Toward a Heat Recovery Chimney
Abstract
: The worldwide population increase and subsequent surge in energy demand leads electricity producers to increase supply in an attempt to generate larger profit margins. However, with Global Climate Change becoming a greater focus in engineering, it is critical for energy to be converted in as environmentally benign a way as possible. There are different sustainable methods to meet the energy demand. However, the focus of this research is in the area of Waste Heat Recovery. The waste heat stored in the exiting condenser cooling water is delivered to the air flow through a water-air cross flow heat exchanger. A converging thermal chimney structure is then applied to increase the velocity of the airflow. The accelerated air can be used to turn on the turbine-generator installed on the top the thermal chimney so that electricity can be generated. This system is effective in generating electricity from otherwise wasted heat.1. Introduction
The environment, and its degradation due to greenhouse gases and other forms of pollution, has become a main topic of discussion and action in both political forums and around the kitchen tables of everyday people. Conventional methods of creating electricity from fossil fuels have significantly contributed to the greenhouse gas build up and improving the efficiency of these systems has become a top priority for industry [1].
Power generation facilities have many inefficiencies leading to a decrease in the amount of power that they can produce and an increase in the fuel that they consume. One of the main areas where inefficiency lies is the waste heat rejected by these steam power generation systems. The condenser in these power plants is used to condense steam into a saturated liquid so that it can be efficiently pumped. The steam from the turbine is cooled with cooling water which is pumped through the condenser, this raises the temperature of the outflow of the cooling water and this warmed water is typically sent to either a cooling tower or lake. Thus, a portion of the fuel that was used to heat the water in the boiler is discarded and unused [2]. Many investigations have been conducted to recover this portion of the waste heat from the power plants [3-5]. In this paper, a thermal chimney system has been developed to capture the waste heat from the power plant and turn it into electricity.
Warmed condenser outflow water will be introduced to a water-air heat exchanger where heat is dissipated to the airflow, which is generated by the fans at the base of a large convergent chimney. As the air flows through the heat exchanger, it will absorb heat and its velocity is also the velocity input into the bottom of the chimney. Due to their specific structure, thermal chimneys have been frequently used in the power generation systems [6]. The shape of the chimney will focuses the rising heated air through its decreasing cross section, thus the air velocity will further increase until it is passed through a vertically mounted shrouded wind turbine which can convert this steady fast moving flow of air into mechanical work. An electric generator coupled to the wind turbine will convert the mechanical work to electric power. In this proposed system, power is generated completely from the waste heat which is typically rejected to the environment. With this system, the total amount of power produced by the power plant will be increased while the fuel consumption remains the same.
2. Thermal Chimney System
The proposed system has been developed for two main objectives. The first is to recover the waste heat; the second objective is to generate electricity with little negative effects to the environment. To reduce the negative environmental effects to the lowest level, the proposed system is suggested be positioned at a location where the waste heat recovery can be conveniently achieved. For example, the system should be installed within or near a steam power plant so that the heat capacity of the cooling water from the condenser will not encounter major losses. The system includes three major components: the heat exchanger, the thermal chimney and the wind turbines. In addition, auxiliary systems such as water pump system and air fan system are also required.
2.1. Heat Exchanger
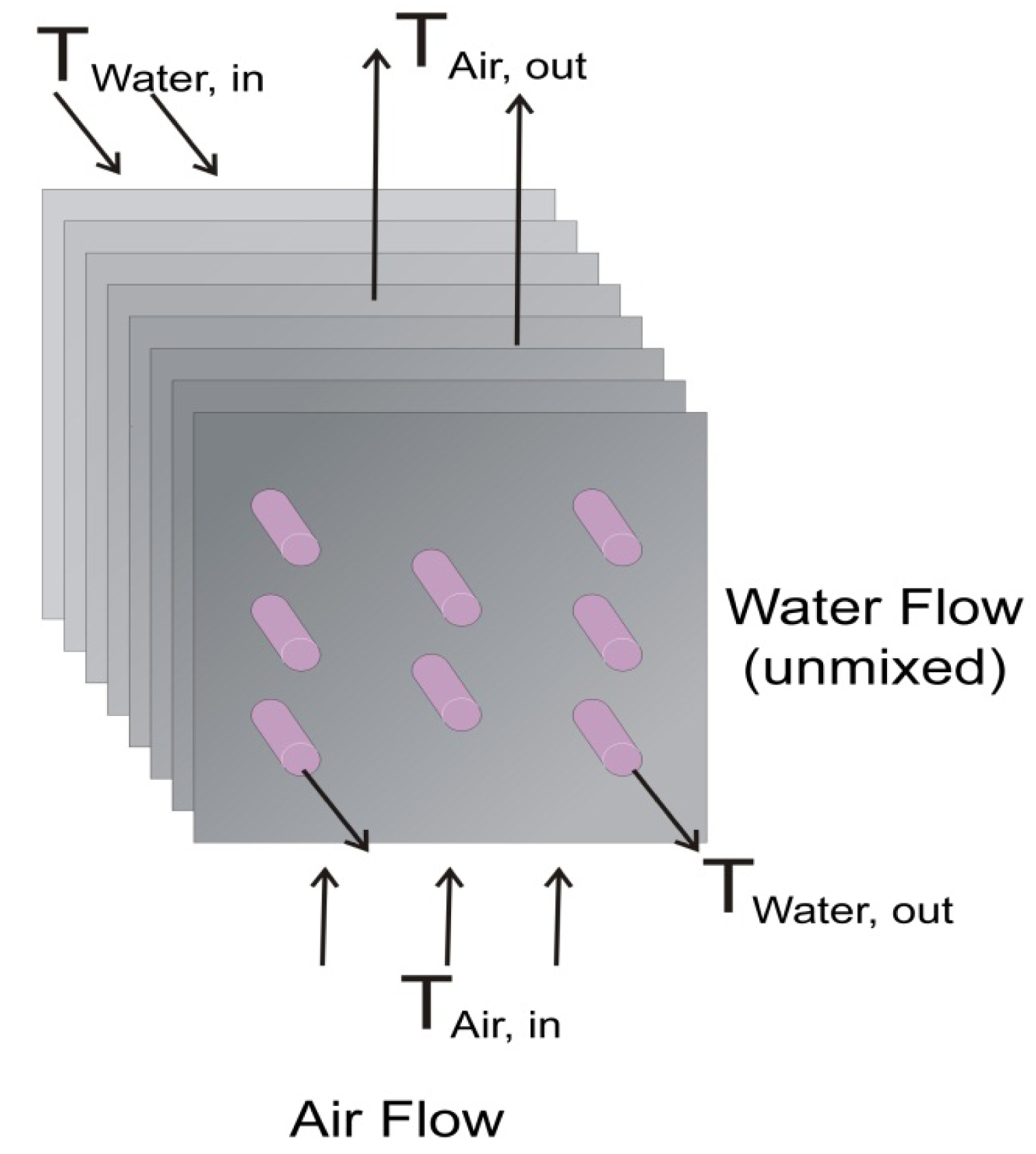
The geometry of the water-air heat exchanger in this system is shown in Figure 1. The warmed water from the condenser (hot fluid) is introduced through water pipes, while the air (cold fluid) flows across the outer surface of the pipes. These two working fluids move perpendicular to each other. To enhance the heat transfer, thin plates are attached to the heat exchanger to regulate the airflow. As a result, this unmixed cross flow compact heat exchanger works similar to a car radiator, and the heat is dissipated from the warm water to the air.
In this heat exchanger, the water is dispersed accordingly to the small, horizontal pipes from a huge central pipe. The copper is chosen as the pipe material due to its high conductivity.
If the specific heat of water is assumed to be constant, the energy balance of the cooling water leads to:
Since warm water is only energy source of the system, mass flow rate and inlet temperature of the water are usually specified, while the water temperature at the exit and heat transfer rate of the heat exchanger usually should be determined. In this paper, water is assumed to be the fluid with high heat capacity rate.
The classic NTU-effectiveness method has been adopted to design this heat exchanger. To calculate the Number of Transfer Unit (NTU), it is necessary to determine the overall heat transfer coefficient (based on the water side surface area), U, which can be calculated with the following equation, if the conduction resistance of the pipes is neglected:
And ho is the heat transfer coefficient between the outer surfaces of the pipes and air, which can be calculated with the following equation [8]:
Based on Equations (3) and (4), as well as the range of the air flow rate and water flow rate of this system, it can be concluded that hi ≫ ho, thus Equation (2) can be simplified as
The Number of the Transfer Unit of this heat exchanger thus can be calculated as:
For this unmixed cross flow heat exchanger, the effectiveness is given by [9]:
The actual rate of heat transfer is then given by:
Therefore the air temperature at the bottom of the chimney Tb can be determined with:
And the exit temperature of the water can be calculated with Equations (1) and (8):
2.2. Converging Chimney
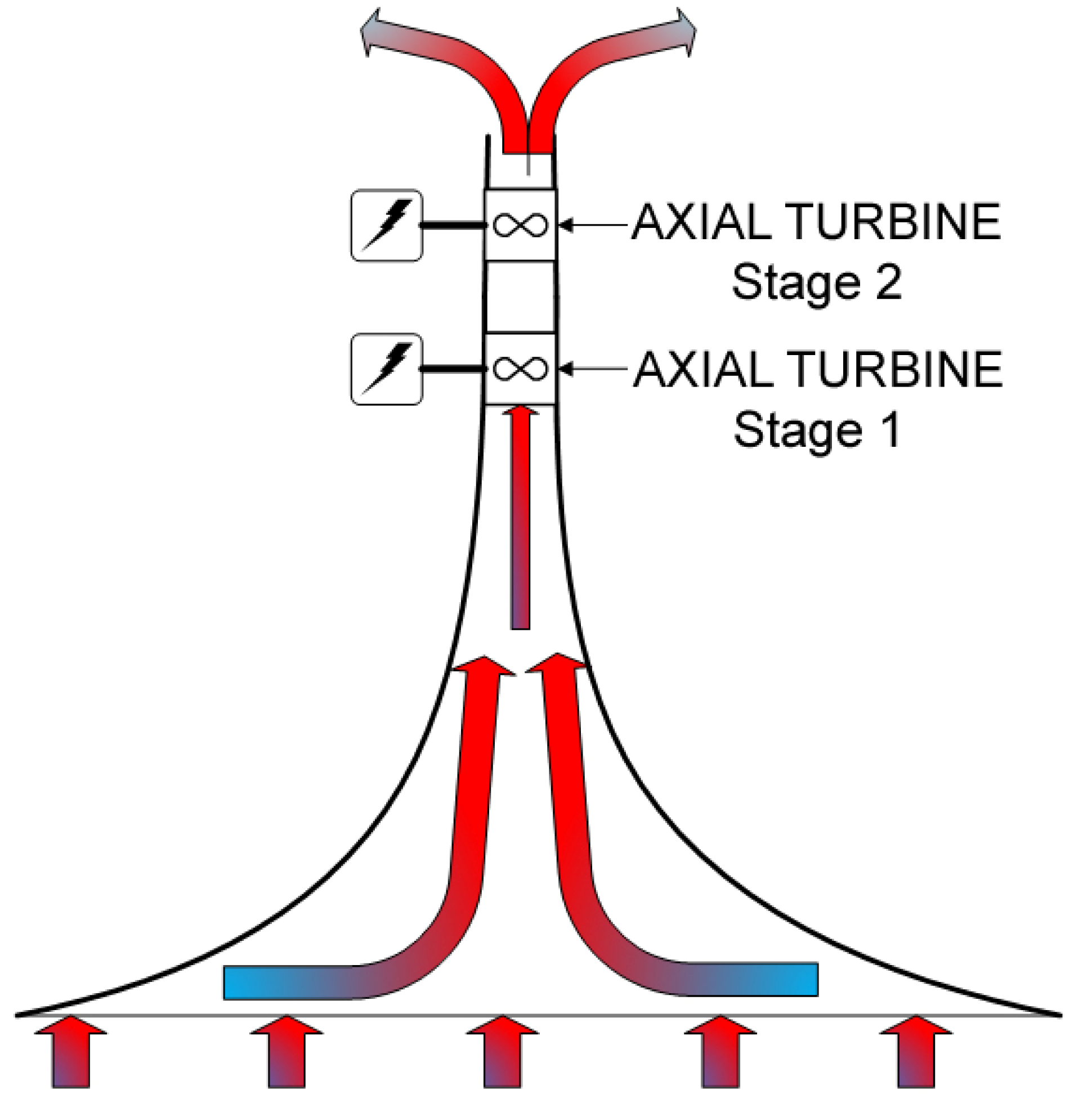
The heat exchanger thus can be installed inside the chimney (shown in Figure 2). This arrangement can better facilitate the air flow towards the turbine, which sits on the top of the chimney. As the air passes through the layers of the heat exchanger and absorbs the heat, it reaches the highest temperature at the bottom entrance of the chimney structure.
The chimney physically constrains the air just like a nozzle. A converging chimney as the one shown in Figure 3 has a variable cross sectional diameter for which the fluid velocity changes because the flow area is different from one section of the chimney to the other. As the cross sectional area decreases with height, the velocity increases. The fluid flow is governed by the conservation of mass as well as the conservation of the energy.
To harvest meaningful kinetic energy from the airflow, the March number of the airflow will exceed 0.3 and thus the airflow can no longer be treated as incompressible fluid.
Based on the continuity equation, the air flow satisfies:
To further simplify the calculations, the air is taken as an ideal gas and the chimney is assumed to be isentropic (no heat losses and friction losses are considered), therefore:
Finally based on the energy balance, if potential energy is negligible
Since
With the assumption that the specific heat is constant, Equation (13) becomes
Thus, if the properties of the air at the bottom of the chimney and the bottom to top cross-sectional area ratio are known, with Equations (11), (12) and (14), the velocity of the air exiting the chimney Vt can be calculated with the following:
The exit velocity calculated using the above equation are ideal and does not take into account friction losses, gravity, and heat losses through the chimney wall.
2.3. Turbine
The selected turbine in this system is a horizontal turbine, which is mounted in an inverted configuration.
In order to harvest the most amount of power from the chimney, multiple wind turbines can be used in series or in parallel. Figure 4 illustrates a turbine configuration at the top of the chimney,
After the air is warmed by the heat exchanger, it rises and gains speed through the chimney. The highest velocity is reached at the top of the chimney where it is focused through the first axial turbine. This turbine produces power by converting kinetic energy to electrical energy. The air exiting each of the turbine stages is roughly one third of the velocity entering, due to the inefficiency of the turbine and its inability to harvest all the power from the air stream. For this reason, multiple stages are used to gain the maximum benefit. Up to three stages have been investigated and it has been determined that the third stage could be unnecessary if the minimal beneficial gain can be found from the additional stage.
The total power output by a wind turbine is given by:
2.4. Auxiliary Systems
Water pumps are needed to pump the cooling water to the heat exchanger. The total pump work required by the system can be easily calculated with the water flow rate as well as geometry of the pipes.
Fans are needed to force the ambient air flow over the warm water pipes. Air flow actually can be initiated purely through natural convection and based on some studies [10], an air velocity of 0.4 m/s can be achieved purely through natural convection. As discussed later in this paper, this velocity is too low for the air to obtain enough velocity at the exit of the chimney for the turbines harvesting meaningful kinetic energy. Therefore, fans are necessary to produce forced convection between the water and airflow.
3. Results and Discussion
3.1. Heat Transfer Rate of the Heat Exchanger
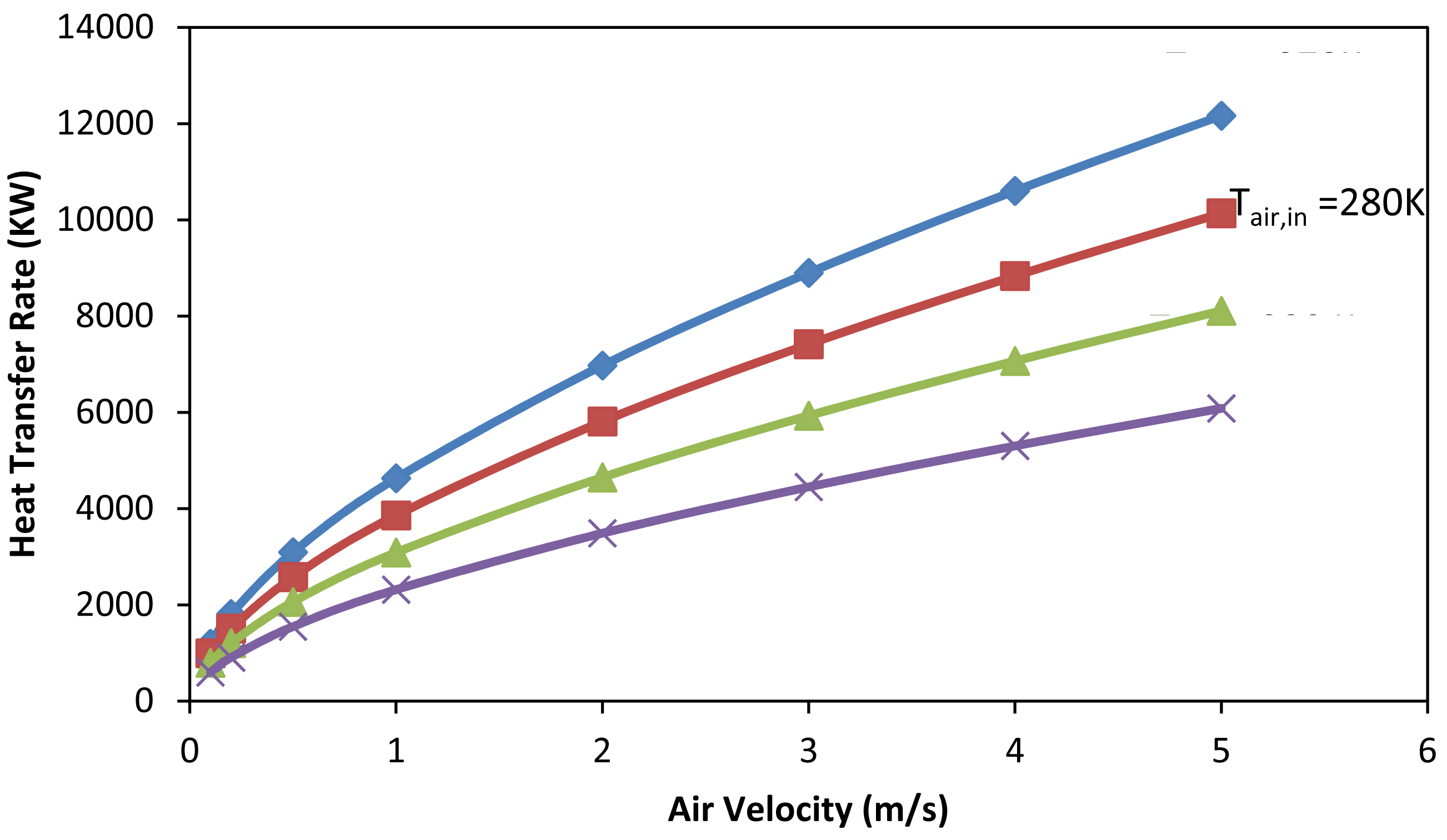
Heat transfer rate of the heat exchanger represents the rate of actual amount of the heat picked by the airflow from the condenser water. Parameters such as air velocity, surface area of the heat exchanger can significantly affect the heat transfer rate. Figure 5 shows the relationship between actual heat transfer rate and air velocity. If the water pipes used has a length of 24 m and a diameter of 28 cm, for a fixed water flow rate of 2000 kg/s and inlet water temperature of 57 °C, the heat transfer rate increases steadily when air velocity increases from 0.1 m/s to 5 m/s. Figure 5 also shows how the number of the water pipes will affect the heat transfer. When air velocity is 5 m/s, if 60 water pipes are used, the heat transfer rate will be 6.09 MW, while if 240 water pipes are used, the heat transfer rate can reach to 21.62 MW. This can be well explained by the increased surface areas with the additional pipes, but more pipes used will lead to higher construction costs as well as more pump work consumed.
Another parameter which affects the heat transfer rate is the inlet air temperature, which is usually the same as the ambient temperature. Figure 6 shows that with a lower inlet air temperature, the higher heat transfer rate can be achieved. For the heat exchanger, the “worst” situation occurs in the hottest day in the summer time with an inlet ambient temperature of over 30 °C. The temperature difference between the two fluids is the smallest comparing with other times of the year. As a result, the heat transfer rate of the heat exchanger is the smallest in this situation. For other days, especially during winter time, the heat transfer rate would be higher due to the bigger temperature difference between the water and the air. Therefore, the heat transfer rate of the heat exchanger would be higher on winter than the hottest days.
3.2. Effectiveness
The effectiveness of this heat exchanger is related with NTU, thus related to the total surface areas of the heat exchanger. As shown in Figure 7, the more water pipes are used, the higher effectiveness will be. Another factor which affects the effectiveness is the air velocity. The higher the air velocity is, the lower its effectiveness will be. This is due to the fact that a higher air exit temperature can be achieved with a lower air velocity. But a lower air velocity will lead to a lower heat transfer rate as well. For example, for a natural convection that has induced an air velocity of 0.2 m/s, its total heat transfer rate of is only 2.35 MW even 240 water pipes are used (shown in Figure 5), although it has a relatively high effectiveness of 0.7273 (shown in Figure 7).
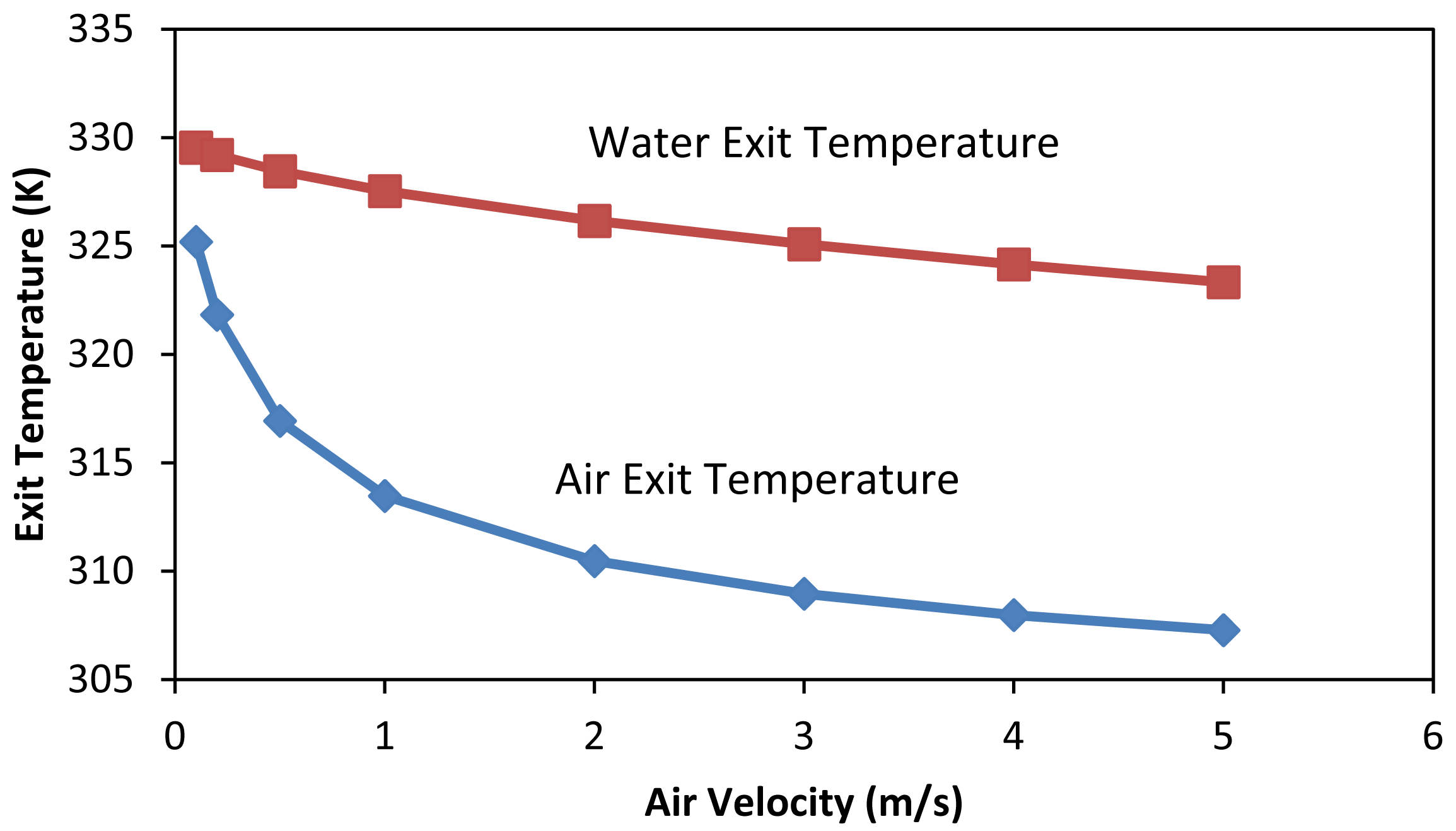
Lower effectiveness leads to higher exit temperature difference between the water and the air. Figure 8 shows how the air velocity affects the temperature difference between these two fluids at the exit of the heat exchanger. It can be seen that with an air velocity less than 0.2 m/s (natural convection induction), the temperature difference could reach as low as 5 K. At the same time it can be seen that the water exit temperature is still high and that shows a low heat transfer rate.
3.3. Air Velocities within the Chimney
Air flow accelerates through the converging chimney due to the variations of the cross section area and the air density. Figure 9 shows the relationship between the air velocities at the top and bottom of the chimney. It can be seen that, with a higher cross section area ratio, air accelerates faster. Since the chimney is proposed to be subsonic, the air velocity at the top of the chimney is expected to be lower than 343 m/s. It can be seen that from Figure 9, with a cross section ratio of 100, the air velocity can reach 300 m/s at the top with a bottom velocity of 1.92 m/s.
Figure 10 shows the air density ratio between inlet and exit of the chimney. This ratio is approximately unity when the air velocity is lower than 50 m/s and can reach as high as 1.55 with an air velocity of 300 m/s.
3.4. Air Temperatures within the Chimney
The chimney is assumed to be isentropic. When the air flow accelerates through the chimney, air temperature decreases while the thermal energy is converted to the kinetic energy. This temperature variation will be negligible if the air velocity is low and air can thus be treated as incompressible. Figure 11 shows a case for a chimney with a cross section area ratio of 100 and a very low air inlet temperature at the heat exchanger (−23 °C), the air temperatures at the bottom of the chimney, Tb, can be lifted as shown in the figure, and it can be found that the temperature difference between Tb and Tf can be as high as 45 °C if a bottom air velocity of 1.92 m/s is initiated, which will lead to a 300 m/s air velocity at the top of the chimney.
3.5. Power Output
Table 1 shows the power outputs of a two-stage wind turbine with two different heat exchanger air velocities. The system operates at a steady flow condition, with a water flow rate of 700 kg/s, and a water inlet temperature of 57 °C. The air inlet temperature at the heat exchanger is 300 K. The heat exchanger has 240 water pipes (each has a length of 24 m and a diameter of 28 cm). The cross section area ratio of the chimney is 50.
It can be found that with a heat exchanger air velocity of 2.75 m/s, the total power output of the system is about 5.7 MW, while with a heat exchanger air velocity of 3.85 m/s, the total power output will reach 19.7 MW.
3.4. Pump and Fan Work
Pump work is related to the water flow rate as well as size and number of the water pipes used in the heat exchanger. For a water flow rate of 2000 kg/s, if 120 water pipes are used in the heat exchanger, the total pump work required is about 73.7 kW, which is very small compared with the total power output of the turbine.
For the fans, if its isentropic efficiency is 80%, for the cases in section 3.5, the total fan work consumption is 19.02 kW for an introduced air velocity of 3.85 m/s, which is also negligible, compared the power output of 19.7 MW of the system.
3.5. Economic Estimation
The benefits of the proposed system directly come from the electricity generated. Since the only energy source is the waste heat, which is obtained at no costs, the major costs come from the financial costs and operating costs such as maintenance and pump work consumptions.
Based on the 19.7 MW power output in section 3.3, with a price of 0.04 $/kwh, the system can generate an additional revenue of 6.9 million dollars for the power plant. If the construction cost is 40 million dollars, for a 25-year loan with an interest rate of 5.0%, the financial cost is about 2.77 million dollars per year, if the operating cost is 2 million dollars per year, the system still may generate a net profit of over 2 million dollars per year.
The system actually can produce a power output more than 19.7 MW, considering the air velocity at the exit of the chimney can be well above 252.4 m/s if higher heat exchanger air velocity is introduced.
4. Conclusions
The Heat Recovery Chimney presented in this paper has shown that part of the heat rejected from the condenser in a typical Rankine cycle can be recovered, and the air can be heated through a water-air heat exchanger and further accelerated through a converging thermal chimney to drive wind turbines which are coupled to a generator. The system produces little impacts of the environment. The implementation and use of the Heat Recovery Chimney will make the conventional steam power cycles more effective without adding much to the pollution of the original system; which is a possible solution to the sustainable problems we are facing today.
5. Future Work
The current research on this system is based on several assumptions such as the isentropic flow within the thermal chimney, where the heat losses and friction losses are not considered. Air flow within the heat exchangers also needs further investigation. A more detailed model and more experimental data are needed for this system.







| Turbine Stages | Heat Exchanger Air Velocity (m/s) | Power Output | ||||
|---|---|---|---|---|---|---|
| Turbine Air Inlet Velocity (m/s) | Max Power Available (kW) | Turbine Efficiency | Total Power (kW) | Turbine Air Exit Velocity (m/s) | ||
| Turbine Stage | 2.75 | 150.9 | 16699.4 | 0.35 | 5195 | 50.3 |
| 1 Calculation | 3.85 | 252.4 | 65406.7 | 0.35 | 17441 | 84.1 |
| Turbine Stage | 2.75 | 50.3 | 1855.5 | 0.35 | 494.8 | 16.8 |
| 2 Calculation | 3.85 | 84.1 | 7261.7 | 0.35 | 2259.2 | 28.0 |
Acknowledgments
The authors appreciate the suggestions and comments from Patrick Merry and Greg Vass for Ontario Power Generations.
References and Notes
- Munson, B.R.; Young, D.G.; Okiishi, T.H. Fundamentals of Fluid Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Cengel, Y.A. Heat and Mass Transfer: A Practical Approach; McGraw-Hill Companies, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Dai, D.; Zhou, Y.; Liu, J. Liquid metal based thermoelectric generation system for waste heat recovery. Renew. Energ. 2011, 36, 3530–3536. [Google Scholar]
- Zhang, X.; Yu, S.; Yu, M.; Lin, Y. Experimental research on condensing heat recovery using phase change material. Appl. Therm. Eng. 2011, 31, 3736–3740. [Google Scholar]
- Anozie, A.N.; Odejobi, O.J. The search for optimum condenser cooling water flow rate in a thermal power plant. Appl. Therm. Eng. 2011, 31, 4083–4090. [Google Scholar]
- Hamdan, M. Analysis of a solar chimney power plant in the Arabian Gulf region. Renew. Energy 2011, 36, 2593–2598. [Google Scholar]
- Cengel, Y.A.; Cimbala, J.M.; Turner, R.H. Fundamentals of Thermal-Fluid Science; McGraw Hills, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Churchill, S.M.; Bernstein, M. A correlating equation for forced convection from gases and liquids to a circular cylinder in cross flow. J. Heat Transfer. 1997, 99, 300–306. [Google Scholar]
- Kays, W.M.; London, A.L. Compact Heat Exchangers, 3rd ed.; McGraw Hills Inc.: New York, NY, USA, 1984. [Google Scholar]
- Pan, M.; Merry, P.; Vass, G. Heat Recovery Chimney; Technical report for University of Ontario Institute of Technology: Oshawa, ON, Canada, 2010. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, D.; Yang, Y.; Pan, M.; Gao, Z. Toward a Heat Recovery Chimney. Sustainability 2011, 3, 2115-2128. https://doi.org/10.3390/su3112115
Zhang D, Yang Y, Pan M, Gao Z. Toward a Heat Recovery Chimney. Sustainability. 2011; 3(11):2115-2128. https://doi.org/10.3390/su3112115
Chicago/Turabian StyleZhang, Dan, Yuelei Yang, Min Pan, and Zhen Gao. 2011. "Toward a Heat Recovery Chimney" Sustainability 3, no. 11: 2115-2128. https://doi.org/10.3390/su3112115




