A Value Function for Assessing Sustainability: Application to Industrial Buildings
Abstract
: Decision support tools based on multi-attribute analysis involve the use of different types of variables. These variables are aimed at providing a framework that allows preferences to be quantified. This is particularly useful in the field of sustainability, where variables with different units are involved. One widely accepted framework for standardizing different units is the value function. Studies of value function are complex and frequently have limited physical meaning. In this context, this paper emphasizes the need to define a general equation that reflects the preferences of the decision maker in a clear and easily applied way. The paper proposes a new general equation that fulfils these requirements. By modifying certain parameters, this general equation represents the most commonly used relationships (linear, convex, concave and S-shaped). The proposed equation is finally applied to four variables used in the field of industrial buildings and sustainability.1. Introduction
This paper deals with the standardization of units used to express different variables (indicators, criteria or attributes) involved in a decision making process and its application in the context of industrial buildings and sustainability. This standardization is achieved using a scale of preference, or the degree to which a certain desired outcome is satisfied. Such a preference usually lacks an objective measure that directly reflects the priority or priorities of the decision makers and their numerical magnitude. In order to estimate such a magnitude, numerous proposals have been put forward [1-9], some of which are highly complex. Such is the case with the method of interdependent attributes [10], which requires that a single function be specified for several different attributes, not just for one. To construct the function it is therefore necessary to combine the concepts of a single-valued surface and the marginal substitution rate [11].
Some proposals use fuzzy techniques, which analyze complex problems with incomplete and inaccurate information describing real situations [5,12-15]. However, these techniques lack the mathematical rigor of probability functions [14].
Other approaches include using probability density functions [16], optimization methods [1], interactive methods [17], and fractals [1], which require the decision maker to have a clear idea of values, the degree of precision required at the moment of evaluation, and the probability of the phenomenon occurring. In the construction sector (the specific area that this paper addresses with industrial buildings) this information is not normally available, and this makes it more difficult to define the function.
With regard to the scales used to assign values, most discussion is centered on the use (or rejection) of negative values. The inclusion of negative values (using, for example, a scale from −1 to +1, as proposed in [12,18]) implies that dissatisfaction (values below zero) can be produced in some variables. If this happens, the value given by other variables is reduced and a situation of dissatisfaction (negative value) may be obtained as a final result. However, most methods [1-7,12-14,17,19] propose the use of only positive values ranging from 0 to 1 or from 0 to 100 [20,21]. Another way of reflecting these preferences is to express them in monetary terms [10].
As far as the area of application is concerned, the value function is widely used in medicine [3], financial project management [4], the construction sector [20,22,23] and in contracting construction projects [14,21,24-26], among others.
Once the different methods for defining and modeling the value function have been set, the difficulty lies in its application, since the majority of cases do not provide a real, physical sense of the variables involved and therefore users who are not well-versed in mathematics may find them difficult to use.
The objective of this paper is to respond to this difficulty by presenting a simple and understandable method for constructing a general value function and applying it in the field of industrial buildings and sustainability. It should be a universal function that allows the decision maker's preferences to be stated directly by modifying a series of physically meaningful variables. Obviously, a specific problem will require the assessment of different variables (actually all the relevant ones) that, in the context of sustainability, should cover the project's whole life cycle. This assessment will vary depending on the viewpoint (building developer, owner, user, etc.), location and time. In some way, the value function objectivizes the subjectivity for a specific variable and viewpoint. This approach was developed by the MIVES project working group and applied to different fields [23,27-35]. MIVES is a decision making model and tool developed by researchers from three Spanish universities and institutes (UPC, UPV and Labein-Tecnalia). It was initially applied in the field of sustainability and industrial buildings.
2. Method for Defining the Value Function
Defining the value function requires measuring preference, or the degree of satisfaction produced by a certain alternative option for a measurement variable (indicator). Each measurement variable may be given in different units; therefore, it is necessary to standardize them into units of value or satisfaction, which is basically what the value function does. The method proposed rates satisfaction on a scale from 0 to 1, where 0 reflects minimum satisfaction (Smin) and 1 reflects maximum satisfaction (Smax).
To determine the satisfaction value for an indicator, the MIVES model [27-30] outlines a procedure consisting of the four following stages:
Definition of the tendency (increase or decrease) of the value function.
Definition of the points corresponding to the minimum (Smin, value 0) and maximum (Smax, value 1) satisfaction.
Definition of the shape of the value function (linear, concave, convex, S-shaped).
Definition of the mathematical expression of the value function.
A description of each of these stages is presented in the sections below.
2.1. Stage 1: Definition of the Tendency of the Value Function (Increasing/Decreasing)
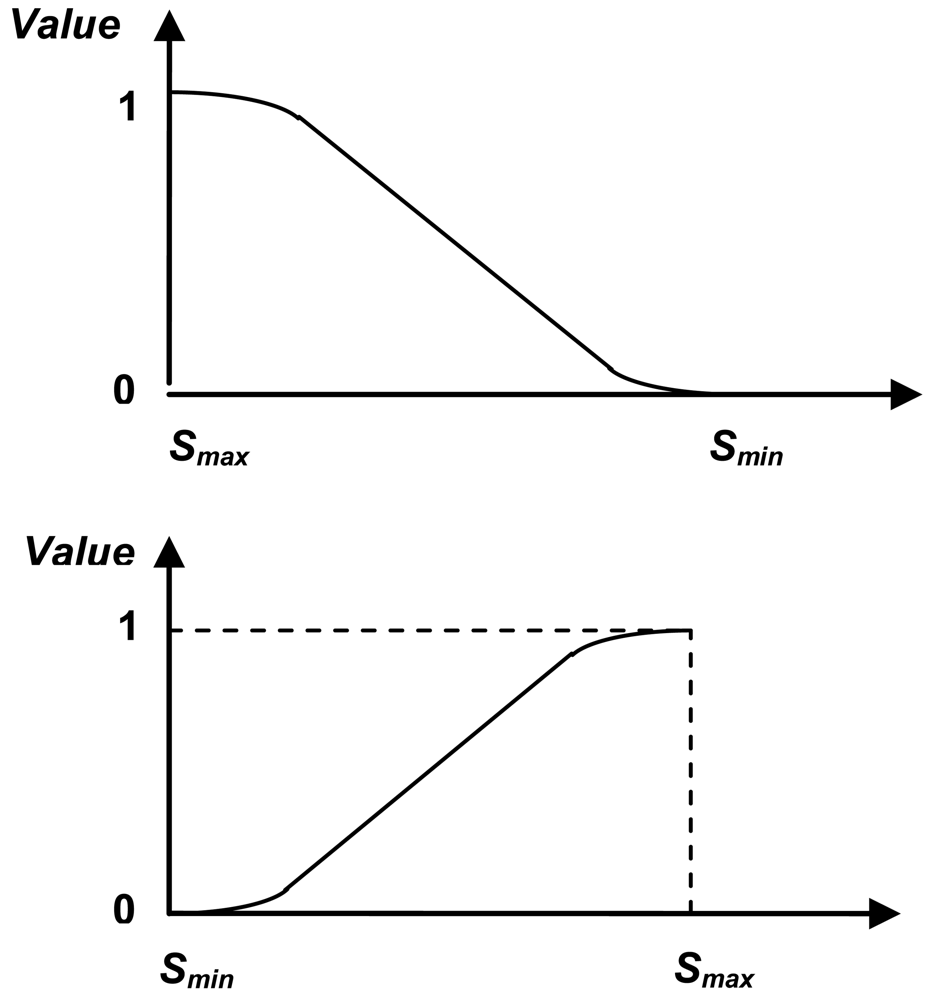
The value function can be increasing or decreasing depending on the nature of the indicator (or measurement variable) to be evaluated. An increasing function is used when an increase in the measurement variable results in an increase in the decision maker's satisfaction. In contrast, a decreasing value function shows that an increase in the measurement unit causes a decrease in satisfaction (see Figure 1).
Examples of indicators with a decreasing tendency as applied to sustainable industrial buildings include economic cost, time of execution, or emissions to the environment. Examples of this type of indicator with an increasing tendency would be those that reflect the proportion of recycled materials used in the building, the degree of adaptability to the surroundings, the flexibility of different elements or components of the industrial building, etc. Defining the different indicators and the corresponding assessment and quantification will naturally vary in difficulty depending on the case.
Other value functions will have a mixed tendency, that is, functions that increase at first but later decrease. This type of function is characteristic of indicators with two points of minimum satisfaction and one maximum between them, as explained in the following section.
2.2. Stage 2: Definition of the Points of Minimum (Smin) and Maximum Satisfaction (Smax)
The points of minimum and maximum satisfaction define the limits of the value function on the x-axis: Smin (point of minimum satisfaction) and Smax (point of maximum satisfaction). These two points have a satisfaction value of 0 (Smin) and 1 (Smax) respectively. These limits correspond to the satisfaction values and not necessarily to the minimum and maximum values of the measurement variables, which may have (and will in general have) a wider range.
These points are usually established according to three criteria: existing rules and regulations, experience with previous projects, and the value produced by the different alternatives with respect to the indicator. A description of each of these follows.
Rules and regulations. The measurement variables are regulated by existing standards and are therefore limited to the values given, or to the minimum and maximum values included within the interval defined by them. The limits that are defined according to this criterion are quite inflexible since they usually must be complied with. As an example, we can consider the minimum fire resistance time of a structure according to the type and dimensions of the structure. In this case the minimum satisfaction is located at the point of minimum fire resistance time established by the corresponding regulations and cannot be changed. In the majority of cases, only one limit (minimum or maximum) is defined (e.g., minimum strength, maximum content). Sometimes, however, both limits (minimum and maximum) may exist (for instance in the case of temperature).
Experience with previous projects. When information on measurement variables is not provided by rules and regulations, these values can be determined by experience, from historical data, from data found in the literature, or from data obtained from previous projects. The range of values is slightly more flexible than when complying with rules and regulations.
The value produced by the different alternatives with respect to an indicator. In this case, the limits of the value function are provided by the minimum and maximum values of the different alternatives with respect to an indicator. Consequently, if a new alternative appears, the limits of the function and the corresponding value of the indicators may change.
In the case of having alternatives that generate values for variables that fall outside the established limits, they can be disregarded if the minimum or maximum values cannot be surpassed (for example if they correspond to regulatory limits) or, alternatively, the value of the limit surpassed (0 or 1) can be assigned to them. Choosing one option over another clearly depends on the variable considered.
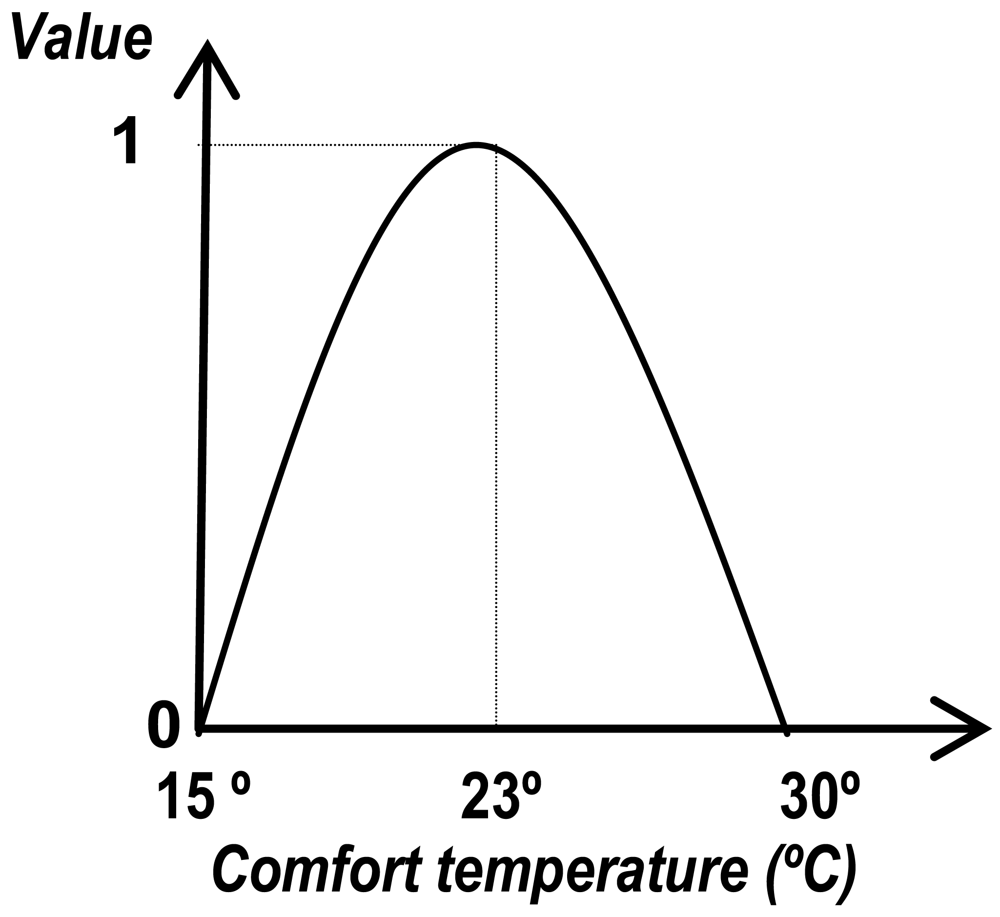
If there are two points of minimum satisfaction and only one maximum, as shown in Figure 2 (where the indicator corresponds to the comfort temperature), it is necessary to adjust the limiting values with respect to the best or most satisfactory value (for instance, the distance to optimum instead of the actual value of the variable) in order to have a continuously increasing or decreasing relationship.
2.3. Stage 3: Definition of the Shape of the Value Function (Linear, Concave, Convex, S-Shaped)
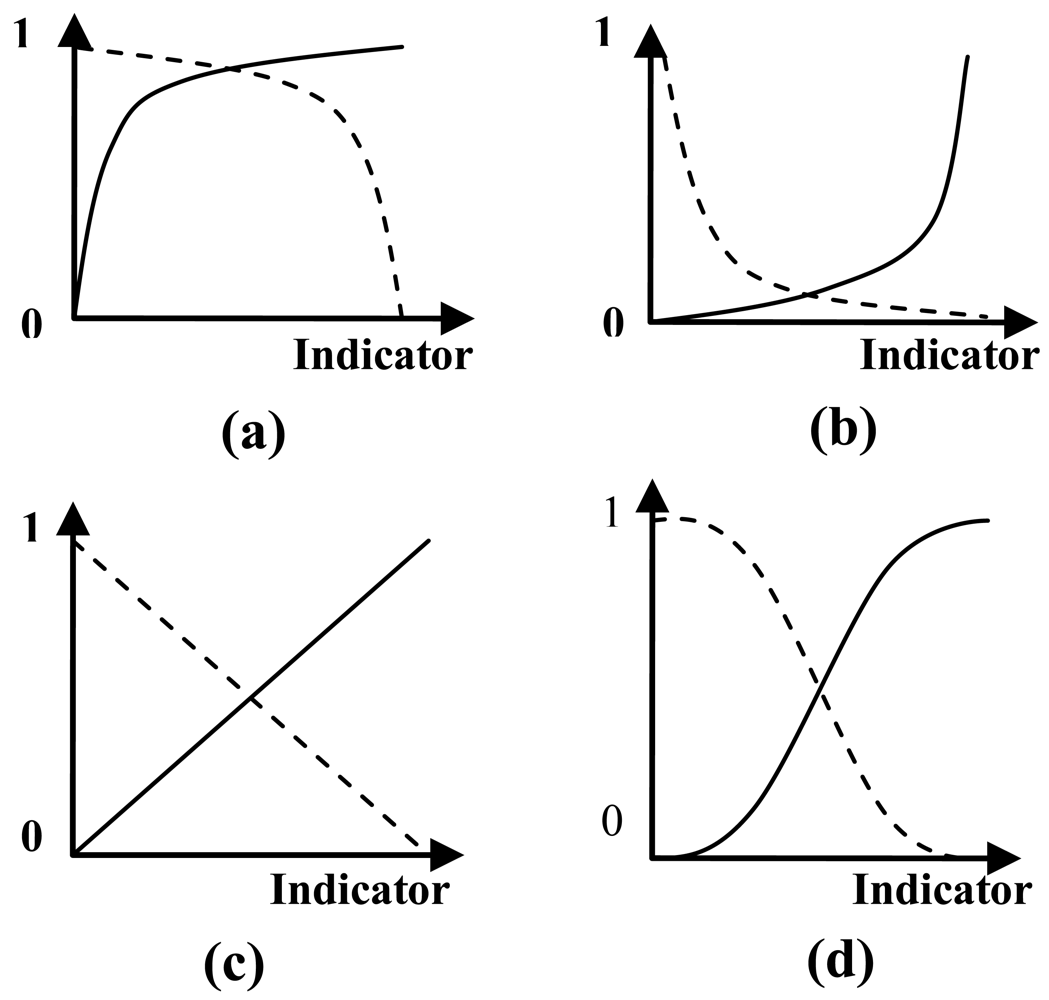
Given that so far two coordinate points, (Smin, 0) and (Smax, 1), have been generated, the objective of this stage is to connect them using some type of function. Four types of functions are suggested: concave, convex, linear and S-shaped. These four curves represent the most common relationships that can be found in practice. They include the modeling of the different behavior of people regarding their indifference, aversion or attraction to risk with respect to the decisions to be taken, in addition to the different strategies that can be defined in order to promote improvement. The latter is related to the range between the points of minimum and maximum satisfaction where the satisfaction increases more rapidly.
A concave curve is used when, starting from a minimum condition, satisfaction rapidly increases at first in relation to the indicator (see Figure 3a). In this case, small changes around the point that generates minimum satisfaction are highly valuated. This type of relationship is chosen when it is more important to move away from the point of minimum satisfaction than to approach the point of maximum satisfaction. It is also used when the majority of alternatives are close to the point of minimum satisfaction. In this case the discrimination between alternatives is better and the incentive for improvement higher.
A convex function is appropriate when there is hardly any increase in satisfaction for small changes around the point that generates minimum satisfaction (see Figure 3b). In contrast to the previous case, this type of relationship is selected when it is more important to approach the point of maximum satisfaction than to move away from the point of minimum satisfaction. This type of function is often used for economic or environmental indicators since the aim is to ensure that the alternatives are located as close to the point of maximum satisfaction as possible. It is also used when the majority of alternatives are close to the point of maximum satisfaction. In this case, as in the previous one, the discrimination of alternatives is better and the incentive for improvement higher.
A linear function reflects a steady increase in the satisfaction produced by the alternatives (see Figure 3c). There is a proportional relationship throughout the range. This function is the default option when no specific criteria can be defined.
An S-shaped function is a combination of the concave and convex functions. A significant increase in satisfaction is detected at central values, while satisfaction changes little as the minimum and maximum points are approached (see Figure 3d). This type of relationship can be chosen when the majority of alternatives are concentrated into a middle range between the points of minimum and maximum satisfaction. In this case, as in the cases of concave and convex curves, the discrimination of alternatives is better and the incentive for improvement higher.
2.4. Stage 4: Definition of the Mathematical Expression of the Value Function
Equation (1) is proposed as a mathematical model for the value function.
where
Vind is the value of the indicator being evaluated.
B is a factor that allows the function to remain within the range from 0 to 1. It is assumed that the highest level of satisfaction has a value of 1. This factor is determined by Equation (2).
Smin is the point of minimum satisfaction, with a value of 0.
Smax is the point of maximum satisfaction, with a value of 1.
X is the abscissa that generates a value equal to Vind.
P defines approximately the shape of the curve: concave, convex, linear or S-shaped. If P < 1 the curve is concave; if P > 1 the curve is convex or S-shaped; if P = 1 it is linear.
C is a parameter that approximately defines the x-value of the point of inflexion for curves with P > 1.
K is a parameter that approximately defines the y-value at the point C.
It can be seen that the shape of the function depends on the values that the parameters P, C and K take in each case. The interpretation of these parameters makes it easier to understand and use Equation (1). Table 1 gives some characteristic values of these parameters for the construction of different types of value functions. This is simply a rough guide as the parameters may vary according to the preferences of the decision maker. The final shape of the value function when specific values for P, C and K are introduced must always be checked in order to assure that it matches the desired relationship.
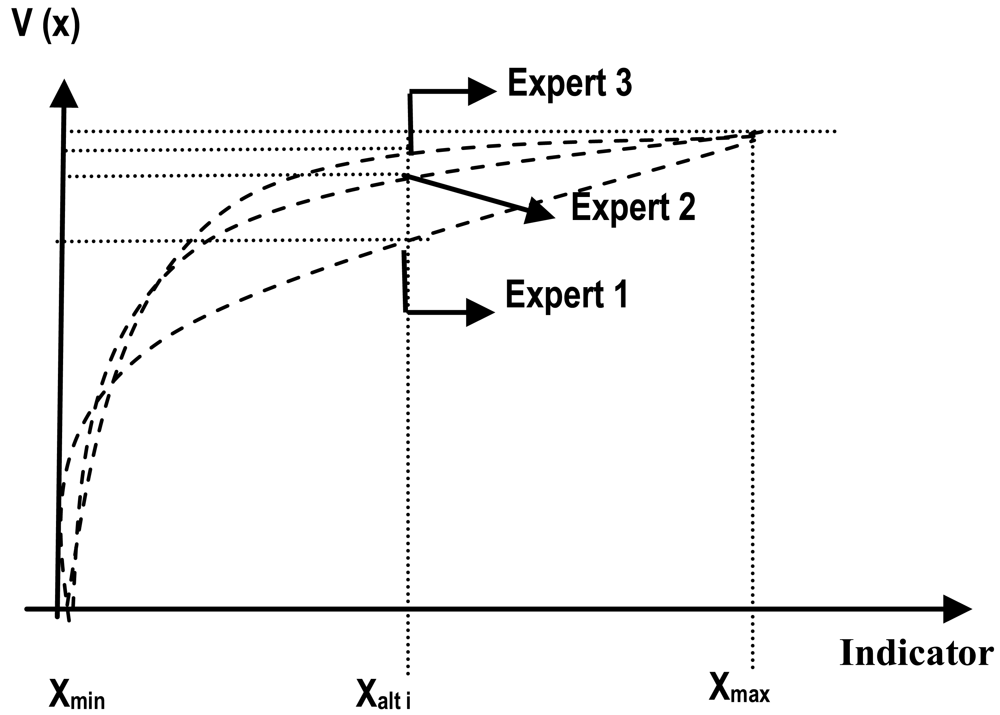
When the specific shape of the value function for an indicator is unclear, it may be defined by a working group. When this is the case, several value functions (discrete or continuous) may initially be defined according to the proposals given by each or some of the members of the group for the measurement variable (indicator). This means that rather than a single function, a family of functions is obtained, as shown in Figure 4.
According to this figure, several values on the y-axis (one for each initial value function) correspond to the value labeled Xalt. As these values are obtained, it is necessary to establish another value that allows each alternative to be evaluated. The simplest way to do this is to take the mean of the different values (after excluding extreme cases, if needed). The parameters P, K and C can then be estimated through a minimum squares approach. It is also possible to work with a range of values in such a way that two values correspond to each y-value: the mean and the standard deviation. This would call for a statistical approach in the subsequent decision process.
3. Value Functions for Some Indicators of an Industrial Building
In this section, the procedure for determining the value function of four of the indicators that may characterize the design of a sustainable industrial building, as proposed in [22], is set out. The indicators selected cover the tendencies (increasing and decreasing) and shapes (concave, convex, linear and S-shaped) previously presented. The variables selected are as follows: the proportion of recycled material in concrete (%), the cost of the building (€/m2), the thermal comfort (°C) and the number of suitable contractors for the job.
3.1. Proportion of Recycled Material in the Concrete (%)
Once a material has come to the end of its useful life in a building, it can be used again as a resource (reused or recycled) in other applications. This process reduces the impact on the environment (fewer natural resources required) and the use of energy (mining of natural resources saved). For this reason, this use is encouraged or enforced by the regulations of different countries [36,37].
In the following points, the stages defined in the previous sections for determining the value function are applied to this indicator.
3.1.1. Stage 1: Definition of the Tendency of the Value Function
As previously mentioned, the use of recycled material in concrete makes a positive contribution to the environment and improves sustainability. Therefore, the higher the percentage of recycled material used in a building, the higher the degree of satisfaction obtained. Consequently, the value function will have an increasing tendency.
3.1.2. Stage 2: Definition of the Points of Minimum and Maximum Satisfaction
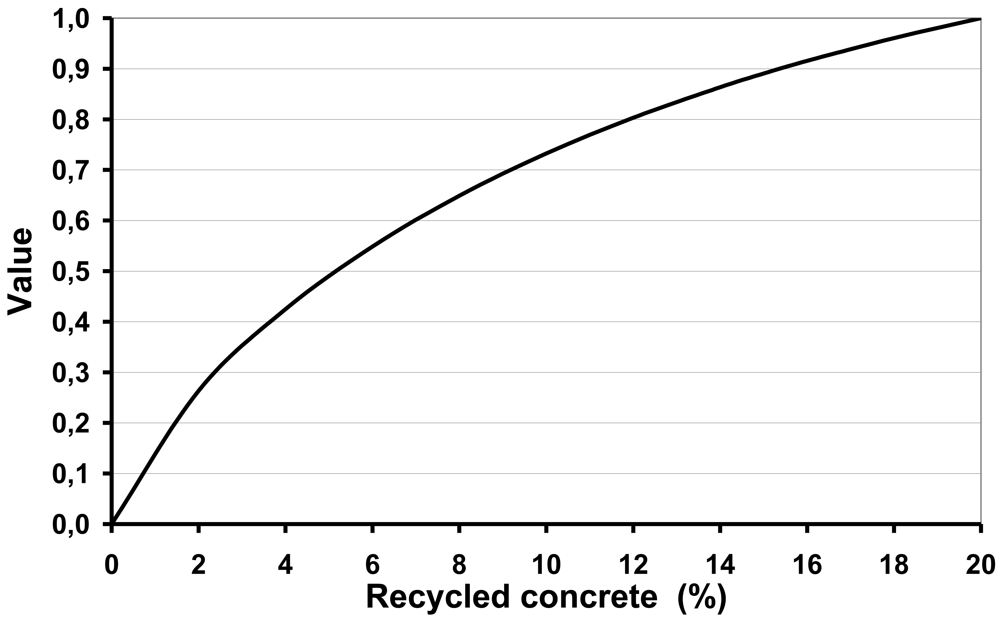
For this indicator, the points of minimum and maximum satisfaction can be defined through the regulations in force where the building is going to be constructed. Since in some countries the use of recycled materials in concrete is not very common, the point of minimum satisfaction can be established as 0%. In relation to the maximum, it is frequent that the regulations define this value based on technical matters (strengths, durability, previous experience, etc.). In the case of Spain, the maximum without having to perform specific studies and tests to justify it is defined as 20% [36,37]. These two values define the range that will be considered in this case for the recycled materials indicator (0–20%).
3.1.3. Stage 3: Definition of the Shape of the Value Function
Given that the use of recycled materials in concrete is not very common in Spain, it is positive to encourage it and a concave value function is proposed, in which small initial improvements are highly valued. The increase in value of the function is therefore maximized near the point of minimum value (Smin), that is, if a recycled material is used, the degree of satisfaction increases considerably. Furthermore, as the point of maximum satisfaction is approached (Smax) the function tends to become more horizontal.
3.1.4. Stage 4: Definition of the Mathematical Expression of the Value Function
Since a concave shape has been decided for the value function in the previous stage, a P value lower than 1 should be defined in agreement with the suggestions laid out in Table 1. In accordance with this, the values P = 0.8, K = 0.8 and C = 10 have been adopted. Figure 5 shows the value function obtained in this case. Obviously, this function can be changed (more or less concave or with another shape; different points of minimum and maximum satisfaction) depending, for example, on the location or on previous experience.
3.2. Cost of Building the Structure (€/m2)
This indicator is used to assess the total cost of the construction of the industrial building. It includes all the costs needed to complete the structure, including such aspects as materials, labor costs, machinery, facilities, transport, etc.
3.2.1. Stage 1: Definition of the Tendency of the Value Function
Naturally, lower costs generally result in greater satisfaction. Therefore, a decreasing tendency function should be defined, so that as costs increase, satisfaction decreases.
3.2.2. Stage 2: Definition of the Points of Minimum and Maximum Satisfaction
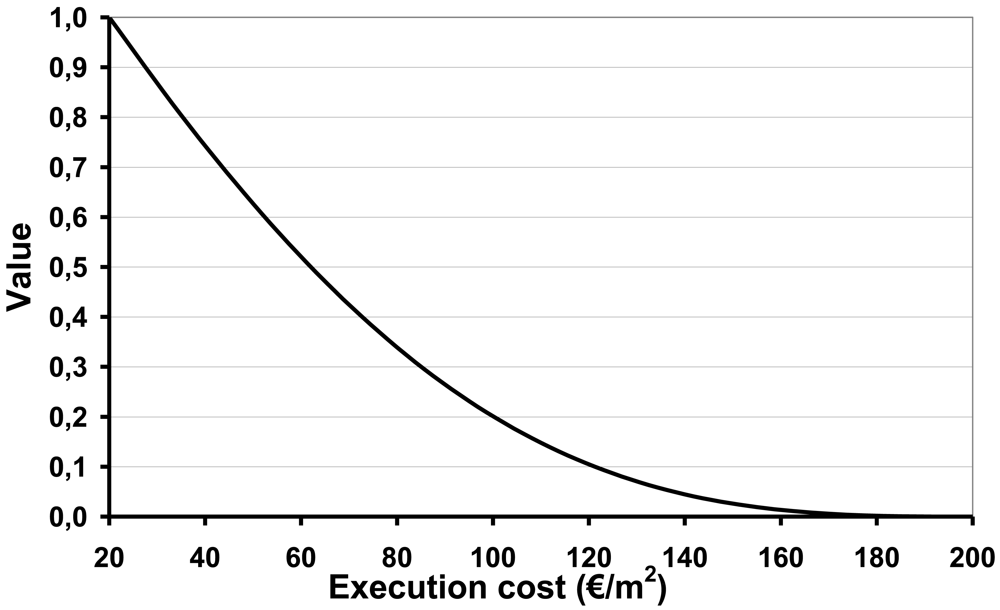
The points of minimum and maximum cost satisfaction in terms of €/m2 can be defined by experience with previous projects and by average market values. Typical values found for the cost of building different types of structures may vary between 20 €/m2 and 200 €/m2. Consequently, the minimum and maximum limits are set in this case at 20 and 200 €/m2 respectively. In more specific cases, smaller ranges can be defined. Cost is a typical indicator (generically with a high variability) in which the range can be adapted to the available alternatives. If this approach is adopted, the minimum and maximum costs would become the points of maximum and minimum satisfaction, respectively.
3.2.3. Stage 3: Definition of the Shape of the Value Function
Given that the objective is to reduce the building costs, a convex value function is proposed. This type of function penalizes severely high and medium costs while significantly rewarding low costs. For this type of function the increase in value is maximized near the point of maximum satisfaction.
3.2.4. Stage 4: Definition of the Mathematical Expression of the Value Function
Since the value function is convex, a P value higher than 1 is defined (Table 1) and the values P = 3, K = 0.05 and C = 90 are adopted. The shape of the value function obtained can be seen in Figure 6.
3.3. Thermal Comfort (°C)
This indicator reflects the temperature in the building related to the comfort of people working inside. Temperature control systems in the building should maintain body temperature at an appropriate level. To calculate the required temperature, we need to consider factors such as the type of work that is performed in the building, the clothes worn by the workers, and the season.
3.3.1. Stage 1: Definition of the Tendency of the Value Function
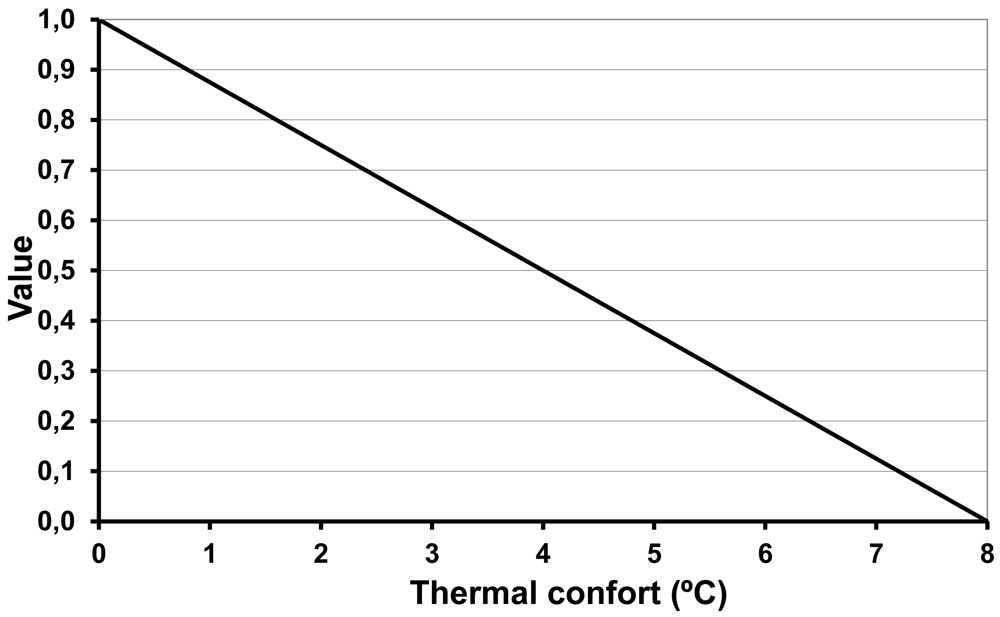
Since very low or very high temperatures are not acceptable (low satisfaction), this indicator will, in general, have an intermediate optimum. This leads to an indicator with a mixed tendency (increasing until the optimum, and then decreasing). In order to define one single tendency, a redefinition of the points of minimum and maximum satisfaction must be established. For example, if temperatures are very low (15 °C) or in contrast very high (30 °C), with regard to what is tolerable for human comfort, then two points of minimum satisfaction are generated while there is only one point of maximum satisfaction, which is reached at the average temperature: 23 °C (see Figure 2).
That said, it becomes necessary (as shown in the next section) to transform the extremes with respect to the optimum temperature. This does not necessarily need to be the average point between the extreme values given above. Thus, if the distance to the optimum is defined as the new variable, a decreasing tendency will apply, since as we move away from the optimum temperature, satisfaction decreases.
3.3.2. Stage 2: Determining the Points of Minimum and Maximum Satisfaction
As explained above, there are three points for this type of function: two points of minimum satisfaction and one of maximum satisfaction (TOPT). Given that the proposed equation in this paper only works for two points, it is necessary to perform a transformation using the distance from the optimum temperature as previously stated:
The range of values resulting from this transformation is 0–8 °C, where 0 °C corresponds to the maximum satisfaction since it is the most comfortable temperature with respect to the average (22−23 °C), while 8 °C represents the least satisfactory temperature as it is the furthest from the optimum temperature (23 − 15 = 8 °C)/(30 − 23 = 7 °C).
3.3.3. Stage 3: Definition of the Shape of the Value Function
A linear value function is proposed for this indicator because the distance from the optimum temperature may be considered proportional to the corresponding dissatisfaction.
3.3.4. Stage 4: Definition of the Mathematical Expression of the Value Function
In this case, the equation that defines the indicator is given by P = 1, K = 0 and C = 10. The shape of the resulting value function is presented in Figure 7.
3.4. Number of Suitable Contractors
This indicator quantifies the number of possible contractors capable of and interested in making an offer for the job according to the system of contracts used in a specific case [26]. An enough number of contractors is relevant to ensure competitive alternatives with reasonable technical solutions and costs and with different characteristics from the sustainability point of view (economic, social, environmental).
3.4.1. Stage 1: Definition of the Tendency of the Value Function
For this indicator, a function with an increasing tendency is defined since as the number of contractors increases the range to choose from also increases with respect to certain evaluation criteria (cost, technical solutions, experience, etc.).
3.4.2. Stage 2: Definition of the Points of Minimum and Maximum Satisfaction
Following the recommendations given in [25,26], when only a few contractors are available (<3) satisfaction is very low, since as there is less competition, the probability of the price increasing is greater.
However, when there are many suitable contractors (n > 6) there is little increase in satisfaction as it is already a large enough number to ensure that the client receives realistic proposals.
Based on these values, setting the points of minimum and maximum satisfaction at 0 and 10, respectively, is recommended. The first figure (0) would cover the case in which there are no suitable contractors. The second figure (10) takes into account that it is not usually realistic to have more than 10 candidates meeting the conditions of a contract.
3.4.3. Stage 3: Definition of the Shape of the Value Function
An S-shaped function is proposed in this case. This function tends to level off as the minimum value is approached for responses of between 0 and 3 alternatives, and also as the maximum value is approached for more than 6 alternatives. For values between 3 and 6, which is the critical range, there is a sharp increase in satisfaction.
3.4.4. Stage 4: Definition of the Mathematical Expression of the Value Function
The equation that defines the mathematical expression for the value function of this indicator is defined by the following parameters P = 3.5, K = 0.15 and C = 3, as shown in Figure 8.
4. Final Remarks and Conclusions
A process that allows step by step definition of value functions to standardize and quantify preferences for different quantitative measurement variables has been presented in this paper. A mathematical formulation based on a continuous and flexible equation that provides a straightforward and understandable way of modeling has also been proposed. The starting points for this methodology are the tendency of the function (increasing or decreasing), the minimum and maximum satisfaction coordinates, Smin and Smax, and its shape (linear, concave, convex or S-shaped).
The value function proposed is modeled through a mathematical expression that depends on three basic parameters. The variation of these parameters leads to value functions that are physically representative and easy to construct, even for non-experts. This flexibility makes it a useful tool that can be applied to any situation requiring multi-criteria analysis within a wide range of applications. The examples presented, relevant to the field of industrial buildings, confirm this flexibility in cases requiring different types of value functions (linear, concave, convex or S-shaped). Even cases presenting an intermediate optimum can be modeled with this methodology through the use of an alternative indicator measuring the distance from the optimum. However it does not cover some complex cases as, for instance, value functions with an intermediate, but asymmetrical, maximum, with more than a maximum or with more than an inflection point, which are, in any case, very unusual, in particular for industrial buildings and in the construction sector.
It is important to emphasize that the sustainability assessment of any project will need the compiling and selection of all the relevant variables covering its whole life cycle. The value function of each variable will objectivize its subjectivity in accordance with a specific viewpoint (building developer, owner, user, etc.), location and time. This means that the value function and the assessment will, in general, vary with such aspects.

| Increasing function | |||
|---|---|---|---|
| Function | C | K | P |
| Linear | C ≈ Xmin | ≈ 0 | ≈ 1 |
| Convex | < 0.5 | >1 | |
| Concave | >0.5 | <1 | |
| S-shaped | 0.2/0.8 >1 | >1 | |
| Decreasing function | |||
| Function | K | K | P |
| Linear | C ≈ Xmin | ≈A0 | ≈1 |
| Convex | <0.5 | >1 | |
| Concave | >0.5 | <1 | |
| S-shaped | 0.2/0.8 | >1 | |
Acknowledgments
The authors wish to acknowledge the aid received through a number of projects funded by the Spanish Government (Spanish Interministerial Science and Technology Commission; MAT 2002-04310, BIA2005-09163-C03-01, BIA2009-14171-C04-01, BIA2010-20789-C04-01).
References and Notes
- Rios, S.; Rios, M.J. Procesos de Decision Multicriterio; EUDEMA Universidad, Ediciones Universidad Complutense: Madrid, Spain, 1989. [Google Scholar]
- Bana e Costa, C.; Vansnick, J. MACBETH—An interactive path towards the construction of cardinal value functions. Int. Trans. Oper. Res. 1994, 1, 489–500. [Google Scholar]
- Gass, N.; Muller-Gass, A. A multicriteria decision model to compute optimal treatment packages under constraint conditions. Method. Psychol. Res. Online 1999, 4, 1–18. [Google Scholar]
- Tiu, C.; Zariphopoulou, T. On level curves of value functions in optimization models of expected utility. Math. Finance 2000, 10, 323–338. [Google Scholar]
- Wong, E.; Norman, G.; Flanagan, R. A fuzzy stochastic technique for project selection. Const. Manag. Econ. 2000, 18, 407–414. [Google Scholar]
- Piantanakulchai, M.; Saengkhao, N. Evaluation of alternatives in transportation planning using multi-stakeholders multi-objectives AHP modeling. Proceedings of the Eastern Asia Society for Transportation Studies, Fukuoka, Japan, 29 October–1 November 2003; Satoh, K., Ed.; Eastern Asia Society for Transportation Studies: Tokyo, Japan, 2003; 4, pp. 1613–1628. [Google Scholar]
- Jimenez, A. Generic Multi-Attribute Analysis System (GMAA). PhD Thesis, Facultad de informatica, Universidad Politecnica de Madrid (UPM), Madrid, Spain, 2003. [Google Scholar]
- Ding, G.K.C. Developing a multicriteria approach for the measurement of sustainable performance. Build. Res. Inf. 2005, 33, 3–16. [Google Scholar]
- Saaty, T.L. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process; RWS Publications: Pittsburgh, PA, USA, 2006; Volume VI of AHP Series. [Google Scholar]
- Norris, G.; Marshall, H. Multiattribute Decision Analysis Method for Evaluating Buildings and Building Systems; NISTR 5663; US Department of Commerce National Institute of Standards & Technology: Gaithersburg, MD, USA, 1995. [Google Scholar]
- Keney, R.; Raiffa, H. Decision with Multiple Objectives. Preferences and Value Tradeoffs, 1st ed.; Willey: New York, NY, USA, 1976; 2nd ed.; Cambridge University Press: London, UK, 1993. [Google Scholar]
- Sanchez, M.; Prats, F.; Agell, N.; Ormazabal, G. Multiple-criteria evaluation for value management in civil engineering. J. Manag. Eng. 2005, 21, 131–137. [Google Scholar]
- Georgy, M.; Chang, L.; Zhang, L. Utility function model for engineering performance assessment. J. Const. Eng. Manag. 2005, 131, 558–568. [Google Scholar]
- Singh, D.; Tiong, R. A fuzzy decision framework for contractor selection. J. Const. Eng. Manag. 2005, 131, 62–70. [Google Scholar]
- Vakili-Ardebili, A.; Boussabaine, A.H. Application of fuzzy techniques to develop an assessment framework for building design eco-drivers. Build. Environ. 2007, 42, 3785–3800. [Google Scholar]
- Springer, M.D. The Algebra of Random Variables; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Gal, T.; Stewart, T.; Hanne, T. Multicriteria Decision Making Advances in MCDM Models, Algorithms Theory, and Applications; Kluwers Academic Publishers: New York, NY, USA, 1999. [Google Scholar]
- Ormazabal Sanchez, G. El IDS: Un Nuevo Sistema Integrado de Toma de Decision Para la Gestion de Proyectos Constructivos. PhD Thesis, Departamento de ingenieria de la construccion, Universidad Politecnica de Cataluna (UPC), Barcelona, Spain, 2002. [Google Scholar]
- Caricheu, O.; Olson, D.; Moshkovich, H.; Mechitov, A. Numerical vs. cardinal measurement in multiattribute decision making. How exact is enough? Organ. Behav. Hum Decision 1995, 64, 9–21. [Google Scholar]
- Griffith, A.; Headley, J. Using a weighted score model as an aid to selecting procurement methods for small building works. Const. Manag. Econ. 1997, 15, 341–348. [Google Scholar]
- Hatush, Z.; Skitmore, M. Contractor selection using multicriteria utility theory: An additive model. Build. Environ. 1998, 33, 105–115. [Google Scholar]
- Alarcon, B. Modelo Integrado de Valor para Estructuras Sostenibles. PhD Thesis, Escuela Tecnica Superior de Ingenieros de Caminos, Canales y Puertos de Barcelona, Universidad Politecnica de Cataluna (UPC), Barcelona, Spain, 2006. [Google Scholar]
- San Jose, J.T.; Garrucho, I. A system approach to the environmental analysis of industrial buildings. Build. Environ. 2010, 45, 673–683. [Google Scholar]
- Neufville, R.; King, D. Risk and needs for work premiums in contractor bidding. J. Const. Eng. Manag. 1991, 117, 659–673. [Google Scholar]
- Palaneeswaran, E.; Kumaraswamy, M. Contractor selection for Design/Build projects. J. Const. Eng. Manag. 2000, 126, 331–339. [Google Scholar]
- Manga, R. Una Nueva Metodologia Para la Toma de Decision en la Gestion de Contratacion de Proyectos. PhD Thesis, Departamento de Ingenieria de la Construccion, Universidad Politecnica de Cataluna (UPC), Barcelona, Spain, 2005. [Google Scholar]
- MIVES I Project: Integrated Model for a Sustainable Constructive Design. Aplication to Industrial and Service Buildings; Ministerio de Ciencia y Educacion: Madrid, Spain, 2002.
- MIVES II Project: Sustainability through Value Analysis Applied to Several Fields; Ministerio de Ciencia y Educacion: Madrid, Spain, 2005.
- MIVES III Project: Towards Sustainability in Construction through Value Analysis with and without Uncertainty; Ministerio de Ciencia y Educacion: Madrid, Spain, 2009.
- MIVES IV Project: Quantification of Sustainability in Construction Engineering with and without Uncertainty; Ministerio de Ciencia y Educacion: Madrid, Spain, 2010.
- Aguado, A.; Manga, R.; Ormazabal, G. Los aspectos conceptuales del proyecto Mives. In La medida de la Sostenibilidad en Edificacion Industrial; UPV, UPC, Labein-Tecnalia: Bilbao, Spain, 2006; Chapter 6; pp. 113–134. [Google Scholar]
- Garrucho, I.; San Jose, T.; Garcia, D. Ejemplo de aplicacion de la herramienta mives. In La Medida de la Sostenibilidad en Edificacion Industrial; UPV, UPC, Labein-Tecnalia: Bilbao, Spain, 2006; Chapter 9; pp. 203–223. [Google Scholar]
- San-Jose, J.T.; Garrucho, I.; Cuadrado, J. The first sustainable industrial building projects. Proc. Inst. Civil Eng. Munic. Eng. 2006, 159, 147–153. [Google Scholar]
- San-Jose, J.T.; Garrucho, I.; Losada, R.; Cuadrado, J. A proposal for environmental indicators towards industrial building sustainable assessment. Int. J. Sustain. Dev. World Eco. 2007, 14, 160–173. [Google Scholar]
- Gomez Lopez, D.; del Cano, A.; de la Cruz, M.P. Sustainability assessment of concrete structures using the Spanish code EHE-2008: Reflections and recommendations. Proceedings of the 13th International Congress on Project Engineering, Badajoz, Spain, July 2009; AEIPRO (Spanish Engineering and Project Management Association): Badajoz, Spain, 2009. [Google Scholar]
- Instruccion de Hormigon Estructural (EHE-98); Ministerio de Fomento: Madrid, Spain, 1998; Real Decreto 2661/1998, de 11 de diciembre.
- Instruccion de Hormigon Estructural (EHE-08); Ministerio de Fomento: Madrid, Spain, 2008; Real Decreto 1247/2008, de 18 de Julio.
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Alarcon, B.; Aguado, A.; Manga, R.; Josa, A. A Value Function for Assessing Sustainability: Application to Industrial Buildings. Sustainability 2011, 3, 35-50. https://doi.org/10.3390/su3010035
Alarcon B, Aguado A, Manga R, Josa A. A Value Function for Assessing Sustainability: Application to Industrial Buildings. Sustainability. 2011; 3(1):35-50. https://doi.org/10.3390/su3010035
Chicago/Turabian StyleAlarcon, Bibiana, Antonio Aguado, Resmundo Manga, and Alejandro Josa. 2011. "A Value Function for Assessing Sustainability: Application to Industrial Buildings" Sustainability 3, no. 1: 35-50. https://doi.org/10.3390/su3010035





