An Investigation of a Supply Chain Model for Co-Ordination of Finished Products and Raw Materials in a Production System under Different Situations
Abstract
:1. Introduction
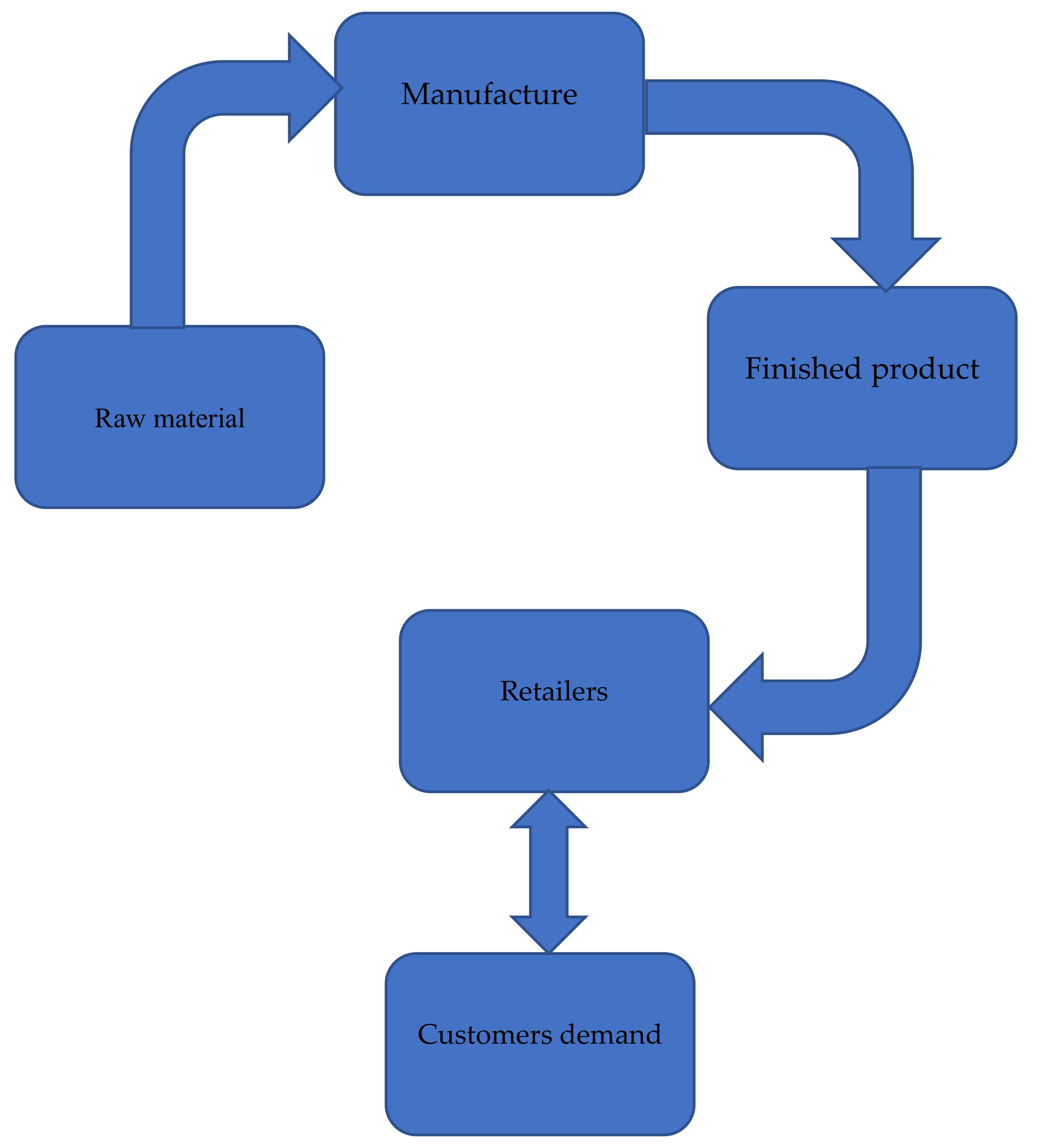
1.1. Motivation (General Problem Description)
1.2. Literature Review
1.3. Research Gap and Contribution
- (i).
- Controllable deterioration, i.e., preservation technology, is introduced;
- (ii).
- Time-varying holding cost is incorporated;
- (iii).
- Shortages are allowed.
2. Nomenclature and Assumptions
2.1. Symbolizations/Nomenclature
- (a)
- = component production cost of the decaying product. [units]
- (b)
- = rate of production. [$/units)]
- (c)
- = persistent deterioration amount of finished products. [quantity unit/unit time]
- (d)
- = resultant deterioration rate .
- (e)
- Reduced deterioration rate of the finished product where
- (f)
- = setup cost. [setup/$]
- (g)
- = demand rate of market from one to three . [$/units/quantity unit]
- (h)
- = selling season of market from one to three . [$/units]
- (i)
- = backlogging cost per unit. [$/unit]
- (j)
- = purchase cost of finished products. [$/unit]
- (k)
- = the purchase cost of finished products. [$/quantity unit/unit time]
- (l)
- = the backlogging cost of finished products. [unit time]
- (m)
- = the total cost of finished products goods [$/units]
- (n)
- = total cost [$/order]
- (o)
- = inventory level in the interval . [units]
- (a)
- = component price of ordering cost. [($/order)]
- (b)
- = component price of raw materials. [unit]
- (c)
- = holding price of raw material per unit time for manufacturing. [unit/unit time]
- (d)
- = constant deterioration rate of raw materials. [unit time]
- (e)
- = resultant deterioration rate of raw materials. [quantity unit/unit]
- (f)
- = procedure unit of raw constituents per finished product. [$/order]
- (g)
- = purchased cost per unit finished product. [quantity unit/unit time]
- (h)
- = transportation cost per lot [$/shipment]
- (i)
- = total cost of raw materials. [$/unit]
- (a)
- = Optimal time. [time unit]
- (b)
- = Number of raw materials deliveries from the supplier to manufacture. [Positive integer]
- (c)
- = Lot-size per delivery from supplier to manufacture. [$/unit]
- (d)
- = Preservation technology (PT) charges for dropping deterioration rate in instruction to preserve the product. [in $].
2.2. Assumptions
- (1)
- (2)
- (3)
- The rate of production is more significant than any selling price rate of demand.
- (4)
- (5)
- Deterioration rates of the materials and finished products are deterministic and controllable [1].
- (6)
- (7)
- (8)
- (9)
- (10)
- (11)
- Demand rate of market have three components [34].
- (12)
- (13)
- (14)
- Preservation technology is one of the most important investments to prevent the product from deteriorating. The deterioration of items can be improved by preservation technology investment and the reduced deterioration rate is , where [17].
- (15)
3. The Mathematical Formulation of the Problem and Solution
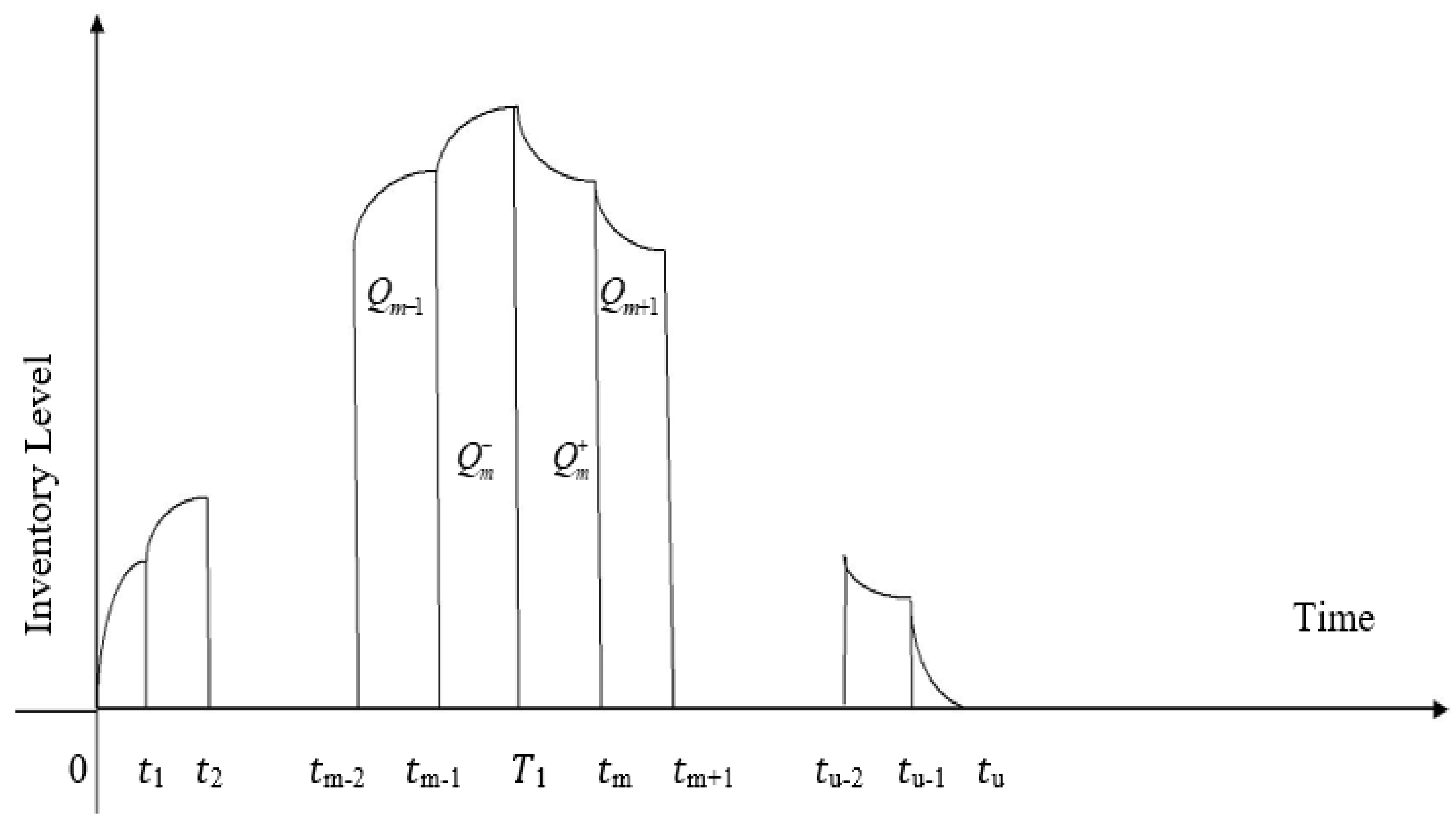
3.1. Finished Products of the Manufactures for the Given Inventory Model
3.2. Calculation of Cost for Finished Products
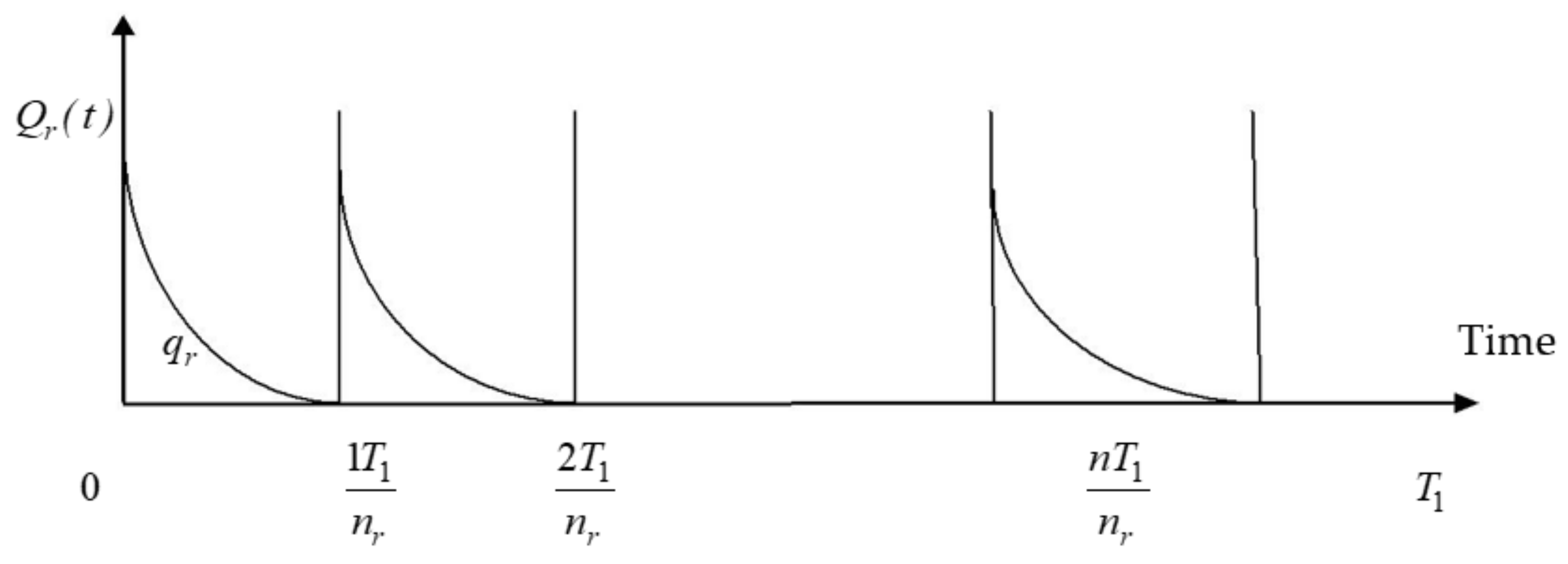
3.3. Manufactories’ Warehouse Raw Materials Inventory Model
3.4. Raw Materials Cost Calculation
- The ordering cost:
- Transportation cost of raw materials:
- The holding cost of raw material:
- The deterioration cost of raw material:
- The preservation technology cost of raw material:
3.5. Model 2: Modal with Shortage Allowed
3.5.1. Manufacture Is Finished Products, Inventory Model
3.5.2. Cost Calculation
3.5.3. Integrated Inventory Model-2 and Solution
4. Objective (Cost Calculation of Raw Material and Manufacture Finished Products)
5. Experimental Analysis
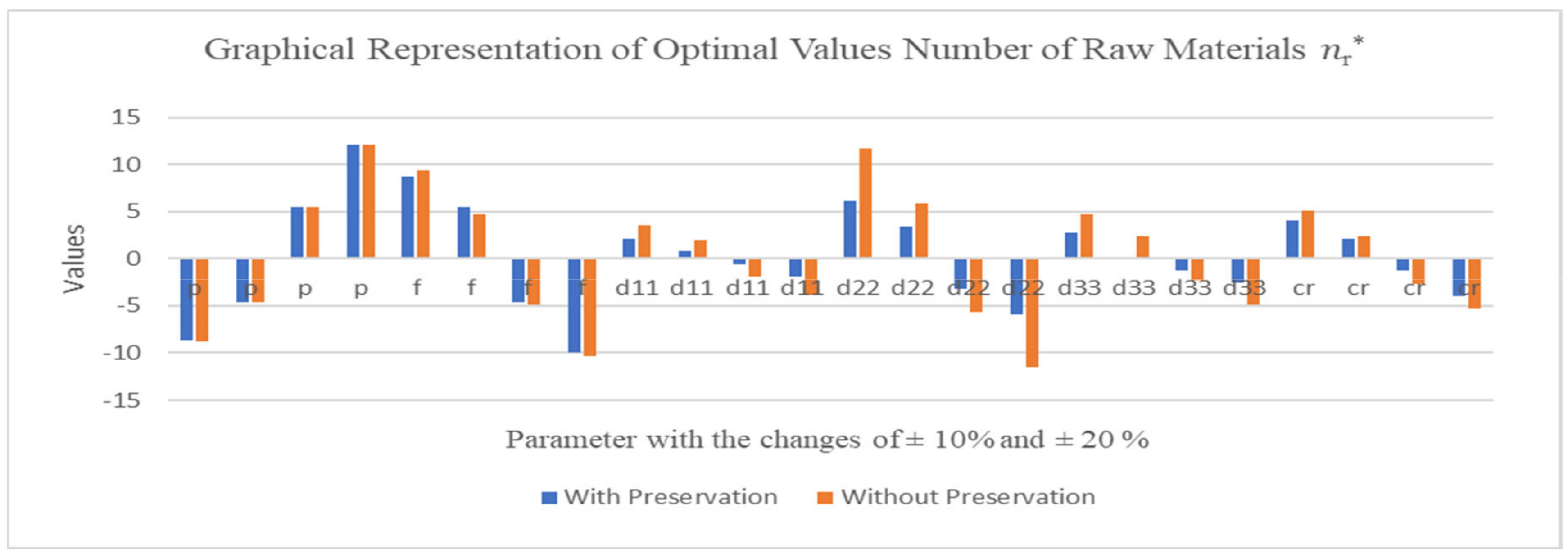
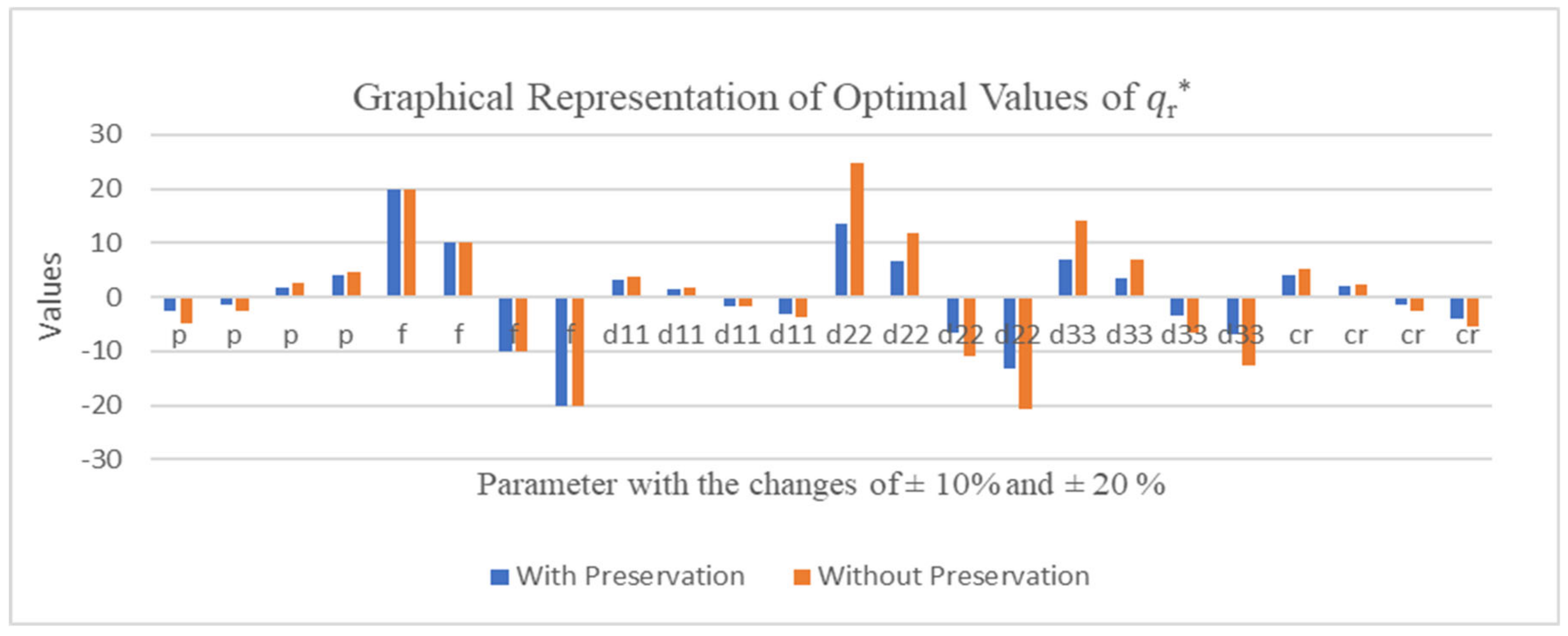
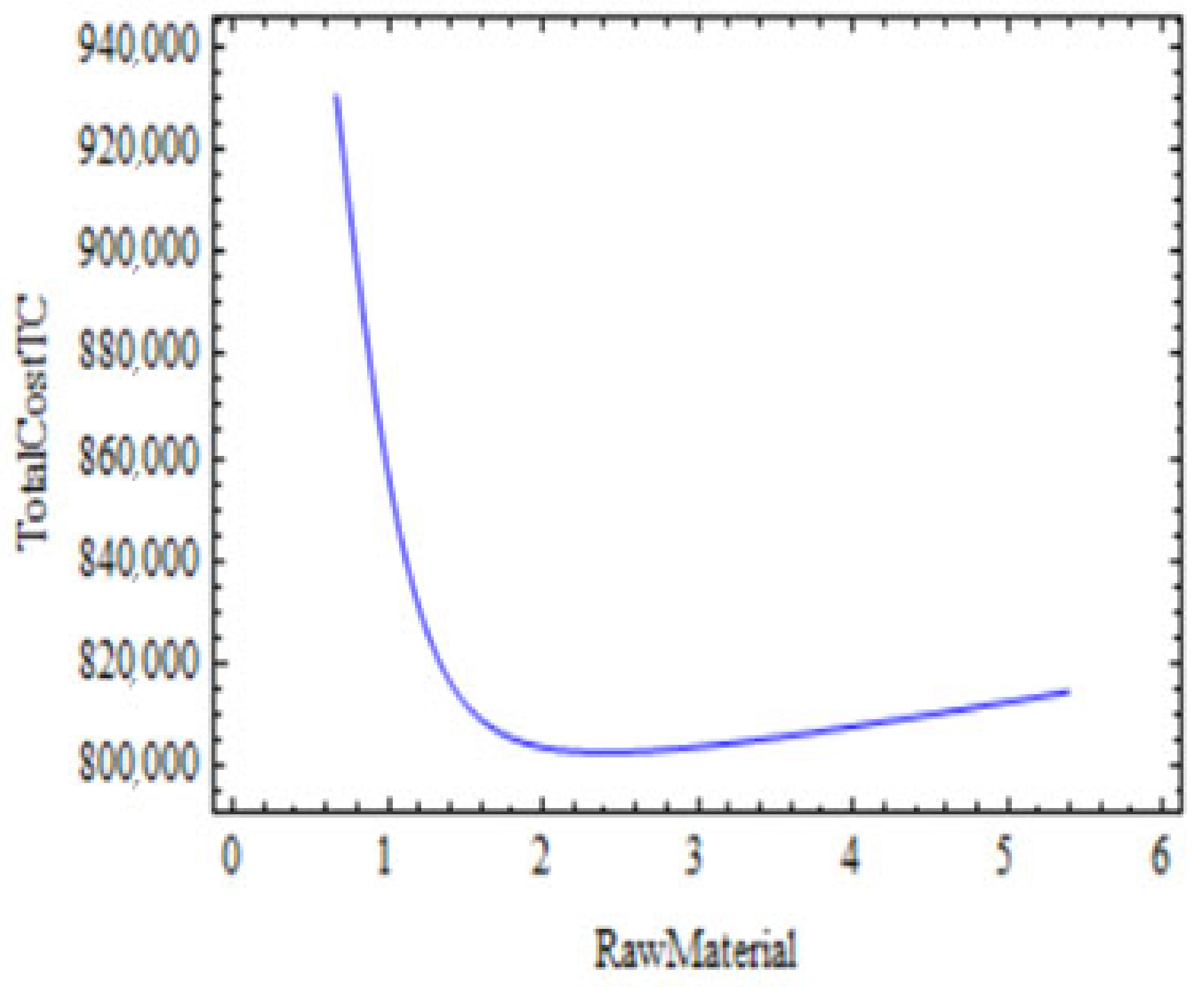
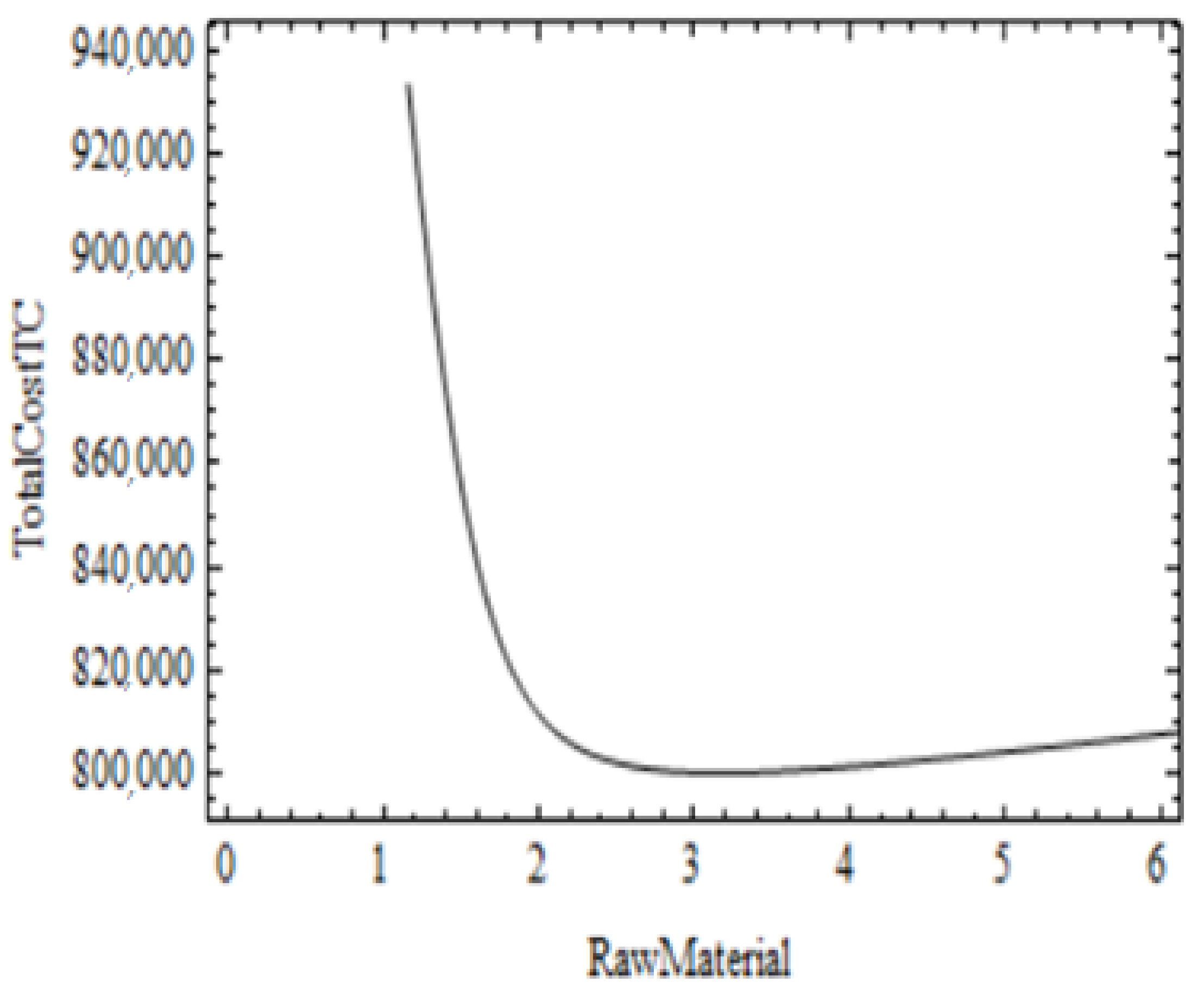
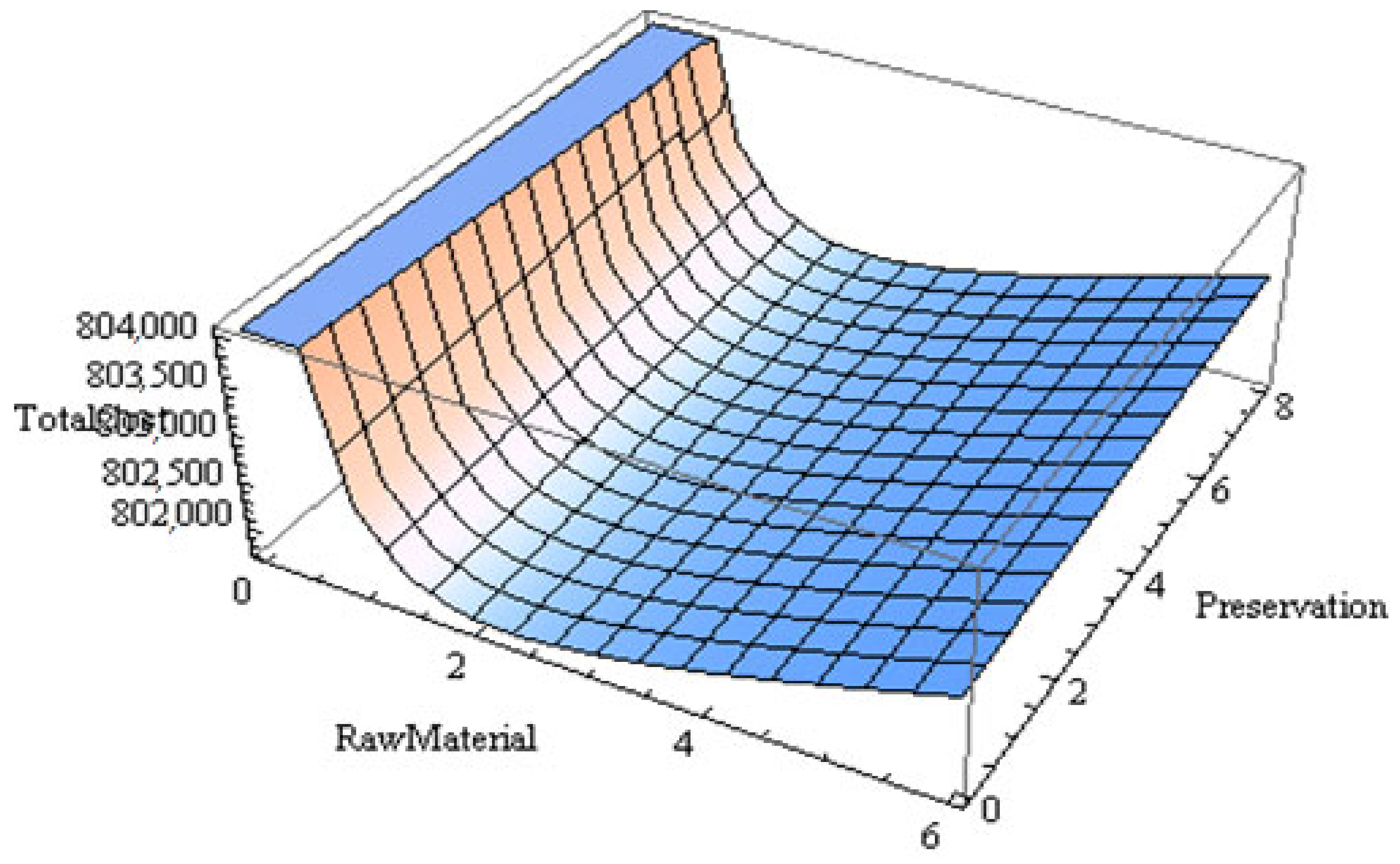
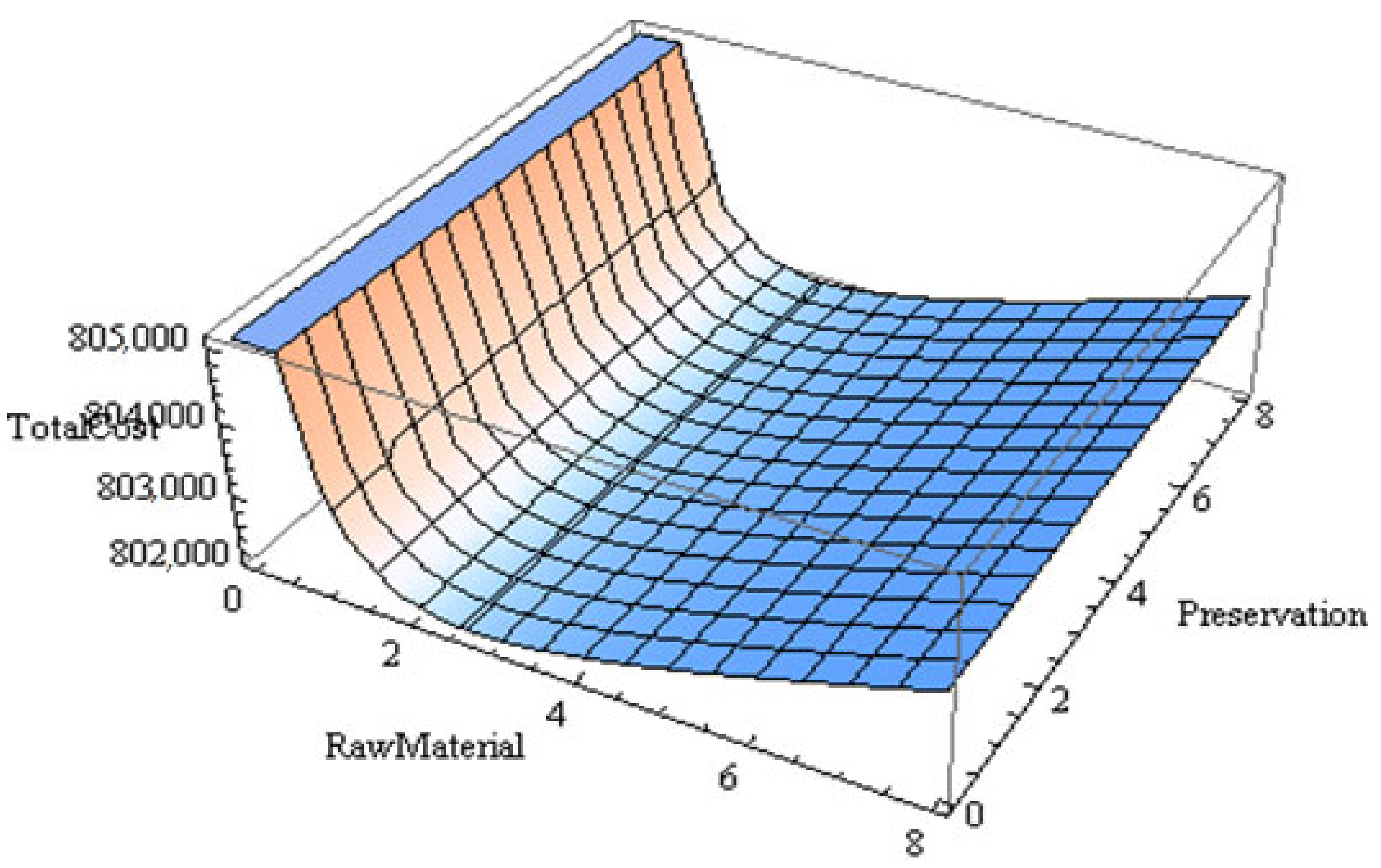
6. Sensitivity Analyses and Graphical Analysis
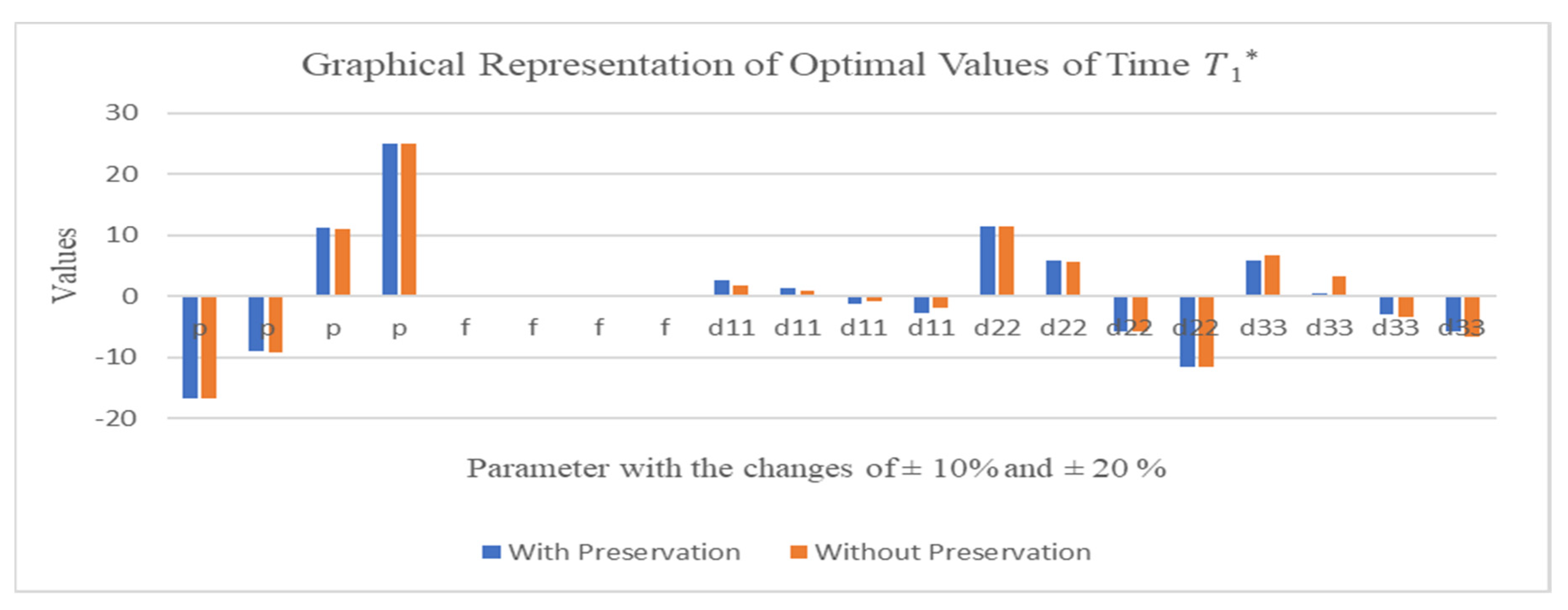
6.1. Sensitivity Analyses
6.2. Graphical Analysis
7. Managerial Implication
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mishra, V.K.; Sahab, S.L. A deteriorating inventory model for time dependent demand and holding cost with partial backlogging. Int. J. Manag. Sci. Eng. Manag. 2011, 6, 267–271. [Google Scholar] [CrossRef]
- Khara, B.; Dey, J.K.; Mondal, S.K. An inventory model under development cost-dependent imperfect production and reliability-dependent demand. J. Manag. Anal. 2017, 4, 258–275. [Google Scholar] [CrossRef]
- Benkherouf, L.; Skouri, K.; Konstantaras, I. Optimal batch production with rework process for products with time-varying demand over finite planning horizon. In Operations Research, Engineering and Cyber Security; Springer: Cham, Switzerland, 2017; Volume 113, pp. 57–68. [Google Scholar]
- Demirag, O.C.; Kumar, S.; Rao, K.M. A note on inventory policies for products with residual-life-dependent demand. Appl. Math. Model. 2017, 43, 647–658. [Google Scholar] [CrossRef]
- Bera, A.K.; Jana, D.K. Multi-item imperfect production inventory model in Bi-fuzzy environments. Opsearch 2017, 54, 260–282. [Google Scholar] [CrossRef]
- Mahata, G.C. A production-inventory model with imperfect production process and partial backlogging under learning considerations in fuzzy random environments. J. Intell. Manuf. 2017, 28, 883–897. [Google Scholar] [CrossRef]
- Nobil, A.H.; Cárdenas-Barrón, L.E. Some observations to: Lot sizing with non-zero setup times for rework. Int. J. Appl. Comput. Math. 2017, 3, 1511–1517. [Google Scholar] [CrossRef]
- Dizbin, N.M.; Tan, B. Optimal control of production-inventory systems with correlated demand inter-arrival and processing times. Int. J. Prod. Econ. 2020, 228, 107692. [Google Scholar]
- Maihami, R.; Kamalabadi, I.N. Joint pricing and inventory control for non- instantaneous deteriorating items with partial backlogging and time and price dependent demand. Int. J. Prod. Econ. 2012, 136, 116–122. [Google Scholar] [CrossRef]
- Ghoreishi, M.; Weber, G.W.; Mirzazadeh, A. An inventory model for non-instantaneous deteriorating items with partial backlogging, permissible delay in payments, inflation-and selling price-dependent demand and customer returns. Ann. Oper. Res. 2015, 226, 221–238. [Google Scholar] [CrossRef]
- Yang, C.T.; Ouyang, L.Y.; Wu, K.S.; Yen, H.F. An optimal replenishment policy for deteriorating items with stock-dependent demand and relaxed terminal conditions under limited storage space. Cent. Eur. J. Oper. Res. 2011, 19, 139–153. [Google Scholar] [CrossRef]
- Banerjee, S.; Agrawal, S. Inventory model for deteriorating items with freshness and price dependent demand, optimal discounting and ordering policies. Appl. Math. Model. 2017, 52, 53–64. [Google Scholar] [CrossRef]
- Hsu, P.H.; Wee, H.M.; Tang, H.M. Preservation technology investment for deteriorating inventory. Int. J. Prod. Econ. 2010, 124, 388–394. [Google Scholar] [CrossRef]
- He, Y.; Huang, H.H. Optimizing inventory and pricing policy for deteriorating seasonal products with preservation technology investment. J. Ind. Eng. 2013, 2013, 793568. [Google Scholar]
- Dye, C.Y. The effect of preservation technology investment on a no instantaneous deteriorating inventory model. Omega 2013, 41, 872–880. [Google Scholar] [CrossRef]
- Mishra, U.; Crdenas-Barrn, L.E.; Tiwari, S.; Shaikh, A.A.; Trevio-Garza, G. An inventory model under price and stock dependent demand for controllable deterioration rate with shortages and preservation technology investment. Ann. Oper. Res. 2017, 252, 165–190. [Google Scholar]
- Shen, Y.; Shen, K.; Yang, C. A production inventory model for deteriorating items with collaborative preservation technology investment under carbon tax. Sustainability 2019, 11, 5027. [Google Scholar] [CrossRef] [Green Version]
- Bardhan, S.; Pal, H.; Giri, B.C. Optimal replenishment policy and preservation technology investment for a non-instantaneous deteriorating item with stock-dependent demand. Oper. Res. 2017, 19, 247–368. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Roy, D.; Daryanto, Y.; Chakrabortty, R.K.; Tseng, M.L. A sustainable inventory model with controllable carbon emissions, deterioration and advance payments. J. Clean. Prod. 2021, 296, 126608. [Google Scholar] [CrossRef]
- Taleizadeh, A.A. A constrained integrated imperfect manufacturing-inventory system with preventive maintenance and partial backordering. Ann. Oper. Res. 2018, 261, 303–337. [Google Scholar] [CrossRef]
- Sarkar, M.; Lee, Y.H. Optimum pricing strategy for complementary products with reservation price in a supply chain model. J. Ind. Manag. Optim. 2017, 13, 1553. [Google Scholar] [CrossRef] [Green Version]
- Alfares, H.K.; Ghaithan, A.M. Inventory and pricing model with price-dependent demand, time-varying holding cost, and quantity discounts. Comput. Ind. Eng. 2016, 94, 170–177. [Google Scholar] [CrossRef]
- Sarkar, B.; Sana, S.S.; Chaudhuri, K. An imperfect production process for time varying demand with inflation and time value of money—an EMQ model. Expert Syst. Appl. 2011, 38, 13543–13548. [Google Scholar] [CrossRef]
- Pervin, M.; Roy, S.K.; Weber, G.W. An integrated inventory model with variable holding cost under two levels of trade-credit policy. Numer. Algebra Control Optim. 2018, 8, 169. [Google Scholar] [CrossRef] [Green Version]
- Cárdenas-Barrón, L.E.; Mandal, B.; Sicilia, J.; San-José, L.A.; Abdul-Jalbar, B. Optimizing price, order quantity, and backordering level using a nonlinear holding cost and a power demand pattern. Comput. Oper. Res. 2021, 133, 105339. [Google Scholar] [CrossRef]
- Palanivel, M.; Suganya, M. Partial backlogging inventory model with price and stock level dependent demand, time varying holding cost and quantity discounts. J. Manag. Anal. 2021, 8, 1–28. [Google Scholar] [CrossRef]
- Mishra, V.K. An inventory model of instantaneous deteriorating items with controllable deterioration rate for time dependent demand and holding cost. J. Ind. Eng. Manag. 2013, 6, 495–509. [Google Scholar] [CrossRef]
- Nasr, W.W.; Salameh, M.K.; Moussawi-Haidar, L. Integrating the economic production model with deteriorating raw material over multi production cycles. Int. J. Prod. Res. 2014, 52, 2477–2489. [Google Scholar] [CrossRef]
- Bhunia, A.; Shaikh, A. A deterministic inventory model for deteriorating items with selling price dependent demand and three-parameter Weibull distributed deterioration. Int. J. Ind. Eng. Comput. 2014, 5, 497–510. [Google Scholar] [CrossRef] [Green Version]
- Duari, N.K.; Chakraborti, T. An order level EOQ model for deteriorating items in a single warehouse system with price depended demand and shortages. Am. J. Eng. Res. 2014, 3, 11–16. [Google Scholar]
- Nobil, A.H.; Sedigh, A.H.A.; Cárdenas-Barrón, L.E. A multiproduct single machine economic production quantity (EPQ) inventory model with discrete delivery order, joint production policy and budget constraints. Ann. Oper. Res. 2020, 286, 265–301. [Google Scholar] [CrossRef]
- AL-Khazraji, H.; Cole, C.; Guo, W. Optimization and simulation of dynamic performance of production–inventory systems with multivariable controls. Mathematics 2021, 9, 568. [Google Scholar] [CrossRef]
- Uthayakumar, R.; Tharani, S. An economic production model for deteriorating items and time dependent demand with rework and multiple production setups. J. Ind. Eng. Int. 2017, 13, 499–512. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Wang, S.Y.; Lai, K.K. An optimal production-inventory model for deteriorating items with multiple-market demand. Eur. J. Oper. Res. 2010, 203, 593–600. [Google Scholar] [CrossRef]
- Singh, S.R.; Malik, A.K.; Gupta, S.K. Two warehouses inventory model with partial back ordering and multi-variate demand under inflation. Int. J. Oper. Res. Optim. 2011, 2, 371–384. [Google Scholar]
- Sajadifar, S.M.; Hashempour, M. An optimal production-inventory model for deteriorating items with multiple-market demand under backlogging. In Proceedings of the 2012 International Conference on Industrial Engineering and Operations Management, Istanbul, Turkey, 3–6 July 2012; pp. 1735–1743. [Google Scholar]
- Malik, A.K.; Shrma, A. An inventory model for deteriorating items with multi-variate demand and partial backlogging under inflation. Int. J. Math. Sci. 2011, 3, 315–321. [Google Scholar]
- He, Y.; Wang, S. Analysis of production-inventory system for deteriorating items with demand disruption. Int. J. Prod. Res. 2012, 50, 4580–4592. [Google Scholar] [CrossRef]
- Karimi, M.; Sadjadi, S.J. Optimization of a multi-Item inventory model for deteriorating items with capacity constraint using dynamic programming. J. Ind. Manag. Optim. 2020, 18, 1–16. [Google Scholar] [CrossRef]
- Singhal, S.; Singh, S.R. Supply chain system for time and quality dependent decaying items with multiple market demand and volume flexibility. Int. J. Oper. Res. 2018, 31, 245–261. [Google Scholar] [CrossRef]
- Chakraborty, D.; Jana, D.K.; Roy, T.K. Multi-warehouse partial backlogging inventory system with inflation for non-instantaneous deteriorating multi-item under imprecise environment. Soft Comput. 2020, 24, 14471–14490. [Google Scholar] [CrossRef]
- Pal, B.; Sana, S.S.; Chaudhuri, K. A three-layer multi-item production–inventory model for multiple suppliers and retailers. Econ. Model. 2012, 29, 2704–2710. [Google Scholar] [CrossRef]
- Khurana, D. Two warehouse inventory model for deteriorating items with time dependent demand under inflation. Int. J. Comput. Appl. 2015, 114, 34–38. [Google Scholar] [CrossRef]
- Tiwari, S.; Jaggi, C.K.; Bhunia, A.K.; Shaikh, A.A.; Goh, M. Two-warehouse inventory model for non-instantaneous deteriorating items with stock-dependent demand and inflation using particle swarm optimization. Ann. Oper. Res. 2017, 254, 401–423. [Google Scholar] [CrossRef]
- Jauhari, A.W.; Pujawan, N.I. Joint economic lot size (JELS) model for single-vendor single-buyer with variable production rate and partial backorder. Int. J. Oper. Res. 2014, 20, 91–108. [Google Scholar] [CrossRef]
- Thinakaran, N.; Jayaprakas, J.; Elanchezhian, C. Survey on inventory model of EOQ & EPQ with partial backorder problems. Mater. Today: Proc. 2019, 16, 629–635. [Google Scholar]
- Taleizadeh, A.A.; Cárdenas-Barrón, E.L.; Mohammadi, B. A deterministic multi product single machine EPQ model with backordering, scraped products, rework and interruption in manufacturing process. Int. J. Prod. Econ. 2014, 150, 9–21. [Google Scholar] [CrossRef]
- Singh, D. Production inventory model of deteriorating items with holding cost, stock, and selling price with backlog. Int. J. Math. Oper. Res. 2019, 14, 290–305. [Google Scholar] [CrossRef]
- Chatterji, D.; Gothi, B.U. EOQ model for deteriorating items under two and three parameter Weibull distribution and constant IHC with partially backlogged shortages. Int. J. Sci. Eng. Technol. Res. (IJSETR) 2015, 4, 3582–3594. [Google Scholar]
- Palanivel, M.; Uthayakumar, R. An EPQ model for deteriorating items with variable production cost, time dependent holding cost and partial backlogging under inflation. Opsearch 2015, 52, 1–17. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, E.L. The derivation of EOQ/EPQ inventory models with two backorders costs using analytic geometry and algebra. Appl. Math. Model. 2011, 35, 2394–2407. [Google Scholar] [CrossRef] [Green Version]
- Taleizadeh, A.; Hazarkhani, B.; Moon, I. Joint pricing and inventory decisions with carbon emission considerations, partial backordering and planned discounts. Ann. Oper. Res. 2020, 290, 95–113. [Google Scholar] [CrossRef]
- Prasad, K.; Mukherjee, B. Optimal inventory model under stock and time dependent demand for time varying deterioration rate with shortages. Ann. Oper. Res. 2016, 243, 323–334. [Google Scholar] [CrossRef]
- De, S.K.; Sana, S.S. An EOQ model with backlogging. Int. J. Manag. Sci. Eng. Manag. 2016, 11, 143–154. [Google Scholar]
- San-José, L.A.; Sicilia, J.; González-De-la-Rosa, M.; Febles-Acosta, J. Optimal inventory policy under power demand pattern and partial backlogging. Appl. Math. Model. 2017, 46, 618–630. [Google Scholar] [CrossRef]
- Sarkar, T.; Ghosh, S.K.; Chaudhuri, K.S. An optimal inventory replenishment policy for a deteriorating item with time-quadratic demand and time-dependent partial backlogging with shortages in all cycles. Appl. Math. Comput. 2012, 218, 9147–9155. [Google Scholar] [CrossRef]
- Choudhury, K.D.; Karmakar, B.; Das, M.; Datta, T.K. An inventory model for deteriorating items with stock-dependent demand, time-varying holding cost and shortages. Opsearch 2015, 52, 55–74. [Google Scholar] [CrossRef]
- Wuu Wu, J.; Chuan Lee, W. An EOQ inventory model for items with Weibull deterioration, shortages and time varying demand. J. Inf. Optim. Sci. 2013, 24, 103–122. [Google Scholar]
- Sarkar, B.; Majumder, A.; Sarkar, M.; Kim, N.; Ullah, M. Effects of variable production rate on quality of products in a single-vendor multi-buyer supply chain management. Int. J. Adv. Manuf. Technol. 2018, 99, 567–581. [Google Scholar] [CrossRef]
- Dey, B.K.; Sarkar, B.; Pareek, S. A two-echelon supply chain management with setup time and cost reduction, quality improvement and variable production rate. Mathematics 2019, 7, 328. [Google Scholar] [CrossRef] [Green Version]
- Sett, B.K.; Dey, B.K.; Sarkar, B. The effect of O2O retail service quality in supply chain management. Mathematics 2020, 8, 1743. [Google Scholar] [CrossRef]
- Dey, B.K.; Bhuniya, S.; Sarkar, B. Involvement of controllable lead time and variable demand for a smart manufacturing system under a supply chain management. Expert Syst. Appl. 2021, 184, 115464. [Google Scholar] [CrossRef]




| Authors | Deterioration (Constraints) | Demand Function | Holding Cost | Preservation | Shortage |
|---|---|---|---|---|---|
| He et al. [34] | Constant | Constant | Constant | No | No |
| Singh et al. [35] | Weibull distribution | Time-dependent | Constant | No | Allowed |
| Sajadifar and Hashempour [36] | Constant | Constant | Constant | No | Allowed |
| Malik and Sharma [37] | Constant | Linear | Constant | No | Allowed |
| He and Wang [38] | Constant | Disruption | Constant | No | No |
| Karimi and Sadjadi [39] | Discrete | Time-dependent | Constant | No | Allowed |
| Singhal and Singh [40] | Weibull distribution | Linear increasing | No | Not Allowed | |
| Chakraborty et al. [41] | Constant overtime | Stock dependent | Constant | No | Allowed |
| Pal et al. [42] | Constant | Time-dependent | Constant | No | Not Allowed |
| Khurana [43] | Weibull distribution | DeterministicLinear | Constant | Yes | Not Allowed |
| Tiwari et al. [44] | Non-instantaneous | Stock dependent | Constant | --------- | Allowed |
| This Paper | Controllable | Constant | Linear | Yes | Allowed |
| With Preservation Technology | Without Preservation Technology | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Without Shortage | With Shortage | Without Shortage | With Shortage | ||||||
| 2 | 6.23 | 20.33 | 3422 | 793,905 | 795,436 | 9.37 | 2282 | 731,044 | 732,575 |
| 3 | 6.25 | 20.33 | 3422 | 793,858 | 795,389 | 9.37 | 2282 | 731,303 | 732,834 |
| With Preservation Technology | Without Preservation Technology | ||||||
|---|---|---|---|---|---|---|---|
| Without Shortage | With Shortage | Without Shortage | With Shortage | ||||
| 2 | 6.23 | 3206 | 793,452 | 794,926 | 2202 | 730,540 | 732,143 |
| 3 | 6.25 | 3206 | 793,402 | 794,845 | 2202 | 730,808 | 732,475 |
| Optimal Values of Previous Work [34] | Optimal Values of This Paper | ||||
|---|---|---|---|---|---|
| Total Cost (Without Shortage) | Total Cost (Without Shortage) | ||||
| 6 | 19.30 | 19,287 | 2 | 11.05 | 17,471 |
| 7 | 19.30 | 19,300 | 3 | 11.05 | 18,780 |
| Parameter | With Preservation Technology | Without Preservation Technology | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Without and with Shortage | Without and with Shortage | |||||||||||
| 20 | 4.00 | −8.60 | −16.63 | −2.68 | −29.51 | −29.40 | −8.82 | −16.67 | −4.89 | −29.30 | −29.18 | |
| 10 | 2.13 | −4.59 | −9.04 | −1.47 | −16.76 | −16.70 | −4.57 | −9.10 | −2.48 | −16.64 | −16.57 | |
| −10 | −2.38 | 5.42 | 11.12 | 1.84 | 22.65 | 22.57 | 5.48 | 11.07 | 2.66 | 22.48 | 22.39 | |
| −20 | −5.02 | 12.09 | 25.00 | 4.20 | 44.33 | 44.12 | 12.05 | 24.94 | 4.57 | 43.88 | 43.68 | |
| 20 | −0.20 | 8.75 | 0.00 | 20.00 | 0.26 | 0.26 | 9.34 | 0.00 | 20.00 | 0.06 | 0.06 | |
| 10 | −0.05 | 5.42 | 0.00 | 10.00 | 0.13 | 0.13 | 4.71 | 0.00 | 10.00 | 0.03 | 0.03 | |
| −10 | 0.05 | −4.59 | 0.00 | −10.00 | −0.13 | −0.13 | −4.95 | 0.00 | −10.00 | −0.03 | −0.03 | |
| −20 | 0.11 | −9.93 | 0.00 | −20.00 | −0.26 | −0.26 | −10.36 | 0.00 | −20.00 | −0.06 | −0.06 | |
| 20 | −0.67 | 2.08 | 2.70 | 3.15 | 10.01 | 10.00 | 3.55 | 1.82 | 3.72 | 9.96 | 9.96 | |
| 10 | −0.36 | 0.75 | 1.40 | 1.57 | 4.93 | 4.93 | 2.00 | 0.89 | 1.85 | 4.91 | 4.91 | |
| −10 | 0.26 | −0.59 | −1.33 | −1.56 | −4.79 | −4.78 | −1.86 | −0.93 | −1.82 | −4.76 | −4.76 | |
| −20 | 0.73 | −1.92 | −2.75 | −3.12 | −9.43 | −9.43 | −3.79 | −1.87 | −3.61 | −9.38 | −9.38 | |
| 20 | −2.84 | 6.08 | 11.48 | 13.59 | 37.71 | 37.61 | 11.66 | 11.46 | 24.90 | 37.38 | 37.28 | |
| 10 | −1.45 | 3.41 | 5.79 | 6.74 | 17.84 | 17.79 | 5.86 | 5.71 | 11.89 | 17.69 | 17.64 | |
| −10 | 1.51 | −3.26 | −5.72 | −6.62 | −15.92 | −15.88 | −5.73 | −5.76 | −10.87 | −15.79 | −15.75 | |
| −20 | 3.22 | −5.93 | −11.53 | −13.12 | −30.04 | −29.97 | −11.52 | −11.51 | −20.80 | −29.78 | −29.71 | |
| 20 | −0.67 | 2.75 | 5.79 | 6.84 | 37.67 | 37.53 | 4.71 | 6.69 | 13.99 | 37.50 | 37.35 | |
| 10 | −0.05 | 0.08 | 2.45 | 3.56 | 17.87 | 17.80 | 2.39 | 3.30 | 6.81 | 17.78 | 17.71 | |
| −10 | 0.42 | −1.26 | −2.87 | −3.37 | −16.04 | −15.98 | −2.25 | −3.34 | −6.46 | −15.96 | −15.90 | |
| −20 | 0.73 | −2.59 | −5.84 | −6.72 | −30.38 | −30.26 | −4.95 | −6.69 | −12.59 | −30.22 | −30.11 | |
| 20 | 0.05 | 4.08 | 0.00 | 0.00 | 0.02 | 0.02 | 5.09 | 0.00 | 0.00 | 0.02 | 0.02 | |
| 10 | 0.05 | 2.08 | 0.00 | 0.00 | 0.01 | 0.01 | 2.39 | 0.00 | 0.00 | 0.01 | 0.01 | |
| −10 | −0.05 | −1.26 | 0.00 | 0.00 | −0.01 | −0.01 | −2.64 | 0.00 | 0.00 | −0.01 | −0.01 | |
| −20 | −0.05 | −3.93 | 0.00 | 0.00 | −0.02 | −0.02 | −5.34 | 0.00 | 0.00 | −0.02 | −0.02 | |
| 20 | −2.69 | 0.00 | 0.00 | 0.00 | 0.62 | 0.62 | 0.00 | 0.00 | 0.00 | 0.62 | 0.62 | |
| 10 | −1.45 | 0.00 | 0.00 | 0.00 | 0.31 | 0.31 | 0.00 | 0.00 | 0.00 | 0.31 | 0.31 | |
| −10 | 1.66 | 0.00 | 0.00 | 0.00 | −0.31 | −0.31 | 0.00 | 0.00 | 0.00 | −0.31 | −0.31 | |
| −20 | 3.53 | 0.00 | 0.00 | 0.00 | −0.62 | −0.62 | 0.00 | 0.00 | 0.00 | −0.62 | −0.62 | |
| 20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.38 | 0.00 | 0.00 | 0.00 | 0.00 | 0.38 | |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | |
| −10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.19 | 0.00 | 0.00 | 0.00 | 0.00 | −0.19 | |
| −20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.38 | 0.00 | 0.00 | 0.00 | 0.00 | −0.38 | |
| 20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.31 | 0.00 | 0.00 | 0.00 | 0.00 | −0.31 | |
| 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.15 | 0.00 | 0.00 | 0.00 | 0.00 | −0.15 | |
| −10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.15 | |
| −20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.31 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, D.; Jayswal, A.; Alharbi, M.G.; Shaikh, A.A. An Investigation of a Supply Chain Model for Co-Ordination of Finished Products and Raw Materials in a Production System under Different Situations. Sustainability 2021, 13, 12601. https://doi.org/10.3390/su132212601
Singh D, Jayswal A, Alharbi MG, Shaikh AA. An Investigation of a Supply Chain Model for Co-Ordination of Finished Products and Raw Materials in a Production System under Different Situations. Sustainability. 2021; 13(22):12601. https://doi.org/10.3390/su132212601
Chicago/Turabian StyleSingh, Dharamender, Anurag Jayswal, Majed G. Alharbi, and Ali Akbar Shaikh. 2021. "An Investigation of a Supply Chain Model for Co-Ordination of Finished Products and Raw Materials in a Production System under Different Situations" Sustainability 13, no. 22: 12601. https://doi.org/10.3390/su132212601






