Model of Color Parameters Variation and Correction in Relation to “Time-View” Image Acquisition Effects in Wheat Crop

Abstract

Many images of agricultural crops are made at different times of the day, images with different spectral information about the same crop in relation to conditions when the picture was taken. A set of 30 digital images of a wheat crop in the BBCH 3-Stem elongation code 32–33 stage was captured between 9 am and 14 (UTC+3), in the 0°–180° variation range of the image acquisition angle on the E-W axis (cardinal directions). A high variation of the spectral data given by the combination of the hour (h) and angle (a) at which the images were captured was found. The interdependence relationship between the analyzed parameters (r, g, and b), and the time (t) and the angle (a) of image acquisition was assessed with the linear correlation coefficient. By calculating the roots of the mathematical expressions of the correlation coefficients dependence on the angles (a) or times of day (t), the optimal angle and time were determined as a combination of the two variables for capturing images and obtaining optimal r_o, g_o, b_o values. The correction coefficients of the normalized r, g, and b values obtained out of the optimal field were determined. To this end, the multiplication of the r(a,t), g(a,t), and b(a,t) values with the ρ_a,t, γ_a,t, and β_a,t correction coefficients was suggested to reach the optimal values for sustainable decisions.

1. Introduction

The imaging-based techniques for earth’s crust, plant cover, and crop investigation have developed and diversified dramatically. As a result, image analysis has come to rely on satellite imagery [1,2,3], aerial images (utility aircraft or drones) [4,5], or terrestrial images taken with commercial cameras or cameras mounted on agricultural machinery and equipment [6,7,8].

To assess agricultural crop vegetation and yield relative to the environmental and technological factors such as fertilizer dosage, irrigation, phytosanitary condition etc., classical methods can be employed, but they are expensive and slow as opposed to imagery techniques [9,10]. As an alternative solution, methods based on imagery analysis have been promoted increasingly in practice and research activities [11,12,13,14].

The new investigation methods bring more precision to agricultural practice, as they provide real-time information for adequate crop management corresponding to the nutritional status, the flowering structure, the phytosanitary condition, the reaction to various stress factors (hydric, thermal etc.,), the yield estimation and even the interventions required to compensate different deficiency in crops [15,16,17,18,19].

Operational environmental factors such as the camera height, the angle to the horizon, and the distance to the target object refer mainly to the image geometry and can be established as being constant, to have a uniform distribution of the absorption and radiation properties of the target area. There are also other environmental factors in the image acquisition area [20,21] such as: a different architecture of wheat plants, the degree of coverage and the green conditions of leaves, the intensity, spectral composition and luminosity of the photographed object. These factors are influenced especially by weather conditions. Consequently, the use of working methods that provide color stability may reduce the degree of uncertainty that characterizes the assessment of the physiological parameters of plants whose study is based on their color.

The purpose of this study was to determine the optimal angle for image capture so that the r, g, and b color indices may not be affected (or be affected in the smallest possible degree) by the moment chosen for taking the photographs. At the same time, the study intended to determine what the best time is to take photos on crops so that the r, g, and b color indices may not be affected by the image capture angle. The determination of these parameters and their simultaneous practical application may lead to a decrease in the variation of the value of the studied color indices. The study proposed a model and correction coefficients of the normalized r, g, and b values obtained for images acquired at other angles or times, then those suggested as optimal in this study.

2. Materials and Methods

2.1. Location and Experimental Conditions

The study was conducted in the Educational and Experimental Station of the Banat University of Agricultural Sciences and Veterinary Medicine “King Michael I of Romania” (BUASVM) from Timisoara, Romania. The experimental field was located in Plot A 363 and had the following geographic coordinates: N 45°28′ and 30.9″, E 21°7′9.8″. The climate characteristics—an average multiannual rainfall of 603.3 mm and an average temperature of 10.9 °C—are specific to the temperate continental climate with Mediterranean influences. In autumn, the field was fertilized with phosphorous, potassium and one-third of the nitrogen dose (mixed granular fertilizer). The remaining nitrogen was applied as urea next spring, before the stem elongation stage, the general fertilization being P₁₀₀K₁₀₀N₁₀₀ (P₁₀₀ represents 100 kg·ha⁻¹ active substance (a.c.) phosphorus (P), and similarly for kallium (K) and for nitrogen (N). This level was considered optimal for the climatic and agro-chemical conditions of the area, for a 6 t ha⁻¹ yield.

2.2. Biological Material and Crop Status

The biological material was Triticum aestivum L. Alex cultivar, a genotype with great yield potential and very good quality indices that is grown not only in Romania, but also in other countries. The main growth stage 3—Stem elongation scale for cereals was selected for image acquisition. Detailing phenological aspects, converted in crop development codes, according to BBCH-scale [22,23], the wheat plants were in the growth stage 3—Stem elongation, more exactly in 32 (Node 2 at least 2 cm above node 1) and 33 stage (Node 3 at least 2 cm above node 2). This growth stage was chosen because it is considered to be very predictable when fertilized with nitrogen and in relation to the further development of the wheat crop [24,25].

2.3. Taking Photos and Digital Images Analyzation

The digital images were taken in a visible spectrum with a commercial digital camera with proper technical parameters: NIKON D300, 12 MP resolution, DX format. The images were acquired from a uniform wheat crop in a sunny day (24 April 2013), during 9.00 to 14.00 (noted in the article as “t”) and at different camera angles (noted “a”, expressed sexagesimal degrees) on the E-W axis (0°, 45°, 90°, 135°, and 180°) (Figure 1). Throughout this paper, the time format used is hh.mm.ss, according to Time Zone UTC+3.00.

The constant parameters were the following: the camera height (1.5 m), the 45° angle to the horizontal line, the 24-mm lens and the 52.4° lens angle, full frame (Figure 2). Each acquired image covered equal crop areas of about 3 m², with a mean density of about 1550 wheat plants. The images were recorded hourly from 9.00 to 14.00, from E to W, at 0°, 45°, 90°, 135°, and 180°, resulting in a set of 30 images in jpg format (Figure 3).

The image resolution was 4288 x 2848 pixels, 300 dpi, 24 bits for Adobe RGB. The average image size was 9.54 MB. The images were processed with ImageJ software [26] to obtain the mean values of the R, G, B parameters (R—spectral values in red channel; G—spectral values in green channel; B—spectral values in blue channel). Based on the values R, G, B normalized values have been calculated, noted as r, g, respectively b (r = R/(R + G + B), g = G/(R + G + B), b = B/(R + G + B)).

Based on them, the normalized r,g,b values [27] and the specific indices intensity—INT [28], Equation (1), normalized difference index—NDI [29] Equation (2), and dark green color index—DGCI [30] Equation (3) were calculated. In Equation (3) H—hue; S—saturation; B—brightness in HSB color system, have been used for calculating DGCI according to [30], and for B in HSB system the symbol B_HSB has been used in order to avoid confusion with B in RGB system.

$$\mathrm{NDI}=\frac{\left(\mathrm{r}-\mathrm{g}\right)}{\left(\mathrm{r}+\mathrm{g}+0.01\right)},$$

(1)

$$\mathrm{INT}=\frac{\left(\mathrm{R}+\mathrm{G}+\mathrm{B}\right)}{3},$$

(2)

$$\mathrm{DGCI}=\left[\frac{\left(\mathrm{H}-60\right)}{60}+\left(1-\mathrm{S}\right)+\left(1-{\mathrm{B}}_{\mathrm{HSB}}\right)\right]/3,$$

(3)

2.4. Experimental Data Analysis

The interdependence relationship between the analyzed parameters (r, g, and b) and the hour (t) and angle (a) of image acquisition was assessed with the linear correlation coefficient. A high correlation indicates a great dependence between the parameters and the determination factors, i.e., a high contribution of the two variables to the values of the indices, while a low correlation indicates the independence from the parameters.

The values of the coefficients of correlation between the r, g, and b series and the moments (t) the images were acquired (9 a.m., 10 a.m., 11 a.m., 12 a.m., 1 p.m., 2 p.m.) in relation to the angles at which the photos were taken (0°, 45°, 90°, 135°, 180°) were calculated; the coefficients of correlation between the r, g, and b series and the angles (a) at which the photos were taken at different moments (t) were calculated as well.

A high correlation coefficient (absolute value, namely close to −1 or 1) will show that a slight change of the moment chosen to take the photo in relation to the angle (a) or a change of the angle in relation to time indicates a change in the r, g, and b color indices. At the same time, a correlation coefficient close to zero will indicate that even a significant change of the time chosen to take the photo in relation to the angle, or vice versa, does not imply a change in the r, g, and b color indices. Next the mathematical expressions of the correlation coefficients dependence on angles (a) or times (t) were determined. By calculating the roots of these expressions, we were able to determine the optimal image acquisition angle so that the color indices might not be affected by time, as well as the optimal time in relation to the angle.

The calculation of the correlation coefficients, their graphic representations, the determination of the regression equations for several variable functions and other calculations were done with Microsoft Excel. The polynomial regression equations were determined with PAST 3 [31]. For the graphic representations of the constant level curves and the algebraic calculus the Wolfram Alpha software was used.

3. Results

3.1. Subheadings Image Acquisition

The combination of the two variables against which the images were acquired, namely the time (6 different hours) and the angle (5 angles on the E-W axis), generated a set of 30 digital images of the same plant cover represented by the autumn wheat crop, Alex cultivar. From the image analysis performed with the ImageJ 1.48r software the spectral data specific to the r, g, and b bands were retrieved. Based on these data, the normalized rgb values and the INT (intensity), NDI (normalized difference index), and DGCI (dark green color index) indices used to characterize the plant cover were calculated. The results are given in

Table 1. Normalized r,g,b and indices values corresponding to the images acquired at different angles and times.

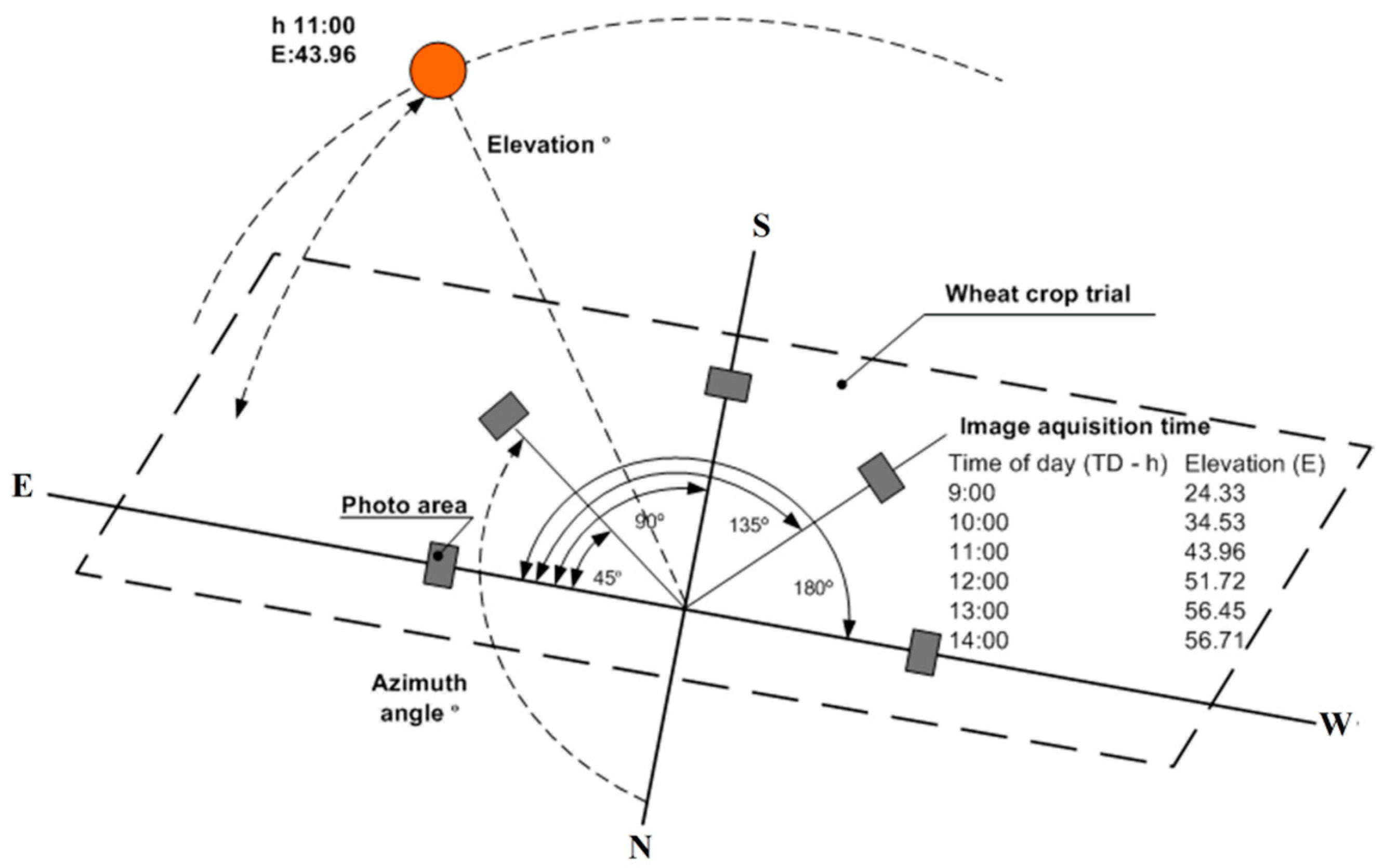
Time (GMT+3) (t)	Azimuth	Elevation	Angle (a)	r	g	b	INT	NDI	DGCI
9	96.63	24.51	0	0.330	0.530	0.139	73.570	−0.229	0.439
			45	0.341	0.517	0.143	64.567	−0.203	0.452
			90	0.323	0.486	0.191	72.433	−0.198	0.513
			135	0.311	0.447	0.242	82.303	−0.177	0.596
			180	0.293	0.455	0.253	64.137	−0.214	0.676
10	108.47	34.53	0	0.369	0.486	0.146	88.147	−0.136	0.383
			45	0.378	0.499	0.123	93.887	−0.136	0.339
			90	0.360	0.474	0.165	102.493	−0.135	0.382
			135	0.339	0.434	0.227	116.137	−0.122	0.466
			180	0.331	0.410	0.259	124.887	−0.105	0.521
11	122.96	43.96	0	0.350	0.471	0.179	95.430	−0.146	0.422
			45	0.369	0.498	0.132	102.140	−0.147	0.340
			90	0.360	0.486	0.154	103.690	−0.148	0.371
			135	0.337	0.450	0.212	107.593	−0.142	0.459
			180	0.325	0.415	0.259	120.507	−0.120	0.536
12	141.51	51.73	0	0.341	0.452	0.208	103.833	−0.138	0.459
			45	0.358	0.487	0.155	93.317	−0.152	0.391
			90	0.365	0.494	0.142	100.000	−0.149	0.359
			135	0.350	0.471	0.179	107.750	−0.145	0.399
			180	0.332	0.432	0.237	114.517	−0.130	0.490
13	165.24	56.46	0	0.329	0.429	0.243	107.740	−0.130	0.521
			45	0.344	0.465	0.191	100.110	−0.149	0.437
			90	0.358	0.486	0.156	102.200	−0.149	0.374
			135	0.359	0.484	0.157	109.273	−0.147	0.364
			180	0.337	0.450	0.213	109.933	−0.142	0.452
14	191.95	56.73	0	0.333	0.415	0.252	118.900	−0.109	0.510
			45	0.340	0.447	0.213	101.363	−0.134	0.472
			90	0.357	0.471	0.172	101.930	−0.136	0.394
			135	0.372	0.492	0.137	105.383	−0.137	0.334
			180	0.354	0.469	0.176	104.350	−0.138	0.391

.

The r, g, and b values series is highly heterogeneous. The variation coefficients obtained by relating the standard deviation to the value mean were 5.5% for r, 6.4% for g, and 22.9% for b. The same was found for the INT, NDI, and DGCI parameters that also had a high variation coefficient in absolute value (15.4%, 19.4%, and 18.15%). This implies a wide variety of color hues (Figure 4), which recovers the colors of the images acquired in the field based on the r, g, and b value set given in Table 1.

3.2. Normalized r,g,b—Time (t) Correlation at Different Angle (a)

Based on the data in Table 1, the data in

Table 2. Values of the coefficients of correlation between normalized r, g, and b and time (t) at different angles (a) of image acquisition.

Angle (a)	r	g	b
0	−0.395	−0.983	0.986
45	−0.395	−0.973	0.873
90	0.588	−0.192	−0.422
135	0.962	0.926	−0.993
180	0.879	0.473	−0.885

have been calculated, which provides the coefficients of linear correlation between the r and t series, then g and t series, respectively b and t series, for each shooting angle in part (a) separately.

Based on the data in Table 2, the expressions of Equations (4)–(6) describing the correlation coefficient variation with the angle were obtained, under very high correlation conditions. These were written as ${\mathrm{f}}_{\mathrm{r}}\left(\mathrm{a}\right),{\mathrm{f}}_{\mathrm{g}}\left(\mathrm{a}\right),{\mathrm{f}}_{\mathrm{b}}\left(\mathrm{a}\right)$ and their polynomial expressions were calculated with Past3. The graphical representations of the Equations (4) to (6) are represented on Figure 5.

$${\mathrm{f}}_{\mathrm{r}}\left(\mathrm{a}\right)=-0.4202-0.009315\mathrm{a}+0.000328{\mathrm{a}}^2-1.316·{10}^{-6}{\mathrm{a}}^3;$$

(4)

$${\mathrm{f}}_{\mathrm{g}}\left(\mathrm{a}\right)=-0.9615-0.02288\mathrm{a}+0.000557{\mathrm{a}}^2-2.143·{10}^{-6}{\mathrm{a}}^3;$$

(5)

$${\mathrm{f}}_{\mathrm{b}}\left(\mathrm{a}\right)=1.014+0.009792\mathrm{a}-0.0004187{\mathrm{a}}^2+1.703·{10}^{-6}{\mathrm{a}}^3;$$

(6)

The roots of Equations (7)–(9) simplified as ${\mathrm{f}}_{\mathrm{r}/\mathrm{g}/\mathrm{b}}\left(\mathrm{a}\right)=0$ (determined with Wolfram Alpha) and marked a_r, a_g, and a_b respectively will indicate the angle at which the correlation coefficient is zero, i.e., the optimal angle at which photos can be taken so that the color indices may not be affected by the image acquisition time. From these roots, only that which is close to angle (a) variation range, i.e., from 0° to 90°, will be chosen.

$${\mathrm{f}}_{\mathrm{r}}\left(\mathrm{a}\right)=0\iff -0.4202-0.009315\mathrm{a}+0.000328{\mathrm{a}}^2-1.316·{10}^{-6}{\mathrm{a}}^3=0\Rightarrow {\mathrm{a}}_{\mathrm{r}}=65.07°,$$

(7)

$${\mathrm{f}}_{\mathrm{g}}\left(\mathrm{a}\right)=0\iff -0.9615-0.02288\mathrm{a}+0.000557{\mathrm{a}}^2-2.143·{10}^{-6}{\mathrm{a}}^3=0\Rightarrow {\mathrm{a}}_{\mathrm{g}}=92.82°,$$

(8)

$${\mathrm{f}}_{\mathrm{b}}\left(\mathrm{a}\right)=0\iff 1.014+0.009792\mathrm{a}-0.0004187{\mathrm{a}}^2+1.703·{10}^{-6}{\mathrm{a}}^3=0\Rightarrow {\mathrm{a}}_{\mathrm{b}}=79.57°,$$

(9)

3.3. Normalized r,g,b—Angle (a) Correlation at Different Time (t)

The values of the coefficients of correlation between the series of r, g, and b values and the angle series (0°, 45°, 90°, 135°, 180°) were calculated similarly. In

Table 3. Values of the coefficients of correlation between normalized r, g, and b and angles (a) of image acquisition at different times of day (t).

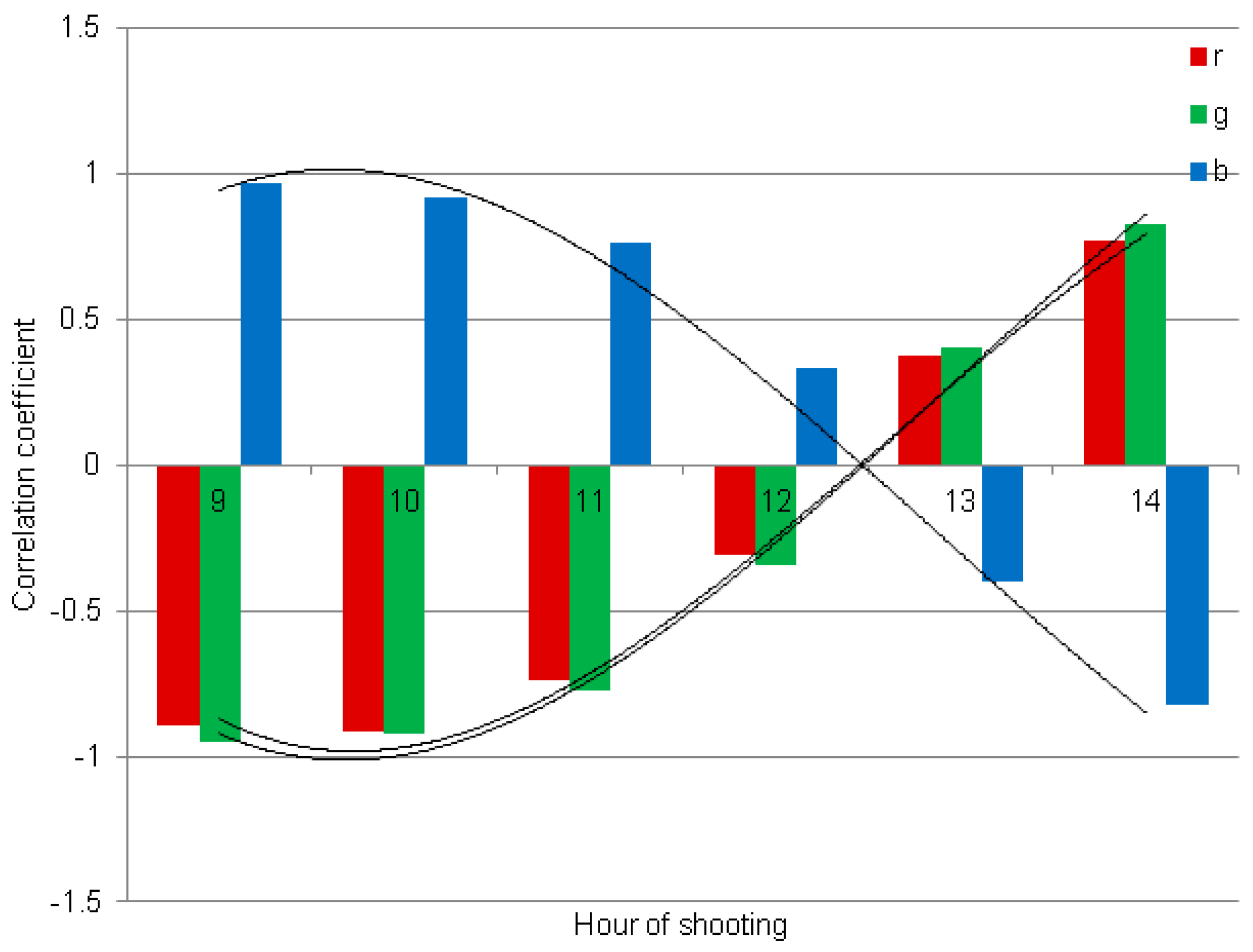
Time (GMT+2)	r	g	b
9	−0.892	−0.949	0.968
10	−0.915	−0.920	0.915
11	−0.737	−0.773	0.759
12	−0.313	−0.348	0.334
13	0.375	0.402	−0.398
14	0.767	0.828	−0.822

, the values of the correlation coefficients are given separately, on each row, to correspond to the image acquisition time.

The graphic representations of the equations describing the variation of the correlation coefficients with time marked h_r(t), h_g(t), h_b(t) (Figure 6), have the analytical expressions given in Equations (10)–(12). For all three equations, the value of the correlation coefficient was very high (0.99)

$${\mathrm{h}}_{\mathrm{r}}\left(\mathrm{t}\right)=37.9-10.12\mathrm{t}+0.8477{\mathrm{t}}^2-0.022244{\mathrm{t}}^3$$

(10)

$${\mathrm{h}}_{\mathrm{g}}\left(\mathrm{t}\right)=33.52-8.929\mathrm{t}+0.7394{\mathrm{t}}^2-0.01916{\mathrm{t}}^3$$

(11)

$${\mathrm{h}}_{\mathrm{b}}\left(\mathrm{t}\right)=-31.36+9.403\mathrm{t}-0.6974{\mathrm{t}}^2+0.01806{\mathrm{t}}^3$$

(12)

The roots of the ${\mathrm{h}}_{\mathrm{r}/\mathrm{g}/\mathrm{b}}\left(\mathrm{t}\right)=0$ equations that are close to the variation range of the studied time range (9–14, UTC+3), determined with the Wolfram Alpha software, will indicate the time when the correlation coefficient is zero, i.e., the optimal time at which the photos can be taken so that the color indices may not be affected by the acquisition angle. The following solutions (16) to Equations (13), (14) and (15) were obtained:

$${\mathrm{h}}_{\mathrm{r}}\left(\mathrm{t}\right)=0\iff 37.9-10.12\mathrm{t}+0.8477{\mathrm{t}}^2-0.02244{\mathrm{t}}^3=0,$$

(13)

$${\mathrm{h}}_{\mathrm{g}}\left(\mathrm{t}\right)=0\iff 33.52-8.929\mathrm{t}+0.7394{\mathrm{t}}^2-0.01916{\mathrm{t}}^3=0,$$

(14)

$${\mathrm{h}}_{\mathrm{b}}\left(\mathrm{t}\right)=0\iff -31.36+8.403\mathrm{t}-0.6974{\mathrm{t}}^2+0.01806{\mathrm{t}}^3=0,$$

(15)

$${\mathrm{t}}_{\mathrm{r}}=12.45\left(12\mathrm{h}27\mathrm{m}\right);{\mathrm{t}}_{\mathrm{g}}=12.47\left(12\mathrm{h}28\mathrm{m}\right);{\mathrm{t}}_{\mathrm{r}}=12.46\left(12\mathrm{h}27\mathrm{m}\right),$$

(16)

As an observation, the mathematical expressions of the correlation coefficients were third-degree polynomials, and the only roots of interest were those close to the studied variation range both for the time and the angle of image acquisition.

The r(a,t) dependence relationships in Equation (17), g(a,t) in Equation (18) and b(a,t) in Equation (19), between the normalized r, g, and b coefficients, the angle (a) value and the time (t) at which they were calculated were determined:

$$\mathrm{r}\left(\mathrm{a},\mathrm{t}\right)=-2.3·{10}^{-6}{\mathrm{a}}^2-0.003{\mathrm{t}}^2-0.00064\mathrm{a}+0.065021\mathrm{t}+8.55·{10}^{-5}\mathrm{at},$$

(17)

$$\mathrm{g}\left(\mathrm{a},\mathrm{t}\right)=-4·{10}^{-6}{\mathrm{a}}^2-0.00502{\mathrm{t}}^2-0.00117\mathrm{a}+0.09939\mathrm{t}+0.000151\mathrm{at},$$

(18)

$$\mathrm{b}\left(\mathrm{a},\mathrm{t}\right)=6.21·{10}^{-6}{\mathrm{a}}^2+0.000679{\mathrm{t}}^2+0.002212\mathrm{a}+0.008693\mathrm{t}-0.00027\mathrm{at},$$

(19)

The regression Equation (17) has a high correlation coefficient value (0.99), and the p values of each separate coefficient of the regression equation reach a maximum of p = 0.0104. For Equation (18), R² = 0.99, and p is smaller than p = 0.0255, respectively for Equation (19) (0.99) and p is smaller than p = 0.0300. In all situations, this provides statistical certainty at $\mathsf{\alpha }=0.05$ level (the calculations were done with Excel/Data analysis/Regression).

The optimal r value was determined for the optimal angle (a) values in Equations (7)–(9), and for the time (t) values in Equation (16), and the optimal values for the r, g, b in relation to time and angle are presented in Equations (20)–(22):

$${\mathrm{r}}_{\mathrm{o}}=\mathrm{r}\left({\mathrm{a}}_{\mathrm{o}},{\mathrm{t}}_{\mathrm{o}}\right)=\mathrm{r}\left(65.07,12.45\right)=0.3623,$$

(20)

$${\mathrm{g}}_{\mathrm{o}}=\mathrm{g}\left({\mathrm{a}}_{\mathrm{o}},{\mathrm{t}}_{\mathrm{o}}\right)=\mathrm{g}\left(92.82,12.47\right)=0.4904,$$

(21)

$${\mathrm{b}}_{\mathrm{o}}=\mathrm{b}\left({\mathrm{a}}_{\mathrm{o}},{\mathrm{t}}_{\mathrm{o}}\right)=\mathrm{b}\left(79.57,12.46\right)=0.1613,$$

(22)

3.4. Corrections Model

Subsequently, the problem was raised to determine the correction coefficients of the normalized r, g, and b values obtained for images acquired at other angles or times than those suggested as optimal in this study. To this end, the multiplication of the r(a,t), g(a,t) și b(a,t) values with the ρ_a,t, γ_a,t, and β_a,t correction coefficients was suggested to reach the optimal values, as shown in Equations (23)–(25):

$${\mathrm{r}}_{\mathrm{o}}=\mathrm{r}\left({\mathrm{a}}_{\mathrm{o}},{\mathrm{t}}_{\mathrm{o}}\right)=\mathrm{r}\left(\mathrm{a},\mathrm{t}\right)\times {\mathsf{\rho }}_{\mathrm{a},\mathrm{t}}\Rightarrow {\mathsf{\rho }}_{\mathrm{a},\mathrm{t}}=\frac{{\mathrm{r}}_{\mathrm{o}}}{\mathrm{r}\left(\mathrm{a},\mathrm{t}\right)},$$

(23)

$${\mathrm{g}}_{\mathrm{o}}=\mathrm{g}\left({\mathrm{a}}_{\mathrm{o}},{\mathrm{t}}_{\mathrm{o}}\right)=\mathrm{g}\left(\mathrm{a},\mathrm{t}\right)\times {\mathsf{\gamma }}_{\mathrm{a},\mathrm{t}}\Rightarrow {\mathsf{\gamma }}_{\mathrm{a},\mathrm{t}}=\frac{{\mathrm{g}}_{\mathrm{o}}}{\mathrm{g}\left(\mathrm{a},\mathrm{t}\right)},$$

(24)

$${\mathrm{b}}_{\mathrm{o}}=\mathrm{b}\left({\mathrm{a}}_{\mathrm{o}},{\mathrm{t}}_{\mathrm{o}}\right)=\mathrm{b}\left(\mathrm{a},\mathrm{t}\right)\times {\mathsf{\beta }}_{\mathrm{a},\mathrm{t}}\Rightarrow {\mathsf{\beta }}_{\mathrm{a},\mathrm{t}}=\frac{\mathrm{b}}{\mathrm{b}\left(\mathrm{a},\mathrm{t}\right)}$$

(25)

As an observation, ${\mathsf{\rho }}_{\mathrm{a},\mathrm{t}},{\mathsf{\gamma }}_{\mathrm{a},\mathrm{t}},{\mathsf{\beta }}_{\mathrm{a},\mathrm{t}}$ are two-dimensional matrices that include the correction coefficients for r, g, and b, and their values were calculated and are given in

Table 4. Matrix of ρ coefficients for r value correction.

Hour/Angle	0°	15°	30°	45°	60°	75°	90°
9	1.059023	1.054631	1.053435	1.055414	1.060604	1.069099	1.081059
10	1.034768	1.026829	1.021986	1.020152	1.021295	1.025435	1.032645
11	1.028831	1.017307	1.008937	1.003572	1.001119	1.001534	1.004825
12	1.040586	1.025066	1.012925	1.003938	0.997946	0.994843	0.994577
13	1.071283	1.050918	1.03436	1.021286	1.011452	1.00468	1.000851
14	1.124396	1.097702	1.07554	1.057439	1.043036	1.032052	1.024285

,

Table 5. Matrix of γ coefficients for g value correction.

Hour/Angle	0°	15°	30°	45°	60°	75°	90°
9	1.005337	1.001366	1.00109	1.004503	1.011682	1.022789	1.038083
10	0.997142	0.9887	0.98394	0.982757	0.985126	0.991097	1.000804
11	1.009517	0.996261	0.986909	0.981253	0.979167	0.980606	0.985601
12	1.044049	1.025002	1.01037	0.999804	0.993064	0.989997	0.990537
13	1.105488	1.078756	1.057373	1.040781	1.02857	1.020449	1.016231
14	1.203548	1.165623	1.13472	1.109916	1.09052	1.076022	1.06606

and

Table 6. Matrix of β coefficients for b value correction.

Hour/Angle	0°	15°	30°	45°	60°	75°	90°
9	1.211144	1.228411	1.219851	1.186519	1.132312	1.06291	0.984449
10	1.042227	1.083681	1.106936	1.109476	1.091017	1.053582	1.000974
11	0.907673	0.961616	1.004588	1.032773	1.043386	1.035318	1.009414
12	0.798488	0.858024	0.912503	0.958201	0.991399	1.009034	1.009351
13	0.7085	0.769565	0.830044	0.887002	0.936901	0.975969	1.000788
14	0.633347	0.693569	0.756407	0.819954	0.881494	0.937547	0.984149

.

Given that real difficulties may occur in practice when determining the exact angle at which images were acquired—for instance, some trips cannot be planned at previously established hours for time reasons (Figure 7) provides graphic representations of the constant level curves that indicate possible combinations between other angle and time values and may lead to r, g, and b values closer to the optimal values. The graphic representations were done with the Wolfram Alpha software. On these images, the suggested optimal values (relative to the stability of the image acquisition process) are marked with a dot. It is easy to notice that their positioning makes them different from the maximum values of the functions. Additionally, the areas around the optimal values to which r, g, and b tend if the angle or time is changed are colored differently. The spectral data-based characterization of vegetation stages, health status or various physiological parameters of plants in agricultural crops or biomass yield has become a common practice in agricultural technologies. Besides the classical satellite-based approach in crop characterization, a series of agricultural machinery have already been equipped with photo/video cameras or high-resolution sensors that capture real-time images of crops [32].

4. Discussion

The acquisition of crop images has often proved inconsistent and the color data are influenced by certain particularities. Studies dealing with such issues have recommended techniques and working models to improve color stability significantly [33,34]. Reflectance is high due to vegetation uniformity [35] and if the soil is not completely covered in vegetation, reflectance may have a dramatic influence on the RGB parameters and may reduce the quality of the correlation between the indices calculated based on spectral or RGB parameters and the nutritional status [24].

The multiple correlations between the plant color, chlorophyll content, and the health or nutritional status of plants show that imaging methods are adequate for agricultural applications [24,25,36]. Chlorophyll absorbs light and transfers light energy to trigger photochemical reactions. It is one of the photo chemically active compounds in photosynthesis. Chlorophyll quantity and quality are reflected in plant color; therefore sunlight is absorbed or reflected in different degrees. Crop reflectance depends on many environmental factors including incident illumination, the physiological status of the crop, and the calibration of the photographic reaction in fields in accordance with the reactions in the measured areas [16,20,21,37,38], and provides the basis for determining plant nutrition deficiencies. In this study, while the crop was uniform, we discovered a certain variation of the color parameters (r, b, and g) relative to the time and angle of image acquisition, following the change of the solar illumination angle in relation to the studied area. This case may occur in real practice, when images are acquired by agricultural machinery in real time, while wheat or other crops are being tended. Reflectance as influenced by the solar illumination angle in some crops has been dealt with in other studies as well [39,40,41,42]. The spectacular evolution of high-definition image acquisition methods in mobile telephony and the development of new mobile applications for the management of various agricultural aspects have created a new niche with great potential for improving applied agricultural research [14].

The literature of on this topic provides different approaches of image acquisition: spectral techniques and photographic techniques. The former (multispectral, hyper spectral imaging) records images to analyze crops and the plant cover with radio spectrographs especially in the visible and infrared range (400–1000 nm). The spectral indices calculated with the reflectance data have proved to have an indirect connection with the nutritional status and the biomass yield of many crops (maize, wheat, soy, cotton, and broccoli), the quantification of the degree of vegetation coverage, and agricultural efficiency [37,43,44,45,46,47,48,49,50,51]. Such techniques usually acquire images from considerable heights using satellites or aircraft and are especially helpful to monitor and analyze larger areas. This spectacular combination of space and imaging technology requires the involvement of governments or multinationals operating in larger farms.

The current technological progress of cameras combined with data storage, processing, and transmission technologies turn cameras and digital capture systems into valuable tools of sustainable, precise agriculture not only in the present, but also in the future. The technical specifications of photographic cameras, such as the optical and electronic parameters and image processing software quality, have reached a high performance level. Remarkable progress has been made in this field. Inexpensive commercial cameras with superior technical characteristics are now available [52]. The photographic techniques applied in visible or infrared ranges with high-definition cameras use RGB or other derived parameters at minimum cost affordable for small and medium-sized farms [13,24,27,52,53,54,55]. Digital camera captures images as a matrix of individual pixels that record the red (R), green (G), and blue (B) intensities. The RGB channels are subsequently used either to classify images or, if combined in spectral indices, to correlate with the relevant parameters [52,56].

RGB or spectral image analysis has been applied in agriculture not only for nutritional status assessment, but also for other purposes like weed identification [57], crop and weed mapping [58], crop and weed discrimination [59], quantification of turf grass color [30], quantitative analysis of specially variable physiological process across leaf surface [60], quantification of damage caused by various crop pathogens [61], seed color test for identification of qualitative and commercial seed traits [62], and research in the in vitro tissue cultures [56].

In both cases, the real research field is dynamic, the methodologies may overlap (multi-spectral photographic cameras), and as a general feature, all results are published faster than before and become available to agricultural practice and farmers [14].

Although wheat crops, given their economic importance, were among the first to be investigated by remote sensing and image analysis, applied research has employed mostly spectral methods and techniques [15,20,35,63,64,65,66], while the photographic techniques in the visible range are not so commonly used and developed afterwards, with the evolution of the photographic digital cameras [24,25,55].

This study has attempted to add to the known approaches the analysis of the influence of certain operational environmental parameters (time and angle) on the RGB image parameters (normalized r, g and b) resulting from the study of a wheat crop based on digital terrestrial images.

5. Conclusions

Following image acquisition in the field, it has been noticed that the time and the angle at which images were captured are the factors leading to different r, g, and b values. Their series were characterized by high variation coefficients (5, 6, 22% respectively), therefore the hues resulted after acquiring the image of the same subject differed. This could lead to false interpretations in the assessment of the physiological status of plants and crop wheat characterization based on color parameters data. As a result, a correction is required of the variation values of the two factors.

The determined constant level curves can provide important information about the selected angle-time combinations. If it is impossible to fall within ranges close to the optimal values, the optimal r, b, and g values can be estimated based on the multiplication with the calculated correction coefficients.

This study may describe only a particular case from among the numerous concrete situations provided by the combination of crop/directions/angle and solar light, but it can represent a calculation model for other particular cases in agricultural holdings.