Air Quality Monitoring Network Design Optimisation for Robust Land Use Regression Models
Abstract
:1. Introduction
2. Related Work
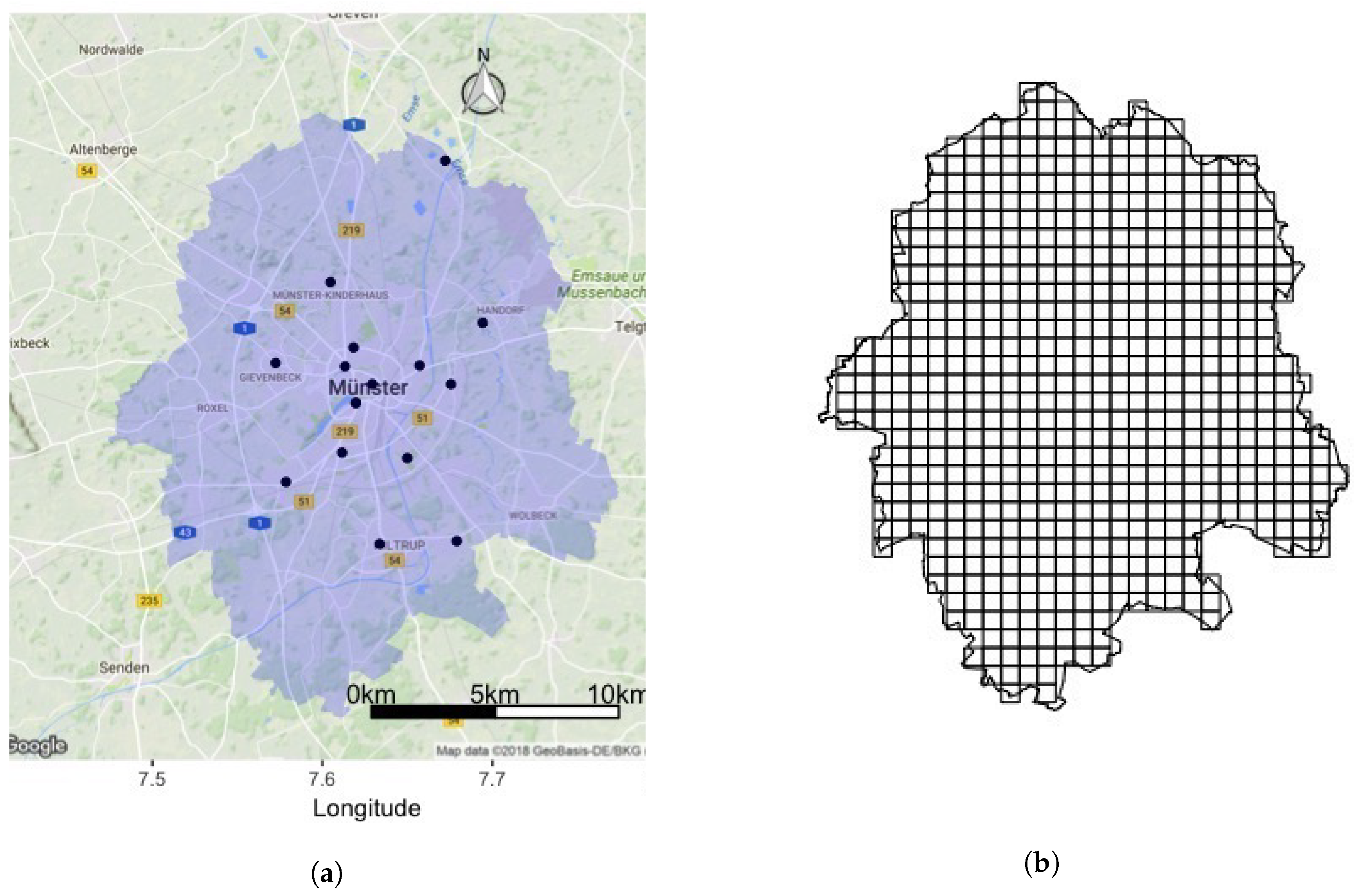
3. Material
- y is an n × 1 vector of air pollution concentration from monitoring sites at any particular time (in our case annual mean concentration at monitoring stations);
- X is an n × k matrix with observations of k independent variables for the n available air pollution monitoring stations;
- is a k × 1 vector of unknown parameters that we want to estimate; and
- is an n × 1 vector of errors, assumed to be independent and identically distributed.
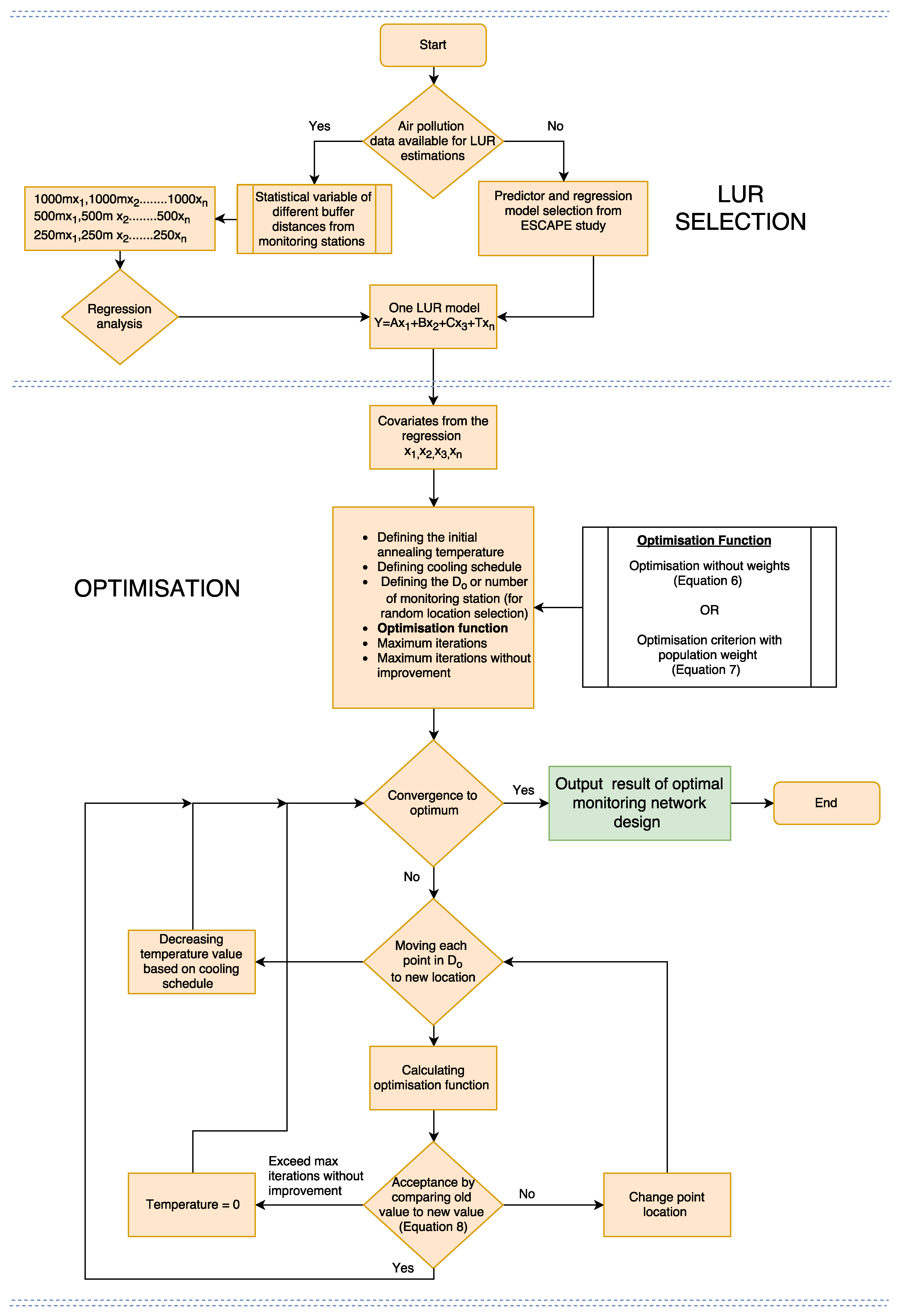
4. Method
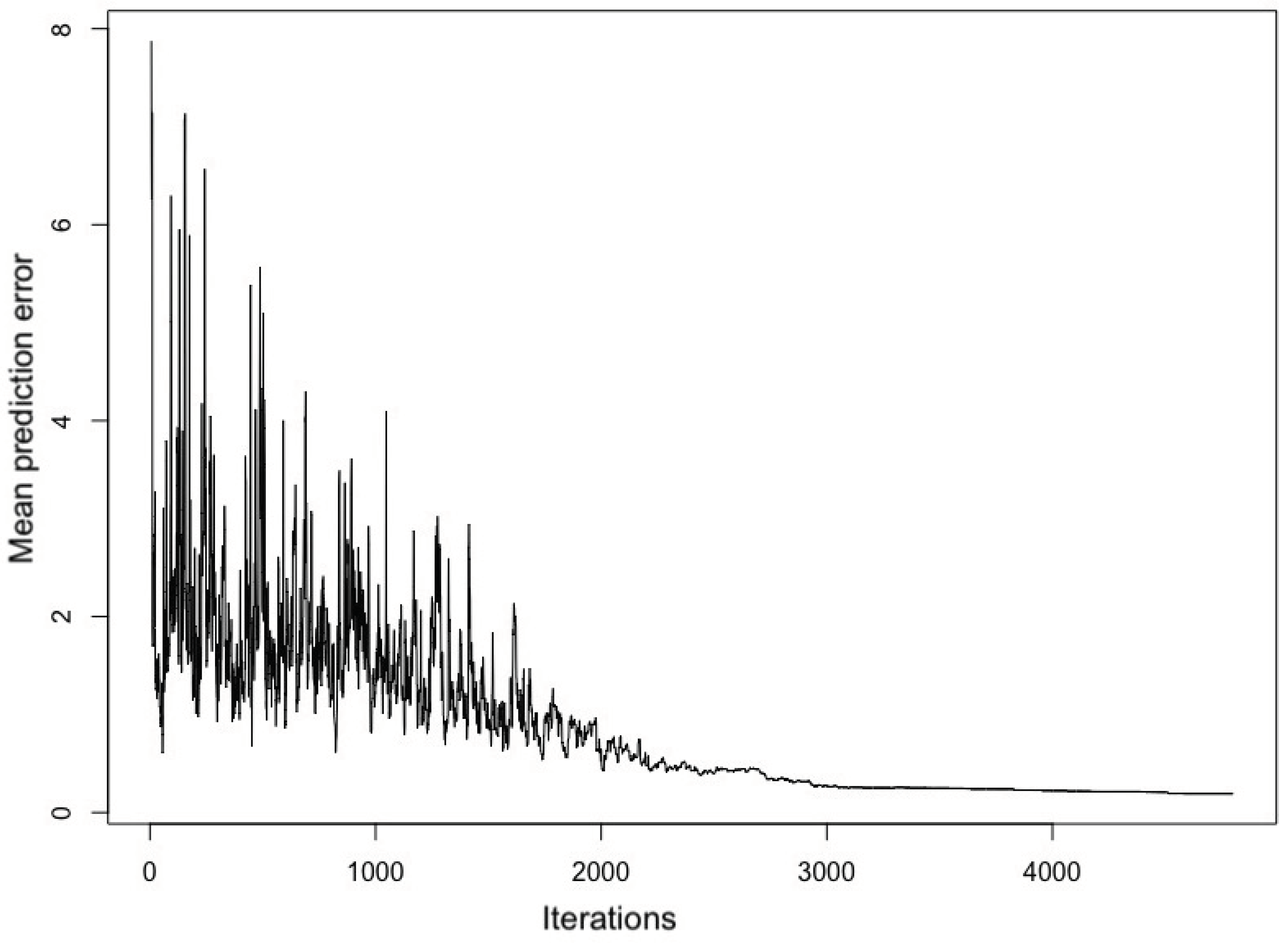
4.1. Spatial Simulated Annealing (SSA)
4.2. Optimisation Criterion Estimation
4.3. The Optimisation Procedure
- A LUR model is chosen for the study area by selecting predictors that explain the air pollutant considered.
- An initial (possibly existing) monitoring design is defined, consisting of n observations to be optimised.
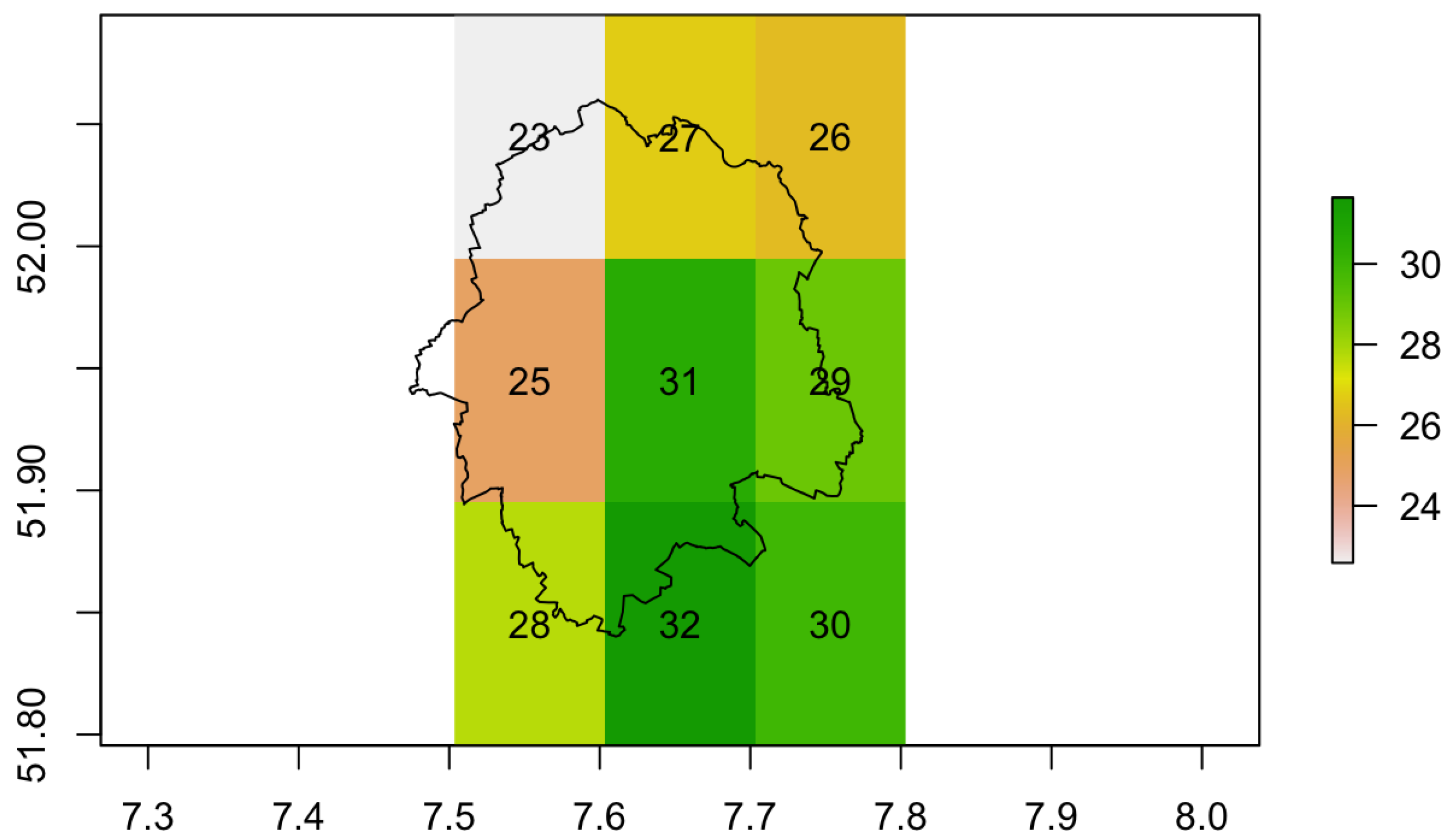
- The area of study A is discretised, the raster is defined with N raster nodes.
- is modified, returning a monitoring design and the new mean prediction error is calculated
- A new monitoring design is accepted if it reduced the optimisation criterion value or rejected as the basis for further optimisation based on Equation (8).
- The optimisation continues until the proposal monitoring designs are no longer accepted, based on energy transition and iteration parameters.
5. Results
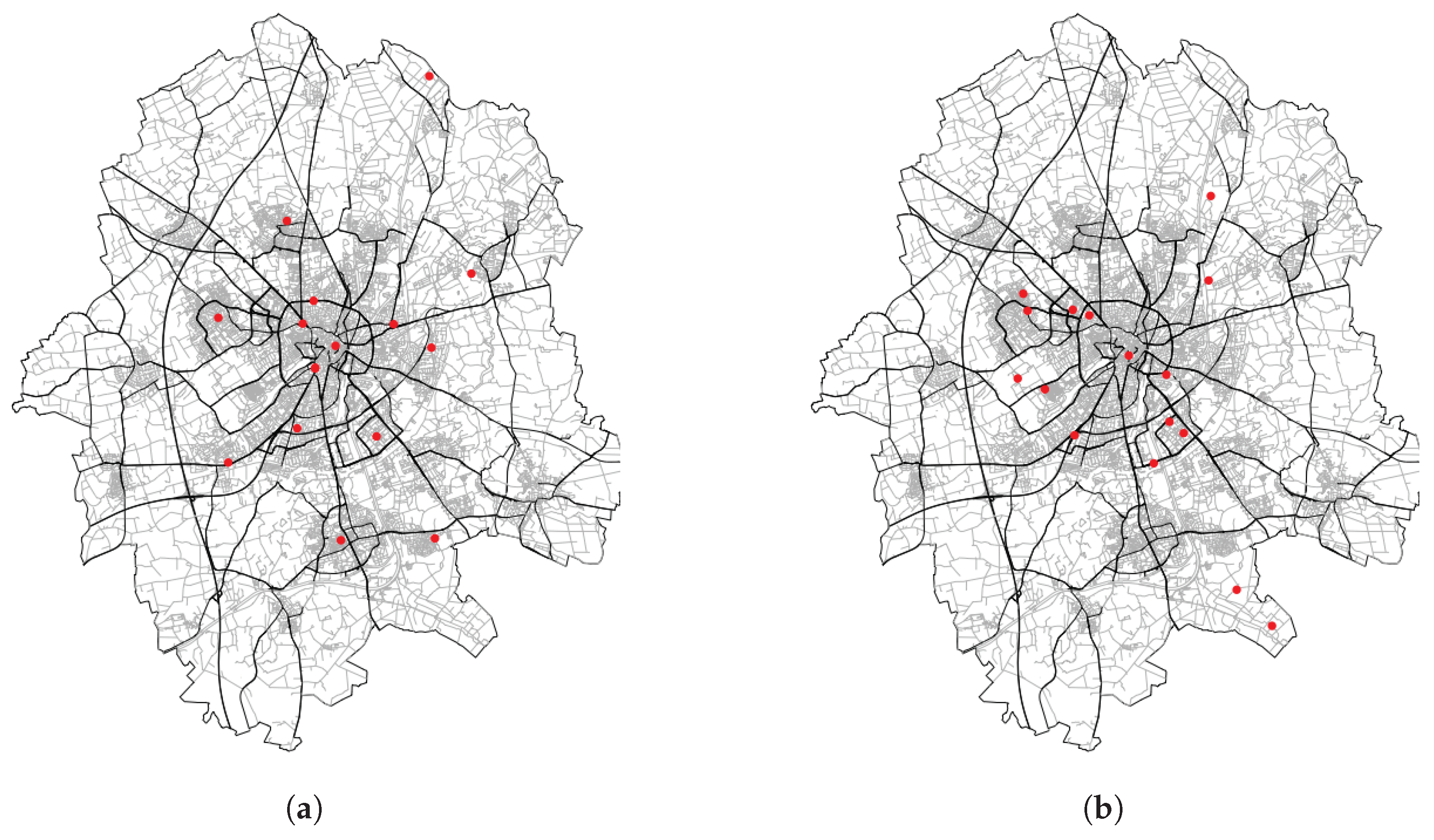
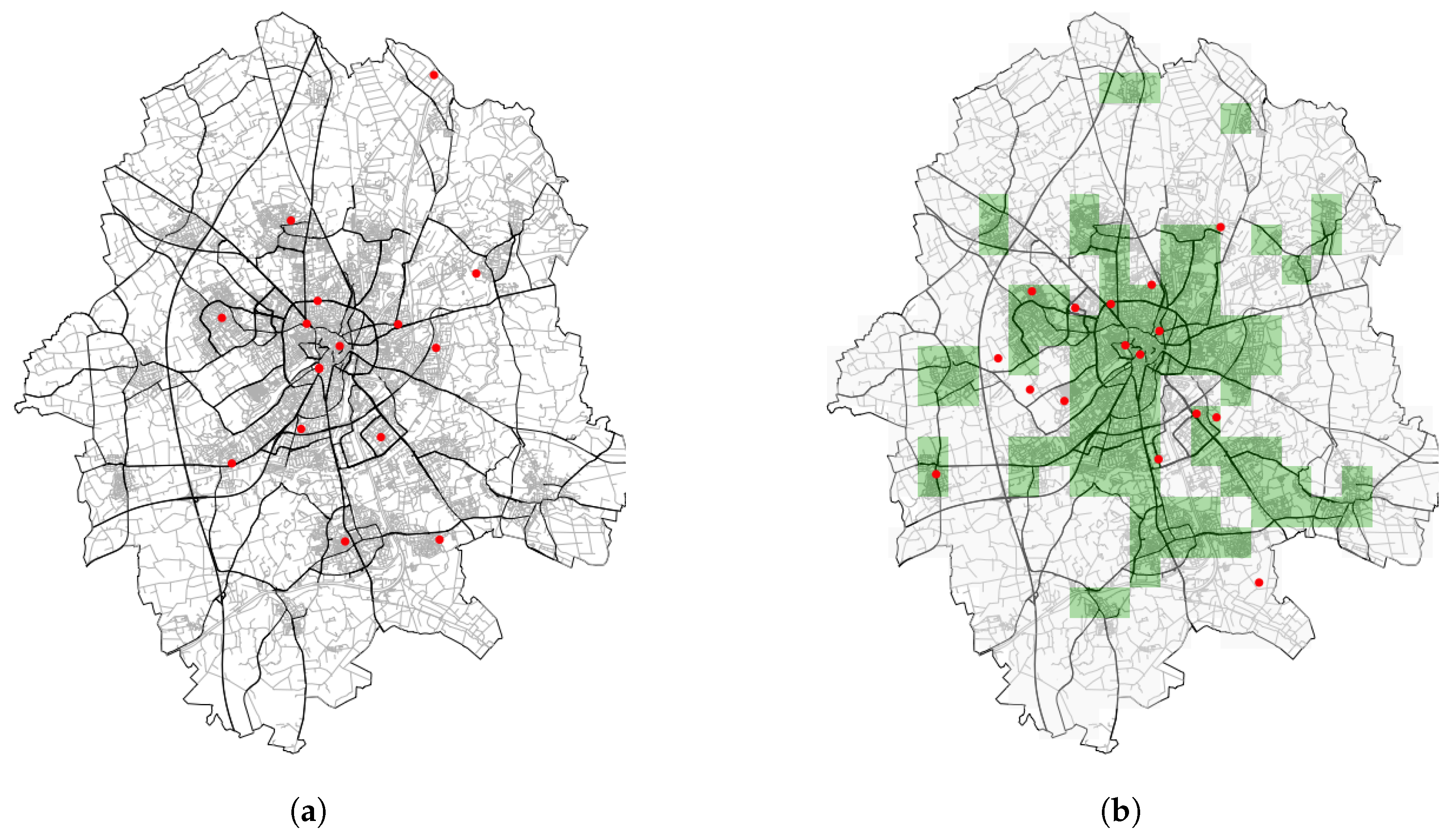
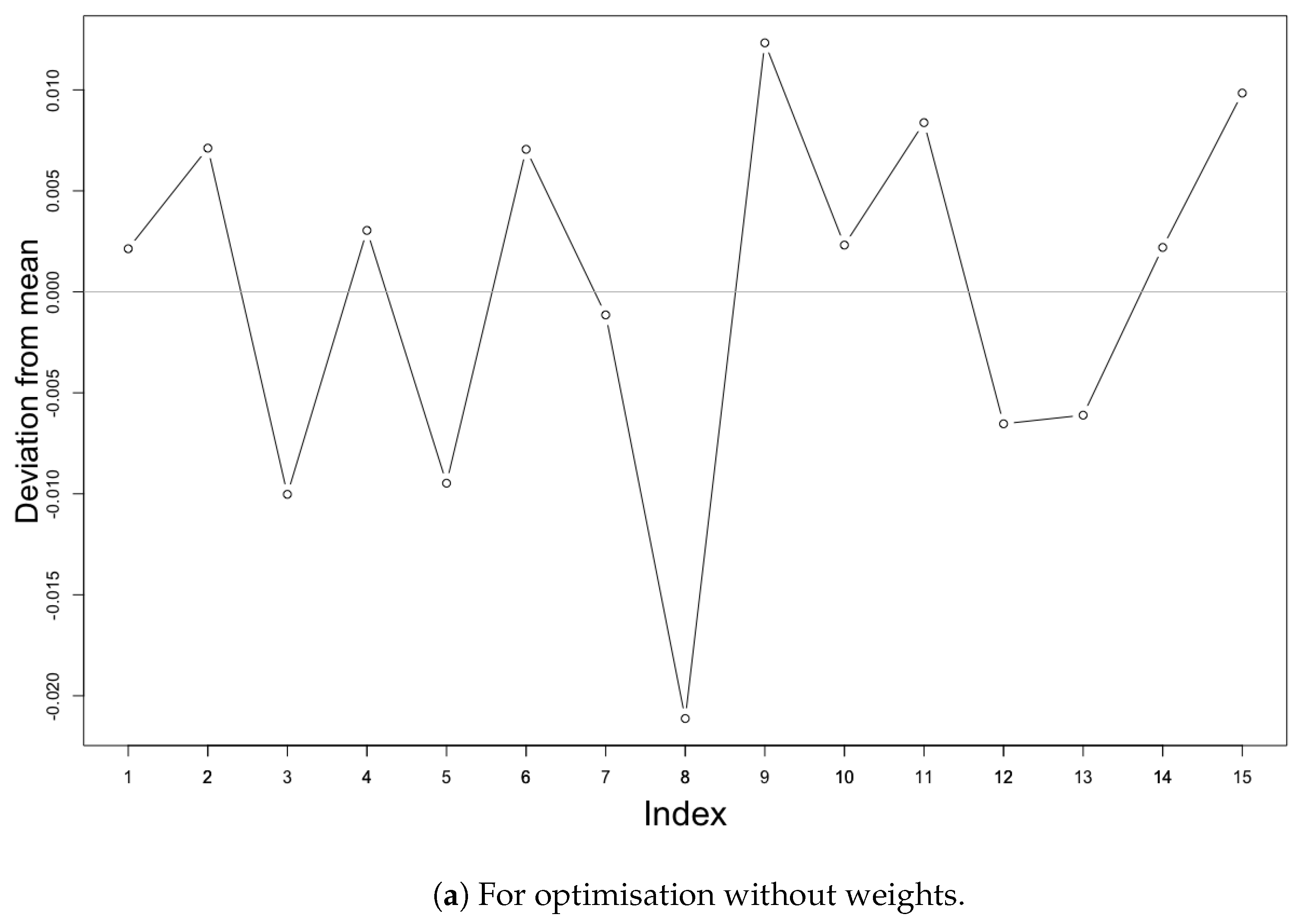
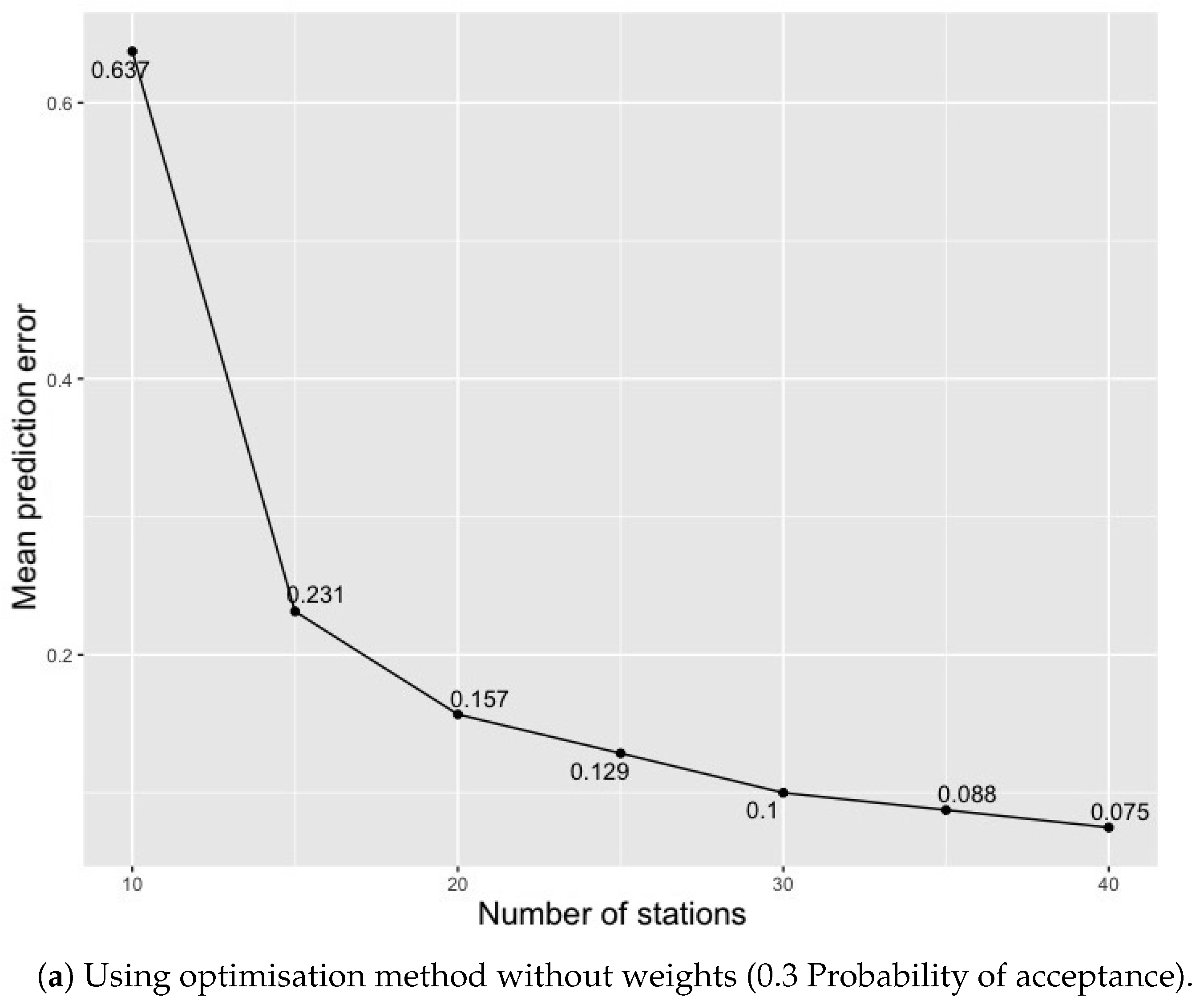
5.1. Optimisation without a Weighted Function for the Study Area
5.2. Optimisation with a Population Weighted Function for the Study Area
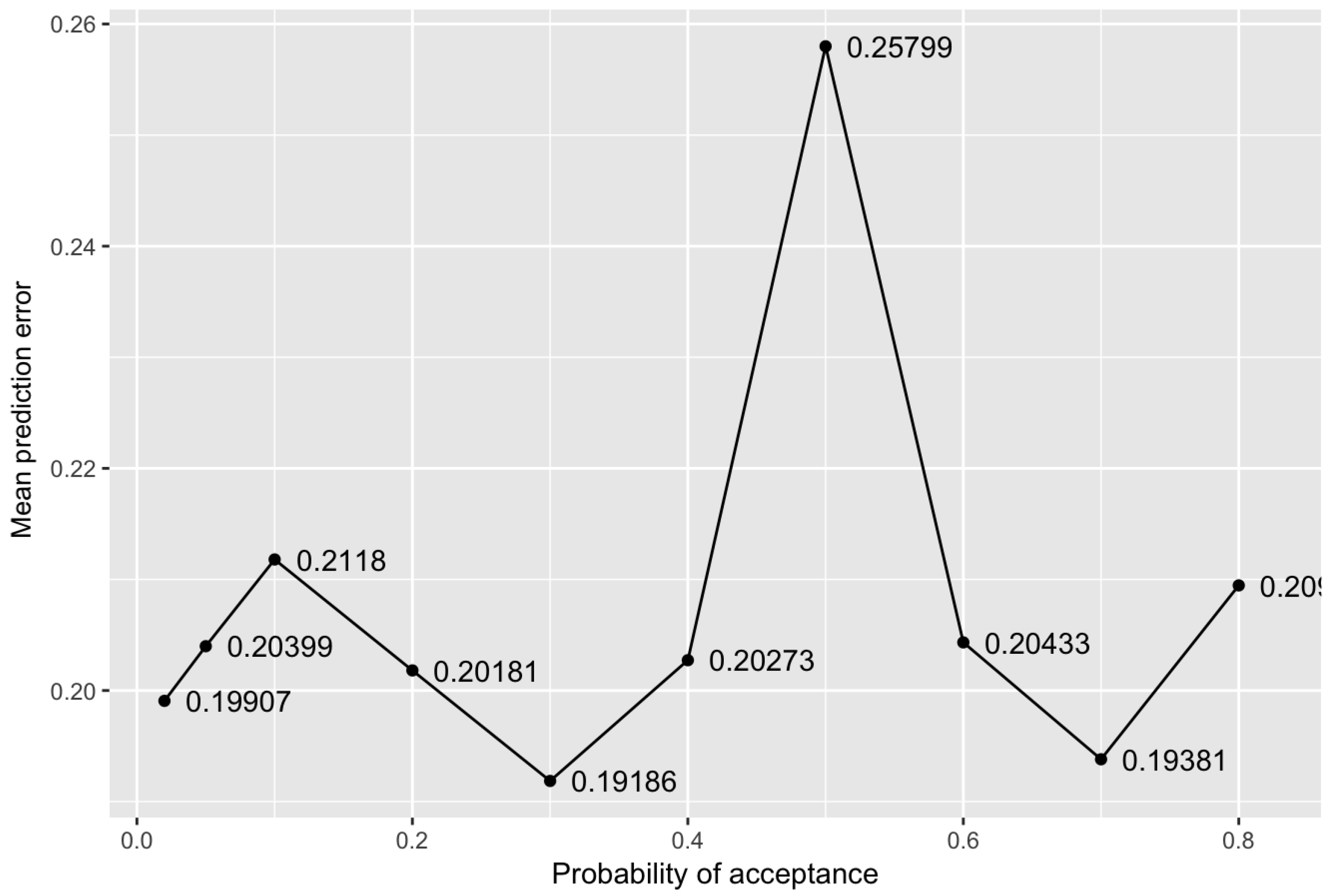
5.3. Sensitivity of the Optimisation Methods
5.4. Comparative Analysis
6. Discussion
Limitations and Future Work
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| MND | Monitoring Network Design |
| LUR | Land Use Regression |
| ESCAPE | European Study of Cohorts for Air Pollution Effects |
| OECD | Organisation for Economic Co-operation and Development |
| WHO | World Health Organisation |
| PM | Particulate Matter |
| EC | Elemental Carbon |
| Ozone | |
| CORINE | coordination of information on the environment |
Appendix A
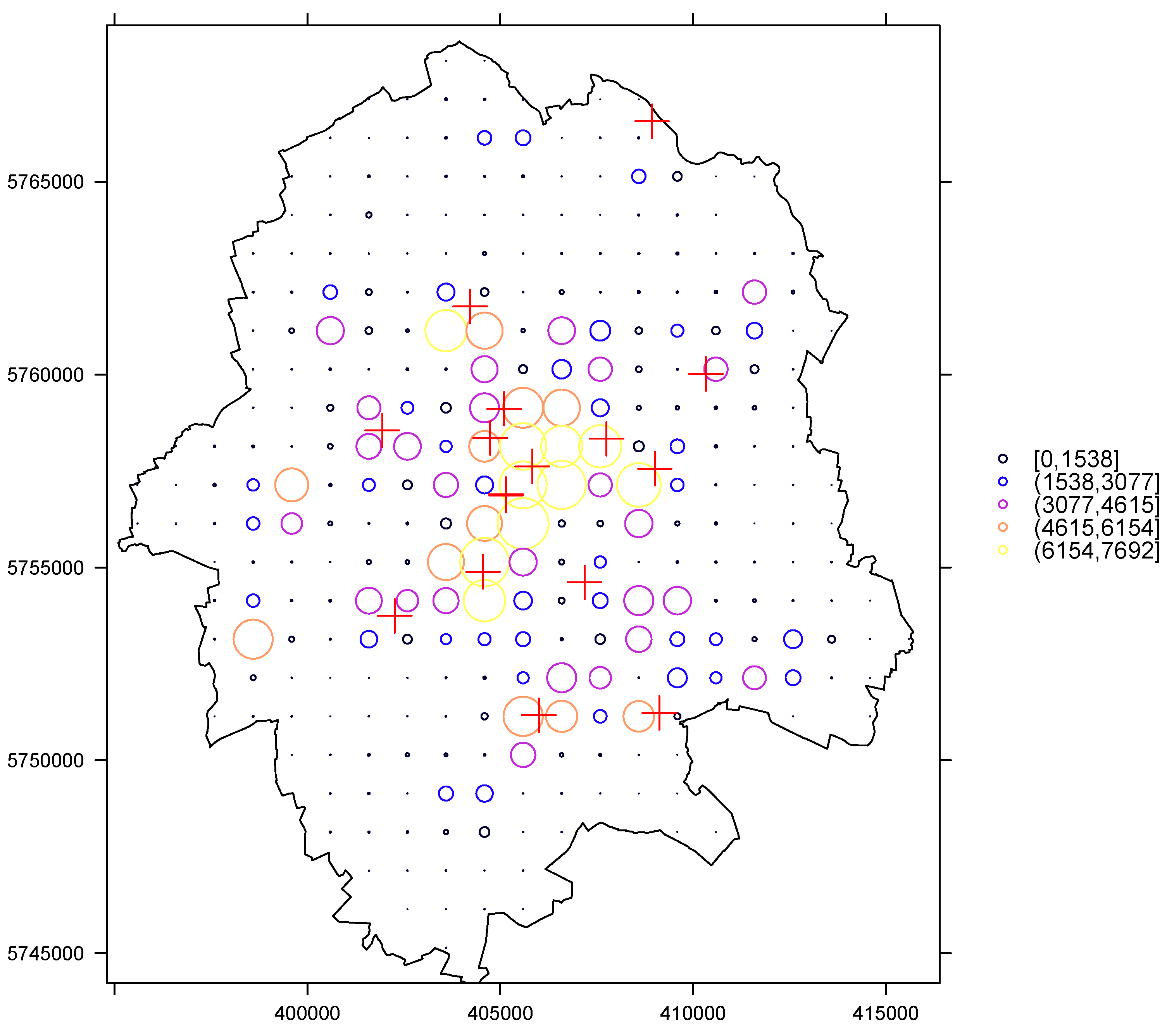
Appendix B
Appendix C
| Various other configurations realised during the study for different probability of acceptance | |
|---|---|
| Without weight optimisation | Population weighted optimisation |
 |  |
| Spatial mean prediction Error: 0.1990 | Spatial mean prediction Error: 404.57 |
 |  |
| Spatial mean prediction Error: 0.2039 | Spatial mean prediction Error: 363.34 |
 |  |
| Spatial mean prediction Error: 0.21179 | Spatial mean prediction Error: 332.86 |
 |  |
| Spatial mean prediction Error: 0.2018 | Spatial mean prediction Error: 370.25 |
 |  |
| Spatial mean prediction Error: 0.1918 | Spatial mean prediction Error: 385.52 |
 |  |
| Spatial mean prediction Error: 0.2027 | Spatial mean prediction Error:405.39 |
 |  |
| Spatial mean prediction Error: 0.2579 | Spatial mean prediction Error: 387.15 |
 |  |
| Spatial mean prediction Error: 0.2043 | Spatial mean prediction Error: 387.57 |
 |  |
| Spatial mean prediction Error: 0.19381 | Spatial mean prediction Error: 27798.28 |
 |  |
| Spatial mean prediction Error: 0.2094 | Spatial mean prediction Error: 333.96 |
References
- United Nations. World Urbanization Prospects: The 2014 Revision, Highlights. Department of Economic and Social Affairs; Population Division; United Nations: New York, NY, USA, 2014. [Google Scholar]
- Marchal, V.; Dellink, R.; Van Vuuren, D.; Clapp, C.; Chateau, J.; Magné, B.; van Vliet, J. OECD Environmental Outlook to 2050; Organization for Economic Co-operation and Development: Paris, France, 2011. [Google Scholar]
- Zivin, J.G.; Neidell, M. Air pollution’s hidden impacts. Science 2018, 359, 39–40. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef]
- Fugiel, A.; Burchart-Korol, D.; Czaplicka-Kolarz, K.; Smoliński, A. Environmental impact and damage categories caused by air pollution emissions from mining and quarrying sectors of European countries. J. Clean. Prod. 2017, 143, 159–168. [Google Scholar] [CrossRef]
- Zhang, Q.; Jiang, X.; Tong, D.; Davis, S.J.; Zhao, H.; Geng, G.; Feng, T.; Zheng, B.; Lu, Z.; Streets, D.G.; et al. Transboundary health impacts of transported global air pollution and international trade. Nature 2017, 543, 705. [Google Scholar] [CrossRef] [PubMed]
- WHO. Global Platform on Air Quality and Health. Available online: http://www.who.int/phe/health_topics/outdoorair/global_platform/en/ (accessed on 1 May 2018).
- Jerrett, M.; Arain, M.A.; Kanaroglou, P.; Beckerman, B.; Crouse, D.; Gilbert, N.L.; Brook, J.R.; Finkelstein, N.; Finkelstein, M.M. Modeling the intraurban variability of ambient traffic pollution in Toronto, Canada. J. Toxicol. Environ. Health Part A 2007, 70, 200–212. [Google Scholar] [CrossRef] [PubMed]
- Khreis, H.; Kelly, C.; Tate, J.; Parslow, R.; Lucas, K.; Nieuwenhuijsen, M. Exposure to traffic-related air pollution and risk of development of childhood asthma: A systematic review and meta-analysis. Environ. Int. 2017, 100, 1–31. [Google Scholar] [CrossRef] [PubMed]
- McConnell, R.; Islam, T.; Shankardass, K.; Jerrett, M.; Lurmann, F.; Gilliland, F.; Gauderman, J.; Avol, E.; Künzli, N.; Yao, L.; et al. Childhood incident asthma and traffic-related air pollution at home and school. Environ. Health Perspect. 2010, 118, 1021. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Health Effects Institute. Panel on the Health Effects of Traffic-Related Air Pollution. Traffic-Related Air Pollution: A Critical Review of the Literature on Emissions, Exposure, and Health Effects; Number 17; Health Effects Institute: Cambridge, MA, USA, 2010. [Google Scholar]
- Charpin, D.; Caillaud, D.M. Air pollution and the nose chronic respiratory disorders. In The Nose and Sinuses in Respiratory Disorders ERS Monograph; European Respiratory Society: Polymouth, UK, 2017; Volume 76, p. 162. [Google Scholar]
- Mayer, H. Air pollution in cities. Atmos. Environ. 1999, 33, 4029–4037. [Google Scholar] [CrossRef]
- Conti, G.O.; Heibati, B.; Kloog, I.; Fiore, M.; Ferrante, M. A review of AirQ Models and their applications for forecasting the air pollution health outcomes. Environ. Sci. Pollut. Res. 2017, 24, 6426–6445. [Google Scholar] [CrossRef] [PubMed]
- Bougoudis, I.; Demertzis, K.; Iliadis, L.; Anezakis, V.D.; Papaleonidas, A. FuSSFFra, a fuzzy semi-supervised forecasting framework: the case of the air pollution in Athens. Neural Comput. Appl. 2018, 29, 375–388. [Google Scholar] [CrossRef]
- Bougoudis, I.; Demertzis, K.; Iliadis, L. Fast and low cost prediction of extreme air pollution values with hybrid unsupervised learning. Integr. Comput.-Aided Eng. 2016, 23, 115–127. [Google Scholar] [CrossRef]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM2. 5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Briggs, D. The role of GIS: Coping with space (and time) in air pollution exposure assessment. J. Toxicol. Environ. Health Part A 2005, 68, 1243–1261. [Google Scholar] [CrossRef] [PubMed]
- Beelen, R.; Hoek, G.; Vienneau, D.; Eeftens, M.; Dimakopoulou, K.; Pedeli, X.; Tsai, M.Y.; Künzli, N.; Schikowski, T.; Marcon, A.; et al. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe–the ESCAPE project. Atmos. Environ. 2013, 72, 10–23. [Google Scholar] [CrossRef]
- European Parliament and Council of the European Union. Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on ambient air quality and cleaner air for Europe. Off. J. Eur. Union 2008, L 152/1–L 152/43. [Google Scholar]
- Raffuse, S.; Sullivan, D.; McCarthy, M.; Penfold, B.; Hafner, H. Ambient air monitoring network assessment guidance, analytical techniques for technical assessments of ambient air monitoring networks. Retrieved July 2007, 20, 2007. [Google Scholar]
- Ott, D.K.; Kumar, N.; Peters, T.M. Passive sampling to capture spatial variability in PM10–2.5. Atmos. Environ. 2008, 42, 746–756. [Google Scholar] [CrossRef]
- Goldstein, I.F.; Landovitz, L. Analysis of air pollution patterns in New York City—I. Can one station represent the large metropolitan area? Atmos. Environ. (1967) 1977, 11, 47–52. [Google Scholar] [CrossRef]
- Kanaroglou, P.S.; Jerrett, M.; Morrison, J.; Beckerman, B.; Arain, M.A.; Gilbert, N.L.; Brook, J.R. Establishing an air pollution monitoring network for intra-urban population exposure assessment: A location-allocation approach. Atmos. Environ. 2005, 39, 2399–2409. [Google Scholar] [CrossRef]
- Nejadkoorki, F.; Nicholson, K.; Hadad, K. The design of long-term air quality monitoring networks in urban areas using a spatiotemporal approach. Environ. Monit. Assess. 2011, 172, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Kuhlbusch, T.A.; Quass, U.; Fuller, G.; Viana, M.; Querol, X.; Katsouyanni, K.; Quincey, P. Air pollution monitoring strategies and technologies for urban areas. In Urban Air Quality in Europe; Springer: Berlin/Heidelberg, Germany, 2013; pp. 277–296. [Google Scholar]
- Mofarrah, A.; Husain, T. A holistic approach for optimal design of air quality monitoring network expansion in an urban area. Atmos. Environ. 2010, 44, 432–440. [Google Scholar] [CrossRef]
- Wu, L.; Bocquet, M.; Chevallier, M. Optimal reduction of the ozone monitoring network over France. Atmos. Environ. 2010, 44, 3071–3083. [Google Scholar] [CrossRef]
- Benis, K.Z.; Fatehifar, E.; Shafiei, S.; Nahr, F.K.; Purfarhadi, Y. Design of a sensitive air quality monitoring network using an integrated optimization approach. Stoch. Environ. Res. Risk Assess. 2016, 30, 779–793. [Google Scholar] [CrossRef]
- Elkamel, A.; Fatehifar, E.; Taheri, M.; Al-Rashidi, M.; Lohi, A. A heuristic optimization approach for Air Quality Monitoring Network design with the simultaneous consideration of multiple pollutants. J. Environ. Manag. 2008, 88, 507–516. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Zhao, H.; Ding, Y.; Li, T.; Hou, L.; Sun, F. Optimization of air pollutant monitoring stations with constraints using genetic algorithm. J. High Speed Netw. 2015, 21, 141–153. [Google Scholar] [CrossRef]
- Van Groenigen, J.W. Constrained Optimisation of Spatial Sampling: A Geostatistical Approach. Ph.D. Thesis, Wageningen University and Research, Wageningen, The Netherlands, 1999. [Google Scholar]
- Sarigiannis, D.A.; Saisana, M. Multi-objective optimization of air quality monitoring. Environ. Monit. Assess. 2008, 136, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Kao, J.J.; Hsieh, M.R. Utilizing multiobjective analysis to determine an air quality monitoring network in an industrial district. Atmos. Environ. 2006, 40, 1092–1103. [Google Scholar] [CrossRef]
- Hoek, G.; Beelen, R.; De Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Marshall, J.D.; Nethery, E.; Brauer, M. Within-urban variability in ambient air pollution: comparison of estimation methods. Atmos. Environ. 2008, 42, 1359–1369. [Google Scholar] [CrossRef]
- Ryan, P.H.; LeMasters, G.K. A review of land-use regression models for characterising intraurban air pollution exposure. Inhal. Toxicol. 2007, 19, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Reis, S.; Lin, C.; Heal, M.R. Effect of monitoring network design on land use regression models for estimating residential NO2 concentration. Atmos. Environ. 2017, 149, 24–33. [Google Scholar] [CrossRef]
- Colette, A.; Andersson, C.; Manders, A.; Mar, K.; Mircea, M.; Pay, M.T.; Raffort, V.; Tsyro, S.; Cuvelier, C.; Adani, M.; et al. EURODELTA-Trends, a multi-model experiment of air quality hindcast in Europe over 1990–2010. Geosci. Model Dev. 2017, 10, 3255. [Google Scholar] [CrossRef]
- Brokamp, C.; Jandarov, R.; Rao, M.; LeMasters, G.; Ryan, P. Exposure assessment models for elemental components of particulate matter in an urban environment: A comparison of regression and random forest approaches. Atmos. Environ. 2017, 151, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Basagaña, X.; Rivera, M.; Aguilera, I.; Agis, D.; Bouso, L.; Elosua, R.; Foraster, M.; de Nazelle, A.; Nieuwenhuijsen, M.; Vila, J.; et al. Effect of the number of measurement sites on land use regression models in estimating local air pollution. Atmos. Environ. 2012, 54, 634–642. [Google Scholar] [CrossRef]
- Wang, M.; Beelen, R.; Eeftens, M.; Meliefste, K.; Hoek, G.; Brunekreef, B. Systematic evaluation of land use regression models for NO2. Environ. Sci. Technol. 2012, 46, 4481–4489. [Google Scholar] [CrossRef] [PubMed]
- Contributors, O. Planet Dump Retrieved from https://planet.osm.org. Available online: https://www.openstreetmap.org (accessed on 1 May 2018).
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Ann. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Röösli, M.; Braun-Fährlander, C.; Künzli, N.; Oglesby, L.; Theis, G.; Camenzind, M.; Mathys, P.; Staehelin, J. Spatial variability of different fractions of particulate matter within an urban environment and between urban and rural sites. J. Air Waste Manag. Assoc. 2000, 50, 1115–1124. [Google Scholar] [CrossRef] [PubMed]
- De Gruijter, J.; Brus, D.J.; Bierkens, M.F.P.; Knotters, M. Sampling for Natural Resource Monitoring; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Lark, R.M. Optimized spatial sampling of soil for estimation of the variogram by maximum likelihood. Geoderma 2002, 105, 49–80. [Google Scholar] [CrossRef]
- Boer, E.P.J.; Dekkers, A.L.M.; Stein, A. Optimization of a monitoring network for sulfur dioxide. J. Environ. Qual. 2002, 31, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Brus, D.J.; Heuvelink, G.B.M. Optimization of sample patterns for universal kriging of environmental variables. Geoderma 2007, 138, 86–95. [Google Scholar] [CrossRef]
- Wang, J.; Ge, Y.; Heuvelink, G.B.M.; Zhou, C. Spatial sampling design for estimating regional GPP with spatial heterogeneities. IEEE Geosci. Remote Sens. Lett. 2014, 11, 539–543. [Google Scholar] [CrossRef]
- Wadoux, A.M.C.; Brus, D.J.; Rico-Ramirez, M.A.; Heuvelink, G.B. Sampling design optimisation for rainfall prediction using a non-stationary geostatistical model. Adv. Water Resour. 2017, 107, 126–138. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Jiang, Z.; De Bruin, S.; Twenhöfel, C.J.W. Optimization of mobile radioactivity monitoring networks. Int. J. Geogr. Inf. Sci. 2010, 24, 365–382. [Google Scholar] [CrossRef]
- Pebesma, E.; Bivand, R.; Rowlingson, B.; Gomez-Rubio, V.; Hijmans, R.; Sumner, M.; MacQueen, D.; Lemon, J.; O’Brien, J.; O’Rourke, J. sp: Classes and Methods for Spatial Data in R. 2015. Available online: https://cran.r-project.org/web/packages/sp/index.html (accessed on 5 May 2018).
- Pebesma, E.; Bivand, R.; Racine, E.; Sumner, M.; Cook, I.; Keitt, T.; Lovelace, R.; Wickham, H.; Ooms, J.; Müller, K. sf: Simple Features for R. R package version 0.5-5. 2018. Available online: https://CRAN.R-project.org/package=sf (accessed on 5 May 2018).
- Samuel-Rosa, A.; dos Anjos, L.H.C.; de Mattos Vasques, G.; Heuvelink, G.B.M.; Pebesma, E.; Skoien, J.; French, J.; Roudier, P.; Brus, D.; Lark, M. Package ‘spsann’. 2017. Available online: https://cran.r-project.org/web/packages/spsann/spsann.pdf (accessed on 23 June 2017).
- Gupta, S. AQ-MND Optimisation. Available online: https://github.com/geohealthshivam/AQ-MND-optimisation (accessed on 1 May 2018).
- Gupta, S.; Mateu, J.; Degbelo, A.; Pebesma, E. Quality of life, big data and the power of statistics. Stat. Probab. Lett. 2018, in press. [Google Scholar] [CrossRef]
- Wang, J.F.; Stein, A.; Gao, B.B.; Ge, Y. A review of spatial sampling. Spat. Stat. 2012, 2, 1–14. [Google Scholar] [CrossRef]
- Johnson, M.; Isakov, V.; Touma, J.; Mukerjee, S.; Özkaynak, H. Evaluation of land-use regression models used to predict air quality concentrations in an urban area. Atmos. Environ. 2010, 44, 3660–3668. [Google Scholar] [CrossRef]
- Allen, R.W.; Amram, O.; Wheeler, A.J.; Brauer, M. The transferability of NO and NO2 land use regression models between cities and pollutants. Atmos. Environ. 2011, 45, 369–378. [Google Scholar] [CrossRef]
- Beelen, R.; Hoek, G.; Pebesma, E.; Vienneau, D.; de Hoogh, K.; Briggs, D.J. Mapping of background air pollution at a fine spatial scale across the European Union. Sci. Total Environ. 2009, 407, 1852–1867. [Google Scholar] [CrossRef] [PubMed]
- Clements, A.L.; Griswold, W.G.; Johnston, J.E.; Herting, M.M.; Thorson, J.; Collier-Oxandale, A.; Hannigan, M. Low-Cost Air Quality Monitoring Tools: From Research to Practice (A Workshop Summary). Sensors 2017, 17, 2478. [Google Scholar] [CrossRef] [PubMed]



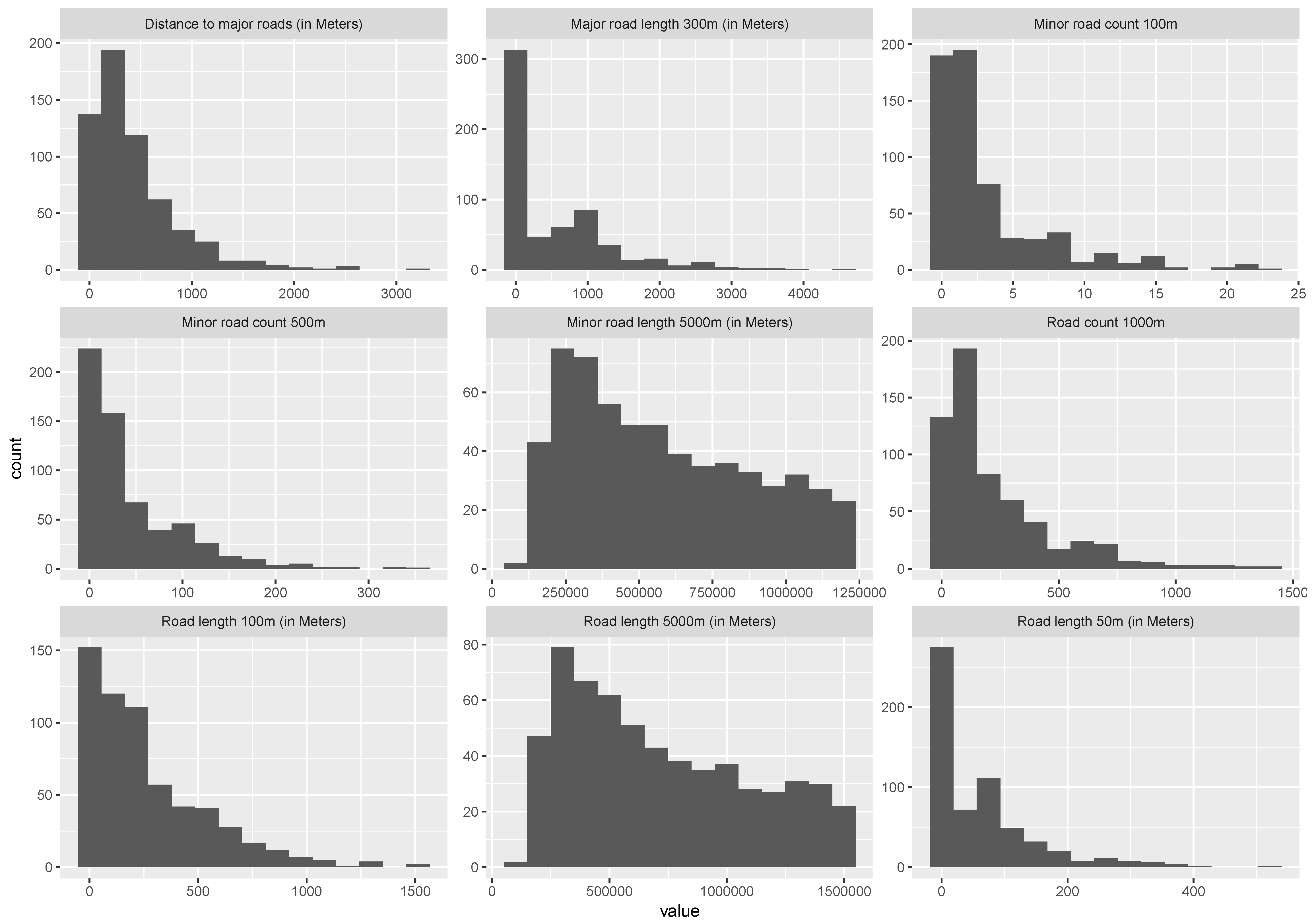
| Variable | Variable Description |
|---|---|
| rdcount_1000 | Road count in 1000 m buffer |
| minrdcount_100 | Minor road count in 100 m buffer |
| minrdcount_500 | Minor road count in 500 m buffer |
| rdlength_100 | Road length count in 100 m buffer |
| rdlength_5000 | Road length count in 5000 m buffer |
| rdlength_50 | Road length count in 50 m buffer |
| mjrdlength_300 | Major road length count in 300 m buffer |
| dist.mjrd | Distance to major roads |
| minrdlength_5000 | Minor road count in 5000 m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, S.; Pebesma, E.; Mateu, J.; Degbelo, A. Air Quality Monitoring Network Design Optimisation for Robust Land Use Regression Models. Sustainability 2018, 10, 1442. https://doi.org/10.3390/su10051442
Gupta S, Pebesma E, Mateu J, Degbelo A. Air Quality Monitoring Network Design Optimisation for Robust Land Use Regression Models. Sustainability. 2018; 10(5):1442. https://doi.org/10.3390/su10051442
Chicago/Turabian StyleGupta, Shivam, Edzer Pebesma, Jorge Mateu, and Auriol Degbelo. 2018. "Air Quality Monitoring Network Design Optimisation for Robust Land Use Regression Models" Sustainability 10, no. 5: 1442. https://doi.org/10.3390/su10051442





