Stand-Alone Battery Thermal Management for Fast Charging of Electric Two Wheelers—Integrated Busbar Cooling †
Abstract
:1. Introduction
2. State of the Art
2.1. Automotive Battery Cooling Systems
2.2. Air Cooling in Electric Two-Wheelers
3. Stand-Alone Battery Thermal Management
3.1. Integration of Battery Thermal Management in Drivetrain Cooling Circuits
3.2. Increasing the Performance and Efficiency and Using Alternative Refrigerants
3.3. Noise Reduction
3.4. Reduction of Refrigerant Charge
3.5. Decreased Water Condensation on Cooling Structures
3.6. Additional Components
3.7. Flammability of Alternative Refrigerants
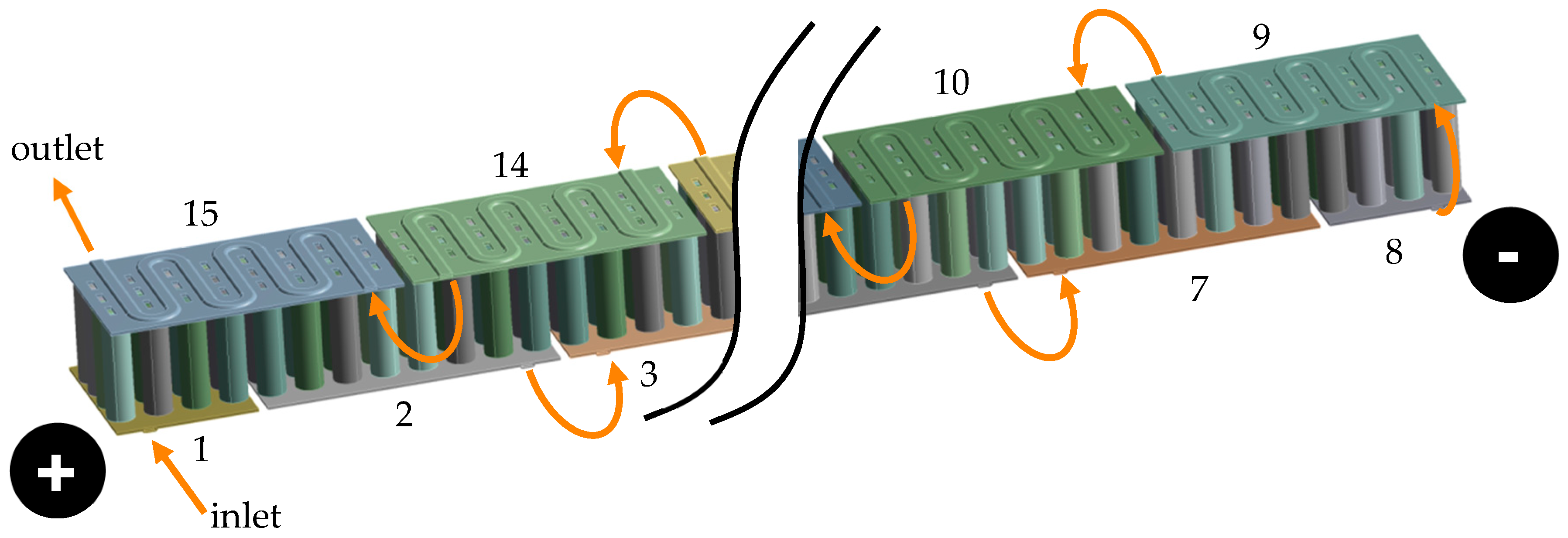
4. Integrated Busbar Cooling
4.1. Boundary Conditions
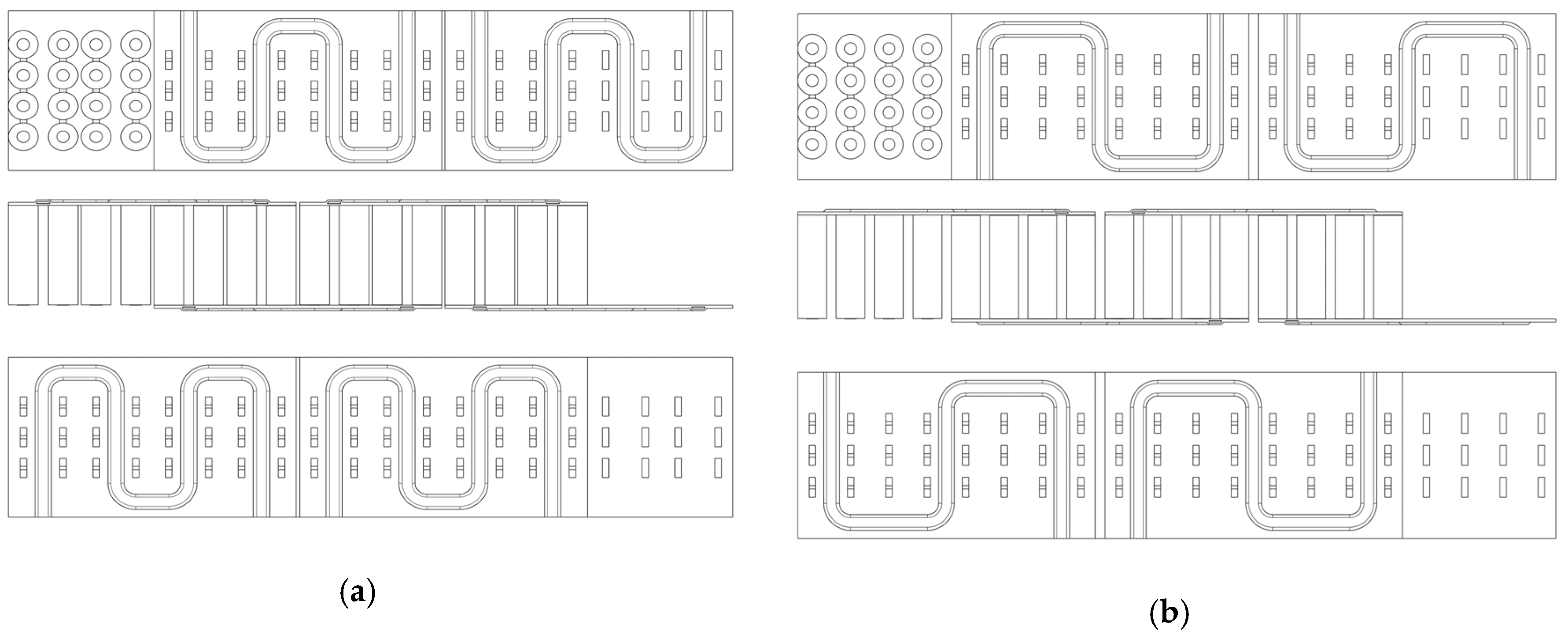
4.2. Geometric Variations
4.3. Target Values
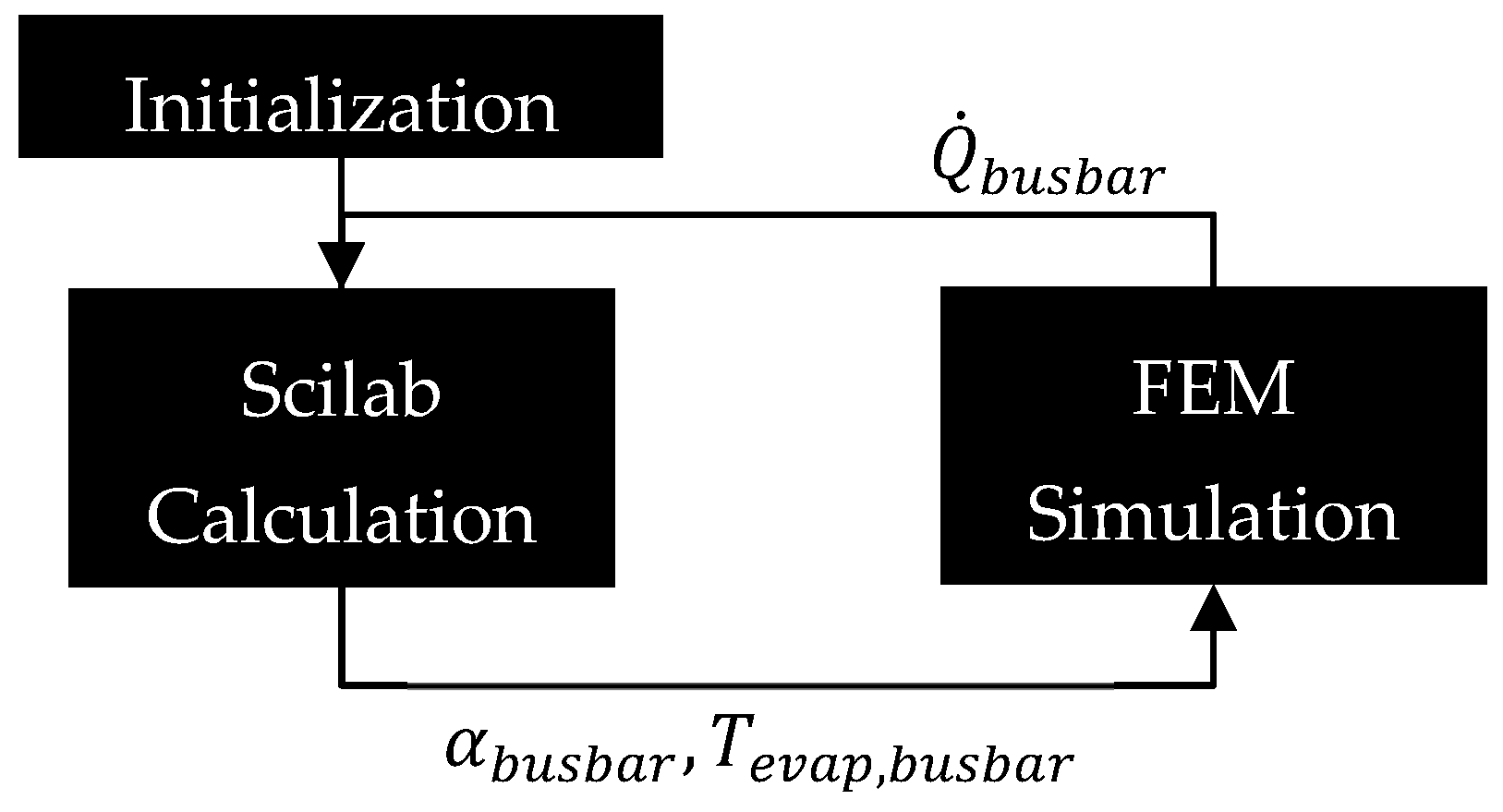
4.4. Methodology
4.5. Results
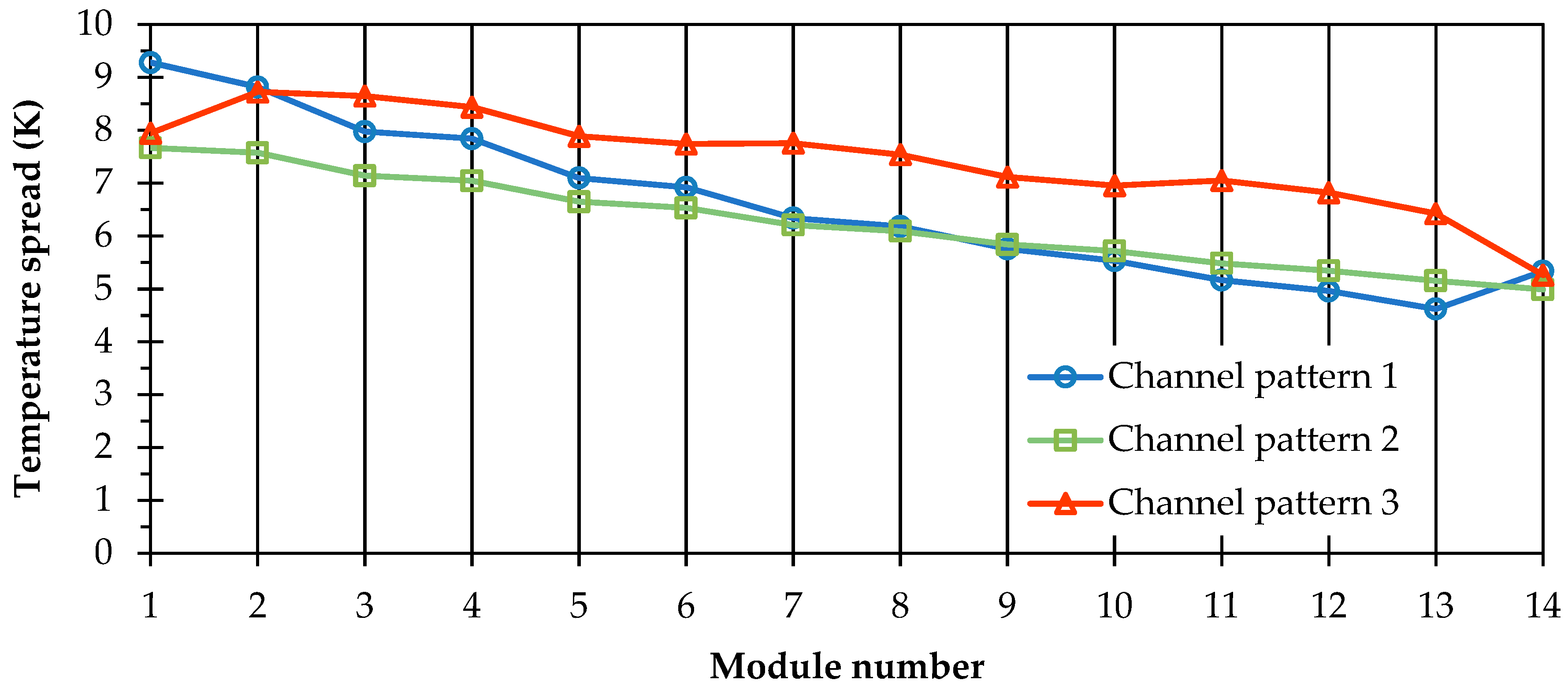
4.5.1. Module Temperatures
4.5.2. Evaporation Temperature
4.5.3. Energy Density
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reber, V. New possibilities by charging at 800 Volt. Porsche Eng. Mag. 2016, 1, 8–15. (In German) [Google Scholar]
- Ochs, T. Technological challenges and chances of Li-metal solid state batteries. In Proceedings of the Batterieforum, Berlin, Germany, 8 April 2016. [Google Scholar]
- Reichardt, K.; Schneider, U.; Dütschke, E. Electromobility on Two Wheels—Experiences from the Model Regions; Fraunhofer ISI: Karlsruhe, Germany, 2012. (In German) [Google Scholar]
- Linzen, D. Impedance-Based Loss Calculation and Thermal Model of Electrochemical Energy Storage Devices for Design Considerations of Automotive Power Systems; RWTH Aachen: Aachen, Germany, 2005. [Google Scholar]
- Wawzyniak, M.; Art, L.; Jung, M.; Ahmed, F.B. Thermal management as prerequisite for electric mobility. Automobiltechnische Zeitung (ATZ) 2017, 9, 53–57. (In German) [Google Scholar] [CrossRef]
- Ebner, C.; Danzer, K.; Platz, C. Batterie package of the E-Scotter concept from BMW motorcycles. Automobiltechnische Zeitung (ATZ) 2012, 114, 248–253. (In German) [Google Scholar]
- Mayer, B.; Schier, M.; Friedrich, H.E. Direct cooling for fast charging of electric vehicles. In Proceedings of the Conference on Future Automotive Technologies (COFAT), Fürstenfeldbruck, Germany, 8 May 2018. [Google Scholar]
- Neumeister, D.; Wiebelt, A.; Hechenberger, T. System integration of a lithium-ion battery in hybrid and electric vehicles. Automobiltechnische Zeitung (ATZ) 2010, 112, 250–255. (In German) [Google Scholar]
- Schoewel, F.; Hochgeiger, E. The high voltage batteries of the BMW i3 and BMW i8. In Proceedings of the Advanced Automotive Battery Conference, Atlanta, GA, USA, 3 February 2014. [Google Scholar]
- Electric Superbike Twente. Available online: https://electricsuperbiketwente.nl/ (accessed on 3 June 2019).
- Eberleh, B. Optimal climate for the battery. E-Mobility 2013, 2, 2–4. (In German) [Google Scholar]
- Jürgensen, H.; Tiedemann, T. Propane in hermetic refrigerant circuits and heat pumps. KI Luft- und Kältetechnik 2003, 3, 121–124. (In German) [Google Scholar]
- Wiebelt, A.; Isermeyer, T.; Siebrecht, T.; Heckenberger, T. Thermal management for lithium ion batteries. Automobiltechnische Zeitung (ATZ) 2009, 111, 500–504. (In German) [Google Scholar] [CrossRef]
- Tahir, M.W. Thermal Characterization, Multi-Scale Thermal Modeling and Experimental Validation of Lithium-Ion Batteries for Automobile Application; Institut für Chemische Verfahrenstechnik der Universität Stuttgart: Stuttgart, Germany, 2016. [Google Scholar]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar]
- Kim, S.-M.; Mudawar, I. Review of databases and predictive methods for heat transfer in condensing and boiling mini/micro-channel flows. Int. J. Heat Mass Transf. 2014, 77, 627–652. [Google Scholar]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. Hydrocarbon refrigerants HC290 (Propane) and HC1270 (Propylene) low GWP long-term substitutes for HFC404A: A comparative analysis in vaporisation inside a small-diameter horizontal smooth tube. Appl. Therm. Eng. 2017, 124, 707–715. [Google Scholar]
- Kim, S.-M.; Mudawar, I. Review of databases and predictive methods for pressure drop in adiabatic, condensing and boiling mini/micro-channel flows. Int. J. Heat Mass Transf. 2014, 77, 74–97. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998. [Google Scholar]








| Refrigerant | R290 (Propane) |
|---|---|
| Mass flow | 3.34 g/s |
| Inlet pressure/inlet temperature | 8.36 bar/20 °C |
| Inlet vapor fraction | 0.26 |
| Axial heat conduction coefficient | 35 W/mK |
| Radial heat conduction coefficient | 1.25 W/mK |
| Variable | Mesh 1 | Mesh 2 | Mesh 3 |
|---|---|---|---|
| No. of elements | 11,188,218 | 4,595,763 | 2,710,836 |
| Average cell temperature | 22.056 °C | 22.04 °C | 21.91 °C |
| GCI (safety factor: 1.25) | GCI12: 0.013% | GCI23: 0.104% | |
| 22.069 | |||
| Error Band | 0.013% |
| Channel Patter | Volumetric Energy Density | Gravimetric Energy Density |
|---|---|---|
| Channel pattern 1 | 241 Wh/litre | 199 Wh/kg |
| Channel pattern 2 | 263 Wh/litre | 201 Wh/kg |
| Channel pattern 3 | 241 Wh/litre | 199 Wh/kg |
| 18650 cells | 653 Wh/litre | 225 Wh/kg |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayer, B.; Schier, M.; Friedrich, H.E. Stand-Alone Battery Thermal Management for Fast Charging of Electric Two Wheelers—Integrated Busbar Cooling. World Electr. Veh. J. 2019, 10, 37. https://doi.org/10.3390/wevj10020037
Mayer B, Schier M, Friedrich HE. Stand-Alone Battery Thermal Management for Fast Charging of Electric Two Wheelers—Integrated Busbar Cooling. World Electric Vehicle Journal. 2019; 10(2):37. https://doi.org/10.3390/wevj10020037
Chicago/Turabian StyleMayer, Bastian, Michael Schier, and Horst E. Friedrich. 2019. "Stand-Alone Battery Thermal Management for Fast Charging of Electric Two Wheelers—Integrated Busbar Cooling" World Electric Vehicle Journal 10, no. 2: 37. https://doi.org/10.3390/wevj10020037





