Signal Detection and Monitoring Based on Longitudinal Healthcare Data
Abstract
:1. Introduction
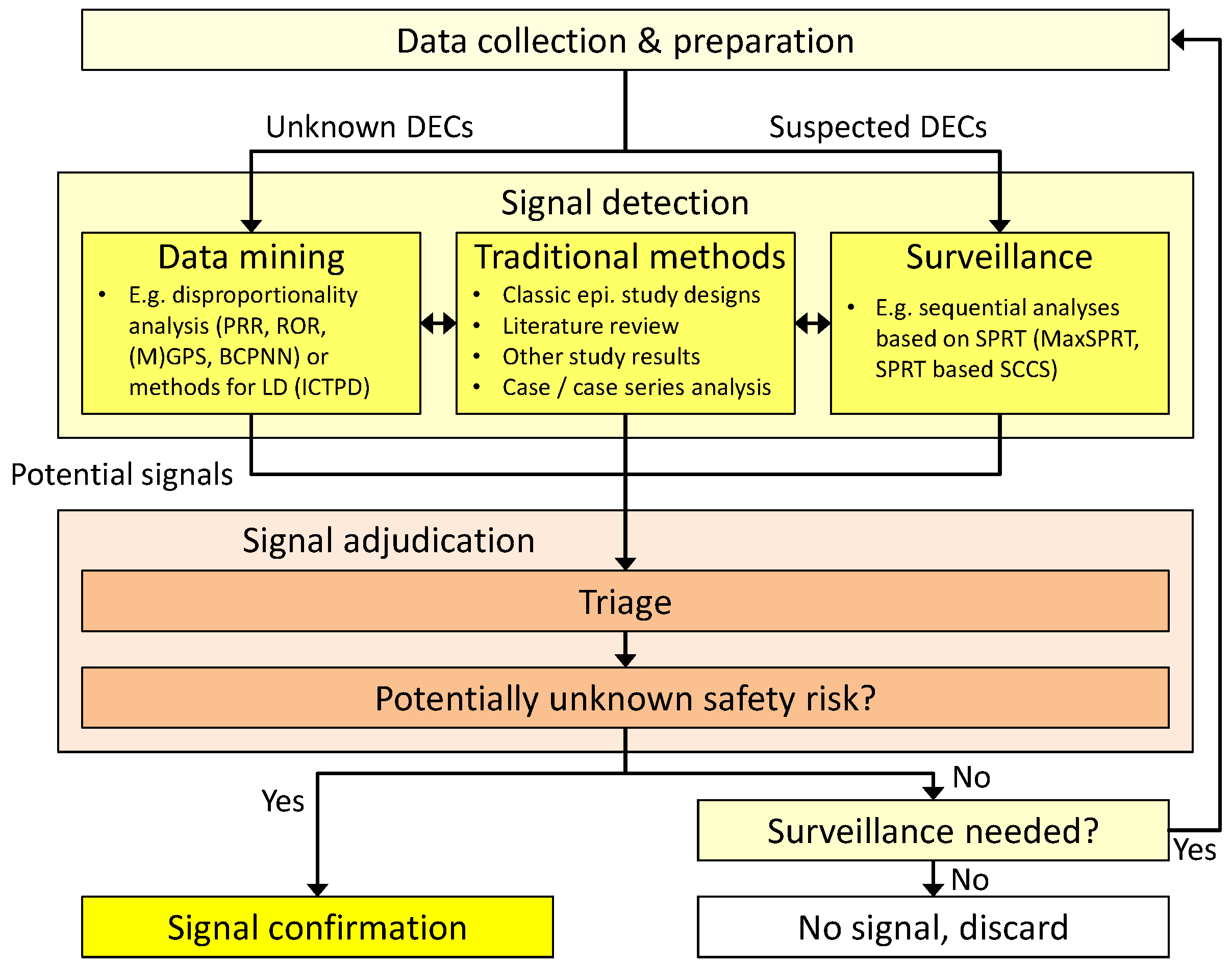
2. General Workflow
- (1)
- Data-mining techniques that strive to uncover so far unknown and unsupected associations. These methods are usually applied to a broad range of combinations of drug exposures and subsequent adverse events, often without limiting the search to pre-defined drug classes or specific medical conditions. They can be regarded as a broad search over the whole spectrum of drug-event combinations (DECs) in the underlying dataset.
- (2)
- If the data-mining search has indicated a possible health risk with a certain DEC, it may be advised to closely monitor this DEC over time to decide whether it should be considered further in confirmatory studies. Surveillance techniques have been developed to consolidate knowledge on these already suspected DECs and are often applied after the first data-mining step.
3. Data Sources
3.1. Overview
- spontaneous reporting databases, like the WHO International Database [22], maintained at the Uppsala Monitoring Centre (UMC) in Uppsala, Sweden; the European Union Drug Regulating Authorities Pharmacovigilance database (EudraVigilance) or a multitude of national databases, e.g., the Adverse Event Reporting System (AERS) as part of MedWatch, the FDA Safety Information and Adverse Event Reporting Program, or the Vaccine Adverse Event Reporting System (VAERS);
- captured data of drug dispensing, e.g., by the New Zealand Intensive Medicines Monitoring Programme [23];
- longitudinal administrative or claims databases from health insurance institutions, like the Medicare database, based on the social insurance program in the U.S., or the German Pharmacoepidemiological Research Database (GePaRD) [24];
- EMRs databases, like the General Practice Research Database (GPRD) in the UK, or data from EHRs, or the Vaccine Safety Datalink (VSD) project [14].
3.2. Spontaneous vs. Longitudinal Data

| Sex | Age | Drug 1 | … | Drug I | Event 1 | … | Event J |
|---|---|---|---|---|---|---|---|
| f | 50 | 0 | … | 1 | 1 | … | 0 |
| m | 80 | 1 | … | 0 | 0 | … | 1 |
| m | 68 | 0 | … | 1 | 1 | … | 1 |
| … | … | … | … | … | … | … | … |
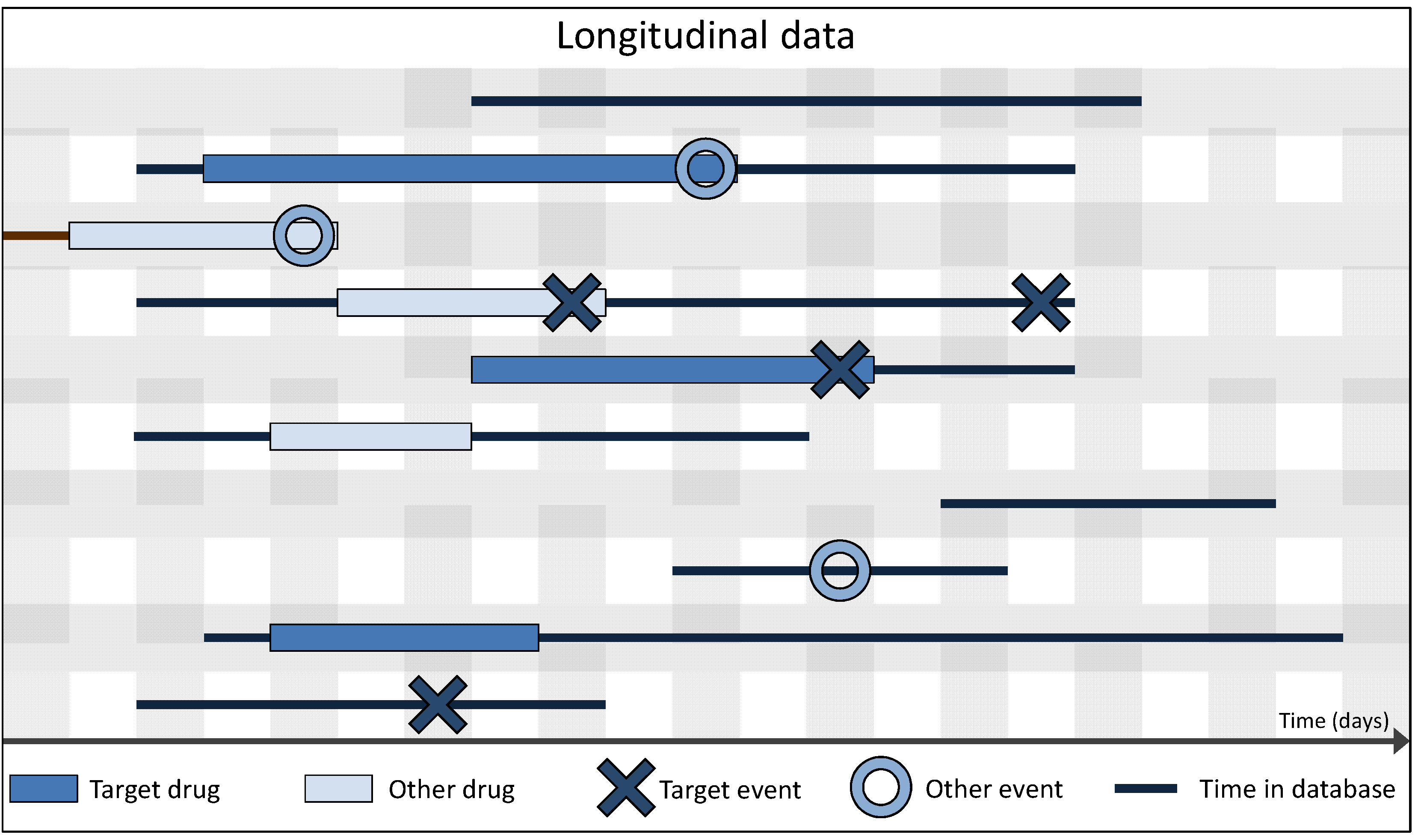
3.3. Data Preparation
| Drug i × ADR j | Event | No event | Total |
|---|---|---|---|
| Exposed | n11 | n10 | n1 |
| Not exposed | n01 | n00 | n0. |
| Total | n.1 | n.0 | n.. |
- (a)
- The basic and most obvious approach is to create “pseudo”-SRs, trying to simulate the exact data structure presented in Table 1. Then, n11 is defined as the number of DEC ij, n01 as the number of events j while not under exposure i, n10 denotes all exposure periods to drug i with a different ADR than event j and n00 is the number of non-j events under non-i exposure (cf. Figure 4(2)). This is a coherent and convenient definition, suffering from the major deficit that information on exposures without events and events without exposures is missing. This approach was discussed and implemented by Schuemie [30] and Zorych et al. [35].
- (b)
- Curtis et al. [34] proposed a method of converting longitudinal data to SR with the possibility to additionally include information on non-exposures and non-events by introducing temporal segmentation of the data. They considered each month per subject to be a single report, consisting of all events that the subject experienced during this specific month and all drugs that were consumed that month or the month before. Thus, reports similar to the structure shown in Table 1 can be generated, plus reports that might contain information on exposures without events or events without exposures (cf. Table 3). Here, n11 is defined as before and denotes the number of reports on DEC ij, n10 is the sum of all reports on drug i without ADR j, n01 is—viceversa—the sum of all reports on ADR j without exposure to drug i and n00 the number of reports containing neither drug i nor ADR j (cf. Figure 4(3)).
- (c)
- A closely related approach to take advantage of the longitudinal information, but without imitating a “reporting structure” was described by Schuemie [30] and Zorych et al. [35]. Here, n11 is defined as the number of distinct DECs ij, n10 and n01 stand for the number of all exposure eras to drug i without the occurrence of ADR j or the number of ADRs j not experienced during exposures to drug i, respectively. Finally, n00 is defined as the number of all non-j events that occur during non-i exposure periods, event-free non-i exposure periods and non-j ADRs when not exposed to any drug (also cf. Figure 4(3)).
- (d)
- The final approach uses even more information than the one presented in c). n11 is defined as number of individuals experiencing event j while exposed to drug i, n10 and n01 are defined as number of persons with exposure to drug i and no occurrence of event j, or an experienced event j and no exposure to drug i, respectively. Finally, n00 includes all individuals that were neither exposed to any drug, nor experienced any ADR (cf. Figure 4(4)). Thus, n11 + n10 + n01 + n00 equals the number n of all subjects contained in the database.
| Sex | Age | Drug 1 | … | Drug I | Event 1 | … | Event J |
|---|---|---|---|---|---|---|---|
| f | 50 | 0 | … | 1 | 1 | … | 0 |
| m | 64 | 0 | … | 0 | 0 | … | 1 |
| m | 80 | 1 | … | 0 | 0 | … | 1 |
| f | 58 | 1 | … | 1 | 0 | … | 0 |
| m | 24 | 0 | … | 0 | 0 | … | 0 |
| … | … | … | … | … | … | … | … |

3.4. Definition of Exposure and Event in Longitudinal Data
4. Analysis Techniques
4.1. Overview
4.2. Disproportionality Analysis Measures for Spontaneous Reporting Data
4.2.1. PRR and ROR—Simple Measures
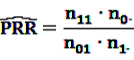
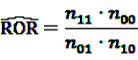
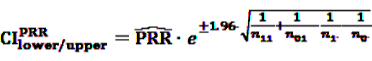
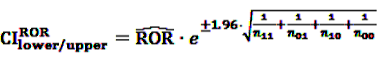 [49]
[49]
 3.85 [50]. Further, rarely applied methods include the crude relative risk (cRR) or Yule’s Q-test [53]. The problems that may arise when using such fixed thresholds are discussed in Section 6 below.
3.85 [50]. Further, rarely applied methods include the crude relative risk (cRR) or Yule’s Q-test [53]. The problems that may arise when using such fixed thresholds are discussed in Section 6 below.4.2.2. BCPNN and GPS—Bayesian Shrinkage
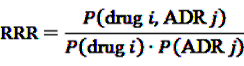
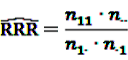
 can easily be interpreted: it simply is the ratio of how many ADRs under exposure were actually observed over the number of expected events under the assumption that ADR and drug exposure were independent.
can easily be interpreted: it simply is the ratio of how many ADRs under exposure were actually observed over the number of expected events under the assumption that ADR and drug exposure were independent. and
and  be random variables to describe the occurrence of drug exposure i and ADR j, respectively. The a priori expectations of X and Y are obtained as:
be random variables to describe the occurrence of drug exposure i and ADR j, respectively. The a priori expectations of X and Y are obtained as: and
and 
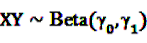
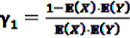 and an a priori expectation of
and an a priori expectation of 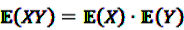 , the expected value under the assumption that X and Y are stochastically independent [56].
, the expected value under the assumption that X and Y are stochastically independent [56].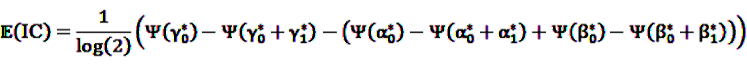
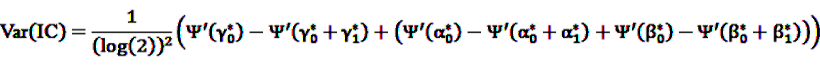
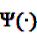 and
and 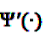 denote the digamma and trigamma function, respectively, and
denote the digamma and trigamma function, respectively, and 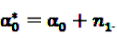 ,
, 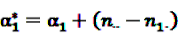 ,
, 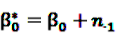 ,
, 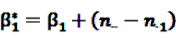 ,
, 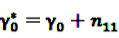 and
and 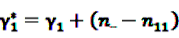 [56].
[56].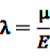
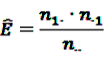
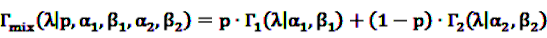
 denotes the negative binomial distribution. The resulting risk measure, the so-called “empirical Bayesian geometric mean” (EBGM) is defined as
denotes the negative binomial distribution. The resulting risk measure, the so-called “empirical Bayesian geometric mean” (EBGM) is defined as
4.2.3. Extension of the GPS: the MGPS
 possible two-way interactions in the set of (n − 1) drugs under inspection and the event A of interest. Given the above set of two drugs (D1, D2) and one ADR (A), the number
possible two-way interactions in the set of (n − 1) drugs under inspection and the event A of interest. Given the above set of two drugs (D1, D2) and one ADR (A), the number  of reports on A after simultaneous exposure to D1 and D2 is considered to be “interesting” if the number of reports involving the two-way interactions (i.e., D1 × D2, D1 × A and D2 × A) does not explain the observed count of the triplet. A log-linear analysis can be conducted to determine if any of the observed frequencies of the two-way combinations depends on the third item. From this analysis one obtains an estimate eAII2F of the frequency of reports on the joint occurrence of D1, D2 and A if all associations were strictly pairwise and independent from the third item. DuMouchel and Pregibon define the EXCESS2 value as number of excess reports on D1, D2 and A over what might be expected if all associations were only pairwise:
of reports on A after simultaneous exposure to D1 and D2 is considered to be “interesting” if the number of reports involving the two-way interactions (i.e., D1 × D2, D1 × A and D2 × A) does not explain the observed count of the triplet. A log-linear analysis can be conducted to determine if any of the observed frequencies of the two-way combinations depends on the third item. From this analysis one obtains an estimate eAII2F of the frequency of reports on the joint occurrence of D1, D2 and A if all associations were strictly pairwise and independent from the third item. DuMouchel and Pregibon define the EXCESS2 value as number of excess reports on D1, D2 and A over what might be expected if all associations were only pairwise:
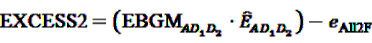
4.3. Analysis Techniques for Longitudinal Data
4.3.1. Adaptation of the MGPS for Longitudinal Data: the LGPS
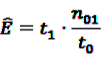
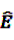 from Equation 11 by Equation 15 to get the plug-in estimator of EBGM (Equation 14) leads to the “longitudinal” GPS (LGPS) algorithm suggested by Schuemie [30].
from Equation 11 by Equation 15 to get the plug-in estimator of EBGM (Equation 14) leads to the “longitudinal” GPS (LGPS) algorithm suggested by Schuemie [30]. 4.3.2. Self-Controlled Case Series
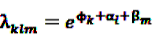
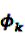 is an effect for individual k, α1 is an effect for age group l, and βm is an effect for risk period m. For the baseline period it is assumed that α0 = β0 = 0, so that the baseline incidence λk00 is simply
is an effect for individual k, α1 is an effect for age group l, and βm is an effect for risk period m. For the baseline period it is assumed that α0 = β0 = 0, so that the baseline incidence λk00 is simply 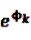 .
. are referred to as relative incidences and are a measure of incidence in risk period m relative to the control period m = 0.
are referred to as relative incidences and are a measure of incidence in risk period m relative to the control period m = 0. observed for the individual k during the observation period, the log likelihood is multinomial:
observed for the individual k during the observation period, the log likelihood is multinomial:
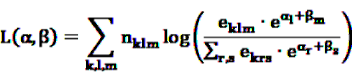
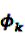 , cancel out in Equation 17. Only age (or other time-dependent covariates) need to be modeled. The model
, cancel out in Equation 17. Only age (or other time-dependent covariates) need to be modeled. The model 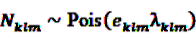 with log link function
with log link function 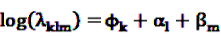 can be fitted using standard statistical analysis software such as STATA® [66] or SAS® [67].
can be fitted using standard statistical analysis software such as STATA® [66] or SAS® [67].4.3.3. IC Temporal Pattern Discovery
 denote the number of prescriptions of drug i with a subsequent event j in the time-window t,
denote the number of prescriptions of drug i with a subsequent event j in the time-window t,  the number of prescriptions to any drug with a subsequent event j in time-window t,
the number of prescriptions to any drug with a subsequent event j in time-window t,  the number of prescription of drug i and any subsequent event in time period t, and
the number of prescription of drug i and any subsequent event in time period t, and  the number of any prescription, followed by any event in time period t. Then the IC, defined in Equation 7, for the time window t can be estimated as
the number of any prescription, followed by any event in time period t. Then the IC, defined in Equation 7, for the time window t can be estimated as
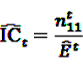
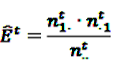
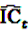 by adding
by adding  to both the nominator an the denominator, resulting in a general shrinkage towards 0.
to both the nominator an the denominator, resulting in a general shrinkage towards 0.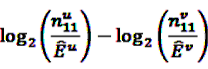
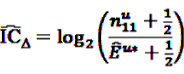
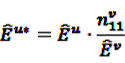
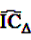 , the shrunk difference between the log observed-to-expected ratios in time periods u and v, can distinguish true temporal associations between an exposure to drug i and the occurrence of an ADR j from a potential tendency of the joint occurrence of i and j in the same patients.
, the shrunk difference between the log observed-to-expected ratios in time periods u and v, can distinguish true temporal associations between an exposure to drug i and the occurrence of an ADR j from a potential tendency of the joint occurrence of i and j in the same patients. 4.4. Applications
4.4.1. Application of the Disproportionality Measures
4.4.2. Application of the LGPS
4.4.3. Comparative Studies
5. Confounder Adjustment
- (1)
- requires the identification of the different data dimensions (e.g., hospitalization data, outpatient care data, outpatient drug dispensation data) in the database;
- (2)
- identifies a pre-specified number of the top most prevalent codes, e.g., ICD or ATC codes (ICD = international statistical classification of diseases and related health problems, ATC = anatomical therapeutic chemical classification system) in each data dimension as candidate covariates;
- (3)
- ranks candidate covariates based on their recurrence (the frequency that the codes are recorded for each individual during the baseline period);
- (4)
- ranks covariates across all data dimensions by their potential for control of confounding based on the bivariate associations of each covariate with the treatment and with the outcome;
- (5)
- selects a pre-specified number of covariates from Step 4 (e.g., 500) for PS modeling, and
- (6)
- estimates the PS based on multivariable logistic regression using the selected covariates plus any pre-specified covariates.
6. Triage—Adjudication of Potential Signals
7. Near Real-Time Surveillance Techniques
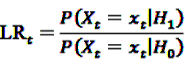
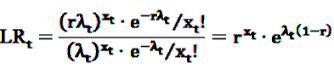
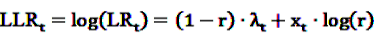
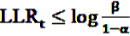 , the alternative is accepted if
, the alternative is accepted if 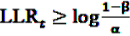 . If LLRt lies between these values, no decision can be made and additional data are needed.
. If LLRt lies between these values, no decision can be made and additional data are needed.7.1. Extensions
 . This leads to a modified test statistic, where the denominator is still given by the simple likelihood of the null hypothesis, but the numerator now is given as the maximum likelihood under the composite alternative hypothesis. The likelihood ratio based test statistic is then
. This leads to a modified test statistic, where the denominator is still given by the simple likelihood of the null hypothesis, but the numerator now is given as the maximum likelihood under the composite alternative hypothesis. The likelihood ratio based test statistic is then
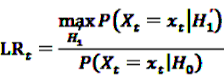
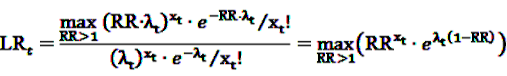
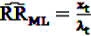 gives
gives
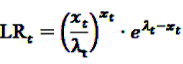
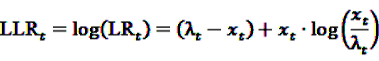
 now used in the test statistic is just an estimate, not the real baseline frequency, and as such it has a variability of its own. If we neglect this variability by simply treating
now used in the test statistic is just an estimate, not the real baseline frequency, and as such it has a variability of its own. If we neglect this variability by simply treating  as if it was the real value, we could spoil the results by assigning
as if it was the real value, we could spoil the results by assigning  a level of certainty it does not possess.
a level of certainty it does not possess.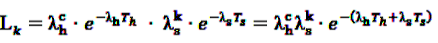
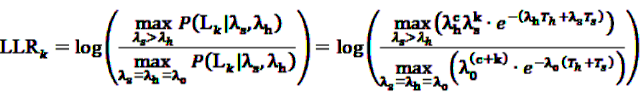
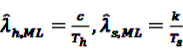 , and
, and 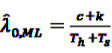 gives
gives
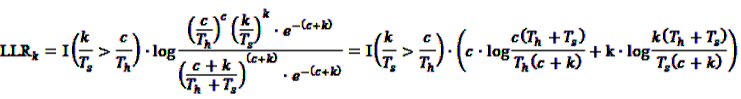
7.2. Application of the SPRT and MaxSPRT
7.3. Further Approaches
8. Discussion
Conflict of Interest
References
- Edwards, I.R.; Biriell, C. Harmonisation in pharmacovigilance. Drug Saf. 1994, 10, 93–102. [Google Scholar] [CrossRef]
- The Council for International Organizations of Medical Science (CIOMS), Practical Aspects of Signal Detection in Pharmacovigilance: Report of CIOMS Working Group VIII; World Health Organization: Geneva, Switzerland, 2010.
- Shibata, A.; Hauben, M. Pharmacovigilance, signal detection and signal intelligence overview. In Information Fusion (FUSION), Proceedings of the 14th International Conference, Chicago, IL, USA, July 5–8 2011; IEEE: New York, NY, USA, 2011; pp. 1–7. [Google Scholar]
- Hauben, M.; Reich, L. Potential utility of data-mining algorithms for early detection of potentially fatal/disabling adverse drug reactions: A retrospective evaluation. J. Clin. Pharmacol. 2005, 45, 378–384. [Google Scholar] [CrossRef]
- Hauben, M.; Madigan, D.; Gerrits, C.M.; Walsh, L.; van Puijenbroek, E.P. The role of data mining in pharmacovigilance. Expert Opin. Drug Saf. 2005, 4, 929–948. [Google Scholar] [CrossRef]
- Almenoff, J.; Tonning, J.M.; Gould, A.L.; Szarfman, A.; Hauben, M.; Ouellet-Hellstrom, R.; Ball, R.; Hornbuckle, K.; Walsh, L.; Yee, C.; et al. Perspectives on the use of data mining in pharmacovigilance. Drug Saf. 2005, 28, 981–1007. [Google Scholar] [CrossRef]
- Goldman, S.A. Limitations and strengths of spontaneous reports data. Clin. Ther. 1998, 20, C40–C44. [Google Scholar] [CrossRef]
- Bates, D.W.; Evans, R.S.; Murff, H.; Stetson, P.D.; Pizziferri, L.; Hripcsak, G. Detecting adverse events using information technology. J. Am. Med. Inform. Assoc. 2003, 10, 115–128. [Google Scholar] [CrossRef]
- Hauben, M.; Bate, A. Data mining in pharmacovigilance. In Pharmaceutical Data Mining; Balakin, K.V., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 339–377. [Google Scholar]
- Bresalier, R.S.; Sandler, R.S.; Quan, H.; Bolognese, J.A.; Oxenius, B.; Horgan, K.; Lines, C.; Riddell, R.; Morton, D.; Lanas, A.; et al. Cardiovascular events associated with rofecoxib in a colorectal adenoma chemoprevention trial. N. Engl. J. Med. 2005, 352, 1092–1102. [Google Scholar] [CrossRef]
- Furberg, C.D.; Pitt, B. Withdrawal of cerivastatin from the world market. Curr. Control. Trials Cardiovasc. Med. 2001, 2, 205–207. [Google Scholar] [CrossRef]
- Schneeweiss, S.; Seeger, J.D.; Landon, J.; Walker, A.M. Aprotinin during coronary-artery bypass grafting and risk of death. N. Engl. J. Med. 2008, 358, 771–783. [Google Scholar] [CrossRef]
- Nissen, S.E.; Wolski, K. Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes. N. Engl. J. Med. 2007, 356, 2457–2471. [Google Scholar]
- DeStefano, F. The Vaccine Safety Datalink project. Pharmacoepidemiol. Drug Saf. 2001, 10, 403–406. [Google Scholar] [CrossRef]
- U.S. Food and Drug Administration (FDA). FDA’s Sentinel Initiative. Available online: http://www.fda.gov/Safety/FDAsSentinelInitiative/default.htm (accessed on 3 February 2012).
- Robb, M.A.; Racoosin, J.A.; Sherman, R.E.; Gross, T.P.; Ball, R.; Reichman, M.E.; Midthun, K.; Woodcock, J. The US Food and Drug Administration’s Sentinel Initiative: Expanding the horizons of medical product safety. Pharmacoepidemiol. Drug Saf. 2012, 21, 9–11. [Google Scholar] [CrossRef]
- Foundation for the National Institutes of Health. Observational Medical Outcomes Partnership (OMOP). Available online: http://omop.fnih.org/ (accessed on 13 July 2011).
- European Medicines Agency. The IMI-PROTECT project (Pharmacoepidemiological Research on Outcomes of Therapeutics by a European ConsorTium). Available online: http://www.imi-protect.eu (accessed on 13 July 2011).
- Arlett, P.R.; Kurz, X. New approaches to strengthen pharmacovigilance. Drug Discov. Today Technol. 2011, 8, e15–e19. [Google Scholar] [CrossRef]
- Trifirò, G.; Pariente, A.; Coloma, P.M.; Kors, J.A.; Polimeni, G.; Miremont-Salamé, G.; Catania, M.A.; Salvo, F.; David, A.; Moore, N.; et al. Data mining on electronic health record databases for signal detection in pharmacovigilance: Which events to monitor? Pharmacoepidemiol. Drug Saf. 2009, 18, 1176–1184. [Google Scholar]
- Trifirò, G.; Patadia, V.; Schuemie, M.J.; Coloma, P.M.; Gini, R.; Herings, R.; Hippisley-Cox, J.; Mazzaglia, G.; Giaquinto, C.; Scotti, L.; et al. EU-ADR healthcare database network vs. spontaneous reporting system database: Preliminary comparison of signal detection. Stud. Health. Technol. Inform. 2011, 166, 25–30. [Google Scholar]
- Olsson, S. The role of the WHO programme on international drug monitoring in coordinating worldwide drug safety efforts. Drug Saf. 1998, 19, 1–10. [Google Scholar] [CrossRef]
- Coulter, D.M. The New Zealand intensive medicines monitoring programme in pro-active safety surveillance. Pharmacoepidemiol. Drug Saf. 2000, 9, 273–280. [Google Scholar] [CrossRef]
- Pigeot, I.; Ahrens, W. Establishment of a pharmacoepidemiological database in Germany: methodological potential, scientific value and practical limitations. Pharmacoepidemiol. Drug Saf. 2008, 17, 215–223. [Google Scholar] [CrossRef]
- Park, M.Y.; Yoon, D.; Lee, K.; Kang, S.Y.; Park, I.; Lee, S.-H.; Kim, W.; Kam, H.J.; Lee, Y.-H.; Kim, J.H.; et al. A novel algorithm for detection of adverse drug reaction signals using a hospital electronic medical record database. Pharmacoepidemiol. Drug Saf. 2011, 20, 598–607. [Google Scholar] [CrossRef]
- Harpaz, R.; DuMouchel, W.; Shah, N.H.; Madigan, D.; Ryan, P.; Friedman, C. Novel data-mining methodologies for adverse drug event discovery and analysis. Clin. Pharmacol. Ther. 2012, 91, 1010–1021. [Google Scholar] [CrossRef]
- Ahmad, S.R. Adverse drug event monitoring at the Food and Drug Administration. J. Gen. Intern. Med. 2003, 18, 57–60. [Google Scholar] [CrossRef]
- Platt, R.; Carnahan, R.M.; Brown, J.S.; Chrischilles, E.; Curtis, L.H.; Hennessy, S.; Nelson, J.C.; Racoosin, J.A.; Robb, M.; Schneeweiss, S.; et al. The U.S. Food and Drug Administration’s Mini-Sentinel program: Status and direction. Pharmacoepidemiol. Drug Saf. 2012, 21, 1–8. [Google Scholar]
- Carnahan, R.M. Mini-Sentinel’s systematic reviews of validated methods for identifying health outcomes using administrative data: Summary of findings and suggestions for future research. Pharmacoepidemiol. Drug Saf. 2012, 21, 90–99. [Google Scholar] [CrossRef]
- Schuemie, M.J. Methods for drug safety signal detection in longitudinal observational databases: LGPS and LEOPARD. Pharmacoepidemiol. Drug Saf. 2011, 20, 292–299. [Google Scholar] [CrossRef]
- Choi, N.-K.; Chang, Y.; Choi, Y.K.; Hahn, S.; Park, B.-J. Signal detection of rosuvastatin compared to other statins: Data-mining study using national health insurance claims database. Pharmacoepidemiol. Drug Saf. 2010, 19, 238–246. [Google Scholar] [CrossRef]
- Choi, N.-K.; Chang, Y.; Kim, J.-Y.; Choi, Y.-K.; Park, B.-J. Comparison and validation of data-mining indices for signal detection: using the Korean national health insurance claims database. Pharmacoepidemiol. Drug Saf. 2011, 20, 1278–1286. [Google Scholar] [CrossRef]
- Kim, J.; Kim, M.; Ha, J.-H.H.; Jang, J.; Hwang, M.; Lee, B.K.; Chung, M.W.; Yoo, T.M.; Kim, M.J. Signal detection of methylphenidate by comparing a spontaneous reporting database with a claims database. Regul. Toxicol. Pharmacol. 2011, 61, 154–160. [Google Scholar] [CrossRef]
- Curtis, J.R.; Cheng, H.; Delzell, E.; Fram, D.; Kilgore, M.; Saag, K.; Yun, H.; DuMouchel, W. Adaptation of Bayesian data mining algorithms to longitudinal claims data: Coxib safety as an example. Med. Care. 2008, 46, 969–975. [Google Scholar] [CrossRef]
- Zorych, I.; Madigan, D.; Ryan, P.; Bate, A. Disproportionality methods for pharmacovigilance in longitudinal observational databases. Stat. Methods Med. Res. 2011. [Google Scholar] [CrossRef]
- Coloma, P.M.; Schuemie, M.J.; Trifirò, G.; Gini, R.; Herings, R.; Hippisley-Cox, J.; Mazzaglia, G.; Giaquinto, C.; Corrao, G.; Pedersen, L.; et al. Combining electronic healthcare databases in Europe to allow for large-scale drug safety monitoring: the EU-ADR Project. Pharmacoepidemiol. Drug Saf. 2011, 20, 1–11. [Google Scholar] [CrossRef]
- Brown, J.S.; Kulldorff, M.; Petronis, K.R.; Reynolds, R.; Chan, K.A.; Davis, R.L.; Graham, D.; Andrade, S.E.; Raebel, M.A.; Herrinton, L.; et al. Early adverse drug event signal detection within population-based health networks using sequential methods: Key methodologic considerations. Pharmacoepidemiol. Drug Saf. 2009, 18, 226–234. [Google Scholar] [CrossRef]
- Madigan, D.; Ryan, P.; Simpson, S.; Zorych, I. Bayesian methods in pharmacovigilance. In Bayesian Statistics 9; Bernardo, J.M., Bayarri, M.J., Berger, J.O., Dawid, A.P., Heckerman, D., Smith, A.F.M., West, M., Eds.; Oxford University Press: Oxford, England, 2011; pp. 421–438. [Google Scholar]
- Wald, A. Sequential tests of statistical hypotheses. Ann. Math. Stat. 1945, 16, 117–186. [Google Scholar] [CrossRef]
- Wald, A. Sequential Analysis; Wiley: New York, NY, USA, 1947. [Google Scholar]
- Mini-Sentinel Coordinating Center (MSCC). Statistical methods development. Available online: http://mini-sentinel.org/foundational_activities/methods_development/ (accessed on 13 February 2012).
- Observational Medical Outcomes Partnership. OMOP methods library. Available online: http://omop.fnih.org/MethodsLibrary (accessed on 13 February 2012).
- Almenoff, J.S.; DuMouchel, W.; Kindman, L.A.; Yang, X.; Fram, D. Disproportionality analysis using empirical Bayes data mining: A tool for the evaluation of drug interactions in the post-marketing setting. Pharmacoepidemiol. Drug Saf. 2003, 12, 517–521. [Google Scholar] [CrossRef]
- Van Puijenbroek, E.P.; Bate, A.; Leufkens, H.G.M.; Lindquist, M.; Orre, R.; Egberts, A.C.G. A comparison of measures of disproportionality for signal detection in spontaneous reporting systems for adverse drug reactions. Pharmacoepidemiol. Drug Saf. 2002, 11, 3–10. [Google Scholar] [CrossRef]
- DuMouchel, W. Bayesian data mining in large frequency tables, with an application to the FDA spontaneous reporting system. Am. Stat. 1999, 53, 177–190. [Google Scholar] [CrossRef]
- DuMouchel, W.; Pregibon, D. Empirical bayes screening for multi-item associations. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 26–29 2001; Association for Computing Machinery: San Francisco, CA, USA, 2001; pp. 67–76. [Google Scholar]
- Bate, A.; Lindquist, M.; Edwards, I.R.; Olsson, S.; Orre, R.; Lansner, A.; de Freitas, R.M. A Bayesian neural network method for adverse drug reaction signal generation. Eur. J. Clin. Pharmacol. 1998, 54, 315–321. [Google Scholar] [CrossRef]
- Evans, S.J.W.; Waller, P.C.; Davis, S. Use of proportional reporting ratios (PRRs) for signal generation from spontaneous adverse drug reaction reports. Pharmacoepidemiol. Drug Saf. 2001, 10, 483–486. [Google Scholar] [CrossRef]
- Lansner, A.; Ekeberg, Ö. A one-layer feedback artificial neural network with a bayesian learning rule. Int. J. Neural Syst. 1989, 1, 77–78. [Google Scholar] [CrossRef]
- Hauben, M.; Bate, A. Decision support methods for the detection of adverse events in post-marketing data. Drug Discov. Today 2009, 14, 343–357. [Google Scholar] [CrossRef]
- Bousquet, C.; Henegar, C.; Lillo-Le Louët, A.; Degoulet, P.; Jaulent, M.-C. Implementation of automated signal generation in pharmacovigilance using a knowledge-based approach. Int. J. Med. Inform. 2005, 74, 563–571. [Google Scholar] [CrossRef]
- Yates, F. Contingency tables involving small numbers and the chi-square-test. Suppl. J. R. Stat. Soc. 1934, 1, 217–235. [Google Scholar] [CrossRef]
- Goodman, L.A. William Henry Kruskal. In Measures of Association for Cross Classification; Springer: New York, NY, USA, 1979. [Google Scholar]
- MacKay, D.J.C. Information Theory. In Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Raiffa, H.; Schlaifer, R. Applied Statistical Decision Theory; Harvard University: Boston, MA, USA, 1961. [Google Scholar]
- Gould, A.L. Practical pharmacovigilance analysis strategies. Pharmacoepidemiol. Drug Saf. 2003, 12, 559–574. [Google Scholar] [CrossRef]
- Norén, G.N.; Bate, A.; Orre, R.; Edwards, I.R. Extending the methods used to screen the WHO drug safety database towards analysis of complex associations and improved accuracy for rare events. Stat. Med. 2006, 25, 3740–3757. [Google Scholar] [CrossRef]
- Ahmed, I.; Poncet, A. PhViD, Version 1.0.4. A R Package for PharmacoVigilance Signal Detection. Available online: http://cran.r-project.org/web/packages/PhViD/ (accessed on 6 December,2012).
- Anonymous. The R Project for Statistical Computing. Available online: http://www.r-project.org/ (accessed on 13 February 2012).
- Pogson, G.W.; Kindred, L.H.; Carper, B.G. Rhabdomyolysis and renal failure associated with cerivastatin-gemfibrozil combination therapy. Am. J. Cardiol. 1999, 83, 1146. [Google Scholar] [CrossRef]
- Van Puijenbroek, E.P.; Egberts, A.C.; Meyboom, R.H.B.; Leufkens, H.G.M. Signalling possible drug-drug interactions in a spontaneous reporting system: delay of withdrawal bleeding during concomitant use of oral contraceptives and itraconazole. Br. J. Clin. Pharmacol. 1999, 47, 689–693. [Google Scholar]
- Van Puijenbroek, E.P.; Egberts, A.C.G.; Heerdink, E.R.; Leufkens, H.G.M. Detecting drug-drug interactions using a database for spontaneous adverse drug reactions: An example with diuretics and non-steroidal anti-inflammatory drugs. Eur. J. Clin. Pharmacol. 2000, 56, 733–738. [Google Scholar] [CrossRef]
- Norén, G.N.; Sundberg, R.; Bate, A.; Edwards, I.R. A statistical methodology for drug–drug interaction surveillance. Stat. Med. 2008, 27, 3057–3070. [Google Scholar] [CrossRef]
- Farrington, C.P. Relative incidence estimation from case series for vaccine safety evaluation. Biometrics 1995, 51, 228–235. [Google Scholar] [CrossRef]
- Taylor, B.; Miller, E.; Farrington, C.P.; Petropoulos, M.C.; Favot-Mayaud, I.; Li, J.; Waight, P.A. Autism and measles, mumps, and rubella vaccine: No epidemiological evidence for a causal association. Lancet 1999, 353, 2026–2029. [Google Scholar]
- Stata Statistical Software, StataCorp: College Station, TX, USA, 2011; Release 12.
- SAS, SAS Institute Inc: Cary, NC, USA, 2011; Release 9.3.
- Hocine, M.N.; Musonda, P.; Andrews, N.J.; Farrington, C.P. Sequential case series analysis for pharmacovigilance. J. R. Stat. Soc. 2009, 172, 213–236. [Google Scholar] [CrossRef]
- Maclure, M.; Fireman, B.; Nelson, J.C.; Hua, W.; Shoaibi, A.; Paredes, A.; Madigan, D. When should case-only designs be used for safety monitoring of medical products? Pharmacoepidemiol. Drug Saf. 2012, 21, 50–61. [Google Scholar] [CrossRef]
- Norén, G.N.; Hopstadius, J.; Bate, A.; Star, K.; Edwards, I.R. Temporal pattern discovery in longitudinal electronic patient records. Data Min. Knowl. Discov. 2010, 20, 361–387. [Google Scholar]
- Murray, R.E.; Ryan, P.B.; Reisinger, S.J. Design and validation of a data simulation model for longitudinal healthcare data. AMIA Annu. Symp. Proc. 2011, 2011, 1176–1185. [Google Scholar]
- OMOP. OSIM-Observational Medical Dataset Simulator. Available online: http://omop.fnih.org/OSIM (accessed on 14 February 2012).
- Thomson Reuters. MarketScan databases. Available online: http://thomsonreuters.com/ (accessed on 14 February 2012).
- Vlug, A.E.; van der Lei, J.; Mosseveld, B.M.Th.; van Wijk, M.A.M.; van der Linden, P.D.; Sturkenboom, M.C.J.M.; van Bemmel, J.H. Postmarketing surveillance based on electronic patient records: The IPCI project. Methods Inf. Med. 1999, 38, 339–344. [Google Scholar]
- Schuemie, M.J.; Coloma, P.M.; Straatman, H.; Herings, R.M.; Trifirò, G.; Matthews, J.N.; Prieto-Merino, D.; Molokhia, M.; Pedersen, L.; Gini, R.; et al. Using electronic health care records for drug safety signal detection: A comparative evaluation of statistical methods. Med. Care. 2012, 10, 890–897. [Google Scholar]
- Ryan, P.B.; Madigan, D.; Stang, P.E.; Marc Overhage, J.; Racoosin, J.A.; Hartzema, A.G. Empirical assessment of methods for risk identification in healthcare data: Results from the experiments of the Observational Medical Outcomes Partnership. Stat. Med. 2012, in press. [Google Scholar]
- Schneeweiss, S.; Rassen, J.A.; Glynn, R.J.; Avorn, J.; Mogun, H.; Brookhart, M.A. High-dimensional propensity score adjustment in studies of treatment effects using health care claims data. Epidemiology 2009, 20, 512–522. [Google Scholar] [CrossRef]
- Rassen, J.A.; Schneeweiss, S. Using high-dimensional propensity scores to automate confounding control in a distributed medical product safety surveillance system. Pharmacoepidemiol. Drug Saf. 2012, 21, 41–49. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar]
- Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge Univ Press: Cambridge, UK, 2008. [Google Scholar]
- Lu, Z. Information technology in pharmacovigilance: Benefits, challenges, and future directions from industry perspectives. Drug Healthc. Patient Saf. 2009, 1, 35–45. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Garbe, E.; Kloss, S.; Suling, M.; Pigeot, I.; Schneeweiss, S. High-dimensional versus conventional propensity scores in a comparative effectiveness study of coxibs and reduced upper gastrointestinal complications. Eur. J. Clin. Pharmacol. 2012. [Google Scholar] [CrossRef]
- Greenland, S. Regression methods for epidemiologic analysis. In Handbook of Epidemiology; Ahrens, W., Pigeot, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 625–691. [Google Scholar]
- Genkin, A.; Lewis, D.D.; Madigan, D. Large-scale Bayesian logistic regression for text categorization. Technometrics 2007, 49, 291–304. [Google Scholar] [CrossRef]
- Caster, O.; Norén, G.N.; Madigan, D.; Bate, A. Large-scale regression-based pattern discovery: The example of screening the WHO global drug safety database. Stat. Anal. Data Min. 2010, 3, 197–208. [Google Scholar]
- Ahmed, I.; Dalmasso, C.; Haramburu, F.; Thiessard, F.; Broët, P.; Tubert-Bitter, P. False discovery rate estimation for frequentistpharmacovigilance signal detection methods. Biometrics 2010, 66, 301–309. [Google Scholar] [CrossRef]
- Ahmed, I.; Thiessard, F.; Miremont-Salamé, G.; Haramburu, F.; Kreft-Jais, C.; Bégaud, B.; Tubert-Bitter, P. Early detection of pharmacovigilance signals with automated methods based on false discovery rates: A comparative study. Drug Saf. 2012, 6, 495–506. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. 1995, 57, 289–300. [Google Scholar]
- Ståhl, M.; Lindquist, M.; Edwards, I.R.; Brown, E.G. Introducing triage logic as a new strategy for the detection of signals in the WHO Drug Monitoring Database. Pharmacoepidemiol. Drug Saf. 2004, 13, 355–363. [Google Scholar] [CrossRef]
- Lindquist, M. Use of triage strategies in the WHO signal-detection process. Drug Saf. 2007, 30, 635–637. [Google Scholar] [CrossRef]
- Horwitz, R.I.; Feinstein, A.R. The problem of protopathic bias in case-control studies. Am. J. Med. 1980, 68, 255–258. [Google Scholar] [CrossRef]
- Schneeweiss, S. A basic study design for expedited safety signal evaluation based on electronic healthcare data. Pharmacoepidemiol. Drug Saf. 2010, 19, 858–868. [Google Scholar] [CrossRef]
- Kulldorff, M.; Davis, R.L.; Kolczak, M.; Lewis, E.; Lieu, T.; Platt, R. A maximized sequential probability ratio test for drug and vaccine safety surveillance. Seq. Anal. 2011, 30, 58–78. [Google Scholar] [CrossRef]
- Li, L.; Kulldorff, M. A conditional maximized sequential probability ratio test for pharmacovigilance. Stat. Med. 2010, 29, 284–295. [Google Scholar]
- Brown, J.S.; Kulldorff, M.; Chan, K.A.; Davis, R.L.; Graham, D.; Pettus, P.T.; Andrade, S.E.; Raebel, M.A.; Herrinton, L.; Roblin, D.; et al. Early detection of adverse drug events within population-based health networks: application of sequential testing methods. Pharmacoepidemiol. Drug Saf. 2007, 16, 1275–1284. [Google Scholar] [CrossRef]
- Platt, R.; Andrade, S.E.; Davis, R.L.; DeStefano, F.; Finkelstein, J.A.; Goodman, M.J.; Gurwitz, J.H.; Go, A.S.; Martinson, B.C.; Raebel, M.A.; et al. Pharmacovigilance in the HMO research network. In Pharmacovigilance; John Wiley & Sons, Ltd.: New York, NY, USA, 2002; pp. 391–398. [Google Scholar]
- Li, L. A conditional sequential sampling procedure for drug safety surveillance. Stat. Med. 2009, 28, 3124–3138. [Google Scholar] [CrossRef]
- Davis, R.L.; Kolczak, M.; Lewis, E.; Nordin, J.; Goodman, M.; Shay, D.K.; Platt, R.; Black, S.; Shinefield, H.; Chen, R.T. Active surveillance of vaccine safety: A system to detect early signs of adverse events. Epidemiology 2005, 3, 336–341. [Google Scholar]
- Yih, W.K.; Kulldorff, M.; Fireman, B.H.; Shui, I.M.; Lewis, E.M.; Klein, N.P.; Baggs, J.; Weintraub, E.S.; Belongia, E.A.; Naleway, A.; et al. Active surveillance for adverse events: The experience of the Vaccine Safety Datalink project. Pediatrics 2011, 127, 54–64. [Google Scholar]
- Li, L.; Kulldorff, M.; Nelson, J.; Cook, A. A propensity score-enhanced sequential analytic method for comparative drug safety surveillance. Stat. Biosci. 2011, 3, 45–62. [Google Scholar] [CrossRef]
- Jin, H.W.; Chen, J.; He, H.; Williams, G.J.; Kelman, C.; O’Keefe, C.M. Mining unexpected temporal associations: applications in detecting adverse drug reactions. IEEE Trans. Inf. Technol. Biomed. 2008, 12, 488–500. [Google Scholar] [CrossRef]
- Jin, H.W.; Chen, J.; He, H.; Kelman, C.; McAullay, D.; O’Keefe, C.M. Signaling potential adverse drug reactions from administrative health databases. IEEE Trans. Knowl. Data Eng. 2010, 22, 839–853. [Google Scholar]
- Grigg, O.; Farewell, V. An overview of risk-adjusted charts. J. R. Stat. Soc. 2004, 167, 523–539. [Google Scholar] [CrossRef]
- Nelson, J.C.; Cook, A.; Yu, O. Evaluation of signal detection methods for use in prospective post licensure medical product safety surveillance. Available online: http://www.regulations.gov/#!documentDetail;D=FDA-2009-N-0192–0002 (accessed on 14 August 2012).
- Spiegelhalter, D.; Grigg, O.; Kinsman, R.; Treasure, T. Risk-adjusted sequential probability ratio tests: applications to Bristol, Shipman and adult cardiac surgery. Int. J. Qual. Health Care 2003, 15, 7–13. [Google Scholar] [CrossRef]
- Norén, G.N.; Bate, A.; Hopstadius, J.; Star, K.; Edwards, I.R. Temporal pattern discovery for trends and transient effects: Its application to patient records. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: Las Vegas, NV, USA, 2008; pp. 963–971. [Google Scholar]
- Hauben, M.; Norén, G.N. A decade of data mining and still counting. Drug Saf. 2010, 33, 527–534. [Google Scholar] [CrossRef]
- Madigan, D.; Ryan, P. Commentary: What can we really learn from observational studies? The need for empirical assessment of methodology for active drug safety surveillance and comparative effectiveness research. Epidemiology 2011, 22, 629. [Google Scholar] [CrossRef]
- Ray, W.A. Improving automated database studies. Epidemiology 2011, 22, 302–304. [Google Scholar] [CrossRef]
- Walker, A.M. Signal detection for vaccine side effects that have not been specified in advance. Pharmacoepidemiol. Drug Saf. 2010, 19, 311–317. [Google Scholar] [CrossRef]
- Reisinger, S.J.; Ryan, P.B.; O’Hara, D.J.; Powell, G.E.; Painter, J.L.; Pattishall, E.N.; Morris, J.A. Development and evaluation of a common data model enabling active drug safety surveillance using disparate healthcare databases. J. Am. Med. Inform. Assoc. 2010, 17, 652–662. [Google Scholar] [CrossRef]
- Avillach, P.; Joubert, M.; Thiessard, F.; Trifirò, G.; Dufour, J.C.; Pariente, A.; Mougin, F.; Polimeni, G.; Catania, M.A.; Giaquinto, C. Design and evaluation of a semantic approach for the homogeneous identification of events in eight patient databases: A contribution to the European EU-ADR project. Stud. Health. Technol. Inform. 2010, 160, 1085. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suling, M.; Pigeot, I. Signal Detection and Monitoring Based on Longitudinal Healthcare Data. Pharmaceutics 2012, 4, 607-640. https://doi.org/10.3390/pharmaceutics4040607
Suling M, Pigeot I. Signal Detection and Monitoring Based on Longitudinal Healthcare Data. Pharmaceutics. 2012; 4(4):607-640. https://doi.org/10.3390/pharmaceutics4040607
Chicago/Turabian StyleSuling, Marc, and Iris Pigeot. 2012. "Signal Detection and Monitoring Based on Longitudinal Healthcare Data" Pharmaceutics 4, no. 4: 607-640. https://doi.org/10.3390/pharmaceutics4040607




