A Linkage among Tree Diameter, Height, Crown Base Height, and Crown Width 4-Variate Distribution and Their Growth Models: A 4-Variate Diffusion Process Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Stochastic Differential Equation Model
2.2. Marginal and Conditional Distributions
2.3. Maximum Likelihood Estimates
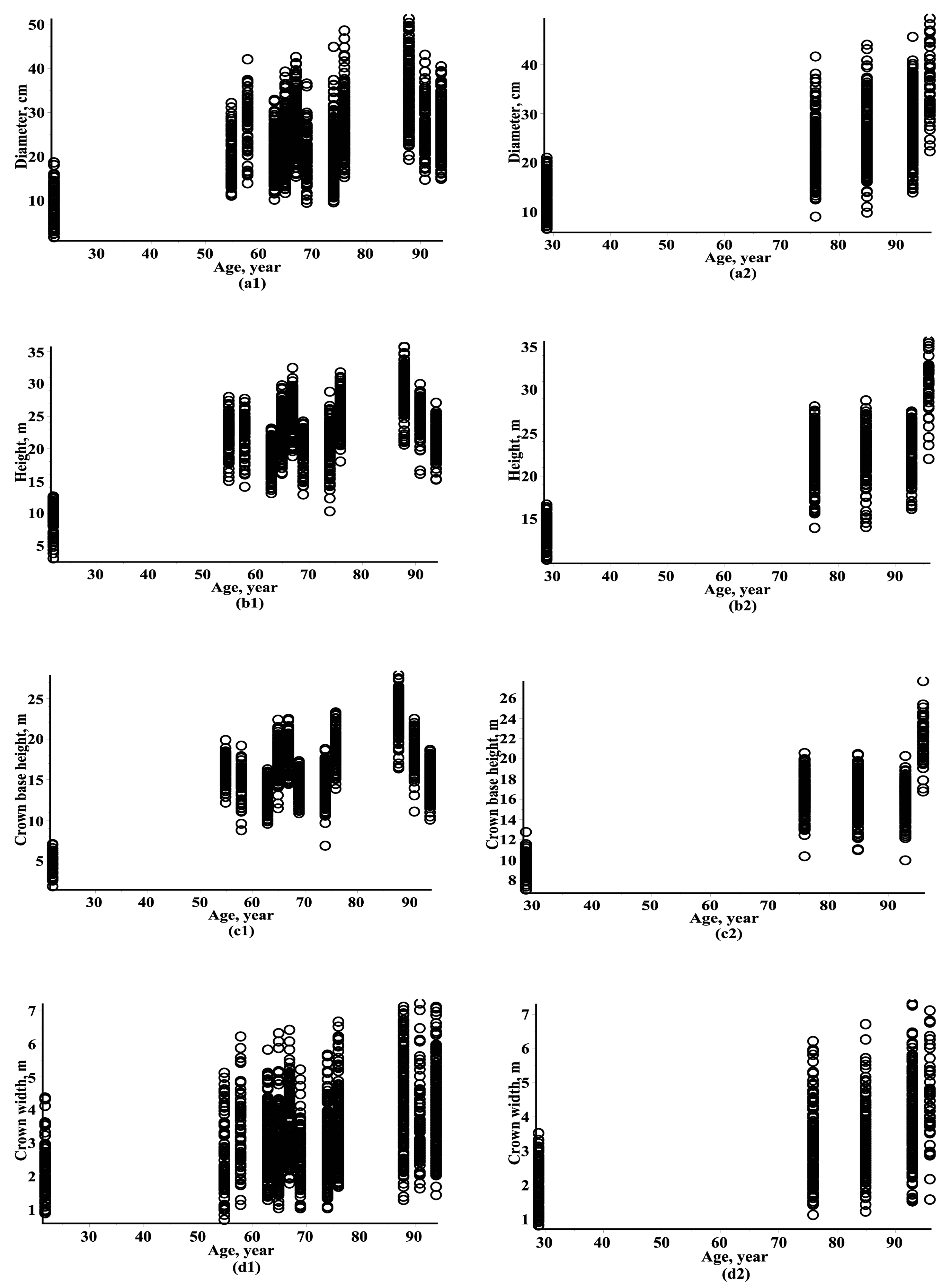
2.4. Data
3. Results and Discussion
3.1. Estimating Results
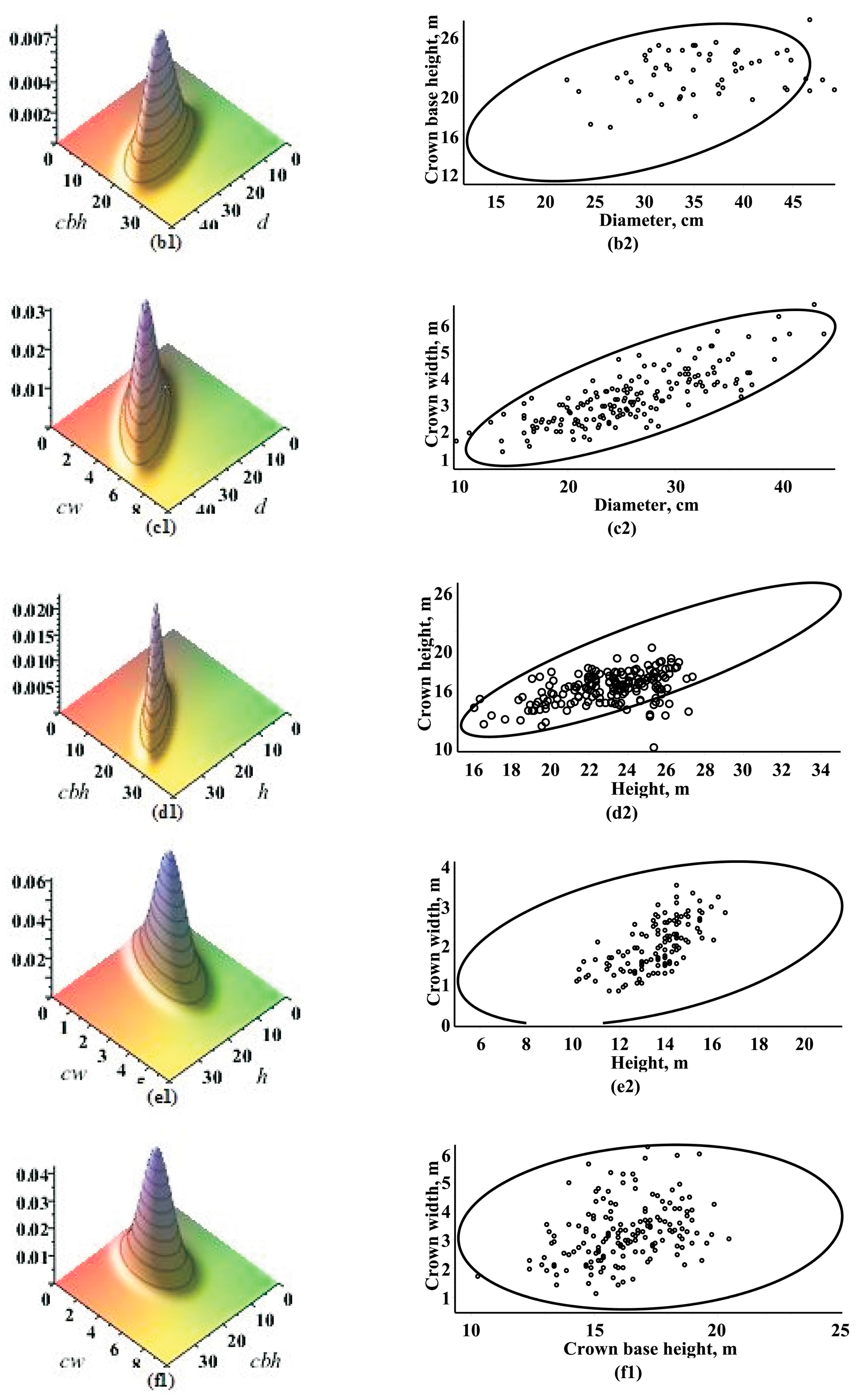
3.2. Marginal Bivariate Distributions
3.3. Coefficient of Correlation
3.4. Diameter, Height, Crown Base Height and Crown Width Dynamical Models
- in the first scenario, a tree size component was linked to tree age (one model, marginal univariate densities are defined by Equations (13) and (14));
- in the second scenario, a tree size component was linked to tree age and one size component (three models, conditional univariate densities are defined by Equations (24) and (25));
- in the third scenario, a tree size component was linked to tree age and two size components (three models, conditional univariate densities are defined by Equations (22) and (23));
- in the fourth scenario, a tree size component was linked to tree age and three size components (one model, conditional univariate densities are defined by Equations (20) and (21)).
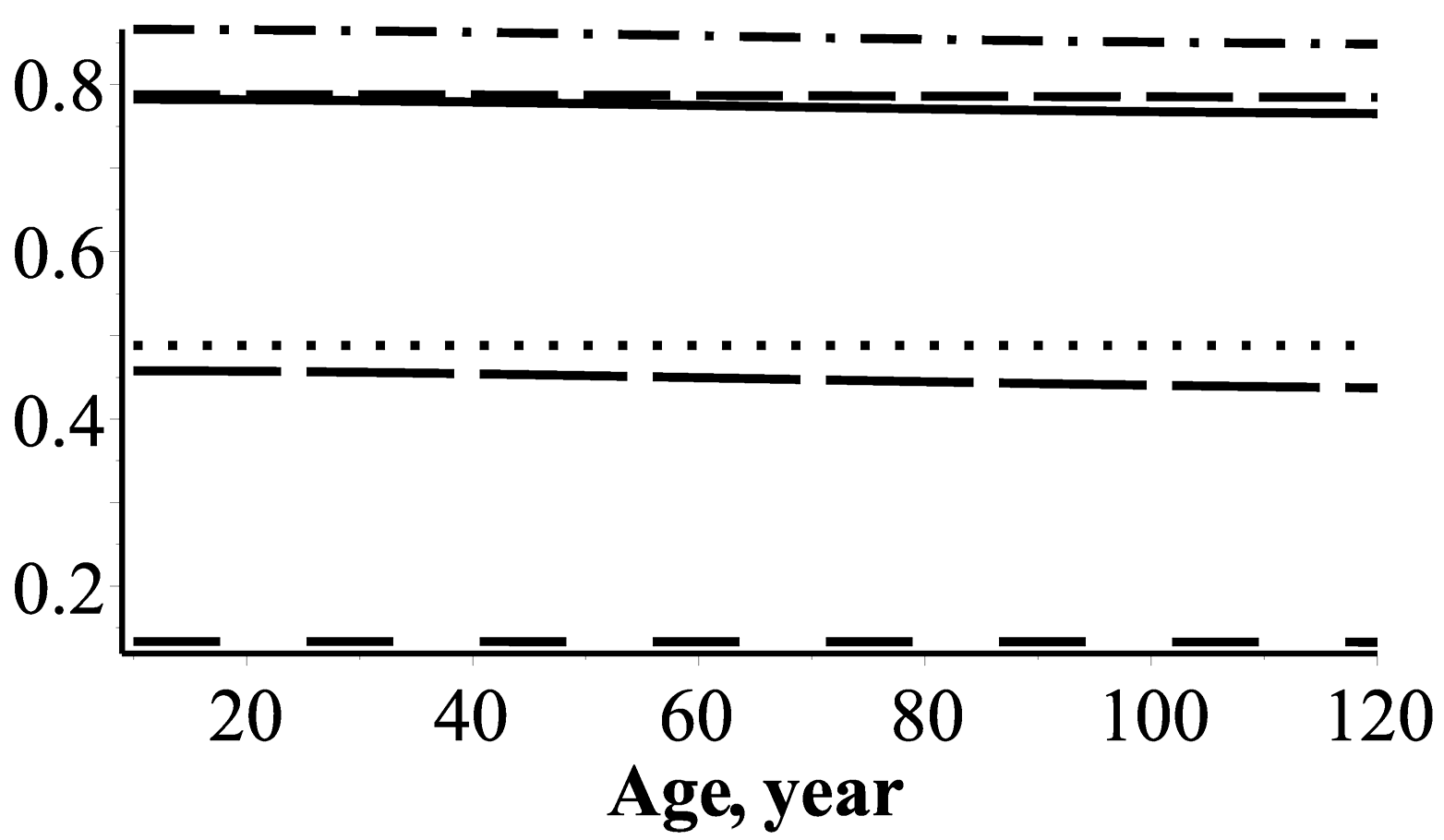
3.5. Slenderness
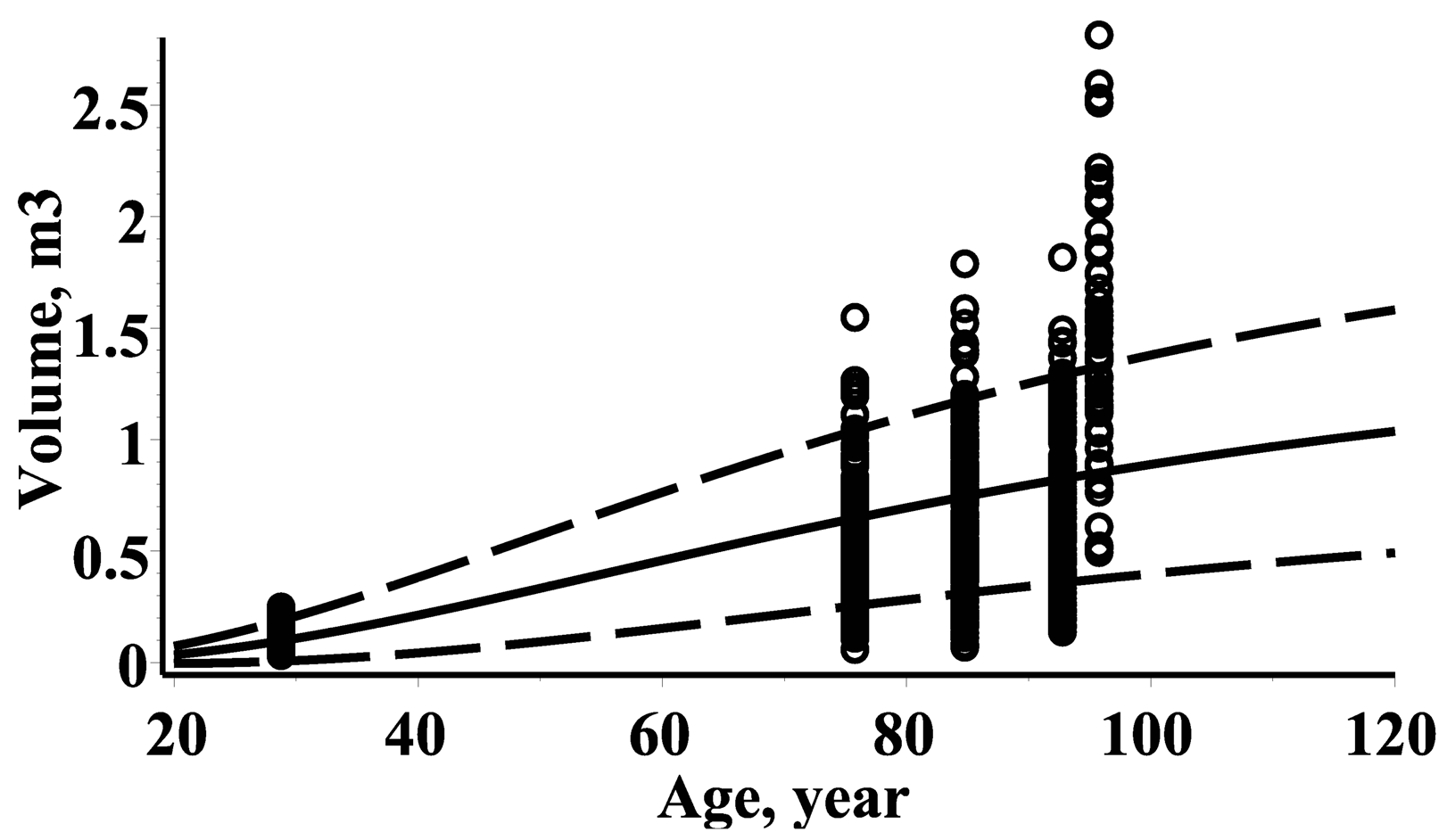
3.6. Mean and Standard Deviation of Stem Volume
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krainovic, P.; Almeida, D.; Sampaio, P. New allometric equations to support sustainable plantation management of rosewood (Aniba rosaeodora Ducke) in the Central Amazon. Forests 2017, 8, 327. [Google Scholar] [CrossRef]
- King, D.A. Size-related changes in tree proportions and their potential influence on the course of height growth. In Size- and Age-Related Changes in Tree Structure and Function; Meinzer, F.C., Lachenbruch, B., Dawson, T.E., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 165–191. [Google Scholar]
- Von Gadow, K.; Zhang, C.Y.; Wehenkel, C.; Pommerening, A.; Corral-Rivas, J.; Korol, M.; Myklush, S.; Hui, G.Y.; Kiviste, A.; Zhao, X.H. Forest structure and diversity. In Continuous Cover Forestry; Pukkala, T., Von Gadow, K., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 29–83. [Google Scholar]
- Mirzaei, M.; Aziz, J.; Mahdavi, A.; Rad, A.M. Modeling frequency distributions of tree height, diameter and crown area by six probability functions for open forests of Quercus persica in Iran. J. For. Res. 2015, 27, 901–906. [Google Scholar] [CrossRef]
- Mohammadalizadeh, A.K.; Namiranian, M.; Zobeiri, M.; Abd-alhosein, H.; Marvie Mohajer, M.R. Modeling of frequency distribution of tree’s height in uneven-aged stands (Case study: Gorazbon district of Khyroud forest). J. For. Wood Prod. 2013, 66, 155–165. [Google Scholar]
- Gorgoso-Varela, J.J.; García-Villabrille, J.D.; Rojo-Alboreca, A.; von Gadow, K.; Álvarez-González, J.G. Comparing Johnson’s SBB, Weibull and Logit-Logistic bivariate distributions for modeling tree diameters and heights using copulas. For. Syst. 2016, 25, 1–5. [Google Scholar] [CrossRef]
- Møller, J.K.; Madsen, H.; Carstensen, J. Parameter estimation in a simple stochastic differential equation for phytoplankton modelling. Ecol. Model. 2011, 222, 1793–1799. [Google Scholar] [CrossRef]
- Rupšys, P. The use of copulas to practical estimation of multivariate stochastic differential equation mixed effects models. AIP Conf. Proc. 2015, 1684, 80011. [Google Scholar] [CrossRef]
- Cai, W.; Pan, J. Stochastic differential equation models for the price of European CO2 Emissions Allowances. Sustainability 2017, 9, 207. [Google Scholar] [CrossRef]
- Rupšys, P.; Petrauskas, E. Analysis of height curves by stochastic differential equations. Int. J. Biomath. 2012, 5, 1–15. [Google Scholar] [CrossRef]
- Rupšys, P. Generalized fixed-effects and mixed-effects parameters height–diameter models with diffusion processes. Int. J. Biomath. 2015, 8, 1–23. [Google Scholar] [CrossRef]
- Rupšys, P. New insights into tree height distribution based on mixed effects univariate diffusion processes. PLoS ONE 2016, 11, e0168507. [Google Scholar] [CrossRef] [PubMed]
- Petrauskas, E.; Bartkevičius, E.; Rupšys, P.; Memgaudas, R. The use of stochastic differential equations to describe stem taper and volume. Balt. For. 2013, 19, 43–151. [Google Scholar]
- Rupšys, P. Stochastic mixed-effects parameters Bertalanffy process, with applications to tree crown width modeling. Math. Probl. Eng. 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Itô, K. On stochastic processes. Jpn. J. Math. 1942, 18, 261–301. [Google Scholar] [CrossRef]
- Arnold, L. Stochastic Differential Equations; John Wiley and Sons: New York, NY, USA, 1973. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of Brownian motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Tong, Y.L. The Multivariate Normal Distribution; Springer Series in Statistics; Springer-Verlag: New York, NY, USA, 1990. [Google Scholar]
- Monagan, M.B.; Geddes, K.O.; Heal, K.M.; Labahn, G.; Vorkoetter, S.M.; Mccarron, J. Maple Advanced Programming Guide; Maplesoft: Waterloo, ON, Canada, 2007. [Google Scholar]
- Rupšys, P.; Petrauskas, E. A new paradigm in modelling the evolution of a stand via the distribution of tree sizes. Sci. Rep. 2017, 7, 15875. [Google Scholar] [CrossRef] [PubMed]
- Uria-Diez, J.; Pommerening, A. Crown plasticity in Scots pine (Pinus sylvestris L.) as a strategy ofadaptation to competition and environmental factors. Ecol. Model. 2017, 356, 117–126. [Google Scholar] [CrossRef]
- Temesgen, H.; LeMay, V.; Mitchell, S.J. Tree crown ratio models for multi-species and multi-layered stands of southeastern British Columbia. For. Chron. 2005, 81, 133–141. [Google Scholar] [CrossRef]
- Petrauskas, E.; Rupšys, P. The Generalised height-diameter equations of Scots pine (Pinus sylvestris L.) trees in Lithuania. Rural Dev. 2013, 6, 407–411. [Google Scholar]


| Parameters of Drift Term | |||||||||
| α1 | β1 | α2 | β2 | α3 | β3 | α4 | β4 | ||
| 37.3302 | 0.0174 | 27.6250 | 0.0277 | 24.0573 | 0.0177 | 4.9822 | 0.0137 | ||
| Parameters of Diffusion Term | |||||||||
| σ11 | σ12 | σ13 | σ14 | σ22 | σ23 | σ24 | σ33 | σ34 | σ44 |
| 1.8334 | 1.0057 | 0.4150 | 0.2242 | 0.9010 | 0.5159 | 0.0913 | 0.3937 | 0.0176 | 0.0441 |
| Estimation | Validation | |||||||
|---|---|---|---|---|---|---|---|---|
| B, m (PB, %) | Model | AE, m (Rank) | R2 (Rank) | B, m (PB, %) | AB, m (PAB, %) | AE, m | R2 | |
| Diameter | ||||||||
| Equation (13) A | −0.006 (−9.079) | 5.452 (26.148) | 6.800 (8) | 0.334 (8) | −0.842 (−10.942) | 5.293 (25.612) | 6.554 (8) | 0.432 (8) |
| Equation (24) A, H | 0.006 (−2.262) | 3.409 (15.243) | 4.302 (5) | 0.733 (5) | 0.382 (−1.976) | 3.260 (14.354) | 4.111 (4) | 0.773 (4) |
| Equation (24) A, CH | 0.004 (−5.865) | 4.751 (22.162) | 5.869 (7) | 0.503 (7) | 0.376 (−5.605) | 4.788 (22.256) | 5.990 (7) | 0.517 (7) |
| Equation (24) A, CW | −0.006 (−4.211) | 3.237 (15.053) | 4.216 (4) | 0.744 (4) | −0.491 (−4.368) | 3.282 (15.189) | 4.186 (5) | 0.766 (5) |
| Equation (22) A, H, CH | 0.00001 (−5.377) | 4.408 (20.330) | 5.452 (6) | 0.571 (6) | 0.311 (−5.098) | 4.441 (20.495) | 5.536 (6) | 0.587 (6) |
| Equation (22) A, H, CW | 0.002 (−1.021) | 2.072 (9.083) | 2.731 (2) | 0.892 (2) | 0.237 (−0.231) | 2.240 (9.887) | 2.873 (2) | 0.889 (2) |
| Equation (22) A, CH, CW | 0.002 (−1.964) | 2.479 (11.002) | 3.285 (3) | 0.844 (3) | 0.461 (−0.531) | 2.784 (12.370) | 3.601 (3) | 0.826 (3) |
| Equation (20) A, H, CH, CW | 0.001 (−0.971) | 2.034 (9.005) | 2.674 (1) | 0.896 (1) | 0.091 (−0.326) | 2.204 (9.964) | 2.804 (1) | 0.892 (1) |
| Height | ||||||||
| Equation (13) A | −0.016 (−4.085) | 3.225 (15.770) | 3.926 (8) | 0.473 (8) | −0.904 (−5.834) | 2.478 (12.032) | 3.328 (8) | 0.592 (8) |
| Equation (24) A, D | −0.013 (−2.078) | 2.014 (9.818) | 2.491 (6) | 0.788 (6) | −0.539 (−2.950) | 1.654 (7.638) | 2.086 (5) | 0.837 (5) |
| Equation (24) A, CH | 0.005 (−0.720) | 1.603 (7.921) | 1.999 (4) | 0.863 (4) | 0.287 (−0.143) | 1.664 (7.977) | 2.178 (6) | 0.813 (6) |
| Equation (24) A, CW | −0.019 (−3.661) | 2.872 (14.161) | 3.510 (7) | 0.578 (7) | −0.786 (−4.669) | 2.192 (10.382) | 2.899 (7) | 0.688 (7) |
| Equation (22) A, D, CH | 0.001 (−0.405) | 0.968 (4.618) | 1.253 (2) | 0.946 (1−2) | 0.191 (0.085) | 1.036 (4.962) | 1.320 (2) | 0.931 (1) |
| Equation (22) A, D, CW | −0.009 (−1.623) | 1.809 (8.672) | 2.276 (5) | 0.822 (5) | −0.492 (−2.801) | 1.612 (7.501) | 2.049 (4) | 0841 (4) |
| Equation (22) A, CH, CW | 0.002 (−0.578) | 1.200 (5.732) | 1.540 (3) | 0.919 (3) | 0.314 (0.445) | 1.291 (6.100) | 1.695 (3) | 0.888 (3) |
| Equation (20) A, D, CH, CW | 0.001 (−0.406) | 0.967 (4.616) | 1.252 (1) | 0.946 (1–2) | 0.074 (1.319) | 1.034 (4.956) | 1.319 (1) | 0.931 (2) |
| Crown Base Height | ||||||||
| Equation (13) A | −0.009 (−5.573) | 2.592 (18.191) | 3.134 (8) | 0.507 (8) | −1.135 (−7.942) | 2.148 (14.535) | 2.683 (8) | 0.554 (8) |
| Equation (24) A, D | −0.008 (−4.718) | (2.206 (15.889) | 2.706 (6) | 0.632 (6) | −0.946 (−6.447) | 1.914 (12.884) | 2.478 (6) | 0.602 (6) |
| Equation (24) A, H | −0.003 (−1.866) | 1.272 (9.134) | 1.586 (4) | 0874 (4) | −0.512 (−2.919) | 1.275 (8.714) | 1.729 (4) | 0.793 (4) |
| Equation (24) A, CW | −0.009 (−5.649) | 2.559 (18.170) | 3.079 (7) | 0.518 (7) | −1.108 (−7.710) | 2.115 (14.330) | 2.670 (7) | 0.554 (7) |
| Equation (22) A, D, H | −0.002 (−1.120) | 1.060 (7.343) | 1.362 (3) | 0.907 (3) | −0.439 (−2.294) | 1.151 (7.925) | 1.500 (2) | 0.844 (3) |
| Equation (22) A, D, CW | −0.006 (−3.432) | 1.917 (13.256) | 2.414 (5) | 0.707 (5) | −0.882 (−6.019) | 1.810 (12.061) | 2.362 (5) | 0.636 (5) |
| Equation (22) A, H, CW | −0.002 (−1.048) | 1.056 (7.159) | 1.358 (2) | 0.907 (2) | −0.477 (−2.672) | 1.130 (7.692) | 1.510 (3) | 0.844 (2) |
| Equation (20) A, D, H, CW | −0.001 (−0.989) | 1.033 (7.027) | 1.329 (1) | 0.911 (1) | −0.451 (−2.417) | 1.121 (7.585) | 1.470 (1) | 0.850 (1) |
| Crown Width | ||||||||
| Equation (13) A | −0.0003 (−13.536) | 0.908 (33.124) | 1.129 (8) | 0.141 (8) | −0.066 (−13.737) | 0.829 (30.005) | 1.048 (8) | 0.284 (7) |
| Equation (24) A, D | 0.003 (−4.829) | 0.540 (18.554) | 0.701 (4) | 0.668 (4) | 0.047 (−3.294) | 0.520 (17.404) | 0.671 (4) | 0.705 (4) |
| Equation (24) A, H | 0.001 (−10.287) | 0.804 (28.622) | 1.008 (6) | 0.313 (6) | 0.054 (−7.652) | 0.711 (24.248) | 0.918 (6) | 0.447 (6) |
| Equation (24) A, CH | 5.7 × 10−6 (−13.161) | 0.898 (32.724) | 1.115 (7) | 0.160 (7) | −0.009 (−12.018) | 0.816 (29.099) | 1.043 (7) | 0.284 (8) |
| Equation (22) A, D, H | −1.5 × 10−5 (−4.311) | 0.4878 (16.699) | 0.6410 (3) | 0.7214 (3) | 0.0163 (−4.661) | 0.497 (17.033) | 0.645 (3) | 0.724 (3) |
| Equation (22) A, D, CH | −0.0002 (−3.980) | 0.474 (16.011) | 0.626 (2) | 0.734 (1−2) | −0.069 (−5.416) | 0.485 (16.477) | 0.631 (2) | 0.739 (1) |
| Equation (22) A, H, CH | 2.3 × 10−5 (−7.117) | 0.670 (22.835) | 0.865 (5) | 0.492 (5) | −0.111 (−8.290) | 0.640 (21.929) | 0.805 (5) | 0.578 (5) |
| Equation (20) A, D, H, CH | −0.0001 (−3.977) | 0.474 (16.010) | 0.6254 (1) | 0.734 (1–2) | −0.065 (−5.291) | 0.484 (16.446) | 0.631 (1) | 0.738 (2) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rupšys, P.; Petrauskas, E. A Linkage among Tree Diameter, Height, Crown Base Height, and Crown Width 4-Variate Distribution and Their Growth Models: A 4-Variate Diffusion Process Approach. Forests 2017, 8, 479. https://doi.org/10.3390/f8120479
Rupšys P, Petrauskas E. A Linkage among Tree Diameter, Height, Crown Base Height, and Crown Width 4-Variate Distribution and Their Growth Models: A 4-Variate Diffusion Process Approach. Forests. 2017; 8(12):479. https://doi.org/10.3390/f8120479
Chicago/Turabian StyleRupšys, Petras, and Edmundas Petrauskas. 2017. "A Linkage among Tree Diameter, Height, Crown Base Height, and Crown Width 4-Variate Distribution and Their Growth Models: A 4-Variate Diffusion Process Approach" Forests 8, no. 12: 479. https://doi.org/10.3390/f8120479
APA StyleRupšys, P., & Petrauskas, E. (2017). A Linkage among Tree Diameter, Height, Crown Base Height, and Crown Width 4-Variate Distribution and Their Growth Models: A 4-Variate Diffusion Process Approach. Forests, 8(12), 479. https://doi.org/10.3390/f8120479





