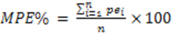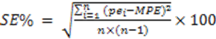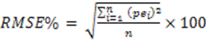1. Introduction
Vegetation clearance has perhaps been the most significant threat to forests and woodlands in the countries of sub-Saharan Africa. The net loss of forests and woodlands in the region was recently estimated at 4 million ha per year over the last two decades (1990–2010) [
1]. Malawi alone lost an estimated 33,000 ha per year, representing a 2.6% annual loss of forests and woodlands on freehold land in the country. During the same period, many landholders in Malawi replanted forests and encouraged regrowth of indigenous woodlands. These restored forest areas contributed over 70% of the total forests (3.2 million hectares) on freehold land in 2010 [
1]. However, as these planted forests and regrowth are not protected from clearing under the Malawi Forest Act of 1997 [
2], there is a serious question over the security of the long-term value they provide to biodiversity and the global carbon cycle. This situation can be improved through revenue earned from carbon credits that is conditioned on areas, that have been planted, being maintained into the future, as is the case under the emissions trading schemes of Clean Development Mechanism (CDM) of the Kyoto Protocol [
3] and the Reducing Emissions from All Land Uses (REALU or REDD++) [
4]. These schemes allow landholders to sell the carbon sequestered in trees and forest stands to industries and governments to offset some of their greenhouse gas emissions [
3].
To begin carbon trading, landholders need reliable estimates of the carbon sequestered in their forest stands. Accurate estimates of carbon stocks depend to a great degree on the availability and adequacy of the allometric equations that are used to estimate tree biomass [
3,
5,
6]. Allometric equations are a fundamental tool for the non-destructive estimation of biomass in woody vegetation and their value depends on the empirical data used to construct such equations [
7]. These equations express tree biomass as a function of easy-to-measure parameters such as diameter, height, wood density, or a combination of these [
6,
8]. The equations are generated from a small sample of trees and are then used to estimate biomass on a larger scale.
Several generalized allometric equations for biomass estimation in broad types of forest ecosystems have been developed for tropical forests, especially in the Amazon Basin [
6,
9,
10,
11,
12,
13]. However, generalized whole ecosystem equations can be inaccurate when used to estimate biomass of individual tree species [
10,
14,
15,
16]. Species-specific models remain more accurate than the generalized models [
16]. This is because individual species allometry takes into account differences in wood density, tree form, and its architecture, all of which can affect the modeled relationship between the easy-to-measure parameters and the biomass of individual trees [
9].
Species-specific allometric equations do exist for many forest ecosystems [
17,
18,
19] but they are not widely available for tropical trees. Even where these models exist, they are not often transferable to the same species growing in a different environment, as they tend to be site specific [
17]. This is due to the fact that tree growth is affected by site characteristics and climatic conditions [
20]. Species- and site-specific allometric equations are the most accurate and precise [
16] and they are recommended for estimating the biomass of high value tree species. Typical examples are the tree species that are planted and/or managed for carbon sequestration potential under the emissions trading schemes of CDM and REDD++ and these tree species require precise and accurate estimates of their biomass in order to attain credibility in the carbon markets [
12].
Jatropha curcas (
Jatropha) is extensively planted by smallholder farmers in Malawi as a high value tree species used as a feedstock for the production of bio fuel. Establishment of
Jatropha has been successful in drier regions of the tropics with an annual rainfall of 300–1000 mm. It favors lower altitudes (0–500 m) with average annual temperatures of 20–28 °C, but can grow at higher altitudes and tolerates slight frost [
21]. Its seeds are rich in highly extractible oil. The oil produces minimal smoke and has better efficiency than diesel in its pure or mixed forms [
21,
22,
23]. The planting of
Jatropha in Malawi is predominantly promoted by a private bio-energy company (Bio-Energy Resources Limited). The company seeks to acquire carbon financial payments through carbon stocks sequestered by the growing of
Jatropha trees. Robust allometric equations that estimate the carbon stocks of the growing trees on the farmers’ fields is a prerequisite to the acquisition of Verified Carbon Units (VCUs) under most existing verification standards (e.g., VCS v3.0 2011 [
24]).
Ghezehei
et al. [
23] and Achten
et al. [
25] developed allometric models for estimating aboveground biomass in
Jatropha. The work by Achten
et al. [
25] was based on data from
Jatropha seedlings and Ghezehei’s work was based on data from
Jatropha trees that were grown under research trial conditions with prescribed and scheduled silvicultural operations. Our study uses data from
Jatropha trees that are planted and managed together with other agricultural crops under smallholder farming systems. Kuyah
et al. [
7] and Brassard
et al. [
26] observed that applying forest-based allometric models to trees that are growing under farm conditions are constrained by factors that influence biomass allocation. For example, trees on a farm are often managed through pruning and coppicing, and they periodically benefit from agricultural operations such as fertilization intended to improve crop production. This study therefore aims to determine local allometric equations for estimating the woody biomass of
Jatropha trees growing under smallholder farming systems.
4. Discussion
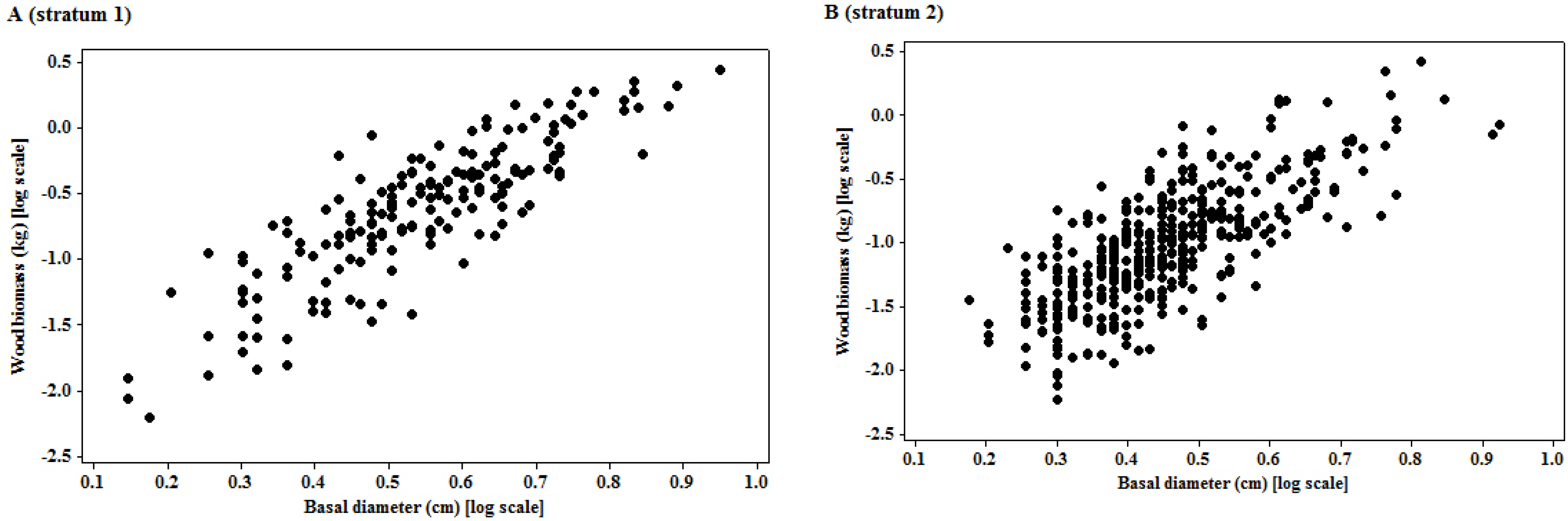
The logarithmic transformation of the basal diameter and woody biomass had put the two variables on a multiplicative scale, which was appropriate for interpreting most size variables, since biological growth is a multiplicative process [
34]. Converting arithmetic data to logarithms, however, is a nonlinear transformation that fundamentally alters the relationship between predictor and response variables [
35]. The change in the relationship is such that influential outliers in the arithmetic domain may be drawn toward the centre of the distribution, and can thereby go undetected, potentially introducing bias into the analysis [
36]. In order to avoid this in our study, the detection of influential outliers was first done on data expressed in arithmetic scale as recommended by Packard
et al. [
36]. Transformation of the two variables was done thereafter.
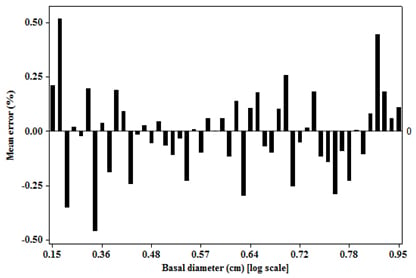
The significant linear relationship observed on the transformed variables is neither surprising nor new. The importance of the relationship of the two variables is underpinned by the size of the mean prediction errors, as the quality of landscape scale measures depend on this [
7]. The unbiased estimates of the woody biomass observed in the study sites are an indication of the robustness of the model in providing such unbiased estimates at the landscape level. However, when considering the prediction of biomass of individual trees, the root mean square error (RMSE), as a measure of deviation of the estimated individual tree biomass from their mean, is more important than bias [
7]. RMSE helped to get the variability of bias, as
zero bias might result when under- or over-estimates cancel out while predicting a lot of trees, but the prediction of an individual tree may be inaccurate. The values of RMSE (%) observed in this study provide a measure of imprecision of the model for individual tree estimations. The imprecision of the model observed in this study might have been introduced by the rotational distortion that accompanies regression analyses performed on logarithms. Because of the nonlinear relationship between values expressed in arithmetic and logarithmic scales, small arithmetic values for predictor and response have a much greater influence than large values on parameters (scaling coefficient,
β0, and exponent,
β1) of the linear equations fitted on logarithmic transformations [
36].
The weak relationship observed between tree height and woody biomass in this study may be due to the fact that the stem of
Jatropha rarely grows to diameter at breast height (DBH) before branching [
23]. Cole and Ewel [
37] reported that complicated branching patterns of woody dicots (in which
Jatropha is a member) obfuscate the form-function relationship that results in a weak relationship between the two size variables. These observations agree with our findings of a weak relationship between tree height that defines tree form and woody biomass (functional variable). Tree height is more tedious to measure in woody dicots and, as noted in this study, may not explain more of the variance at the site where the data originated. Ketterings
et al. [
38] observed, however, that the incorporation of tree height in allometric models has the advantage of increasing the equation’s potential applicability to different sites. This argument might apply for monocots, which show a strong relationship between the two size variables [
37].
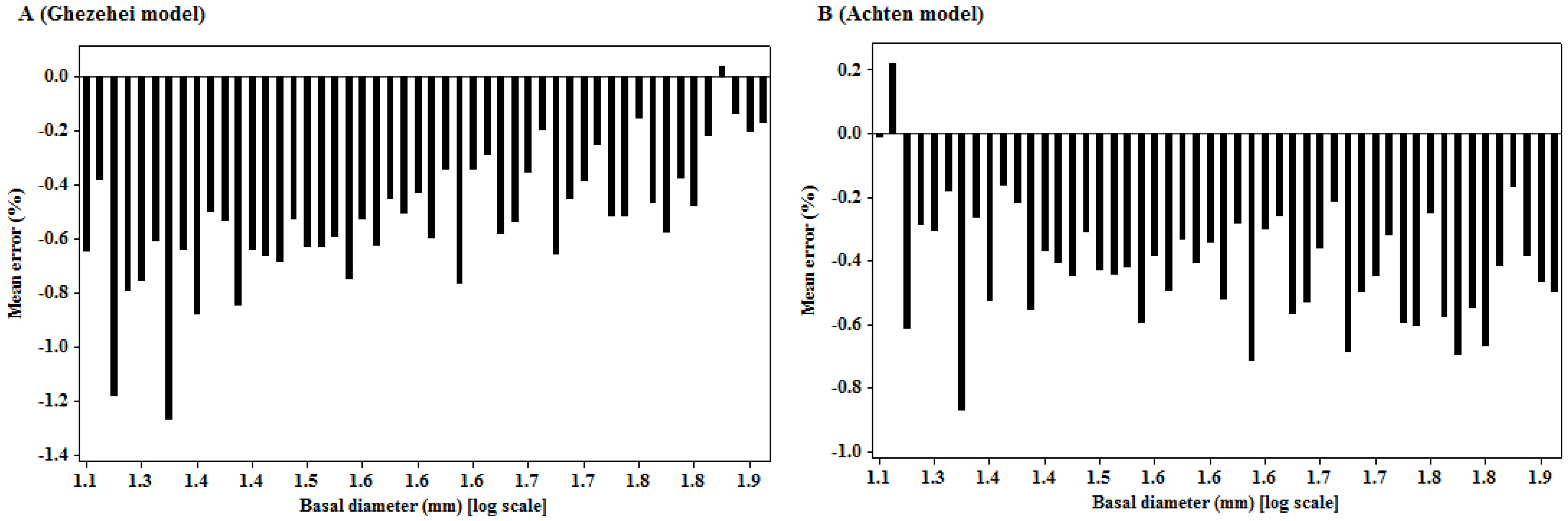
The consistent over-estimation of tree biomass estimates across the basal diameter size classes by other published
Jatropha models (Ghezehei
et al. [
23] and Achten
et al. [
25]) indicates that these models are not appropriate for application in their present form for our study sites. The variations are mainly due to differences in the site characteristics, silvicultural practices, and development stage of the
Jatropha plants on which allometric data was collected. Our study used data from actively growing
Jatropha plants aged 12 to 33 months old that were planted and managed under smallholder farming systems, whereas the work by Achten
et al. [
25] was based on data from
Jatropha seedlings that were planted in greenhouses, and Ghezehei’s work [
23] was based on data from
Jatropha trees that were grown under trial conditions with prescribed and scheduled silvicultural operations.
The most recent allometric research in trees and forests tends to focus on explaining the scaling of structural and functional properties of trees with measures of their body sizes (e.g., diameters, heights) [
36]. West
et al. [
29] suggested that the scaling exponent (
β1) should scale against tree diameter with a universal exponent
β1 ≈ 2.67 on trees whose height increments are at their maximum. Pilli
et al. [
10] confirmed this theoretical value for adult plants and showed that the scaling exponent values are lower for younger trees (
β1≈ 2.08–2.51). The lower exponent values for young trees (seedlings) were confirmed by Achten
at al. [
25]. The scaling exponent values for our study (
β1 ≈2.891 and 2.769 for stratum 1 and 2 respectively) lie within 2.53 and 3.16 at the 95% confidence limits (
Table 4). As such the above presented empirical allometric relationship of woody biomass fits well in a universal model [
10] and confirms the results of Achten
et al. [
25] that
Jatropha follows the universal allometric model described by [
29] and confirmed by [
5,
10].
5. Conclusions
The present work has developed an allometric model for estimating the woody biomass of
Jatropha planted on an agricultural landscape under a smallholder farming systems in Malawi. The predictive performance of the model was assessed and provided satisfactory estimates of woody biomass in the study sites with insignificant biases. The results of the statistical fits of the model were generally good, enabling one to use the model with confidence for the estimation of woody biomass in
Jatropha stands on agricultural landscapes from which they were derived. The published
Jatropha models of Achten
et al. [
25] and Ghezehei
et al. [
23] were tested and the results showed consistent over-estimation of tree biomass across the basal diameter classes, rendering them unsuitable for application in estimating tree biomass in our study sites.
Although the model provides precise estimates of the woody biomass of Jatropha, its use is limited to the range of the tree sizes that were used in its development and sites from where the data was collected (Salima, Nkhotakota, Dowa, Kasungu, and Mzimba districts). Outside these ranges, the model needs to be tested against the field data to determine its appropriateness. The observed robustness and precision of the model could have been enhanced if the effects of rotational distortion that accompanies regression analyses performed on logarithms was detected and eliminated, thereby reducing the imprecision of estimating individual tree biomass.