Application of the 3-PG Model for Gross Primary Productivity Estimation in Deciduous Broadleaf Forests: A Study Area in Japan
Abstract
: The physiological principles predicting growth (3-PG) model is generally used to estimate gross primary productivity (GPP) in forest plantations. All existing parameter values in the 3-PG model for GPP estimation have been set as the standard values for eucalyptus and pine plantations. We propose that the 3-PG model can be applied to deciduous broadleaf forests dominated by Betula platyphylla via appropriate parameterization of their structure and functions. The allometric relationships between stem biomass and stem diameter, and between foliage biomass and stem biomass, were determined for the biomass partitioning ratio. Additionally, a temperature modifier was considered appropriate because it affected canopy quantum efficiency. After parameterization, the model showed a good correlation between the estimated results and the data from experimental plots in central and northern Japan. At both sites, GPP peaked around August and was 0 during the winter, when the canopy is bare of leaves. Furthermore, a sensitivity analysis was conducted to determine the most influential parameter relative to the output. GPP was sensitive to changes in canopy quantum efficiency and optimum temperature. Among the meteorological data used, solar radiation and temperature had great impacts on GPP, therefore, these parameters should be carefully considered to produce accurate results.1. Introduction
Process-based models, which were created in response to studies examining changes in environmental factors or management interventions [1,2], have the potential to reflect the nonlinear relationships between physiological processes and environmental factors. In forests, environmental factors affect the canopy structure, canopy density, biomass partitioning, and physiological processes. Intensive studies of the effects of environmental factors improve researchers' understanding of processes influencing forest growth [3].
Among process-based models, the physiological principles predicting growth (3-PG) model is often used to estimate forest properties in fast-growing forests and forest plantations [3-7]. The 3-PG model has been used to bridge the gap between conventional empirical, mensuration-based growth and yield models, and process-based carbon balance models [8]. The 3-PG model is primarily used for forest plantations or even-aged, relatively homogeneous forests, but this type of model can also be applied to various environments and species. However, parameterization is needed for individual species [9]. Eucalyptus globulus and E. grandis were initially parameterized by Sands and Landsberg [10] and Almeida et al. [11]. For other species, parameter values were adjusted to fit the output based on in situ measurements. Dye [7] and Dye et al. [12] used the 3-PG model to predict the growth and water use of Pinus patula and eucalyptus plantations. This model has been applied to analyses of forest productivity of various species in countries such as Australia, Brazil, Canada, New Zealand, South Africa, and the U.S. [3,4,13-16]. However, parameterizations are still lacking, especially for natural forests which can act as carbon sinks. To develop parameter values for natural forests, in situ measurements are required.
Forest ecosystems in middle and high latitudes of the northern hemisphere have large effects on the carbon cycle, because leaf phenological processes of forests in these regions, such as deciduous broadleaf forests, correspond to carbon sequestration. In this paper we attempted parameterization of the 3-PG model for deciduous broadleaf forests in Japan. We focused on parameters related to biomass production because biomass related to outputs as GPP provides valuable information that will aid in understanding the carbon status of the biosphere. The objective of this study was to assign standard parameter values for deciduous broadleaf forests in the 3-PG model that the original model and previous studies have not calibrated. Our results should make the 3-PG model more applicable to additional species. Moreover, sensitivity analyses were conducted to investigate the parameters with the most influence on output. Parameters identified as sensitive could then be carefully parameterized to calculate output with higher accuracy.
2. The 3-PG Model
2.1. Overview
Landsberg and Waring [8] initiated the 3-PG model as a simple process-based model, on the stand level, for forest growth. The model is composed of five sub-models: assimilation of carbohydrates; biomass partitioning to foliage, stem, and roots; determination of stem number; soil water balance; and the conversion of biomass into variables of interest to forest managers.
2.2. Data Inputs
The main input parameters required are site factors and species-specific data of the species of interest (Table 1). The site factors include latitude, maximum available soil water (ASWx: mm), soil texture (sandy, sandy loam, clay, or clay loam), and fertility rating (FR). Species-specific parameter values are adjusted for each species. If the parameter values for a species do not exist, parameterization of the new site-specific parameter is necessary. Another input is meteorological variables, including mean air temperature (Ta: °C), mean solar radiation (SR: MJ m−2 day−1), total precipitation (R: mm), frost days (dF: days per month), and vapor pressure deficit (VPD: mbar). If VPD is not available, it can be calculated from the maximum and minimum temperatures (Tx and Tn: °C) as half the difference between the saturated vapor pressure at Tx and Tn. The meteorological inputs can be actual monthly data or long-term monthly averages.
2.3. Data Outputs
The outputs are primarily foliage, root, and stem biomass (WF, WR, and WS: t ha−1), gross primary productivity (GPP: t ha−1), and net primary productivity (NPP: t ha−1). Other stand-level outputs can be leaf area index (LAI), specific leaf area (SLA), stem volume (V: m3 ha−1), stem number (N: trees ha−1), average stem diameter at breast height (B: cm), and mean annual stem-volume increment (MAI: m3 ha−1 year−1). 3-PG outputs can be estimated monthly or annually, as well as over longer periods.
2.4. Major Elements of the 3-PG Model for Parameterization
In this study, we focused on parameterization of deciduous broadleaf forests for GPP. The species-specific parameters involved in estimating GPP are part of biomass partitioning and biomass production. Biomass partitioning is related to biomass allocation to the stem, foliage, and roots, each of which is influenced by the GPP. Biomass partitioning is controlled by the ratio of foliage to stem biomass allocation. Root biomass allocation is influenced by soil nutrition and available soil water. However, root data were not available in this study. The partitioning ratio between foliage biomass and stem biomass (pFS) is a function of stem diameter, as shown in the allometric relationship in Equation (1):
To obtain as and ns (Equation (2)), we determine the relationship between Ws and B by fitting the allometric relationship from the observed data. aF and nF (Equation (3)) are from the allometric relationship between WF and B.
In biomass production, growth modifiers directly influence GPP. This modification accounts for environmental conditions affecting forest growth. The six growth modifiers are temperature (fT), frost day (fF), site nutrition (fN), available soil water (fθ), vapor pressure deficit (fD), and stand age (fAGE). The value of each modifier ranges from 0 to 1. As a modifier approaches 0, it has a stronger influence on forest growth [8,10]. Temperature and frost effects control biomass production in this study area. The equations describing each modifier are as follows. The other modifiers have been reported by Landsberg and Waring [8].
2.5. Temperature Modifier
This parameter is given by the expression:
2.6. Frost Day Modifier
This parameter is calculated by the expression:
GPP is calculated as shown in Equation (6), by converting absorbed photosynthetically active radiation (APAR, ϕpa) to GPP using the canopy quantum efficiency (αC), which is constrained by the growth modifiers [8,10]:
Then, GPP is estimated using Equation (8):
3. Materials and Methods
3.1. Site Description
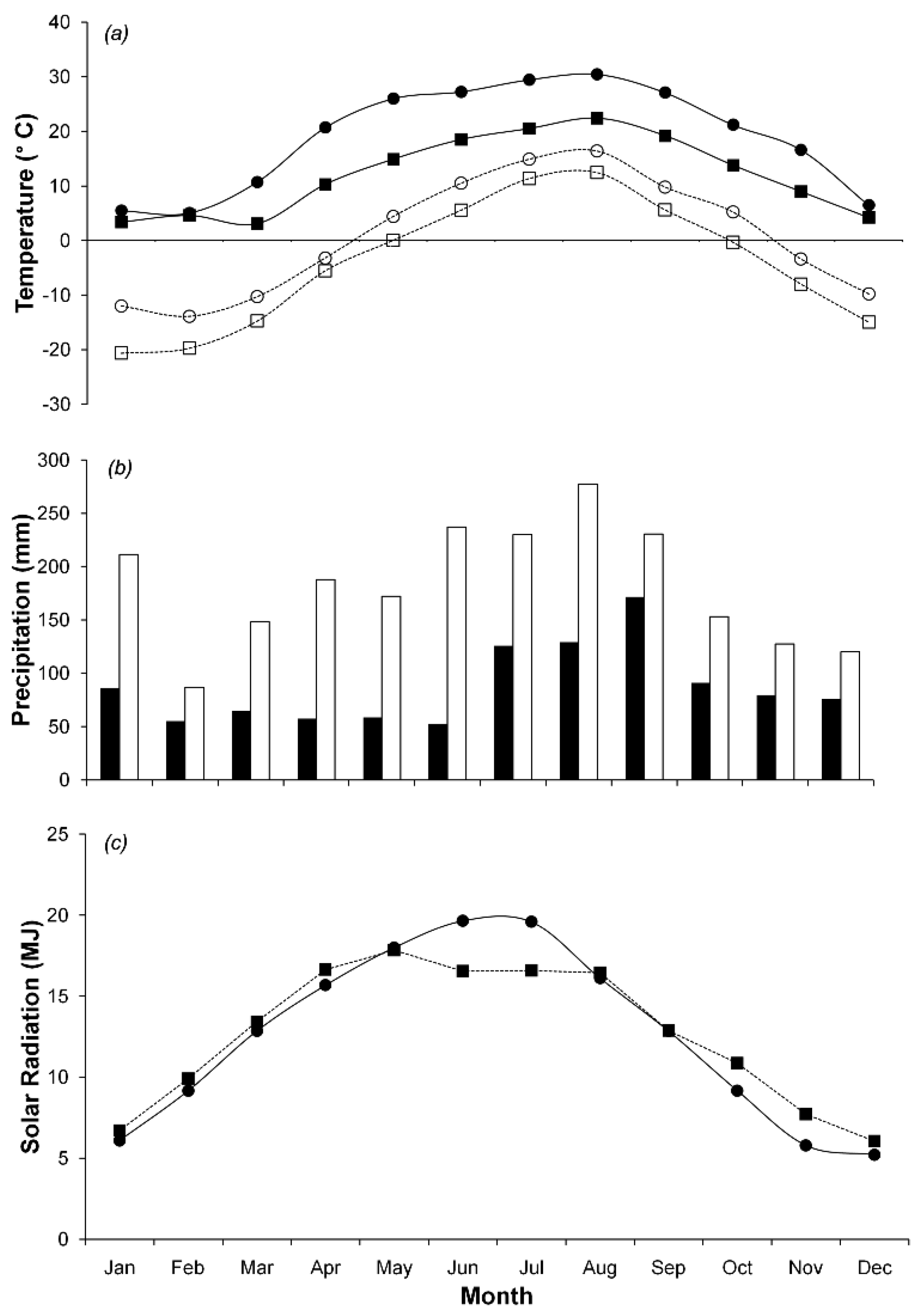
We collected data at two study sites, Hitsujigaoka and Takayama. Hitsujigaoka is located in northern Japan at 42°59′13″ N and 141°23′7″ E and is 180 m above sea level. Takayama is in central Japan at 36°8′46″ N and 137°25′23″ E and is 1,420 m above sea level. At each site, a flux tower collected meteorological data and ecological characteristics. Averaged over five years, from 2001 to 2006 (Figure 1), the maximum temperatures at Hitsugaoka and Takayama were 24.9 ± 1.8 °C and 22.4 ± 1.6 °C in August, while the minimum temperatures were −12.4 ± 1.7 °C and −11.7 ± 2.1 °C in February, respectively. The mean annual precipitation and mean annual solar radiation at Hitsujigaoka were 1,047 ± 174 mm and 12.25 ± 0.4 MJ m−2 day−1, respectively, whereas at Takayama they were 2,275 ± 165 mm and 12.43 ± 0.3 MJ m−2 day−1, respectively. Both sites experience snow cover in the winter (December to April) to a depth of 1 m.
The main vegetation type was deciduous broadleaf natural forest, and the dominant species was Betula platyphylla. The stand basal area for this species accounted for around 81% and 63% of the total basal area at Hitsujigaoka and Takayama, respectively. Tree height ranged from 14 to 28 m. Overstory trees at Hitsujigaoka (around 100 years) were older than those at Takayama (around 50 years; [19,20]). The mean DBH was larger at Hitsujigaoka (23.0 cm) than at Takayama (11.4 cm; [19]). We note that the flux tower at Hitsujigaoka was compromised and the forest around the flux tower was severely damaged by a typhoon in 2003. Data from Takayama were used for calibration, while data from Hitsujigaoka were used for validation. The different locations did not significantly influence the model output because the two sites are located in the same climatic zone and are characterized by the same canopy species. Site data is summarized in Table 2.
3.2. Flux Tower Measurements
Each site has two flux towers. The first tower continuously monitored meteorological data. The second monitored only ecological properties. Meteorological data, including air temperature, precipitation, global solar radiation, humidity, wind speed, and soil temperature were collected every 30 min. The 3-PG model requires data on air temperature, precipitation, and solar radiation. Figure 1 shows monthly meteorological data, which were used as input parameters, for Hitsujigaoka and Takayama from 2001–2006. Vapor pressure deficit was calculated based on maximum and minimum temperatures. Days when the temperature was below 2 °C were counted as frost days. CO2 flux was measured by the eddy covariance method [21]. These data were collected in 30-min increments and used to validate the results. CO2 flux was used to estimate net ecosystem exchange (NEE). Then, GPP was estimated by NEE and ecosystem respiration. Canopy respiration was not observed in the study, therefore NPP is not available.
3.3. Parameterization for Deciduous Broadleaf Forests
3.3.1. Biomass Partitioning
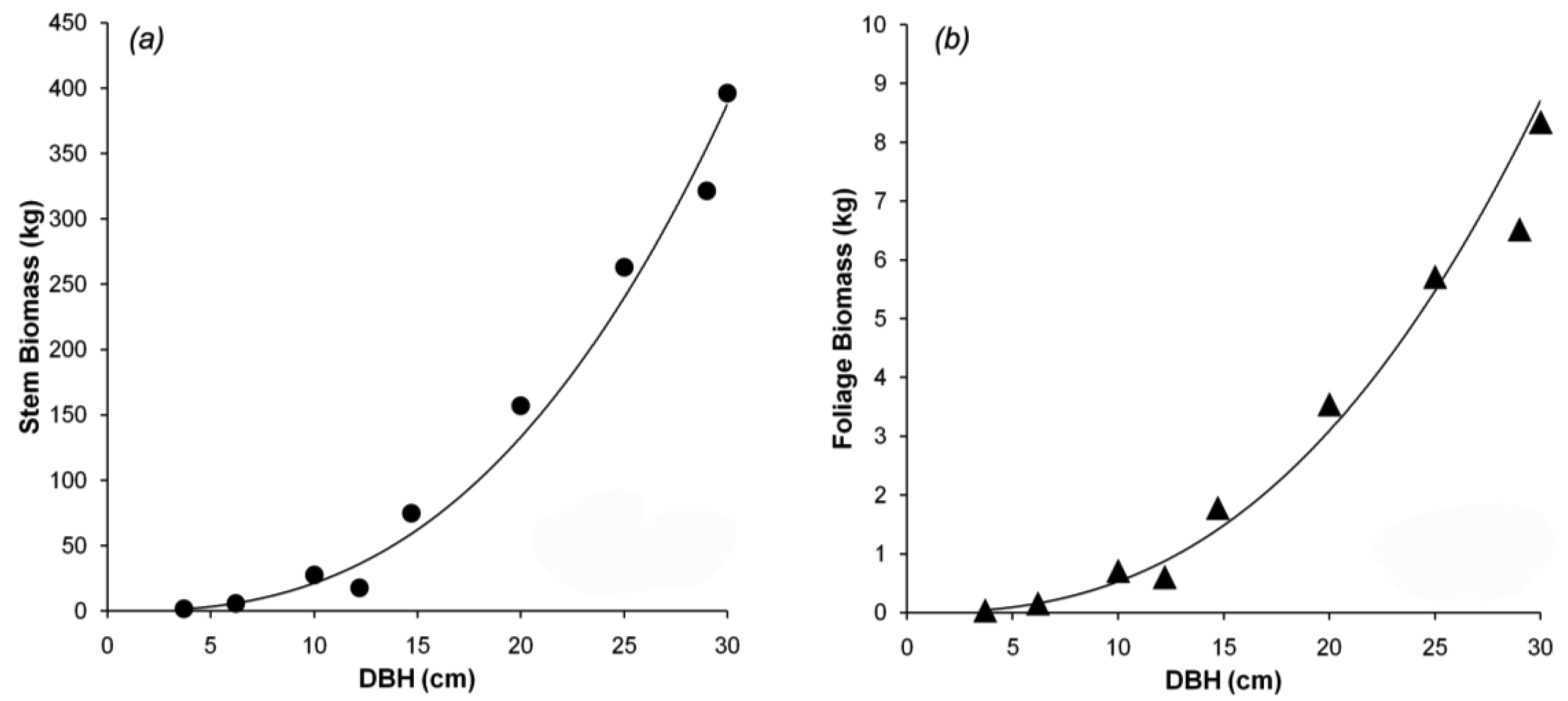
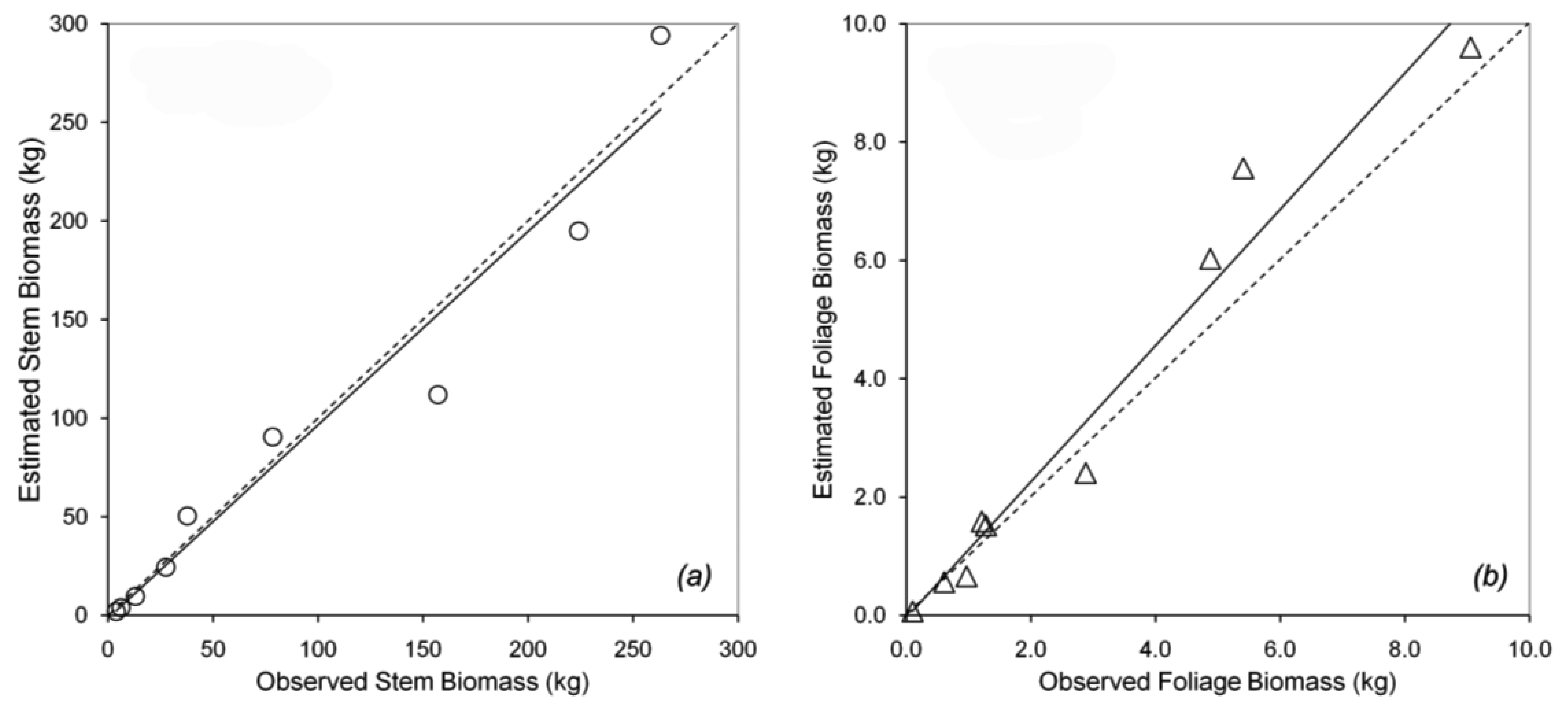
Tree canopy properties were measured in a 100 m × 100 m permanent plot near the flux tower at Takayama [19]. Within the plot, 24 trees (comprising several species) were selected to measure DBH, height, and tree density. Trees with DBH from 1.7 to 29.0 cm were selected to represent the different stand ages, because the actual stand age was not identified. Nine of the 24 sampled trees were B. platyphylla, with a range of small to large DBH. The different DBHs can be used to predict forest growth. The trees were harvested for biomass calculation using the dry mass of the stem and the foliage. Data for B. platyphylla were used for parameterization in biomass partitioning. Figure 2a shows the allometric relationship between DBH and stem biomass. Figure 2b shows the allometric relationship between DBH and foliage biomass. The allometric parameters gave an excellent fit to the trend lines, with r2 = 0.97 and 0.98 for stem and foliage biomass, respectively. The equations in Figure 2 were used to re-estimate stem and foliage biomass at Hitsujigaoka for validation. The results are shown in Figure 3, where the plots of estimated versus observed stem and foliage biomass were close to one-to-one linear relationships. Stem biomass was underestimated by around 3%, whereas foliage biomass was overestimated by about 15%.
From those relationships, as, ns, aF, and nF were calculated as 0.049, 2.64, 0.002, and 2.56, respectively (r2 = 0.97 for stem biomass and 0.98 for foliage biomass). Based on the allometric relationships, aP and nP were computed by substituting as, ns, aF, and nF, to retrieve aP and nP. pFS2 and pFS20 were 0.03 and 0.02, respectively, in these deciduous broadleaf forests of B. platyphylla.
3.3.2. Growth Modifiers
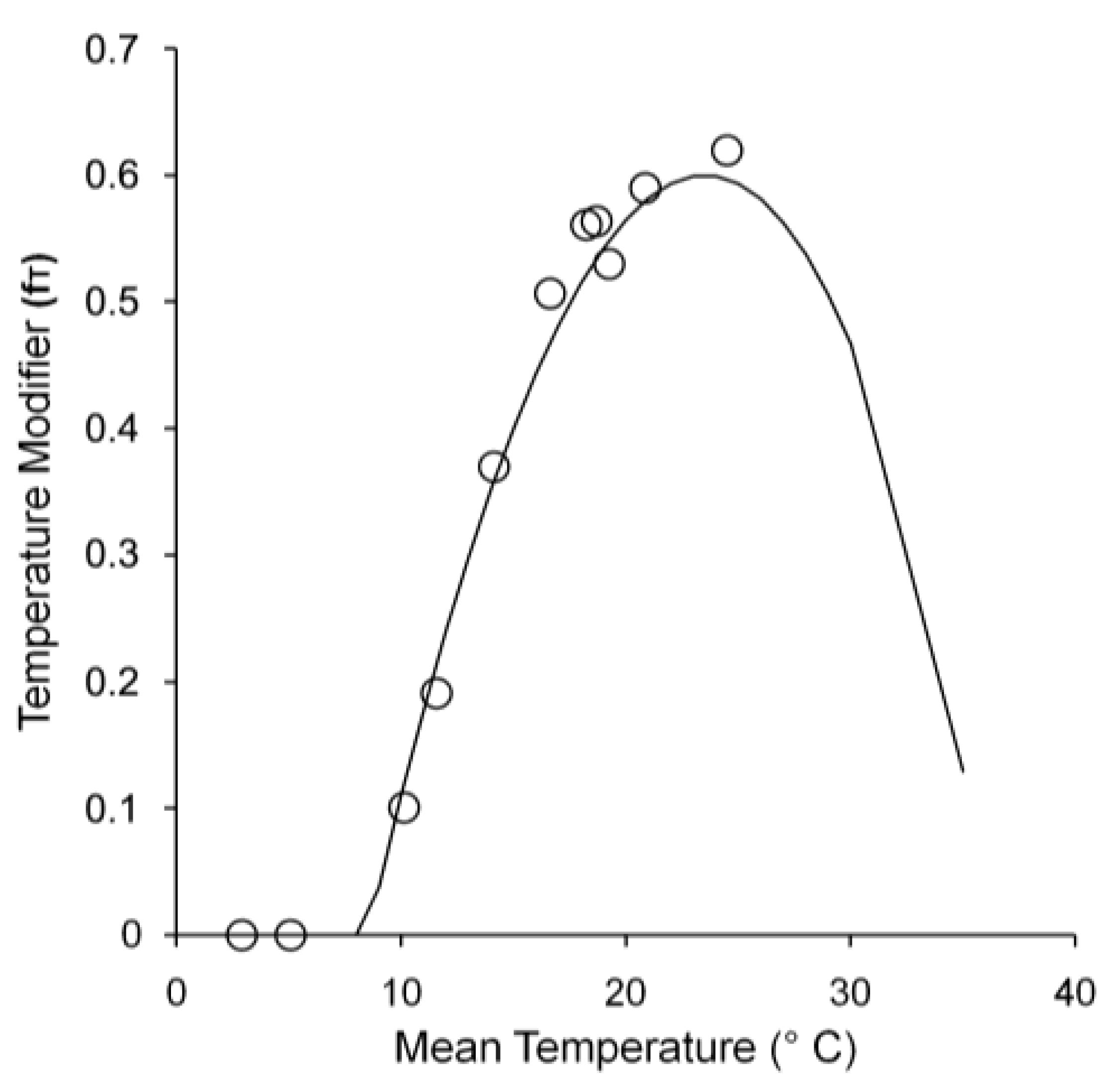
GPP was influenced by LAI and solar radiation, as well as environmental conditions, especially temperature. Figure 4a plots observed GPP with average temperature, solar radiation, and LAI throughout the year. GPP occurred from May to October and was highest in July. Conversely, there was no GPP from November to April. GPP responded to leaf phenology, with leaves emerging in May and falling in November. Solar radiation and LAI peaked in July, resulting in high levels of intercepted solar radiation (Figure 4b) and maximum GPP. The temperature modifier affected quantum efficiency. Figure 5 shows the relationship between mean annual temperature and the temperature modifier to determine Tn, Topt, and Tx for growth. Thus, in this study, Tn, Topt, and Tx were 8.5 °C, 24.5 °C, and 36 °C, respectively. If the mean temperature was less than Tn or greater than Tx, αC was 0 and caused GPP to also be 0.
3.3.3. Other Parameters
Other parameters related to biomass production were assigned values based on direct field measurements. If data were not available for parameterization, a best-fit method was applied by tuning the parameter to obtain an output that corresponded with observed data.
LAI data were obtained using the fish-eye camera method with a Nikon CoolPix camera fitted with a fish-eye lens (Nikon FC-E8). Photos were automatically taken every 2 min during the day and those from 2004 to 2006 were used [22]. Clear sky condition photographs were selected to calculate LAI. LAI data were used to initialize specific leaf area. Litterfall data were collected using 14 traps in a 100 m × 100 m area. Each trap was 1 m2 and was set up for the entire growing season. Tree canopy density was counted based on the amount of tree canopy within the permanent plot. The ratio of NPP/GPP was used to convert GPP to NPP [23]. Note that sites were not constrained by site nutrition or available soil water factors. Parameter values not available for biomass partitioning and biomass production were set as the default values based on the original 3-PG model and did not significantly affect output. All parameter values derived in this study are presented in Table 3.
3.4. Sensitivity Analysis
A sensitivity analysis was carried out to examine how parameter values influenced the output. The parameters examined were as and ns, biomass partitioning ratio at B = 2 and 20 cm, maximum canopy quantum efficiency (αCx), Tn, and Topt. These are the main parameters of biomass partitioning and biomass production, and the most influential for GPP estimation. We determined the effects of changes in these parameters on Ws, Wf, and GPP. Additionally, sensitivity to meteorological data was analyzed with the GPP results. The parameter values changed by −20%, −10%, +10%, and +20% from the default values, except for temperature, which was changed to degrees Celsius (−2 °C, −1 °C, +1 °C, and +2 °C) since changes in degrees Celsius usually showed a more significant effect than those in percentage.
4. Results
Because the study site was a mature forest we do not present an age-series analysis. In this study, we were interested in biomass production because biomass directly relates to the amount of carbon stored by the tree canopy. Our results were validated with the observed data, and a linear regression was applied to investigate accuracy.
4.1. Biomass Calculation
Biomass can be divided into three parts: stem, foliage, and root biomass. We did not examine root biomass because empirical data were not available. Figure 6 shows the estimated stem and foliage biomass versus the observed biomass at each site. Both relationships were close to one-to-one linear relationships. Linear regression showed a high correlation between the estimated and observed values (r2 = 0.89 and 0.94 for stem and foliage biomass, respectively). These values were close to the one-to-one line, in which the estimated values should be equal to the observed values. Foliage and stem biomass at Takayama were slightly overestimated compared to those at Hitsujigaoka. This difference was likely because the canopy at Takayama is younger than that at Hitsujigaoka. A summary of regression statistics is given in Table 4.
4.2. Gross Primary Productivity
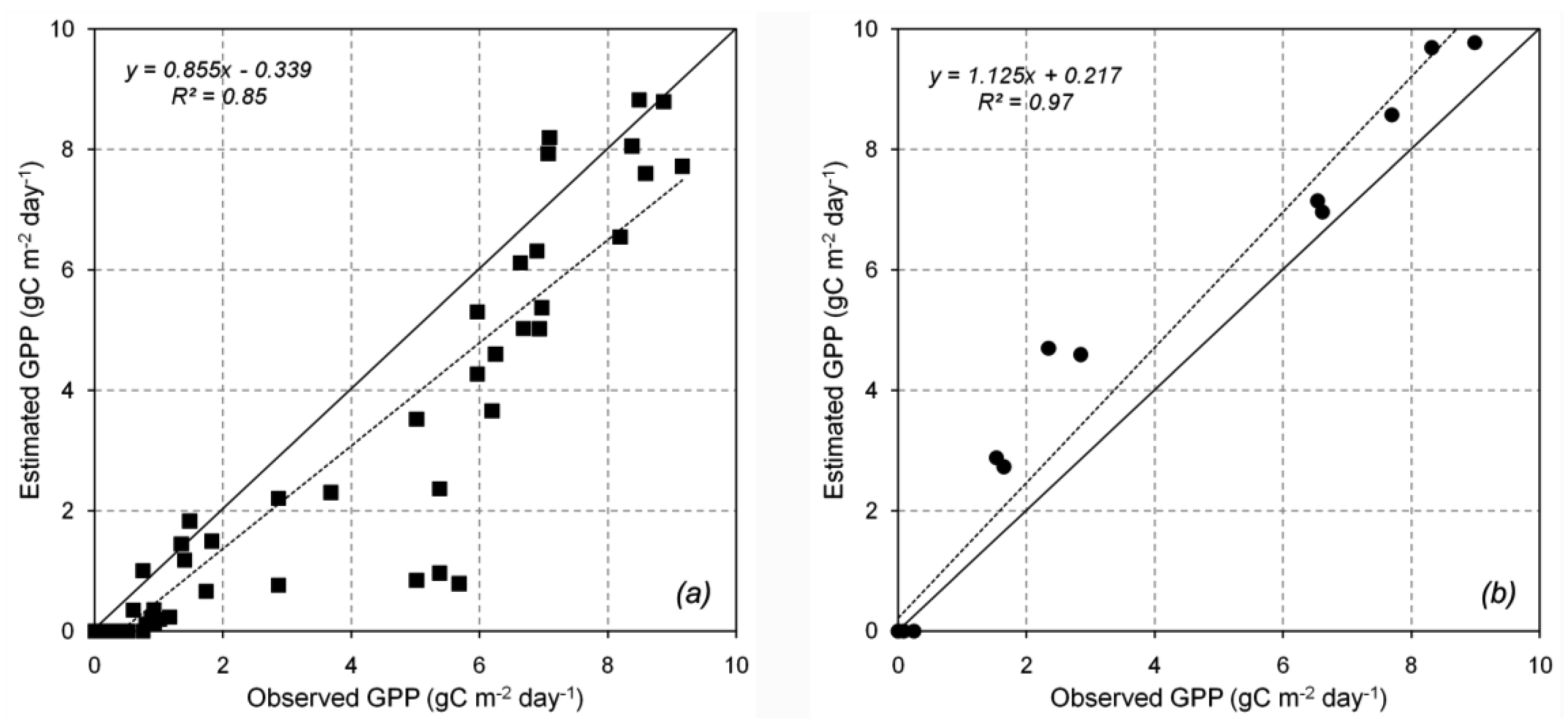
The GPP estimation at Hitsujigaoka and Takayama is presented in Figure 7a and 7b, respectively. The monthly estimated GPP was compared with the observed GPP from 2000 to 2004. The results for both locations showed a good correlation in terms of the linear regression, with r2 = 0.85 and 0.97 at Takayama and Hitsujigoaka, respectively. The 3-PG model indicated that inter-annual GPP peaked around July and August and was 0 in winter (November to April). GPP was lower at Takayama than at Hitsujigaoka because of the smaller LAI at Takayama. Thus, the interception of radiation was lower at Takayama. The GPP at Takayama was underestimated because of the mixed age of the trees in the plot and the influence of the temperature modifier. The low value of the latter at the beginning of the growing season resulted in the low estimate for GPP (low points in the graph). At Hitsujigaoka, the GPP was overestimated because the large tree leaves could absorb more solar radiation for photosynthesis. The average GPP over 5 years was 973.30 g C m−2 (Takayama) and 1255.21 g C m−2 (Hitsujigaoka). Table 4 compares the estimated and observed values of GPP in terms of root mean square error.
4.3. Sensitivity Analysis
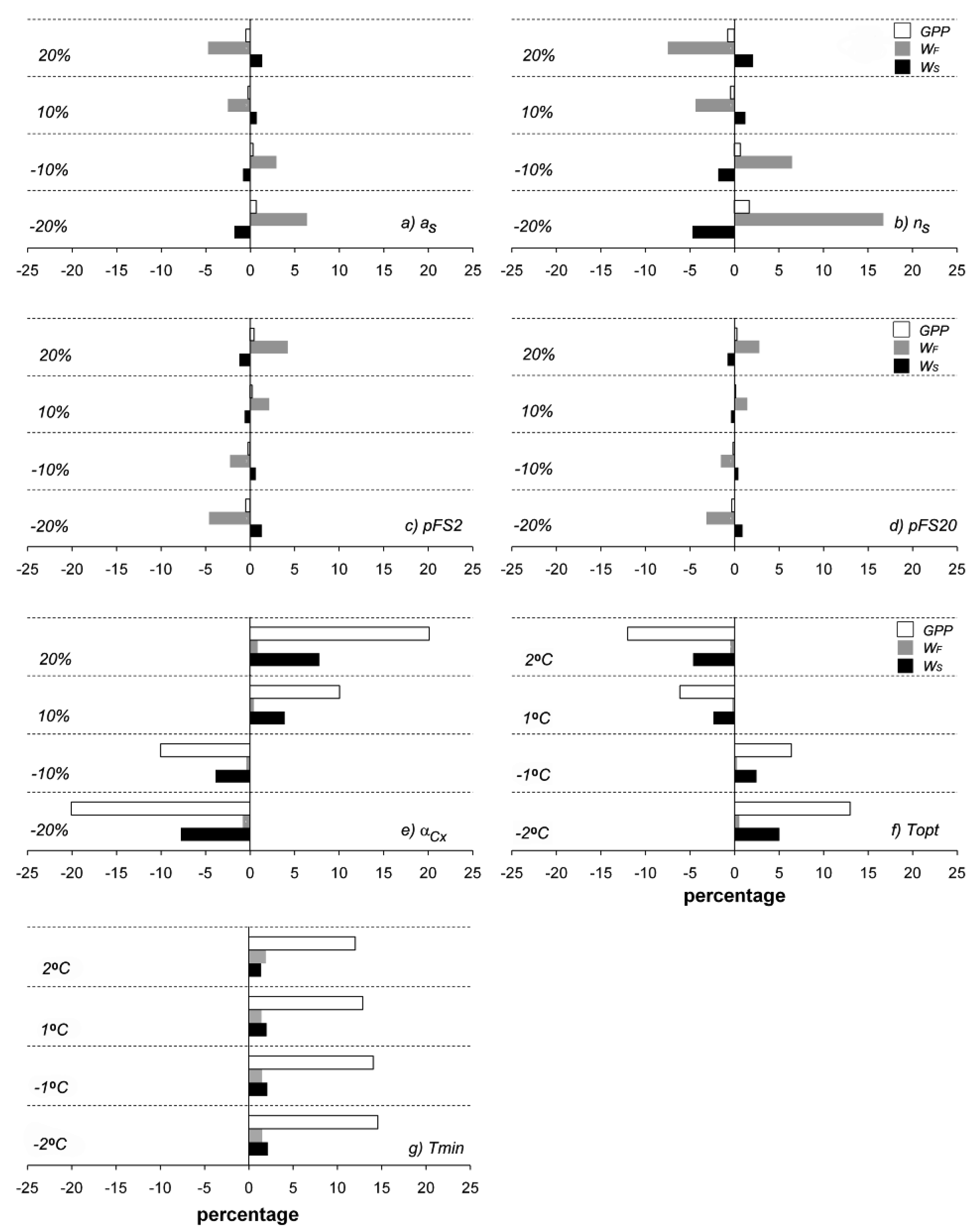
Changing selected parameter values from −20 to 20% had different effects on the estimated output. Figure 8 shows the effects of changes in as, ns, pFS2, pFS20, αCx, Tn, Topt, WF, and Ws. Changes in as (Figure 8a) and ns (Figure 8b) primarily affected WF; when as and ns were changed by −20%, WF differed by around 16% and 6%, respectively. However, the selected outputs were less sensitive to changes in pFS20 (Figure 8d) than pFS2 (Figure 8c). GPP was highly sensitive to αCx (Figure 8e) and to Topt (Figure 8f). Ws was also sensitive to both of those parameters, but not as sensitive as GPP. Tn (Figure 8g) most affected GPP when it was changed by 20 °C. From these results, we recommend that αCx, Topt, and Tn be carefully measured if accurate results are desired, especially in GPP calculations.
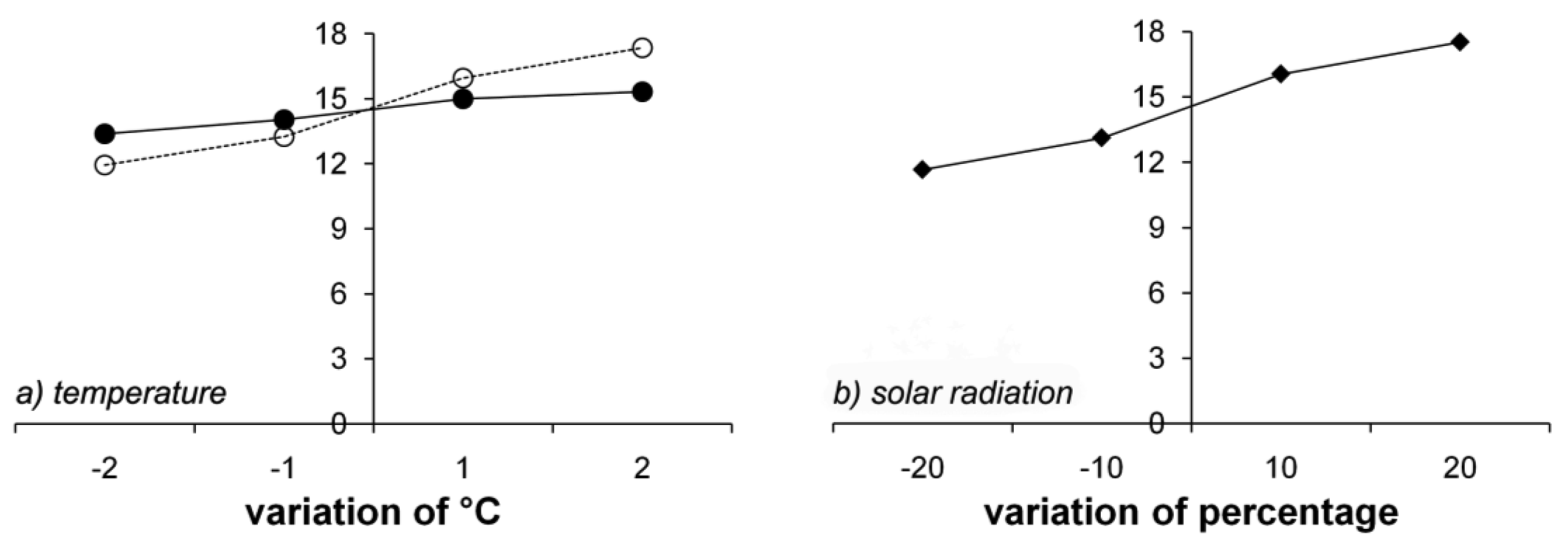
Figure 9 shows the effects of meteorological data on GPP. Solar radiation (Figure 9b) and Tn (Figure 9a) had significant impacts on GPP, with differences around ± 3 g C m−2, but Tx had only a slight effect (Figure 9a). Increased solar radiation and Tn increased GPP. However, GPP was not sensitive to frost days or precipitation, since the study sites are not limited by water. Snow melt increases the soil water content in the summer. The effect of frost days on GPP was large in the winter, as large as the effect of temperature. However, frost days did not affect GPP in the summer, during which GPP was most affected by temperature and solar radiation.
5. Discussion
This study determined the 3-PG model parameter values for a deciduous broadleaf forest dominated by B. platyphylla. The original parameter values were proposed for Eucalyptus forest plantations in Australia [10]. Some authors have directly applied these available parameters to other tree species or indirectly applied tuning methods [12,13,16,24]. The parameter values determined in this study corresponded to mature forest, focusing on biomass production. Data from young forests were not available, so we could not investigate forest growth rate or complete an age-series analysis with the 3-PG model.
An allometric analysis was performed to parameterize biomass partitioning between WS and WF. Our model results were in agreement with empirical data (Figure 6) after parameterization. Even though some default parameter values were used, doing so did not cause significant errors in the output [17]. pFS2 and pFS20 values were moderately different from previous studies [7,10,11]. Deciduous broadleaf forests have annual leaf cycles, and biomass is typically stored in stems and branches throughout the year. However, DBH growth is small due to the short growing season in cool-temperate forests [25,26]. Even though age-series data were not available, trees with different DBH were present, and were assumed to represent different tree ages; these trees were used to find the relationship between relative annual growth rate and above-ground biomass. The relative annual growth rate of estimated above-ground biomass had a trend similar to the observed one. Foliage biomass was highly responsive to leaf phenology (i.e., leaf growth, maturation, senescence, and leaf fall). Litterfall was calculated as a constant fraction of foliage biomass corresponding to leaf growing conditions.
In parameterization, growth modifiers are the main factors affecting GPP calculations [8]. Among the growth modifiers, the temperature modifier had the most effect on αCx. Because our study site was constrained by temperature, the 3-PG model was run so that GPP = 0 when the temperature was lower than Tn or higher than Tx. The temperature at both study sites never reached Tx because it is a cool-temperate area; thus, Tx had no effect on GPP calculations. However, the temperature in the winter was always lower than Tn, and this affected the number of frost days. Thus, the 3-PG model generated GPP values of 0 at Hitsujigaoka and Takayama during winter. GPP is a function of environmental factors and the interception of radiation for photosynthetic processes. Thus, solar radiation (Figure 9b) increased GPP in relation to leaf area. Soil water may be limited at other forest sites, as found in Eucalyptus forest plantations by Esprey et al. [27]. In that case, increased precipitation resulted in increased stand volume, which is relevant to stem biomass. However, our study sites were not limited by water stress because they were located in an Asian monsoon climate region with high precipitation [28]. Additionally, snow melt increases the amount of soil water in the summer. Therefore, precipitation had no effect on GPP.
Biomass production, especially Ws and GPP, was controlled by αCx and Topt (Figure 8). αCx can be highly sensitive, relative to other input parameters [16,27], and directly affects the calculation of GPP. Changes in αCx result in significant differences in GPP. Topt had an inverse relationship with GPP, such that lower temperatures resulted in higher GPP. Tn influenced GPP in the deciduous broadleaf forest examined here, but had no effect in previous studies [27,29]. The large differences in as and ns had strong influences on WF. Almeida et al. [11] also reported the effect of as and ns on WF for E. grandis. Increased ns resulted in increased WF partitioning. However, it is important to note that the various output types had different sensitivity to changes in each parameter.
Even though the growing cycle of deciduous broadleaf forests differs from that of other forest types, such as tropical forest, the set of parameter values indicates that it is not necessary to use a different ratio. Since the parameter values were determined over the entire growing season and there were no leaves in the winter, 3-PG will calculate a GPP of 0 if LAI equals 0. Therefore, there were not increases or losses of biomass during winter. One caveat regarding this study is that root biomass was not included because root data were unavailable at the study site.
The 3-PG model can be applied to estimate biomass production for the deciduous broadleaf tree B. platyphylla. However, long-term empirical data are needed for better understanding parameterization, validating models, and making further improvements in the performance of the 3-PG model.
6. Conclusions
After parameterization, the 3-PG model is applicable to mature, non-water limited deciduous broadleaf forests. The main parameters affecting biomass production are assigned appropriate values from a set of standard parameter values. Some parameters are determined based on empirical data such as the allometric relationships between stem biomass and stem diameter, or between foliage biomass and stem diameter, as well as growth modifiers. Parameters for which empirical data are not available are determined by fitting the output to the observed data. The parameterization in this study emphasized biomass production. Default values were used for parameters that are not involved in biomass production.


| Description of parameter | Symbol | Units |
|---|---|---|
| Biomass partitioning and turnover | ||
| Allometric relationships & partitioning | ||
| Ratio of foliage:stem partitioning at B = 2 cm | p2 | – |
| Ratio of foliage:stem partitioning at B = 20 cm | p20 | – |
| Constant in stem mass v diam. relationship | aS | – |
| Power in stem mass v diam. relationship | nS | – |
| Maximum fraction of NPP to roots | Rx | – |
| Minimum fraction of NPP to roots | Rn | – |
| Litterfall & root turnover | ||
| Litterfall rate at t = 0 | F0 | month−1 |
| Litterfall rate for mature stands | F1 | month−1 |
| Age at which litterfall rate has median value | tF | month |
| Average monthly root turnover rate | R | month−1 |
| Growth modifiers | ||
| Temperature modifier | ||
| Minimum temperature for growth | Tn | °C |
| Optimum temperature for growth | Topt | °C |
| Maximum temperature for growth | Tx | °C |
| Frost modifier | ||
| Number of days production lost for each frost day | kF | days |
| Fertility modifiers | ||
| Value of m when FR = 0 | m0 | – |
| Value of fN when FR = 0 | fN0 | – |
| Power of (1-FR) in fN | nfN | – |
| VPD modifier | ||
| Defines stomatal response to VPD | kD | mbar |
| Soil water modifier | ||
| Moisture ratio deficit which gives fθ = 0.5 | cθ | – |
| Power of moisture ratio deficit in fθ | nθ | – |
| Age modifier | ||
| Maximum stand age used to computer relative age | tx | yr |
| Power of relative age in fage | nage | – |
| Relative age to give fage = 0.5 | rage | – |
| Conductance | ||
| Maximum canopy conductance | gCx | m s−1 |
| Canopy LAI for maximum canopy conductance | LCx | m2 m−2 |
| Canopy boundary layer conductance | gB | m s−1 |
| Canopy structure and processes | ||
| Specific leaf area | ||
| Specific leaf area at stand age 0 | σ0 | m2 kg−1 |
| Specific leaf area for mature aged stands | σ1 | m2 kg−1 |
| Age at which specific leaf area = ½(σ0+σ1) | tσ | yr |
| Rainfall interception | ||
| Maximum fraction of rainfall intercepted by canopy | iRx | – |
| LAI for maximum rainfall interception | Lix | m2 m−2 |
| Light interception, production and respiration | ||
| Extinction coefficient for PAR absorption by canopy | k | – |
| Age at full canopy cover | tc | yr |
| Maximum canopy quantum efficiency | αCx | – |
| Ratio NPP/GPP | Y | – |
| Wood and stand properties | ||
| Basic density | ||
| Minimum basic density—for young trees | ρ0 | t m−3 |
| Maximum basic density—for older trees | ρ1 | t m−3 |
| Age at which ρ = ½ density of old and young trees | tρ | yr |
| Conversion factors | ||
| Intercept of net radiation and solar radiation relationship | Qa | W m−2 |
| Slope of net radiation and solar radiation relationship | Qb | – |
| Molecular weight of dry matter | g mol−1 | |
| Conversion of solar radiation to PAR | mol MJ−1 | |
Source: Sands and Landbergs [10].
| Takayama | Hitsujigaoka | |
|---|---|---|
| Latitude | 36°8′46″ N | 42°59′13″ N |
| Longitude | 137°25′23″ E | 141°23′7″ E |
| Maximum Temperature (°C) | 22.4 | 24.9 |
| Minimum Temperature (°C) | −11.7 | −12.4 |
| Precipitation (mm) | 2,275 | 1,047 |
| Solar Radiation (MJ m−2 day−1) | 12.43 | 12.25 |
| Dominant Species | Betula platyphylla | Betula platyphylla |
| Average Canopy Age (year) | 50 | 100 |
| Mean DBH (cm) | 11.4 | 23 |
| Mean Tree Height (m) | 22 | 24 |
| Description of parameter | Symbol | Units | Default Value | O/L |
|---|---|---|---|---|
| Allometric relationships & partitioning | ||||
| Ratio of foliage:stem partitioning at B = 2 cm | pFS2 | – | 0.03 | O |
| Ratio of foliage:stem partitioning at B = 20 cm | pFS20 | – | 0.02 | O |
| Constant in stem mass v diam. relationship | aS | – | 0.06 | O |
| Power in stem mass v diam. relationship | nS | – | 2.6 | O |
| Litterfall & root turnover | ||||
| Litterfall rate at t = 0 | F0 | month−1 | 0.083 | O |
| Litterfall rate for mature stands | F1 | month−1 | 0.083 | O |
| Age at which litterfall rate has median value | tF | month | 24 | O |
| Average monthly root turnover rate | R | month−1 | 0.083 | L |
| Temperature modifier | ||||
| Minimum temperature for growth | Tn | °C | 8.5 | O |
| Optimum temperature for growth | Topt | °C | 24.5 | O |
| Maximum temperature for growth | Tx | °C | 36 | O |
| Frost modifier | ||||
| Number of days production lost for each frost day | kF | days | 1 | O |
| VPD modifier | ||||
| Defines stomatal response to VPD | kD | mbar | 0.05 | O |
| Stem Number | ||||
| Basic density | ρ | t m−3 | 0.6 | O |
| Maximum tree stem mass for 1,000 trees ha−1 | wSx1000 | kg tree−1 | 180 | O |
| Conductance | ||||
| Maximum canopy conductance | gCx | m s−1 | 0.02 | O |
| Canopy LAI for maximum canopy conductance | LCx | m2 m−2 | 3.33 | O |
| Specific leaf area | ||||
| Specific leaf area at stand age 0 | σ0 | m2 kg−1 | 16 | L |
| Specific leaf area for mature aged stands | σ1 | m2 kg−1 | 16 | L |
| Age at which specific leaf area = ½(σ0 + σ1) | tσ | yr | 2.5 | L |
| Light interception, production and respiration | ||||
| Extinction coefficient for PAR absorption by canopy | k | – | 0.565 | O |
| Maximum canopy quantum efficiency | αCx | – | 0.012 | O |
| Ratio NPP/GPP | Y | – | 0.422 | O |
| Parameters | Site | N | Equation | RMSE | Standard deviation |
|---|---|---|---|---|---|
| Ws | HTJ | 9 | 0.98X − 1.59 | 0.95 | 14.40 |
| TKY | 9 | 1.02X + 3.79 | 0.96 | 12.66 | |
| All | 18 | 1.01X + 0.02 | 0.94 | 16.22 | |
| WF | HTJ | 9 | 1.15X − 0.04 | 0.96 | 0.25 |
| TKY | 9 | 1.04X − 0.07 | 0.94 | 0.26 | |
| All | 18 | 1.09X + 0.02 | 0.89 | 0.28 | |
| GPP | HTJ | 24 | 1.13X + 0.22 | 0.97 | 3.21 |
| TKY | 60 | 0.86X − 0.34 | 0.85 | 4.01 |
Acknowledgments
We would like to sincerely thank to National Institute of Advanced Industrial Science and Technology (AIST), Gifu University and Shin Nagai for providing us the flux tower data at Takayama, as well as Kenlo Nishida Nasahara for LAI data. Furthermore, we would like to give special thank Hokkaido Research Center, Forestry and Forest Products Research Institute (FFPRI) especially Hajime Utsugi for the data at Hitsujigaoka. We deeply thank to Takahiro Endo for his valuable comments and all kind supports.
References
- Farquhar, G.D.; Von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar]
- Landsberg, J.J.; Gower, S. Application of Physiological Ecology to Forest Management; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Waring, R.H. A process-based model analysis of environmental limitations on growth of Sitka spruce plantations in Great Britain. Forestry 2000, 73, 65–79. [Google Scholar]
- Coops, N.C.; Waring, R.H.; Landsberg, J.J. Assessing forest productivity in Australia and New Zealand using a physiologically-based model driven with averaged monthly weather data and satellite derived estimates of canopy photosynthetic capacity. Forest. Ecol. Manage. 1998, 104, 113–127. [Google Scholar]
- Landsberg, J.J.; Johnsen, K.H.; Albaugh, T.J.; Allen, L.; McKeand, S.E. Applying 3-PG, a simple process-based model designed to produce practical results, to data from loblolly pine experiments. Forest. Sci. 2000, 47, 43–51. [Google Scholar]
- Law, B.E.; Waring, R.H.; Anthoni, P.M.; Aber, J.D. Measurements of gross and net ecosystem productivity and water vapour exchange of a Pinus ponderosa ecosystem, and an evaluation of two generalized models. Glob. Change Biol. 2000, 6, 155–168. [Google Scholar]
- Dye, P.J. Modelling growth and water use in four Pinus patula stands with the 3-PG model. South Afr. Forest. J. 2001, 191, 53–63. [Google Scholar]
- Landsberg, J.J.; Waring, R.H. A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning. Forest. Ecol. Manage. 1997, 95, 209–228. [Google Scholar]
- Landsberg, J.J.; Waring, R.H.; Coops, N.C. Performance of the forest productivity model 3-PG applied to a wide range of forest types. Forest. Ecol. Manage. 2003, 172, 199–214. [Google Scholar]
- Sands, P.J.; Landbergs, J.J. Parameterisation of 3-PG for plantation grown Eucalyptus globules. Forest. Ecol. Manage. 2002, 163, 273–292. [Google Scholar]
- Almeida, A.C.; Landsberg, J.J.; Sands, P.J. Parameterisation of 3-PG model for fast-growing Eucalyptus grandis plantations. Forest. Ecol. Manage. 2004, 193, 179–195. [Google Scholar]
- Dye, P.J.; Jacobs, S.; Drew, D. Verification of 3-PG growth and water-use predictions in twelve Eucalyptus plantation stands in Zululand, South Africa. Forest. Ecol. Manage. 2004, 193, 197–218. [Google Scholar]
- Coops, N.C.; Waring, R.H. Estimating forest productivity in the eastern Siskiyou Mountains of southwest Oregon using a satellite driven process model, 3-PGS. Can. J. Forest. Res. 2001, 31, 143–154. [Google Scholar]
- Coops, N.C.; Waring, R.H. The use of multiscale remote sensing imagery to derive regional estimates of forest growth capacity using 3-PGS. Remote Sens. Environ. 2001, 75, 324–334. [Google Scholar]
- Whitehead, D.; Hall, G.M.J.; Walcroft, A.S.; Brown, K.J.; Landsberg, J.J.; Tissue, D.T.; Turnbull, M.H.; Griffin, K.L.; Schuster, W.S.F.; Carswell, F.E.; Trotter, C.M.; James, I.L.; Norton, D.A. Analysis of the growth of rimu (Dacrydium cupressinum) in South Westland, New Zealand, using process-based simulation models. Int. J. Biometeorol. 2002, 46, 66–75. [Google Scholar]
- Almeida, A.C.; Landsberg, J.J.; Sands, P.J.; Ambrogi, M.S.; Fonseca, S.; Barddal, S.M.; Bertolucci, F.L. Needs and opportunities for using a process-based productivity model as a practical tool in fast growing Eucalyptus plantation. Forest. Ecol. Manage. 2004, 193, 167–177. [Google Scholar]
- Arneth, A.; Kelliher, F.M.; McSeveny, T.M.; Byers, J.N. Net ecosystem productivity, net primary productivity and ecosystem carbon sequestration in a Pinus radiata plantation subject to soil water deficit. Tree Physiol. 1998, 18, 785–793. [Google Scholar]
- Waring, R.H.; Landsberg, J.J.; Williams, M. Net primary production of forests: A constant fraction of gross primary production. Tree Physiol. 1998, 18, 129–134. [Google Scholar]
- Ohtsuka, T.; Akiyama, T.; Hashimoto, Y.; Inatomi, M.; Sakai, T.; Jia, S.; Mo, W.; Tsuda, S.; Koizumi, H. Biometric based estimates of net primary production (NPP) in a cool-temperate deciduous forest stand beneath a flux tower. Agr. Forest. Meteorol. 2005, 143, 27–38. [Google Scholar]
- Site Information. Asiaflux: Tsukuba, Japan, 2009. Available online: http://www.asiaflux.net/sf_fsreast.html (accessed on 9 May 2009).
- Saigusa, N.; Yamamoto, S.; Murayama, S.; Kondo, H.; Nishimura, N. Gross primary production and net ecosystem exchange of a cool-temperate deciduous forest estimated by the eddy covariance method. Agr. Forest. Meteorol. 2002, 112, 203–215. [Google Scholar]
- Nasahara, K.N.; Muraoka, H.; Nagai, S.; Mikami, H. Vertical integration of leaf area index in a Japanese deciduous broad-leaved forest. Agr. Forest. Meteorol. 2008, 148, 1136–1146. [Google Scholar]
- Nakai, Y.; Kitamura, K.; Suzuki, S.; Abe, S. Year-long carbon dioxide exchange above a broadleaf deciduous forest in Sapporo, Northern Japan. Tellus 2003, 55B, 305–312. [Google Scholar]
- Nightingale, J.M.; Hill, M.J.; Phinn, S.R.; Davies, I.D.; Held, A.A.; Erskine, P.D. Use of 3-PG and 3-PGS to simulate forest growth dynamics of Australian tropical rainforest: I. Parameterisation and calibration for old-growth, regenerating and plantation forests. Forest. Ecol. Manage. 2008, 254, 122–133. [Google Scholar]
- Maruyama, K.; Fukumoto, Y.; Kamitani, T. The daily radial fluctuation of trunks of some deciduous broad-leaved tree and its controlling factors. J. Jpn. Forest. Soc. 1985, 67, 148–152. (in Japanese). [Google Scholar]
- Komiyama, A.; Inoue, S.; Ishikawa, T. Characteristics of the seasonal diameter growth of twenty-five species of deciduous broad-leaved trees. J. Jpn. Forest. Soc. 1987, 69, 379–385. (in Japanese). [Google Scholar]
- Esprey, L.J.; Sands, P.J.; Smith, C.W. Understanding 3-PG using a sensitivity analysis. Forest. Ecol. Manage. 2004, 193, 235–250. [Google Scholar]
- Ito, A.; Saigusa, N.; Murayama, S.; Yamamoto, S. Modeling of gross and net carbon dioxide exchange over a cool-temperate deciduous broad-leaved forest in Japan: Analysis of seasonal and interannual change. Agr. Forest. Meteorol. 2005, 134, 122–134. [Google Scholar]
- Battaglia, M.; Sands, P.J. Application of sensitivity analysis to model of Eucalyptus globules plantation productivity. Ecol. Model. 1998, 111, 237–259. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Potithep, S.; Yasuoka, Y. Application of the 3-PG Model for Gross Primary Productivity Estimation in Deciduous Broadleaf Forests: A Study Area in Japan. Forests 2011, 2, 590-609. https://doi.org/10.3390/f2020590
Potithep S, Yasuoka Y. Application of the 3-PG Model for Gross Primary Productivity Estimation in Deciduous Broadleaf Forests: A Study Area in Japan. Forests. 2011; 2(2):590-609. https://doi.org/10.3390/f2020590
Chicago/Turabian StylePotithep, Supannika, and Yoshifumi Yasuoka. 2011. "Application of the 3-PG Model for Gross Primary Productivity Estimation in Deciduous Broadleaf Forests: A Study Area in Japan" Forests 2, no. 2: 590-609. https://doi.org/10.3390/f2020590




