Similar to the algorithm by Lenstra
et al. [
2], our approximation algorithm uses an estimation
T of the maximum load of a vertex in an optimal orientation as a parameter. The algorithm GB2W presented below as Algorithm 1 finds a solution of value at most
if a solution of value at most
T exists. We combine this algorithm with a binary search procedure to find the smallest value for
T for which an orientation with load at most
for the graph balancing problem with two weights is found: if for a given
T the algorithm does not find a solution of value at most
then the value of
T is increased in the binary search; otherwise it is decreased. By the above property of our algorithm this smallest value of
T must be less than or equal to the value of an optimum solution, hence our algorithm has approximation ratio
.
The remainder of this section gives Lemmas 1–4 which provide the subroutines used by our algorithm, then in Theorem 5 we prove our algorithm is a -approximation algorithm for GBP2W. First, we present Lemma 1 which covers Step 4 of our algorithm. Note that in Step 1 the algorithm scales the weights so the estimation for the optimum load is . We define a big edge e to be an edge with weight ; otherwise, we call an edge small. Let the value for an optimum solution for the problem be denoted as . From this point forward, we assume that as edges are oriented in Steps 4–5.3, they are removed from G.
2.2. Step 5.1
Next, we consider the case handled in Step 5.1 of the algorithm, namely when
and
so
. In Lemma 2, we utilize the property that
, which means that if
, then no small edge can be oriented with a big edge towards a given vertex without causing the maximal load to be greater than 1.
Lemma 2. For any , there is a polynomial-time algorithm for the graph balancing problem with two rational weights , where and that either finds a solution of value at most or proves that .
Proof. If
, since
, for any optimal orientation either at most a big edge is oriented towards a vertex, or at most
k small edges are oriented towards a vertex. This property is natural to encode into a flow network. To find an orientation for the edges of the weighted multigraph
, we use a multi-level flow network similar to that in [
9].
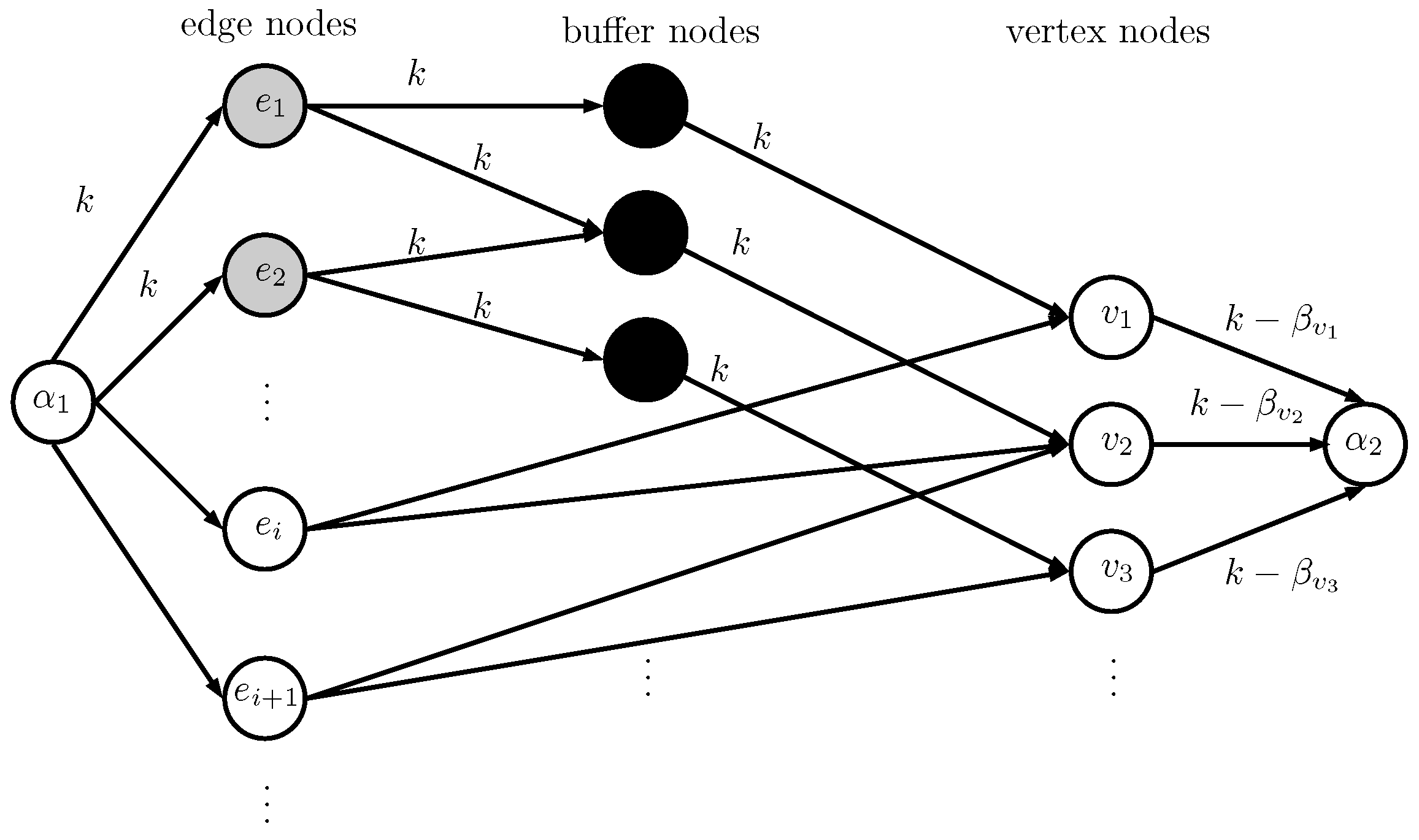
We build a flow network
N as follows. First, we consider the dedicated loads of the vertices. For each vertex
, define a value
as follows: if
, set
; otherwise there is a non-negative integer
so that
, assign
. The flow network will have a source
and sink
. We will describe the network level by level. First, we have a level of nodes in the network called
edge nodes. These are nodes corresponding to the edges in the multigraph. There are two types of edge nodes: big edge nodes for edges with weight
s; and small edge nodes for those with weight
r. From source
, add an arc from
to each edge node, and set its capacity to
k if it is to a big edge node, and 1 otherwise. The next level consists of
buffer nodes, one for each vertex. The buffer nodes are added to prevent excess flow from being contributed by the big edge nodes. While this part of the network is not important for proving this lemma, it will be vital for how we later use this network in Lemma 3. For each big edge
, add arcs with capacity
k from its big edge node to buffer nodes
u and
v. For the next level of the network, create a
vertex node that will correspond to each vertex in the multigraph. For each buffer node for
, add an arc from its buffer node to its vertex node with capacity
k. Next, for each small edge
, include arcs with capacity 1 from its small edge node to vertex nodes
u and
v. Finally, for each vertex
, add an arc from vertex node
v to sink
with capacity
. The resulting flow network is shown in
Figure 1.
Before we proceed to describe the algorithm, we show that this network has the following property: if
, an integral maximum flow on this network saturates all the arcs leaving source
. Consider any optimal orientation
. Using
we construct a flow function in which every small edge node receives 1 unit of flow, and each big edge node receives
k units of flow from the source
. For each big edge
of
G with
, if
u is the big edge node for
send
k units of flow from
to
u,
k units of flow from
u to buffer node
,
k units of flow from buffer node
to vertex node
, and
k units of flow from
to the sink
. Similarly, for each edge
represented by small edge node
u and
, send 1 unit of flow from
to
u, from
u to vertex node
, and from
to
. It is not hard to see that this flow function is feasible and that no additional flow can be sent through the network.
| Algorithm 3: BigSmall_rs |
- Input:
Multigraph G. Note that . - Output:
An orientation γ for the edges in E with maximum vertex load at most or FAIL. If FAIL is returned there is no orientation for E with maximum vertex load 1.
Build the flow network N. Compute an integral maximum flow f of N. If all the arcs leaving the source are not saturated in f, then return FAIL. Construct bipartite graph , where is the set of big edge nodes, is the set of buffer nodes that receive at least units of flow from a big edge node, and
Compute a matching on that matches each node in with a unique vertex in . For each arc in the matching of Step 5, orient big edge u towards vertex . For each small edge node u and vertex node with , orient u towards . Return orientation for the edges of G.
|
The time complexity of algorithm BigSmall_
(Algorithm 3) is polynomial. Now we prove that this algorithm finds an orientation with maximal load at most
if
. If
, then as shown above, every small edge node receives 1 unit of flow from
. By flow conservation, each small edge node
u sends its one unit of flow to a vertex node
, and the algorithm orients small edge
u towards vertex
. As a result, every small edge is oriented by the algorithm. What remains to be shown is that all the big edges are oriented. The orientation of each big edge is determined by the matching computed by the algorithm. We must show this matching exists. Consider any subset
, and denote the neighbourhood in
of this subset of nodes as
. Note that
. To show the above matching exists, we prove
. Two key observations are that the outdegree of every edge node is 2, and every big edge node is sent at most
k units of flow. Furthermore, by flow conservation every big edge node must send at most
k units of flow to the buffer nodes. We have two cases:
If k is odd, a buffer node in can receive at least units of flow from only one big edge node in because . Furthermore, since , each big edge node in has degree 1. Hence, .
If k is even, , and a buffer node can receive units of flow from at most two big edge nodes. Partition into two disjoint sets and , where contains the buffer nodes that receive more than units of flow from a big edge node, and has the buffer nodes that receive units of flow from a big edge node. Similar to when k is odd, each big edge node in is adjacent to only one buffer node in , and so each buffer node in has degree 1 in . This leaves vertices adjacent to buffer nodes in . The indegree of each buffer node in is at least one (and no more than 2), but the outdegree of every big edge node adjacent to the buffer nodes in is exactly 2. This implies that the . Putting this together, .
Since
, by Hall’s Theorem [
16], a matching covering
exists. Hence, the algorithm computes an orientation if
and reports
FAIL otherwise.
Consider the orientation produced by the algorithm. If vertex
v has
, then the edge from
v to
in
N has capacity zero which implies that no edge is oriented towards
v, so the load of
v is
. Next we check when
v has
.
First, let v be a vertex with a big edge oriented towards it. Since a big edge oriented towards v implies a big edge node sends at least units of flow to the vertex node for v, at most units of flow can be additionally sent to this vertex node by small edge nodes; hence at most additional small edges are oriented towards v.
Second, the capacity from any vertex node v to is , so any vertex that is not assigned a big edge has at most small edges oriented towards it.
Hence, the load of a vertex
v is at most
2.3. Step 5.2
Next, we cover the case when
and
. In this case, it is possible that
. If
, at most one big edge can be oriented along with one small edge toward the same vertex; we exploit this property below.
Lemma 3. For any , there is a polynomial-time algorithm for the graph balancing problem with two rational weights , where and that either finds a solution of value at most or proves that .
Proof. We consider two cases: , and . Assuming , if either at most one big edge is oriented towards a vertex or at most k small edges are oriented towards a vertex; apply Lemma 2 to obtain an orientation where each vertex has load at most , if such an orientation exists.
From this point forward, assume
. Observe that
. If
, an optimal orientation either has at most a big edge oriented along with a small edge towards the same vertex, or at most
k small edges are oriented towards a vertex. Like Lemma 2, compute a value
for the dedicated load of each
. When
, set
. Otherwise, if
set
, and if not, assign
where
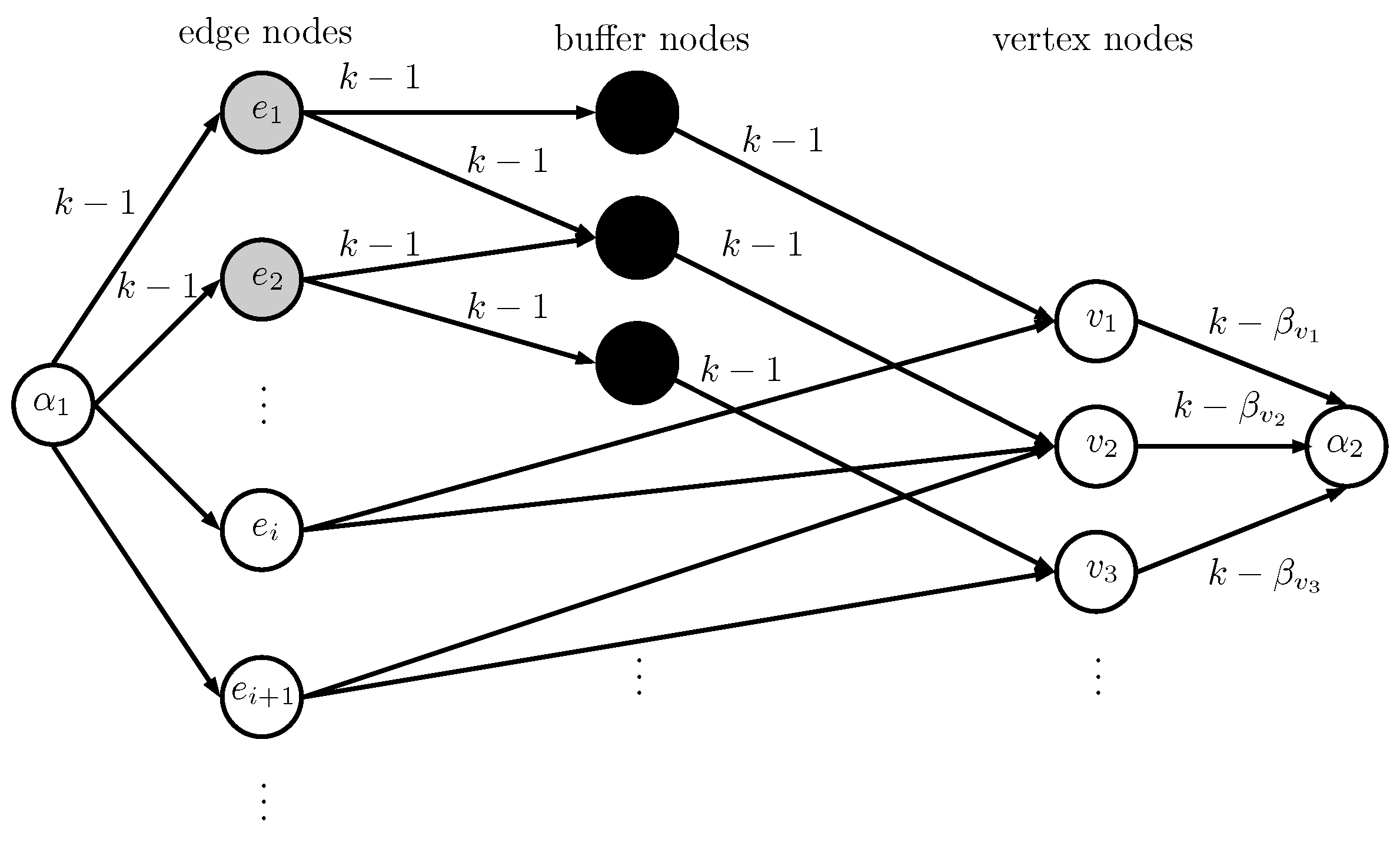
. The algorithm will build a modified version of the flow network
N of Lemma 2, which we describe now. First, change the capacities on the arcs incident on the big edge nodes from
k to
. Second, for each
, set the capacity of the arc from buffer node
v to vertex node
v to
instead of
k. Leave the capacities from the vertex nodes to the sink
as
. We show this flow network in
Figure 2. It is straightforward to see that this modified network maintains the same property that all the arcs leaving
are saturated in an integral maximum flow if
.
We modify the algorithm from Lemma 2 as follows. We refer the reader to BigSmall_
(Algorithm 3). The modified flow network we described above is built for Step 1. Steps 2–3 are the same as before. In Step 4, when constructing the bipartite graph
between the big edge nodes and buffer nodes,
remains the same, but
contains buffer nodes that receive instead at least
units of flow from a big edge node and
steps 5–8 remain the same as before. Since the capacities of the arcs leaving the buffer nodes and the incoming flow to the big edge nodes are one less than in the network in Lemma 2, one can show a matching on
exists if
by replacing
k with
and switching the even and odd cases of our original argument in Lemma 2.
Consider the load of a vertex
v in the orientation produced by the algorithm. Clearly any vertex
v with
has
and
. No flow is sent to these vertex nodes, so the load of these vertices is at most 1. Now, examine vertices with
. If
, then at most one additional small edge can be oriented towards
v. Hence, the load of
v when
is at most
since
. Finally, consider when
and
.
Let v be a vertex with a big edge oriented towards it. At least units of flow are sent from its big edge node to v. Then, at most small edges can be oriented along with the big edge towards v.
Let v not have a big edge oriented towards it. At most small edges are oriented towards v.
Therefore, the load of
v is at most
2.4. Step 5.3
For the final case in Step 5 of our algorithm, we apply a variant of the algorithm by Ebenlendr
et al. [
7]. First we give a brief explanation of their original algorithm that has approximation ratio
.
Let be the set of big edges and let be the subgraph of G consisting of big edges. If , every connected component of with b vertices contains at most b edges, which implies that each component has at most one cycle. For each connected component, identify a cycle if it exists, then orient every big edge not in the cycle away from the cycle and remove each oriented edge. Add the weight of each oriented big edge to the dedicated load of the endpoint farther from the cycle. is now a disjoint union of trees and cycles.
As shorthand, if
v is a vertex and
e is an edge,
means “
v is incident to
e”. For any
, let
where each
is called a
leaf pair of
T. Consider any tree
. Assuming
, since
T has one more vertex than edges, at most one edge in the set of leaf pairs can be oriented away from its leaf. This leads to what is called the
tree constraint (Tree
T) in linear program 1 (LP1) shown below, which is a relaxation of an integer program formulation of the graph balancing problem. A variable
is defined for each edge
and endpoint
v of
e. If
,
e is oriented towards
v. If
, we say that
e is
fractionally oriented towards
v.
Solve LP1 to obtain a fractional solution
. As a brief remark, there can be exponentially many trees, but there is a separation oracle that can be used to solve LP1 in polynomial time with the ellipsoid method [
7]. Let
. Also, let
and
. If a feasible solution is not found for LP1, then
.
The algorithm then considers fractionally oriented edges in
, and performs a rounding procedure to determine their final orientations. It is assumed that as edges are oriented,
and
are updated accordingly. If there is a vertex
v of degree 1 in
and
for edge
then
Leaf assignment: if , e is oriented towards v;
Tree assignment: if note that e then is a big edge and the connected component of containing e must be a tree T. Orient all edges in T away from v.
Finally, if no vertex v as above is found, then there must be a cycle. If so, perform a walk around the cycle changing the values of the edges in the cycle by the minimum amount δ that makes at least one of these values zero and the loads on the vertices remain unchanged. Note that when traversing to find a cycle, big edges are taken in priority over small edges. This step is called rotation. The algorithm terminates once no longer has an edge.
The rounding performed by a leaf assignment increases the load of a vertex u by at most if the edge e under consideration is big or it increases by at most if e is small. Furthermore, a tree assignment can increase the load of a vertex u by at most . A vertex u can have its load increased by either only one leaf assignment or by a tree assignment plus a leaf assignment involving a small edge. In either case the maximum load of a vertex is at most . Note that a rotation does not change loads.
Now we show how to modify this algorithm for our problem.
Lemma 4. For every positive integer , there is a polynomial-time algorithm for the graph balancing problem with two rational weights , where and that either finds a solution of value at most or proves that .
Proof. We make the following modifications to the algorithm in [
7]. Consider any tree
. Every big edge
e has weight
, so we simplify the tree constraint to
Also, in the rounding procedure of [
7] we change the leaf assignment and tree assignment:
New leaf assignment: if , e is oriented towards v.
New tree assignment: if , then e is a big edge and the connected component of containing e is a tree T. Orient all edges in T away from v.
Use the algorithm of Ebenlendr
et al. [
7] with the above modifications. If no fractional solution is found then no orientation exists; report
FAIL if this is the case. Since modifying the above threshold from
to
will still allow all fractionally oriented edges to be rounded, the algorithm still finds an orientation in polynomial time.
We can extend the arguments by Ebenlendr
et al. [
7] to show that the algorithm has approximation ratio
in our case. It is not hard to modify the proof of Theorem 1 in [
7] to show that the following conditions are maintained by each vertex
before and after each step in the rounding procedure.
- (1)
The load of v is at most .
- (2)
If is incident on v, then v has load at most .
- (3)
If is a big edge in incident on v, the load of v is at most 1.
- (4)
For any tree T that is a subgraph of , the tree constraint (Tree T) is never violated.
For completeness we sketch a proof that the above conditions hold throughout the rounding procedure. At the beginning of the algorithm, after the modified LP1 is solved, all the conditions above are satisfied and the load of each vertex is at most 1. Next, we show conditions (1)–(4) are preserved for any vertex that changes its load during the rounding procedure.
Tree assignment: In a tree assignment, only vertices in the tree
containing big edge
for which
and
v is a leaf of
T have their loads modified. Every vertex in
T is incident with a big edge in
. Hence before this step is performed, by condition (3), each one of these vertices has load at most 1. Consider vertex
in
T after the tree assignment has been performed. If
, the load of
v is decreased as big edges are oriented away from
v. If
, there exists a path
P in
T from
to
v. Say this path begins at edge
. As
P is a subtree of
T, it must satisfy our tightened tree constraint of LP1 and so
All the edges in
P are big, so
. Hence, the load of
increases by at most
, and conditions (1) and (2) are satisfied for vertex
. Note that since fractional edge assignments in
T have been eliminated,
cannot be incident on a big edge following a tree assignment. Thus, condition (3) does not apply to this case and condition
is satisfied.
Leaf assignment: In a leaf assignment, edges are oriented towards a leaf vertex. Say vertex v is a leaf. We consider two cases for edge such that : , and .
If , then v is incident on a big edge and so by condition (3), the load of v is at most 1 before the leaf assignment. Since , then following the leaf assignment, the load of v is at most .
If
, then
. By condition (2), before the leaf assignment the load of
v is at most
. So after the leaf assignment the load of
v is at most
In any case, after a leaf assignment
v is isolated in
, so conditions
–
are satisfied.
Rotation: The rotation step does not change the vertex loads so conditions (1)–(3) hold. The argument showing that condition (4) holds is essentially the same as that in [
7] and since it is a bit lengthy we omit it here.
Therefore, by condition (1), the load of a vertex is at most . ☐