A Geometric Orthogonal Projection Strategy for Computing the Minimum Distance Between a Point and a Spatial Parametric Curve
Abstract
:1. Introduction
2. Orthogonal Projection onto a Spatial Parametric Curve
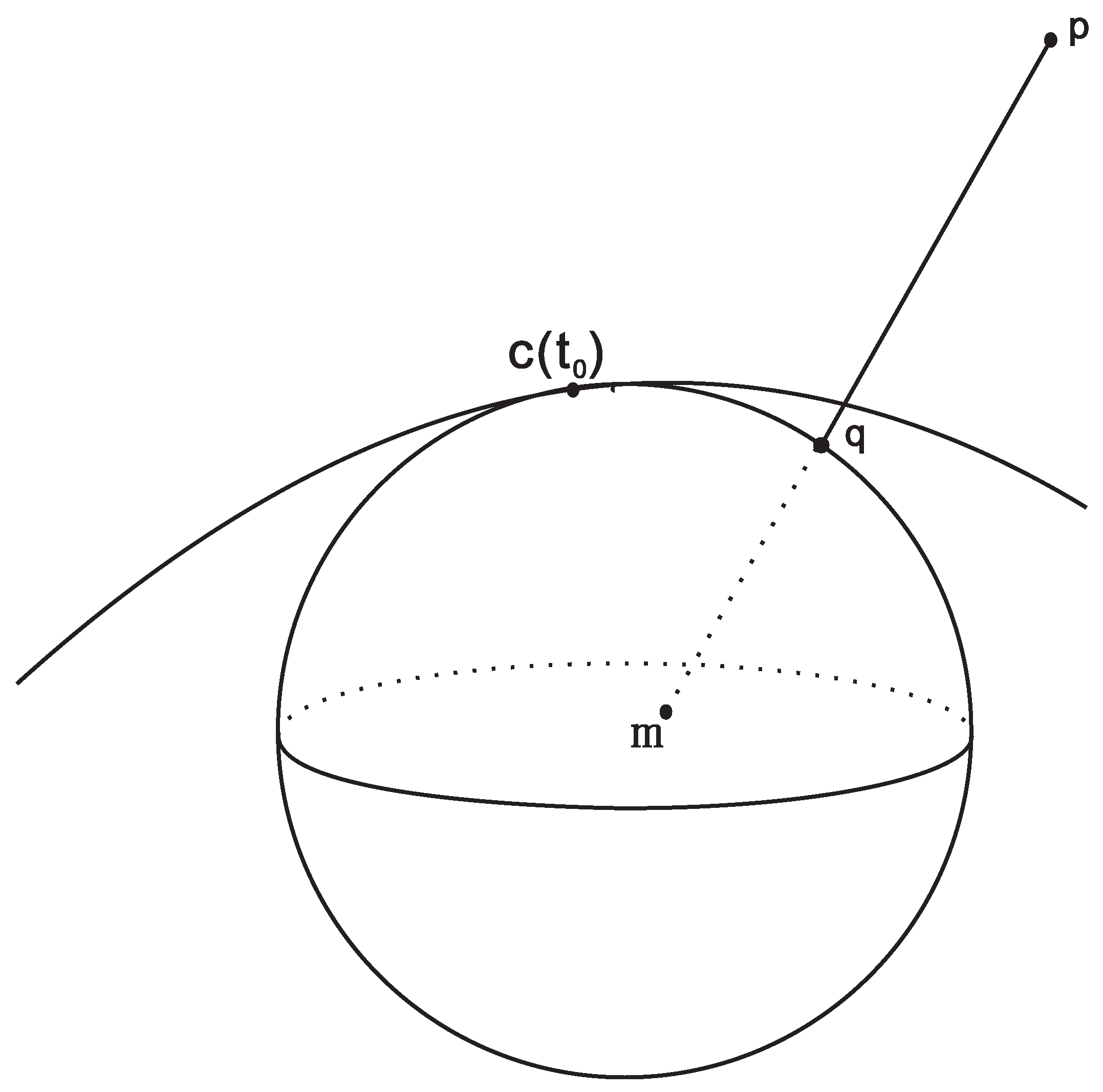
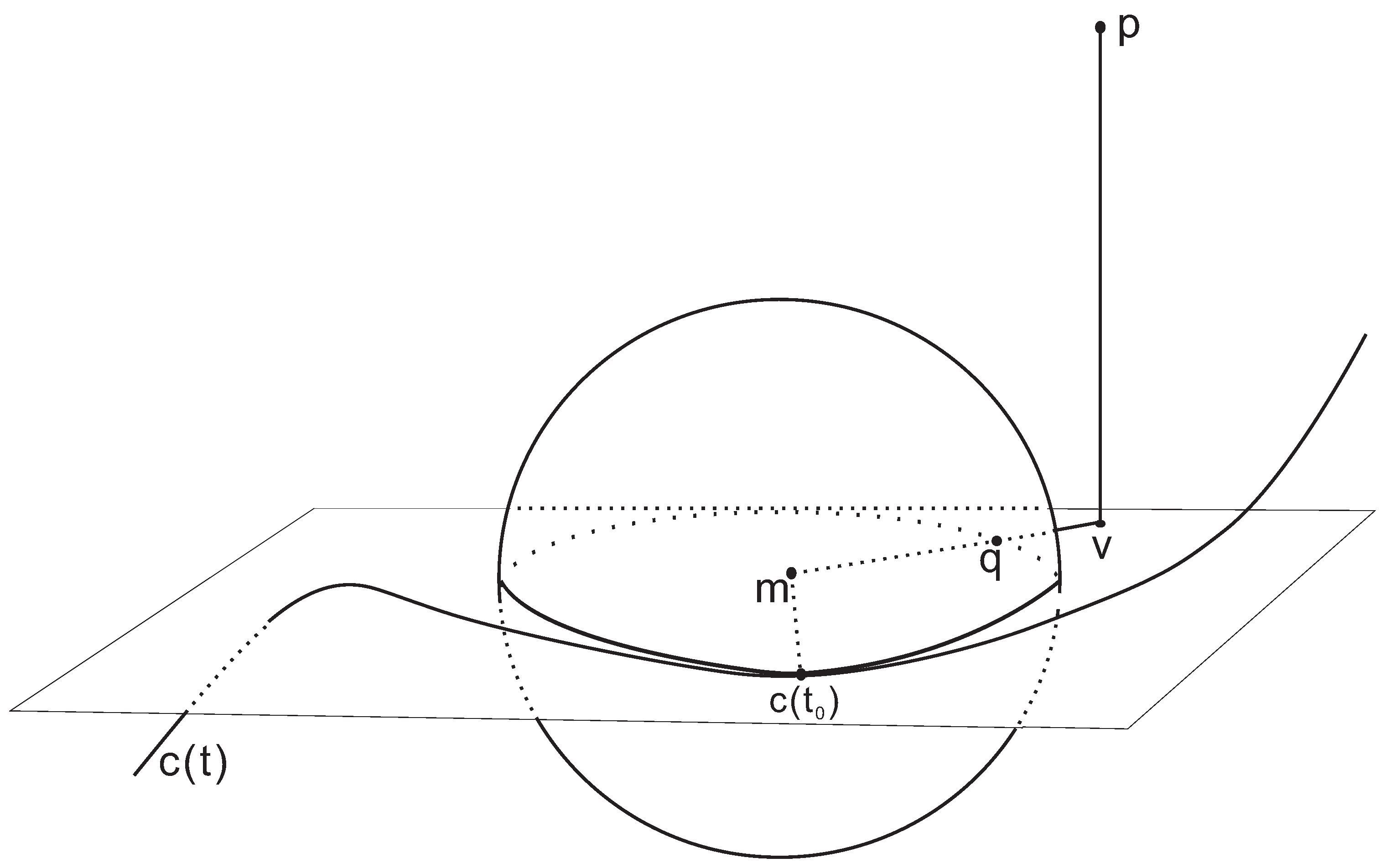
3. Convergence Analysis
4. Numerical Examples
| p = (1, 1, 1), t0 = 1.5 | |||||||
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Δt1 | −3.4e−1 | −1.2e−1 | −1.7e−2 | −2.9e−4 | −8.3e−8 | −6.7e−15 | 0 |
| Δt2 | −4.2e−1 | −6.3e−2 | −1.3e−3 | −5.0e−7 | −7.8e−14 | 7.3e−18 | 0 |
| p = (1, 1, 1), t0 = −0.85 | |||||||
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Δt1 | 1.03 | 6.3 | −2.1 | −1.43 | −9.1e-1 | −5.6e−1 | −3.1e−1 |
| Step | 8 | 9 | 10 | 11 | 12 | ||
| Δt1 | −1.1e−2 | −1.3e−4 | −1.6e−8 | −2.2e−16 | 0 | ||
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Δt2 | 1.2 | 6.5e−1 | 1.2e−2 | −4.1e−5 | −5.2e−10 | 7.4e−18 | 0 |
| p = (2, 2, 0), t0 = −0.32 | |||||||
| Step | 1 | 2 | 3 | 4 | 5 | 6 | |
| Δt1 | NC | NC | NC | NC | NC | NC | |
| Δt2 | 1.82 | 2.8e−1 | 2.1e−3 | 8.3e−7 | 1.4e−13 | 0 | |
| p = (2, 2, 0), t0 = 4.2 | |||||||
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Δt1 | NC | NC | NC | NC | NC | NC | NC |
| Δt2 | −7.2e−1 | −1.65 | −4.1e−2 | 3.5e−4 | 2.5e−8 | 2.2e−16 | 0 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ma, Y.L.; Hewitt, W.T. Point inversion and projection for NURBS curve and surface: Control polygon approach. Comput. Aided Geometric Des. 2003, 20, 79–99. [Google Scholar] [CrossRef]
- Yang, H.P.; Wang, W.P.; Sun, J.G. Control point adjustment for B-spline curve approximation. Comput. Aided Design 2004, 36, 639–652. [Google Scholar] [CrossRef] [Green Version]
- Johnson, D.E.; Cohen, E. A Framework for efficient minimum distance computations. In Proceedings of IEEE Intemational Conference on Robotics & Automation, Leuven, Belgium, 16–20 May 1998.
- Piegl, L.; Tiller, W. Parametrization for surface fitting in reverse engineering. Comput. Aided Des. 2001, 33, 593–603. [Google Scholar] [CrossRef]
- Pegna, J.; Wolter, F.E. Surface curve design by orthogonal projection of space curves onto free-form surfaces. J. Mech. Design ASME Trans. 1996, 118, 45–52. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Mortenson, M.E. Geometric Modeling; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Zhou, J.M.; Sherbrooke, E.C.; Patrikalakis, N. Computation of stationary points of distance functions. Engin. Comput. 1993, 9, 231–246. [Google Scholar] [CrossRef]
- Johnson, D.E.; Cohen, E. Distance extrema for spline models using tangent cones. In Proceedings of the 2005 Conference on Graphics Interface, Victoria, BC, Canada, 9–11 May 2005.
- Hartmann, E. On the curvature of curves and surfaces defined by normalforms. Comput. Aided Geometric Des. 1999, 16, 355–376. [Google Scholar] [CrossRef]
- Limaien, A.; Trochu, F. Geometric algorithms for the intersection of curves and surfaces. Comput. Gr. 1995, 19, 391–403. [Google Scholar]
- Polak, E.; Royset, J.O. Algorithms with adaptive smoothing for finite minimax problems. J. Optim. Theory Appl. 2003, 119, 459–284. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: NewYork, NY, USA, 1992. [Google Scholar]
- Elber, G.; Kim, M.S. Geometric Constraint solver using multivariate rational spline functions. In Proceedings of the Sixth ACM Symposiumon Solidmodeling and Applications, New York, NY, USA, 1 May 2001; pp. 1–10.
- Patrikalakis, N.; Maekawa, T. Shape Interrogation for Computer Aided Design and Manufacturing; Springer: Berlin, Germany, 2001. [Google Scholar]
- Chen, X.D.; Zhou, Y.; Shu, Z.Y.; Su, H.; Paul, J.C. Improved Algebraic Algorithmon Point Projection for Bézier Curves; The University of Iowa: Des Moines, IA, USA, 2007. [Google Scholar]
- Selimovic, I. Improved algorithms for the projection of points on NURBS curves and surfaces. Comput. Aided Geometric Des. 2006, 23, 439–445. [Google Scholar] [CrossRef]
- Boehm, W. Inserting new knots into B-spline curves. Comput. Aided Des. 1980, 12, 199–201. [Google Scholar] [CrossRef]
- Cohen, E.; Lyche, T.; Riesebfeld, R. Discrete B-splines and subdivision techniques in computer-aided geometric design and computer graphics. Comput. Gr. Image Process. 1980, 14, 87–111. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Springer: New York, NY, USA, 1995. [Google Scholar]
- Chen, X.D.; Yong, J.H.; Wang, G.Z.; Paul, J.C.; Xu, G. Computing the minimum distance between a point and a NURBS curve. Comput. Aided Des. 2008, 40, 1051–1054. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.M.; Wallner, J. A second-order algorithm for orthogonal projection onto curves and surfaces. Comput. Aided Geometric Des. 2005, 22, 251–260. [Google Scholar] [CrossRef]
- Schulz, C. Bézier clipping is quadratically convergent. Comput. Aided Geometric Des. 2009, 26, 61–74. [Google Scholar] [CrossRef]
- Li, X.W.; Mu, C.L.; Ma, J.W.; Wang, C. Sixteenth-order method for nonlinear equations. Appl. Math. Comput. 2010, 215, 3754–3758. [Google Scholar] [CrossRef]
- Liang, J.; Li, X.W.; Wu, Z.W.; Zhang, M.S.; Wang, L.; Pan, F. Fifth-order iterative method for solving multiple roots of the highest multiplicity of nonlinear equation. Algorithms 2015, 8, 656–668. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J. L.; Martínez, E.; Torregrosa, J. R. A modified Newton-Jarratt’s composition. Numer. Algor. 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Grau-Sanchez, M.; Noguera, M.; Amat, S. On the approximation of derivatives using divided difference operators preserving the local convergence order of iterative methods. J. Comput. Appl. Math. 2013, 237, 363–372. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solutions of Equations and Systems of Equations; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Melmant, A. Geometry and Convergence of Euler’s and Halley’s Methods. SIAM Rev. 1997, 39, 728–735. [Google Scholar] [CrossRef]
- Traub, J.F. A Class of Globally Convergent Iteration Functions for the Solution of Polynomial Equations. Math. Comput. 1966, 20, 113–138. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wu, Z.; Hou, L.; Wang, L.; Yue, C.; Xin, Q. A Geometric Orthogonal Projection Strategy for Computing the Minimum Distance Between a Point and a Spatial Parametric Curve. Algorithms 2016, 9, 15. https://doi.org/10.3390/a9010015
Li X, Wu Z, Hou L, Wang L, Yue C, Xin Q. A Geometric Orthogonal Projection Strategy for Computing the Minimum Distance Between a Point and a Spatial Parametric Curve. Algorithms. 2016; 9(1):15. https://doi.org/10.3390/a9010015
Chicago/Turabian StyleLi, Xiaowu, Zhinan Wu, Linke Hou, Lin Wang, Chunguang Yue, and Qiao Xin. 2016. "A Geometric Orthogonal Projection Strategy for Computing the Minimum Distance Between a Point and a Spatial Parametric Curve" Algorithms 9, no. 1: 15. https://doi.org/10.3390/a9010015





