1. Introduction
The
-puzzle is defined as follows. Given
numbered tiles arranged in row-major order in an
grid leaving a blank space in the last position where one tile is missing, the aim is to scramble the puzzle and return it to the initial configuration by repeatedly sliding an adjacent tile into the blank location. When
the puzzle is also called the
-puzzle. For example,
Figure 1 shows an example for the 15-puzzle of the solved configuration (left) and a random configuration (right).
Figure 1.
The solved 15-puzzle (left), and a random configuration (right).
Figure 1.
The solved 15-puzzle (left), and a random configuration (right).
The 15-puzzle has a long and interesting history (see, for example, Hordern [
1]) that is said to date back to the 1870s. More recently, the 15-puzzle has appeared in the form of various apps on mobile devices and as minigames inside larger games. For example, the 15-puzzle can be found in the original
Final Fantasy (Square Enix, 1987) and
The Legend of Zelda: The Windwaker (Nintendo 2003), and the 8-puzzle can be found in
Machinarium (Amanita Design, 2009).
Ratner and Warmuth [
2] have proved that the problem of finding the minimum number of moves for the
-puzzle is NP-hard, and they demonstrate that a polynomial time approximation algorithm exists. Kornhauser, Miller, and Spirakis [
3] show an
time algorithm for the
-puzzle, which therefore uses
moves in the worst case.
Parberry [
4] gave worst case upper and lower bounds of
and
, respectively, on the number of moves required to solve the
-puzzle using a greedy algorithm. Whilst upper bounds are certainly interesting, a hypothetical player faced with solving a random configuration of the puzzle is likely be more concerned about the expected number of moves than the worst case. Parberry [
4] also gave lower bounds of at least
for the expected number of moves, and at least
moves for a random configuration with probability one.
We extend this work by showing both theoretically and experimentally that the greedy algorithm solves the
-puzzle in expected number of moves
. The main body of this paper is divided into three sections.
Section 2 contains a brief description of the greedy algorithm.
Section 3 contains the average-case analysis of the number of moves required.
Section 4 contains an experimental verification of this analysis.
2. The Greedy Algorithm
The greedy algorithm for the
-puzzle work as follows (for more details see, for example, Parberry [
4]). There are sequences of five moves that bring a tile one place horizontally or vertically, and a sequence of six moves that brings a tile one place diagonally. Move the blank to the position immediately above the first tile, then use a sequence of these moves to bring that tile to the top left corner. Repeat this for the remaining tiles in the first row, taking care not to disturb the work that has already been done. The last two tiles in the row require a few extra moves to flip into place. Once the first row has been completed, do likewise for the first column. Once the first row and column are in place, recurse on the remaining
-puzzle. The base of the recursion can be solved by brute force, for example, the 3-puzzle can be solved in six moves, the 8-puzzle can be solved in 31 moves (Reinefeld [
5]) and the 15-puzzle can be solved in 80 moves (Brüngger
et al. [
6]).
3. Theoretical Analysis
Suppose
n is even (the case where
k is odd is similar). Consider the expected number of moves required to solve the first half of the first row of the puzzle. For each of those
tiles
, the expected number of moves required to move tile
to position
will be equal to the sum over all positions
p of the number of moves required to move
t from position
p to position
, divided by
. We will do this in three parts, the number of moves required to move the blank into place above tile
t (
Section 3.1), and the number of moves required to move
t to position
once the blank is in place (
Section 3.2), and the total number of moves (
Section 3.3).
3.1. The Blank
The sum of the number of moves required to move the blank from position
to each of the
possible destinations is:
For example, with
, looking at
Figure 2 (left) and numbering the rows from 0 to
top-to-bottom, row
i has sum
. For position
,
, the sum is:
See, for example,
Figure 2 with
and
from left to right. The difference between the leftmost table and the other tables is that
k rightmost columns are replaced with
k columns with lower values (which are the same as columns 1 through
k in the leftmost table). However, the difference in value of each replaced cell is constant
. Since there are
k replaced columns with
n rows, Equation (
2) follows.
Figure 2.
Number of moves required to move the blank to each position from the first half of the first row of the 63-puzzle.
Figure 2.
Number of moves required to move the blank to each position from the first half of the first row of the 63-puzzle.
Therefore, summing Equation (
2) for
to
, the total number of moves for positioning the blank above tiles
is:
Hence, the total number of moves for moving the blank into place while solving the first row and the first column is less than four times Equation (
3) minus Equation (
1) (the latter to avoid counting cell
twice), that is,
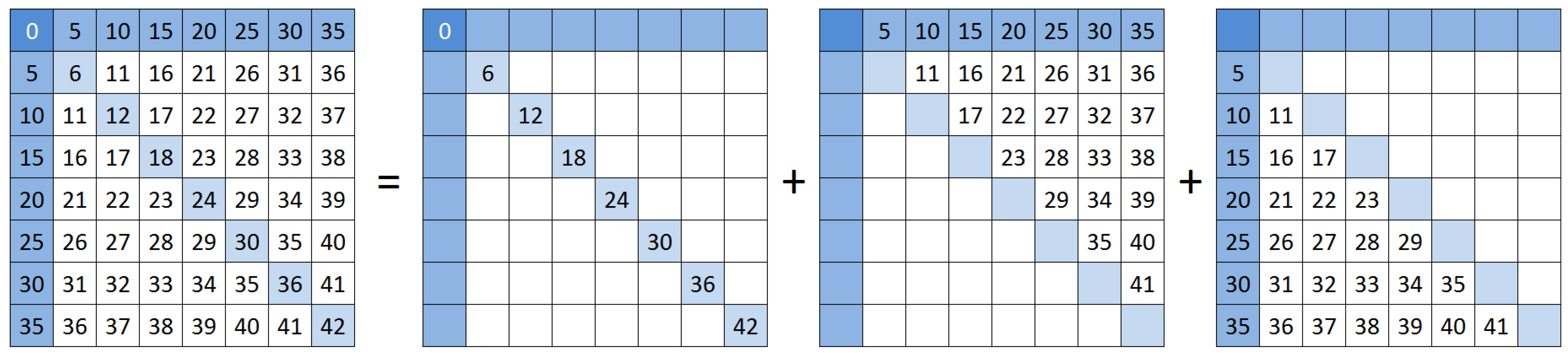
3.2. The Tiles
The sum of the number of moves required to move tile
to position
from all of the
possible sources is (see the leftmost entry of
Figure 3, and
Figure 4):
Similarly, for position
,
, the sum is (see
Figure 3):
Figure 3.
Number of moves required to move a tile from each position to the first half of the first row of the 63-puzzle.
Figure 3.
Number of moves required to move a tile from each position to the first half of the first row of the 63-puzzle.
Therefore, the total number of moves for moving tiles
into place in the first half of the first row is:
and the total number of moves for moving the first row and column tiles into place is, by Equations (
5) and (
7), at most:
The astute reader will have noticed that we have under-counted by
to bring the blank into position at the start, and
for the last tile in the row and column. This is more than compensated for by the fact that we have over-counted by
when moving the blank in
Section 3.1 since there is never any need to move the blank to the last row.
Figure 4.
Decomposing the leftmost entry of
Figure 3 to show the structure of Equation (
5).
Figure 4.
Decomposing the leftmost entry of
Figure 3 to show the structure of Equation (
5).
3.3. Tiles and Blank Together
The total number of moves used to solve the first row and column is at most the sum of the results of Equations (
4) and (
8). That is,
The expected number of moves to solve the first row and column is the total number of moves from Equation (
9) divided by the number of tiles (which is
), that is,
. The argument so far has assumed that
n is even. One can prove similarly the expected number of moves for odd
n is also
.
Having put the first row and column of the
puzzle into place, the remaining
sub-puzzle is then solved recursively, Note that if every even permutation of the
tiles in the
puzzle is equally likely, then since the moves made to put the first row and column into place depend only on the position of those tiles in the permutation (and not, for example, on the values of any of the tiles), the resulting even permutation of the
tiles in the
sub-puzzle on which we recurse is equally likely to be any even permutation of the remaining
tiles. Therefore, the expected number of moves to solve the whole puzzle is bounded above by:
4. Experimental Analysis
We generated 10,000 random instances of the
-puzzle for all
n such that
using the standard algorithm for generating a random even permutation based on the Mersenne Twister (Matsumoto and Nishimura [
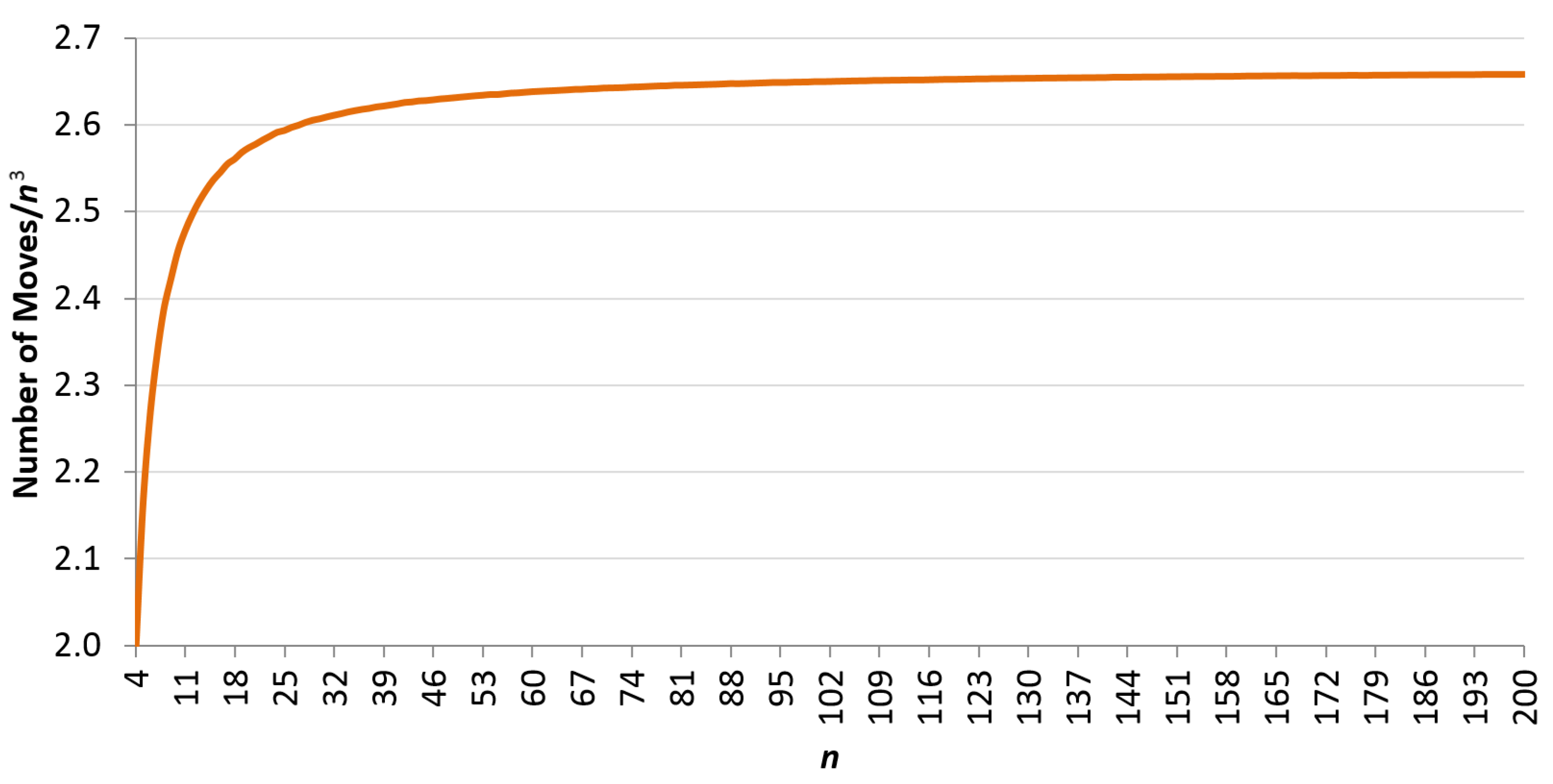
7]). We then solved each instance using the greedy algorithm and measured the average number of moves required to solve each size, which should approximate the expected value if the sample size is large enough. We found that the average number of moves tends to
with an
value of
(see
Figure 5). In fact, the number of moves divided by
is less than
for
(see
Figure 6). Consider that the theoretical bound is the expected number of moves, while the experimental bound is the average number of moves over a relatively small (compared to the solution space) random sample. The fact that the theoretical and experimental results agree so closely in this case is quite remarkable.
Figure 5.
The average number of moves required to solve 10,000 random instances of the -puzzle for .
Figure 5.
The average number of moves required to solve 10,000 random instances of the -puzzle for .
Figure 6.
The average number of moves required to solve 10,000 random instances of the -puzzle divided by for .
Figure 6.
The average number of moves required to solve 10,000 random instances of the -puzzle divided by for .