1. Introduction
In recent years there has been growing interest in swarm intelligence, a distributed mode of computation utilising interaction between simple agents [
1]. Such systems have often been inspired by observing interactions between social insects: ants, bees, birds (
cf. ant algorithms and particle swarm optimisers); see Bonabeau [
2] for a comprehensive review. Swarm Intelligence algorithms also include methods inspired by natural evolution, such as genetic algorithms [
3,
4] and evolutionary algorithms [
5]. The problem solving ability of swarm intelligence methods emerges from positive feedback reinforcing potentially good solutions and the spatial/temporal characteristics of their agent interactions.
Independently of these algorithms, stochastic diffusion search (SDS) was first described in 1989 as a population-based, pattern-matching algorithm [
6]. Unlike stigmergetic communication employed in ant algorithms, which is based on the modification of the physical properties of a simulated environment, SDS uses a form of direct communication between the agents similar to the tandem calling mechanism employed by one species of ant,
Leptothorax acervorum, [
7].
SDS is an efficient probabilistic multi-agent global search and optimisation technique [
8] that has been applied to diverse problems, such as site selection for wireless networks [
9], mobile robots self-localisation [
10], object recognition [
11] and text search [
6]. Additionally, a hybrid SDS and n-tuple RAM[
12] technique has been used to track facial features in video sequences [
11,
13].
Previous analysis of SDS has investigated its global convergence [
14], linear time complexity [
15] and resource allocation properties [
16], under a variety of search conditions.
1.1. Global Optimisation
Global optimisation algorithms have recently been partitioned, in terms of their theoretical foundations, into four distinct classes [
17]:
incomplete methods; heuristic searches with no safeguards against trapping in a local minimum;
asymptotically complete; methods reaching the global optimum with probability one if allowed to run indefinitely without means to ascertain when the global optimum has been found;
complete; methods reaching the global optimum with probability one in infinite time that know after a finite time that an approximate solution has been found to within prescribed tolerances;
rigorous; methods typically reaching the global solution with certainty and within given tolerances.
In heuristic multi-agent systems, the above characterisation is related to the concept of the stability of intermediate solutions, because the probability that any single agent will lose the best solution is often greater than zero. This may result in a lack of stability of the found solutions, or in the worst case, the non-convergence of the algorithm. Thus, for multi-agent systems, it is desirable to characterise the stability of the discovered solutions. For example, it is known that many variants of genetic algorithms do not converge, and so, the optimal solution may disappear from the next population. Consequently, in practice, either an elitist selection mechanism is utilised or the information about the best solution has to be maintained throughout the entire evolution process.
In this paper, we demonstrate that the solutions discovered by SDS are exceptionally stable, and we illustrate some implications of the resource allocation mechanisms employed by SDS concerning the stability and accuracy of the algorithm, as well as its convergence behaviour.
In the next section, we will introduce stochastic diffusion search, and we will briefly introduce the models of SDS on which the results of this paper are based. The following section will analyse the results obtained contrasting SDS with RANSAC (random sample consensus). The final section will include a discussion and conclusions.
2. Stochastic Diffusion Search
SDS is based on distributed computation, in which the operations of simple computational units, or agents, are inherently probabilistic. Agents collectively construct the solution by performing independent searches, followed by the diffusion of information through the population. Positive feedback promotes better solutions by allocating to them more agents for their exploration. Limited resources induce strong competition from which the largest population of agents corresponding to the best-fit solution rapidly emerges. A comprehensive introduction and review is provided in [
18].
In many search problems, the solution can be thought of as composed of many subparts, and in contrast to most swarm intelligence methods SDS explicitly utilises such decomposition to increase the search efficiency of individual agents. In SDS, each agent poses a hypothesis about the possible solution and evaluates it partially. Successful agents repeatedly test their hypothesis, while recruiting unsuccessful agents by direct communication. This creates a positive feedback mechanism ensuring the rapid convergence of agents onto promising solutions in the space of all solutions. Regions of the solution space labelled by the presence of agent clusters can be interpreted as good candidate solutions. A global solution is thus constructed from the interaction of many simple, locally operating, agents forming the largest cluster. Such a cluster is dynamic in nature, yet stable, analogous to, “a forest whose contours do not change but whose individual trees do”, [
19,
20]. The search mechanism is illustrated in the following analogy.
2.1. The Restaurant Game Analogy
A group of delegates attend a long conference in an unfamiliar town. Each night, they have to find somewhere to dine. There is a large choice of restaurants, each of which offers a large variety of meals. The problem the group faces is finding the best restaurant; that is, the restaurant where the maximum number of delegates would enjoy dining. Even a parallel exhaustive search through the restaurant and meal combinations would take too long to accomplish. To solve the problem, the delegates decide to employ a stochastic diffusion search.
Each delegate acts as an agent maintaining a hypothesis identifying the best restaurant in town; the delegate starts by randomly selecting a restaurant. Each night, each delegate tests his hypothesis by dining at the identified restaurant and randomly selecting one of the meals on offer. The next morning at breakfast, every delegate who did not enjoy his meal the previous night asks one randomly selected colleague to share his dinner impressions: if the experience was good, he also adopts this restaurant as his choice. Otherwise, he simply selects another restaurant at random.
Using this strategy, it is found that, very rapidly, a significant number of delegates congregate around the best restaurant in town.
By iterating through test and diffusion phases, agents stochastically explore the solution space. However, since tests succeed more often on good candidate solutions than in regions with irrelevant information, an individual agent will spend more time examining good regions, at the same time recruiting other agents, which, in turn, recruit even more agents. Candidate solutions are thus identified by concentrations of a substantial population of agents.
Central to the power of SDS is its ability to escape local minima. This is achieved by the probabilistic outcome of the partial hypothesis evaluation in combination with the reallocation of resources (agents) via stochastic recruitment mechanisms. Partial hypothesis evaluation allows an agent to quickly form its opinion on the quality of the investigated solution without exhaustive testing (e.g., it can find the best restaurant in town without having to try all the meals available in each).
| Algorithm 1 Algorithmic description of the restaurant game. |
Initialisation phase All agents (delegates) generate an initial hypothesis (select a restaurant at random) loop Test phase Each agent (delegate) evaluates evidence for its hypothesis (meal quality). Agents are partitioned into active (happy) and inactive (disgruntled) groups (of diners). Diffusion phase Inactive agents (delegates) adopt a new hypothesis by communication with another randomly selected agent (who may have had a good meal at a restaurant), or, if the selected agent is also inactive (bad meal), the selecting agent must adopt a new hypothesis (restaurant) at random. end loop
|
3. Standard SDS
SDS searches for and finds the best match of a given model in a given search space; for example, a particular word (the model) in a text document (the search space). During the searching process, each agent operates entirely independently of the other agents, only reconvening to exchange information about what they have found. There is no concept in SDS of the time taken for an agent to travel to its hypothesis position, only spatial concerns (the size of the search space); there is, however, the cost of evaluating the hypothesis once selected: the cost of the test function. During SDS, each agent is able to access the entirety of the search space and also to carry with it information about the entirety of its target model. For example, each agent has access to an entire document of text, along with the whole word that is being searched for. As seen previously with the restaurant game, an agent becomes active when its selected hypothesis’ test function returns a positive result; otherwise the agent remains inactive. For the word search example, a hypothesis could be an index position in the document, along with an offset from this position; the hypothesis could be evaluated by, rather than checking to see if the whole word (model) is precisely at this location, checking a single character at an offset from the index against a character at the same offset in the model. There are various strategies that can be deployed for how the agents communicate with each other (diffusion) once they have all evaluated their respective hypotheses.
3.1. Initialise
During the initialisation phase, all agents randomly select a hypothesis from the search space. All agents are set to inactive. All agents are given access to the target model. The random initialisation of hypothesis positions can be biased in favour of some positions, given what can be described as a-priori knowledge. As shown by Bishop [
11], there are two types of such knowledge that may influence the initialisation phase:
- (i)
The ratio of the size of the model to the size of the search space is greater than one; this guarantees that at least one agent is initialised with the best hypothesis.
- (ii)
The previous location of the model is known; this is useful when performing successive searches on similar search spaces; for example, consecutive frames of video.
| Algorithm 2 Standard SDS algorithm. |
Initialisation phase All agents generate an initial hypothesis while Halting criteria not satisfied do Test phase All agents perform hypothesis evaluation Diffusion phase All agents deploy a communication strategy Relate phase Optional; active agents with the same hypothesis randomly deactivate Halt phase Evaluation of halting criteria end while
|
3.2. Test
During the test phase, the agent determines whether it should set itself to be active or inactive. This is achieved by applying a test function to its current hypothesis. This test function is a partial evaluation of the hypothesis position. The test function will differ depending on the application domain. Agents are set to active if this partial evaluation of the hypothesis returns success; otherwise, they remain inactive.
3.3. Diffusion
During the diffusion phase, agents exchange hypothesis information. The idea is for active agents to disseminate their current hypothesis to inactive agents. There are three differing strategies for this dissemination, termed recruitment strategies: passive recruitment, active recruitment and a combination of the two.
This exchanging of information leads to agents with good hypotheses recruiting inactive agents to their position. Eventually, large numbers of agents congregate around the best hypothesis (or hypotheses if the related phase is used) available in the search space. The standard SDS recruitment strategy deployed is passive.
3.3.1. Passive Recruitment
During passive recruitment, inactive agents randomly select other agents and adopt their hypothesis if they are themselves active. Thus, it is possible, albeit extremely unlikely, that the population of agents will converge to the ideal hypothesis in one iteration.
3.3.2. Active Recruitment
During active recruitment, agents that are themselves active randomly select other agents; if the selected agents are inactive, they are given the selecting agent’s hypothesis; this limits the growth of active agents to a maximum of double the original size.
| Algorithm 3 Passive recruitment algorithm. |
for each agentX in population do if agentX NOT Active then select random agentY from population if agentY Active then agentX adopts agentY’s hypothesis end if if agentY NOT Active) then agentX adopts a new random hypothesis end if end if end for
|
| Algorithm 4 Active recruitment algorithm. |
for each agentX in population do if (agentX Active) then select random agentY from population if (agentY NOT Active) then agentY adopts agentX’s hypothesis agentY becomes Engaged end if end if end for for each agentX in population do if (agentX NOT Active AND agentX NOT Engaged) then agentX receives new random hypothesis end if end for
|
During active recruitment, each agent must also maintain a further variable, engaged, that indicates whether the agent’s hypothesis has changed or not. Should an inactive agent not receive a hypothesis from an active agent during recruitment, it must receive a new random hypothesis, to avoid inactive agents remaining at the same hypothesis position over time.
3.3.3. Combination (or ‘Dual’) Recruitment
The combination recruitment strategy is simply passive recruitment immediately followed by active recruitment.
3.4. Relate
The relate phase is an optional phase, introduced if multiple models are extant in the search space. The technique allows a degree of dynamic re-allocation of agents and the maintenance of multiple clusters of active agents around multiple good hypotheses. The relate phase can also assist with dynamic search spaces, allowing clusters of agents to re-align themselves successfully with the correct hypothesis. The relate phase has two modes: context free and context sensitive [
16].
3.4.1. Context-Free Mode
This dictates that all active agents select another agent at random; if this other agent is also active, the selecting agent deactivates (becomes inactive) and selects a new random hypothesis. This should ensure that when a good hypothesis is discovered (or multiple good hypotheses), approximately half the population is left inactive to continue roaming the search space.
| Algorithm 5 Relate context free. |
for each agentX in population do if (agentX Active) then select random agentY from population if (agentY Active) then agentX set to inactive agentX adopts a new random hypothesis end if end if end for
|
3.4.2. Context-Sensitive Mode
This mode is identical to context free, with the exception that when selecting a random agent, the selecting agent will only deactivate and select a new random hypothesis if the selected agent is active and both agents share the same hypothesis. This should ensure that at most, half of the agent population is associated with any one good hypothesis.
| Algorithm 6 Relate context sensitive. |
for each agentX in population do if agentX Active then select random agentY from population if agentY Active AND agentY hypothesis == agentX hypothesis then agentX set to inactive agentX adopts a new random hypothesis end if end if end for
|
3.5. Halting
After each test and diffuse iteration (and optionally, relate phase), the SDS process determines whether the agent population has reached a state that determines the completion of the search: the halting criteria. Ideally, the search will stop as soon as the best hypothesis (or hypotheses) in the search space is found. This can be difficult to ascertain, particularly with noisy data.
During the initial iterations of the search, the active agent populations will remain small, until an agent hits a good/optimal hypothesis; the population (cluster) around this hypothesis will then grow as more and more agents are recruited to it. Depending on the search space and model parameters, the cluster around the optimal hypothesis (or hypotheses, if the relate phase is used) will stabilise. There are two types of criteria to apply that determine when the SDS search process should come to an end: weak halting criteria and strong halting criteria [
16].
3.6. Weak Halting Criteria
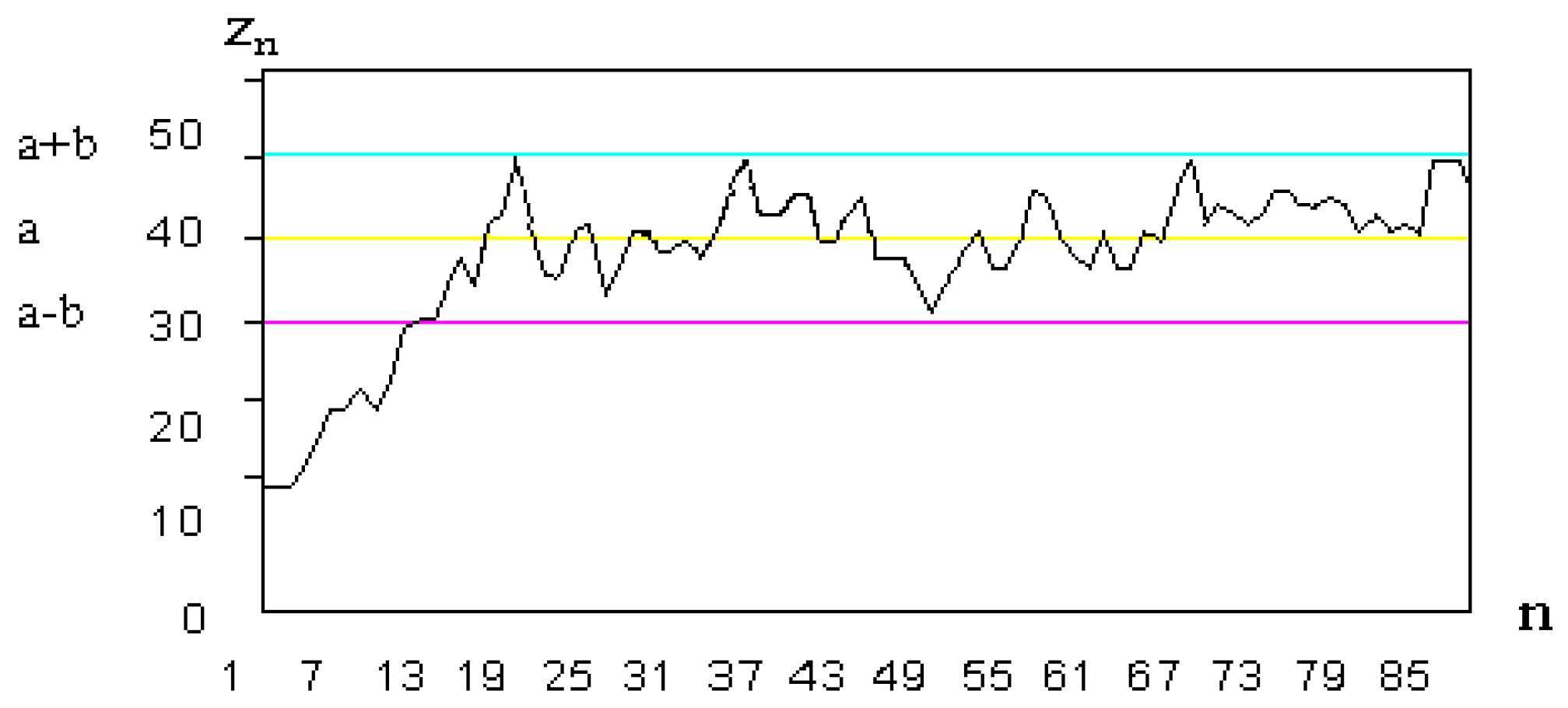
Weak halting criteria states that SDS should stop when a certain percentage of all agents are active, regardless of their hypothesis. Once above this threshold, the population should then stabilise at a certain level. This stabilisation can be seen as the population of active agents remaining steady, with a margin of tolerance, for a certain number of iterations. Once these criteria have been met, the search stops.
Figure 1.
SDS cluster stabilisation. (a) The threshold level; (b) the amount of tolerance; the x-axis describes the number of iterations, n, while the y-axis describes the percentage of active agents.
Figure 1.
SDS cluster stabilisation. (a) The threshold level; (b) the amount of tolerance; the x-axis describes the number of iterations, n, while the y-axis describes the percentage of active agents.
3.7. Strong Halting Criteria
This defines the halt state as being concerned with the percentage of active agents in the largest cluster; i.e., looking at the hypothesis that has the most agents clustered around it and applying the same threshold/tolerance rule as with the weak halting state, but looking instead at the percentage of agents that are active within this largest cluster.
4. Hyperplane Estimation
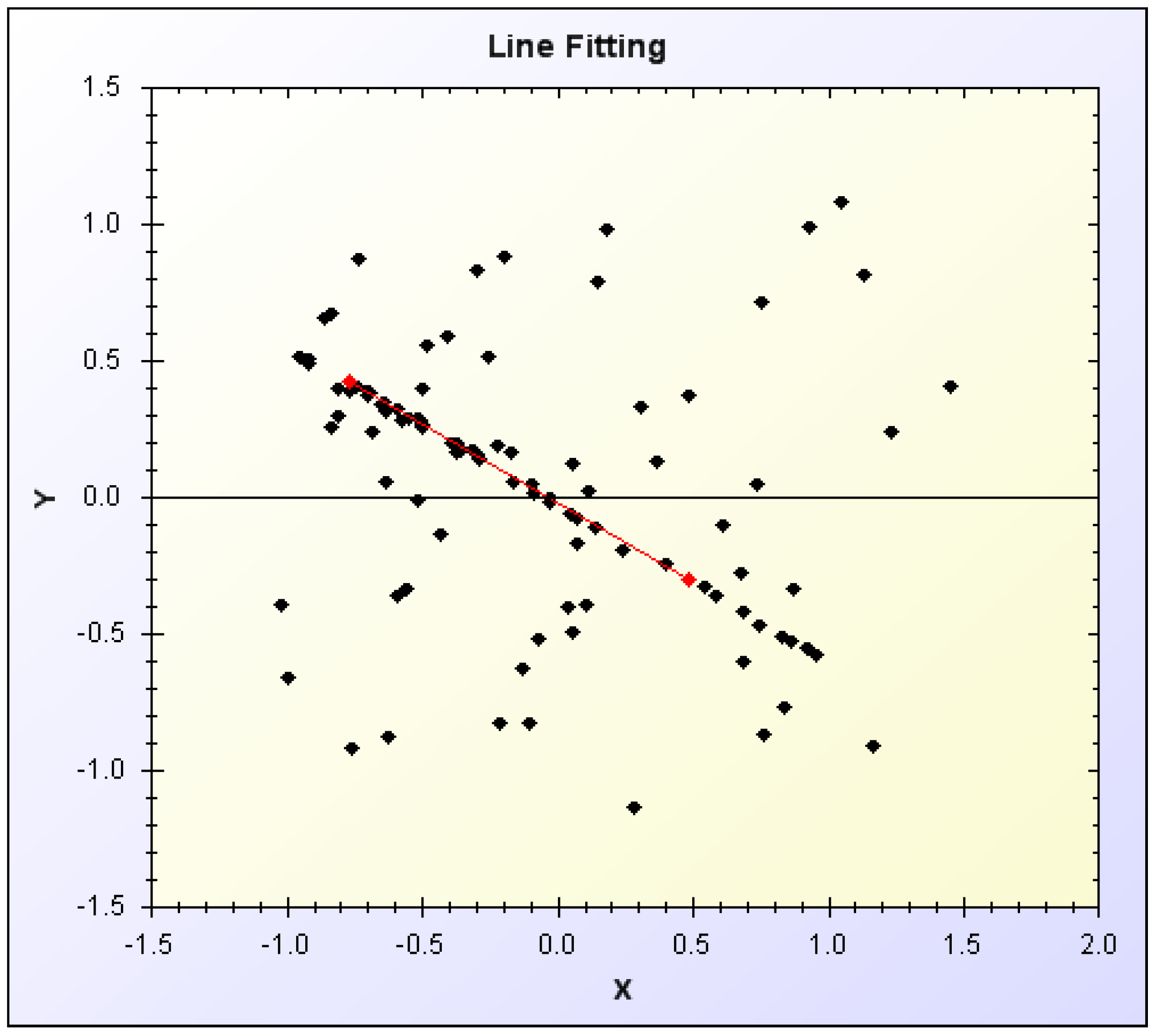
Parameter estimation is the task of finding a suitable fit of data in a given search space to a model. A simple parameter estimation task is that of line fitting: given a set of points on a two-dimensional plane, can a set of points that form a line be estimated?
Figure 2.
Simple line fitting by parameter estimation.
Figure 2.
Simple line fitting by parameter estimation.
Robust parameter estimation is an extension of parameter estimation that is able to fit a set of parameters in the presence of outliers; points that are not on the line, perhaps due to noisy observational data or the presence of multiple line candidates [
18].
A traditional technique for estimating these types of parameters is the Hough transformation [
21].
Latterly, the most popular robust estimators are those based on the stochastic principles introduced by the RANSAC algorithm [
22].
The main task that this research is concerned with is that of hyperplane estimation in multiple dimensions in the presence of increasing noise.
A line can be seen as a hyperplane in two-dimensional space. Given a set of data points in two dimensions, the inliers are seen as those points that lie on the line, while the outliers are seen as those scattered points that do not fit the model. Generally, it is assumed that inliers are perturbed orthogonally from the hyperplane by a zero mean Gaussian with probability distribution:
σ is the standard deviation and x the Euclidean distance from the hyperplane. The inliers are scattered around a true hyperplane, with the described amount of noise.
A hyperplane in three dimensions can be seen as a sheet through three-dimensional space, analogous to a line through two-dimensional space. Hyperplanes in higher dimensions are difficult to visualise.
Hyperplanes (and other manifolds) can be described using a minimal set of data. A hyperplane in two-dimensional space is able to be described using two points: termed the minimum set. A hyperplane in three-dimensional space can be described with three points. This relationship holds as the dimensions increase.
4.1. Hyperplane Hypothesis Generation and Evaluation by Singular Value Decomposition (SVD)
In order to fit data to a model for hyperplane estimation, a method is needed to generate hypothetical hyperplanes for evaluation against the data set. A widely used technique to solve a linear system of equations is the least squares solution from the components of singular value decomposition (SVD) [
23], a technique with which to describe a matrix in a decomposed form in terms of other matrices. A given matrix,
M, can be described, after SVD has been performed, to generate
U (the real orthogonal matrix),
D (the rectangular diagonal matrix, whose diagonal entries are the singular values of
M) and
V (the real orthogonal matrix) as:
The details of the SVD calculation are not given here.
However, one is able to solve a linear system described by a matrix, M, by taking the SVD and subsequently taking the right-hand column of the calculated V as the solution.
For example, in two dimensions, given the equation of a line:
Along with two points (
x1 y1 1) and (
x2 y2 1), in homogeneous form, one can construct the matrix:
and vector:
Thus, the system is described as:
Taking the SVD of
M and using the values in the right-hand column of
V, a solution for
t is obtained. For two rows, this will solve Equation (
6) exactly, but as more rows are added, it will give the least squares solution.
In order to extend this beyond two dimensions, we simply increase the size of the vector described in Equation (
5); needing, where
n denotes the number of dimensions,
n rows in
M, in order to uniquely identify a hyperplane in this way.
Thus, M can be thought of as the minimal set required to describe a hyperplane. This minimal set is used as an agent’s hypothesis.
Finally, a method is required for evaluating the hypothesis against a data point. This Euclidean distance measure is called the residual distance of a point from a hyperplane. To calculate this, we must first convert the hyperplane to Hessian normal form [
24], which then allows us to easily calculate the orthogonal distance from the hyperplane by taking the dot product of the point (with homogeneous coordinates) with the vector of hyperplane parameters,
t. This also applies identically in
n dimensions [
24].
5. Beyond Standard SDS
Standard SDS, as described in the restaurant game, has been shown to be a good search and optimisation method, able to converge to the optimum solution under the right search space conditions. However, standard SDS is only easily applicable on optimisation problems with a decomposable objective functions (such as best-fit template matching)—objective functions that can be evaluated partially.
Rifaie
et al. [
25] and Omran
et al. [
26], have shown how SDS can be an effective technique for continuous optimisation problems. Rifaie’s work suggests that the powerful resource allocation mechanisms deployed in SDS have the potential to improve the optimisation capabilities of classical evolutionary algorithms.
The main weakness of standard SDS is its approach to hypothesis selection. Generally, and particularly in parameter estimation tasks, randomly selecting hypotheses from the entire search space is unlikely to yield good results [
18]. Following Rifaie and Bishop [
18], who, in turn, have adopted methods highlighted by the work on RANSAC [
22] and its minimal set selection to describe a hypothesis, it is possible to improve SDS and allow it to perform more complex search and optimisation tasks by giving it a mechanism that drives the hypothesis selection from the available data space, rather than drawing hypotheses from the total search space. Following RANSAC, SDS can now also be used on regression problems using minimal sample sets to drive hypothesis selection. Two variants of SDS, with this methodology at their core, are now detailed.
5.1. Data-Driven SDS (DDSDS) for Hyperplane Estimation
Data-driven SDS [
18] retains all the core components and simplicity of standard SDS, as seen in the algorithm detailed in
Section 2, with some crucial differences at each stage of the algorithm.
5.2. DDSDS Initialise
During the initialisation phase, all agents randomly select a hypothesis from the search space. For Data-driven SDS (DDSDS), as applied to hyperplane estimation, this entails randomly selecting a minimal set of points required to describe a hyperplane (n points, in n dimensions) from the available data points provided as the search space (as opposed to all possible points in continuous space) and performing singular value decomposition as previously described in order to generate the hypothesised hyperplane solution. A further point, p, drawn from the agent’s minimal set, is stored as part of the agent’s hypothesis; this p is thought of as the data hypothesis and is put to use in the test phase.
5.3. DDSDS Test
During the test phase, each agent now selects a data point with which to test its hypothesis. The data point selected is not taken from the entire set of data, but rather from the set of data points currently associated with other agents. Hence, data points that are associated with many agents are more likely to be selected than data points associated with only a few agents. Data points that are not associated with any agents cannot be selected. Significantly, the set of points that is tested for fitting with the hypothesis is dynamically constrained by the search, rather than being the entire data set. As a consequence, the search will always converge to 100% agent activity, as the test set is ultimately constrained to only those generated by the inlier distribution [
18].
Once selected, the data point is evaluated against the hypothesis; if the Euclidean distance, the residual (calculated as previously illustrated), is under a certain threshold, t, the agent becomes active; otherwise, the agent remains inactive.
During experimentation, it was found that varying the numbers of these residual tests (each agent might pick and test two data points, rather than just one, and become active if either meets the threshold test) had a significant impact on the convergence time of the algorithm. Unfortunately, as we shall see later, this technique also has an impact on the accuracy of the algorithm.
5.4. DDSDS Diffusion
Diffusion proceeds in the usual SDS manner, based on the recruitment strategies employed. However, as the data point, p, now forms part of the agent’s hypothesis, this value is also transferred from active to inactive agents during recruitment. Should an inactive agent not receive a new hypothesis from another agent during the diffusion phase, the agent selects both a new random hypothesis, along with a new data point, p, from the minimal set. This allows the convergence of the entire data set during the test phase, as even though only data points for testing are selected from the population of agents, newly minted hypotheses are drawn from the entire data set.
5.5. Coupled SDS (CSDS) for Hyperplane Estimation
Introduced by Rifaie and Bishop [
18], coupled SDS (CSDS) is essentially a modification of DDSDS. During DDSDS for hyperplane estimation, an agent’s hypothesis can be seen as a composite hypothesis comprising the manifold hypothesis, derived from the minimal set via singular value decomposition, in addition to the data hypothesis: simply, a point,
p, from the minimal set. More generally, the manifold hypothesis in hyperplane estimation can be termed the model hypothesis. Bishop notes that this composite hypothesis can be easily split, leading to the concept of two decoupled agent populations, each maintaining and exchanging information about one half of the composite hypothesis.
Essentially, the standard phases of SDS remain in place, with the following modifications.
5.6. CSDS Initialise
During the initialisation phase, two independent agent populations are generated; one to maintain the model hypothesis; one to maintain the data hypothesis. As before, the model hypotheses are generated by randomly selecting a minimal set of data points and performing SVD. A data hypothesis is a data point, p, selected at random from the data set.
| Algorithm 7 Coupled SDS. |
Initialisation phase Two populations are initialised: 1. A data hypothesis population 2. A model hypothesis population while Halting criteria not satisfied do Test phase Hypothesis evaluation Randomly select an agent from each population Model agent and data agent form a complete hypothesis Diffusion phase All agents deploy a communication strategy The two populations act independently Relate phase (optional) In each population: Active agents with the same hypothesis randomly deactivate Halt phase Evaluation of halting criteria end while
|
5.7. CSDS Test
During the test phase, hypothesis evaluation is performed by forming a complete hypothesis. This is done by selecting an agent from each of the independent populations, combining a model hypothesis with a data hypothesis and calculating the appropriate residual; should this residual fall under the necessary threshold, both agents become active; otherwise, inactive.
5.8. CSDS Diffusion
During the diffusion phase, each population of agents acts independently, in the sense that they only communicate with other agents from their own population. Otherwise, the usual SDS recruitment strategies can be applied. As before, should an agent not receive a new hypothesis from a fellow agent, it is required to generate a new random hypothesis. For model agents, this requires the usual minimal set selection plus SVD, while for data agents, simply selecting another data point.
5.9. CSDS Synchronicity and Context Sensitivity
A further complication introduced by the decoupling of agent populations in CSDS is that of sequencing the phases and selecting appropriate population sizes. Generally, in other variants of SDS, only one population is maintained, hence the test and diffuse phases are simply executed in order. Applied to CSDS, this can be thought of as synchronous CSDS, in the sense that each population iterates through its cycles, in turn; perhaps, the model population iterates first, followed by the data population.
Asynchronous CSDS, however, proceeds by allowing each agent population to act in parallel; implemented here, this equates to interleaving the iteration of each population; for example, the model population selects one agent, forms a complete hypothesis with a data agent and performs the test phase; following this, a data agent will do so similarly; next, the model agent will perform diffusion, followed by the data agent; finally, the relate phase is performed in a similar manner. It was found experimentally that asynchronous operation yields the best performance.
As with DDSDS, the population size chosen is critical. Interestingly, in CSDS, it is possible to vary the size of both the model populations and the data populations. Increasing the size of the model population leads to a wider variety of hypotheses to test and, thus, more SVD calculations to perform, while increasing the data agent population leads to a larger number of residual calculations. Residual calculation is far less computationally expensive than SVD calculation, though SDS tends to perform more of them. Generally, the convergence of the system as a whole is determined by the convergence properties of the model population.
5.10. Master/Slave Synchronous CSDS
In this mode of operation, one of the agent populations is selected to be the master population, with the other population as a slave. Complete hypotheses are tested by sequentially moving through the agents in the master population and randomly selecting an agent from the slave population.
5.11. Sequential Master/Slave Synchronous CSDS
In this mode, each agent population takes a turn at being the master population. For example, the model population takes the first turn at being the master population; each agent in this population randomly selects an agent from the data population and tests the complete hypothesis formed. After all model agents have been cycled, the data agent population takes its turn at being the master population. Again, all data agents are cycled through, this time selecting a random model hypothesis to test.
5.12. Context Sensitivity
The relate phase can be applied to CSDS in the usual manner in order to allow the system to maintain multiple proposed good quality hypotheses in a dynamically changing environment.
6. Experimental Investigation: Hyperplane Estimation Techniques
An investigation was performed on the task of hyperplane estimation in many different dimensions and with varying levels of noise. Each of the two data-driven approaches to SDS, DDSDS and CSDS, were compared, in different incarnations, against RANSAC, a good benchmark for the best available parameter estimation technique (potentially superior techniques are available, such as MLESAC[
27] and NAPSAC[
28], though these are both derived from RANSAC).
6.1. Search Environment Properties
As previously discussed, a hyperplane can be thought of as a line in two dimensions, a sheet, or plane, in three dimensions, and so on for higher dimensions. The crucial idea is that a hyperplane can be described by a linear equation, determined by, for example, in three dimensions:
where the solution (
a,
b,
c,
d) determines the orientation of the plane in the three-dimensional space. This linear description of a plane holds as the dimensions increase. For example, in five dimensions, the hyperplane can be described:
To uniquely describe a hyperplane, one requires a minimal set of points of size equal to the number of dimensions of the space containing the hyperplane. For three dimensions, three points make up the minimal set; for five dimensions, five points.
It was necessary to generate synthetic data with which to test the algorithms. Hence, some data set was needed, residing within which a hyperplane whose points were perturbed orthogonally by Gaussian noise (the inliers) could be found. All points not associated with the hyperplane are thus termed outliers.
Generation of this data is relatively straight forward once the singular value decomposition technique previously described is known. Random minimal sets can be determined, the system solved for (a,b,c,d,...) and, consequently, a set of inlier points generated with each axis co-ordinate perturbed by Gaussian noise at an appropriate level.
The ratio of inliers to outliers determines the overall noisiness of the environment (distinct from the noise perturbations on the inliers themselves).
Thus, two main variables can be evaluated: the number of dimensions and the overall noisiness of the environment. The minimal set size is equivalent to the number of dimensions. Increasing the dimensions increases the search space size, without the need for additional data points. There is a combinatorial explosion in the search space size as the dimensions increase.
For all the trials, dimensions and noise detailed below, 1000 data points were used as the search space. A randomly positioned hyperplane was placed within this space for each trial. The level of environmental noise determines the proportion of inliers to outliers; a level of 50% implies 500 data points making up the inliers (the generated hyperplane) and the remaining 500 evenly distributed outliers. The inliers were disturbed orthogonally from the true hyperplane by Gaussian noise, as described previously. For each measure, 10 trials were run and the average measurement taken (of both convergence time and accuracy). SDS convergence occurred at the 100% agent activity level.
The convergence times of the trials have been used as a guide to computational expense. Another method is to compare the number of singular value decompositions and residual calculations needed for convergence; however, upon analysis, the correlation between the time to convergence in milliseconds and the number of SVDs (the most computationally-intensive process) performed is very close, and hence, the actual time taken is used as a more illustrative measure of overall performance.
To measure the accuracy of the algorithms, the hypothesis converged as the optimal solution was tested against all points in the data space; the percentage classed as inliers are seen to be the score of the hypothesis. The accuracy of the hypothesis is a measure of the percentage of inliers in the data that are described by the solution.
The size of the population of agents in standard SDS has a bearing on the number of iterations required for SDS to converge; similarly for data-driven variants. Too large a population, for a given search, will require SDS to perform far too many SVDs, thus reducing its speed of convergence; too small a population may lead to a lack of accuracy, with the benefit of speeding up the algorithm.
7. Results
After experimentation with coupled and data-driven modes of SDS, it was found that varying the size of the population of agents holding a model hypothesis had a large impact on the convergence performance of the technique; there are also implications for the accuracy of the algorithm. For CSDS, a small model population generally allowed for quicker convergence times at the expense of some accuracy; similarly a larger model population converged more slowly, but produced better accuracy measures. Remembering that as the dimensions increase, there is a combinatorial explosion of the number of possible hypotheses available, it stands to reason that a larger number of model hypotheses entertained by CSDS and DDSDS should lead to better solutions being found (i.e., the risk of overlooking an optimal solution is smaller).
Experimentally, for CSDS, a rule of thumb relationship between the dimensions of the data and the number of model agents was roughly established as: . The larger numbers of model agents gives the algorithm a better chance of finding a good solution in the exploding number of possible hypotheses in higher dimensions. Using too many agents results in very long computation times per iteration, while too few cannot cover the search space adequately to converge on a solution quickly.
Variance in SDS convergence time and accuracy is known to be sensitive to noise and initial state. For example, should a population be instantiated with a high degree of agents at the optimal solution, the convergence time will be shortened. The trends presented are representative of convergence times and accuracy. At high noise and in high dimensions, variance increases. A more detailed analysis of these issues is provided in [
14].
Using a data space size of 1,000 points, results for the following population sizes are presented (in
n dimensions):
Two residual tests were performed during the test phase. This gives a hypothesis two chances of becoming/staying active during the test phase (the agent activates if either of its residual tests fall under the desired threshold).
Results are presented here in comparison with RANSAC performing the same parameter estimation task.
7.1. Dimension Trials
For the dimension trials, all parameters were as described above, with the environmental noise fixed at 50%.
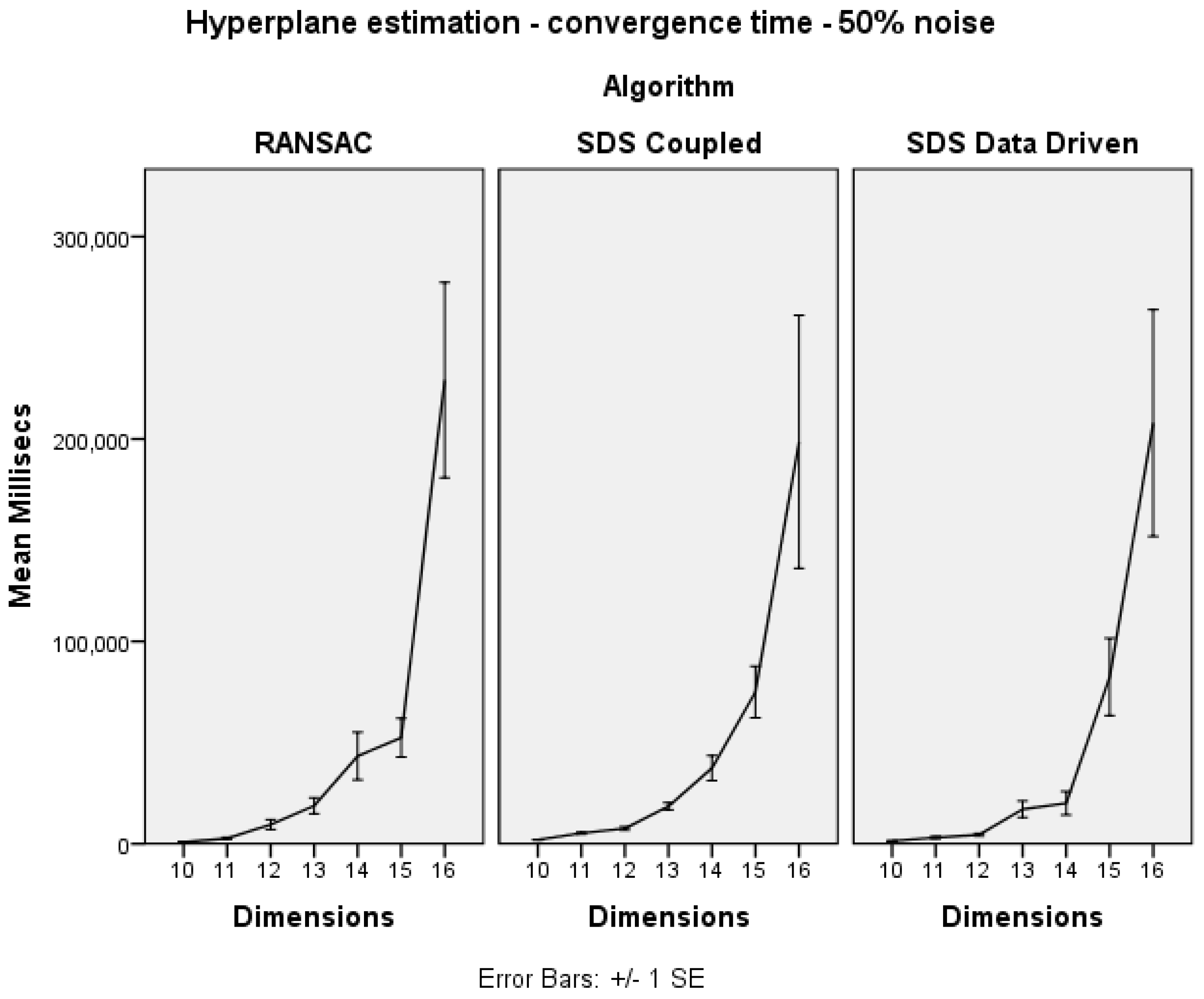
As shown in
Figure 3, the convergence time of each algorithm is similar in increasing dimensions.
Figure 3.
Hyperplane estimation dimension trials: convergence time.
Figure 3.
Hyperplane estimation dimension trials: convergence time.
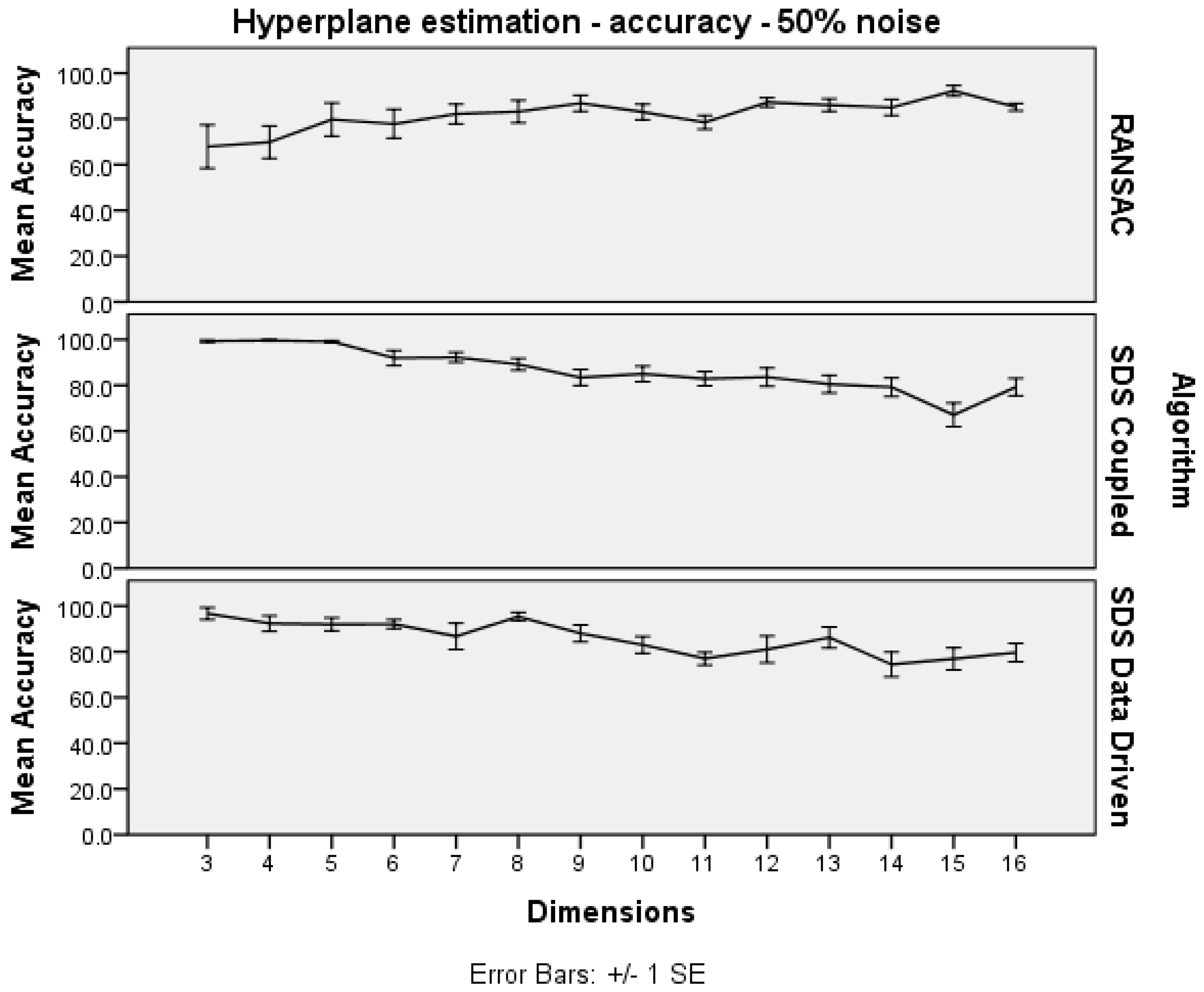
Figure 4 shows that the SDS algorithms are able to maintain good accuracy, dropping off in 15 dimensions and higher. The worrying trend, for SDS, is that the accuracy gradually diminishes as the number of dimensions increases.
Figure 4.
Hyperplane estimation dimensions trials: accuracy.
Figure 4.
Hyperplane estimation dimensions trials: accuracy.
7.2. Noise Trials
Having reported the dimension properties of the three algorithms, at a fixed 50% environmental noise level, the other side of the story can be investigated: increasing environmental noise, at a fixed 10 dimensions.
Figure 5 shows that both varieties of SDS broadly match the performance of RANSAC in increasing noise at 10 dimensions. In high noise, RANSAC is superior. CSDS outperforms DDSDS.
In
Figure 6, it is interesting to note that CSDS is able to outperform RANSAC in terms of accuracy at up to around 50% environmental noise, after which the performance of each algorithm is roughly equivalent.
Figure 5.
Hyperplane estimation noise trials: convergence time.
Figure 5.
Hyperplane estimation noise trials: convergence time.
Figure 6.
Hyperplane estimation noise trials: accuracy.
Figure 6.
Hyperplane estimation noise trials: accuracy.
7.3. Discussion
Looking at the results obtained by each algorithm in the many different noise and dimension environments, it is apparent that there is no obvious winner in all situations. The optimum choice of algorithm is very much dependent on the particular situation to be solved, though this is to be expected, in line with Wolpert and Macready’s no free lunch theorems [
29,
30].
Given a certain set of search space conditions, a particular SDS variant could be configured to give the best performance. However, sometimes, RANSAC would be the best choice. In general, the best performing SDS variant is coupled SDS, with the model agent population linked to the dimensions of the data. There is a scope for fine tuning this agent population to maximise the benefits, though major leaps in performance are unlikely. SDS can perform as well as RANSAC in most hyperplane estimation situations, which should be of interest for computer vision applications. Further customisation and tuning of the algorithms to specific applications and scenarios should produce improved results.
8. Conclusions
Stochastic diffusion search has been placed in the context of swarm intelligence techniques in contrast to more traditional search and optimisation methods.
A variable population size has been shown to be a key factor when designing SDS systems, with coupled SDS shown to be the most flexible and best performing variant of SDS.
All SDS varieties appear to suffer from the no free lunch issue; configured to perform well for a certain problem (for example, hyperplane estimation in twelve dimensions) automatically sets them up to perform badly on another problem (for example, hyperplane estimation in three dimensions). For this reason, it is suggested that further work is carried out to provide SDS with some mechanism of auto-tuning itself; dynamically modifying population size along with some method of varying the number of datum checked during the test phase.
There may be some fundamental relationship between the number of hypothesis agents (in CSDS) needed for best performance and the total number of hypotheses in the system. Given the data-driven techniques adopted, this possible number of hypotheses is finite. Similarly, it seems plausible that there is an optimum number of data agents required for any given problem; some fraction of the total number of data elements, for example. While some attempts have been made here to approximate these relationships, further work is necessary to establish their fundamental properties or simply to provide better heuristics to guide their approximation.
SDS has been shown to be an excellent swarm intelligence search and optimisation technique. This is due to SDS’s partial evaluation of the objective function, in comparison with many existing techniques’ approach of full evaluation. The communication phase of SDS allows good hypotheses to spread throughout the agent population quickly and efficiently, while the discarding of bad hypotheses is generally reliable.
Given that the relate phase can be applied to CSDS in the usual manner, further work in, for example, the realm of image and video analysis could include an investigation into the performance of SDS in context-sensitive modes in order to entertain multiple hypothesis solutions in a dynamic search space; something RANSAC is unable to achieve. For example, applying this kind of technique to object recognition during real-time video analysis appears to offer a rich vein of potential.