Tractabilities and Intractabilities on Geometric Intersection Graphs †
Abstract
:1. Introduction
2. Preliminaries
3. Polynomial Time Algorithms for the Bandwidth Problem
| Algorithm 1: Bandwidth of a general graph |
| Input : Graph G = (V,E) |
| Output: generate a proper interval graph that gives a minimum completion of G make the unique proper interval representation of find a point p such that for any other point on |
| returen (). |
3.1. Linear Time Algorithm for a Threshold Graph
- For , corresponds to the point i, that is, .
- For , corresponds to the interval , where j is the minimum index with .

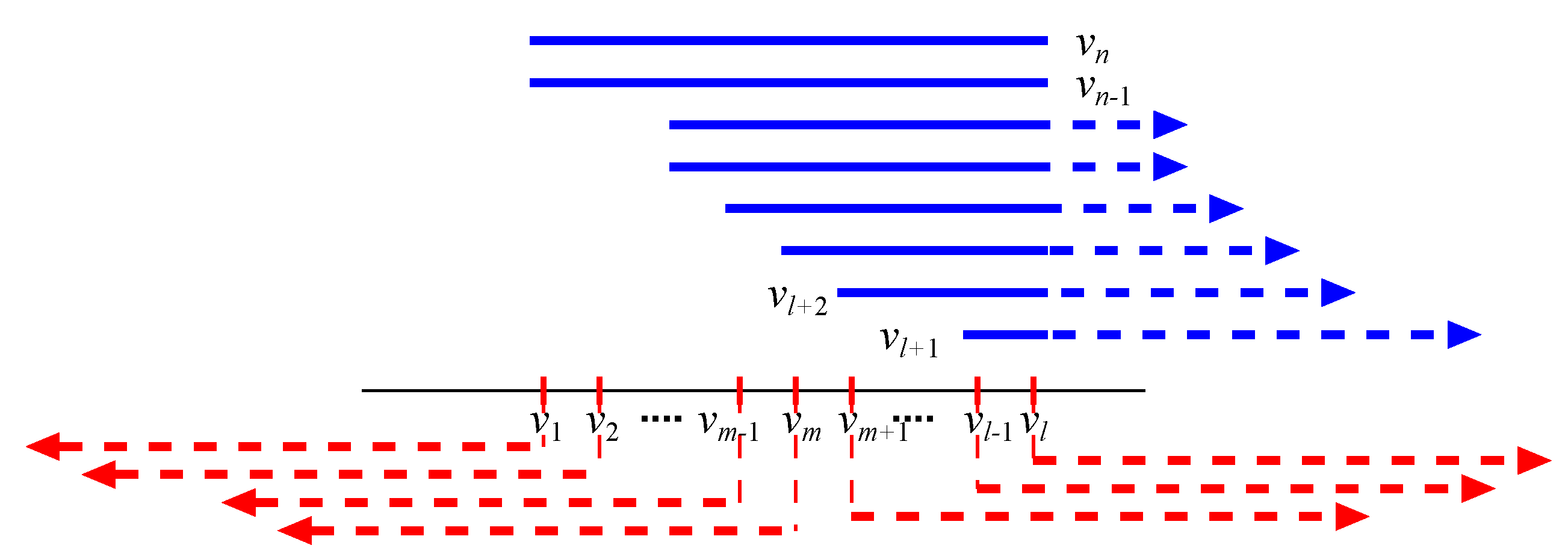
| Algorithm 2: Bandwidth of a threshold graph |
| Input : Threshold graph G = (V, E) with w(v1 ≤ w(v2) ≤ … ≤ w(vn) and t Output: let ℓ be the minimum index with set  |
- let j be the minimum index with ;
- set ;
3.2. Linear Time Algorithm for a Chain Graph
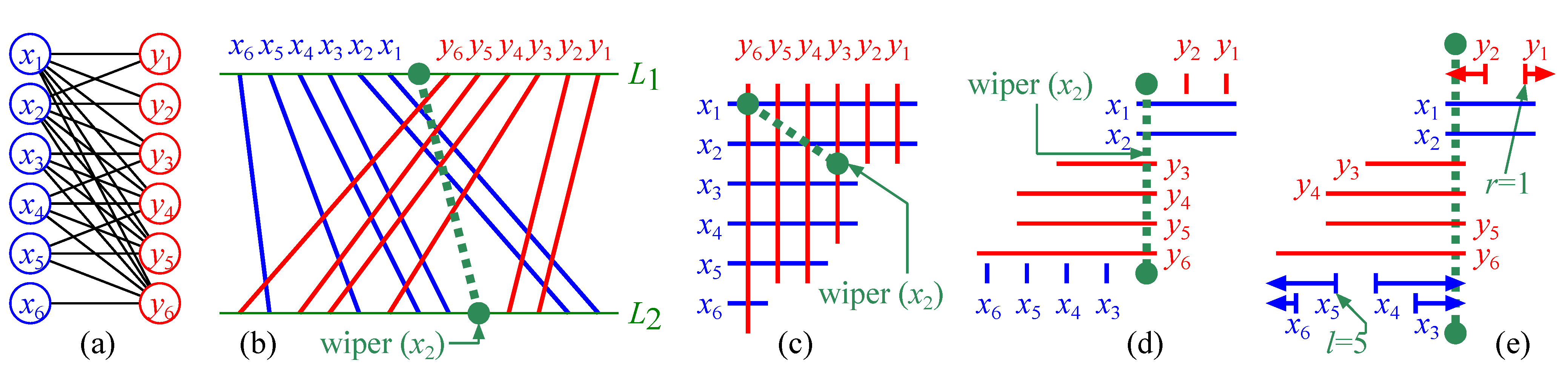
| Algorithm 3: Bandwidth of a chain graph |
| Input : Chain graph G = (X, Y, E) with N(xn) ⊆ † ⊆ N(y1) ⊆ … ⊆ N(yn′) Output: by Algorithm 2  |
4. Intractable Problems on a (Unit) Grid Intersection Graph
4.1. The Hamiltonian Cycle Problem


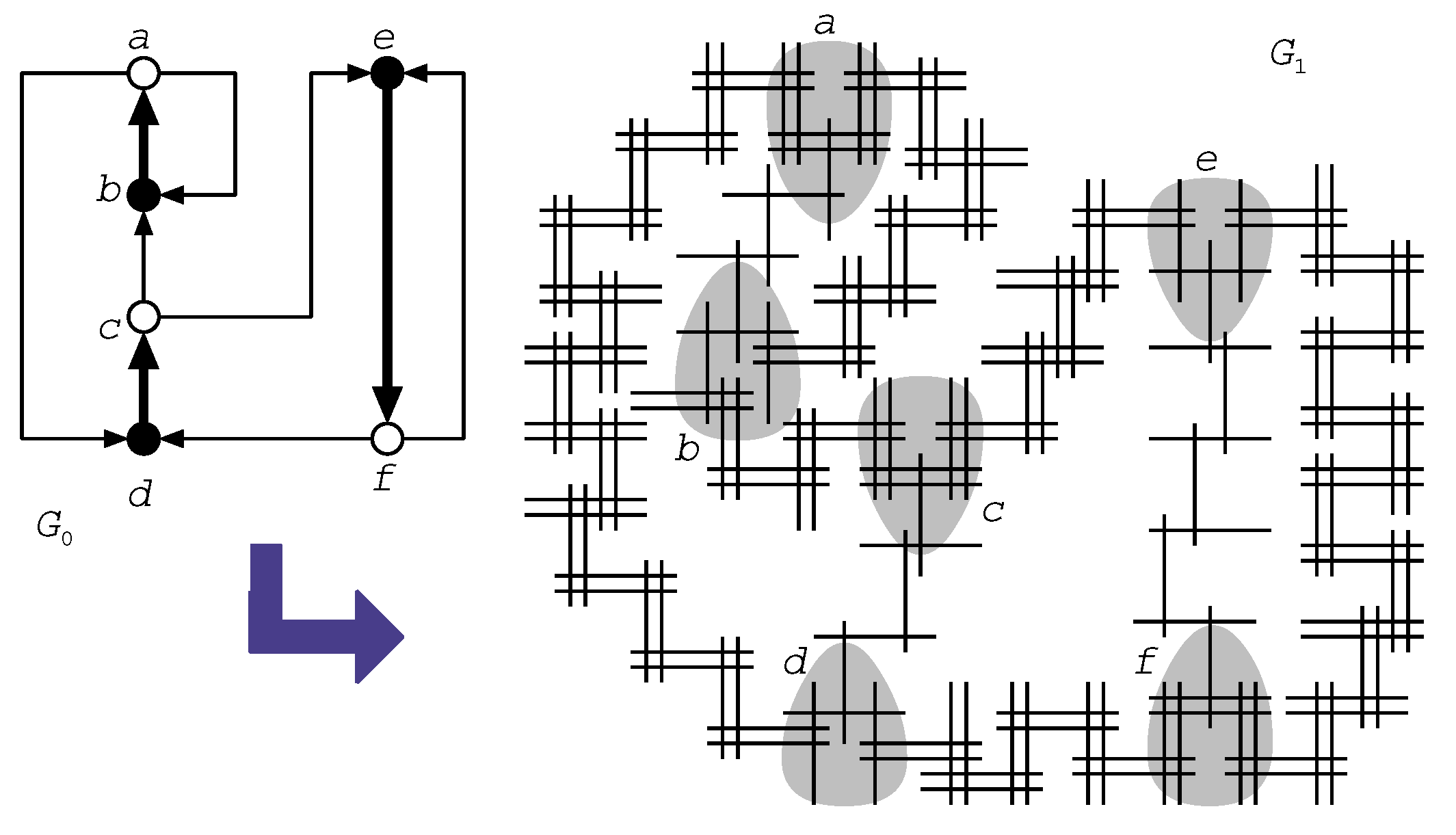
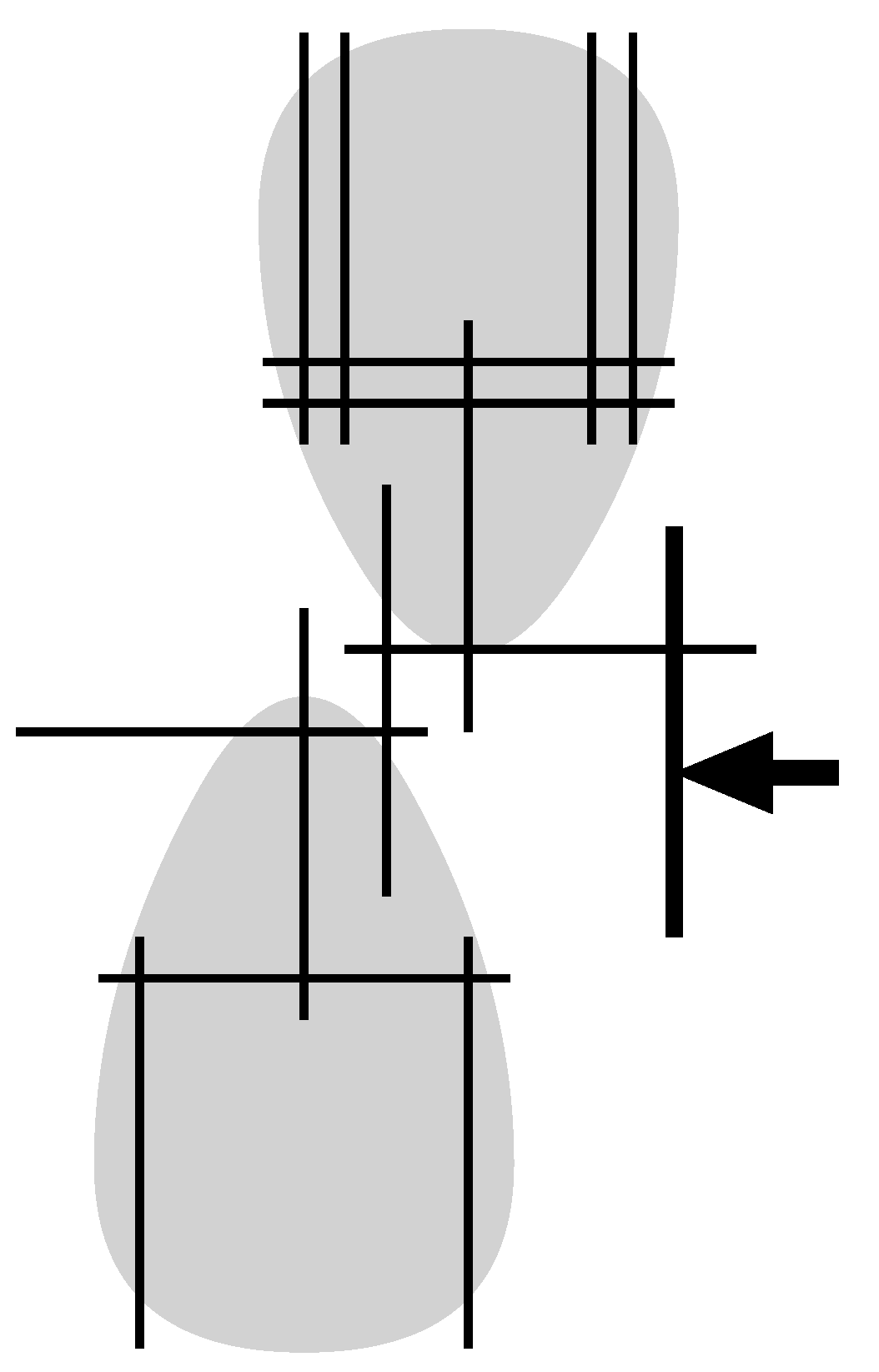
4.2. The Graph Isomorphism Problem
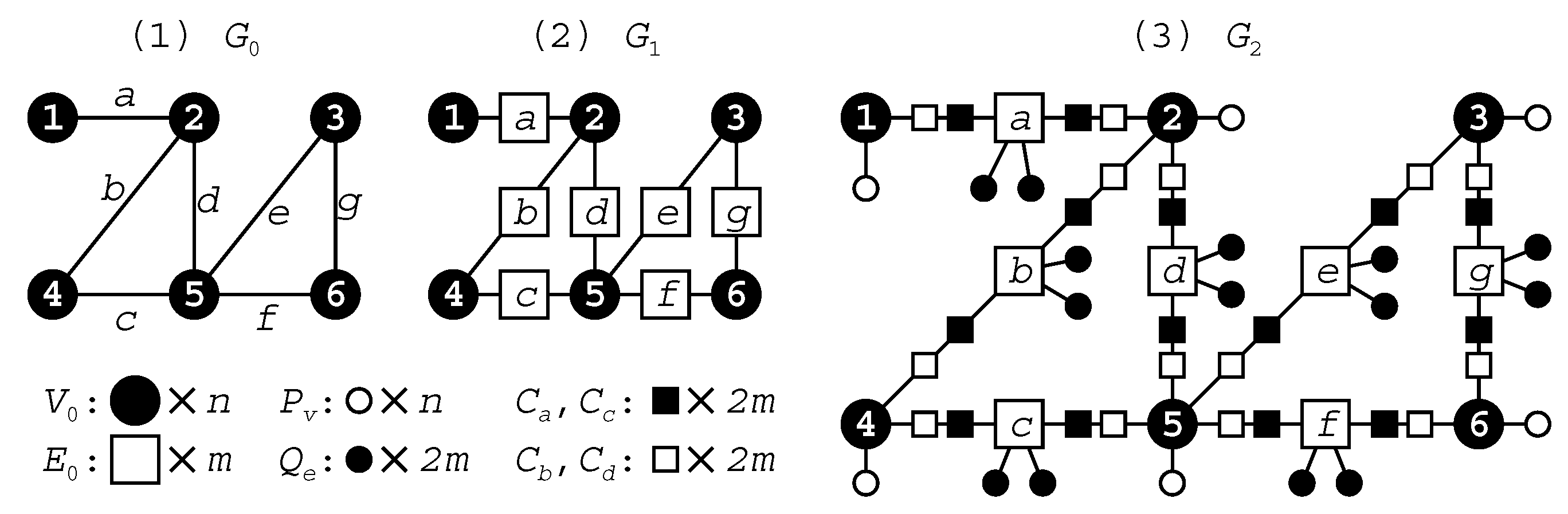
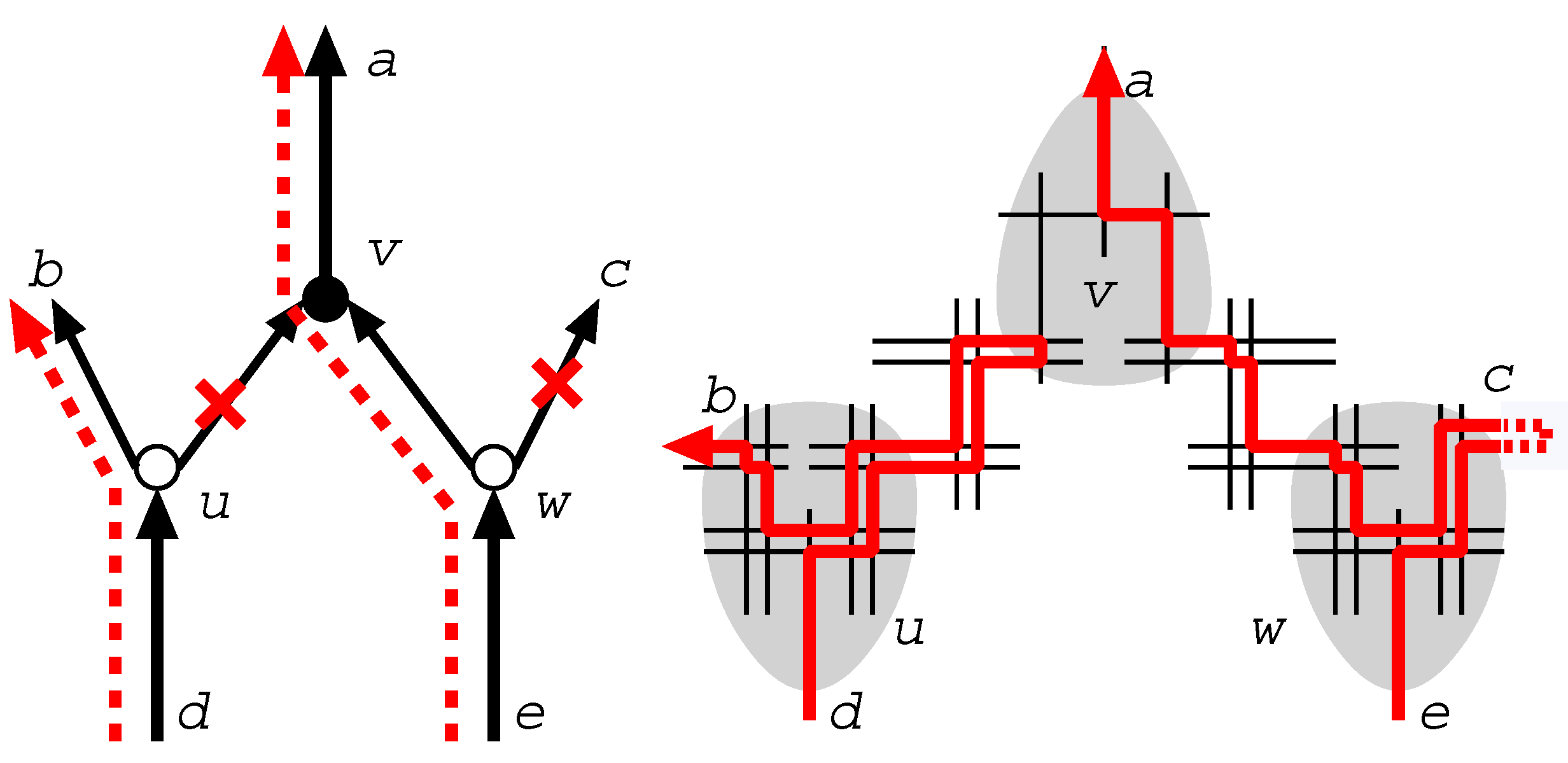
- , ; we let , , where for some .
- ; each vertex in is called pendant and , . That is, we have and .
- ; each vertex in is called connector, and , , , and .
- For each i with , each pendant is joined to . That is, for each i with .
- For each j with , two pendants and are joined to . That is, for each j with .
- For each with , we have two vertices and with . For the three vertices , , , we add , , , , , into . Intuitively, each edge in is replaced by a path of length 3 that consists of one vertex in and the other one in .

5. Conclusions
Appendix
A. Algorithm by Kleitman and Vohra
| Algorithm 4: Algorithm KV |
| Input : An interval graph G = (V, E) and a positive intrger k. Output: A Layout realizing if it exists. Set and for all where . Set and ; Select with smallest (break ties by selecting the interval with smallest ) and set ; Set and . If , stop, all vertices have been labeled; If overlaps i and set Let . If for all , go to step 7; There is a j such that . Stop, for the bandwidth of the graph is ; Find the smallest value , such that ; Select with smallest (break ties as in Step 2). Set and go to Step 3. |
References
- Golumbic, M. Algorithmic Graph Theory and Perfect Graphs, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Spinrad, J. Efficient Graph Representations; American Mathematical Society: Providence, RI, USA, 2003. [Google Scholar]
- Fishburn, P.C. Interval Orders and Interval Graphs; Wiley & Sons, Inc.: Hoboken, NJ, USA, 1985. [Google Scholar]
- McKee, T.; McMorris, F. Topics in Intersection Graph Theory; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Uehara, R. Simple Geometrical Intersection Graphs. In Proceedings of the Workshop on Algorithms and Computation (WALCOM 2008); Springer-Verlag: Berlin/Heidelberg, Germany, 2008; pp. 25–33. [Google Scholar]
- Uehara, R. Bandwidth of Bipartite Permutation Graphs. In Proceedings of the Annual International Symposium on Algorithms and Computation (ISAAC 2008); Springer-Verlag: Berlin/Heidelberg, Germany, 2008; pp. 824–835. [Google Scholar]
- Lai, Y.L.; Williams, K. A survey of solved problems and applications on bandwidth, edgesum, and profile of graphs. J. Graph Theory 1999, 31, 75–94. [Google Scholar] [CrossRef]
- Chinn, P.Z.; Chvátalová, J.; Dewdney, A.K.; Gibbs, N.E. The bandwidth problem for graphs and matrices—A survey. J. Graph Theory 1982, 6, 223–254. [Google Scholar] [CrossRef]
- Kaplan, H.; Shamir, R. Pathwidth, bandwidth, and completion problems to proper interval graphs with small cliques. SIAM J. Comput. 1996, 25, 540–561. [Google Scholar] [CrossRef]
- Kaplan, H.; Shamir, R.; Tarjan, R. Tractability of parameterized completion problems on chordal, strongly chordal, and proper interval graphs. SIAM J. Comput. 1999, 28, 1906–1922. [Google Scholar] [CrossRef]
- Papadimitriou, C.H. The NP-completeness of the bandwidth minimization problem. Computing 1976, 16, 263–270. [Google Scholar] [CrossRef]
- Garey, M.; Johnson, D. Computers and Intractability—A Guide to the Theory of NP-Completeness; Freeman: Gordonsville, VA, USA, 1979. [Google Scholar]
- Monien, B. The bandwidth minimization problem for caterpillars with hair length 3 is NP-complete. SIAM J. Alg. Disc. Meth. 1986, 7, 505–512. [Google Scholar] [CrossRef]
- Kloks, T.; Kratsch, D.; Borgne, Y.L.; Müller, H. Bandwidth of Split and Circular Permutation Graphs. In Proceedings of the WG 2000; Springer-Verlag: Berlin/Heidelberg, Germany, 2000; pp. 243–254. [Google Scholar]
- Shrestha, A.M.S.; Tayu, S.; Ueno, S. Bandwidth of Convex Bipartite Graphs and Related Graphs. In Proceedings of the COCOON 2011; Springer-Verlag: Berlin/Heidelberg, Germany, 2011; pp. 307–318. [Google Scholar]
- Feige, U. Coping with the NP-Hardness of the Graph Bandwidth Problem. In Proceedings of the 7th Scandinavian Workshop on Algorithm Theory (SWAT 2000); Springer-Verlag: Berlin/Heidelberg, Germany, 2000; pp. 10–19. [Google Scholar]
- Cygan, M.; Pilipczuk, M. Exact and approximate bandwidth. Theor. Comput. Sci. 2010, 411, 3701–3713. [Google Scholar] [CrossRef]
- Cygan, M.; Pilipczuk, M. Even faster exact bandwidth. ACM Trans. Algorithm 2012, 8, 1–14. [Google Scholar] [CrossRef]
- Cygan, M.; Pilipczuk, M. Bandwidth and distortion revisited. Discrete Appl. Math. 2012, 160, 494–504. [Google Scholar] [CrossRef]
- Haralambides, J.; Makedon, F.; Monien, B. Bandwidth minimization: An approximation algorithm for caterpillars. Theory Comput. Syst. 1991, 24, 169–177. [Google Scholar] [CrossRef]
- Kloks, T.; Kratsch, D.; Müller, H. Approximating the bandwidth for asteroidal triple-free graphs. J. Algorithm 1999, 32, 41–57. [Google Scholar] [CrossRef]
- Karpinski, M.; Wirtgen, J.; Zelikovsky, A. An Approximation Algorithm for the Bandwidth Problem on Dense Graphs. TR-97-017, Electronic Colloquium on Computational Complexity (ECCC). 1997. Available online: http://eccc.hpi-web.de/report/1997/017/ (accessed on 24 January 2013).
- Gupta, A. Improved bandwidth approximation for trees and chordal graphs. J. Algorithm 2001, 40, 24–36. [Google Scholar] [CrossRef]
- Kloks, T.; Kratsch, D.; Müller, H. Bandwidth of chain graphs. Inf. Process. Lett. 1998, 68, 313–315. [Google Scholar] [CrossRef]
- Kloks, T.; Tan, R.B. Bandwidth and topological bandwidth of graphs with few P4’s. Discrete Appl. Math. 2001, 115, 117–133. [Google Scholar] [CrossRef]
- Kleitman, D.; Vohra, R. Computing the Bandwidth of Interval Graphs. SIAM J. Disc. Math. 1990, 3, 373–375. [Google Scholar] [CrossRef]
- Mahesh, R.; Rangan, C.P.; Srinivasan, A. On finding the minimum bandwidth of interval graphs. Inf. Comput. 1991, 95, 218–224. [Google Scholar] [CrossRef]
- Sprague, A. An O(nlogn) algorithm for bandwidth of interval graphs. SIAM J. Discrete Math. 1994, 7, 213–220. [Google Scholar] [CrossRef]
- Heggernes, P.; Kratsch, D.; Meister, D. Bandwidth of bipartite permutation graphs in polynomial time. J. Discret. Algorithm 2009, 7, 533–544. [Google Scholar] [CrossRef]
- Kratsch, D. Finding the minimum bandwidth of an interval graph. Inf. Comput. 1987, 74, 140–158. [Google Scholar] [CrossRef]
- Booth, K.; Lueker, G. Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms. J. Comput. Syst. Sci. 1976, 13, 335–379. [Google Scholar] [CrossRef]
- Lueker, G.; Booth, K. A linear time algorithm for deciding interval graph isomorphism. J. ACM 1979, 26, 183–195. [Google Scholar] [CrossRef]
- Brandstädt, A.; Lozin, V. On the linear structure and clique-width of bipartite permutation graphs. Ars Comb. 2003, 67, 273–281. [Google Scholar]
- Uehara, R.; Valiente, G. Linear structure of bipartite permutation graphs with an application. Inf. Process. Lett. 2007, 103, 71–77. [Google Scholar] [CrossRef]
- Otachi, Y.; Okamoto, Y.; Yamazaki, K. Relationships between the class of unit grid intersection graphs and other classes of bipartite graphs. Discrete Appl. Math. 2007, 155, 2383–2390. [Google Scholar] [CrossRef]
- Keil, J. Finding hamiltonian circuits in interval graphs. Inf. Process. Lett. 1985, 20, 201–206. [Google Scholar] [CrossRef]
- Müller, H. Hamiltonian circuit in chordal bipartite graphs. Discret. Math. 1996, 156, 291–298. [Google Scholar] [CrossRef]
- Uehara, R.; Toda, S.; Nagoya, T. Graph isomorphism completeness for chordal bipartite graphs and strongly chordal graphs. Discret. Appl. Math. 2004, 145, 479–482. [Google Scholar] [CrossRef]
- Wu, T.H. An O(n3) isomorphism test for circular-arc graphs. Ph.D. Thesis, Applied Mathematics and Statistics, SUNY-Stonybrook, New York, NY, USA, 1983. [Google Scholar]
- Eschen, E.M. Circular-arc graph recognition and related problems. Ph.D. Thesis, Department of Computer Science, Vanderbilt University, Nashville, TE, USA, 1997. [Google Scholar]
- Hsu, W.L. O(M·N) Algorithms for the recognition and isomorphism problem on circular-arc graphs. SIAM J. Comput. 1995, 24, 411–439. [Google Scholar] [CrossRef]
- Curtis, A.R.; Lin, M.C.; McConnell, R.M.; Nussbaum, Y.; Soulignac, F.J.; Spinrad, J.P.; Szwarcfiter, J.L. Isomorphism of graph classes related to the circular-ones property. arXiv:1203.4822v1.
- Roberts, F.S. Indifference Graphs. In Proof Techniques in Graph Theory; Harary, F., Ed.; Academic Press: Waltham, MA, USA, 1969; pp. 139–146. [Google Scholar]
- Bogart, K.P.; West, D.B. A short proof that “proper=unit”. Discret. Math. 1999, 201, 21–23. [Google Scholar] [CrossRef]
- Deng, X.; Hell, P.; Huang, J. Linear-time representation algorithms for proper circular-arc graphs and proper interval graphs. SIAM J. Comput. 1996, 25, 390–403. [Google Scholar] [CrossRef]
- Uehara, R.; Uno, Y. On computing longest paths in small graph classes. Int. J. Found. Comput. Sci. 2007, 18, 911–930. [Google Scholar] [CrossRef]
- Saitoh, T.; Otachi, Y.; Yamanaka, K.; Uehara, R. Random Generation and Enumeration of Bipartite Permutation Graphs. In Proceedings of the 20th International Symposium on Algorithms and Computation (ISAAC 2009); Springer-Verlag: Berlin/Heidelberg, Germany, 2009; pp. 1104–1113. [Google Scholar]
- Brandstädt, A.; Le, V.; Spinrad, J. Graph Classes: A Survey; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Müller, H. Recognizing interval digraphs and interval bigraphs in polynomial time. Disc. Appl. Math. 1997, 78, 189–205. Available online: http://www.comp.leeds.ac.uk/hm/pub/node1.html (accessed on 22 January 2013). [Google Scholar] [CrossRef]
- Hell, P.; Huang, J. Interval bigraphs and circular Arc graphs. J. Graph Theory 2004, 46, 313–327. [Google Scholar] [CrossRef]
- Rafiey, A. Recognizing interval bigraphs using forbidden patterns. Unpublished work. 2012. [Google Scholar]
- Uehara, R. Canonical Data Structure for Interval Probe Graphs. In Proceedings of the 15th Annual International Symposium on Algorithms and Computation (ISAAC 2004); Lecture Notes in Computer Science Volume 3341. Springer-Verlag: Berlin/Heidelberg, Germany, 2004; pp. 859–870. [Google Scholar]
- Colbourn, C. On testing isomorphism of permutation graphs. Networks 1981, 11, 13–21. [Google Scholar] [CrossRef]
- Babel, L.; Ponomarenko, I.; Tinhofer, G. The isomorphism problem for directed path graphs and for rooted directed path graphs. J. Algorithm 1996, 21, 542–564. [Google Scholar] [CrossRef]
- Nakano, S.-I.; Uehara, R.; Uno, T. A New Approach to Graph Recognition and Applications to Distance Hereditary Graphs. In Proceedings of the 4th Annual Conference on Theory and Applications of Models of Computation (TAMC 07); Springer-Verlag: Berlin/Heidelberg, Germany, 2007; pp. 115–127. [Google Scholar]
- Knuth, D. Sorting and Searching. In The Art of Computer Programming, 2nd ed.; Addison-Wesley Publishing Company: Boston, MA, USA, 1998. [Google Scholar]
- Uehara, R.; Iwata, S. Generalized Hi-Q is NP-Complete. Trans. IEICE 1990, E73, 270–273. Available online: http://www.jaist.ac.jp/˜uehara/pdf/phd7.ps.gz (accessed on 22 January 2013). [Google Scholar]
- Plesník, J. The NP-completeness of the hamiltonian cycle problem in planar digraphs with degree bound two. Inf. Process. Lett. 1979, 8, 199–201. [Google Scholar] [CrossRef]
- Downey, R.; Fellows, M. Parameterized Complexity; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Spinrad, J. Open Problem List. 1995. Available online: http://www.vuse.vanderbilt.edu/~spin/open.html (accessed on 22 January 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Uehara, R. Tractabilities and Intractabilities on Geometric Intersection Graphs. Algorithms 2013, 6, 60-83. https://doi.org/10.3390/a6010060
Uehara R. Tractabilities and Intractabilities on Geometric Intersection Graphs. Algorithms. 2013; 6(1):60-83. https://doi.org/10.3390/a6010060
Chicago/Turabian StyleUehara, Ryuhei. 2013. "Tractabilities and Intractabilities on Geometric Intersection Graphs" Algorithms 6, no. 1: 60-83. https://doi.org/10.3390/a6010060
APA StyleUehara, R. (2013). Tractabilities and Intractabilities on Geometric Intersection Graphs. Algorithms, 6(1), 60-83. https://doi.org/10.3390/a6010060



