An Open-Source Implementation of the Critical-Line Algorithm for Portfolio Optimization
Abstract
:1. Introduction
2. The Problem
- is a set of indices that number the investment universe.
- is the (nx1) vector of asset weights, which is our optimization variable.
- l is the (nx1) vector of lower bounds, with .
- u is the (nx1) vector of upper bounds, with .
- is the subset of free assets, where . In words, free assets are those that do not lie on their respective boundaries. F has length .
- is the subset of weights that lie on one of the bounds. By definition, .
3. The Solution
- mean: The (nx1) vector of means.
- covar: The (nxn) covariance matrix.
- lB: The (nx1) vector that sets the lower boundaries for each weight.
- uB: The (nx1) vector that sets the upper boundaries for each weight.
- w: A list with the (nx1) vector of weights at each turning point.
- l: The value of at each turning point.
- g: The value of at each turning point.
- f: For each turning point, a list of elements that constitute F.
4. A Few Utilities
4.1. Search for the Minimum Variance Portfolio
4.2. Search for the Maximum Sharpe Ratio Portfolio
- obj: The objective function on which the extreme will be found.
- a: The leftmost extreme of search.
- b: The rightmost extreme of search.
- **kargs: Keyworded variable-length argument list.
4.3. Computing the Efficient Frontier
5. A Numerical Example
| L Bound | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| U Bound | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Mean | 1.175 | 1.19 | 0.396 | 1.12 | 0.346 | 0.679 | 0.089 | 0.73 | 0.481 | 1.08 |
| Cov | 0.4075516 | |||||||||
| 0.0317584 | 0.9063047 | |||||||||
| 0.0518392 | 0.0313639 | 0.194909 | ||||||||
| 0.056639 | 0.0268726 | 0.0440849 | 0.1952847 | |||||||
| 0.0330226 | 0.0191717 | 0.0300677 | 0.0277735 | 0.3405911 | ||||||
| 0.0082778 | 0.0093438 | 0.0132274 | 0.0052667 | 0.0077706 | 0.1598387 | |||||
| 0.0216594 | 0.0249504 | 0.0352597 | 0.0137581 | 0.0206784 | 0.0210558 | 0.6805671 | ||||
| 0.0133242 | 0.0076104 | 0.0115493 | 0.0078088 | 0.0073641 | 0.0051869 | 0.0137788 | 0.9552692 | |||
| 0.0343476 | 0.0287487 | 0.0427563 | 0.0291418 | 0.0254266 | 0.0172374 | 0.0462703 | 0.0106553 | 0.3168158 | ||
| 0.022499 | 0.0133687 | 0.020573 | 0.0164038 | 0.0128408 | 0.0072378 | 0.0192609 | 0.0076096 | 0.0185432 | 0.1107929 |
- Row 1: Headers
- Row 2: Mean vector
- Row 3: Lower bounds
- Row 4: Upper bounds
- Row 5 and successive: Covariance matrix
- cla = CLA.CLA(mean, covar, lB, uB): This creates a CLA object named cla, with the input parameters read from the csv file.
- cla.w contains a list of all turning points.
- cla.l and cla.g respectively contain the values of and for every turning point.
- cla.f contains the composition of F used to compute every turning point.
| CP Num | Return | Risk | Lambda | X(1) | X(2) | X(3) | X(4) | X(5) | X(6) | X(7) | X(8) | X(9) | X(10) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.190 | 0.952 | 58.303 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 1.180 | 0.546 | 4.174 | 0.649 | 0.351 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 3 | 1.160 | 0.417 | 1.946 | 0.434 | 0.231 | 0.000 | 0.335 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 4 | 1.111 | 0.267 | 0.165 | 0.127 | 0.072 | 0.000 | 0.281 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.520 |
| 5 | 1.108 | 0.265 | 0.147 | 0.123 | 0.070 | 0.000 | 0.279 | 0.000 | 0.000 | 0.000 | 0.006 | 0.000 | 0.521 |
| 6 | 1.022 | 0.230 | 0.056 | 0.087 | 0.050 | 0.000 | 0.224 | 0.000 | 0.174 | 0.000 | 0.030 | 0.000 | 0.435 |
| 7 | 1.015 | 0.228 | 0.052 | 0.085 | 0.049 | 0.000 | 0.220 | 0.000 | 0.180 | 0.000 | 0.031 | 0.006 | 0.429 |
| 8 | 0.973 | 0.220 | 0.037 | 0.074 | 0.044 | 0.000 | 0.199 | 0.026 | 0.198 | 0.000 | 0.033 | 0.028 | 0.398 |
| 9 | 0.950 | 0.216 | 0.031 | 0.068 | 0.041 | 0.015 | 0.188 | 0.034 | 0.202 | 0.000 | 0.034 | 0.034 | 0.383 |
| 10 | 0.803 | 0.205 | 0.000 | 0.037 | 0.027 | 0.095 | 0.126 | 0.077 | 0.219 | 0.030 | 0.036 | 0.061 | 0.292 |
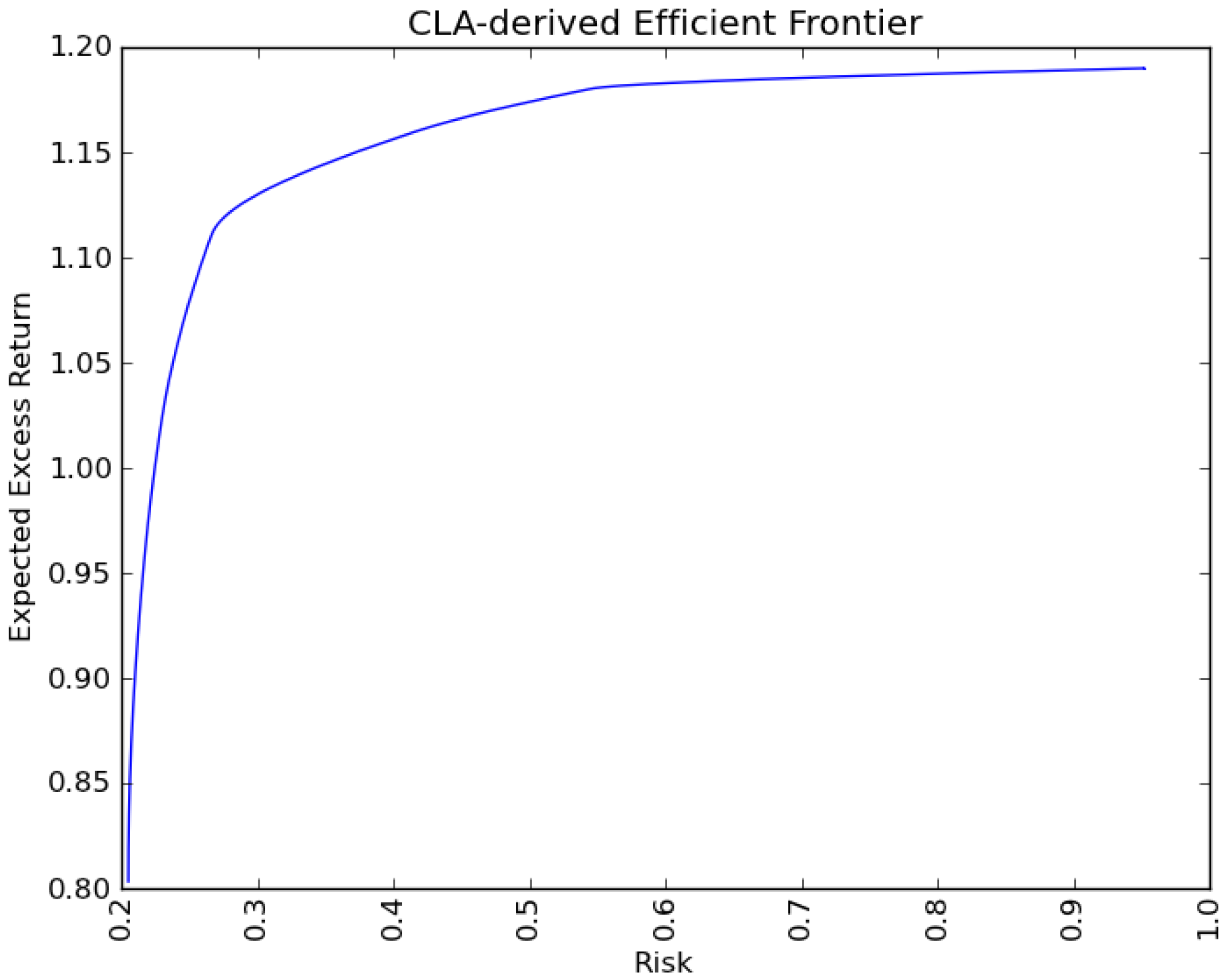
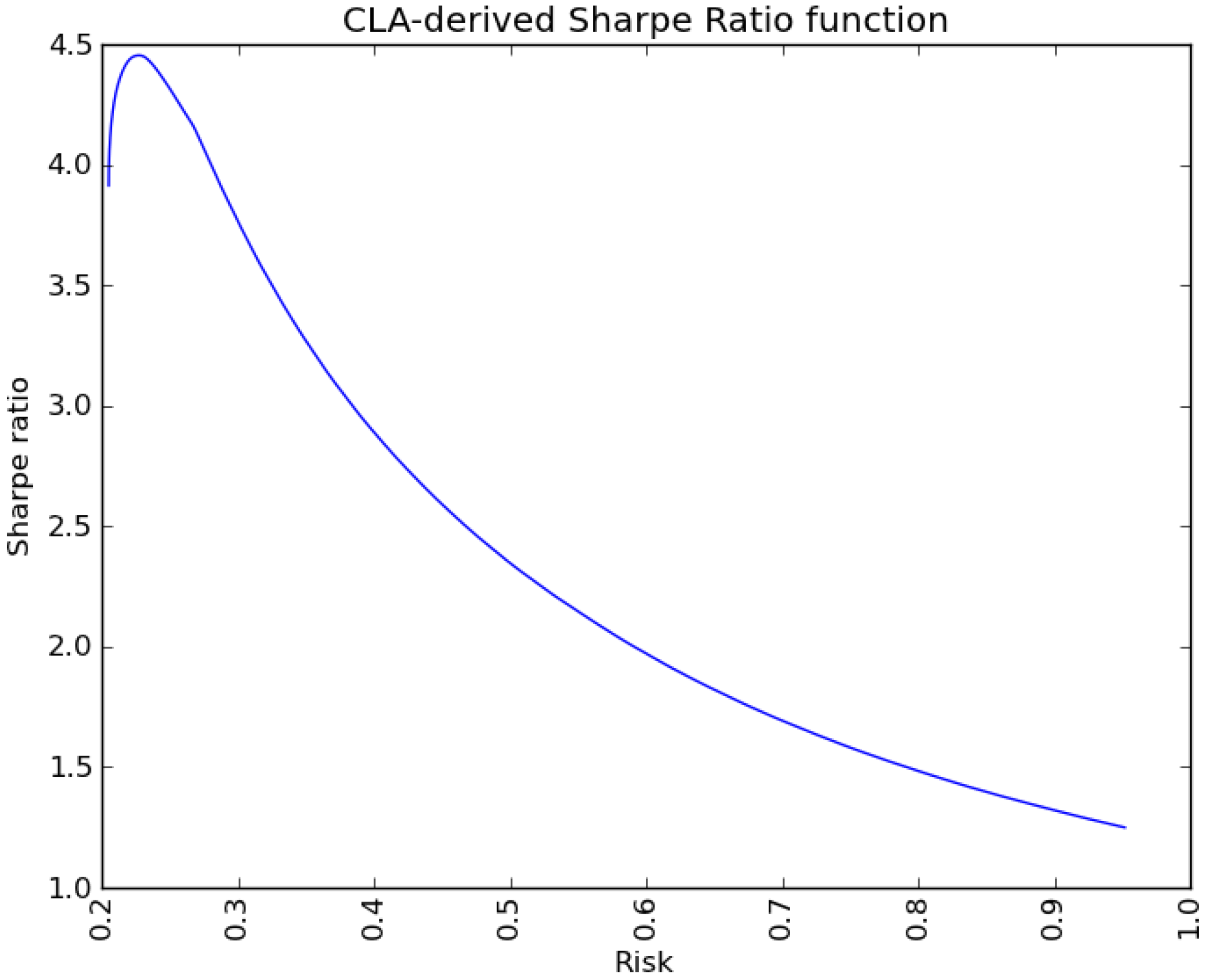
6. Conclusions
Acknowledgments
Appendix
A.1. Python Implementation of the Critical Line Algorithm
- purgeNumErr(): It removes turning points which violate the inequality conditions, as a result of a near-singular covariance matrix .
- purgeExcess(): It removes turning points that violate the convex hull, as a result of unnecessary drops in .
References
- Markowitz, H.M. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Beardsley, B.; Donnadieu, H.; Kramer, K.; Kumar, M.; Maguire, A.; Morel, P.; Tang, T. Capturing Growth in Adverse Times: Global Asset Management 2012. Research Paper, The Boston Consulting Group, Boston, MA, USA, 2012. [Google Scholar]
- Markowitz, H.M. The optimization of a quadratic function subject to linear constraints. Nav. Res. Logist. Q. 1956, 3, 111–133. [Google Scholar] [CrossRef]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investments, 1st ed.; John Wiley and Sons: New York, NY, USA, 1959. [Google Scholar]
- Wolfe, P. The simplex method for quadratic programming. Econometrica 1959, 27, 382–398. [Google Scholar] [CrossRef]
- Markowitz, H.M.; Todd, G.P. Mean Variance Analysis in Portfolio Choice and Capital Markets, 1st ed.; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
- Markowitz, H.M.; Malhotra, A.; Pazel, D.P. The EAS-E application development system: principles and language summary. Commun. ACM 1984, 27, 785–799. [Google Scholar] [CrossRef]
- Steuer, R.E.; Qi, Y.; Hirschberger, M. Portfolio optimization: New capabilities and future methods. Z. Betriebswirtschaft 2006, 76, 199–219. [Google Scholar] [CrossRef]
- Kwak, J. The importance of Excel. The Baseline Scenario, 9 February 2013. Available online: http://baselinescenario.com/2013/02/09/the-importance-of-excel/ (accessed on 21 March 2013).
- Hirschberger, M.; Qi, Y.; Steuer, R.E. Quadratic Parametric Programming for Portfolio Selection with Random Problem Generation and Computational Experience. Working Paper, Terry College of Business, University of Georgia, Athens, GA, USA, 2004. [Google Scholar]
- Niedermayer, A.; Niedermayer, D. Applying Markowitz’s Critical Line Algorithm. Research Paper Series, Department of Economics, University of Bern, Bern, Switzerland, 2007. [Google Scholar]
- Black, F.; Litterman, R. Global portfolio optimization. Financ. Anal. J. 1992, 48, 28–43. [Google Scholar] [CrossRef]
- Bailey, D.H.; López de Prado, M. The sharpe ratio efficient frontier. J. Risk 2012, 15, 3–44. [Google Scholar] [CrossRef]
- Meucci, A. Risk and Asset Allocation, 1st ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Kopman, L.; Liu, S. Maximizing the Sharpe Ratio. MSCI Barra Research Paper No. 2009-22. MSCI Barra: New York, NY, USA, 2009. [Google Scholar]
- Avriel, M.; Wilde, D. Optimality proof for the symmetric Fibonacci search technique. Fibonacci Q. 1966, 4, 265–269. [Google Scholar]
- Dalton, S. Financial Applications Using Excel Add-in Development in C/C++, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2007; pp. 13–14. [Google Scholar]
- Kiefer, J. Sequential minimax search for a maximum. Proc. Am. Math. Soc. 1953, 4, 502–506. [Google Scholar] [CrossRef]
- David, H. Bailey’s Research Website. Available online: www.davidhbailey.com (accessed on 21 March 2013).
- Marcos López de Prado’s Research Website. Available online: www.quantresearch.info (accessed on 21 March 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bailey, D.H.; López de Prado, M. An Open-Source Implementation of the Critical-Line Algorithm for Portfolio Optimization. Algorithms 2013, 6, 169-196. https://doi.org/10.3390/a6010169
Bailey DH, López de Prado M. An Open-Source Implementation of the Critical-Line Algorithm for Portfolio Optimization. Algorithms. 2013; 6(1):169-196. https://doi.org/10.3390/a6010169
Chicago/Turabian StyleBailey, David H., and Marcos López de Prado. 2013. "An Open-Source Implementation of the Critical-Line Algorithm for Portfolio Optimization" Algorithms 6, no. 1: 169-196. https://doi.org/10.3390/a6010169
APA StyleBailey, D. H., & López de Prado, M. (2013). An Open-Source Implementation of the Critical-Line Algorithm for Portfolio Optimization. Algorithms, 6(1), 169-196. https://doi.org/10.3390/a6010169




