Mammographic Segmentation Using WaveCluster
Abstract
:1. Introduction
2. Background
2.1. Mammographic Segmentation
2.2. WaveCluster
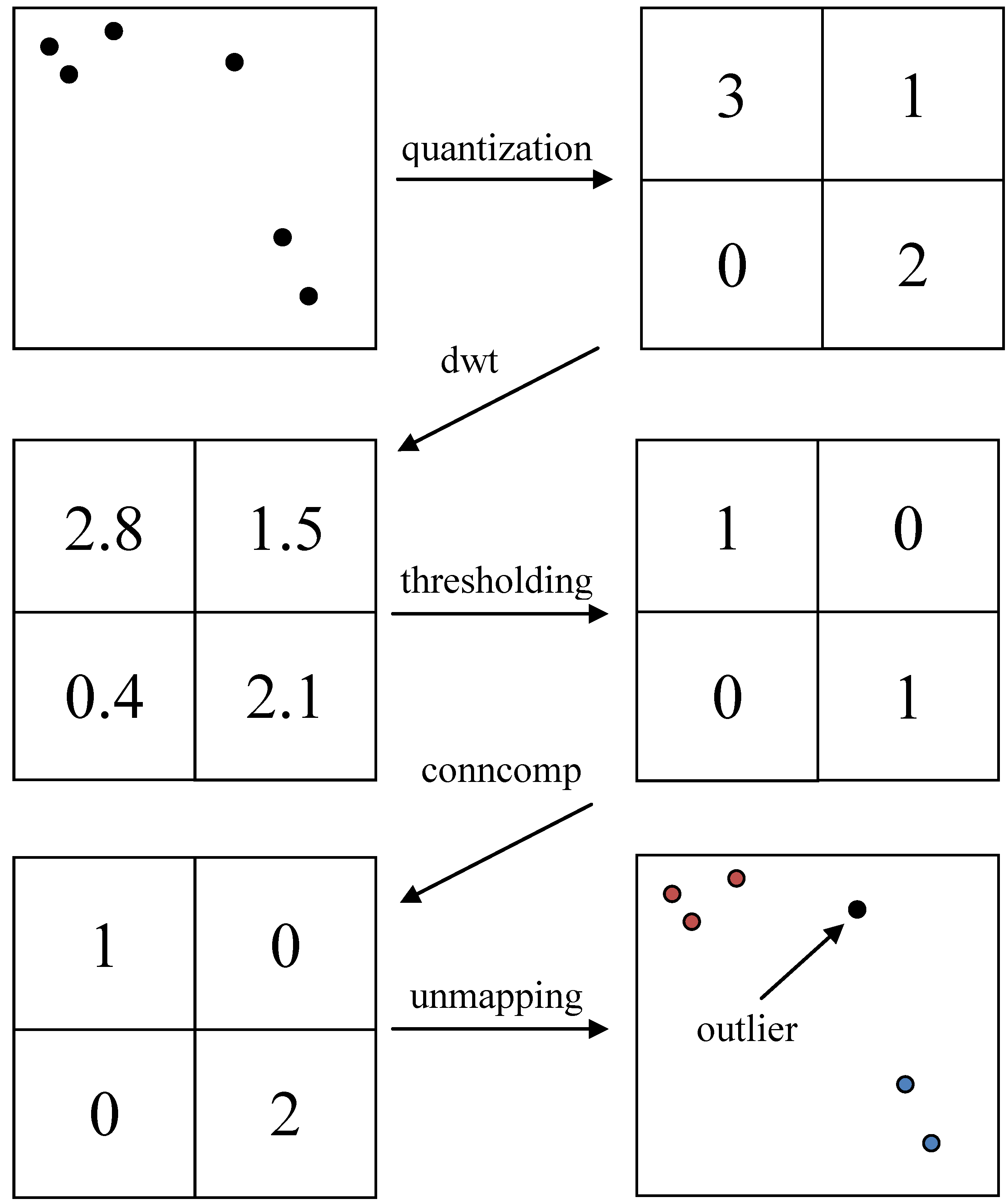
2.2.1. WaveCluster Algorithm
- • Quantize data to a grid, using the cell counts in place of the original data.
- • Apply a wavelet transformation using a hat-shaped wavelet (such as the 2.2 or 4.2 biorthogonal wavelets), retaining the approximation coefficients. These wavelets have the effect of emphasizing dense regions and suppressing sparse ones.
- • Threshold cells in the transformed space. Cells with values above a user-specified density threshold are “significant”, while other cells are dropped.
- • Apply a connected component algorithm to the significant cells to discover and label clusters.
- • Map the cells back to the data using a lookup table built during quantization.
2.2.2. WaveCluster Parameters
- • Increasing the number of cells increases the resolution of the analysis, allowing the algorithm to detect finer patterns but reducing the amount of neighborhood information which is incorporated in the clustering.
- • Increasing the density threshold reduces the number of cells which are considered “significant”, resulting in fewer “bridges” between clusters and a smaller number of “stronger” but more isolated clusters. The optimal value of this parameter is application-dependent: too low and the entire image may be merged into one cluster, too high and regions of the same cluster will break apart. At extremely high values, no clusters are detected whatsoever.
- • The wavelet function can be thought of as a convolution kernel applied to each pixel of the image. “Hat-shaped” wavelets are useful for clustering applications because they emphasize dense regions and suppress sparse ones, but more complex wavelet functions may be useful in niche applications, such as clustering highly anisotropic data.
3. Results and Discussion
3.1. Dataset
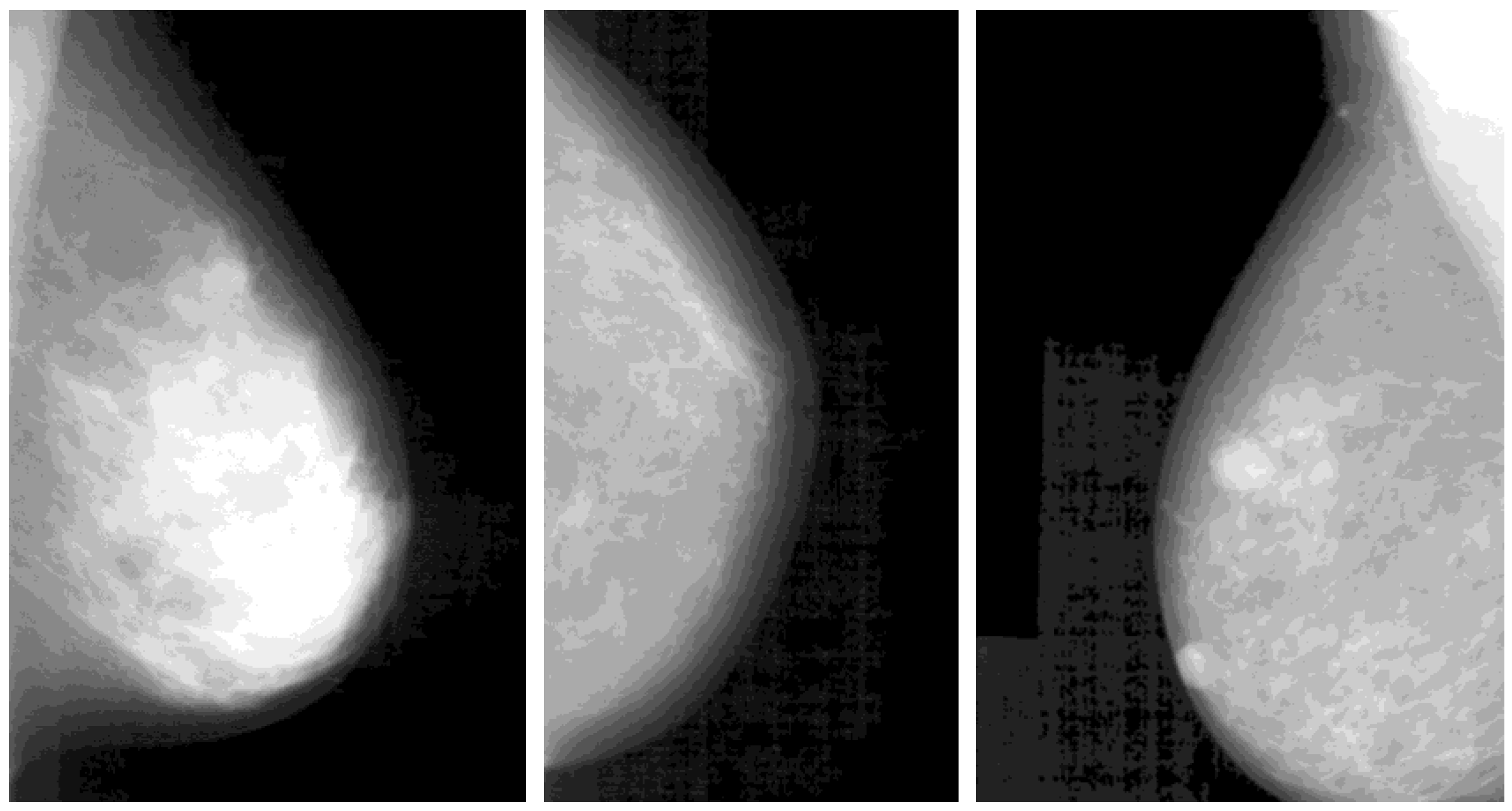
3.2. Breast Profile Segmentation
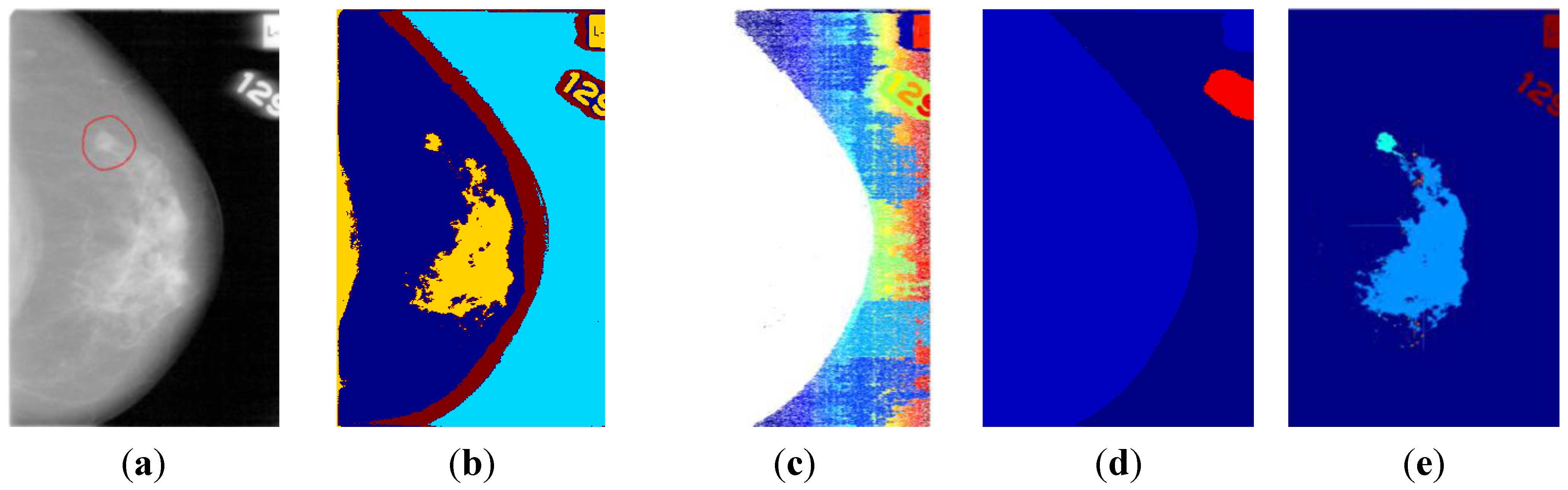
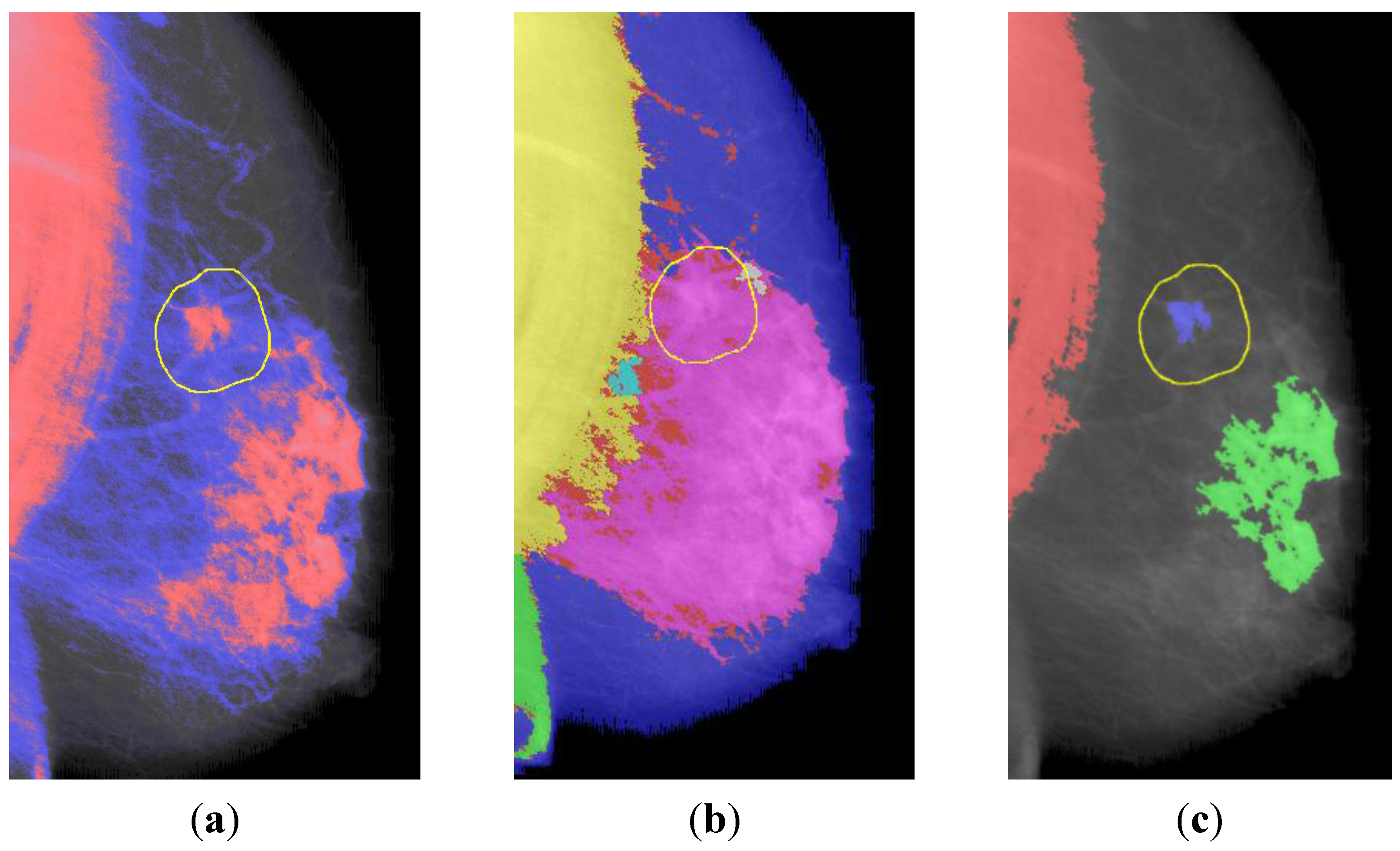
3.3. ROI Segmentation
3.4. Performance
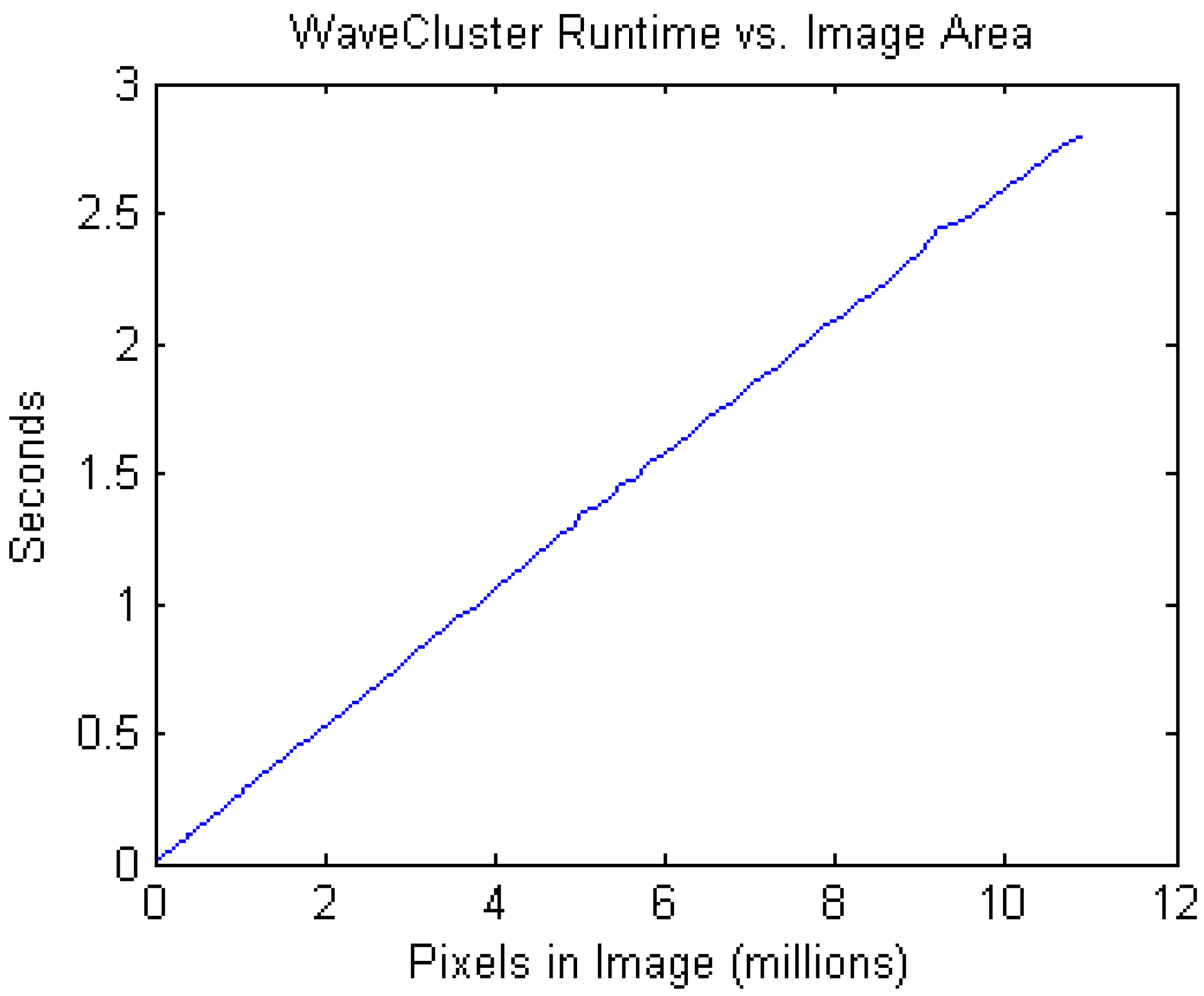
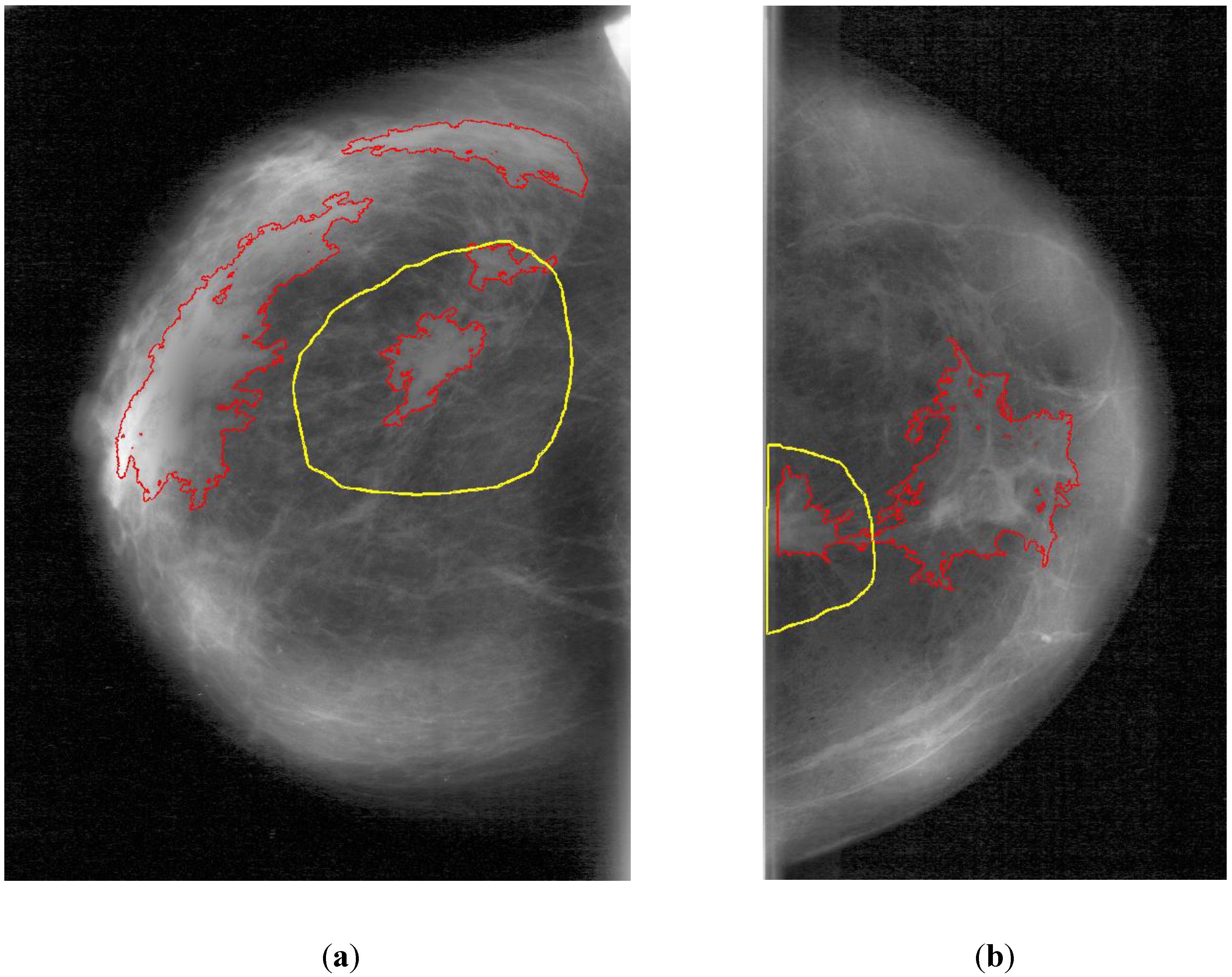
3.5. Comparison
- • WaveCluster was run with an 85% density threshold and the 2.2 biorthogonal wavelet.
- • WaveCluster and watershed segmentation were evaluated by considering a cluster a true positive if and only if at least half of the cluster fell within the bounds of a ground truth ROI.
- • Naïve watershed segmentation is prone to severe oversegmentation. In practice, watershed segmentation requires an h-minima transform as a preprocessing step. The h-minima transform removes all minima in the image of depth less than h. h = 0.075 was chosen empirically.
- • Fuzzy c-means was run with c = 5. Since each pixel can have multiple cluster memberships, a cluster was considered a true positive if at least 50% of the sum of cluster weights came from pixels within the ground truth ROI.
- • All methods were run with the morphological post-filtering described above. This particularly improved performance on the watershed segmentation approach.
| WaveCluster | Fuzzy 5-means | Watershed | |
|---|---|---|---|
| Sensitivity: | 81% | 23%/78% | 33% |
| False Positives: | 0.96/image | N/A | 1.17/image |
| Average Runtime: | 5.2 s/image | 325 s/image | 7.3 s/image |
4. Experimental Section
4.1. Breast Profile Segmentation
4.2. ROI Segmentation
- • The density threshold is raised to the 85th percentile. This places the entire background and most of the breast beneath the significance threshold, yielding a clustering in which only the most dense regions within the breast are considered significant.
- • Morphological noise filtering was not performed prior to clustering, as the low-power noise did not affect the significantly more dense regions of interest.
- • Clusters <30 pixels in radius were discarded using morphological opening by reconstruction, which preserves the shape of the remaining clusters.

5. Conclusions
References
- Lee, S.; Lo, C.; Wang, C.; Chung, P.; Chang, C.; Yang, C.; Hsu, P. A computer-aided design mammography screening system for detection and classification of microcalcifications. Int. J. Med. Inform. 2000, 60, 29–57. [Google Scholar] [CrossRef]
- Oliver, A.; Freixenet, J.; Martí, R.; Pont, J.; Pérez, E.; Denton, E.; Zwiggelaar, R. A novel breast tissue density classification methodology. IEEE Trans. Inform. Technol. Biomed. 2008, 12, 55–65. [Google Scholar] [CrossRef]
- Torrent, A.; Bardera, A.; Oliver, A.; Freixenet, J.; Boada, I.; Feixes, M.; Martí, R.; Lladó, X.; Pont, J.; Pérez, E.; et al. Breast Density Segmentation: A Comparison of Clustering and Region Based Techniques. In Proceedings of the 9th International Workshop on Digital Mammography, Tucson, AZ, USA, 20–23 July 2008; pp. 9–16.
- Khuzi, A.M.; Besar, R.; Zaki, W.W.; Ahmad, N.N. Identification of masses in digital mammogram using gray level co-occurrence matrices. Biomed. Imaging Interv. J. 2009, 5. [Google Scholar] [CrossRef]
- Alhadidi, B.; Zu’bi, M.H.; Suleiman, H.N. Mammogram breast cancer image detection using image processing functions. Inf. Technol. J. 2007, 6, 217–221. [Google Scholar] [CrossRef]
- Sheikholeslami, G.; Chatterjee, S.; Zhang, A. WaveCluster: A wavelet-Based clustering approach for spatial data. VLDB J. 2000, 8, 289–304. [Google Scholar] [CrossRef]
- Barnathan, M. Mining Complex High-Order Datasets. Dissertation. Ph.D. Thesis, Temple University, Philadelphia, PA, USA, April 2010. [Google Scholar]
- Oliver, A. Automatic Mass Segmentation in Mammographic Images. Ph.D. Thesis, Universitat de Girona, Girona, Spain, July 2007. [Google Scholar]
- Sholl, D.A. Dendritic organization in the neurons of the visual and motor cortices of the cat. J. Anat. 1953, 87, 387–406. [Google Scholar]
- Guliato, D.; Rangayyan, R.M.; Carvalho, J.D.; Santiago, S.A. Polygonal modeling of contours of breast tumors with the preservation of spicules. IEEE Trans. Biomed. Eng. 2008, 55, 14–20. [Google Scholar] [CrossRef]
- Nagi, J.; Abdul Kareem, S.; Nagi, F.; Khaleel Ahmed, S. Automated Breast Profile Segmentation for ROI Detection Using Digital Mammograms. In Proceedings of2010 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 30 November–2 December 2010; pp. 87–92.
- Heath, M.; Bowyer, K.; Kopans, D.; Moore, R.; Kegelmeyer, W.P. The Digital Database for Screening Mammography. In Proceedings of the Fifth International Workshop on Digital Mammography, Toronto, Canada, June 2000; Medical Physics Publishing: Madison, WI, USA; pp. 212–218.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barnathan, M. Mammographic Segmentation Using WaveCluster. Algorithms 2012, 5, 318-329. https://doi.org/10.3390/a5030318
Barnathan M. Mammographic Segmentation Using WaveCluster. Algorithms. 2012; 5(3):318-329. https://doi.org/10.3390/a5030318
Chicago/Turabian StyleBarnathan, Michael. 2012. "Mammographic Segmentation Using WaveCluster" Algorithms 5, no. 3: 318-329. https://doi.org/10.3390/a5030318




