Edit Distance with Block Deletions
Abstract
: Several variants of the edit distance problem with block deletions are considered. Polynomial time optimal algorithms are presented for the edit distance with block deletions allowing character insertions and character moves, but without block moves. We show that the edit distance with block moves and block deletions is NP-complete (Nondeterministic Polynomial time problems in which any given solution to such problem can be verified in polynomial time, and any NP problem can be converted into it in polynomial time), and that it can be reduced to the problem of non-recursive block moves and block deletions within a constant factor.1. Introduction
The traditional edit distance problem considers character insertions, deletions and sometimes exchanges, in order to find the minimum number of such operations required to convert a given string to another. Although a simple quadratic time dynamic programming algorithm can be used for the edit distance problem (see the book of Gusfield [1] for more information), when generalized to include the operations block move, block delete, and block copy it is NP-complete. Here we consider block deletions with or without character insertions, character moves and block moves. These variations are shown to be solved optimally in polynomial time using dynamic programming, except when including block moves, where the problem is then NP-hard, and we show how to reduce the problem within a constant factor to non-recursive block moves. One way to model block moves is by viewing strings as linked lists, and allowing operations to apply to pointers associated with characters as well as the characters themselves; although in practice, it is unlikely that linked lists would be used for this purpose, this model captures the fact that both moving and deleting substrings are done in O(1) processing time with standard edit operations.
Given two strings, S of length n and T of length m, in this paper we study the edit distance problem which is the minimum number of insertions, deletions, and moves used to convert S into T. The sequence <i/d/m> is used to denote a variant of the edit distance problem, where i refers to insertions, d refers to deletions and m refers to moves, and i, d and m are either character or block operations, or no corresponding operation, denoted by “c”, “b” or “-”, respectively. As an example, <c/c/b> denotes the edit distance variant with character insertions, character deletions, and block moves. Variants including block insertions are not included, since it is not captured in the linked list model, and block insertions are in fact repeatedly inserting individual characters. The known results and the ones achieved in this paper are summarized in Table 1:
Section 2 summarizes related research; Section 3 presents formal definitions of the generalized edit distance operations. In Section 4 we prove that edit distance with block moves and block deletions is NP-hard, and show that eliminating recursion can be done within a constant factor. In Section 5 we present optimal algorithms for solving variations of edit distance with block deletions.
2. Related Work
Ukkonen [5] extends the set of allowed edit operations (character insertions, character deletions and character exchanges) to include transpositions of adjacent characters, block insertions, block deletions and block replacements. For the case of block operations he considers a restricted block edit problem for which the edit operations must be in a restricted order, which illustrates the behaviors of non recursive block operations, discussed in Section 4.2. Ukkonen presents polynomial dynamic programming algorithms that compute the edit distance (extended and original) d of two strings of length m and n in time and space O(d · min(n,m)), for uniform and non-uniform costs of the operations involved. Since the edit distance is at most max(n,m), the algorithms proposed for character operations are asymptotically at least as efficient as the traditional O(nm) algorithm(Gusfield [1]). Ann et al. [6] noted that for the case of block operations the running time is in fact O(d2·min(n2,m2)). Our algorithms improve this running time to O(n2·m + |Σ|).
Muthukrishnan and Sahinalp [7,8] consider the edit distance with block moves, deletes, copies and reversals. They approximate this problem, called also the nearest neighbors problem, to a factor of O(log(n)·(log*(n))2), using an embedding of strings into the vector space. Cormode and Muthukrishnan [9] achieve a factor of O(log(n)·log*(n)) when considering the edit distance with moves only. They embed the strings into the L1 vector space. Cormode, et al. [10] consider the hamming and Levenshtein distances, and define the LZ distance, which employs block copies and block deletions, together with the usual single character operations. Given two strings S and T, they consider the problem of starting from an empty string and producing T using copies from S, in a minimum number of operations. Here, copies are not allowed, and we consider the minimum number of operations performed on S in order to produce T. Ergun et al. [11] consider the edit distance with block moves, deletes and copies and present a polynomial time algorithm with a factor of 12 approximation to optimal.
Shapira and Storer [4] consider the standard edit distance problem augmented with block moves, where a sequence of characters are moved from one location in the string to another with constant cost, and present a log(n) factor approximation algorithm to optimal for a sub-family of strings (finding an optimal solution is NP-hard [4]). The proposed greedy algorithm reduces the two given strings to (possibly) shorter strings by replacing repeatedly a longest common substring by a new single character. The traditional edit distance is then applied on the new strings. Chrobak et al. [12] consider the Minimum Common String Partition (MCSP) problem, that receives two input strings and tries to minimize the number of partitions of the strings into the same collection of substrings. They refer to several versions of this problem by limiting the number of times each character can occur in both input strings, and study the approximation of a greedy algorithm for MCSP that at each step extracts a longest common substring from the given strings. In the case of 2-MCSP, where each character can occur at most twice in each input string, the approximation of 3 is shown. For 4-MCSP the approximation ratio of the greedy algorithm is at least Ω(log n), and for the general problem they present an approximation ratio between Ω(n0.43) and O(n0.69). An implication of this bound is that the log(n)-approximation greedy algorithm presented in Shapira and Storer [4] for a sub-family of strings cannot be extended to provide a log(n)-approximation for all inputs. Shafrir and Kaplan [13] improve the lower bound on the approximation guarantee of the greedy algorithm for MCSP to Ω(n0.46).
Ann et al. [6] present polynomial-time optimization algorithms for the edit distance problem which involves character insertions, character deletions, block copies and block deletions, when some restrictions are applied, such as allowing only left to right non recursive operations to be applied on the source string in order to get the target string. They refer to different versions of edit problems where internal copies (copy of a substring of the current string), external copies (copy of a substring of the original string), and shifted copies (copy of a shifted substring) are allowed. They also consider various costs of the operations such as constant, linear (the cost of a block operation is proportional to the length of the block) and nested costs (in which they allow the copied substring to be further edited).
Bafna and Pevzner [14] consider the case that S is a permutation of the integers 1 through n, and give a 1.5 approximation algorithm for minimizing the number of moves needed to transform S into another permutation T. The restriction that all characters are distinct makes the problem easier. Lopresti and Tompkins [15] compare two strings by extracting collections of substrings and placing them into the corresponding order. Tichy [16] considers block copies and looks for the minimal covering set of one string with respect to another. In Hannenhalli [17], one can only swap a prefix or suffix of one chromosome with a prefix or suffix of another.
Durand et al. [18] consider the best alignment. There are several types of two-sequence alignments. The global alignment is the traditional edit-distance, where the goal is to match the entire sequence. The local alignment is to see whether a substring in one sequence aligns well with a substring in the other, thus, deleting prefixes or suffixes is free. The semi-global alignment is when the input is constructed from two sequences, one short and one long, and the goal is to find whether the short one is a part of the long one. These variations are addressed by Smith and Waterman [19]. In the alignment problem, the term gap is used instead of a block deletion in the edit distance problem. A gap is a maximal consecutive run of spaces in a single string of a given alignment. The affine gap penalty is when k consecutive deletions are not simply the cost of k individual single character deletions. The penalty combines the cost of opening a gap and k times the cost of extending a gap. Introduction of gaps into sequence alignments allows the alignment to be extended into regions where one sequence may have lost or gained sequence characters not found in the other. The gap penalty is used to help decide whether or not to accept a gap or insertion in an alignment when it is possible to achieve a good alignment at some other point in the sequence. When aligning two sequences it is often required to insert gaps in them in order to optimize the alignment.
The classical algorithm for computing the similarity between two sequences uses a dynamic programming matrix, and compares two strings of size n in O(n2) time. Masek and Paterson [2], apply the “Four-Russians technique” and reduce the running-time to O(n2/log n) by exploiting repetitions in the strings. A drawback of the Masek and Paterson algorithm is that it can only be applied when the given scoring function is rational. Crochemore et al. [3] also present a O(n2/log n) time algorithm by dividing the dynamic programming matrix into variable sized blocks, as induced by Lempel-Ziv-Welch parsing of both strings. For most texts, the time complexity is O(hn2/log n) where h ≤ 1 is the entropy of the text. Hermelin et al. [20] generalize the idea of applying edit distance on the compressed forms of the strings and present a generic platform for popular compression schemes such as the LZ-family, Run-Length Encoding, Byte-Pair Encoding and dictionary methods. In this paper we use basic dynamic programming which can be adapted to a O(n2/log n) processing time by applying compression techniques to the underlying strings.
3. Definitions of the Generalized Operations
We now give a formal description of the operations involved: insert, delete and move, all of which are with respect to strings of characters over a finite alphabet.
Let S = S1⋯Sn:
Insert: For a string S and a position 1 ≤ p ≤ n, the operation insert (σ, p) inserts the character σ to the pth position of S. After performing this operation, S becomes S1⋯Sp−1σSp⋯Sn.
Delete: The operation delete(p, ℓ) deletes ℓ, (1 ≤ ℓ ≤ n − p +1), consecutive characters which occur at positions p,⋯, p + ℓ − 1 of S, i.e., S becomes S1⋯Sp−1Sp+ℓ⋯Sn.
Move: Given two distinct positions 1 ≤ p1 ≠ p2 ≤ n and a length ℓ, move(ℓ, p1, p2) moves the string at position p1 of length ℓ to position p2. After performing the move operation, if p1 < p2 and ℓ ≤ p2 − p1 then S becomes S1⋯Sp1−1Sp1+ℓ⋯Sp2−1Sp1⋯Sp1+ℓ−1Sp2⋯Sn; and if p2 < p1 and 1 ≤ ℓ ≤ n − p1 + 1, S becomes: S1⋯Sp2−1Sp1⋯Sp1+ℓ−1Sp2⋯Sp1−1Sp1+ℓ⋯Sn.
When ℓ = 1 we refer to the operations as delete-character, and move-character, and when ℓ > 1 we refer to the operations as block-deletion, and block-move Alternatively, we sometimes write delete(str, p)/move(str, p1, p2), where str specifies the string which is deleted or moved, rather than its length. We even use delete/move (str) when the indices are clear.
4. Edit Distance with Block Moves, Block Deletions, Character Insertions
In this section we first note that finding the minimum edit-distance to transform S to T using character insertions, block deletions and block moves is NP-complete. Second, we introduce the notation of recursive moves and recursive-moves-deletes, and simplify the problem of finding an approximation algorithm by showing that eliminating recursive-moves-deletes cannot change the edit distance by more than a constant factor.
4.1. NP-Completeness
We first prove the NP-completeness of edit distance with block moves, block deletions, and character insertions.
Theorem 1
Given two strings S and T, and a positive integer l, performing only the three unit-cost operations character insertions, block deletions, and block moves on S, it is NP-complete to determine if S can be converted to T with cost ≤ l.
Proof
Since a non-deterministic algorithm need only guess the operations and check in polynomial time that S is converted to T with cost ≤ l, the problem is in NP. Shapira and Storer [4] show that the edit distance problem with only block moves is NP complete. In other words: suppose you are given a string S′, a permutation T′ of S′ and a positive integer k. Determining whether S′ can be converted to T′ in a cost less than or equal to k, performing only move operations, is NP complete. We employ a transformation from the edit distance problem with only moves. Given an instance S′, T′ (which is a permutation of the characters in S′), and an integer k, of the edit distance problem with only moves, let: S = S′; T = T′; l = k. As T is a permutation of the characters of S′, every delete character operation will require an insert of the characters. This means that character insertions and deletions (especially block deletions) are useless in the sense of minimizing the edit-distance. Therefore, S can be converted to T with a cost ≤ l using character inserts, block moves and block deletes, if and only if S′ can be converted to T with cost ≤ k using only moves.
Using the notation above, Theorem 1 uses a reduction from the edit distance problem with no insertions, with no deletions, and with block moves, <-/-/b>, to show that <c/b/b> is also NP-hard. The same proof can be applied to 7 more versions of the edit distance problem proving they are also NP Complete: <-/c/b>, <-/b/b>, <c/-/b>, <c/c/b>, <b/-/b>, <b/c/b>, and <b/b/b> (the last three allow block insertions).
4.2. Non Recursive Block Moves and Deletions
Recursive operations allow one to deal with substrings that have already been dealt with, and which do not occur consecutively in the original string. In the following, we define when moves and deletes are considered recursive. Ukkonen [5] gives a similar definition to non recursive block operations called “restricted editing sequences”.
Definition
A sequence of operations applied to a string is recursive with respect to move operations if it contains an operation which moves a substring whose characters do not occur consecutively in the original string. For example, if S is the string abcde and the character b is moved to obtain the string T = acdbe, then moving the substring dbe or ac are both considered as recursive moves.
Definition
A sequence of operations including character insertions, block moves, and block deletions is recursive with respect to move and delete operations if it moves or deletes a substring whose characters do not occur consecutively in the original string.
For example, if S is the string abcde and the character b is moved to obtain the string T = acdbe, then deleting the substring dbe or ac are both recursive with respect to move and delete operations.
Theorem 2
If there is a sequence of k recursive move operations that convert S into T, then there is a non-recursive sequence of no more than 3k moves that convert S to T.
Proof
By induction on k.
Base case: k = 1. One move operation converts S to T. Since this move is not recursive, S is converted to T in less than three non-recursive operations.
Inductive hypothesis: Assume that for every recursive sequence of l < k moves that convert S to T, there is a conversion of S to T of a non-recursive sequence of no more than 3l moves. We prove that this holds for l = k.
Induction step: Consider any recursive sequence of k moves that convert S to T. Remove the last move of this sequence. Denote the obtained string by T′. There is a recursive sequence of k − 1 moves that convert S to T′. Using the inductive hypothesis, a non-recursive sequence converts S to T′ by not more than 3(k − 1) operations. These 3(k − 1) operations introduce a parsing of S into r blocks {A1, A2, ⋯, Ar}, where each block Ai contains consecutive characters in S. A move operation of a block b introduces at most two boundaries in the source location, where the substrings to the left of the left boundary, and the substring to the right of the right boundary can be either blocks that were originally there, or blocks that were transferred to that location by previous operations. A move operation of b also introduces a boundary in its destination. Therefore not all substrings Ai are necessarily substrings that were moved. This way a move operation introduces 3 additional blocks, two in its source location and one in its destination. More formally, b is of the form , where is a suffix of the block Ai−1 and is a prefix of Aj+1. The symbols and will denote the remaining prefix and suffix of the corresponding blocks, respectively. Every block Ax, i ≤ x ≤ j, which was already moved by non-recursive moves, could be moved straight to its final location. If blocks Ai−1 and Aj+1 were moved within the first 3(k − 1) operations, then when non-recursive operations are considered, only the partial blocks and are moved. However, the blocks and must move to their final location, which adds a cost of two to the number of operations by splitting the original blocks Ai−1 and Aj+1(if Ai−1 and Aj+1 were not moved in previous operation, this additional cost is left for future cost). We show that the inner blocks {Ai, ⋯, Aj} of b, which were not moved within the first 3(k − 1) operations, are moved to their final location with no additional cost. Blocks which were never moved, are located in different blocks since there was a block, which was moved in between them or from between them, in one of the previous operations. In the case a block was moved out from between two blocks, this operation was “charged” by three non recursive moves, instead of one (since this is a non recursive move to start with), so these blocks are now moved for free. In case a block was moved in between two blocks that were never moved, without loss of generality, the block to the left of the border can be moved for free using the cost that was charged for this operation in its destination. By assigning the charge for each border to the block to its left, we are left with at most a single block for which the block to its right was moved out (otherwise it is a block to the left of a border of a block which was moved in, and is moved for free) or this block is one of the ends of b. In any of these cases the block can be moved for free using the charge that was applied to a block move source. Using the induction hypothesis, we have “charged” this move by three non recursive moves instead of one. Therefore, we can move the two adjacent blocks without charging it again. The worst case uses three more operations in order to convert T′ to T. Adding it to the number of operations executed in order to convert S into T′ we get 3 + 3(k − 1) = 3k operations.
Theorem 3
The bound of Theorem 2 is tight.
Proof
The following example builds two strings S and T of n substrings of the form Sn and Tn respectively, where Sn and Tn are defined recursively, such that the non-recursive edit distance of S and T is three times the recursive edit distance of these strings. For simplicity, because each character will not occur more than once in both S and T, for this example we use the notation move(s) for moving a substring s of S, without stating its source and destination locations.
First consider the alphabet Σ = {L0, L1, M0, R0}. Let S1 = L1L0M0R0 and T1 = L1M0L0R0. Suppose S1 is a substring of S, not aligned with the substring T1 of T, and therefore must be moved. The recursive edit distance is 2 (move(M0) and move(L1M0L0R0)) and the non-recursive edit distance is 4 (move(L1), move(M0), move(L0) and move(R0)).
In general, we use the following definition:
We get that
Using the above definition of Sn and Tn, we continue taking out a mid part of a block (thus, breaking a continuous string into three parts), and putting it into another block, and again breaking a continuous string. This way we add three blocks by each move operation. If Sn should be recursively moved (given the assumption that Sn and Tn are not aligned in the entire strings S and T), these previous move operations turn into recursive ones, and cannot be performed by the non-recursive sequence of moves. A non-recursive sequence of moves must move each block separately to its final location. Since every recursive operation adds three more blocks, the non-recursive edit distance increases by three.
The recursive edit distance of S and T (which include Sn and Tn as non aligned substrings) is n + 1 (including the move of the entire block). We have 3n blocks in addition to the one block we have started with, which require 1 + 3n non-recursive moves. If n is unbounded, .
We still have to define S and T so that Sn must be moved in S in order to be aligned with Tn in T. As we would like the other parts of S not to be moved instead of the substring Sn, moving them must cost more than moving Sn. In order to achieve this we construct 2n strings, and , of the form of Sn and Tn, respectively. The strings and are constructed from the same characters but their characters differ from any other pair and . Let and . As the blocks in T occur in the reversed order of the blocks of S, at least n − 1 blocks should be moved. The recursive edit distance of S and T is (n − 1)·(n + 1) + n, as we should use n operations in each of the n − 1 blocks before or after they have moved, and n more operations in the block which stands still. The non-recursive edit distance of S and T is (n − 1)·(1 + 3n) + n, as it should perform 1 + 3n operations for the n − 1 blocks which are moved, and exactly the same operations of the recursive algorithm in the block that stays still. If n goes to infinity then we obtain the factor of three by: .
Theorem 4
A recursive sequence of k block moves and block deletes that converts S to T, can be implemented by a non recursive sequence of no more than 3k non recursive operations.
Proof
Given a sequence of k recursive block moves and block deletes that converts S to T, we construct a sequence of k recursive block moves that converts S′ to T′ in the following way: For simplicity let $ be a character which does not occur in the alphabet of S and T. Define S′ = S$ and T′ to be the string starting with T$ as its prefix followed by the concatenation of all substrings that were deleted in the original recursive sequence, in the exact order of block deletions. We use the same sequence of recursive operations, but instead of performing a block deletion we move the block to the end of the generated string. At the end of this process we will obtain T′ using only recursive moves. We now use Theorem 3 that the recursive sequence of k moves that converts S′ to T′ can be implemented by a non recursive sequence, A′, of no more than 3k non recursive operations. We use A′ to construct a non-recursive sequence of moves and deletes that convert S to T. We denote by T″ the suffix of T′ that remains after eliminating its prefix T$, i.e., T′ = T$T″. Note that T″ is obtained by moving substrings that are deleted from S (and therefore from S′), and all characters that moved to T″ remain there until the end of the process. We use one block deletion for each of these special block moves, thus the number of operations remains the same. Starting from a non-recursive sequence of block moves implies a non-recursive sequence of block moves and block deletes with the exact number of operations 3k.
5. Edit Distance with Block Deletions
In the previous section we have shown that the problem of finding the edit-distance with block moves and block deletions is NP-complete. In this section we consider several variations of the edit distance problem with block deletions without block moves and show that for the following set of operations, the problem can be solved optimally, in polynomial time, using variations of the traditional dynamic programming method:
Block deletions.
Block deletions and character insertions.
Block deletions, character insertions, and character moves.
In the last case we prove that we can apply the dynamic programming algorithm for block deletions and character insertions and modify the way we calculate the cost.
5.1. Block Deletions with or without Character Insertions
Given two strings S and T, where T is a sub-sequence of S (i.e., it is possible to delete characters from S to obtain T), we are interested in the smallest integer k such that T is partitioned into k blocks (substrings), and the blocks of T are substrings of S, and occur in S in the same order as in T. If k = 1 this is the traditional pattern matching problem, which returns whether the pattern T occurs in S or not. Consider for example S = bcxyabczfdlmefij and T = abcdef. In this case there are three blocks in S occurring in the same order as in T. Define S′ = $S$, where $ is a new character not occurring in S nor T. Finding the minimum number of blocks of S so that the blocks of T occur in S in the same order as in T is equivalent to finding the minimum number of block deletions minus 1, performed on S′ so that S′ is identical to T. The difference of 1 in the cost is since every block deletion of S′ can be matched with the corresponding preceding block of S, except for the first block of S′.
The block deletion problem can be solved in polynomial time using dynamic programming. Allowing character insertions in addition to block deletions requires small changes in the algorithm. Let o be a block deletion which deletes a substring that ends with a character c, o |c denotes the substring o after truncating its last character. If o does not end with c, o |c is equal to o. The following lemma refers to the case of block deletions only, and implies a recurrence formula which is the basis of the dynamic programming algorithm presented in Algorithm 2.
Lemma 1
Let S = s1⋯sn and T = t1⋯tm be two strings of lengths n and m, respectively, and let O = {o1,…ok} be an optimal sequence of block deletions which converts S into T. If ok ends with the character sn, then O′ = {o1,…ok |sn} is an optimal sequence of block deletions which converts S1⋯sn−1 into T. Otherwise, O is an optimal sequence of block deletions which converts s1⋯sn−1 into t1⋯tm−1.
Proof
Assume that ok ends with the character sn:
If ok deletes sn alone (being ok a character deletion) then O′ = {o1,…ok−1} is an optimal sequence of block deletions which converts S = s1⋯sn−1 into T. Otherwise, if O′ is not optimal, let {õ1,…õℓ} be an optimal sequence of block deletions converting s1⋯sn−1 into T with cost less than O′. Define Õ = {õ1,…õℓ, ok}. The sequence Õ of block deletions is a sequence of block deletions which converts S into T with cost less than O, which contradicts the optimality of O.
If ok deletes sn, and sn is deleted within a block deletion of length greater than 1, the block deletion charge is applied to some previous character, and sn is deleted for free. Thus, shortening ok to not include sn is done within the same cost, and O′ = {o1,…ok |sn} is an optimal sequence of block deletions which converts s1⋯sn−1 into T. Otherwise, if O′ is not optimal, let {õ1,…õℓ} be an optimal sequence of block deletions converting s1⋯sn−1 into T with cost less than O′ (meaning ℓ < k). Let i be the minimum index 1 ≤ i ≤ ℓ so that the block deletion õi deletes some character which is also deleted by . Define ôi to be a block deletion of the continues substring starting with characters deleted by õi concatenated to the characters deleted by ok, and let Õ = {õ1,…õi−1, ôi}. The sequence Õ of block deletions includes i ≤ ℓ < k block deletions, which converts S into T, contradicting the optimality of O.
Assume that ok does not end with the character sn:
In this case sn is equal to tm, and O is also an optimal sequence of block deletions which converts s1⋯sn−1 into t1⋯tm−1. Otherwise, if O is not optimal, let Õ = {õ1,…õℓ} be an optimal sequence of block deletions which converts s1⋯sn−1 into t1⋯tm−1 with cost less than O. Then Õ is a sequence of block deletions which converts S into T with cost less than O, which contradicts the optimality of O.
The last lemma implies the following recurrence formula for the edit distance problem with block deletions <-,b,->,
The dynamic programming algorithm is given in Algorithm 2. It uses a table A[i,j], where rows correspond to S and columns correspond to T. An assistant function, During_Deletion, is given in Algorithm 1. It receives the current cell in the dynamic programming table, A, indexed by (i,j) and returns whether the cheapest sequence of operations converting s1⋯si into t1⋯tj ends with a block deletion, i.e., whether A[i,j] =A[i − 1, j] + 1 (si starts a block deletion) or A[i,j] = A[i − 1, j] (si is an internal character of a block deletion). In the later case it should be verified that there exists an index 0 < i0 < i such that si0 starts a block deletion, i.e., such that A[i0,j] = A[i − 1,j] + 1. If si+1 follows a block deletion, there is no need in recharging a cost of a block deletion if si+1 should be deleted too, it could be deleted “for free” with the cost applied to the first character, si0, of the block deletion. The Delete function presented in Algorithm 2 is given two strings S and T of lengths n and m, respectively, and returns the minimum number of block deletions applied to S in order to convert it into T. If both strings are empty there is no cost to convert S into T. If only S is empty, the cost is infinity, since block deletions are applied to S. If T is empty, the cost is 1 since a single block deletion of the entire string S converts it into T.
| Algorithm 1. During Deletion function—returns whether cell (i,j) is involved in a block deletion operation. |
| function During_Deletion(i,j) { |
| while (i > 1) and (A[i,j] == A[i − 1,j]) |
| i--; |
| return ((i ≠ 0) and (A[i,j] == A[i − 1,j] + 1)) |
| } |
After the dynamic programming table is initialized, the cost of converting s1⋯si into t1⋯tj is calculated and stored in cell A[i,j] of the dynamic programming table. If the characters si and tj are identical, the cost of converting s1⋯si into t1⋯tj is equal to converting s1⋯si−1 into t1⋯tj−1, unless it is cheaper to apply a block deletion to the character si. The character si can be deleted among other characters, and the cost of a block deletion is constant, no matter how many characters are deleted.
| Algorithm 2. Edit distance with block deletion. |
| function Delete(S,T) { |
| A[0,0] ← 0 |
| for 1 ≤ i ≤ n do A[i,0] ← 1 |
| for 1 ≤ j ≤ m do A[0,j] ← ∞ |
| for i = 1 to n do |
| for j = 1 to m do |
| if si = tj then { |
| if during_deletion(i − 1j) |
| then A[i,j] ← min(A[i − 1, j − 1], A[i − 1, j]) |
| else A[i,j] ← min(A[i − 1, j − 1], A[i − 1j] + 1) |
| } |
| else { |
| if (during_deletion(i − 1j)) |
| then A[i,j] ← A[i − 1,j] |
| else, A [i,j] ← A[i − 1, j] + 1 |
| } |
| return A [n,m] |
| } |
Two cases are distinguished, the case for which its previous character was deleted, and the case its previous character was not deleted. In the former case there is no new charge for deleting si since the block deletion is charged by the first character of the block. In this case A[i,j] has the same cost as A[i − 1,j]. Otherwise, it is worthwhile starting a block deletion with si, charging the first character of the block. In this case A[i,j] is equal to A[i − 1, j] + 1 (we assume that ∞ + 1 = ∞). If the characters si and tj are not identical, si should be deleted. In order to determine the cost, it has to be checked if si shall be the first character of a block deletion or not, as done previously. Since the during_deletion function runs in linear time in the size of S, the total running time of the edit distance with block deletion algorithm is O(n2 m).
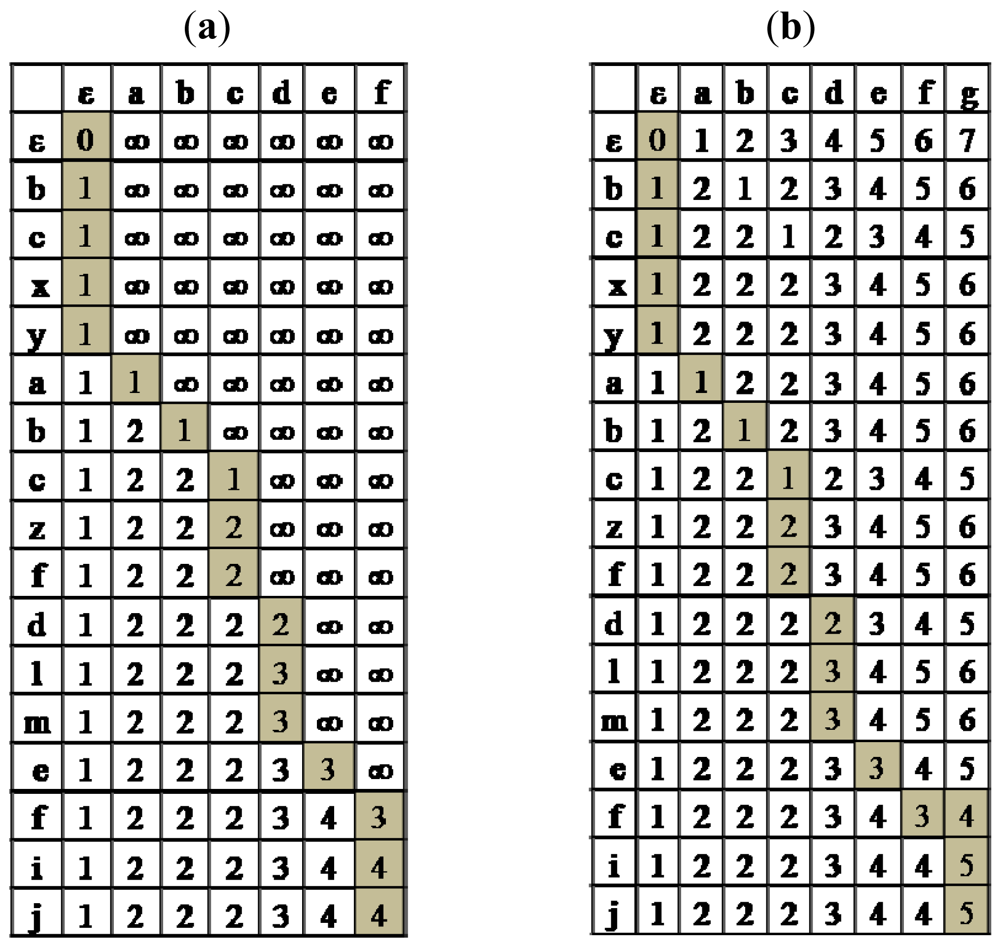
Running Algorithm 2 on the above example, S = bcxyabczfdlmefij and T = abcdef, produces Figure 1a. The optimal path from the bottom right cell (corresponding to S and T) to the upper left cell (corresponding to S = ε and T = ε) is illustrated by gray colored cells. The number of block deletions is 4, and the deleted blocks are {bcxy,zf,lm,ij}.
The block deletion problem is now extended to include character insertions, and requires small modifications to the algorithm presented in Algorithm 2. An optimal solution to the edit distance problem of character insertions and block deletions will not insert a character c into S followed by a block deletion that includes c, since the insertion of c is unnecessary. Thus, block deletions and character insertions can be ordered so that all insertions follow block deletions. The following lemma refers to the case of character insertions and block deletions, but does not separate them, and considers both operations in every step, so that the two dimension table is traversed only once. The lemma is followed by a recurrence formula which is the basis of the polynomial time dynamic programming algorithm presented in Algorithm 3.
Lemma 2
Let S = s1⋯sn and T = t1⋯tm be two strings of lengths n and m, respectively, and let O = {o1,…ok} be an optimal sequence of block deletions and character insertions which converts S into T.
If ok is a character insertion: then if it is an insert of the character tm then O′ = {o1,…ok−1} is an optimal sequence of character insertions and block deletions which converts S into t1 ⋯ tm−1. Otherwise, if ok is a character insertion of a character different than tm, then O is an optimal sequence of block deletions and character insertions which converts s1⋯sn−1 into t1⋯tm−1.
If ok is a block deletion that ends with the character sn, then O′ = {o1,…ok |sn} is an optimal sequence of character insertions and block deletions which converts s1⋯sn−1 into T. Otherwise, O is an optimal sequence of character insertions and block deletions which converts s1⋯sn−1 into t1⋯tm−1.
Proof
If ok is a block deletion, the proof is constructed the same as the proof of Lemma 1, only that the set of operations {o1,…ok−1} is an optimal sequence of block deletions and character insertions.
If ok is a character insertion:
If ok is a character insertion of tm then O′ = {o1,…ok−1} is an optimal sequence of character insertions and block deletions which converts S into t1⋯tm−1. Otherwise, if O′ is not optimal, let {õ1,…õℓ} be an optimal sequence of block deletions and character insertions converting s1⋯sn−1 into T with cost less than O′ .= Define Õ = {õ1,…õℓ, ok}. The sequence Õ of block deletions and character insertions is a sequence which converts S into T with cost less than O, which contradicts the optimality of O.
If ok is a character insertion of a character different than tm, and using the fact that there is no block deletion that involves sn (otherwise it was treated in case 1), then sn is equal to tm and O is an optimal sequence of block deletions and character insertions which converts s1⋯sn−1 into t1⋯tm−1. Otherwise, if O is not optimal, let Õ = {õ1,…õℓ} be an optimal sequence of block deletions which converts s1⋯sn−1 into t1⋯tm−1 with cost less than O. Then Õ is a sequence of block deletions which converts S into T with cost less than O, which contradicts the optimality of O.
The last lemma implies the following recurrence formula for the edit distance problem with block deletions and character insertions, <c,b,->,
| Algorithm 3. Edit Distance with Block Deletions and Character Insertion. |
| function Delete_Insert(S,T) { |
| A[0,0] ← 0 |
| for 1 ≤ i ≤ n do A[i,0]← 1 |
| for 1 ≤ j ≤ m do A[0,j] ← j |
| for i = 1 to n do |
| for j = 1 to m do |
| if si = tj then { |
| if during_deletion(i − 1,j) |
| then A[i,j]← min(A[i − 1,j − 1], A[i − 1,j], |
| A[i,j −1] + 1) |
| else A[i,j]← min(A[i − 1,j−1], A[i − 1,j] + 1, |
| A[i,j − 1] + 1) |
| } |
| else { |
| if (during_deletion(i − 1,j)) |
| then A[i,j] ← min(A[i − 1,j], A[i,j − 1] + 1) |
| else A[i,j] ← min(A[i − 1,j] + 1, A[i,j − 1] + 1) |
| } |
| return A [n,m] |
| } |
While the algorithm of Algorithm 2 deals only with block deletions, the one in Algorithm 3 also permits character insertions to be applied to S. The algorithm is similar to the previous one, but with the following difference. In each stage it also allows inserting tj right after s1⋯si, if it makes the cost cheaper than deleting si within a block deletion, or having the same cost of converting s1⋯si−1 to t1⋯tj−1 in case the characters are equal. The running time of the algorithm is O(n2 m) since during_deletion is linear.
Running Algorithm 3 on the example, S = bcxyabczfdlmefij and T = abcdefg, produces the table presented in Figure 1b. The number of character insertions and block deletions is 5, and corresponds to deleting the blocks {bcxy,zf,lm,ij} and inserting character “g”.
5.2. Block Deletions with Character Moves
We now consider the minimum number of block deletions, character insertions and character moves applied to S in order to attain T. We use the dynamic programming algorithm introduced in the previous section taking into account character moves. A character move is an insert and a delete of the same character. Therefore, when performing dynamic programming, we try to reduce the cost by exchanging insertions and deletions with moves. We first consider the case of character deletions, character insertions, and character moves for general costs. Replacing the character deletion with block deletions is considered for uniform costs and is solved using dynamic programming.
Shapira and Storer [4] showed that in the case of uniform costs of character insertions, character deletions and character moves, the minimal edit distance occurs in any optimal path transforming S to T of the traditional edit distance. We now generalize this to all cases. We use the following notations: P and P′ denote paths in a constructed dynamic table, starting at the left most upper cell and ending at the right lower cell (the final cell). denote the number of character insertions and character deletions of σ ∈ Σ when converting S into T in path P, and c(x) denotes the cost of operation x, where x is either an insert character or a delete character or a move character. The traditional edit distance, including only character insertions and character deletions, is denoted by ed, and the edit distance of S and T, including character moves is denoted by edm. Thus, edP and edmP refer to paths in the traditional and move edit distance, respectively, i.e., if path P in the model of edit distance with moves includes both an insertion and a deletion of some character σ, the cost is calculated as the cost of a move, subtracting the cost of a delete and an insert.
Fact
For any two paths P and P′ and every σ ∈ Σ,
The proof appears in Shapira and Storer [4], and is included here for completeness.
Proof
Denote by and the number of appearances of a character σ in the strings S and T respectively. For any path P which converts S into T, .
The following lemma only considers the edit distance problem with character insertions, character deletions and character moves. Character moves are irrelevant unless the cost of a move is cheaper than the cost of a character insert and the cost of a character delete. Then block deletion is added to the set of operations, and a dynamic programming algorithm is presented, which is optimal under the assumption of unit costs.
Lemma 3
For any positive costs of character insertion, character deletion, and character move, denoted c(insert), c(delete) and c(move) respectively, such that c(move) < c(insert) + c(delete), the minimal edit distance including character moves can be reconstructed from every optimal path of the traditional edit-distance.
Proof
A character move is deleting the character from its source location and inserting it again at its destination. By splitting characters according to the number of operations performed on them in path P, we have:
Let P and P′ be two paths converting S into T, such that edP < edP′. By using Equations 1 and 2 we find that:
By using Equations 1 and 3 we conclude that edmP < edmP′.
Lemma 4
For unit costs of character insertion, block deletion, and character move, the minimal edit distance including character moves can be reconstructed from every optimal path of the edit-distance table constructed using the algorithm presented in Algorithm 3 of character insertions and block deletions.
Proof
Let a ∈ Σ. Since a cost of an insert is the same cost as a move operation, replacing an insert of a and a deletion of a within a block deletion, by a move operation of a, has the same cost, unless a is deleted by a character deletion. In the case of a character deletion, Lemma 3 proves that the minimal edit distance including character moves can be reconstructed from every optimal path of the traditional edit-distance, which is a special case of the algorithm of character insertions and block deletions. Otherwise, since there are no changes in the costs, the minimal edit distance including character moves can be reconstructed from every optimal path of the edit-distance table constructed using the algorithm of character insertions and block deletions.
Lemma 4 can also be applied when the cost of a character move is less than the cost of a character insert and a delete operation, and the cost of a character insertion is equal to the cost of a character move. If there is an optimal path that leads to a cell and consists of an insert and a delete of the same character, and none of these operations were converted into a move operation yet in the current path, we reduce the cost of the cell (assuming that a move operation is cheaper than the cost of insertion and deletion). To determine the final cost of the cell, we refer to the (two) characters associated with it. We distinguish between two different cases. Consider first the case where the character is deleted among other characters, and the same character is inserted within the same path. In this case it is not worth replacing this character by a character move, since the cost of an insert character is less than the cost of a move character together with the cost of a block deletion (assuming the cost of a block deletion is positive). The reason is that when a character is deleted among other characters within a block deletion, it is not charged an additional cost for this deletion, since all characters are deleted in a single operation. However, when converting the deletion of this character into a move operation, we must partition the deleted block into two sub-blocks while adding another block deletion, unless it occurs at one of the block ends. In case the character is not at one of the block ends, this additional charge makes this case more expensive than the one without moves in the case where a character insertion operation is cheaper than a character move and a block deletion. In case the character is deleted at one of the block ends, shortening the block deletion to not include that character does not change the cost using the assumption that the cost of a character insert is equal to the cost of a character move. The situation is different when converting a character deletion and character insertion (of the same character), both performed in the same path, to a move operation, when this character was deleted alone. The former case of a character deletion we should subtract the cost of an insert and a delete, and add the cost of a move to the cost of the current cell, since we have charged it while deleting it and while inserting it, but need to charge it for the move. This is true when a cost of a move is less than a cost of an insert and a delete. For simplicity, the algorithm presented in Algorithm 4 is given for the case of uniform costs, but can be easily adapted to the case the above assumptions on the costs are valid.
Using the reasoning above regarding the conversion of insert and delete character into a move character, only in the case that the character was not deleted within a block deletion, the optimal algorithm for the edit distance problem with block deletions, character insertions, and character moves first computes the edit distance with character insertions and block deletions presented in Algorithm 3, and then chooses any optimal path in the constructed table, and reduces its final cost by exchanging the cost of an insert and a delete of the same character by the cost of a move. The following algorithm shows the way to traverse the dynamic programming table constructed by the Delete-Insert algorithm, based on Lemma 4. It uses two associative arrays Insert and Delete, for storing the information gathered during traversal. For simplicity the algorithm only outputs the operations for converting S into T. By storing the indices of the characters, more precise information can be output, such as the source and destination locations for a move operation. After applying the Delete-Insert algorithm of Algorithm 3 and constructing a dynamic programming table, A, the algorithm traverses A starting with cell A[n,m], and ending at cell A[0,0]. At each cell the algorithm reconstructs the optimal operation that led to that cell. In case the cell was determined from the cell to its left, it indicates a character insertion of tj, and this information is saved in the Insert table in the location for tj. In case the cell was determined from the cell above, it indicates a block deletion of si. The table is checked to see whether this character is deleted alone. If so, this information is saved in the Delete table in the location for si. Otherwise, a block deletion (of at least two characters) is identified and output. Once cell A[0,0] is reached, the information stored in the Delete and Insert tables is retrieved, and the number of character insertions, character deletions and character moves is computed and output. The Delete-Insert function runs in time O(n2·m), Traversing the dynamic programming table takes O(n·m), therefore, the total running time is O(n2·m + |Σ|), where Σ is the alphabet.
| Algorithm 4. Edit Distance with Block Deletions, Character Insertion and Character Moves. |
| function Delete_Insert_Move(S, T) { |
| A ← Delete_Insert(S, T) |
| for 1 ≤ i ≤ |Σ| do |
| Insert [si] ← 0 |
| Delete [si] ← 0 |
| i ← n,j ← m |
| while (i > 0) or (j > 0){ |
| if si = tj and A[i,j] ← A[i − 1, j − 1] |
| i--, j-- |
| // character insertion of tj |
| if A[i,j] == A[i,j − 1] + 1 |
| Insert[tj]++ |
| j-- |
| // character deletion of si |
| else if A[i,j] = A[i − 1,j] + 1 and (i = n or A[i + 1,j]≠A[ij]) |
| Delete [si]++ |
| i-- |
| else // block deletion |
| output si is deleted within a block deletion |
| } |
| for 1 ≤ i ≤ |Σ| do { |
| m ← Insert[si] − Delete[si] |
| output si is moved |m| times |
| if (m > 0) |
| output si is inserted Insert[si] − m times |
| else |
| output si is deleted Delete[si] + m times |
| } |
| } |
| } |
Lemma 5
The algorithm presented in Algorithm 4 produces an optimal solution for the edit distance problem with character insertions, block deletions and character moves.
Proof
Assume, by contradiction that the algorithm presented in Algorithm 4 is not optimal, and let O = {o1,…ok} be an optimal sequence of block deletions, character insertions and character moves (<c,b,c>), which converts S into T. We define as follows: if oi is a character insertion or a block deletion then . Otherwise, oi, which is a move of a character a, is replaced by two operations for inserting the character a, and for deleting the character a. Obviously, the operations of O′ convert S into T. From the fact above, any sequence of operations which convert S into T, has the same difference between the number of its insertions and the number of its deletions for every character σ ∈ Σ. Formally, , where and stand for the number of insertions and deletions of σ in O′, and and denote the number of insertions and deletions of an optimal conversion of S into T using only character insertions and block deletions (e.g., an output of Algorithm 3).
If for all σ ∈ Σ, then it applies that for all σ ∈ Σ. Thus, the algorithm presented in Algorithm 4 gives the same cost of the optimal sequence of operations (converting and back into a move character oi) and it is optimal, which contradicts our assumption. Therefore, there exist a character σ in Σ such that, . We show that there exists a character σ ∈ Σ for which . Otherwise, if for all σ ∈ Σ, , then it applies that which contradicts the optimality of <b,c,-> (Lemma 2).
Let σ be such character in Σ for which , thus . We divide the deletion operations in O′ into two groups and as follows. If is a block deletion, and σ is deleted alone, belongs to , otherwise, if σ occurs within belongs to . Obviously, . We now construct a third sequence of operations Õ for converting S into T, which uses character insertions, block deletions and character moves. Õ includes the same operations as O except those operations where σ is involved. Instead, the operations applied to σ are replaced by character moves of σ from the location where it is deleted to the location where it is inserted. Thus move operations are replaced by operations. Since and , and Õ contradicts the optimality of O and the algorithm presented in Algorithm 4 is optimal.
Figure 2 presents the dynamic table constructed, after applying the algorithm of Algorithm 4 of edit distance with unit cost operations (insert, delete, and move) on the strings S = abcbcbcabcabcaa and T = bcabcabcyabca. The light and dark gray cells represent an optimal path. The light gray cells represent an insert (vertical) and a delete (horizontal) of a character a, so the final cost for the edit distance including character moves is 4, which is block deletion of abc, character insertion of a, character insertion of y and a character deletion of a, reducing the cost to 3. The character insert and character delete can be replaced by a character move of a. Notice that another more expensive option is replacing the insert character of a and shortening the block deletion to only delete bc by a move operation of a, but it is not optimal.
6. Conclusions
We have shown that the problem of finding the edit-distance considering only block deletion is solved in polynomial time using dynamic programming, and the addition of insert character requires small changes in the algorithm. Adding character moves is solved using dynamic programming, and traversing any optimal path in order to reduce the cost. However, adding block moves to the set of operations, changes the problem to be NP-complete, and can be reduced to the problem of non-recursive block moves and block deletions within a constant factor. An interesting open question is whether the problem remains NP-complete when block sizes are restricted in some fashion.

| Problem | Complexity | Remarks |
|---|---|---|
| <c/c/-> | O(n2/log(n)) | Masek and Paterson [2], Crochemore et al. [3], assuming m = n |
| <c/c/b> | NPC | Shapira and Storer [4] |
| <c/b/b> | NPC | Current paper (4.1) |
| <-/b/-> | O(n2 · m) | Current paper (5.1) |
| <c/b/-> | O(n2 · m) | Current paper (5.1) |
| <c/c/c> | O(n2 · m + |Σ|) | Shapira and Storer [4] |
| <c/b/c> | O(n2 · m + |Σ|) | Current paper (5.2) |
References
- Gusfield, D. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology; Press Syndicate of the University of Cambridge: New York, NY, USA, 2007. [Google Scholar]
- Masek, W.J.; Paterson, M.S. A Faster Algorithm for Computing String Edit Distances. J. Comput. Syst. Sci. Int. 1980, 20, 18–31. [Google Scholar]
- Crochemore, M.; Landau, G.M.; Ziv-ukelson, M. A sub-quadratic sequence alignment algorithm for unrestricted cost matrices. SIAM J.Comput. 2003, 32, 1654–1673. [Google Scholar]
- Shapira, D.; Storer, J.A. Edit Distance with Move Operations. J. Discrete Algorithms 2007, 5, 380–392. [Google Scholar]
- Ukkonen, E. Algorithms for approximate string matching. Inf. Control 1985, 64, 100–118. [Google Scholar]
- Ann, Y.; Peng, L. Efficient algorithms for the block-edit problems. Inf. Comput. 2010, 208, 221–229. [Google Scholar]
- Muthukrishnan, S.; Sahinalp, S.C. Approximate Nearest Neighbors and Sequence Comparison with Block Operations. Proceeding of the Thirty-Second Annual ACM Symposium on Theory of Computing; ACM Press: New York, NY, USA, 2000; pp. 416–424. [Google Scholar]
- Muthukrishnan, S.; Sahinalp, S.C. Simple and Practical Sequence Nearest Neighbors with Block Operations. Springer Lect. Notes Comput. Sci. 2002, 2373, 262–278. [Google Scholar]
- Cormode, G.; Muthukrishnan, S. The String Edit Distance Matching Problem with Moves. ACM Trans. Algorithms 2007, 3. [Google Scholar] [CrossRef]
- Cormode, G.; Paterson, M.; Sahinalp, S.C.; Vishkin, U. Communication Complexity of Document Exchange. In Symp., Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000; pp. 197–206. [Google Scholar]
- Ergun, F.; Muthukrishnan, S.; Sahinalp, S.C. Comparing Sequences with Segment Rearrangements. Lect. Notes in Comput. Sci. 2003, 2914, 183–194. [Google Scholar]
- Chrobak, M.; Kolman, P.; Sgall, J. The Greedy Algorithm for the Minimum Common String Partition Problem. ACM Trans. Algorithms 2004, 1, 84–95. [Google Scholar]
- Shafrir, N.; Kaplan, H. The Greedy Algorithm for Edit Distance with Moves. Inf. Process. Lett. 2006, 1, 23–27. [Google Scholar]
- Bafna, V.; Pevzner, P. A. Sorting by Transpositions. SIAM J. Discrete Math. 199, 11, 124–240. [Google Scholar]
- Lopresti, D.; Tomkins, A. Block Edit Models for Approximate String Matching. Theor. Comput. Sci. 1997, 181, 159–179. [Google Scholar]
- Tichy, W.F. The String to String Correction Problem with Block Moves. ACM Trans. Comput. Syst. 1984, 2, 309–321. [Google Scholar]
- Hannenhalli, S. Polynomial-Time Algorithm for Computing Translocation Distance between Genomes. Discrete Appl. Math. 1996, 71, 137–151. [Google Scholar]
- Durand, D.; Farach, M.; Ravi, R.; Singh, M. A Short Course in Computational Molecular Biology; DIMACS Technical Report 97-63; Center for Discrete Mathematics & Theoretical Computer Science: Piscataway, NJ, USA, 1997. [Google Scholar]
- Smith, T.F.; Waterman, M.S. Identification of Common Molecular Sequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar]
- Hermelin, D.; Landau, G.M.; Landau, S.; Weimann, O. A Unified Algorithm for Accelerating Edit-Distance Computation via Text-Compression. Symp. Theor. Aspects Comput. Sci. 2009 2009, 529–540. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shapira, D.; Storer, J.A. Edit Distance with Block Deletions. Algorithms 2011, 4, 40-60. https://doi.org/10.3390/a4010040
Shapira D, Storer JA. Edit Distance with Block Deletions. Algorithms. 2011; 4(1):40-60. https://doi.org/10.3390/a4010040
Chicago/Turabian StyleShapira, Dana, and James A. Storer. 2011. "Edit Distance with Block Deletions" Algorithms 4, no. 1: 40-60. https://doi.org/10.3390/a4010040
APA StyleShapira, D., & Storer, J. A. (2011). Edit Distance with Block Deletions. Algorithms, 4(1), 40-60. https://doi.org/10.3390/a4010040




