A Prediction of Precipitation Data Based on Support Vector Machine and Particle Swarm Optimization (PSO-SVM) Algorithms
Abstract
:1. Introduction
2. Algorithm
2.1. SVM
2.2. Particle Swarm Optimization
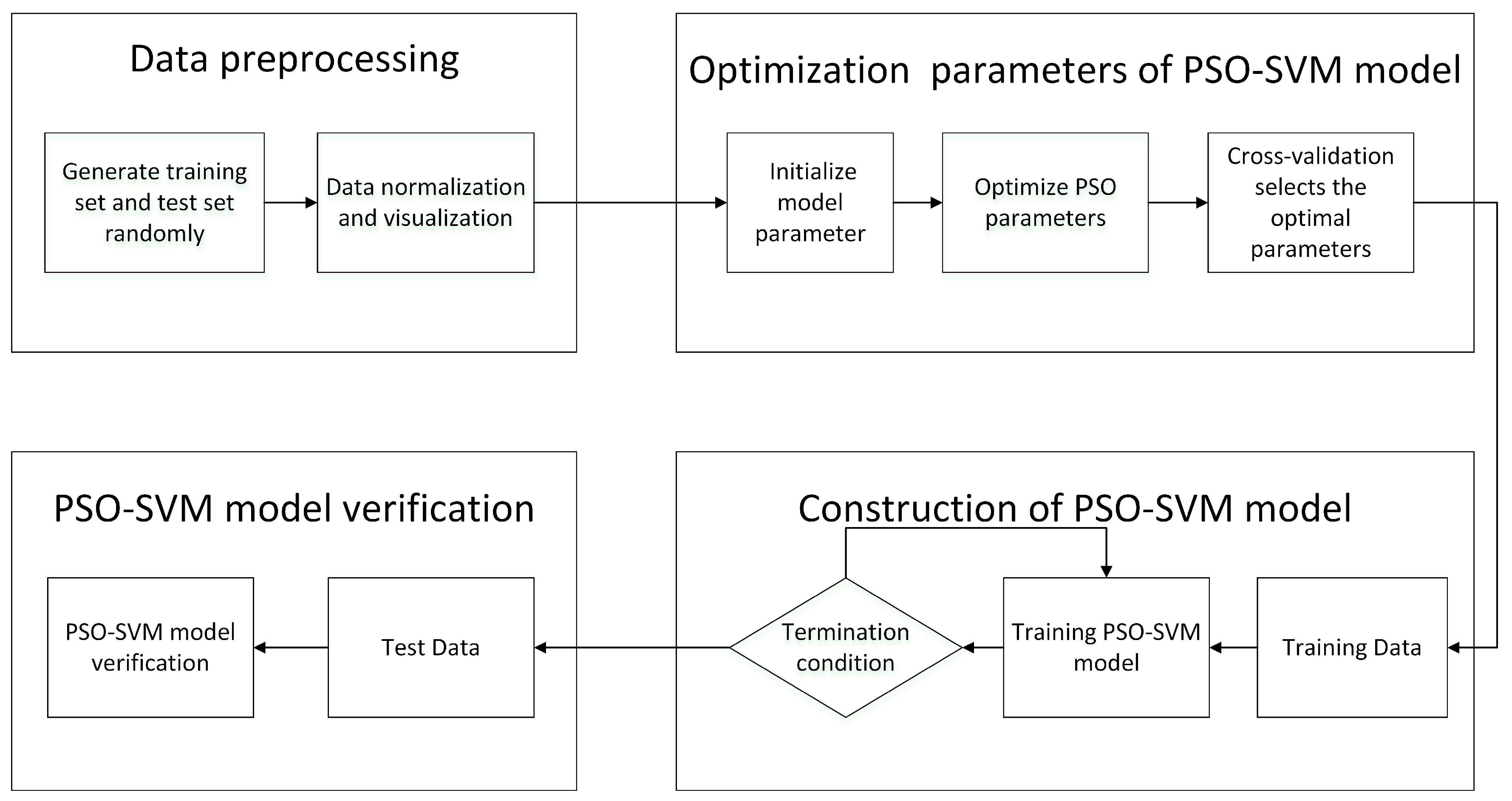
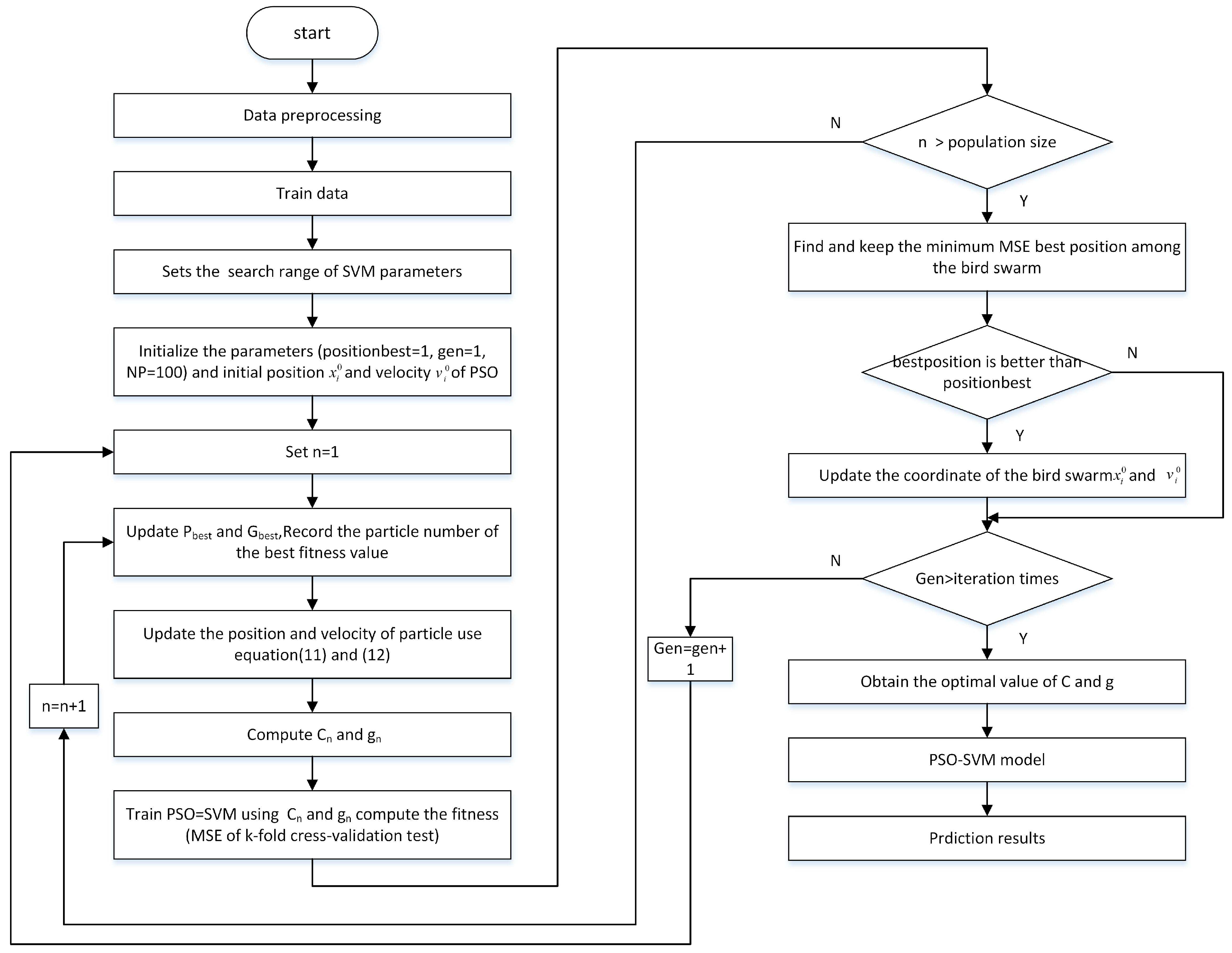
3. SVM Based on the PSO
- (1)
- Time-consuming—when the data size becomes large, or the number of parameters exceeds two, it takes a very long time to calculate.
- (2)
- It is difficult to find the optimal parameters accurately. The method needs to select a reasonable range for parameters, and the optimal parameters may not be in the range. For the practical problem, the above method can only find the local optimal solution in the candidate parameter combination.
4. Experiments
4.1. Data Collection and Preprocessing
- Training set—take 80% of the samples randomly from the dataset as the training set.
- Text set—for the text data set, we used other data remaining in the data set, which contained all the attributes except the rainfall data that the model is supposed to predict. The test set was never used for the training of any of the models.
4.2. Data Normalization
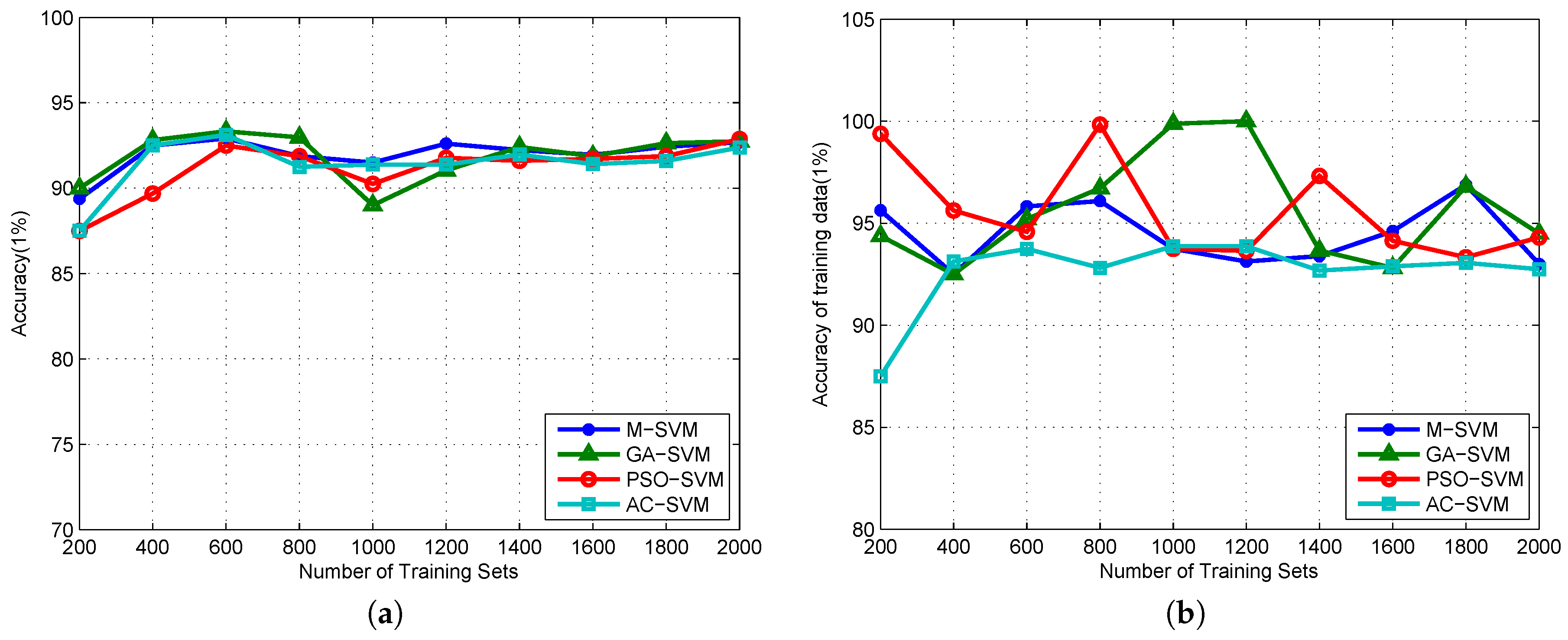
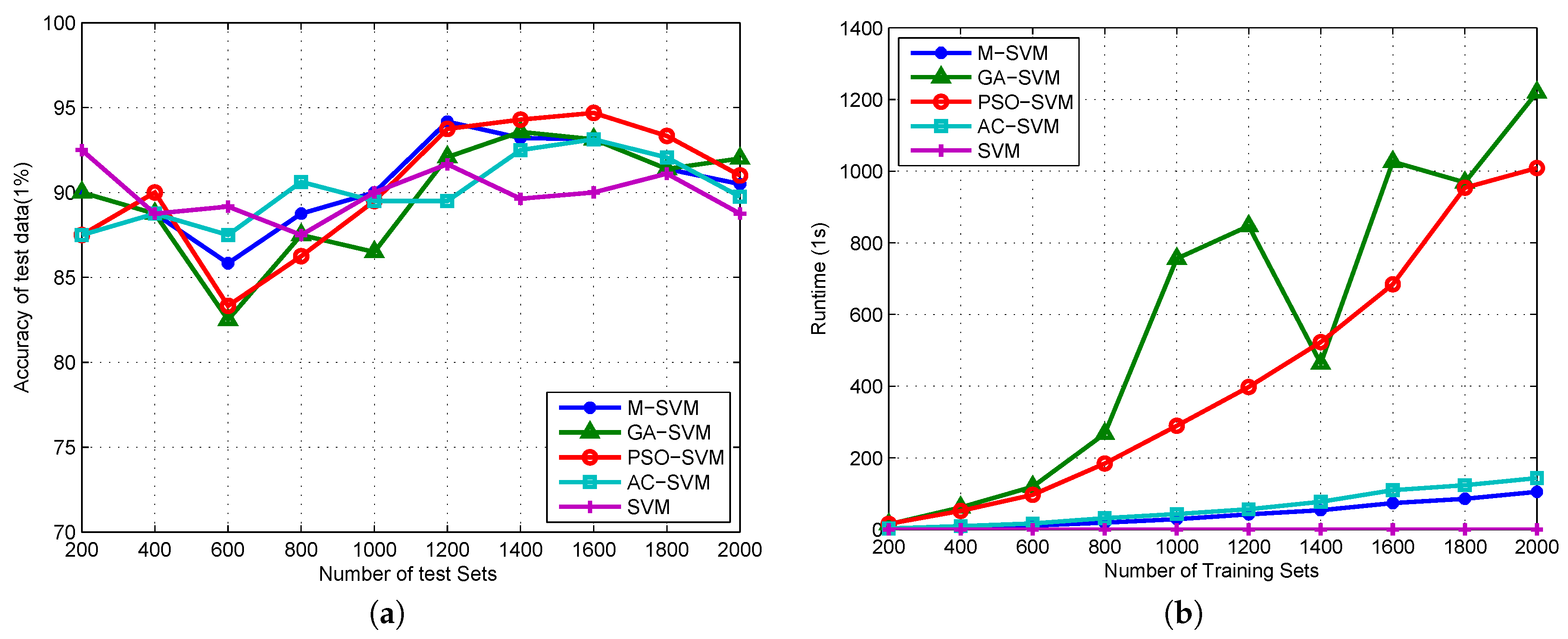
4.3. Algorithm Validation
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Geetha, A.; Nasira, G.M. Data mining for meteorological applications: Decision trees for modeling rainfall prediction. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 18–20 December 2014; pp. 1–4. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques; Elsevier: Harrisburg, PA, USA, 2011; ISBN 10: 9380931913. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Witten, I.H., Frank, E., Eds.; Elsevier: Burlington, MA, USA, 2014; ISBN 9787111453819. [Google Scholar]
- Yin, Y.; Zhao, Y.; Li, C.; Zhang, B. Improving Multi-Instance Multi-Label Learning by Extreme Learning Machine. Appl. Sci. 2016, 6, 160. [Google Scholar] [CrossRef]
- Annas, S.; Kanai, T.; Koyama, S. Assessing daily tropical rainfall variations using a neuro-fuzzy classification model. Ecol. Inform. 2007, 2, 159–166. [Google Scholar] [CrossRef]
- Prasad, N.; Reddy, P.K.; Naidu, M.M. A Novel Decision Tree Approach for the Prediction of Precipitation Using Entropy in SLIQ. In Proceedings of the 2013 UKSim 15th International Conference on Computer Modelling and Simulation (UKSim), Cambridge, UK, 10–12 April 2013; pp. 209–217. [Google Scholar]
- Lu, K.; Wang, L. A novel nonlinear combination model based on support vector machine for rainfall prediction. In Proceedings of the IEEE 4th International Joint Conference on Computational Sciences and Optimization (CSO 2011), Kunming and Lijiang City, China, 15–19 April 2011; pp. 1343–1347. [Google Scholar]
- Kisi, O.; Cimen, M. Precipitation forecasting by using wavelet-support vector machine conjunction model. Eng. Appl. Artif. Intell. 2012, 25, 783–792. [Google Scholar] [CrossRef]
- Ortiz-Garcia, E.G.; Salcedo-Sanz, S.; Casanova-Mateom, C. Accurate precipitation prediction with support vector classifiers: A study including novel predictive variables and observational data. Atmos. Res. 2014, 139, 128–136. [Google Scholar] [CrossRef]
- Sanchez-Monedero, J.; Salcedo-Sanz, S.; Gutierrez, P.A.; Casanova-Mateo, C.; Hervas-Martinez, C. Simultaneous modelling of rainfall occurrence and amount using a hierarchical nominal-rdinal support vector classifier. Eng. Appl. Artif. Intell. 2014, 34, 199–207. [Google Scholar] [CrossRef]
- Sehad, M.; Lazri, M.; Ameur, S. Novel SVM-based technique to improve rainfall estimation over the Mediterranean region (north of Algeria) using the multispectral MSG SEVIRI imagery. Adv. Space Res. 2017, 59, 1381–1394. [Google Scholar] [CrossRef]
- Young, C.C.; Liu, W.C.; Wu, M.C. A physically based and machine learning hybrid approach for accurate rainfall-runoff modeling during extreme typhoon events. Appl. Soft Comput. 2017, 53, 205–216. [Google Scholar] [CrossRef]
- Wei, J.; Huang, Z.; Su, S.; Zuo, Z. Using Multidimensional ADTPE and SVM for Optical Modulation Real-Time Recognition. Entropy 2016, 18, 30. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Lang, R.; Qin, H.; Zhou, K.; Cao, Y. A Real-Time Interference Monitoring Technique for GNSS Based on a Twin Support Vector Machine Method. Sensors 2016, 16, 329. [Google Scholar] [CrossRef] [PubMed]
- Sonnenschein, A.; Fishman, P.M. Radiometric detection of spread-spectrum signals in noise of uncertain power. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 654–660. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Campilongo, S.; Ficarella, A.; Congedo, P.M. Comparison between wind power prediction models based on wavelet decomposition with least-squares support vector machine (LS-SVM) and artificial neural network (ANN). Energies 2014, 7, 5251–5272. [Google Scholar] [CrossRef]
- Xiao, C.C.; Hao, K.R.; Ding, Y.S. The bi-directional prediction of carbon fiber production using a combination of improved particle swarm optimization and support vector machine. Materials 2015, 8, 117–136. [Google Scholar] [CrossRef]
- Huang, C.L.; Dun, J.F. A distributed PSO-SVM hybrid system with feature selection and parameter optimization. Appl. Soft Comput. 2008, 8, 1381–1391. [Google Scholar] [CrossRef]
- Ren, F.; Wu, X.; Zhang, K.; Niu, R. Application of wavelet analysis and a particle swarm-optimized support vector machine to predict the displacement of the Shuping landslide in the Three Gorges, China. Environ. Earth Sci. 2015, 73, 4791–4804. [Google Scholar] [CrossRef]
- Zhao, H.; Yin, S. Geomechanical parameters identification by particle swarm optimization and support vector machine. Appl. Math. Model 2009, 33, 3997–4012. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. Classification of fruits using computer vision and a multiclass support vector machine. Sensors 2012, 12, 12489–12505. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.D.; Dong, Z.C.; Liu, A.J.; Wang, S.H.; Ji, G.L.; Zhang, Z.; Yang, J.Q. Magnetic resonance brain image classification via stationary wavelet transform and generalized eigenvalue proximal support vector machine. J. Med. Imaging Health Inform. 2015, 5, 1395–1403. [Google Scholar] [CrossRef]
- Wu, J.; Liu, M.; Jin, L. A hybrid support vector regression approach for rainfall forecasting using particle swarm optimization and projection pursuit technology. Int. J. Comput. Intell. Appl. 2010, 9, 87–104. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. IEEE Proc. Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Hassan, R.; Cohanim, B.; De Weck, O.; Venter, G. A comparison of particle swarm optimization and the genetic algorithm. In Proceedings of the 46th AIAA Multidisciplinary Design Optimization Specialist Conference, Austin, TX, USA, 18–21 April 2005; pp. 18–21. [Google Scholar]
- Selakov, A.; Cvijetinovic, D.; Milovic, L.; Mellon, S.; Bekut, D. Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank. Appl. Soft Comput. 2014, 16, 80–88. [Google Scholar] [CrossRef]
- Shieh, M.Y.; Chiou, J.S.; Hu, Y.C.; Wang, K.Y. Applications of PCA and SVM-PSO based real-time face recognition system. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Nong, J.F.; Jin, L. Application of support vector machine to predict precipitation. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chingqing, China, 25–27 June 2008; pp. 8975–8980. [Google Scholar]
- Wang, S.H.; Yang, X.J.; Zhang, Y.D.; Phillips, P.; Yang, J.F.; Yuan, T.F. Identification of green, oolong and black teas in China via wavelet packet entropy and fuzzy support vector machine. Entropy 2015, 17, 6663–6682. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Dong, Z.C.; Wang, S.H.; Ji, G.L.; Yang, J.Q. Preclinical diagnosis of magnetic resonance (MR) brain images via discrete wavelet packet transform with Tsallis entropy and generalized eigenvalue proximal support vector machine (GEPSVM). Entropy 2015, 17, 1795–1813. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 1st ed.; Springer-Verlag: New York, NY, USA, 1995; ISBN 978-1-4757-2442-4. [Google Scholar]
- Vapnik, V.N.; Chervonenkis, A. On the Uniform Convergence of Relative Frequencies of Events to Their Probabilities; Theory of Probability and Its Applications; Springer International Publishing: New York, NY, USA, 1971; pp. 264–280. ISBN 978-3-319-21851-9. [Google Scholar]
- Kuhn, H.; Tucker, A. Nonlinear Programming. In Proceedings of the 2nd Berkeley Symposium on Mathematical Statistics and Probabilistics, Berkeley, CA, USA, 31 July–12 August 1950; pp. 481–492. [Google Scholar]
- Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree species classification using hyperspectral imagery: A comparison of two classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef]
- Kennedy, J. Particle Swarm Optimization. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2011; pp. 760–766. ISBN 978-0-387-30768-8. [Google Scholar]
- Chi, D.C.; Zhang, L.F.; Xue, L.I.; Wang, K.; Xiu-Ming, W.U.; Zhang, T.N. Drought Prediction Model Based on Genetic Algorithm Optimization Support Vector Machine (SVM). J. Shenyang Agric. Univ. 2013, 2, 013. [Google Scholar] [CrossRef]
- Zang, S.Y.; Zhang, C.; Zhang, L.J.; Zhang, Y.H. Wetland Remote Sensing Classification Using Support Vector Machine Optimized with Genetic Algorithm: A Case Study in Honghe Nature National Reserve. Sci. Geograph. Sin. 2012, 4, 007. [Google Scholar] [CrossRef]
- Gao, L.F.; Zhang, X.L.; Wang, F. Application of improved ant colony algorithm in SVM parameter optimization selection. Comput. Eng. Appl. 2015, 51, 139–144. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Ni, L.P.; Ni, Z.W.; Li, F.G.; Pan, Y.G. SVM model selection based on ant colony algorithm. Comput. Technol. Dev. 2007, 17, 95–98. (In Chinese) [Google Scholar]

| PRS (hPa) | PRS_Sea (hPa) | WIN_D () | WIN_S (0.1 m/s) | TEM (C) | RHU (1%) | PRE_1h (mm) |
|---|---|---|---|---|---|---|
| 1031.2 | 1035.8 | 89 | 2.5 | 77 | 2 | 0 |
| 1030.8 | 1035.4 | 113 | 2.9 | 61 | 6.4 | 0 |
| 1027.3 | 1031.9 | 153 | 2.1 | 49 | 8.3 | 0 |
| 1026.2 | 1030.8 | 122 | 2 | 55 | 7.1 | 0 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 1027.1 | 1031.7 | 121 | 0.7 | 71 | 4.1 | 0 |
| MSE | M-SVM | GA-SVM | AC-SVM | PSO-SVM |
|---|---|---|---|---|
| 200 | 0.3162 | 0.3162 | 0.3536 | 0.3536 |
| 400 | 0.4183 | 0.3354 | 0.3354 | 0.3354 |
| 600 | 0.3873 | 0.3416 | 0.3536 | 0.3651 |
| 800 | 0.3708 | 0.3708 | 0.3062 | 0.3354 |
| 1000 | 0.3162 | 0.324 | 0.324 | 0.3162 |
| 1200 | 0.2814 | 0.25 | 0.25 | 0.2415 |
| 1400 | 0.2892 | 0.2809 | 0.2739 | 0.2597 |
| 1600 | 0.2622 | 0.25 | 0.2622 | 0.2305 |
| 1800 | 0.2934 | 0.2635 | 0.2635 | 0.2582 |
| 2000 | 0.3082 | 0.2872 | 0.2872 | 0.2782 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Liu, Y.; Yu, Y.; Yan, W. A Prediction of Precipitation Data Based on Support Vector Machine and Particle Swarm Optimization (PSO-SVM) Algorithms. Algorithms 2017, 10, 57. https://doi.org/10.3390/a10020057
Du J, Liu Y, Yu Y, Yan W. A Prediction of Precipitation Data Based on Support Vector Machine and Particle Swarm Optimization (PSO-SVM) Algorithms. Algorithms. 2017; 10(2):57. https://doi.org/10.3390/a10020057
Chicago/Turabian StyleDu, Jinglin, Yayun Liu, Yanan Yu, and Weilan Yan. 2017. "A Prediction of Precipitation Data Based on Support Vector Machine and Particle Swarm Optimization (PSO-SVM) Algorithms" Algorithms 10, no. 2: 57. https://doi.org/10.3390/a10020057






