An Efficient Sixth-Order Newton-Type Method for Solving Nonlinear Systems
Abstract
:1. Introduction
2. The New Method and Analysis of Convergence
3. Computational Efficiency
- 1.
- for all
- 2.
- for all
- 3.
- for all
- Based on the expression (26), the relation between SNAM and M6 can be given by:Subtracting the denominator from the numerator of (27), we have:Equation (28) is positive for Thus, we get for all and
- The relation between CHM and M6 is given by:Subtracting the denominator from the numerator of (29), we have:Equation (30) is positive for Thus, we get for all and
- The relation between CHM and M6 can be given by:Subtracting the denominator from the numerator of (31), we have:Equation (32) is positive for Thus, we obtain for all and . This completes the proof.
- 1.
- for all
- 2.
- for all
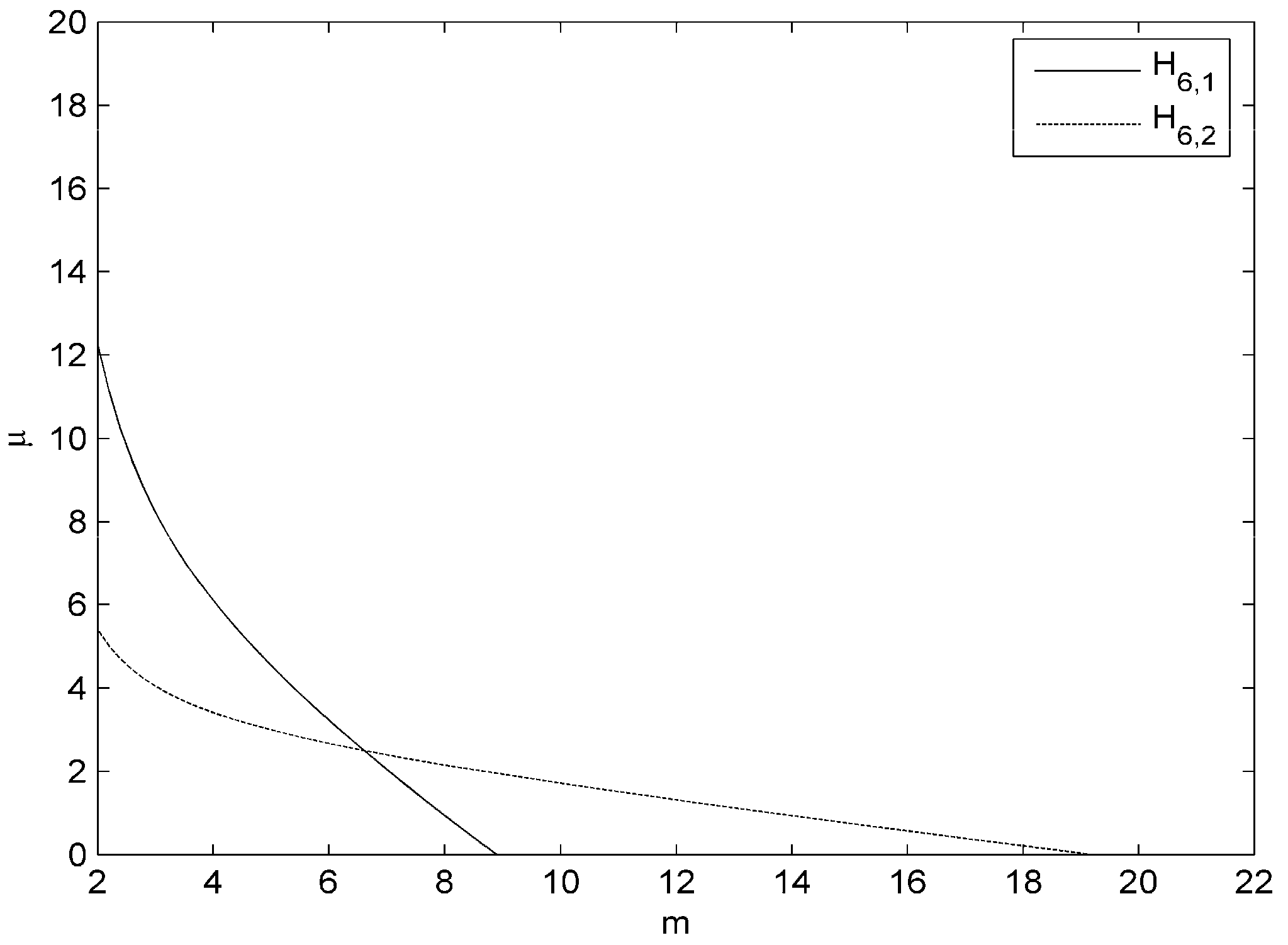
- From expression (26) and Table 1, we get the following relation between NM and M6:We consider the boundary . The boundary can be given by the following equation:where over it (see Figure 1). Boundary (34) cuts axes at points and . Thus, we get since for all and
- The relation between CM4 and M6 is given by:We consider the boundary . The boundary can be given by the following equation:where over it (see Figure 1). Boundary (36) cuts axes at points and . Thus, we get since for all and
4. Numerical Examples
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kelley, C.T. Solving Nonlinear Equations with Newton’s Method; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Ortega, J.M.; Rheinbolt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Cordero, A.; Martínez, E.; Torregrosa, J.R. Iterative methods of order four and five for systems of nonlinear equations. J. Comput. Appl. Math. 2009, 231, 541–551. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Matínez, E.; Torregrosa, J.R. Increasing the convergence order of an iterative method for nonlinear systems. Appl. Math. Lett. 2012, 25, 2369–2374. [Google Scholar] [CrossRef]
- Sánchez, M.G.; Noguera, M.; Amat, S. On the approximation of derivatives using divided difference operators preserving the local convergence order of iterative methods. J. Comput. Appl. Math. 2013, 237, 263–272. [Google Scholar]
- Cordero, A.; Hueso, J.L.; Matínez, E.; Torregrosa, J.R. Efficient high-order methods based on golden ratio for nonlinear systems. Appl. Math. Comput. 2011, 217, 4548–4556. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. Pseudocomposition: A technique to design predictor-corrector methods for systems of nonlinear equations. Appl. Math. Comput. 2012, 218, 11496–11504. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Grau, À.; Sánchez, M.G.; Hernández, M.A. On the efficiency of two variants of Kurchatov’s method for solving nonlinear systems. Numer. Algorithms 2013, 64, 685–698. [Google Scholar] [CrossRef]
- Potra, F.A.; Pták, V. Nondiscrete Induction and Iterative Processes; Pitman Publishing: Boston, MA, USA, 1984. [Google Scholar]
- Ezquerro, J.A.; Grau, À.; Sánchez, M.G.; Hernández, M.A.; Noguera, M. Analysing the efficiency of some modifications of the secant method. Comput. Math. Appl. 2012, 64, 2066–2073. [Google Scholar] [CrossRef]
- Sánchez, M.G.; Grau, À.; Noguera, M. On the computational efficiency index and some iterative methods for solving systems of nonlinear equations. J. Comput. Appl. Math. 2011, 236, 1259–1266. [Google Scholar] [CrossRef]
- Sánchez, M.G.; Grau, À.; Noguera, M. Frozen divided difference scheme for solving systems of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 739–1743. [Google Scholar]
- Ezquerro, J.A.; Hernández, M.A.; Romero, N. Solving nonlinear integral equations of Fredholm type with high order iterative methods. J. Comput. Appl. Math. 2011, 236, 1449–1463. [Google Scholar] [CrossRef]
- Argyros, I.K.; Hilout, S. On the local convergence of fast two-step Newton-like methods for solving nonlinear equations. J. Comput. Appl. Math. 2013, 245, 1–9. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Grau, À.; Sánchez, M.G. Maximum efficiency for a family of Newton-like methods with frozen derivatives and some applications. Appl. Math. Comput. 2013, 219, 7954–7963. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T. A family of Steffensen type methods with seventh-order convergence. Numer. Algorithms 2013, 62, 429–444. [Google Scholar] [CrossRef]
- Sharma, J.R.; Guha, R.K.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algorithms 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T.; Qian, W.; Teng, M. Seventh-order derivative-free iterative method for solving nonlinear systems. Numer. Algorithms 2015, 70, 545–558. [Google Scholar] [CrossRef]
- Păvăloiu, I. On approximating the inverse of a matrix. Creative Math. 2003, 12, 15–20. [Google Scholar]
- Diaconu, A.; Păvăloiu, I. Asupra unor metode iterative pentru rezolvarea ecuaţiilor operaţionale neliniare. Rev. Anal. Numer. Teor. Aproximaţiei 1973, 2, 61–69. [Google Scholar]
| Methods | ||||
|---|---|---|---|---|
| NM | 2 | |||
| CM4 | 4 | |||
| SNAM | 6 | |||
| CHM | 6 | |||
| CTVM | 6 | |||
| M6 | 6 |
| 5 | 1.0055606 | 1.0052450 | 1.0049895 | 1.0052838 | 1.0055283 | 1.0050600 |
| 7 | 1.0025422 | 1.0025753 | 1.0023729 | 1.0025126 | 1.0026423 | 1.0025375 |
| 9 | 1.0013845 | 1.0014870 | 1.0013340 | 1.0014096 | 1.0014831 | 1.0014905 |
| 11 | 1.0008405 | 1.0009480 | 1.0008314 | 1.0008761 | 1.0009207 | 1.0009643 |
| 20 | 1.0001777 | 1.0002326 | 1.0001898 | 1.0001978 | 1.0002060 | 1.0002482 |
| 50 | 1.0000141 | 1.0000224 | 1.0000165 | 1.0000169 | 1.0000173 | 1.0000258 |
| 100 | 1.0000019 | 1.0000034 | 1.0000023 | 1.0000024 | 1.0000024 | 1.0000040 |
| 200 | 1.0000002 | 1.0000005 | 1.0000003 | 1.0000003 | 1.0000003 | 1.0000006 |
| 5 | 1.0028332 | 1.0027489 | 1.0028941 | 1.0029907 | 1.0030675 | 1.0029177 |
| 7 | 1.0013956 | 1.0014055 | 1.0014554 | 1.0015068 | 1.0015525 | 1.0015157 |
| 9 | 1.0008054 | 1.0008390 | 1.0008536 | 1.0008839 | 1.0009123 | 1.0009150 |
| 11 | 1.0005124 | 1.0005505 | 1.0005504 | 1.0005697 | 1.0005882 | 1.0006057 |
| 20 | 1.0001242 | 1.0001488 | 1.0001391 | 1.0001434 | 1.0001476 | 1.0001681 |
| 50 | 1.0000117 | 1.0000168 | 1.0000139 | 1.0000141 | 1.0000144 | 1.0000199 |
| 100 | 1.0000017 | 1.0000028 | 1.0000021 | 1.0000021 | 1.0000022 | 1.0000034 |
| 200 | 1.0000002 | 1.0000004 | 1.0000003 | 1.0000003 | 1.0000003 | 1.0000005 |
| Function | Method | ||||
|---|---|---|---|---|---|
| NM | 8 | 2.42128 × 10−192 | 1.06480 × 10−383 | 1.99667 | |
| CM4 | 5 | 5.59843 × 10−147 | 2.69120 × 10−586 | 4.00129 | |
| SNAM | 4 | 3.76810 × 10−39 | 3.25655 × 10−227 | 6.09363 | |
| CHM | 4 | 4.18959 × 10−123 | 4.03125 × 10−736 | 5.99962 | |
| CTVM | 4 | 2.07203 × 10−100 | 2.63883 × 10−597 | 6.00033 | |
| M6 | 4 | 7.65662 × 10−119 | 1.55028 × 10−710 | 6.00589 | |
| NM | 9 | 3.41596 × 10−116 | 2.48971 × 10−232 | 1.97549 | |
| CM4 | 5 | 3.73825 × 10−90 | 1.20501 × 10−359 | 4.02761 | |
| SNAM | 4 | 9.18821 × 10−35 | 6.76819 × 10−207 | 5.98999 | |
| CHM | 4 | 8.31995 × 10−52 | 8.11818 × 10−310 | 5.72008 | |
| CTVM | 4 | 3.82928 × 10−42 | 4.59455 × 10−251 | 5.85429 | |
| M6 | 4 | 8.13364 × 10−65 | 6.14607 × 10−387 | 5.99644 | |
| NM | 22 | 2.71070 × 10−196 | 2.20459 × 10−392 | 1.99900 | |
| CM4 | 6 | 2.26562 × 10−115 | 1.03777 × 10−460 | 4.00061 | |
| SNAM | nc | ||||
| CHM | 5 | 2.79450 × 10−99 | 4.68047 × 10−594 | 5.92903 | |
| CTVM | 5 | 5.12075 × 10−193 | 1.30600 × 10−1157 | 5.97091 | |
| M6 | 5 | 1.99499 × 10−161 | 3.41913 × 10−967 | 6.08153 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, Y. An Efficient Sixth-Order Newton-Type Method for Solving Nonlinear Systems. Algorithms 2017, 10, 45. https://doi.org/10.3390/a10020045
Wang X, Li Y. An Efficient Sixth-Order Newton-Type Method for Solving Nonlinear Systems. Algorithms. 2017; 10(2):45. https://doi.org/10.3390/a10020045
Chicago/Turabian StyleWang, Xiaofeng, and Yang Li. 2017. "An Efficient Sixth-Order Newton-Type Method for Solving Nonlinear Systems" Algorithms 10, no. 2: 45. https://doi.org/10.3390/a10020045







