Pressure-Induced Phase Transition and Mechanical Properties of Mg2Sr Intermetallics
Abstract
:1. Introduction
2. Computational Methods
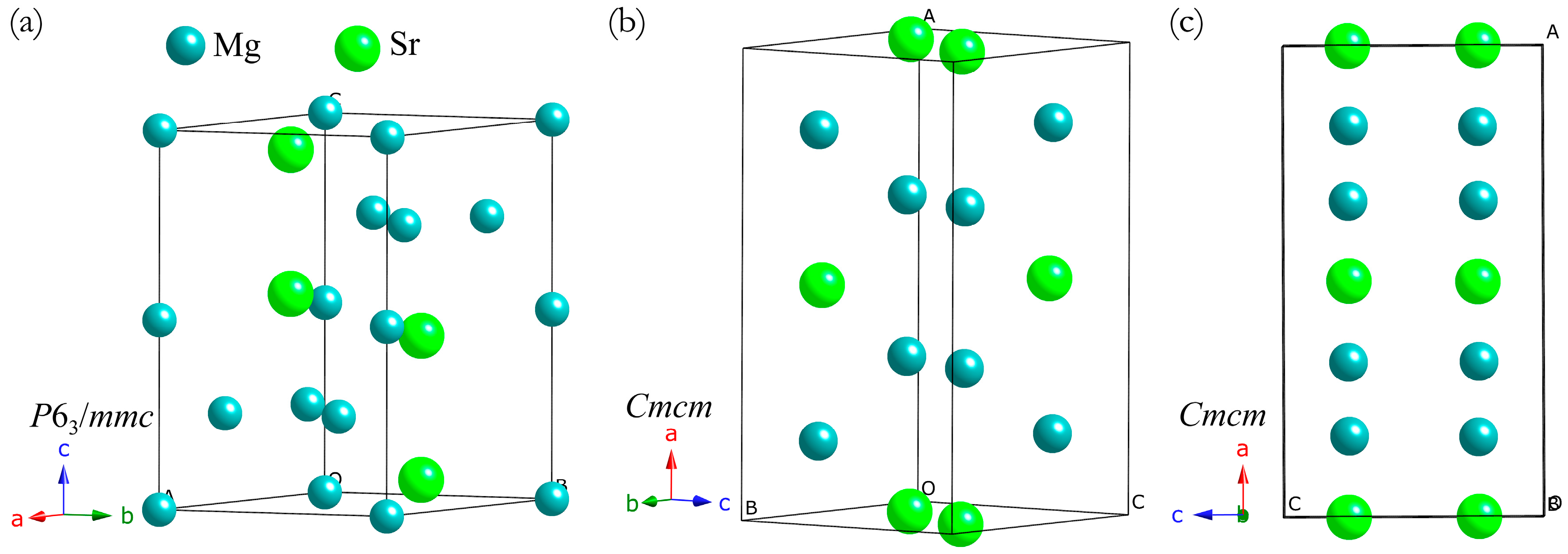
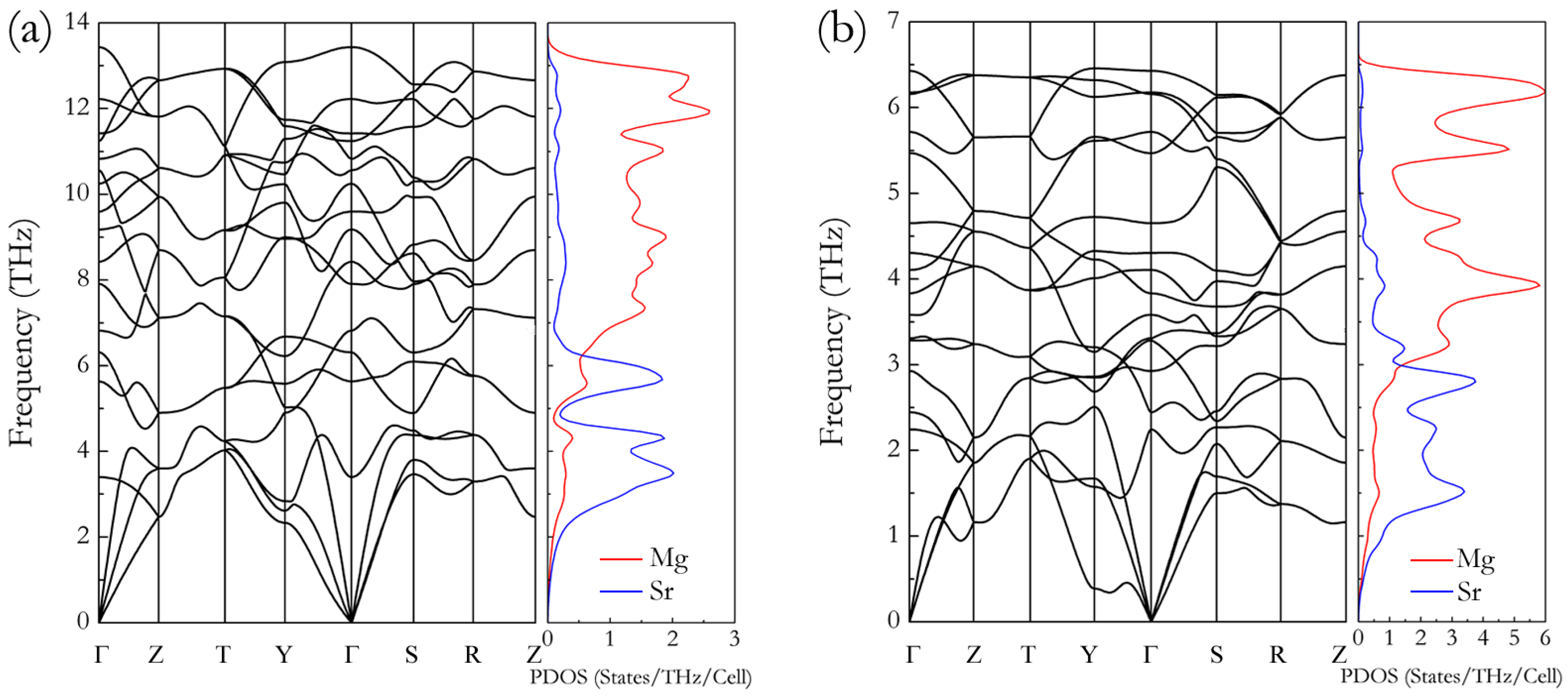
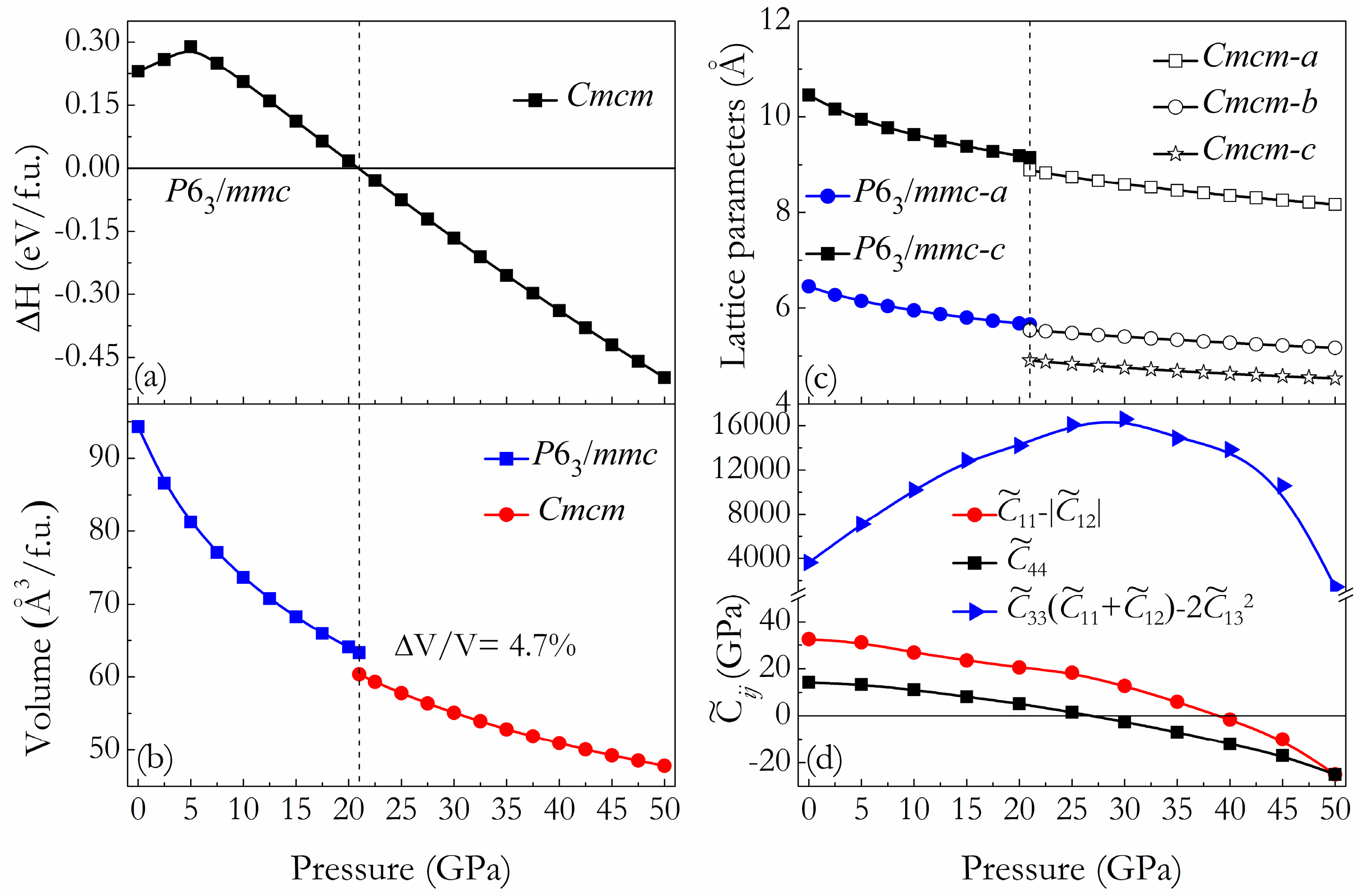
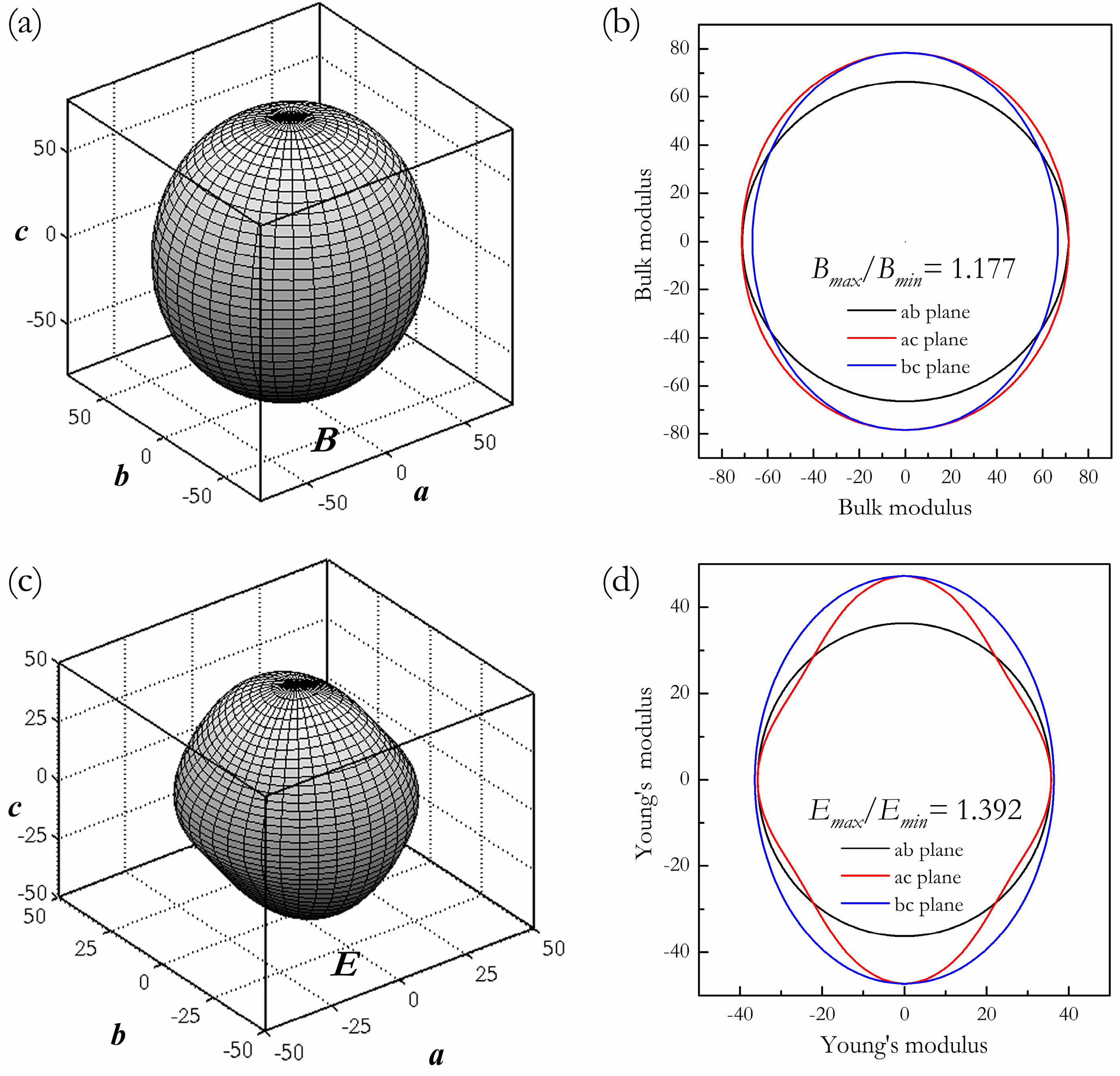
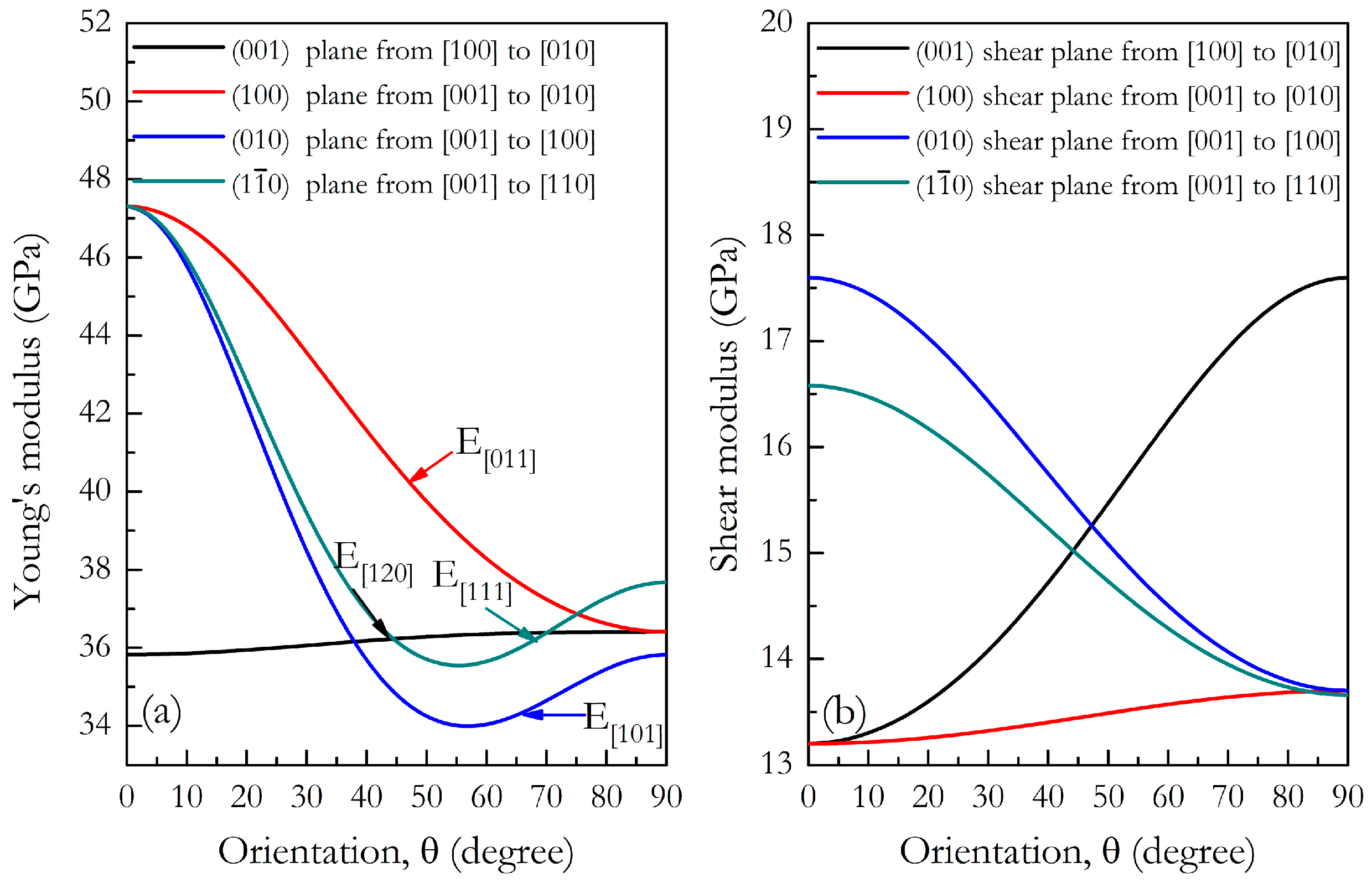
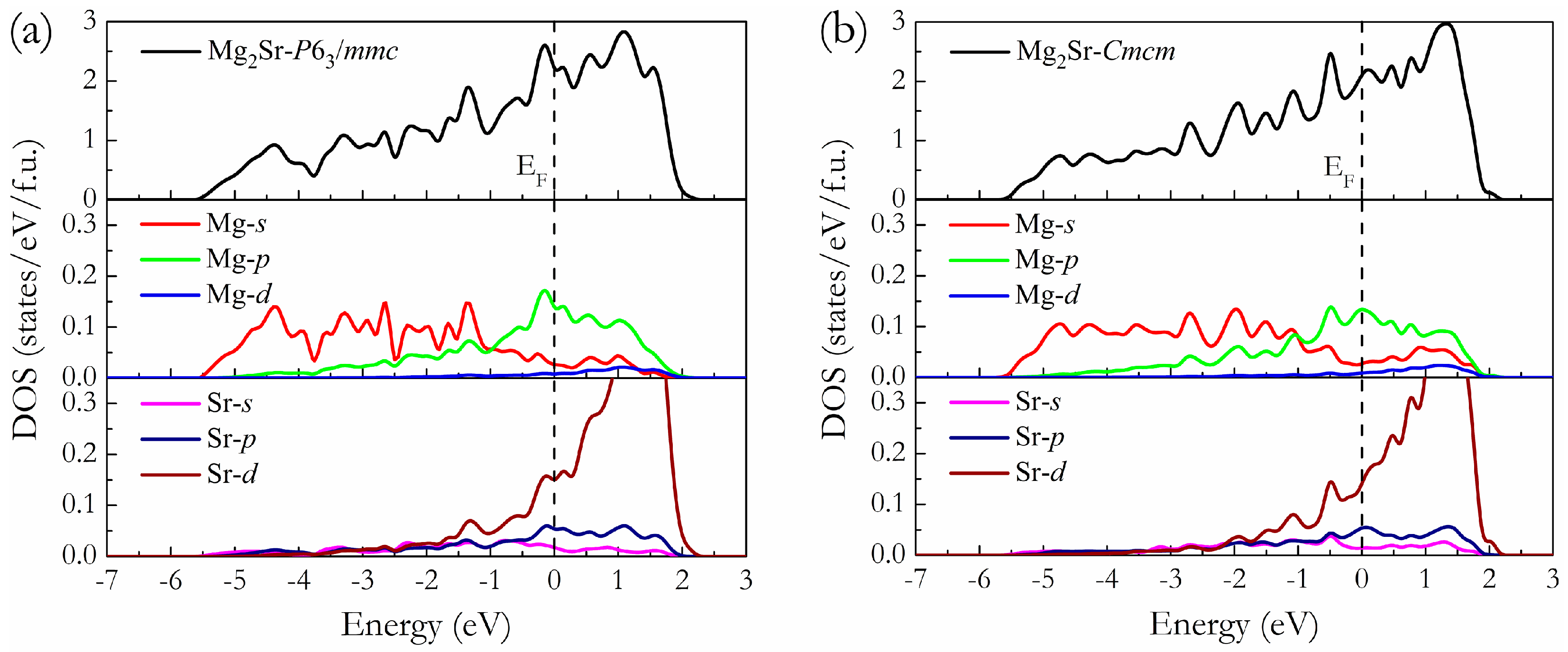
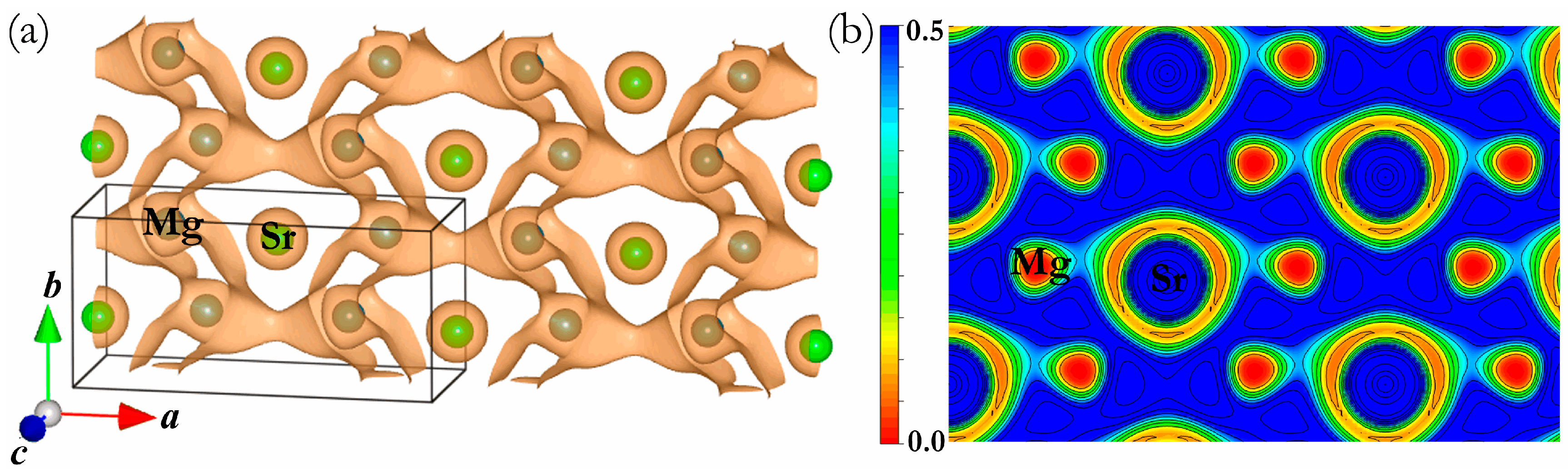
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bastami, M.; Chaboki-Khiabani, A.; Baghbadrani, M.; Kordi, M. Performance of high strength concretes at elevated temperatures. Sci. Iran. 2011, 18, 1028–1036. [Google Scholar] [CrossRef]
- Williamsa, J.C.; Stark, E.A. Progress in structural materials for aerospace systems. Acta Mater. 2003, 51, 5775–5799. [Google Scholar]
- Aljarrah, M.; Medraj, M.; Wang, X.; Essadiqi, E.; Muntasar, A.; Dénès, G. Experimental investigation of the MgAlCa system. J. Alloys Compd. 2007, 436, 131–141. [Google Scholar] [CrossRef]
- Zhong, Y.; Ozturk, K.; Liu, Z.K.; Luo, A.A. Magnesium Technology; Hryn, J., Ed.; TMS: Seattle, WA, USA, 2002; pp. 69–73. [Google Scholar]
- Miskell, C.F. Intermetallic Compounds in the Systems Sr-Mg and Ba-Mg. Ph.D. Thesis, Syracuse University, Syracuse, NY, USA, 1966. [Google Scholar]
- Nayeb-Hashemi, A.A.; Clark, J.B. The Ca-Mg (Calcium-Magnesium) system. J. Phase Equilib. 1987, 8, 58–65. [Google Scholar] [CrossRef]
- Nayeb-Hashemi, A.A.; Clark, J.B. The Sr-Mg (Magnesium-Strontium) system. Bull. Alloy Phase Diagr. 1986, 7, 149–156. [Google Scholar] [CrossRef]
- Nayeb-Hashemi, A.A.; Clark, J.B. The Ba-Mg (Barium-Magnesium) system. Bull. Alloy Phase Diagr. 1986, 7, 144–149. [Google Scholar] [CrossRef]
- Hellner, E.; Laves, F. The crystal structure of SrMg2, BaMg2, and CaLi2. Z. Krist. 1943, A105, 134–143. [Google Scholar]
- Wang, F.E.; Kanda, F.A.; MiskelI, C.F.; King, A.J. The crystal structures of Sr6Mg23, SrMg4, Ba6Mg23, andBaLi4. Acta Crystallogr. 1965, 18, 24–31. [Google Scholar] [CrossRef]
- Kanda, F.A.; Carter, W. Refined crystal structure of Sr2Mg17 and Ba2Mg17. J. Less Common Met. 1973, 32, 97–102. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, W.C.; Li, D.J.; Li, K.; Jin, H.L.; Xu, C.S.; Zeng, X.Q. Mechanical, electronic and thermodynamic properties of C14-type AMg2 (A = Ca, Sr and Ba) compounds from first principles calculations. Comput. Mater. Sci. 2015, 97, 75–85. [Google Scholar] [CrossRef]
- Zhang, H.; Shang, S.L.; Wang, Y.; Chen, L.Q.; Liu, Z.K. Thermodynamic properties of Laves phases in the Mg-Al-Ca system at finite temperature from first-principles. Intermetallics 2012, 22, 17–23. [Google Scholar] [CrossRef]
- King, R.C.; Kleppa, O.J. A thermochemical study of some selected laves phases. Acta Metall. 1964, 12, 87–97. [Google Scholar] [CrossRef]
- Aljarrah, M.; Medraj, M. Thermodynamic modelling of the Mg-Ca, Mg-Sr, Ca-Sr and Mg-Ca-Sr systems using the modified quasichemical model. Calphad 2008, 32, 240–251. [Google Scholar] [CrossRef]
- Yang, Z.W.; Du, J.L.; Wen, B.; Hu, C.Z.; Melnik, R. First principles studies on the structural, elastic, electronic properties and heats of formation of Mg-AE (AE = Ca, Sr, Ba) intermetallics. Intermetallics 2013, 32, 156–161. [Google Scholar] [CrossRef]
- Mao, P.L.; Yu, B.; Liu, Z.; Wang, F.; Ju, Y. First-principles investigation on mechanical, electronic, and thermodynamic properties of Mg2Sr under high pressure. J. Appl. Phys. 2015, 117, 115903. [Google Scholar] [CrossRef]
- Huan, T.D.; Tuoc, V.N.; Le, N.B.; Minh, N.V.; Woods, L.M. High-pressure phases of Mg2Si from first principles. Phys. Rev. B 2016, 93, 094109. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lv, J.; Zhu, L.; Ma, Y.M. Crystal structure prediction via particle swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lv, J.; Zhu, L.; Ma, Y.M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Lv, J.; Wang, Y.C.; Zhu, L.; Ma, Y.M. Predicted novel high-pressure phases of lithium. Phys. Rev. Lett. 2011, 106, 015503. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Wang, H.; Wang, Y.C.; Lv, J.; Ma, Y.M.; Cui, Q.L.; Ma, Y.M.; Zou, G.T. Substitutional alloy of Bi and Te at high pressure. Phys. Rev. Lett. 2011, 106, 145501. [Google Scholar] [CrossRef] [PubMed]
- Nishio-Hamane, D.; Zhang, M.G.; Yagi, T.; Ma, Y.M. High pressure and high-temperature phase transitions in FeTiO3 and a new dense FeTi3O7 structure. Am. Mineral. 2012, 97, 568–572. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, D.; Zheng, W.T.; Ma, Y.M.; Chen, C.F. Global structural optimization of tungsten borides. Phys. Rev. Lett. 2013, 110, 136403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Liu, H.Y.; Li, Q.; Gao, B.; Wang, Y.C.; Li, H.D.; Chen, C.F.; Ma, Y.M. Superhard BC3 in cubic diamond structure. Phys. Rev. Lett. 2015, 114, 015502. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.W.; Hao, J.; Liu, H.Y.; Li, Y.L.; Ma, Y.M. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 2014, 140, 174712. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Amerioun, S.; Yokosawa, T.; Lidin, S.; Ha1ussermann, U. Phase stability in the systems AeAl2-xMgx (Ae = Ca, Sr, Ba): Electron concentration and size controlled variations on the Laves phase structural theme. Inorg. Chem. 2004, 43, 4751–4760. [Google Scholar] [CrossRef]
- Sin’ko, G.V.; Smirnov, N.A. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure. J. Phys. Condens. Matter 2002, 14, 6989–7005. [Google Scholar]
- Karki, B.B.; Ackland, G.J.; Crain, J. Elastic instabilities in crystals from ab initio stress-strain relations. J. Phys. Condens. Matter 1997, 9, 8579–8589. [Google Scholar] [CrossRef]
- Wang, J.H.; Li, J.; Yip, S.; Phillpot, S.; Wolf, D. Mechanical instabilities of homogeneous crystals. Phys. Rev. B 1995, 52, 12627. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Slutsky, L.J.; Garland, C.W. Elastic constants of Magnesium from 4.2 K to 300 K. Phys. Rev. 1957, 107, 972–976. [Google Scholar] [CrossRef]
- Zhang, M.G.; Yan, H.Y. Elastic anisotropy and thermodynamic properties of iron tetraboride under high pressure and high temperature. Solid State Commun. 2014, 187, 53–58. [Google Scholar] [CrossRef]
- He, Y.; Schwarz, R.B.; Migliori, A.; Whang, S.H. Elastic constants of single crystal γ-TiAl. J. Mater. Sci. 1995, 10, 1187–1195. [Google Scholar] [CrossRef]
| Mg2Sr | Source | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | B | G | E | ν |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C14-type | Present | 49.9 | - | 56.9 | 14.2 | - | - | 17.4 | 10.2 | - | 25.8 | 16.6 | 41.0 | 0.235 |
| Theory a | 43.8 | - | 57.2 | 12.4 | - | - | 19.8 | 10.6 | - | 25.2 | 13.8 | 36.1 | 0.360 | |
| Theory b | 43.7 | - | 56.5 | 12.4 | - | - | 20.1 | 11.9 | - | 25.4 | 13.7 | 34.8 | 0.230 | |
| HP | Present | 43.1 | 42.9 | 52.0 | 17.6 | 13.2 | 13.7 | 15.7 | 12.6 | 10.7 | 24.0 | 15.3 | 37.9 | 0.237 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Han, X.; Zheng, B. Pressure-Induced Phase Transition and Mechanical Properties of Mg2Sr Intermetallics. Materials 2016, 9, 902. https://doi.org/10.3390/ma9110902
Yan H, Han X, Zheng B. Pressure-Induced Phase Transition and Mechanical Properties of Mg2Sr Intermetallics. Materials. 2016; 9(11):902. https://doi.org/10.3390/ma9110902
Chicago/Turabian StyleYan, Haiyan, Xingming Han, and Baobing Zheng. 2016. "Pressure-Induced Phase Transition and Mechanical Properties of Mg2Sr Intermetallics" Materials 9, no. 11: 902. https://doi.org/10.3390/ma9110902
APA StyleYan, H., Han, X., & Zheng, B. (2016). Pressure-Induced Phase Transition and Mechanical Properties of Mg2Sr Intermetallics. Materials, 9(11), 902. https://doi.org/10.3390/ma9110902






