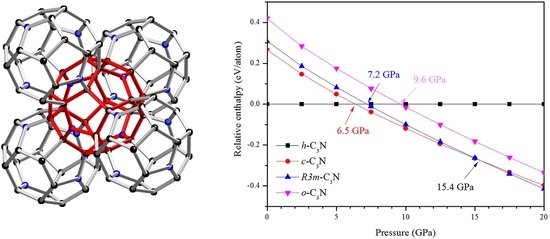
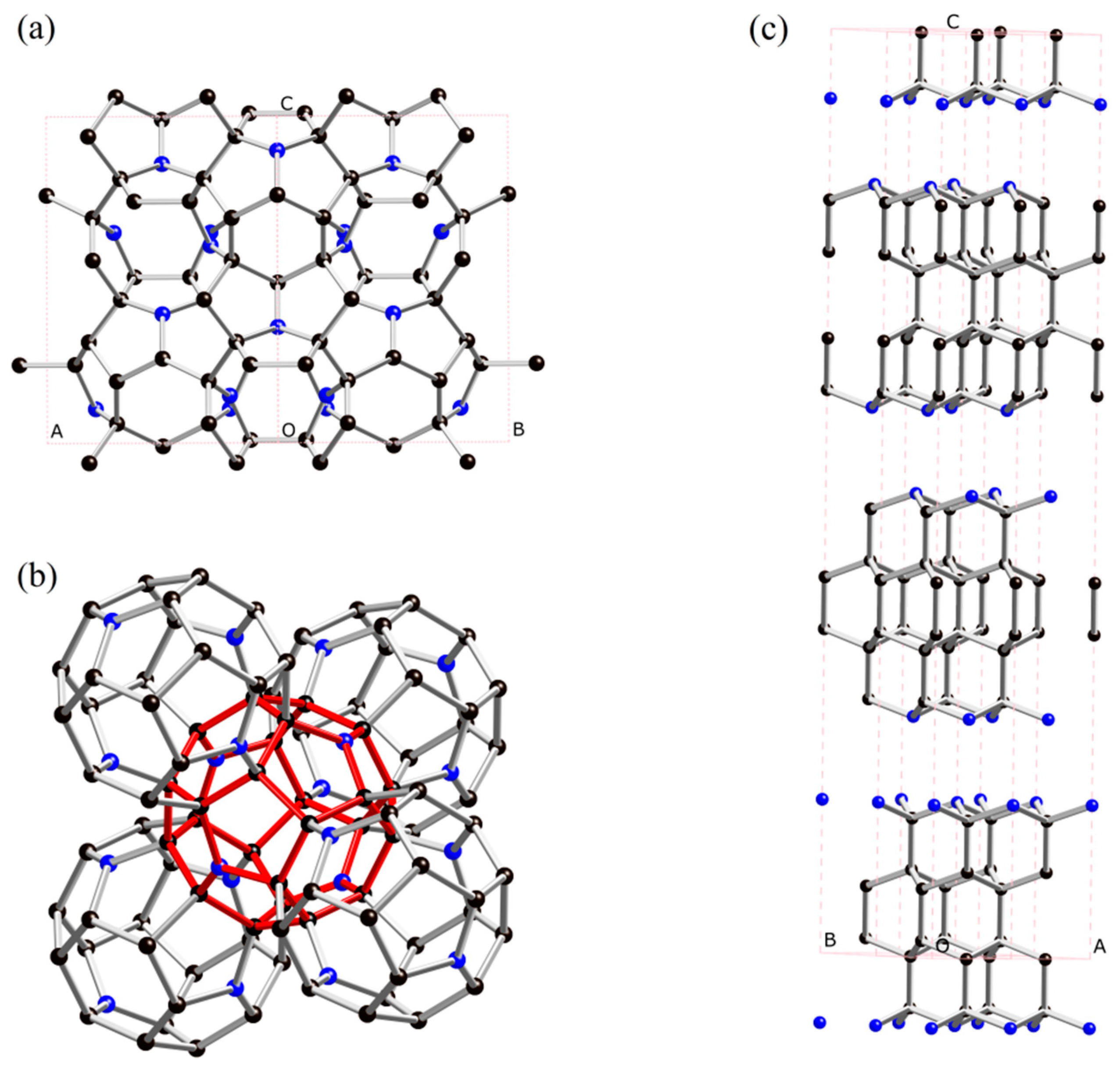
Cubic C3N: A New Superhard Phase of Carbon-Rich Nitride
Abstract
:1. Introduction
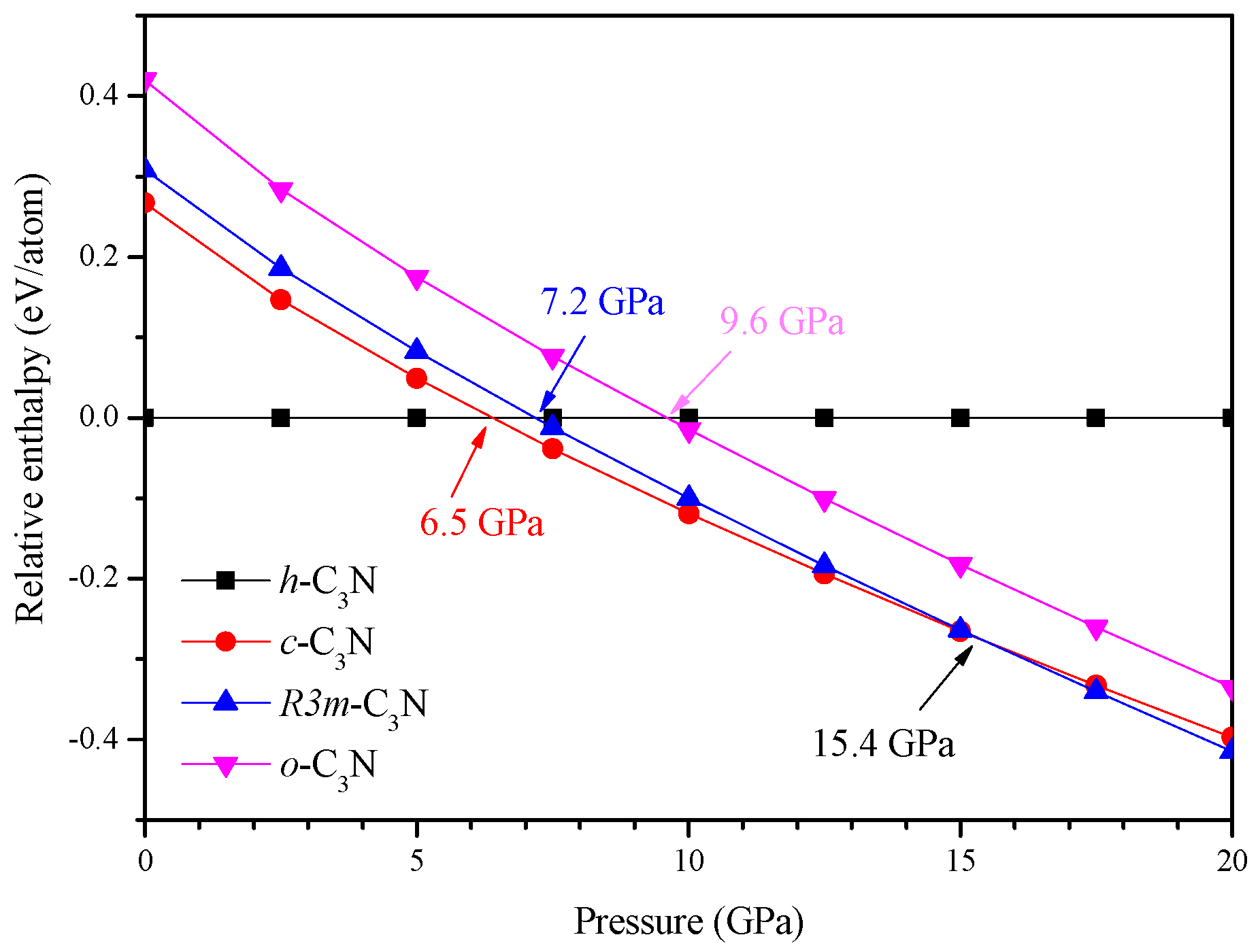
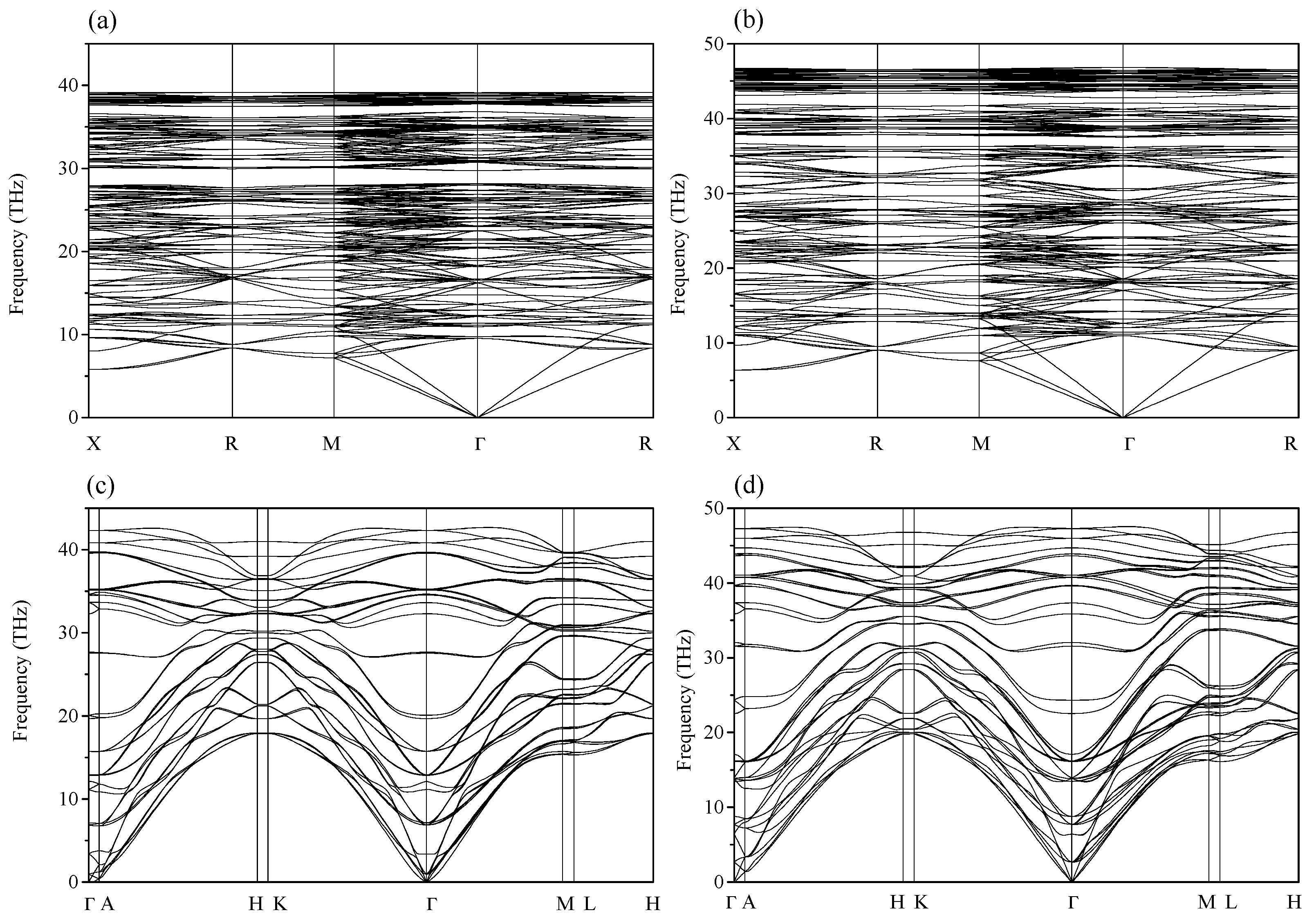
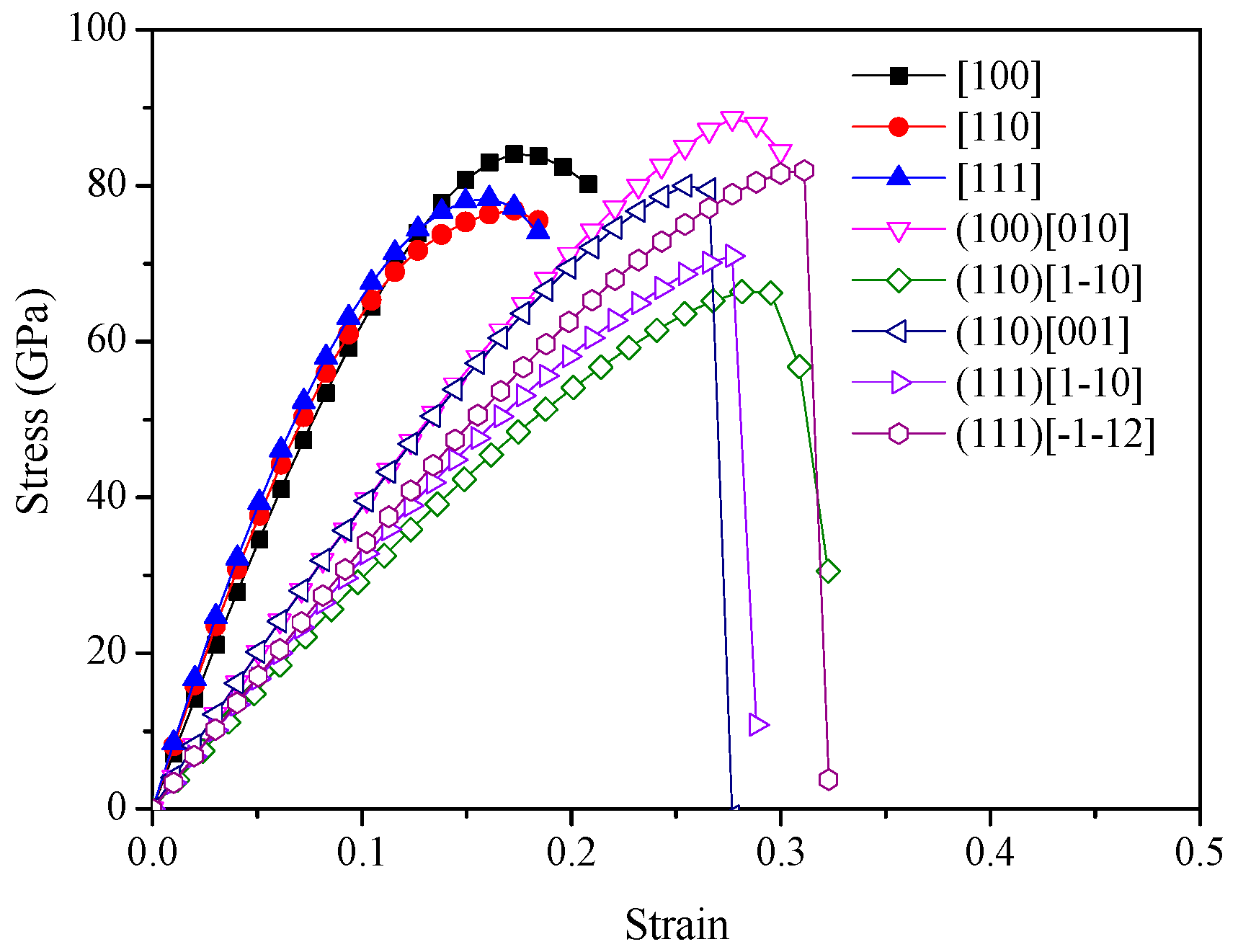
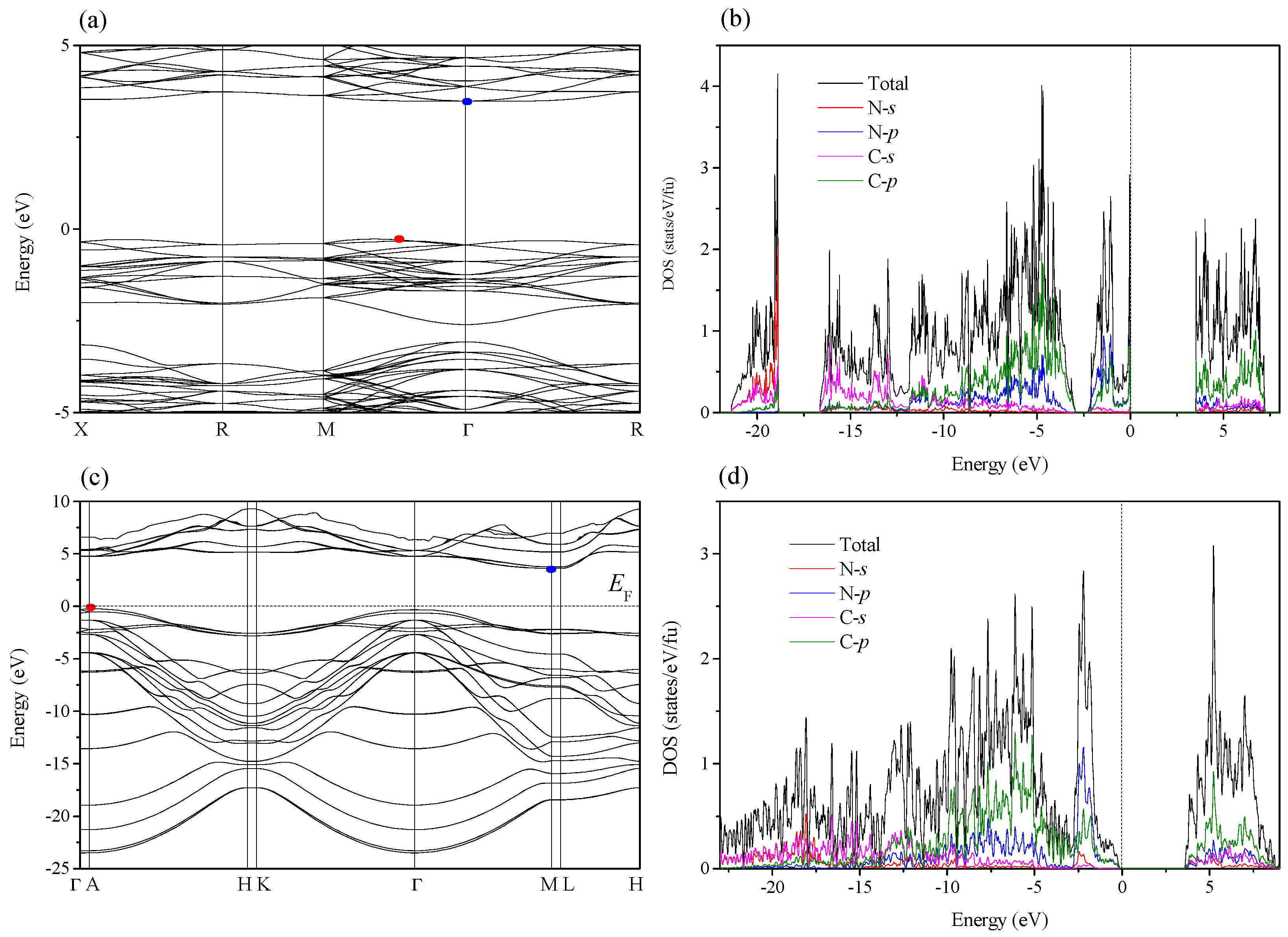
2. Results and Discussion
3. Computational Methods
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, Z.; Lu, M.; Zhu, L.; Zhu, L.; Li, Y.; Zhang, M.; Li, Q. Orthorhombic BN: A novel superhard boron nitride allotrope. Phys. Lett. A 2014, 378, 741–744. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Yu, D.; Ma, Y.; Wang, Y.; Jiang, Y.; Hu, W.; Tang, C.; Gao, Y.; Luo, K. Ultrahard nanotwinned cubic boron nitride. Nature 2013, 493, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wang, Q.; Kawazoe, Y.; Jena, P. Three-dimensional metallic boron nitride. J. Am. Chem. Soc. 2013, 135, 18216–18221. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Wei, Q.; Yan, H.; Zhang, M.; Zhang, Z.; Zhang, J.; Zhang, D. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80–87. [Google Scholar] [CrossRef]
- He, C.; Sun, L.; Zhang, C.; Peng, X.; Zhang, K.; Zhong, J. Z-BN: A novel superhard boron nitride phase. Phys. Chem. Chem. Phys. 2012, 14, 10967. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Hao, J.; Liu, H.; Lu, S.; Tse, J.S. High-energy density and superhard nitrogen-rich B-N compounds. Phys. Rev. Lett. 2015, 115, 105502. [Google Scholar] [CrossRef] [PubMed]
- Teter, D.M.; Hemley, R.J. Low-compressibility carbon nitrides. Science 1996, 271, 53–55. [Google Scholar] [CrossRef]
- Wang, X. Polymorphic phases of sp3-hybridized superhard CN. J. Chem. Phys. 2012, 137, 184506. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Guo, L.; Guo, X.; Liu, R.; Tian, Y.; Wang, H.; Gao, C. Predicting hardness of dense C3N4 polymorphs. Appl. Phys. Lett. 2006, 88, 101906. [Google Scholar] [CrossRef]
- Tian, F.; Wang, J.; He, Z.; Ma, Y.; Wang, L.; Cui, T.; Chen, C.; Liu, B.; Zou, G. Superhard semiconducting C3N2 compounds predicted via first-principles calculations. Phys. Rev. B 2008, 78, 235431. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, Q.; Yan, H.; Zhao, Y.; Wang, H. A novel superhard tetragonal carbon mononitride. J. Phys. Chem. C 2014, 118, 3202–3208. [Google Scholar] [CrossRef]
- Dong, H.; Oganov, A.R.; Zhu, Q.; Qian, G.R. The phase diagram and hardness of carbon nitrides. Sci. Rep. 2015, 5, 9870. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Liu, H.; Zhou, D.; Zheng, W.; Wu, Z.; Ma, Y. A novel low compressible and superhard carbon nitride: Body-centered tetragonal CN2. Phys. Chem. Chem. Phys. 2012, 14, 13081. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Zhang, M.; Yan, H.; Li, R.; Zhu, X.; Lin, Z.; Yao, R. A new superhard phase of C3N2 polymorphs. Z. Naturforsch. A 2015, 70, 1001. [Google Scholar] [CrossRef]
- Tang, X.; Hao, J.; Li, Y. First-principle study of orthorhombic CN as a potential superhard material. Phys. Chem. Chem. Phys. 2015, 17, 27821–27825. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Liu, H.; Lei, W.; Tang, X.; Lu, J.; Liu, D.; Li, Y. Prediction of a superhard carbon-rich C–N compound comparable to diamond. J. Phys. Chem. C 2015, 119, 28614–28619. [Google Scholar] [CrossRef]
- Hart, J.N.; Claeyssens, F.; Allan, N.L.; May, P.W. Carbon nitride: Ab initio investigation of carbon-rich phases. Phys. Rev. B 2009, 80, 174111. [Google Scholar] [CrossRef]
- Sandre, E.; Pickard, C.J.; Colliex, C. What are the possible structures for CN compounds? The example of C3N. Chem. Phys. Lett. 2000, 325, 53–60. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Calypso: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, H.; Li, Q.; Gao, B.; Wang, Y.; Li, H.; Chen, C.; Ma, Y. Superhard BC3 in cubic diamond structure. Phys. Rev. Lett. 2015, 114, 015502. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Ma, Y.; Oganov, A.R.; Wang, H.; Wang, H.; Xu, Y.; Cui, T.; Mao, H.-K.; Zou, G. Superhard monoclinic polymorph of carbon. Phys. Rev. Lett. 2009, 102, 175506. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhou, D.; Zheng, W.; Ma, Y.; Chen, C. Global structural optimization of tungsten borides. Phys. Rev. Lett. 2013, 110, 136403. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Wei, Q.; Chang, S.; Guo, P. Ab initio study of ultra-incompressible ternary BeCN2 polymorph. J. Phys. Chem. Solids 2011, 72, 667–672. [Google Scholar] [CrossRef]
- Chen, X.-Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Rivelino, R.; Santos, R.B.D.; Mota, F.D.B.; Gueorguiev, G.K. Conformational effects on structure, electron states, and Raman scattering properties of linear carbon chains terminated by graphene-like pieces. J. Phys. Chem. C 2010, 114, 16367–16372. [Google Scholar] [CrossRef]
- Santos, R.B.D.; Rivelino, R.; Mota, F.D.B.; Gueorguiev, G.K. Exploring Hydrogenation and Fluorination in Curved 2D Carbon Systems: A Density Functional Theory Study on Corannulene. J. Phys. Chem. A 2012, 116, 9080–9087. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Zhang, M.; Yan, H.; Lin, Z.; Zhu, X. Structural, electronic and mechanical properties of Imma-carbon. EPL 2014, 107, 27007. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
| Phase | a, b, c (Å) | Atomic Coordinates | dC–C (Å) | dC–N (Å) |
|---|---|---|---|---|
| c-C3N | a = 9.5342 | C 96g (0.93983, 0.93983, 0.75924) N 32e (0.35488, 0.35488, 0.35488) | 1.551 1.623 | 1.429 |
| R3m-C3N | a = 2.4519 c = 31.7508 | C 3a (0.33333, 0.66667, 0.07030) C 3a (0.33333, 0.66667, 0.02080) C 3a (0.33333, 0.66667, 0.28862) C 3a (0.66667, 0.33333, 0.08675) C 3a (0.66667, 0.33333, 0.00436) C 3a (0.66667, 0.33333, 0.13582) N 3a (0.66667, 0.33333, 0.27269) N 3a (0.00000, 0.00000, 0.15174) | 1.558 1.572 1.553 1.509 | 1.503 |
| Crystal | Reference | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | E | B | G | G/B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| o-C3N | This work | 1105 | 806 | 804 | 484 | 424 | 424 | 122 | 125 | 222 | - | 404 | 409 | 1.01 |
| - | [16] | 1092 | 797 | 796 | 482 | 398 | 392 | 131 | 132 | 222 | 918 | 406 | 401 | 0.99 |
| c-C3N | This work | 766 | - | - | 403 | - | - | 133 | - | - | 810 | 344 | 365 | 1.06 |
| Diamond | [4] | 1052 | - | - | 563 | - | - | 120 | - | - | - | 431 | 522 | 1.2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Q.; Zhang, Q.; Yan, H.; Zhang, M. Cubic C3N: A New Superhard Phase of Carbon-Rich Nitride. Materials 2016, 9, 840. https://doi.org/10.3390/ma9100840
Wei Q, Zhang Q, Yan H, Zhang M. Cubic C3N: A New Superhard Phase of Carbon-Rich Nitride. Materials. 2016; 9(10):840. https://doi.org/10.3390/ma9100840
Chicago/Turabian StyleWei, Qun, Quan Zhang, Haiyan Yan, and Meiguang Zhang. 2016. "Cubic C3N: A New Superhard Phase of Carbon-Rich Nitride" Materials 9, no. 10: 840. https://doi.org/10.3390/ma9100840
APA StyleWei, Q., Zhang, Q., Yan, H., & Zhang, M. (2016). Cubic C3N: A New Superhard Phase of Carbon-Rich Nitride. Materials, 9(10), 840. https://doi.org/10.3390/ma9100840