1. Introduction
Many dimension stones used for the construction of historical buildings show, after a certain time, superficial degradations in the first centimeters that do however not affect the stone below this depth. That is the case, for instance, during the formation of scales in a sandstone during a spalling process. These alterations are formed parallel to the outer surface and are independant of the stone bedding orientation, suggesting that a combination of transport properties and environmental exposure causes the stress from a degradation process to reach critical levels only at a certain depth. An example of such alteration is presented in
Figure 1a.
When decisions are made to restore these stones, the question is how to remediate these alterations: should the degraded part of the stone be replaced by another stone, or by an appropriate mortar? Since the alteration is generally superficial, a reinstatement of natural stones would imply a removal of potentially sound original material to a depth of at least 10 cm to ensure a good placement [
1], while the use of a plastic mortar that can be substituted for the lost parts would result in a minimal loss of historical material and, in addition, extend its lifetime. The latter practice is called “reprofiling” or “filling”, while the piece itself is called “plastic repair” [
2], “piecing-in” [
1], “fill” or “patch”. This strategy complies with modern building conservation principles that favour a minimal intervention and the retaining of as much historical material as possible [
2]. It is one of the reasons that explains the increasing use of repair mortar in conservation, as pointed out by Torney in Scotland [
2], and the increasing research undertaken, in both the philosophical side of the repair [
3,
4,
5] and the material science side, with the development of compatibility criteria, upon which Isebaert wrote a recent review [
6], as well as new mortar formulations [
7] sometimes based on polymers [
8].
Figure 1.
(a) Common dimension of a flake in a historical building molasse sandstone; (b) Old acrylic-based mortar used in Lausanne, after more than 30 years; (c) Reversibility of the old acrylic-based mortar.
Figure 1.
(a) Common dimension of a flake in a historical building molasse sandstone; (b) Old acrylic-based mortar used in Lausanne, after more than 30 years; (c) Reversibility of the old acrylic-based mortar.
The present work was initiated by the curiosity and questioning of stone carvers who used an acrylic-based mortar for the repair of calcareous sandstones in the late seventies in Switzerland. This mortar was developed at that time by Professor Furlan’s team in the Ecole Polytechnique Fédérale de Lausanne, and applied in the townhall of Lausanne, in locations protected from the direct sun but washed weekly by a high-pressure water hose to clean the remnants of the market. More than thirty years later, the mortar is in most of the locations still in place, and the repairs have been judged durable and successful by the stone carvers from the point of view of the integrity of the natural stone it aimed to repair, as shown in
Figure 1b. The stone carvers thus proposed this mortar for the restoration of the Catholic Church of Notre-Dame de Vevey, Vevey, Switzerland, where it was used in 2011. However, owing to the very different natures of the original stone and the repair mortar, a more comprehensive understanding of the interactions between them would provide the foundation to decide in which situations this material could be beneficial or not.
The development of an acrylic-based repair mortar by Professor Furlan’s team originated in the confluence of three factors: the particular mode of alteration of the local stone, the resurgence of interest towards repair mortars due to the spreading of the minimal-intervention approach, and the increasing use of polymers in conservation.
Indeed, many of the Swiss historical buildings have been erected with the soft stone present in the Swiss Plateau, a sandstone called molasse, mainly composed of quartz and felspars cemented by calcite and clays [
9]. This stone is sensitive to wetting and drying cycles that commonly lead to granular desintegration and spalling of flakes of 0.5 to 3 cm [
10], but the stone is often in good conditions above this limit, as illustrated by
Figure 1a.
Eventually, the properties of reversibility, transparency and stability generally attributed to acrylic polymers [
1,
11] oriented the team towards devising a mortar with an acrylic binder. These properties contributed to the large use of acrylic polymers in the conservation of heritage materials. Since the early 1930’ s, where they were used as picture varnishes [
12], they have been applied on glass pigments, paper, silver, iron, wood and stone [
13]. In the particular field of stone conservation, they have mainly been used, alone or mixed with other polymers, as consolidants or protective agents [
1,
11]. The search for better and more stable polymers led to the development of many formulations; in a recent handbook Princi listed 31 different commercial acrylic resins applied to stone conservation [
11]. However, even though they are often used for the conservation of stone objects, there are no detailed records in the scientific literature. Moreover, to the best of the authors’ knowledge, there are no reports of their use as the sole binder in a repair mortar, to the exception of Kemp who describes the repair of marble using artificial stones based on Paraloid [
14].
The mortar that is the subject of this paper is made by mixing a stone powder with a dispersion of methacrylic ester-acrylic ester copolymer. The hardening occurs through the drying of the dispersion and the subsequent coalescence of the polymer particles, that ultimately bind the grains together. Due do its slow drying time, this artificial stone is better indicated for repairs no thicker than a couple of centimeters, while lateral dimensions can reach few tens of centimeters, which overall agrees well with the maximum dimensions generally accepted for a repair. In the hardened state, the polymer represents 10 % of the weight of the stone powder and is the only binder between the grains. This has several consequences : because it is transparent, the color of the artificial stone is the color of the stone powder, making it easy to match the color of the natural stone; because the polymer can be dissolved in an organic solvent, the mortar is reversible and can be removed without breaking the original stone substrate when, or if, time has come for another repair. It has to be noted that the reversibility is still effective after more than thirty years of use in the townhall of Lausanne, as can be seen in
Figure 1c. The stone repaired in this study is a calcareous sandstone but the repair material could potentially be used on any stone that would benefit from a small-size repair and that does not display any visible pattern or layering. Another interesting feature lies in its ability to be worked like the sandstone due to its similar stiffness, thus making the integration of the repair possible by the normal tools of a stone carver.
However, repair with an acrylic-based mortar does not correspond to the "like-for-like" principle of building conservation, that would favour using a similar material for a repair [
5]. The sandstone is indeed a soft elastic material, while the mortar displays the physical properties of the acrylic resin, among which viscoelasticity, namely time and temperature-dependent physical properties, and a thermal expansion coefficient more than twice that of the molasse sandstone. This raises questions about the magnitude of the thermal stresses induced in the two materials. Indeed, on one hand, on repairs exposed outdoors and subject to temperature variations, the thermal expansion mismatch could lead to high thermal stresses in the two materials. On the other hand, the viscoelastic character of the repair mortar may attenuate the development of these thermal stresses, so that they should not only depend on the temperature difference, but also on the rate at which this temperature difference develops. The magnitude of the thermal stresses is thus dictated by the site exposure and developing a general treatment to evaluate their importance represents an important objective for providing more confidence in the use of such repair materials from case to case.
The aim of this work is thus to calculate the thermal stresses arising in the two materials at heating and cooling rates representative of field exposure. We present the general approach for this and illustrate its use with site specific numerical examples. For this, we use temperature variations that have been recorded over a year at different depths in a wall where the repair mortar has recently been applied, in the Catholic Church of Notre-Dame de Vevey. The physical properties of the materials, namely the thermal expansion coefficient, the elastic moduli, and the viscoelastic modulus of the artificial stone have been measured in the laboratory. The numerical evaluation is achieved through the development of an analytical solution presented in the next section.
2. Mechanical Analysis of the Repair
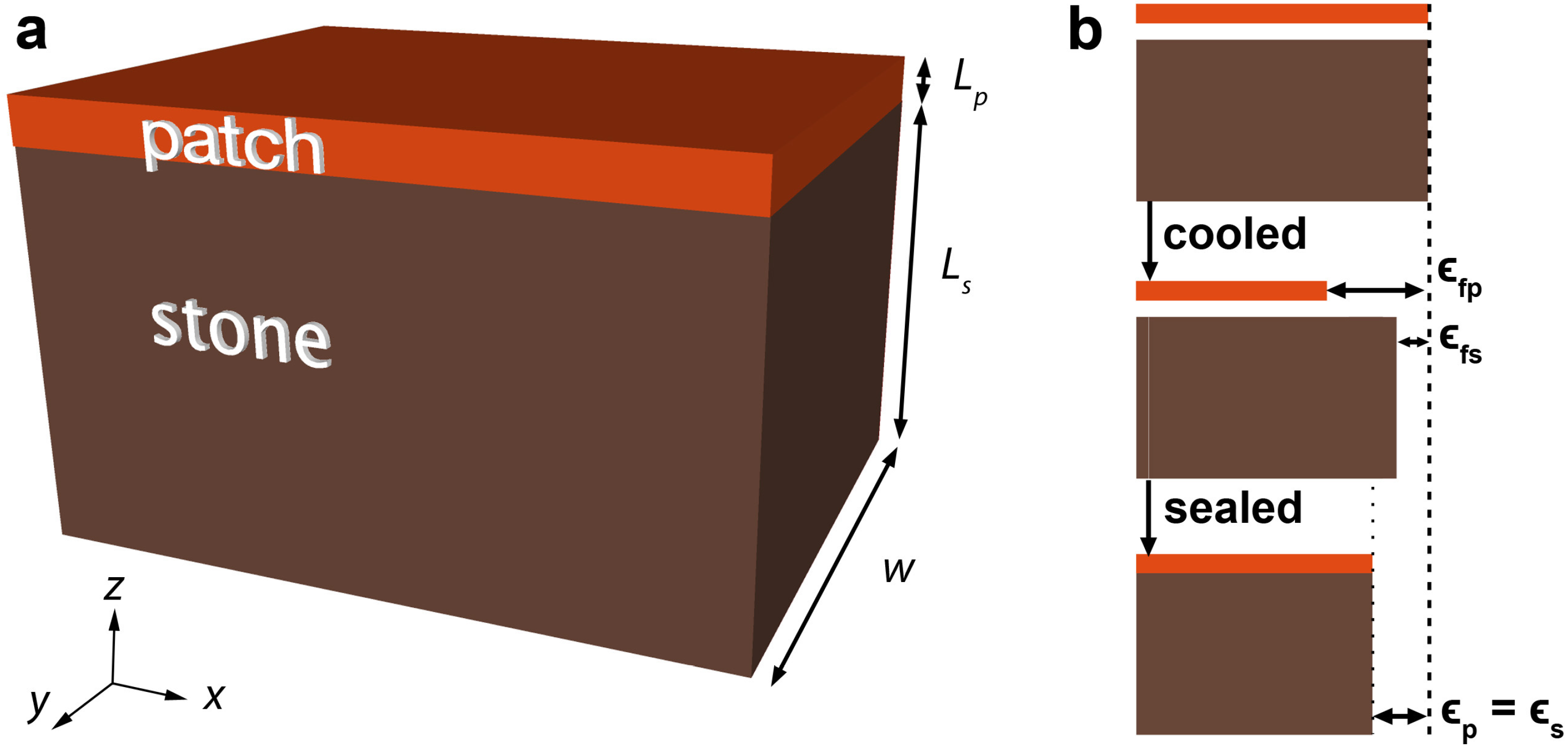
The simplest case of reprofiling can be seen as a bilayer composite material made of a thin mortar layer (“patch”) on a thick stone substrate. If we extract a part of the composite from the wall, it would look like the scheme of
Figure 2a.
Figure 2.
(a) Schematic of the patch layer on top of the stone substrate; (b) Illustration of the thermal expansion mismatch between the two materials.
Figure 2.
(a) Schematic of the patch layer on top of the stone substrate; (b) Illustration of the thermal expansion mismatch between the two materials.
When two materials are bound together, if they have dissimilar expansion properties, mismatch forces arise at the interface and internal stresses build up. That is the case for thermal expansion mismatch, as is illustrated in
Figure 2b. Consider two plates of repair mortar and natural stone of equal length; after cooling, the patch contracts by
and the stone by
, respectively the free strain of the patch and the stone. However, if they were connected, they would have contracted by an amount
intermediate between
and
. This imposed strain is, as we shall see, dictated by the elastic moduli, the Poisson’s ratios and the relative thicknesses of both materials, and leads to the creation of internal stresses. But, since the repair material has a polymeric nature and exhibits a viscoelastic behaviour, the stresses developed in it might be relaxed. Consequently the stresses affecting the natural stone might decrease, depending on the temperature of the material and on the heating or cooling rate. This section develops an analytical description to quantify whether this is the case or not, and if so under which conditions of temperature. This analysis follows the steps and the notation developed in the analysis of the sandwich seal [
15]. The stone is considered linear elastic and the acrylic-based repair material is considered viscoelastic.
Let us define a Cartesian coordinate system where the x and y-axis are parallel to the layers. Since the composite is not constrained in the z-direction,
= 0 ; and due to the symmetry of the composite,
in the two layers. In all the subsequent equations, the subscripts
p and
s stand for patch and stone. If the materials are considered isotropic, and the stress in the z-direction is zero, the constitutive equations connecting stress and strain can be written:
and
where
stands for the free strain of the material;
E for the elastic modulus; and
ν for the Poisson’s ratio. Due to the bond between the two materials, the layers have strained equally in the central region of the repair, so
=
. Thus,
Another equation to define
can be obtained by considering the edge of the composite, where the net force in the isolated sample must be zero. Let us call the thicknesses of the layers
for the patch and
for the stone substrate; they share the same width
w, and thus we have:
or
Combining Equation (
3) and Equation (
5), we find:
with
n the stiffness ratio defined as:
In a typical reprofiling the thickness of the patch is very small compared to the thickness of the stone substrate, on the order of 1/20. If we consider
, then
n → 0 and the stress is maximal in the repair layer; on the other side, the repair layer does not exert significant stress on the stone. The maximal elastic stress exerted by the stone on the repair layer is then expressed by:
The free strain
is the unconstrained change of dimension of the material. It is given by:
and
with
and
the coefficient of thermal expansion of the stone and the patch; and
and
the infinitesimal temperature variation of the stone and the patch, respectively. Since the coefficients of thermal expansion are taken independent of the temperature, the elastic thermal stress can be written:
with ΔT the temperature differences. This equation thus describes the maximal stresses that can appear in the repair material. The viscoelastic solution, according to the correspondence principle, is found by substituting the elastic quantities by their appropriate transformed quantities in the Laplace domain [
15,
16,
17,
18]. When using a dash superscript to indicate the Laplace transform, the Equation (
8) in the Laplace domain is written:
where the elastic modulus is transformed into an apparent modulus
M and the Poisson’s ratio into an apparent Poisson’s ratio
N; here, the relaxation of Poisson’s ratio is ignored. The apparent modulus
M is related to the elastic modulus
E through the transform of the relaxation function
. In case of a uniaxial stress, M is written:
where
is the instantaneous elastic modulus of the patch and
p is the Laplace transform parameter. It follows that
The solution in the Laplace domain has to be inverted to find the solution in the time domain. The stress in the patch becomes:
where
ξ is the reduced time defined as
and thus
in which the relaxation time of the artificial stone is
τ. As is confirmed in the experimental section, the relaxation function has the form of a stretched exponential:
which, together with Equation (
17), when substituted into Equation (
15), gives:
In Equation (
19) the relaxation time is written as
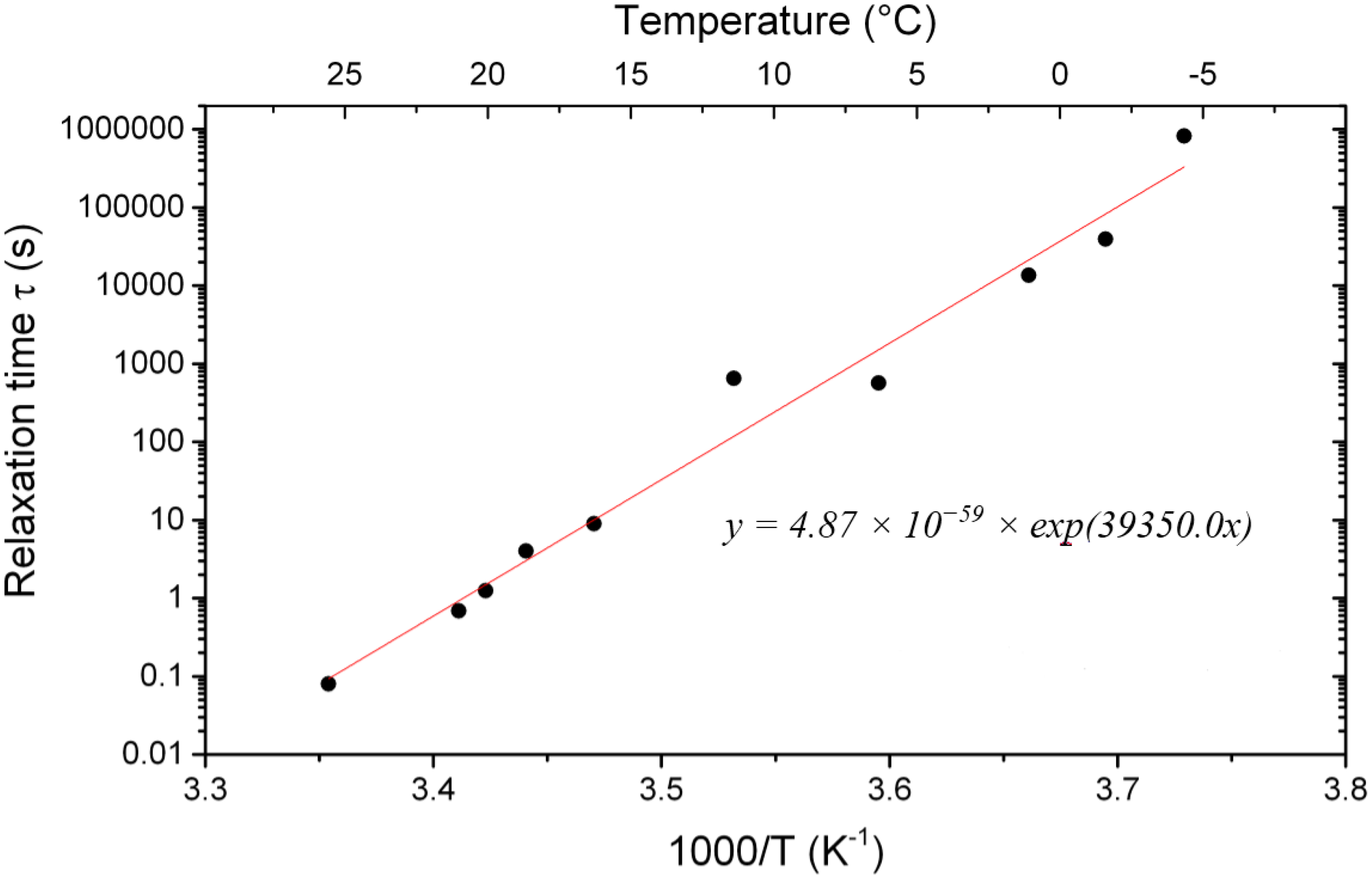
since it is temperature dependent. From the stress relaxation experiments at different temperatures, the artificial stone shows a thermorheologically simple behaviour that can be described by an Arrhenius law (see results in corresponding section). The dependence of the relaxation time with the temperature is thus written :
and can be incorporated in Equation (
19):
Since the temperatures of the two materials are different, then
The derivative in
ξ can be transformed in derivative in
t thanks to Equation (
17). By dividing by
the previous equation thus becomes
and we need to distinguish the integrals for the two materials in Equation (
21). They are written:
and
The stress in the patch is thus finally written:
This equation can be used to calculate the stresses induced by a thick elastic substrate in a thin viscoelastic layer on the central region of the composite, with the two materials having different inner temperatures. In turn, this makes it possible to calculate the stresses affecting the thick elastic layer (the stone), simply by using Equation (
5). The risk of delamination by adhesion failure is not covered in this analysis, and even though there is no indication from field experience to suggest that it is a problem, it is a question that will be further investigated in future work. Of course, the stresses that might contribute to delamination or decohesion also relax at about the same rate as the in-plane stresses that we examine.
Among the hypotheses involved, the bond-slip effect that can occur between the sandstone substrate and the mortar patch is ignored. Indeed, the roughness of the sandstone surface makes a mechanical interlocking of the patch with the stone likely. Furthermore, before the application of the patch, the sandstone is brushed with diluted resin to enhance the adhesion; these combined effects are assumed to prevent slippage. Another assumption concern the coefficients of thermal expansion that are taken to be constant in the range of temperature considered, as well as the elastic moduli and the Poisson’s ratio of both materials. Finally, the viscoelasticity of the thin layer is described by a stretched exponential function, that incorporates the temperature dependence of the relaxation time. The limitation of this function concerns the calculation of the stresses during a long period of time, for example when the input is a temperature evolution covering several months, and for which excessively long computation time is needed. A solution to this issue is to use a sum of exponential terms instead of a stretched exponential relaxation function, which, as described in
Appendix, is far more efficient.
3. Materials and Methods
3.1. Measuring the Thermal Expansion
The thermal expansion was measured on cubes of 1 cm using a Dynamic Mechanical Analyser DMA 7e from Perkin Elmer (Perkin Elmer (Schweiz), Schwerzenbach, Switzerland). The dynamic mode is not used in this experiment, which is thus equivalent to use the device as a thermo-mechanical analyser. The temperature range went from −20 to 60 °C with a heating rate of 0.5 under nitrogen flow. The force exerted by the displacement sensor was kept as low as possible, namely 10 mN thus 127 Pa.
3.2. Measuring the Tensile Strength of the Materials
The direct tensile strength tests were performed on a universal testing machine Zwick 1454 equipped with a 10 kN load cell (Zwick GmbH, Ulm, Germany) on six specimens of natural stone and five of artificial stone. The cylindrical samples had diameters of 20 mm and lengths of 50 mm in average. The natural stone was a Ostermundigen blue sandstone, widely spread in the historical buildings in Switzerland. The bedding has been chosen perpendicular to the strain.
The artificial stone was prepared with ground Ostermundigen blue mixed with 20% m of Plextol D512 (Synthomer Deutschland GmbH, Marl, Germany). Since the glass transition temperature of the polymer is around 20 °C, and consequently the relaxation of the stresses at room temperature is very fast, the samples were conditioned in a climatic chamber and wrapped in rockwool before the test to ensure an inner temperature lower than 15 °C, as measured by a thermocouple embedded in a sample. The strain rate adopted was 0.5 mm/min.
The tensile strength is the force at break divided by the cross-sectional area of the sample, in accordance with reference [
19].
3.3. Measuring the Elastic Modulus by Ultrasound Pulse Velocity
The instantaneous elastic modulus
represents the purely elastic mechanical property of the repair material. An approximative quantification is obtained by measuring the ultrasonic pulse velocity through a cubic sample with 5 cm edge using a Pundit Lab (Proceq SA, Schwerzenbach, Switzerland), equipped with transducers operating at a frequency of 54 kHz. The velocity is linked to the elastic modulus through the relation:
with
ρ the density and
v the velocity of the wave [
20];
K is determined from the dynamic Poisson’s ratio as following:
We take
, in accordance with reference [
21].
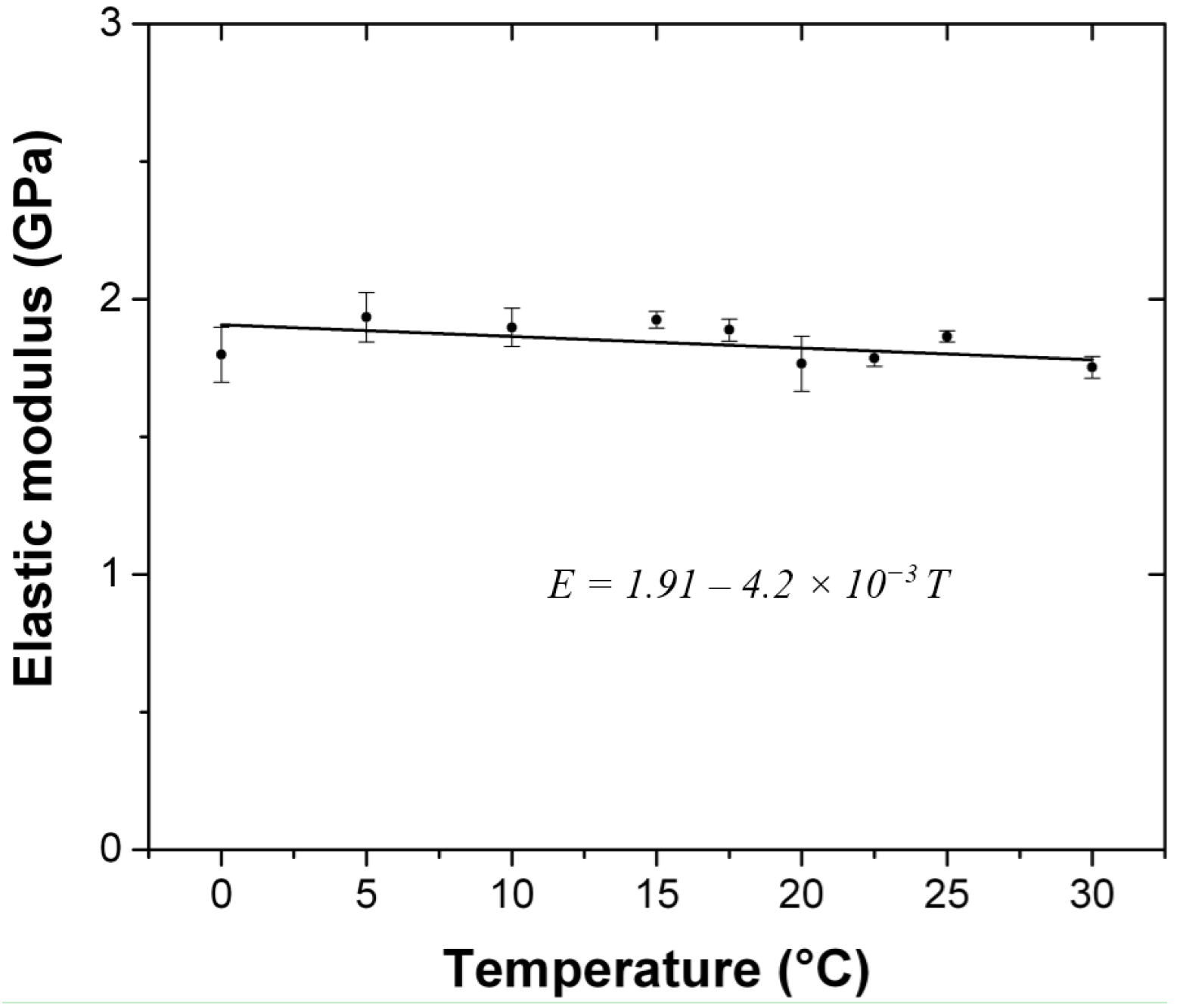
The evolution of the elastic modulus with the temperature has been studied between 0 and 30 °C, a range of temperature that encompasses the glass transition temperature of the acrylic polymer.
3.4. Measuring the Stress Relaxation
The viscoelasticity of the artificial stone is studied through the measurement of the relaxation of a load at a constant strain.
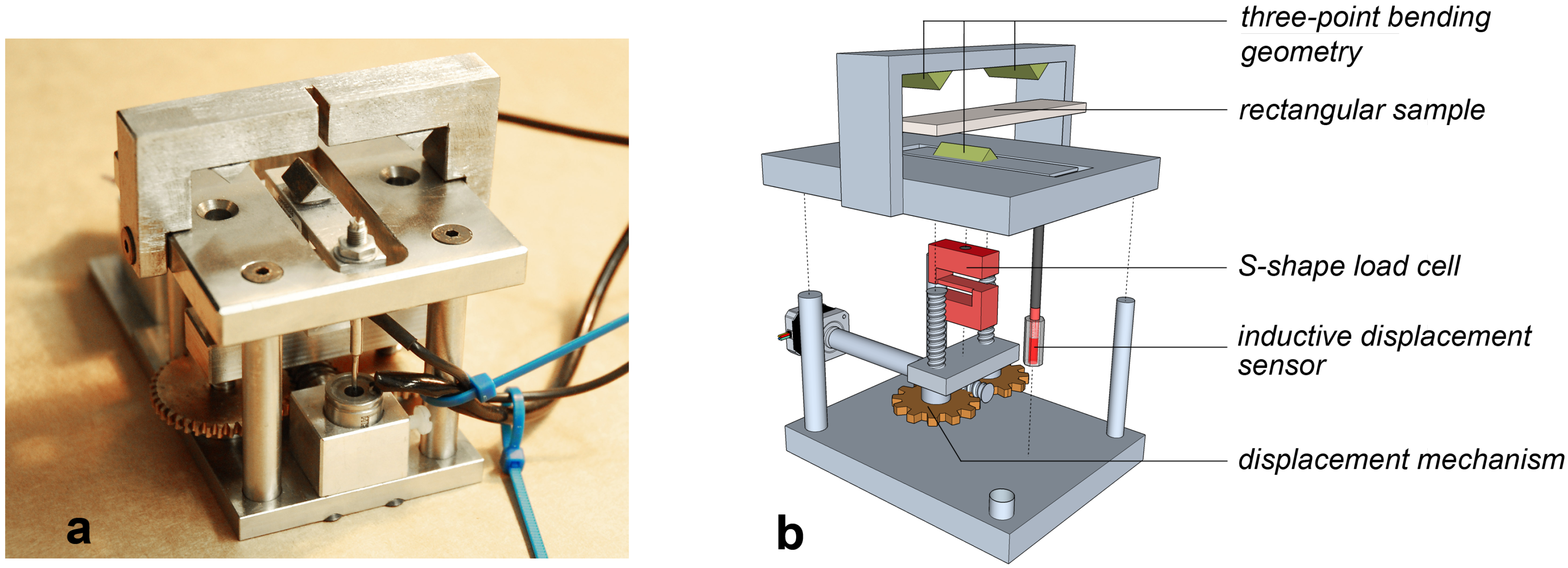
The relaxation tests are three-point bending tests performed with a home-made device consisting of a mechanical-loading stage and a computer-assisted control unit. The device is shown in
Figure 3, and a thorough description is given by Wei [
22]. The mechanical-loading stage is composed of a PRECIstep two-phase stepper motor mounted with a zero-backlash spur gearhead (1/900 ratio) (Faulhaber Precistep SA, La Chaux de Fonds, Switzerland), a Transmetra KD24S 100 N load cell (accuracy of ± 0.1%, Transmetra GmbH, Flurlingen, Switzerland), a HBM linear-variable displacement transducer W1EL/0 (accuracy of ± 2
, Hottinger Baldwin Messtechnik AG, Volketswil, Switzerland) and a high-precision micro-transmission system used to integrate these components. A program coded in Labview controls the rotation of the motor, displays and saves the force and displacement data.
The specimens are in the form of rectangular beams with thickness of 4 mm, width of 12 mm and length of 50 mm, while the length of the support span is 48 mm, allowing an aspect ratio of 1:3:12. The strain rate adopted was 0.045 mm/min.
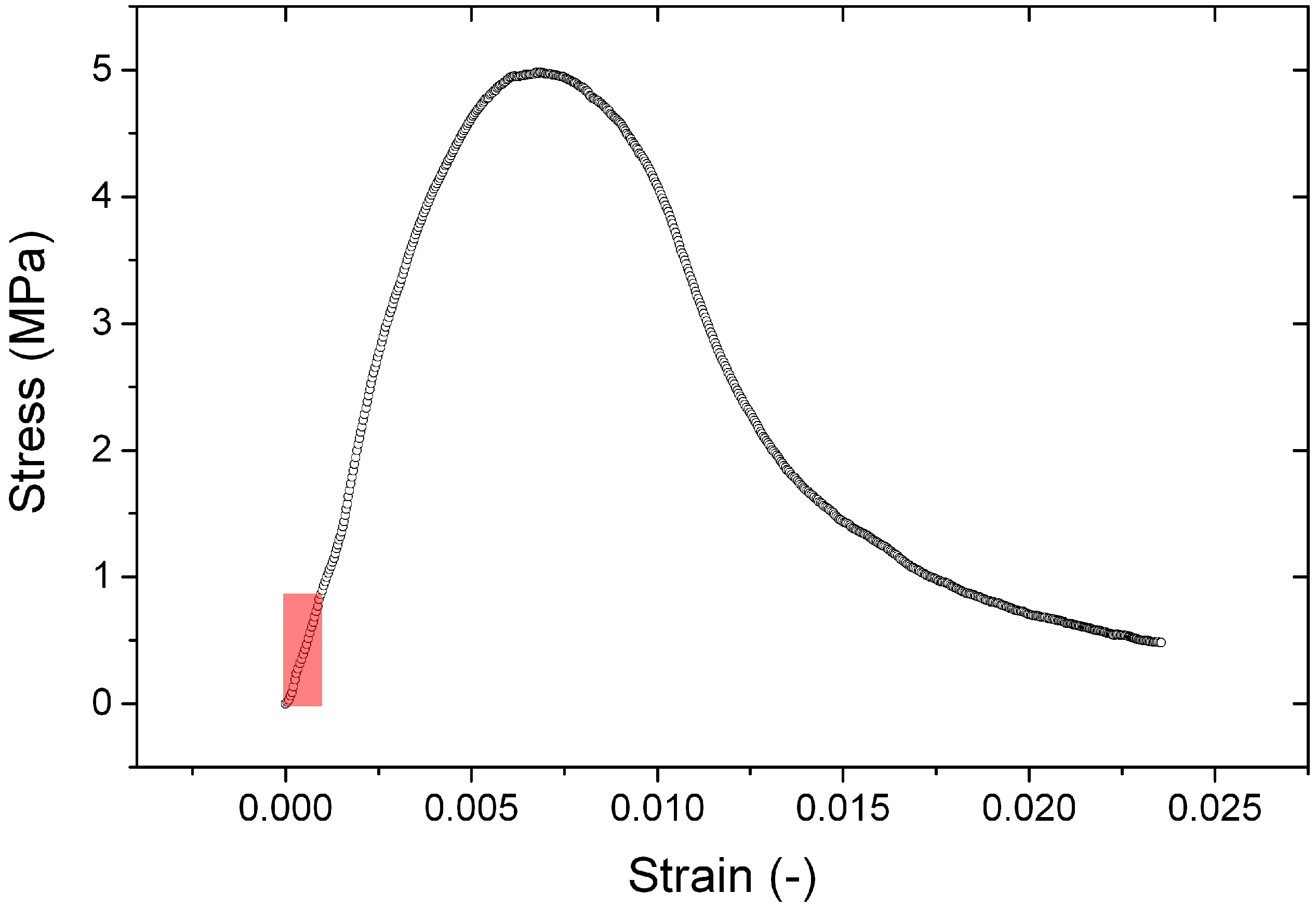
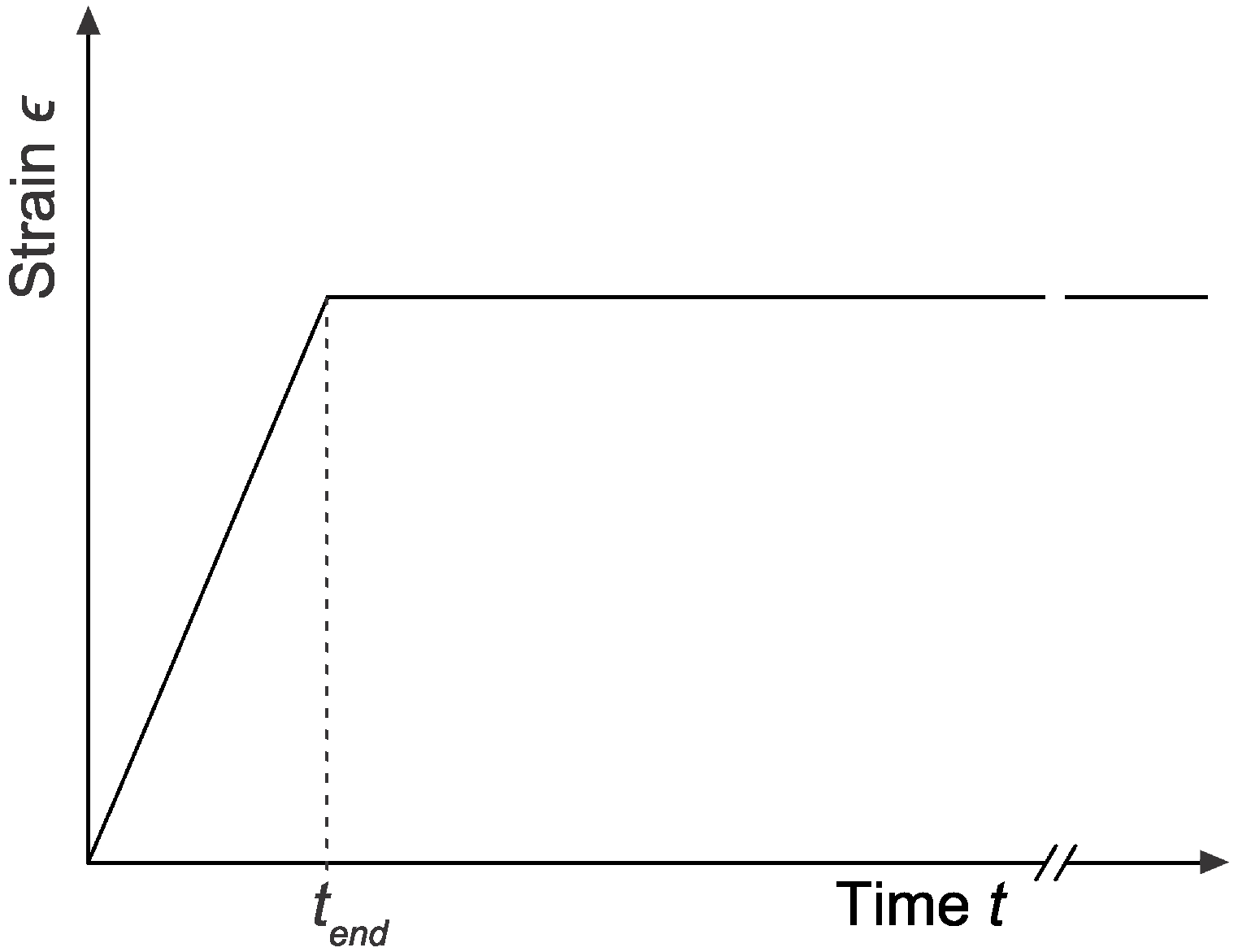
The stress relaxation is studied by loading the sample far from its load at break as illustrated in
Figure 4.
Figure 3.
(a) Stress relaxation setup; (b) and its detailed diagram.
Figure 3.
(a) Stress relaxation setup; (b) and its detailed diagram.
Figure 4.
Typical stress-strain curve of the artificial stone. Note the high critical deformation. The red rectangle indicates the area of stress and strain investigated during the relaxation tests.
Figure 4.
Typical stress-strain curve of the artificial stone. Note the high critical deformation. The red rectangle indicates the area of stress and strain investigated during the relaxation tests.
The dependence of the relaxation on temperature is studied by repeating the measurement in a climatic chamber at temperatures from −5 to 25 °C. Higher temperatures, even though often reached during summer at the surface of the building, are not relevant because they are higher than the glass transition temperature of the polymer (≈ 20 °C), where the relaxation is quasi-instantaneous.
The relative humidity in the climatic chamber has been kept below 65 %, since it has been noted that the relaxation time is strongly affected by the relative humidity; measuring the relaxation below 65 % RH ensures the relaxation to be the slowest, and thus put us in the worst case.
Table 1.
Temperatures investigated and number of runs performed.
Table 1.
Temperatures investigated and number of runs performed.
| Temperatures Investigated (°C) | −5 | −2.5 | 0 | 5 | 10 | 15 | 17.5 | 19 | 20 | 25 |
|---|
| Number of Runs | 1 | 1 | 2 | 3 | 2 | 2 | 2 | 1 | 2 | 1 |
3.5. Measuring the Temperature On-Site
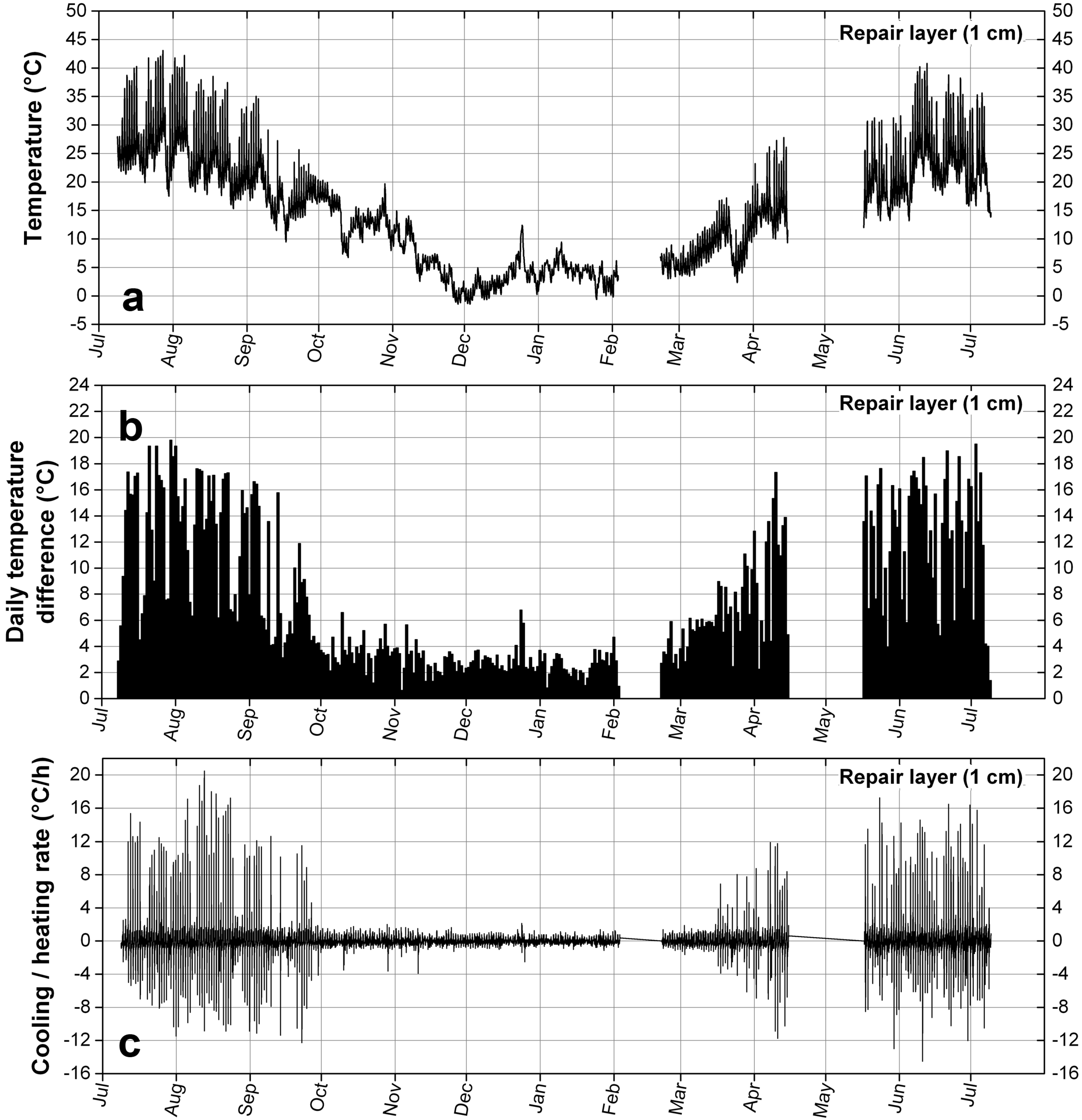
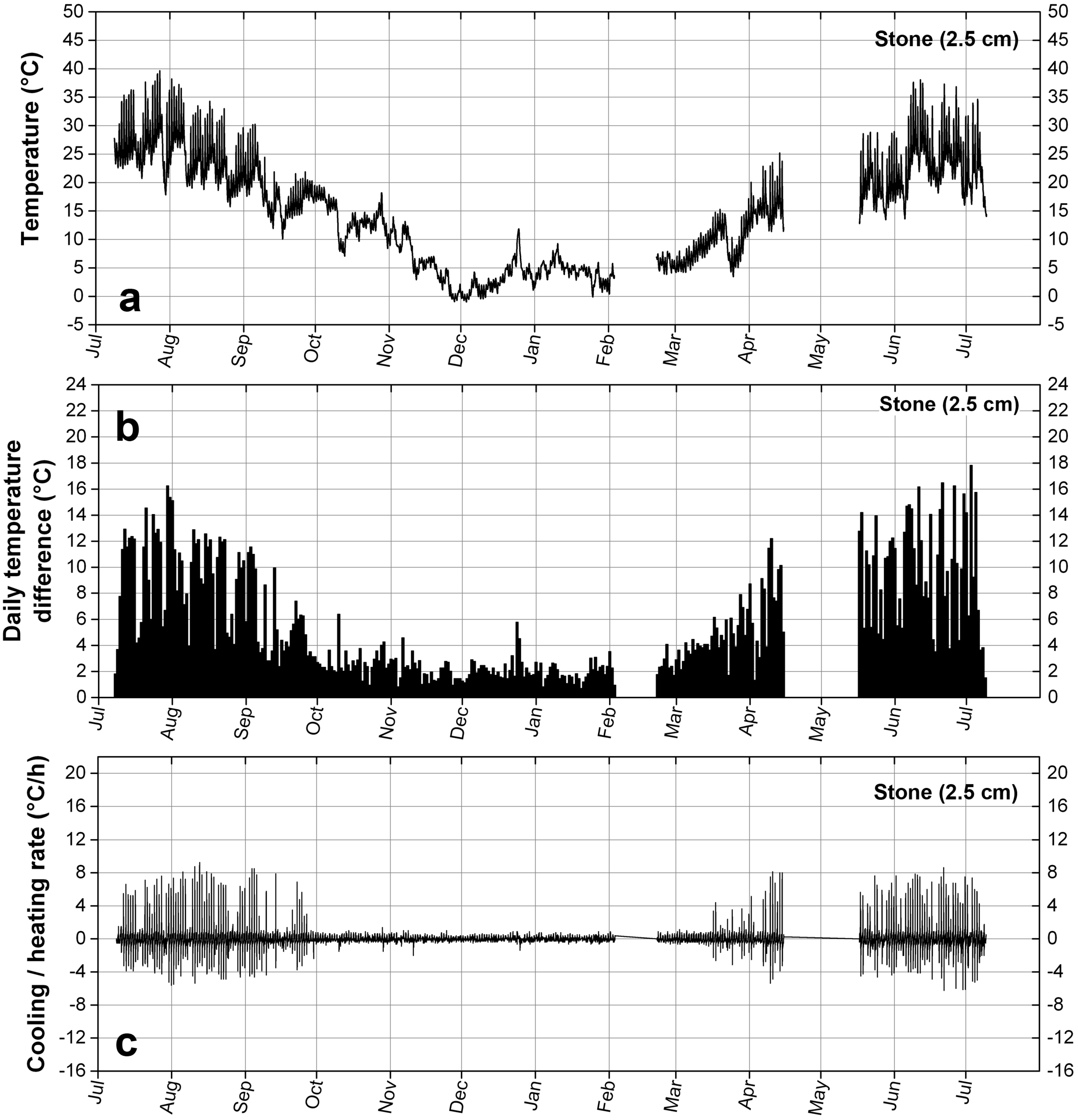
On the monument considered in this study (Catholic Church of Notre Dame de Vevey, Vevey, Switzerland), the temperature was recorded at different depths in a stone that had been repaired with the acrylic-based mortar, from July 2013 to July 2014. It was measured by capacitive Hygrochron loggers (Maxim Integrated, San Jose, CA, USA), put together in a cylindrical shape and separated by expanded Polyvinyl Chloride, a material with a low thermal conductivity (0.06 W/m.K, against 2.30 W/m.K for the molasse). The cylinder is protected by a shrink-fit tube and placed in a hole drilled in the artificial stone and the natural stone it covers. A view of the church and of the equipment installed on site is given in
Figure 5. More information about the setup can be found in references [
23,
24].
The sensors function through the 1-Wire protocol, which permits as many wires as sensors plus one for the ground, hence keeping as low as possible the physical impact of any sensor on the measurement, as the quality could be reduced by water infiltration or thermal heating of the wires. Moreover, each sensor being autonomous, the need for a central acquisition system is avoided, thus reducing the invasive nature of the installation. The sensors measure the temperature in a range of −20 to 85 °C with a resolution of 0.06 °C and an accuracy of 0.5 °C between −10 and 65 °C, that extends beyond the conditions observed during the campaign. The sampling interval was 30 min.
The best location to position the sensors was determined by its potential of receving sun on a repair. This was identified on the buttress of an apse, approximately six meters above the ground. The selected location is facing west and receives the warm sun of the afternoon during summer, causing large temperature variations interesting for our purpose.
Figure 5.
The church where the sensors have been applied in Vevey, and a close view of the equipment.
Figure 5.
The church where the sensors have been applied in Vevey, and a close view of the equipment.
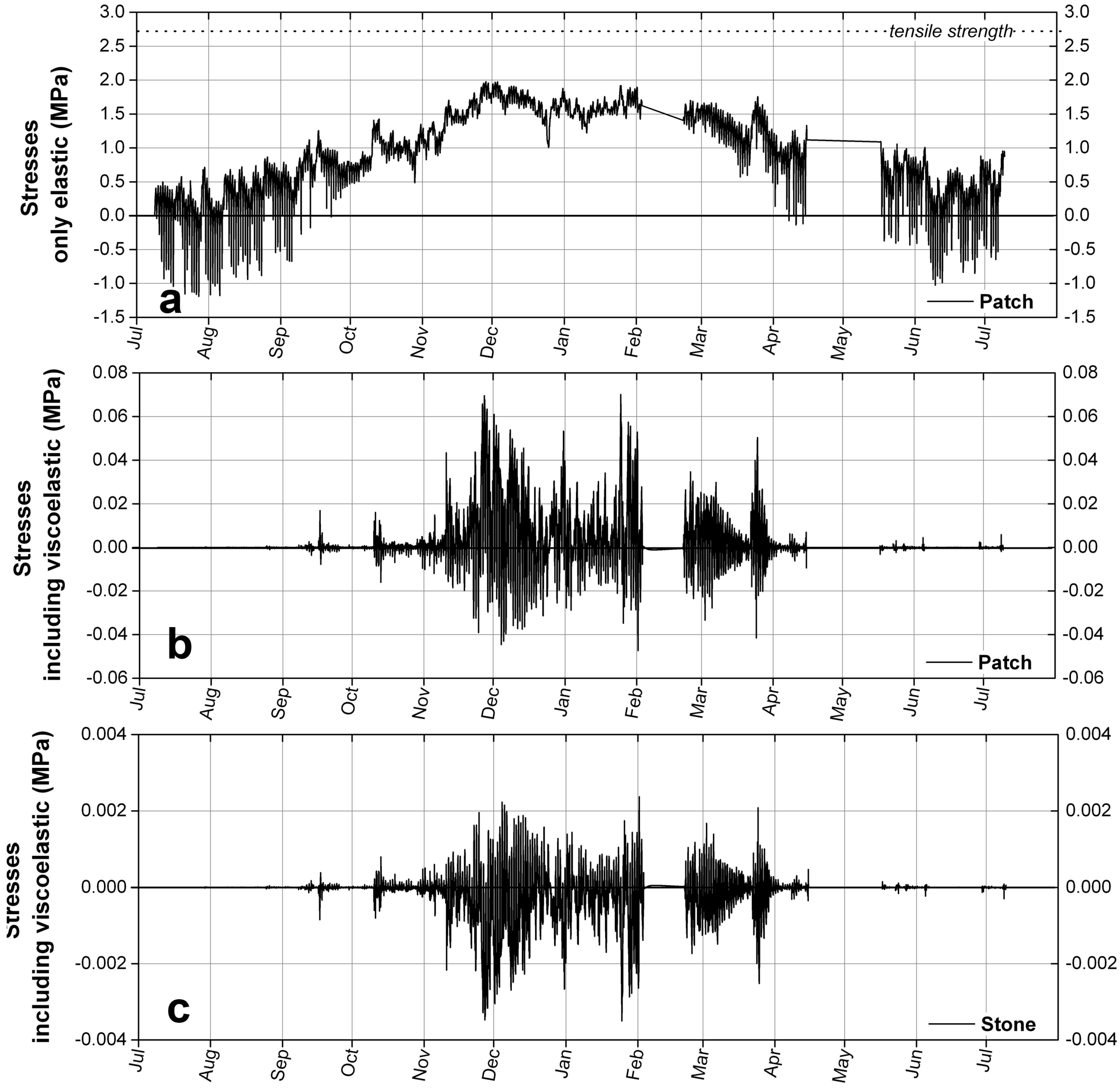
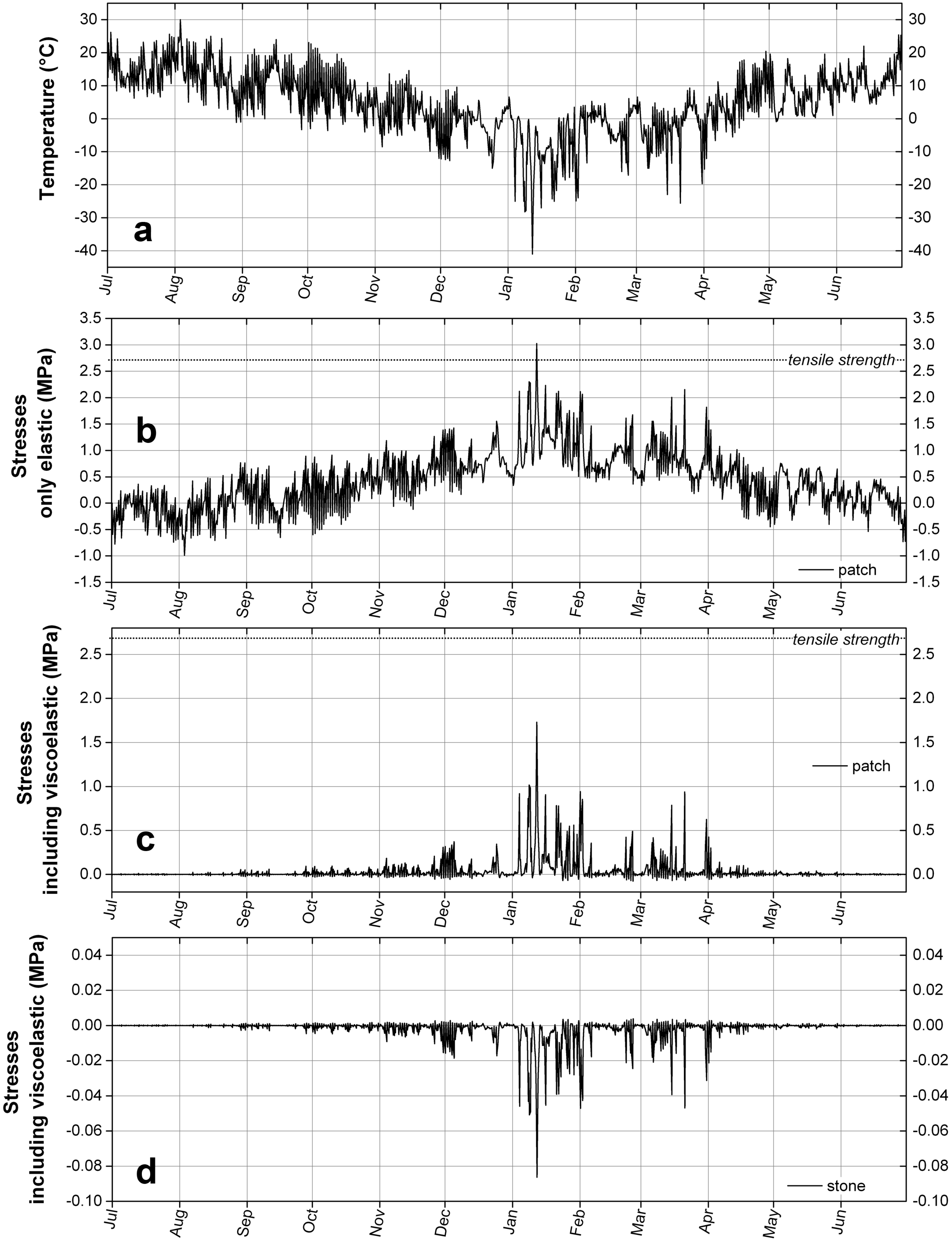
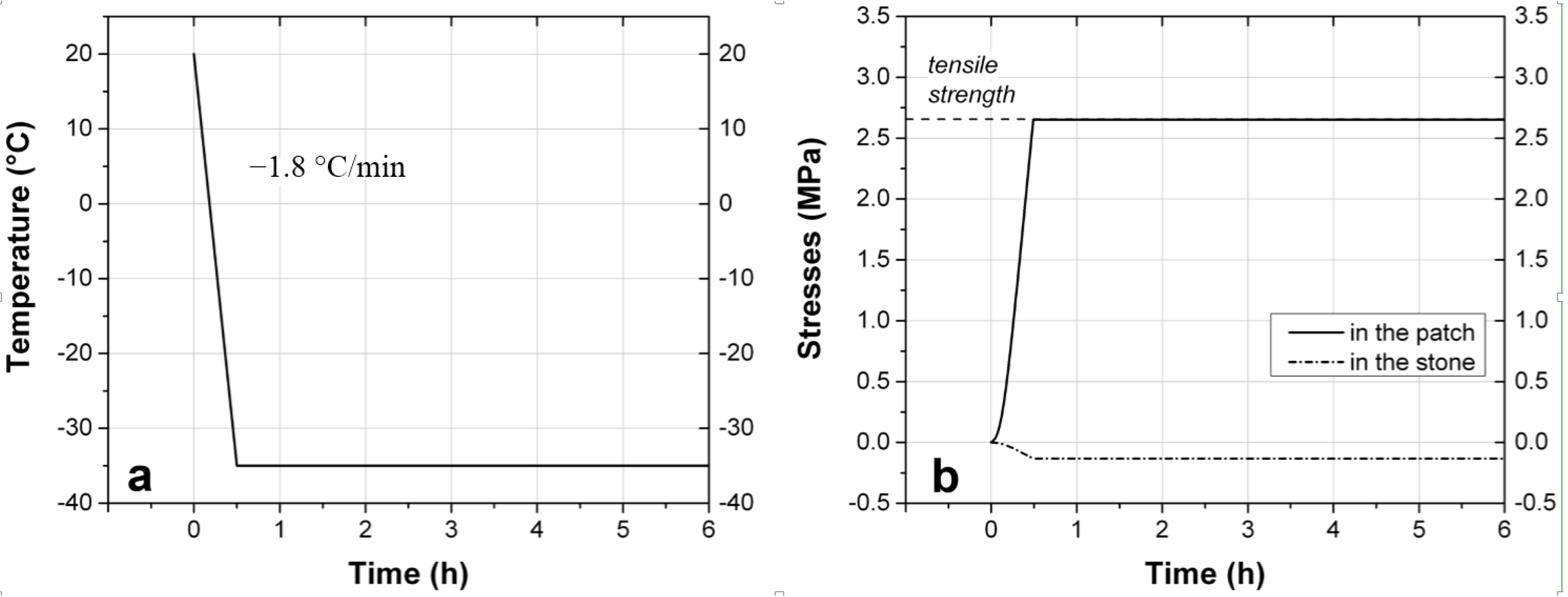
6. Conclusions
We have examined the question of thermo-mechanical compatibility of an acrylic-based repair mortar and a sandstone, in case of a typical reprofiling, that is a thick stone substrate which imposes its deformation on a thin layer of repair material. The repair mortar is characterized by a low strength and elastic modulus, as well as a high viscoelastic relaxation. Such properties make it adequate for patches, but the creep characteristics associated with viscoelasticity do not make it suitable for any structural application. Given the large thermal expansion coefficient mismatch between the acrylic-based mortar and the sandstone it aims to repair, the question of the magnitude of the thermal stresses that could be induced in the two materials is legitimate. Indeed, a calculation that would treat the repair mortar as a purely elastic material would deliver a result of stress higher than the tensile strength of the repair material. However, since the acrylic-based mortar displays viscoelastic properties associated with a relatively low (20 °C), the relaxation processes specific to this type of material have to be considered. The amplitude of the temperature variations, the value of the coldest temperature reached and the rate at which the temperature variations occur all play a role in the magnitude of the thermal stresses. Even by considering the worst case-scenario, the analysis shows that the thermal stresses are not high enough to harm the repair material, and more importantly, are insignificant for the integrity of the historical substrate. The key role of the glass transition temperature has to be stressed: choosing an acrylic polymer with a in the range of temperatures found on-site allows to benefit from an interesting property of the polymer from a conservation point of view, namely its reversibility, without having to suffer from one of its drawback, a high thermal expansion coefficient.
With respect to the ultimate durability of such patches other issues also have to be considered, for example water migration and salt crystallization might be modified around the hydrophobic patch.