Study on the Carbonation Behavior of Cement Mortar by Electrochemical Impedance Spectroscopy
Abstract
: A new electrochemical model has been carefully established to explain the carbonation behavior of cement mortar, and the model has been validated by the experimental results. In fact, it is shown by this study that the electrochemical impedance behavior of mortars varies in the process of carbonation. With the cement/sand ratio reduced, the carbonation rate reveals more remarkable. The carbonation process can be quantitatively accessed by a parameter, which can be obtained by means of the electrochemical impedance spectroscopy (EIS)-based electrochemical model. It has been found that the parameter is a function of carbonation depth and of carbonation time. Thereby, prediction of carbonation depth can be achieved.1. Introduction
Mortar has always found wide application in the construction industry, which plays a bonding, padding and protective role in concrete structures. Due to its high strength, low cost and convenient fabrication, mortars have been used as isolating lining materials in cisterns, wells, aqueducts, shafts and duct drains, as well as supporting materials for pavement sand mosaics, plasters on external and internal walls, supporting materials for frescoes, and as joint mortars of masonry structures [1]. The properties of mortar exert a great influence in concrete structure as mortar occupies a large amount of volume inside concrete. Much has been published in the literature: mortars are often affected by environmental degradation [2], causing a severe reduction of the durability of the reinforced concrete or masonry structure. Among all the aggressive elements (e.g., ions attack, freeze thawing), carbonation is the most common as well as the most harmful. In this sense, investigation of carbonation properties of mortars is of great value to durability design of concrete structure. Carbonation is actually a neutralization reaction. Reacting with the CO2 dissolved in the pore water, the highly alkaline components in concrete like Ca(OH)2, hydrated calcium silicate (C-S-H), etc. can be transformed into calcite crystals CaCO3 [3–9]. On the one hand, carbonation causes the reduction of pH value in the concrete pore solution, which leads to destroy the passivation oxide layer on the surface of the steel reinforcement [10–15]. On the other hand, contraction of concrete is very likely to be aggravated, giving rise to more cracks in concrete [16,17]. Therefore, carbonation has a considerable impact on durability of concrete structure [18–22].
One of the traditional ways of determining carbonation depth is to spray phenolphthalein indicator onto the surface of a split concrete prism [23]. Although the method retains its popularity nowadays, there are obvious disadvantages to this method. The biggest one is that the test must take samples out of the concrete structure, which indicates a destructive test. In addition, not easily detecting the pH value in a partially carbonated zone and vision illusion caused by darkly colored aggregate are also challenges [23]. Another negative side to be mentioned is that accuracy of measurement relies on the skill and experience of the person who performs the test.
As a sort of nondestructive testing, the electrochemical impedance spectroscopy (EIS) method is able to reflect the micro-structural changes in the cementitious materials under variously natural exposure environments, which has been viewed as a promising way to study the physical and chemical properties of cementitious materials [24–30].
The objective of this paper is firstly to obtain the electrochemical impedance data of the carbonated mortar then, to apply the electrochemical model to describe the carbonation behavior of mortar. Finally, obtaining the functional relationship between the fitted parameter of the model and the carbonation time, the prediction of carbonation depth is thought to be achieved.
2. Experimental Section
Cement: P.O 52.5 Portland cement, a product of the Starfish Onoda cement limited company of Shenzhen.
Water: normal tap water.
Sand: The standard sand derived from Xiamen ISO Stand Sand Company, China.
Mortar specimens with dimensions of 160 mm (length) × 40 mm (height) × 40 mm (thickness) were prepared with a cement/sand ratio of 1:2, 1:3 and 1:4 at the room temperature 20 °C as well as 95% of relative humidity. All specimens were water-cured for 28 days.
Before exposing the mortars to accelerating carbonation, they were sealed with wax, with both ends of the specimens left open to carbonation (see Figure 1a). The carbonation is carried out in a carbonation accelerating chamber filled with 20% commercial CO2 concentration. Regarding temperature and humidity, the carbonation test is set as 29–31 °C and 65%–70%, respectively.
EIS measurement was carried out by Princeton Applied Research Co. (PAR, Oak Ridge, TN, USA) Potentiostat/Galvanostat 283 with a frequency range of 0.01 Hz–1 MHz. The test was performed at 0, 3, 7, 14, 28, 36, 60 days, respectively. The mold for electrochemical impedance measurement is shown in Figure 1b.
The carbonation depth was measured according to Chinese Standard (GBJ820-85) “Standard for test methods of long-term performance and durability of ordinary concrete” [31]. To start with, the test specimens were taken out of the carbonation chamber at given carbonation ages of 0, 3, 7, 14, 28, 36, 60, 90 and 120 days, and then split into two blocks with transverse exposed fresh surfaces. The next step was to cleaning and spraying the fresh surface with the phenolphthalein pH indicator (1% ethanol solution with 1g phenolphthalein and 90 mL 95.0% (V/V) ethanol diluted in water to 100 mL solution). In order to alleviate the experimental error, the carbonation depth was measured at 7 different points along the carbonation front. Measuring to nearest 0.1 mm with a digital caliper, the average depth value was calculated as the final experimental result.
3. Results and Discussion
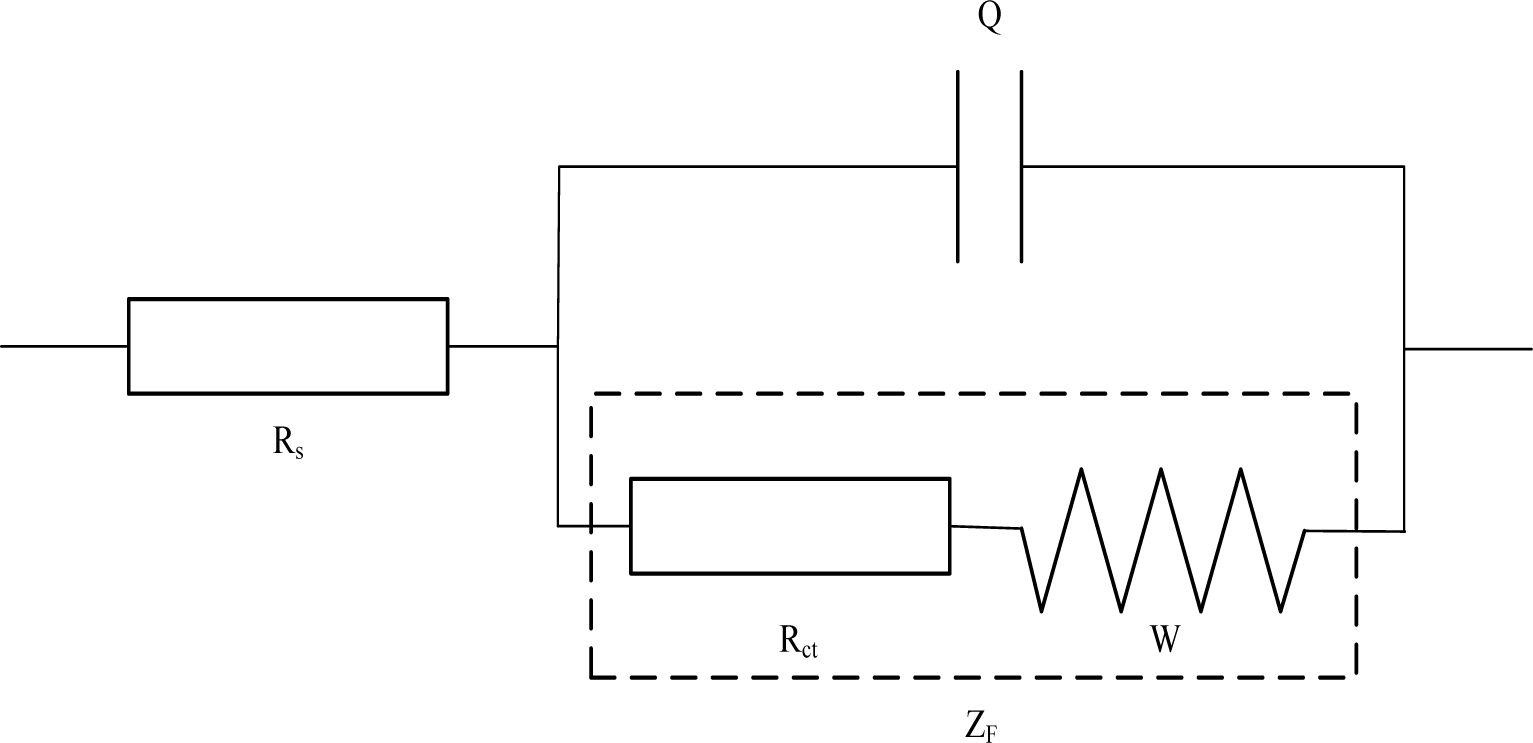
Generally, a simple electrochemical system can be simulated as a typical equivalent circuit shown in Figure 2, which can be described as Rs(Q(RctW)) by CDC (circuit description code).Where, Rs is the solution resistance, Q corresponds to the double-layer capacitance of the electrodes/electrolyte interface [32]. It should be emphasized that the value of Q is associated with CPE (constant phase element), which is generally attributed to distributed surface reactivity, surface inhomogeneity, roughness or fractal geometry, electrode porosity, and also to the current and potential distributions associated with electrode geometry. ZF stands for the impedance of the Faraday’s procedure that occurs on the surface of the electrodes. Faraday’s procedure includes charge transfer procedure and charge diffusion procedure. As a result, Faraday impedance is represented by a serious connection of Rct and W, in which Rct stands for charge transfer resistance of the electrodes/electrolyte interface and W stands for Warburg resistance that caused by charge diffusion procedure.
As far as Rs(Q(RctW))’s concerned, electrolyte in this electrochemical system is regarded as a relatively stable component, only considering the electrochemical resistance (Rct). In this sense, other reactions are overlooked except the electrode reaction. However, the microstructure of cement-based materials is very complex [33], which includes air voids, capillary pores and gel pores [34]. These pores, always filled with solution, can be viewed as the spaces among solid phase like C-S-H gel and sand. The interfaces between the C-S-H gel and pore solution can have a great influence on the electrochemical behavior of cement-based materials [35]. Thereby, when it comes to study the electrochemical impedance of mortar materials, not only the reaction on the surface of the electrodes, but also the interaction between solid cement and liquid solution (solid/liquid double-phase) needs to be considered.
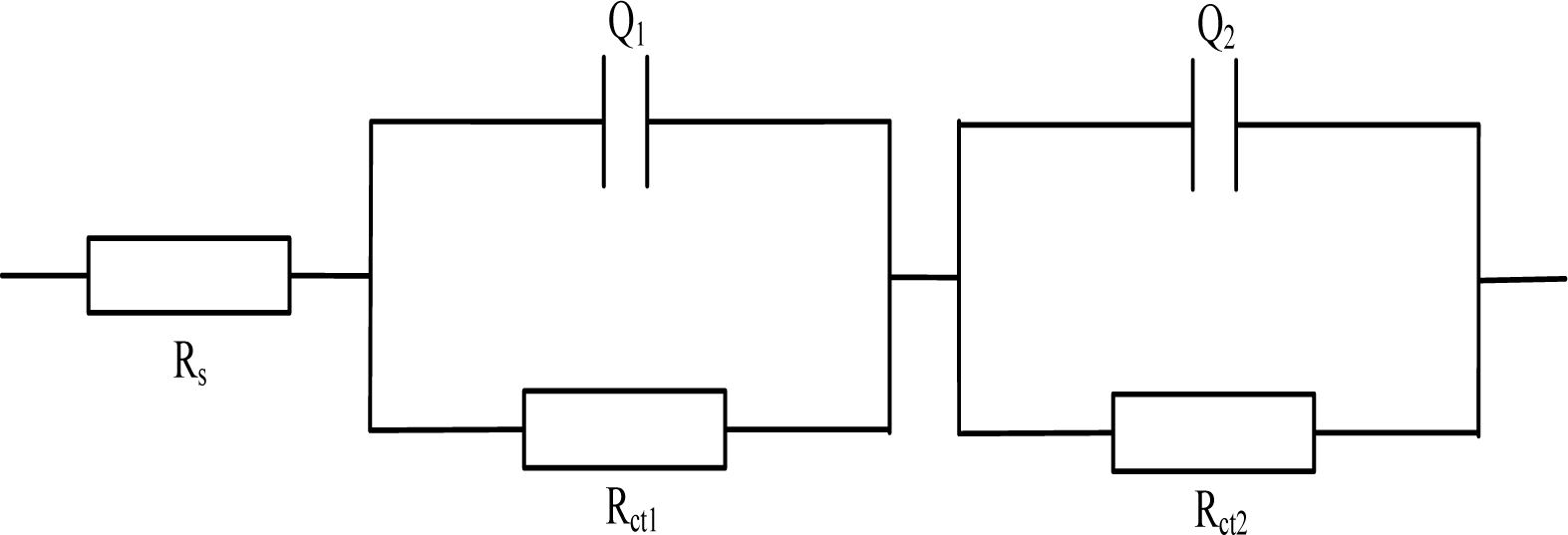
In view of the mechanism, Gu Ping, et al. [36] put forward an electrical equivalent circuit model to study the impedance behavior of cement mortar, with roots in “solid-liquid interfaces” conceived. In view of the effect of the charge transfer and the outside testing electrode, the whole Rs(Q1Rct1)(Q2Rct2) system (shown in Figure 3) was formed, where Rs represents the resistance of the electrolyte solution, Q1 corresponds to the double layer capacitance between the solid/liquid phases, Rct1 stands for the resistance caused by ion transfer procedure inside the cement mortar sample, Q2 stands for the double layer capacitance between cement mortar and electrodes; Rct2 stands for the resistance caused by the charge transfer procedure on the surface of the electrodes.
The electrochemical model Rs(Q1Rct1)(Q2Rct2) effectively characterizes the electrochemical impedance spectroscopy when the cement mortars are in dry condition. For dry specimens, as the pore solution in the materials is rather little and the ions scarcely diffuse on a large scale. It is therefore to say that the charge diffusion procedure impedance (Warburg impedance) is insignificant to mention in this case. However, as to the moist mortars (especially the ones that used in the neighborhood of seaside), the interior amount of solution is apparently higher, the Warburg impedance is supposed to be considered.
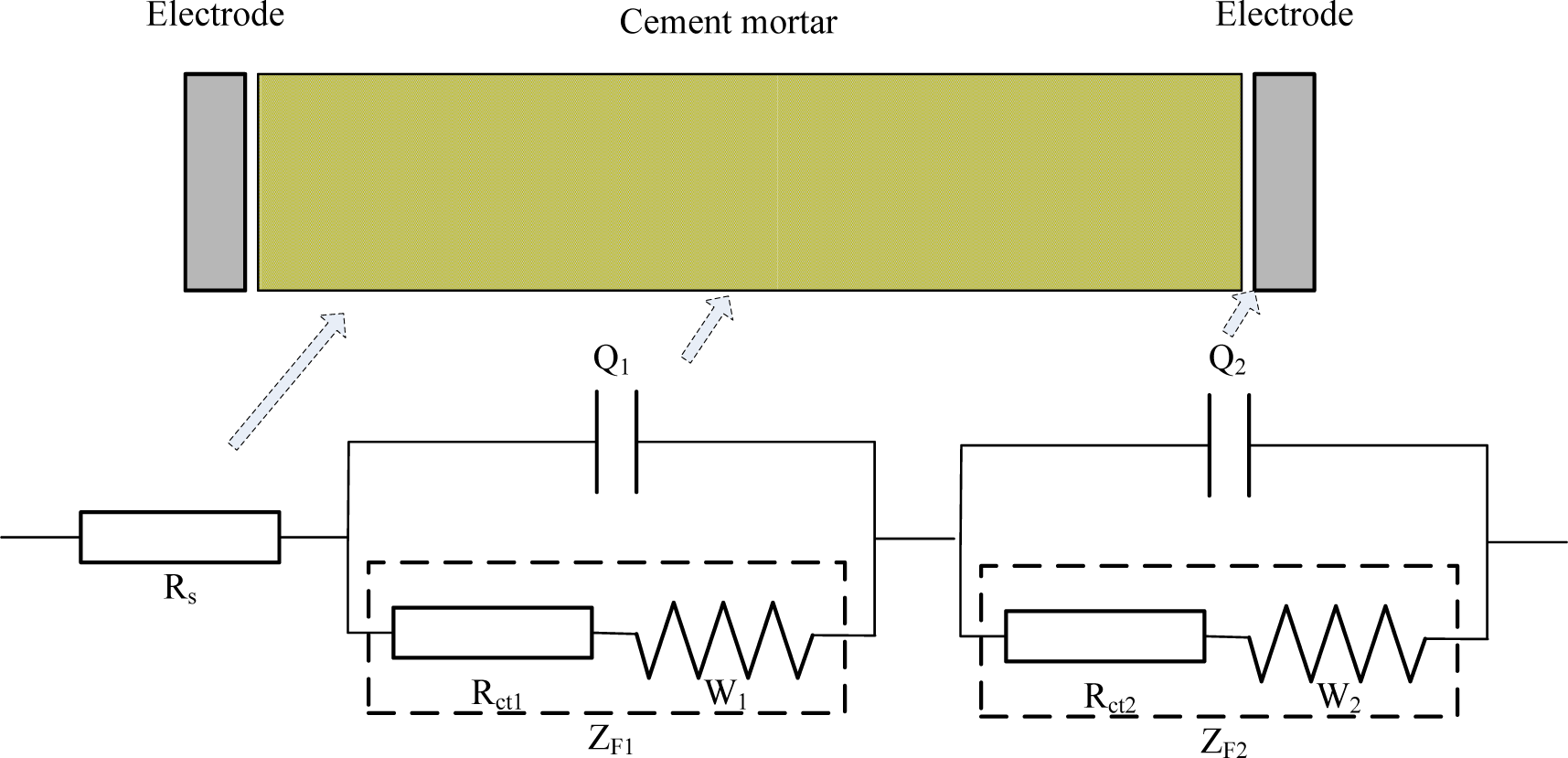
After consideration of the fact that ions in mortar would transfer on a large scale, a novel electrical circuit model is proposed for investigation of mortar’s carbonation (illustrated in Figure 4).
Where, Rs stands for the resistance of pore solution in mortar; Q1 stands for the double layer capacitance between the solid/liquid phases; Rct1 stands for the resistance caused by ions transfer procedure inside the mortar; W1 stands for Warburg resistance caused by ions diffusion procedure inside the mortar; Q2 stands for the double layer capacitance between mortar and electrodes; Rct2 stands for the resistance caused by the charge transfer procedure on the surface of the electrodes; W2 stands for Warburg resistance caused by the ion diffusion procedure on the surface of the electrodes. The CDC (Circuit Description Code) for this new equivalent circuit can then be described as Rs(Q1(Rct1W1))(Q2(Rct2W2)), in which Rct1 + W1 = ZF1, standing for the Faraday impedance caused by the Faraday’s procedure inside the mortar; while Rct2 + W2 = ZF2, standing for the Faraday impedance caused by the Faraday’s procedure between the mortar and electrodes.
As concerning the mentioned-above equivalent electrical circuit model, the total impedance can be stated by the mathematical equation as below:
The real part of Z is:
And imaginary part of Z is:
where, σ1: the conductivity of cement mortar; σ2: the conductivity of electrodes; .
(1) When (Very high frequency), that is,
then
Based on Equations (6) and (7), the following equation can be derived:
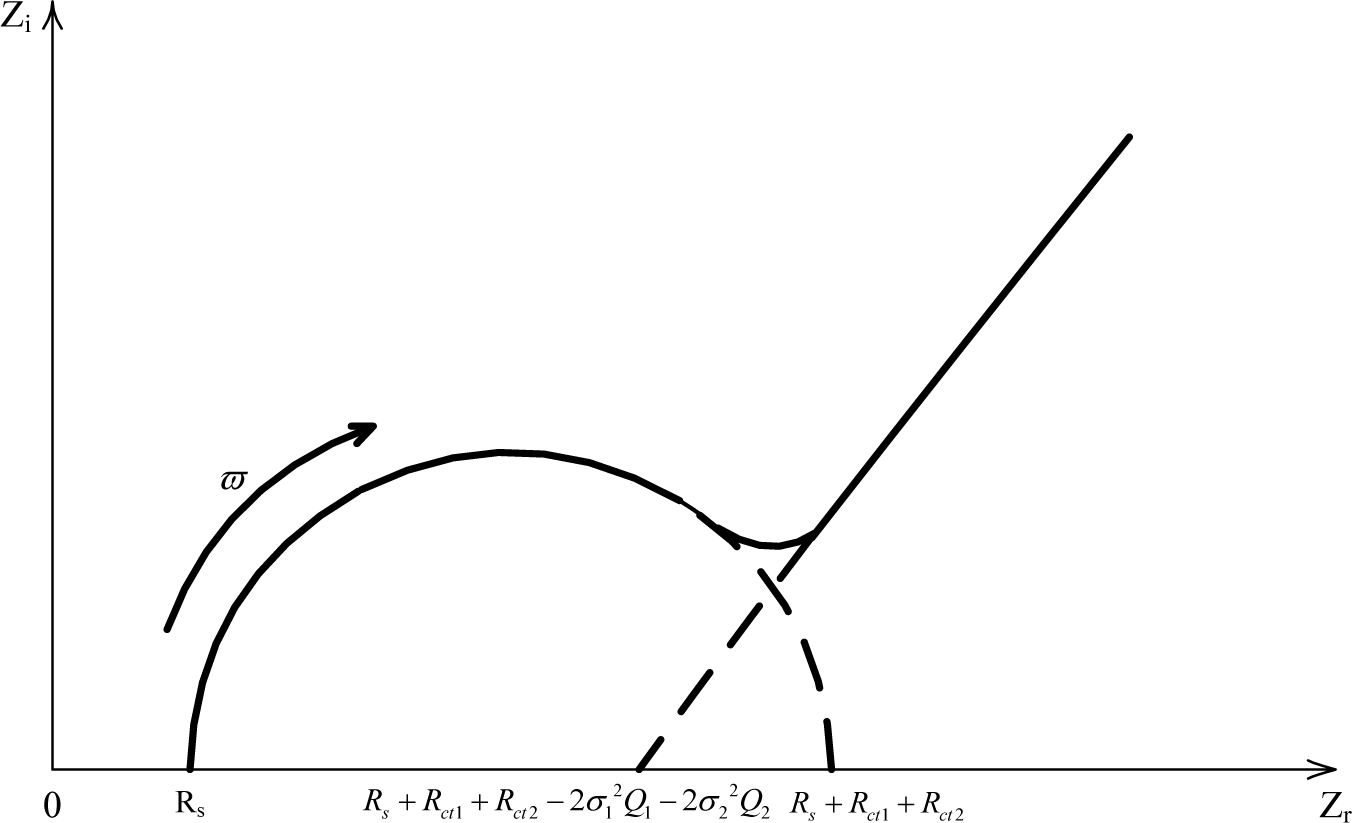
It is an equation standing for a half circle in the first quadrant.
When ω → 0 (Very low frequency);
Based on Equations (9) and (10), the following equation can be derived:
This is a linear equation.
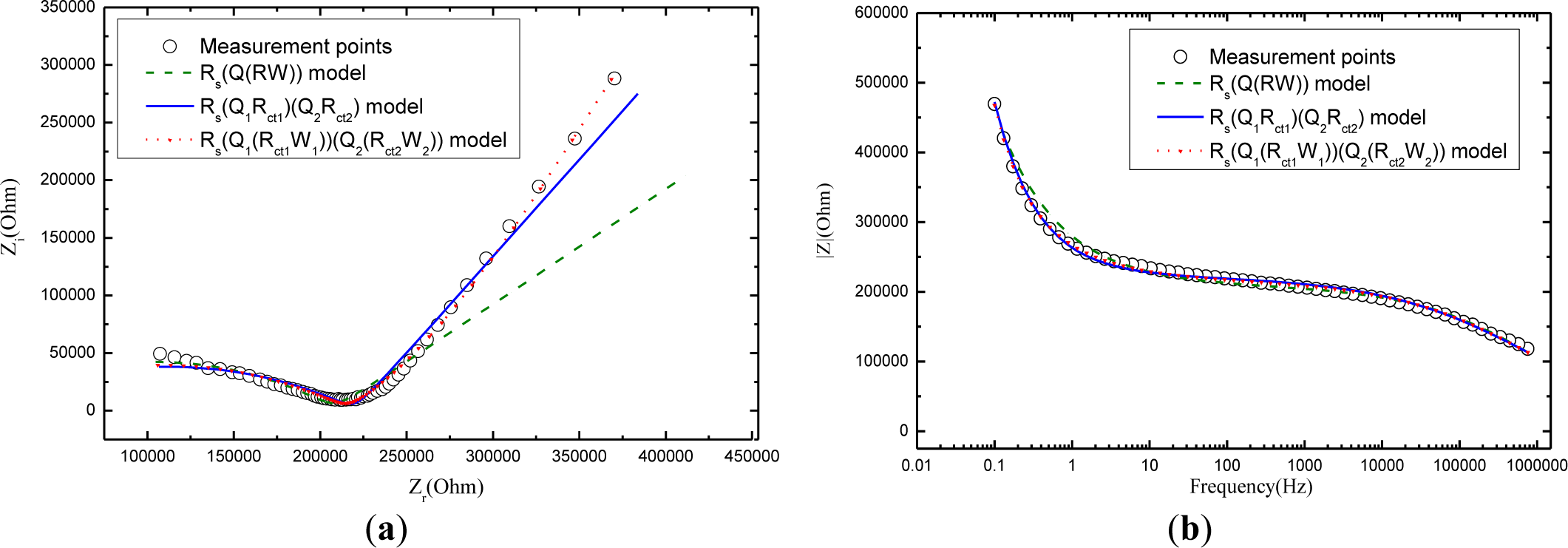
Based on the derivation in Equations (8) and (11), a typical Nyquist curve of the electrochemical impedance spectroscopy for carbonation procedure in mortar can be drawn as Figure 5.
Figure 6 compares the fitting results of electrochemical impedance measurement among the Randles model Rs(Q(RctW)), the model Rs(Q1Rct1)(Q2Rct2), and the model Rs(Q1(Rct1W1))(Q2(Rct2W2)) in the Nyquist figure. It can see clearly that model Rs(Q1(Rct1W1))(Q2(Rct2W2)) that considers the charge diffusion procedure impedance (Warburg) in mortar performs the best fit for the impedance spectroscopy data while the Randles model Rs(Q(RctW)) shows a poor fit, demonstrating that the traditional model Rs(Q(RctW)) is not probable to study the carbonation mechanism of mortar. Although the more comprehensive model Rs(Q1Rct1)(Q2Rct2) makes a good figure, it is inferior to the model Rs(Q1(Rct1W1))(Q2(Rct2W2)). The phenomenon is not hard to explain: The samples in the whole experimental work are wettish (cured for 28 days in water and then kept in carbonation chamber of 95% relative humidity). As noted above, Warburg impedance is supposed to be taken into account for those of mortars in wet state. But model Rs(Q1Rct1)(Q2Rct2)leaves out the Warburg impedance of the mortar. If the mortar turn dry, the most comprehensive model Rs(Q1(Rct1W1))(Q2(Rct2W2)) will convert to electrical equivalent circuit of Rs(Q1Rct1)(Q2Rct2) as the “W1” and “W2” are cleared away.
In the light of the fitting results above, conclusion can naturally be drawn that the new model Rs(Q1(Rct1W1))(Q2(Rct2W2)) proposed in this paper is able to explore the properties of carbonation of mortar.
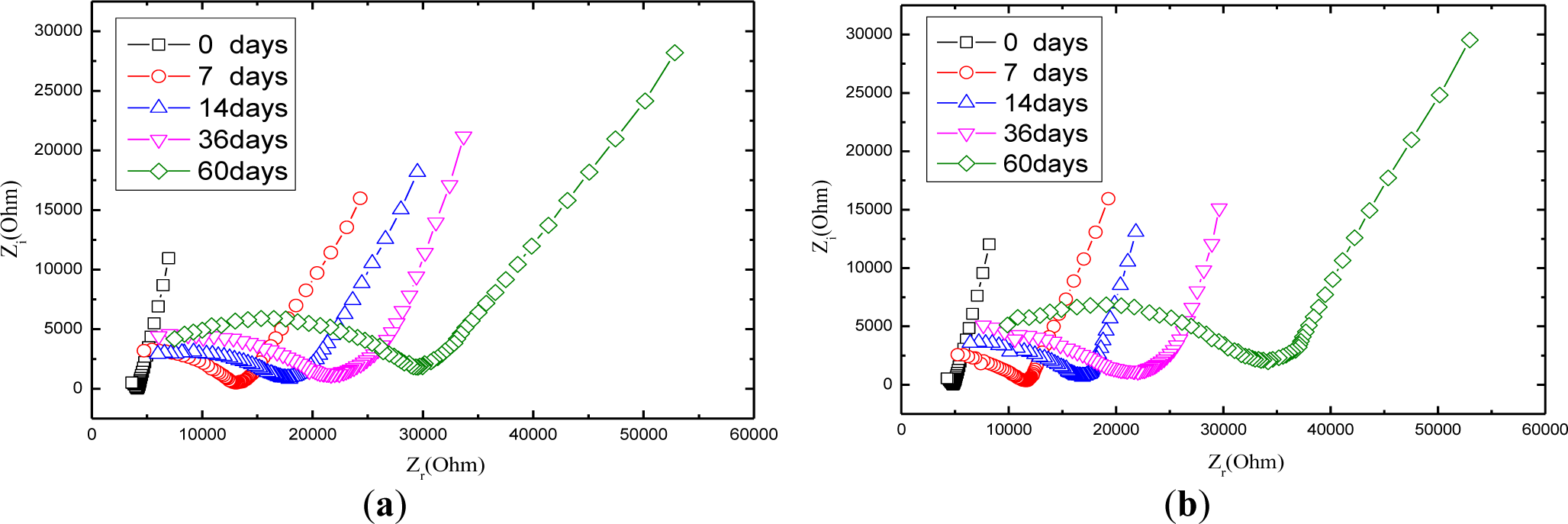
Figure 7 shows the Nyquist curve of mortars with carbonation time. It is obvious that the radius of the half circle of Nyquist curve increases while the carbonation time extends, which is attributed partially to that CO2 dissolved in the electrolyte solution reacts with OH− ions generated by the hydration of the cement so that the concentration of OH− ions tends to decline. Among all the ions in the cement-based materials, OH− ion is thought of as the most conductive [37]. In the light of what has been mentioned above, carbonation can lead to increase the resistance of charge transfer. Another factor that contributes to increase the Nyquist arc is that calcium carbonate has a very low solubility and precipitates inside the concrete pores, reducing the porosity and increasing the density of mortar [38,39], which consequently tends to rises the resistance of the ions transfer process.
With the purpose to investigate the quantized links between the resistance caused by ion transfer procedure inside the mortar sample (Rct1) and carbonation depth, the fitting parameter Rct1 of Rs(Q1(Rct1W1))(Q2(Rct2W2)) model at different carbonation time is listed in Table 1. Through the results obtained, we notice that Rct1 is an increasingly linear proportion to the carbonation time. In order to explore the quantitatively functional correlation between Rct1 and carbonation depth, the test of the carbonation depth for the mortar is carried out with the same carbonation cycle. The results shown in Table 2 and Figure 8 claim that the link between the carbonation depth and carbonation time is in line with the square-root-t-law, that is:
where, D is the carbonation depth; k is the carbonation coefficient, determined by the material properties.
The experimental results are in perfect agreement with other researchers [40–45].
Given that Rct1 value is linear with time while carbonation depth (D) follows the square-root-t-law, strong relations exist between carbonation depth (D) and Rct1 value:
A comparison between the experimental values and the estimated values of the carbonation depth both at 90 days and 120 days is shown in Figure 9 as well as Table 3. In Table 3, a calculated result of carbonation depth (C/S = 1:2) is estimated to reach 3.56 mm, while the measured carbonation depth is 3.40 mm. The relative error (%) between the experimental result and the prediction is only 4.71%. As to mortar of cement/sand ratio = 1:3, the carbonation depth is predicted as 5.59 mm, while the measured value is 5.53 mm, which claims the error of 1.08%. The 120 d carbonation depth also shows a good prediction. It demonstrates that electrochemical impedance spectroscopy fitting parameter Rct1 based on Rs(Q1(Rct1W1))(Q2(Rct2W2)) model can be used to predict the cement carbonation depth in an acceptable manner.
4. Conclusions
Based on the test and the analytical results, the following conclusions could be drawn:
It is of theoretical and practical significance to characterize the carbonation behavior and to predict the carbonation depth of mortar by EIS measurement. This approach can overcome the inherent constraints of phenolphthalein solution test.
A novel equivalent circuit model with Rs(Q1(Rct1W1))(Q2(Rct2W2)) has been proposed to provide detailed insight on the carbonation behavior of mortar, taking into account both the solid/liquid double-phase interaction and the Warburg impedance. The curve fitting results based on the proposed model show a high consistency with the experimental results.
Rct1 value obtained by fitting calculation of the impedance data with the new electric circuit can be applied to characterize the carbonation behaviors of the mortar. Comparing with the experimental results and with modeling parameters, it is found that carbonation depth is the function of Rct1: . This relationship can be utilized to predict the carbonation depth precisely. Experimental results demonstrate that the prediction is ≤11% error for most of the specimens.
Acknowledgments
The authors would like to acknowledge financial support provided by National Key Basic Research Program funded by MOST (Project No. 2011CB013600; Issue No. 2011CB013604) and National Natural Science Foundation of China (No. 51120185002/51272160); Foundation for technology innovation project in Higher Education of Guangdong, China (No. 2012KJCX0091).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moropoulou, A.; Bakolas, A.; Bisbikou, A. Investigation of the technology of historic mortars. J. Cult. Herit 2000, 1, 45–58. [Google Scholar]
- Sabbioni, C.; Zappia, G.; Riontino, C.; Blanco-Varela, M.T.; Aguilerac, J.; Puertasc, F.; Van Balend, K.; Toumbakarid, E.E. Atmospheric deterioration of ancient and modern hydraulic mortars. Atmospheric Environ 2001, 35, 539–548. [Google Scholar]
- Johannesson, B.; Utgenannt, P. Microstructural changes caused by carbonation of cement mortar. Cem. Concr. Res 2001.
- Rabehi, M.; Mezghiche, B.; Guettala, S. Correlation between initial absorption of the cover concrete, the compressive strength and carbonation depth. Constr. Build. Mater 2013, 45, 123–129. [Google Scholar]
- Thiery, M.; Villain, G.; Dangla, P.; Platret, G. Investigation of the carbonation front shape on cementitious materials: Effects of the chemical kinetics. Cem. Concr. Res 2007, 37, 1047–1058. [Google Scholar]
- Meier, S.A.; Peter, M.A.; Muntean, A.; Böhm, M. Dynamics of the internal reaction layer arising during carbonation of concrete. Chem. Eng. Sci 2007, 62, 1125–1137. [Google Scholar]
- Atiş, C.D. Accelerated carbonation and testing of concrete made with fly ash. Constr. Build. Mater 2003, 17, 147–152. [Google Scholar]
- Marques, P.F.; Chastre, C.; Nunes, Â. Carbonation service life modeling of RC structures for concrete with Portland and blended cements. Cem. Concr. Compos 2013, 37, 171–184. [Google Scholar]
- Muntean, A.; Böhm, M. A moving-boundary problem for concrete carbonation: Global existence and uniqueness of weak solutions. J. Math. Anal. Appl 2009, 350, 234–251. [Google Scholar]
- Bary, B.; Sellier, A. Coupled moisture—Carbon dioxide–calcium transfer model for carbonation of concrete. Cem. Concr. Res 2004, 34, 1859–1872. [Google Scholar]
- Villain, G.; Thiery, M.; Platret, G. Measurement methods of carbonation profiles in concrete: Thermogravimetry, chemical analysis and gammadensimetry. Cem. Concr. Res 2007, 37, 1182–1192. [Google Scholar]
- Fabbri, A.; Corvisier, J.; Schubnel, A.; Bruneta, F.; Gofféa, B.; Rimmeleb, G.; Barlet-Gouédard, V. Effect of carbonation on the hydro-mechanical properties of Portland cements. Cem. Concr. Res 2009, 39, 1156–1163. [Google Scholar]
- Duong, V.B.; Sahamitmongkol, R.; Tangtermsirikul, S. Effect of leaching on carbonation resistance and steel corrosion of cement-based materials. Constr. Build. Mater 2013, 40, 1066–1075. [Google Scholar]
- Huet, B.; L’Hostis, V.; Miserque, F.; Idrissi, H. Electrochemical behavior of mild steel in concrete: Influence of pH and carbonate content of concrete pore solution. Electrochim. Acta 2005, 51, 172–180. [Google Scholar]
- Valcarce, M.B.; Vázquez, M. Carbon steel passivity examined in solutions with a low degree of carbonation: The effect of chloride and nitrite ions. Mater. Chem. Phys 2009, 115, 313–321. [Google Scholar]
- Metalssi, O.O.; Aït-Mokhtar, A.; Turcry, P.; Ruot, B. Consequences of carbonation on microstructure and drying shrinkage of a mortar with cellulose ether. Constr. Build. Mater 2012, 34, 218–225. [Google Scholar]
- Ngala, V.T.; Page, C.L. Effects of carbonation on pore structure and diffusional properties of hydrated cement pastes. Cem. Concr. Res 1997, 27, 995–1007. [Google Scholar]
- Rozière, E.; Loukili, A.; Cussigh, F. A performance based approach for durability of concrete exposed to carbonation. Constr. Build. Mater 2009, 23, 190–199. [Google Scholar]
- Isgor, O.B.; Razaqpur, A.G. Finite element modeling of coupled heat transfer, moisture transport and carbonation processes in concrete structures. Cem. Concr. Compos 2002, 26, 57–73. [Google Scholar]
- Steffens, A.; Dinkler, D.; Ahrens, H. Modeling carbonation for corrosion risk prediction of concrete structure. Cem. Concr. Res 2002, 32, 935–941. [Google Scholar]
- Jiang, L.; Lin, B.; Cai, Y. A model for predicting carbonation of high-volume fly ash concrete. Cem. Concr. Res 2000, 30, 699–702. [Google Scholar]
- Bertos, M.F.; Simons, S.J.R.; Hills, C.D.; Carey, P.J. A review of accelerated carbonation technology in the treatment of cement-based materials and sequestration of CO2 (review article). J. Hazard. Mater 2004, 112, 193–205. [Google Scholar]
- Lo, Y.; Lee, H.M. Curing effects on carbonation of concrete using a phenolphthalein indicator and Fourier-transform infrared spectroscopy. Build. Environ 2002, 37, 507–514. [Google Scholar]
- Song, G. Equivalent circuit model for AC electrochemical impedance spectroscopy of concrete. Cem. Concr. Res 2000, 30, 1723–1730. [Google Scholar]
- McCarter, W.J.; Garvin, S.; Bouzid, N. Impedance measurements on cement paste. J. Mater. Sci. Lett 1998, 7(1), 1056–1057. [Google Scholar]
- McCarter, W.J.; Brousseau, R. The A.C. response of hardened cement paste. Cem. Concr. Res 1990, 20, 891–900. [Google Scholar]
- Gu, P.; Xie, P.; Beaudoin, J.J.; Brousseau, R. A.C. impedance spectroscopy (II): Microstructural characterization of hydrating cement-silicafume systems. Cem. Concr. Res 1993, 23, 157–168. [Google Scholar]
- Brantervik, K.; Niklasson, G.A. Circuit models for cement based materials obtained form impedance spectroscopy. Cem. Concr. Res 1991, 21, 496–508. [Google Scholar]
- An, X.P.; Shi, C.J.; He, F.; Wang, D. AC impedance characteristics of ternary cementitious materials. J. Chin. Ceram. Soc 2012, 40, 1059–1066. [Google Scholar]
- Ye, C.-Q.; Hu, R.-G.; Dong, S.-G.; Zhang, X.-J.; Hou, R.-Q.; Du, R.-G.; Lin, C.-J.; Pan, J.-S. EIS analysis on chloride-induced corrosion behavior of reinforcement steel in simulated carbonated concrete pore solutions. J. Electro Anal. Chem 2013, 688, 275–281. [Google Scholar]
- Chinese National Standards, Standard for Test Methods of Long-term Performance and Durability of Ordinary Concrete; GBJ820-8527; Ministry of Housing and Urban-Rural Development: Beijing, China, 2010.
- Macdonald, J.R. Impedance Spectroscopy Theory, Experiment, and Applications; John Wiley & Sons, Inc: Hoboken, NJ, USA; Volume 2005, pp. 306–308.
- Chen, X.D.; Wu, S.X. Influence of water-to-cement ratio and curing period on pore structure of cement mortar. Constr. Build. Mater 2013, 38, 804–812. [Google Scholar]
- Diamond, S. A critical comparison of mercury porosimetry and capillary condensation pore size distributions of Portland cement pastes. Cem. Concr. Res 1971, 1, 531–545. [Google Scholar]
- Xie, P.; Gu, P.; Xu, Z.; Beaudoin, J.J. A rationalized A.C. impedance model for microstructural characterization of hydrating cement systems. Cem. Concr. Res 1993, 23, 359–367. [Google Scholar]
- Gu, P.; Xie, P.; Beaudion, J.J. Microstructural characterization of the transition zone in cement systems by mean of A.C. impedance spectroscopy. Cem. Concr. Res 1993, 23, 581–591. [Google Scholar]
- Snydera, K.A.; Fenga, X.; Keenc, B.D.; Masonb, T.O. Estimating the electrical conductivity of cement paste pore solutions from OH−, K+ and Na+ concentrations. Cem. Concr. Res 2003, 33, 793–798. [Google Scholar]
- Arandigoyen, M.; Bicer-Simsir, B.; Alvarez, J.I.; Langeb, D.A. Variation of microstructure with carbonation in lime and blended pastes. Appl. Surf. Sci 2006, 252, 7562–7571. [Google Scholar]
- Montemor, M.F.; Cunha, M.P.; Ferreira, M.G.; Simões, A.M. Corrosion behaviour of rebars in fly ash mortar exposed to carbon dioxide and chlorides. Cem. Concr. Compos 2002, 24, 45–53. [Google Scholar]
- Zhang, X.; Zhou, X.; Zhou, H.; Gaoa, K.; Wang, Z. Studies on forecasting of carbonation depth of slag high performance concrete considering gas permeability. Appl. Clay Sci 2013, 79, 36–40. [Google Scholar]
- Sisomphon, K.; Franke, L. Carbonation rates of concretes containing high volume of pozzolanic materials. Cem. Concr. Res 2007, 37, 1647–1653. [Google Scholar]
- Ji, Y.S. Performance and Prediction of Reinforced Concrete in Full Service Life Due to Corrosion Damage; China Railway Publishing House: Beijing, China, 2011; pp. 49–53. [Google Scholar]
- Niu, D.T.; Dong, Z.P.; Pu, J.X. Random model of predicting the carbonated concrete depth. Ind. Constr 1999, 29, 41–45. [Google Scholar]
- Dhir, R.K.; Hewlett, P.C.; Chan, Y.N. Near surface characteristics of concrete: Prediction of carbonation resistance. Mag. Concr. Res 1989, 41, 137–143. [Google Scholar]
- Yoon, I.; Çopuroğlu, O.; Park, K. Effect of global climatic change on carbonation progress of concrete. Atmospheric Environ 2007, 41, 7274–7285. [Google Scholar]




| Carbonation time (day) | Rct1 value calculated from Rs(Q1(Rct1W1))(Q2(Rct2W2)) model (Ohm)
| ||
|---|---|---|---|
| C/S = 1:2 | C/S = 1:3 | C/S = 1:4 | |
| 0 | 66,200 | 77,330 | 136,200 |
| 3 | 118,900 | 139,800 | 178,600 |
| 7 | 211,000 | 185,100 | 201,300 |
| 14 | 292,000 | 216,600 | 343,300 |
| 36 | 358,000 | 354,500 | 460,600 |
| 60 | 467,000 | 534,600 | 697,300 |
| 90 | 663,200 | 745,800 | 968,100 |
| 120 | 854,600 | 957,800 | 1,238,900 |
| Carbonation time (day) | Carbonation depth (mm)
| ||
|---|---|---|---|
| C/S = 1:2 | C/S = 1:3 | C/S = 1:4 | |
| 0 | 0.00 | 0.00 | 0.00 |
| 3 | 0.89 | 1.80 | 1.02 |
| 7 | 1.55 | 2.54 | 2.18 |
| 14 | 1.96 | 2.67 | 3.29 |
| 36 | 2.60 | 3.68 | 3.94 |
| 60 | 3.18 | 4.32 | 4.61 |
| 90 | 3.40 | 5.53 | 5.62 |
| 120 | 3.60 | 5.80 | 6.46 |
| Carbonation Depth | Cement/Sand Ratio
| |||
|---|---|---|---|---|
| 1:2 | 1:3 | 1:4 | ||
| 90 day | Measured carbonation depth (mm) | 3.40 | 5.53 | 5.62 |
| Calculated value (mm) | 3.56 | 5.59 | 6.04 | |
| Variation (%) | 4.71 | 1.08 | 7.47 | |
| 120 day | Measured carbonation depth (mm) | 3.60 | 5.80 | 6.46 |
| Calculated value (mm) | 4.09 | 6.42 | 7.00 | |
| Variation (%) | 13.61 | 10.69 | 8.36 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dong, B.; Qiu, Q.; Xiang, J.; Huang, C.; Xing, F.; Han, N. Study on the Carbonation Behavior of Cement Mortar by Electrochemical Impedance Spectroscopy. Materials 2014, 7, 218-231. https://doi.org/10.3390/ma7010218
Dong B, Qiu Q, Xiang J, Huang C, Xing F, Han N. Study on the Carbonation Behavior of Cement Mortar by Electrochemical Impedance Spectroscopy. Materials. 2014; 7(1):218-231. https://doi.org/10.3390/ma7010218
Chicago/Turabian StyleDong, Biqin, Qiwen Qiu, Jiaqi Xiang, Canjie Huang, Feng Xing, and Ningxu Han. 2014. "Study on the Carbonation Behavior of Cement Mortar by Electrochemical Impedance Spectroscopy" Materials 7, no. 1: 218-231. https://doi.org/10.3390/ma7010218




