Generalized Fractional Derivative Anisotropic Viscoelastic Characterization
Abstract
:1. Introduction
2. Analysis
2.1. Material Property Dependence on Temperature
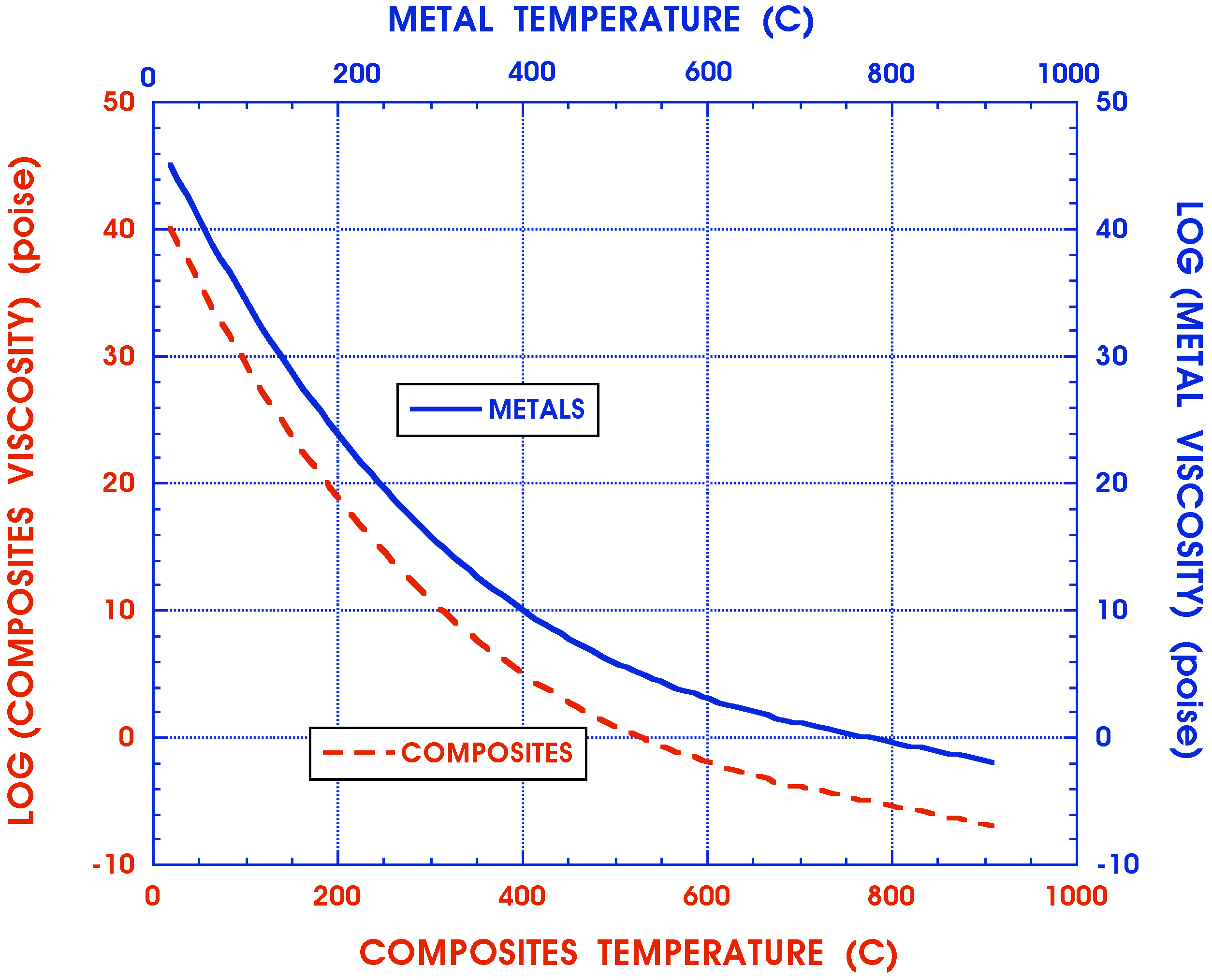
| Temperature | Modulus | Type of Constitutive Relations, Equation (2) | Type of Material |
|---|---|---|---|
| convolution | homogeneous | ||
| convolution | non-homogeneous | ||
| convolution | non-homogeneous | ||
| non-convolution | non-homogeneous |
2.2. General Concepts—Isotropic Materials
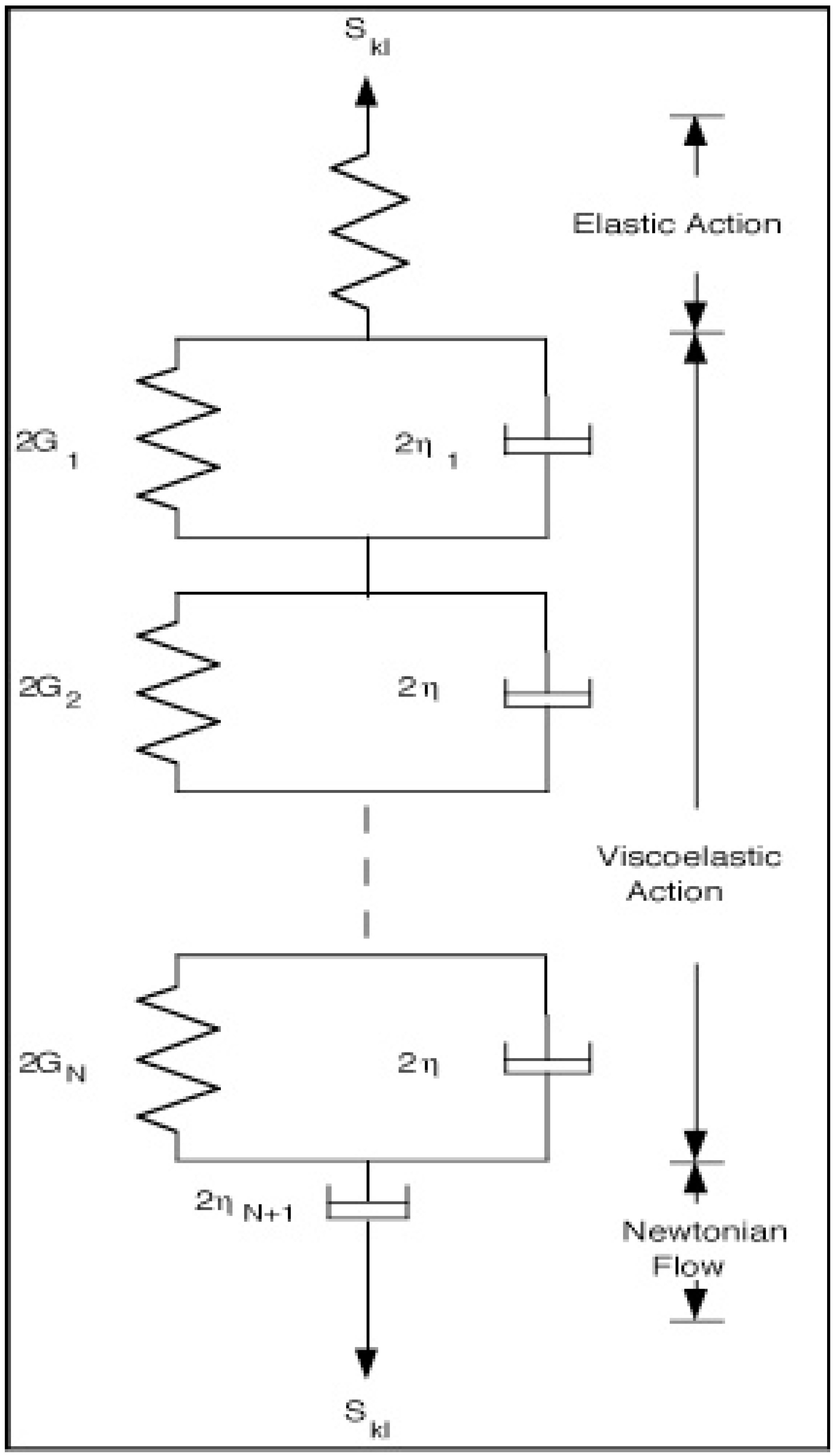
2.3. Anisotropic Relations
- (1)
- different parametric values and with equal numbers N in all directions
- (2)
- same parameters and in all directions but with distinct , thus generating different numbers of GKM parameters in each direction
- (3)
- combinations of (1) and (2) above
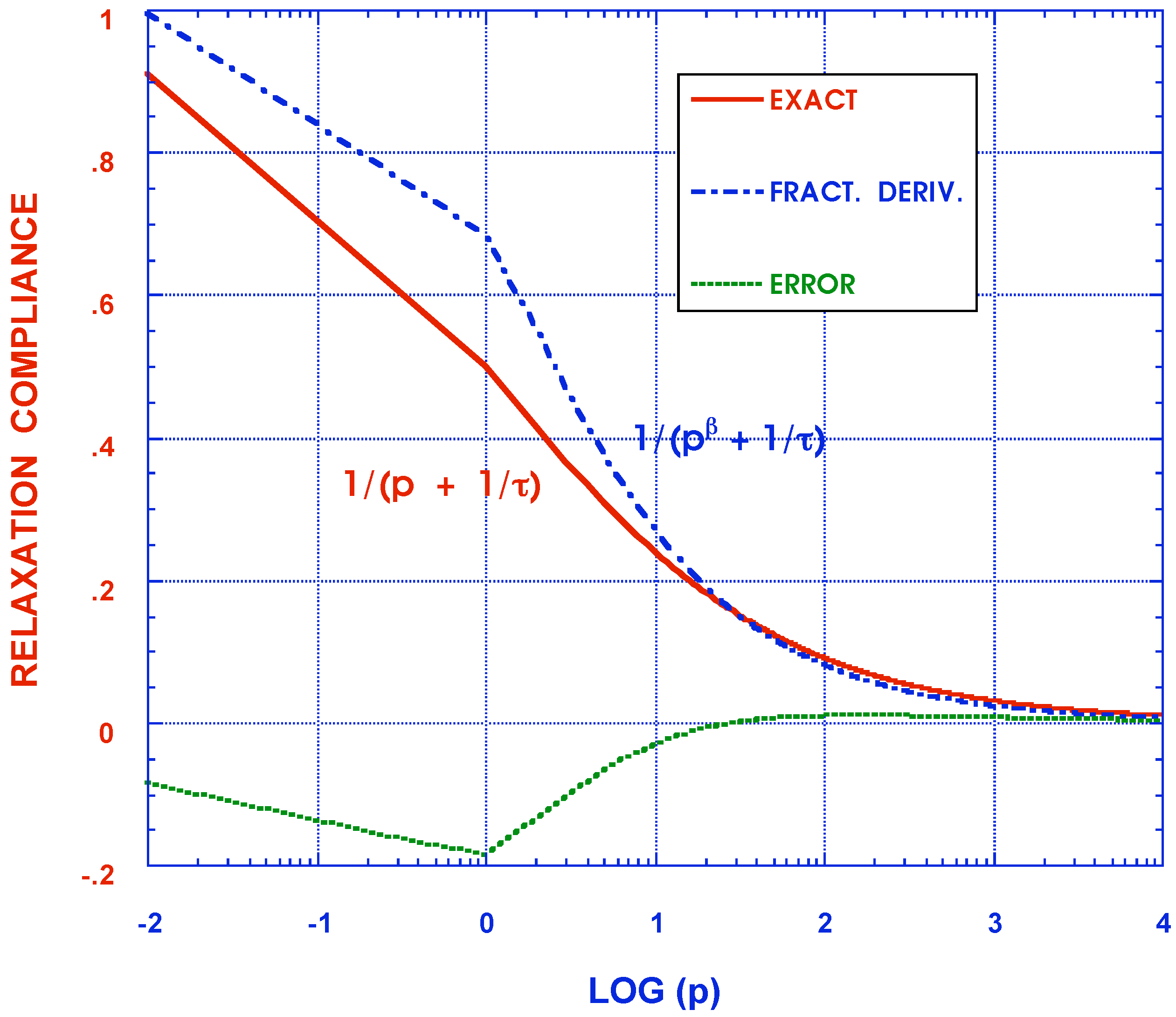
3. Discussion
- (a)
- Performing “simple” experiments for which analytic solution can be formulated and evaluated
- (b)
- Curve fitting of actual creep and/or relaxation data by least square or other methods in order to determine modulus, creep function or compliance parameters
- (c)
- Inversion of FT or LT expressions for moduli, stresses and deformations
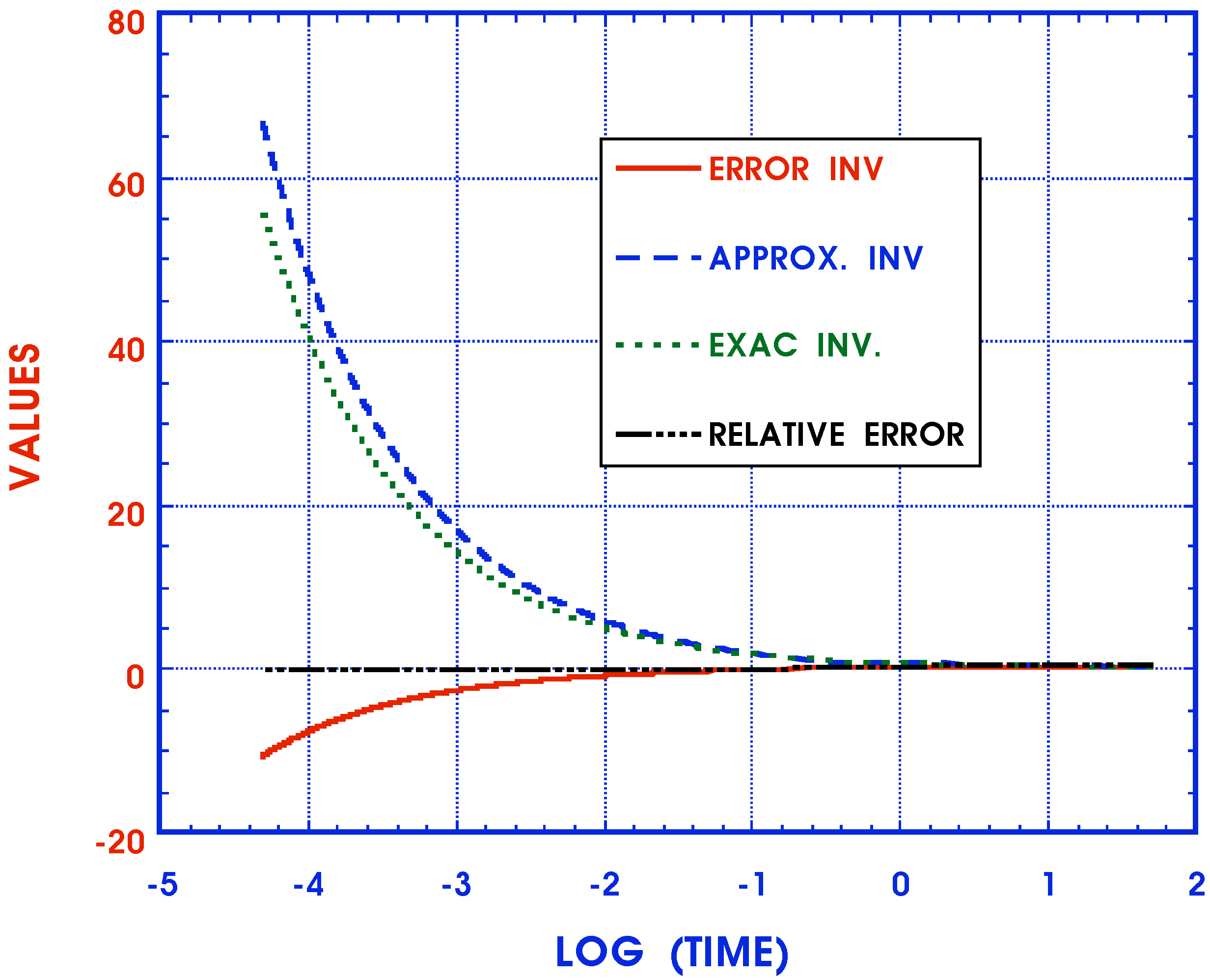
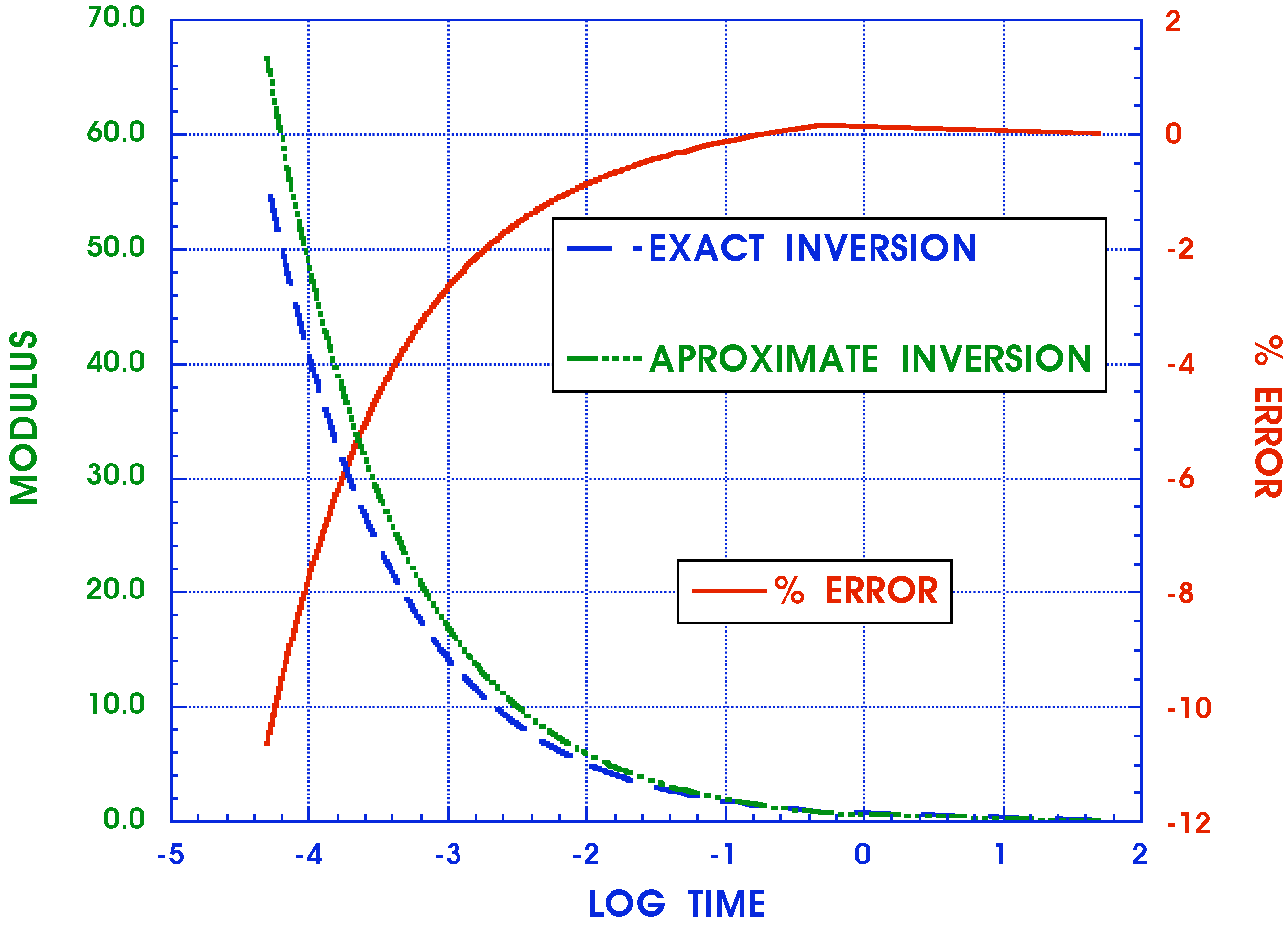
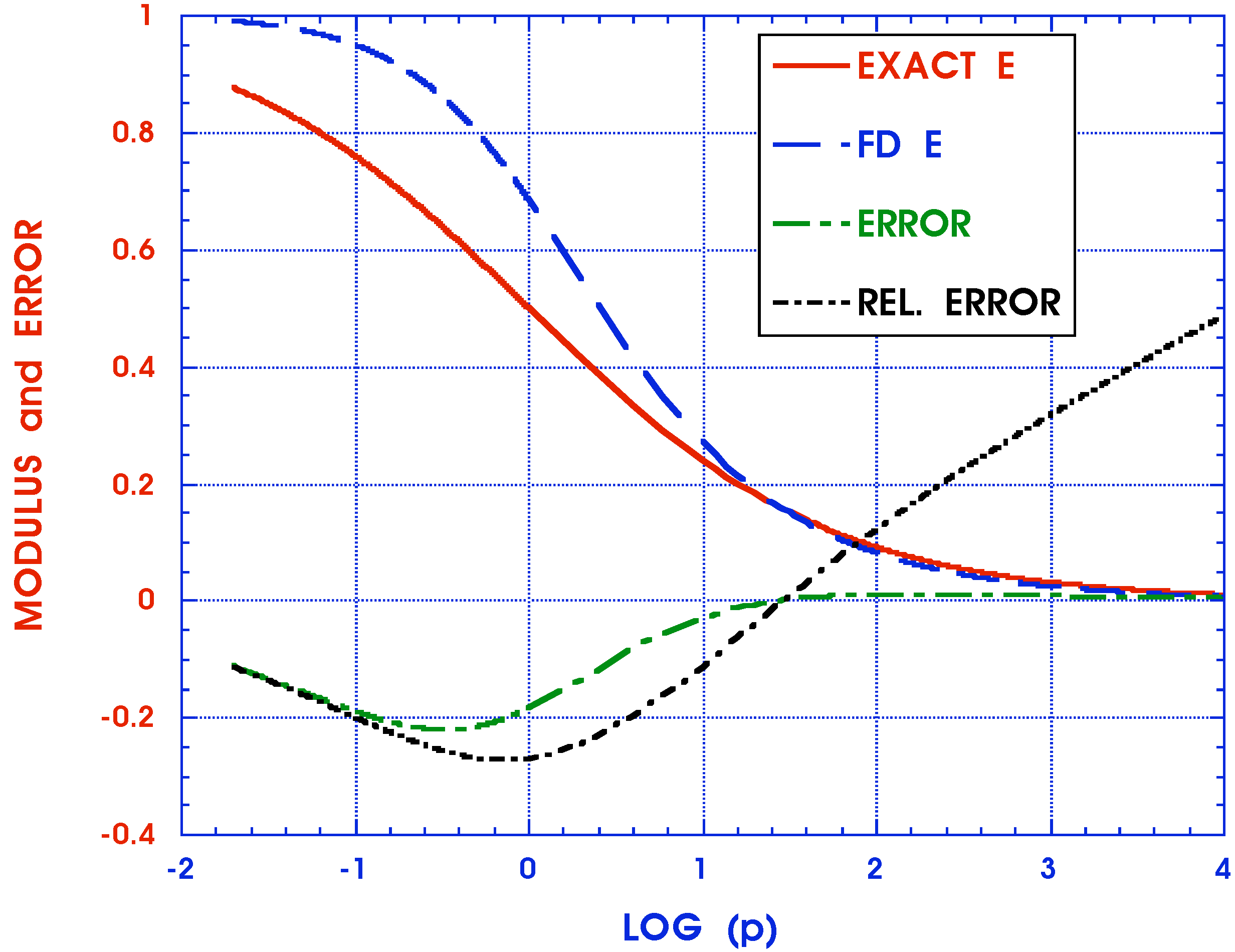
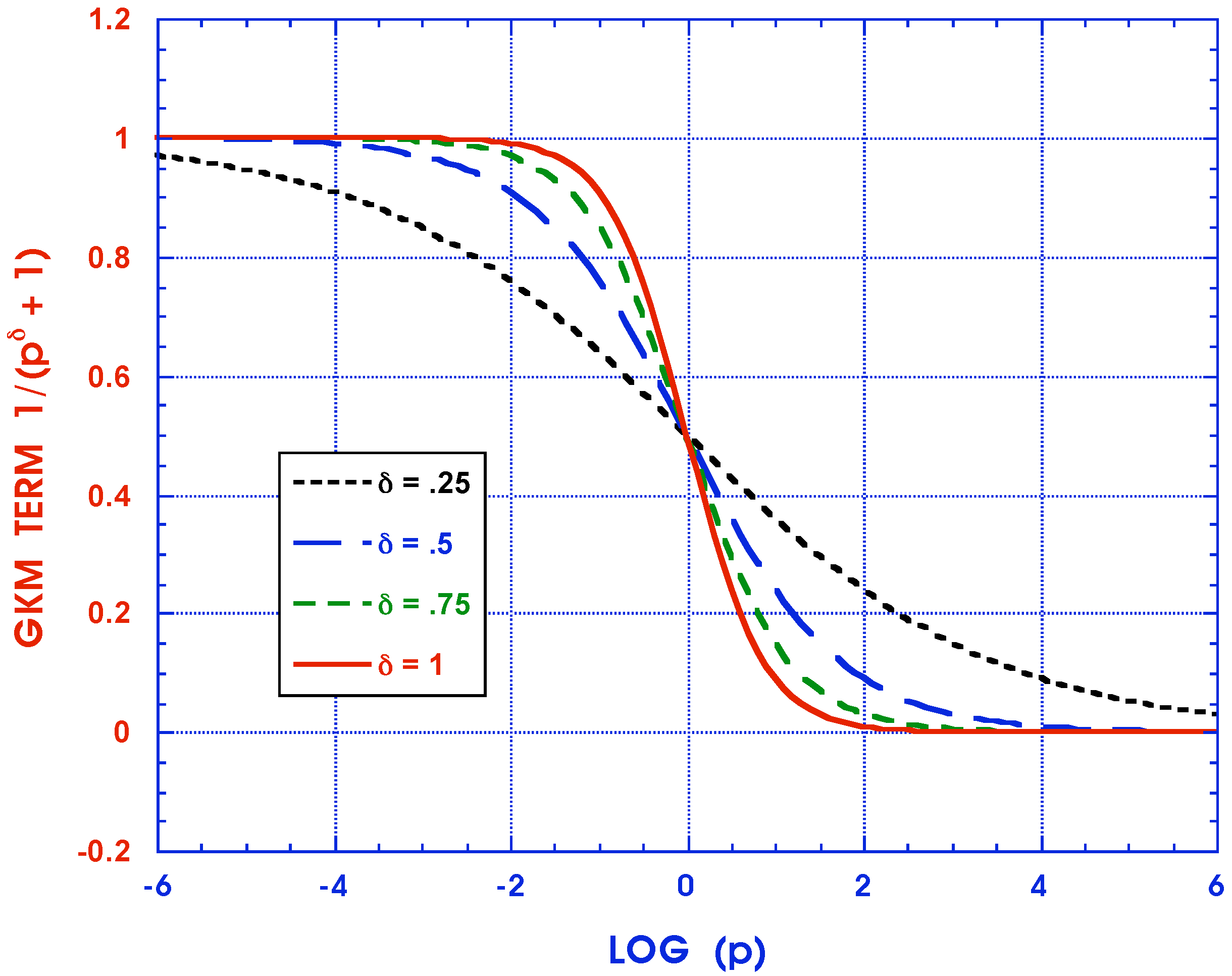
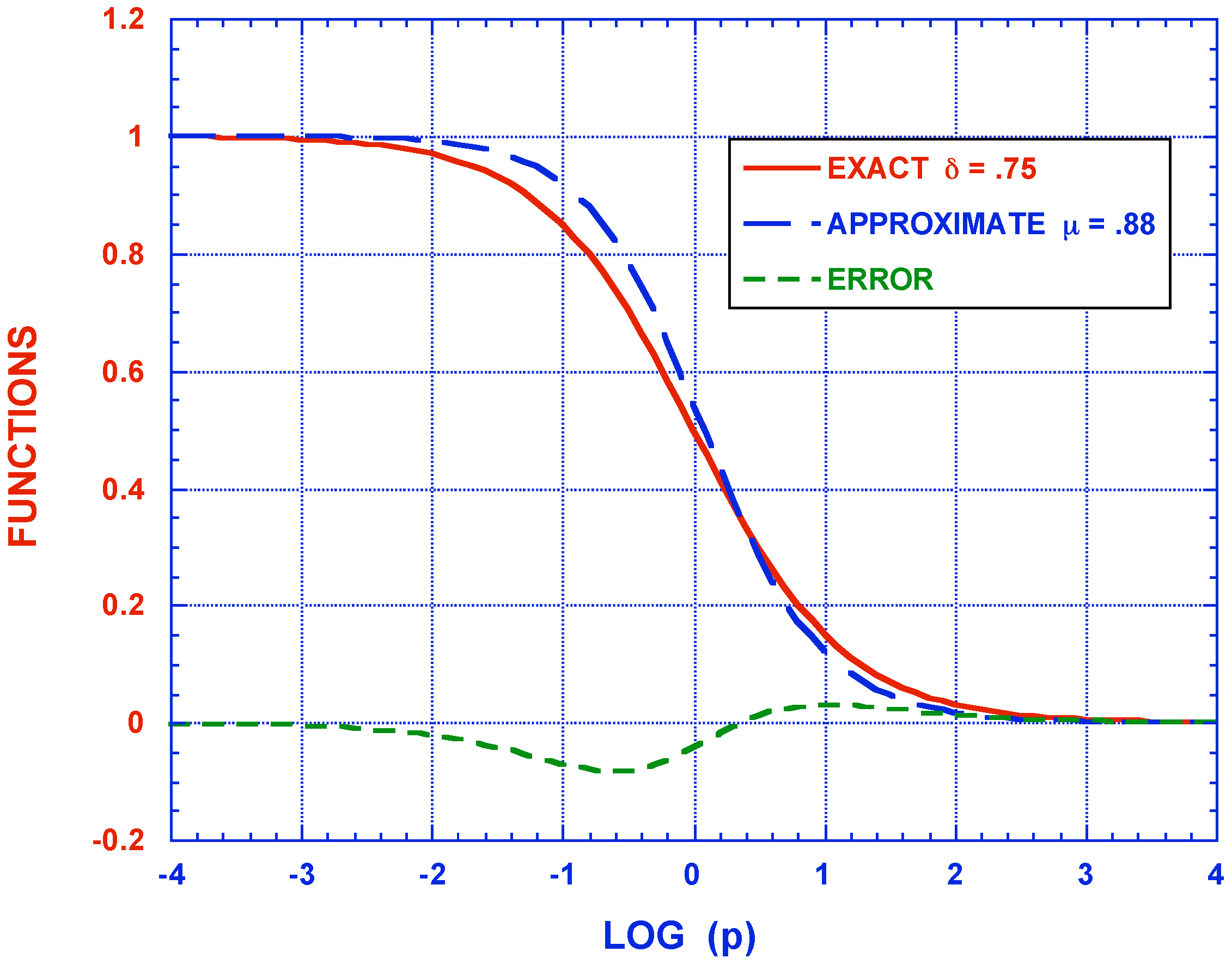
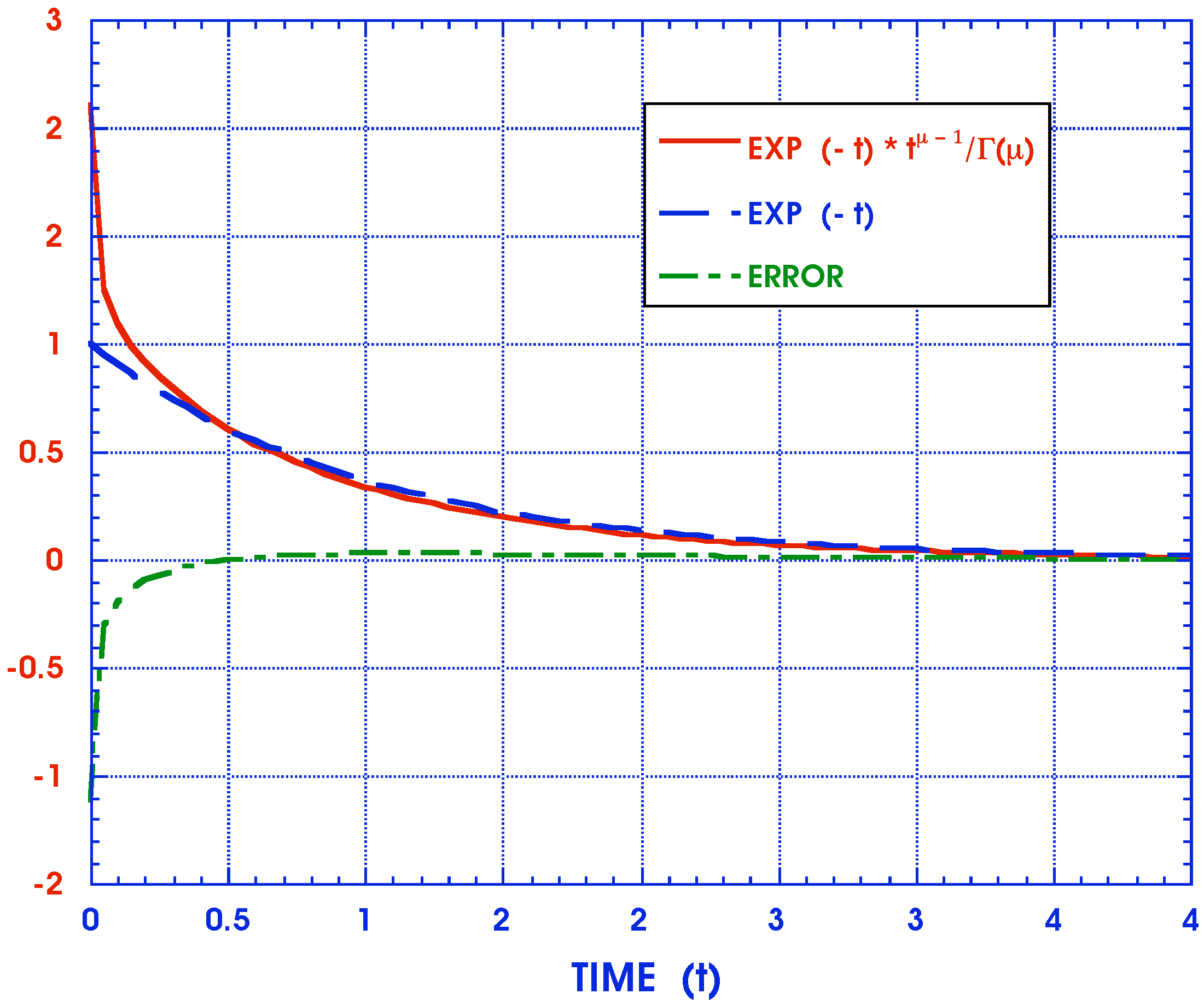
4. Conclusions
Acknowledgement
References
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity: An Introduction; Springer: New York, NY, USA, 2008. [Google Scholar]
- Christensen, R.M. Theory of Viscoelasticity—An Introduction, 2nd ed.; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Hilton, H.H. An Introduction to viscoelastic analysis. In Engineering Design for Plastics; Baer, E., Ed.; Reinhold Publishing Corp.: New York, NY, USA, 1964; pp. 199–276. [Google Scholar]
- Lakes, R.S. Viscoelastic Solids; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Lakes, R.S. Viscoelastic Materials; Cambridge University Press: London, UK, 2009. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. A generalized derivative model for an elastomer damper. Shock Vib. Bull. 1979, 49, 135–143. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. Fractional calculus—A different approach to the finite element analysis of viscoelastically damped structures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201:1–201:10. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133:1–133:23. [Google Scholar] [CrossRef]
- Bagley, R.L. Power law and fractional calculus model of viscoelasticity. AIAA J. 1987, 27, 1412–1417. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. ASME J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Koeller, R.C. Polynomial operators, Stieltjes convolution, and fractional calculus in hereditary mechanics. Acta Mech. 1986, 58, 251–264. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behavior of real materials. ASME J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Rogers, L. Operators and fractional derivatives for viscoelastic constitutive equations. J. Rheol. 1983, 27, 351–372. [Google Scholar] [CrossRef]
- Kiryakova, V.S. Generalized Fractional Calculus and Applications; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; John Willey and Sons: New York, NY, USA, 1993. [Google Scholar]
- McBride, A.C. Fractional Calculus and Integral Transforms of Generalized Functions; Pitman Advanced Publishing Program: San Francisco, CA, USA, 1979. [Google Scholar]
- Nishimoto, K. Fractional Calculus; Descartes Press Co.: Koriyama, Japan, 1984, 1987, 1989, 1991; Volumes 1–4. [Google Scholar]
- Nishimoto, K. The Essence of Nishimoto’s Fractional Calculus; Descartes Press Co.: Koriyama, Japan, 1991. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus—Theory and Applications of Differentiation and Integration of Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives—Theory and Applications; Gordon & Beach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Bagley, R.L. The thermorheologically complex material. Intern. J. Eng. Sci. 1991, 29, 797–806. [Google Scholar] [CrossRef]
- Volterra, V. Sulle equazioni integrodifferenzialli dela teoria dell’elastica. Atti Reale Accademi Lincei 1909, 18, 295–301. [Google Scholar]
- Boltzmann, L. Zur theorie der elastischen nachwirkung. Sitzungsberichte Kaiserliche Akademie Wissenhaft Wien Mathematische-Naturwissenhaft 1874, 70, 275–306. [Google Scholar]
- Biot, M.A. Theory of stress-strain relations in anisotropic viscoelasticity and relaxation phenomena. J. Appl. Phys. 1954, 25, 1385:1–1385:7. [Google Scholar] [CrossRef]
- Biot, M.A. Dynamics of viscoelastic anisotropic media. In Proceedings Second Midwestern Conference on Solid Mechanics, Urbana, IL, USA, 1955; pp. 94–108.
- Edelstein, W.S.; Gurtin, M.E. Uniqueness theorems in the linear dynamic theory of anisotropic viscoelastic solids. Arch. Ration. Mech. Anal. 1964, 7, 47–60. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Sternberg, E. A reciprocal theory of anisotropic viscoelastic solids. SIAM J. 1963, 11, 607–613. [Google Scholar]
- Hilton, H.H. On the inadmissibility of separation of variables solutions in linear anisotropic viscoelasticity. Intern. J. Comput. Mater. Struct. 1996, 3, 97–100. [Google Scholar]
- Vosteen, L.F. Effect of Temperature on Dynamic Modulus of Elasticity on Structural Alloys; NACA TN 4348; US Gov. Printing Office: Washington, DC, USA, 1958. [Google Scholar]
- Mathauser, E.E. Compressive Stress-Strain Properties of 2024-T3 Aluminum Alloy Sheet at Elevated Temperatures; US Gov. Printing Office: Washington, DC, USA, 1956. [Google Scholar]
- Williams, M.L.; Landel, R.L.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Hilton, H.H.; Dong, S.B. An Analogy for Anisotropic, nonhomogeneous linear viscoelasticity including thermal stresses. In Development in Mechanics; Pergamon Press: New York, NY, USA, 1964; pp. 58–73. [Google Scholar]
- Fourier, J.B.J. Théorie de la Chaleur; Didot: Paris, France, 1822. [Google Scholar]
- Ross, B. A Brief History and Exposition of the Fundamental Theory of Fractional Calculus; Springer-Verlag: Berlin, Germany, 1975; volume 451, pp. 1–36. [Google Scholar]
- Liouville, J. Mémoire sur quelques quéstions de géometrie et de mécanique et sur un nouveau genre de calcul pour résoundre ces quéstions. J. l’École Poly. Paris 1832, 13, 1–69. [Google Scholar]
- Liouville, J. Mémoire sur le changement de la variable dans le calcul des differentielles à indices quelconques. J. l’École Poly. Paris 1835, 15, 17–54. [Google Scholar]
- Riemann, G.F.B. Versuchung einer allgemeinen auffassung der integration und differentiation (1847). In Gesammelte Mathematische Werke und Wissensschaflicher Nachlass; B.G. Teubner: Leipzig, Germany, 1876; pp. 331–344. [Google Scholar]
- Loan, C.V. Computational Frameworks for the Fast Fourier Transform; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Lakes, R.S.; Wineman, A. On Poisson’s ratio in linearly viscoelastic solids. J. Elast. 2006, 85, 45–63. [Google Scholar] [CrossRef]
- Tschoegl, N.W. Time dependence in material properties: An overview. Mech. Time-Depend. Mater. 1997, 1, 3–31. [Google Scholar] [CrossRef]
- Tschoegl, N.W.; Wolfgang, G.; Knauss, W.G.; Igor Emri, I. Poisson’s ratio in linear viscoelasticity—A critical review. Mech. Time-Depend. Mater. 2002, 6, 3–51. [Google Scholar] [CrossRef]
- Hilton, H.H.; Yi, S. The significance of anisotropic viscoelastic Poisson ratio stress and time dependencies. Intern. J. Solids Struct. 1998, 35, 3081–3095. [Google Scholar] [CrossRef]
- Hilton, H.H. Implications and constraints of time independent Poisson ratios in linear isotropic and anisotropic viscoelasticity. J. Elast. 2001, 63, 221–251. [Google Scholar] [CrossRef]
- Hilton, H.H. The elusive and fickle viscoelastic Poisson’s ratio and its relation to the elastic-viscoelastic correspondence principle. J. Mech. Mater. Struct. 2009, 4, 1341–1364. [Google Scholar] [CrossRef]
- Hilton, H.H. Clarifications of certain ambiguities and failings of Poisson’s ratios in linear viscoelasticity. J. Elast. 2011, 104, 303–318. [Google Scholar] [CrossRef]
- Yi, S.; Hilton, H.H. Dynamic finite element analysis of viscoelastic composite plates in the time domain. Intern. J. Num. Meth. Eng. 1994, 37, 4081–4096. [Google Scholar] [CrossRef]
- Brinson, L.C.; Gates, T.S. Effects of physical aging on long term creep behavior of polymers and polymer matrix composites. Intern. J. Solids Struct. 1994, 32, 827–846. [Google Scholar] [CrossRef]
- Monaghan, M.R.; Brinson, L.C.; Bradshaw, R.D. Analysis of variable stress history on polymeric composite materials with physical aging. Compos. Eng. 1994, 4, 1023–1032. [Google Scholar] [CrossRef]
- Harper, B.D. Optimal cooling paths for a class of thermorheologically complex viscoelastic materials. ASME J. Appl. Mech. 1985, 52, 634–638. [Google Scholar] [CrossRef]
- Harper, B.D.; Weitsman, Y. Characterization method for a class of thermorheologically complex materials. J. Rheol. 1985, 29, 49–66. [Google Scholar] [CrossRef]
- Yi, S.; Hilton, H.H. Constitutive relations for thermosetting resins during curing processes. In Proceedings AIAA/ASME/ASCE/AHS/ASC 36th SDM Conference, Reston, VA, USA, April 1995. AIAA Paper 95–1428.
- Yi, S.; Hilton, H.H.; Ahmad, M.F. Nonlinear thermoviscoelastic analysis of interlaminar stresses in laminated composites. ASME J. Appl. Mech. 1996, 3, 97–100. [Google Scholar]
- Yi, S.; Ling, S.F.; Ying, M.; Hilton, H.H.; Vinson, J.R. Finite element formulation for anisotropic coupled piezo-hygro-thermo-viscoelasto-dynamic problems. Intern. J. Num. Meth. Eng. 1999, 45, 1531–1546. [Google Scholar] [CrossRef]
- Schapery, R.A. On the characterization of nonlinear viscoelastic materials. Polym. Eng. Sci. 1969, 9, 295–310. [Google Scholar] [CrossRef]
- Schapery, R.A. Approximate methods of transform inversion for viscoelastic stress analysis. In Proceedings of the 4th US Nattional Congress of Application Mechanics, Berkeley, CA, USA, June 1962; Volume 2, pp. 1075–1085.
- Prony, G.C.F.R. Essai experimental et analytique. J. l’École Poly. Paris 1755, 1, 24–76. [Google Scholar]
- Michaeli, M.; Shtark, A.; Grosbein, H.; Hilton, H.H. Analytical, Experimental and computational viscoelastic material characterizations absent Poisson’s ratios. In Proceedings of the Fifty-second AIAA/ASME/ASCE/AHS/ASC SDM Conference, Denver, CO, USA, April 2011. AIAA Paper 2011-1809.
- Shtark, A.; Grosbein, H.; Sameach, G.; Hilton, H.H. An alternate protocol for determining viscoelastic material properties based on tensile tests without use of Poisson ratios. In Proceedings of the ASME 2007 International Mechanical Engineering Congress and Exposition (IMECE2007), Seattle, WA, USA, 11–15 November 2007.
- Shtark, A.; Grosbein, H.; Hilton, H.H. Analytical determination without use of Poisson ratios of temperature dependent viscoelastic material properties based on uniaxial tensile experiments. In Proceedings of the 2009 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, January 2009. ASME Paper IMECE 2009-10332.
- Shtark, A.; Grosbein, H.; Sameach, G.; Hilton, H.H. An alternate protocol for determining viscoelastic material properties based on tensile tests without use of Poisson ratios. ASME J. Appl. Mech. 2012, in press. [Google Scholar]
- Post, E.L. Generalized differentiation. Trans. Am. Math. Soc. 1930, 32, 723–781. [Google Scholar] [CrossRef]
- Yi, S. Finite Element Analysis of Viscoelastic Structures and Analytical Determination of Optimum Viscoelastic Materials. Ph. D. Dissertation, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 1992. [Google Scholar]
- Knauss, W.G. Uniaxial wave propagation in a viscoelastic material using measured material properties. ASME J. Appl. Mech. 1968, 35, 449–453. [Google Scholar] [CrossRef]
- Sackman, J.L. A remark on transient stresses in nonhomogeneous viscoelastic materials. J. Aerosp. Sci. 1962, 29, 1015–1016. [Google Scholar]
- Sackman, J.L.; Kaya, I. On the propagation of transient pulses in linear viscoelastic media. ASME J. Appl. Mech. 1968, 16, 349–356. [Google Scholar]
- Pipkin, A.C. Convolutions as products in viscoelastic theory. In Recent Advances in Elasticity, Viscoelasticity and Inelasticity; Rajagopal, K.R., Ed.; World Scientific: Singapore, 1995; pp. 82–107. [Google Scholar]
- Beldica, C.E.; Hilton, H.H. Analytical and computational simulations of experimental determinations of deterministic and random linear viscoelastic constitutive relations. J. Sandw. Struct. Mater. 2012, in press. [Google Scholar]
- Bellman, R.E.; Lockett, J.A.; Kalaba, R.E. Numerical Inversion of the Laplace Transform: Applications to Biology, Economics, Engineering and Physics; Elsevier: New York, NY, USA, 1966. [Google Scholar]
- Cost, T.L. Approximate Laplace transform inversions in viscoelastic stress analysis. AIAA J. 1964, 2, 2197–2166. [Google Scholar]
- Cost, T.L.; Becker, E.B. A multidata method of approximate Laplace transform inversion. Intern. J. Num. Meth. Eng. 1970, 2, 207–219. [Google Scholar] [CrossRef]
- Dubner, H.; Abate, J. Numerical inversion of Laplace transforms by relating them to the finite Fourier cosine transform. J. Assoc. Comput. Mach. 1968, 15, 115–123. [Google Scholar] [CrossRef]
- Durbin, F. Numerical inversion of Laplace transforms: An efficient improvement to Dubner and Abate’s method. Comput. J. 1974, 17, 371–376. [Google Scholar] [CrossRef]
- Eldred, L.B.; Baker, W.P.; Palazzo, A.P. Kelvin-Voigt vs. fractional derivative model as constitutive relations for viscoelastic materials. AIAA J. 1995, 33, 547–550. [Google Scholar] [CrossRef]
- Hilton, H.H.; Sossou, S. An efficient protocol for evaluating viscoelastic Prony series hereditary integrals. J. Num. Meth. Eng. 2011. submited for publication. [Google Scholar]
© 2012 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hilton, H.H. Generalized Fractional Derivative Anisotropic Viscoelastic Characterization. Materials 2012, 5, 169-191. https://doi.org/10.3390/ma5010169
Hilton HH. Generalized Fractional Derivative Anisotropic Viscoelastic Characterization. Materials. 2012; 5(1):169-191. https://doi.org/10.3390/ma5010169
Chicago/Turabian StyleHilton, Harry H. 2012. "Generalized Fractional Derivative Anisotropic Viscoelastic Characterization" Materials 5, no. 1: 169-191. https://doi.org/10.3390/ma5010169
APA StyleHilton, H. H. (2012). Generalized Fractional Derivative Anisotropic Viscoelastic Characterization. Materials, 5(1), 169-191. https://doi.org/10.3390/ma5010169




