Investigation of the Cementing Efficiency of Fly Ash Activated by Microsilica in Low-Cement Concrete
Abstract
:1. Introduction
2. Materials and Methods
3. Results
- −
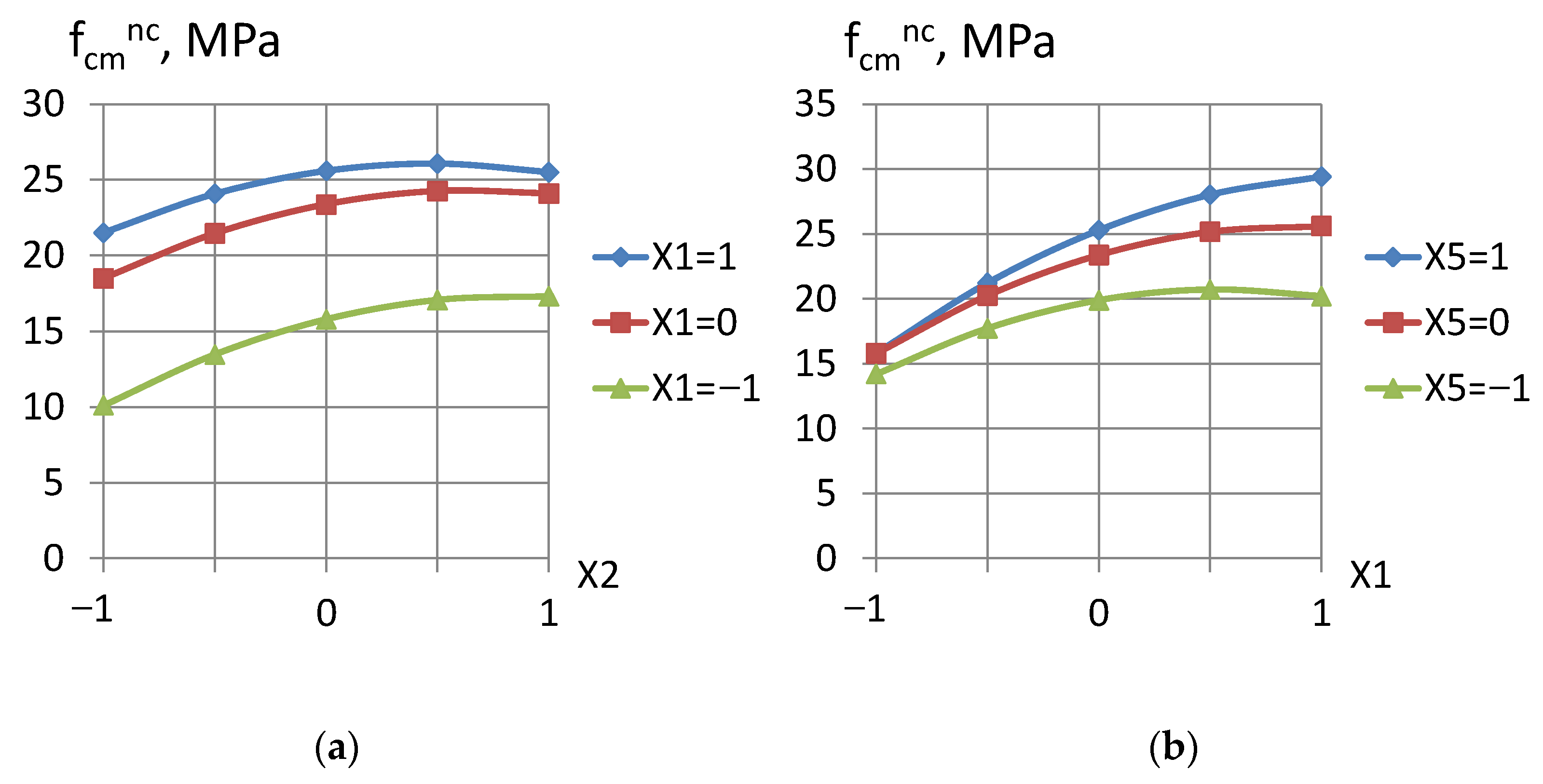
- Concrete compressive strength after 28 days of normal curing
- −
- Concrete compressive strength after steaming
- −
- Criterion L for concrete compressive strength after 28 days of normal curing
- −
- Criterion L for concrete compressive strength after steaming
- −
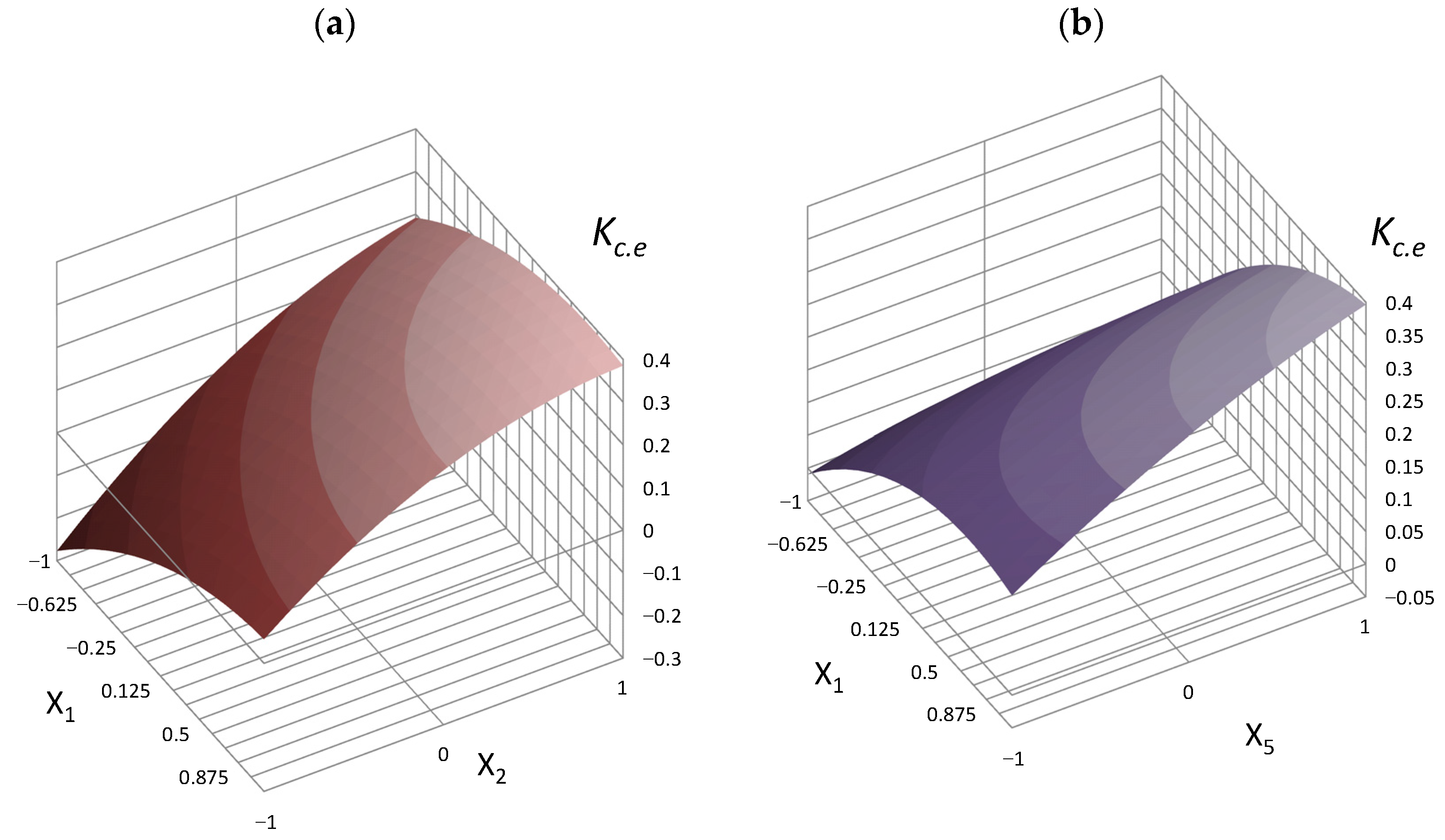
- Cementing efficiency coefficient Kc.e for concrete compressive strength after 28 days of normal curing
- −
- Cementing efficiency coefficient Kc.e for concrete compressive strength after steaming
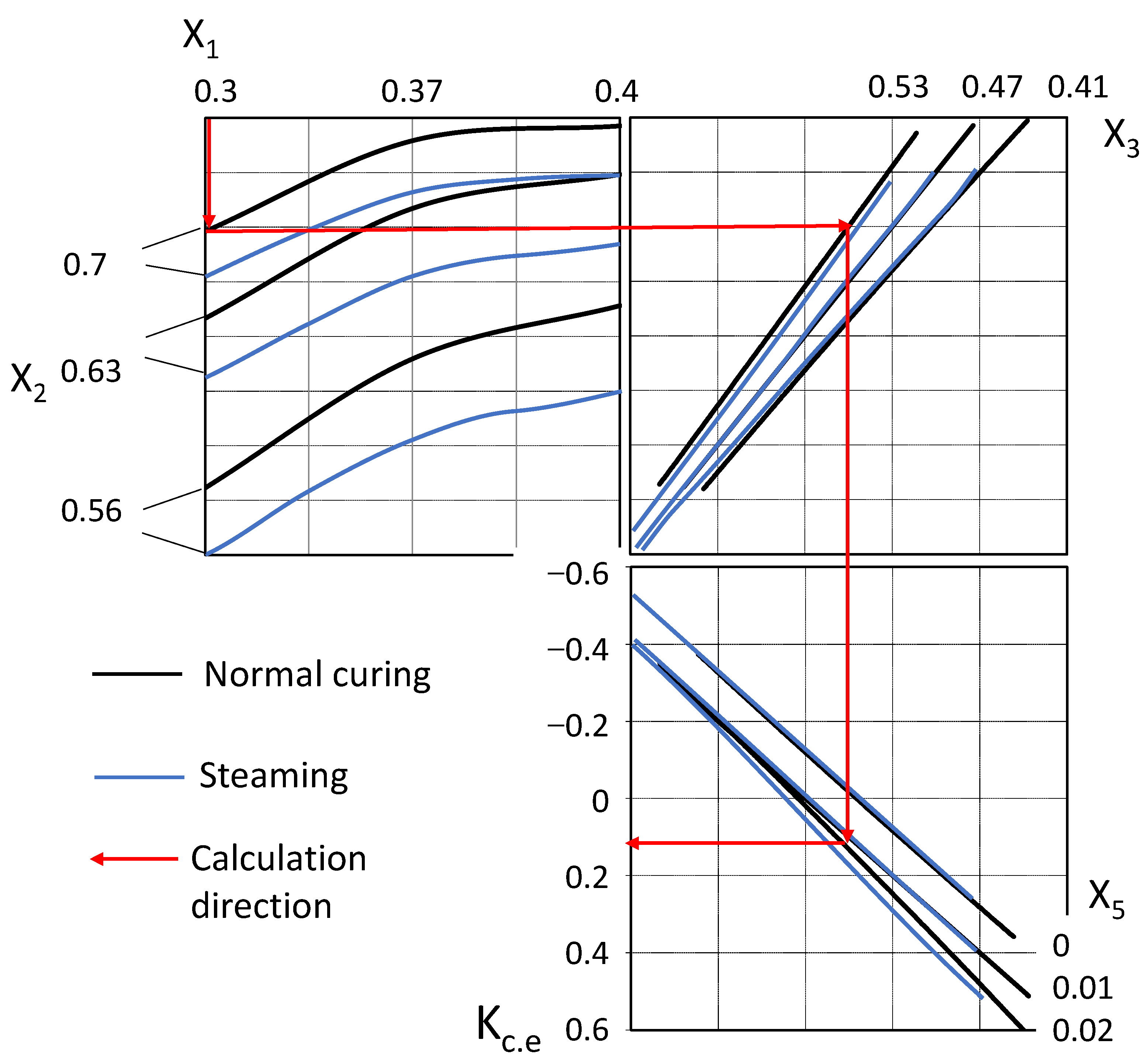
- The part of the activator (microsilica) in the volume of the active mineral additive (X1) is:
- 2.
- The part of the active mineral additive in the binder volume (X2) is:
- 3.
- The part of the binder in the binding paste volume (X3) is:
- 4.
- The part of the superplasticizer in the aqueous solution (X5) is:
- 5.
- From Equation (14) or according to the nomogram (Figure 5), the value of Kc.e is:
- Kc.e = 0.11.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Campos, H.F.; Klein, N.S.; Marques Filho, J.; Bianchini, M. Low-cement high-strength concrete with partial replacement of Portland cement with stone powder and silica fume designed by particle packing optimization. J. Clean. Prod. 2020, 261, 121228. [Google Scholar] [CrossRef]
- Damineli, B.L.; Kemeid, F.M.; Aguiar, P.S.; John, V.M. Measuring the eco-efficiency of cement use. Cem. Concr. Compos. 2010, 32, 555–562. [Google Scholar] [CrossRef]
- Güneyisi, E.; Gesoğlu, M.; Karaoğlu, S.; Mermerdaş, K. Strength, permeability and shrinkage cracking of silica fume and metakaolin concretes. Constr. Build. Mater. 2012, 34, 120–130. [Google Scholar] [CrossRef]
- Konieczna, K.; Chilmon, K.; Jackiewicz-Rek, W. Investigation of Mechanical Properties, Durability and Microstructure of Low-Clinker High-Performance Concretes Incorporating Ground Granulated Blast Furnace Slag, Siliceous Fly Ash and Silica Fume. Appl. Sci. 2021, 11, 830. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, H.; Gao, X.; Wu, W. Adsorption and desorption of polycarboxylate ether superplasticizer in fresh cementitious materials blended with mineral admixtures. J. Mater. Res. Technol. 2022, 17, 1740–1751. [Google Scholar] [CrossRef]
- Bapat, J.D. Mineral Admixtures in Cement and Concrete; CRC Press: Boca Raton, FL, USA, 2012; 310p. [Google Scholar]
- Shvarzman, A.; Kovler, K.; Schamban, I.; Grader, G.S.; Shter, G.E. Influence of chemical and phase composition of mineral admixtures on their pozzolanic activity. Adv. Cem. Res. 2002, 14, 35–41. [Google Scholar] [CrossRef]
- Papayianni, I.; Anastasiou, E. Production of high-strength concrete using high volume of industrial by-products. Constr. Build. Mater. 2010, 24, 1412–1417. [Google Scholar] [CrossRef]
- Dvorkin, L.; Zhitkovsky, V.; Sitarz, M.; Hager, I. Cement with Fly Ash and Metakaolin Blend—Drive towards a More Sustainable Construction. Energies 2022, 15, 3556. [Google Scholar] [CrossRef]
- Smith, I.A. The design of fly ash concretes. Proc. Inst. Civ. Eng. 1967, 36, 769–790. [Google Scholar] [CrossRef]
- Stolnikov, V.V. Using Fly Ash from Combustion of Pulverized Fuel at Thermal Power Plants; Energiya: Leningrad, Russia, 1989; 50p. (In Russian) [Google Scholar]
- Golewski, G.L. The Effect of the Addition of Coal Fly Ash (CFA) on the Control of Water Movement within the Structure of the Concrete. Materials 2023, 16, 5218. [Google Scholar] [CrossRef] [PubMed]
- Dvorkin, L.I. Effective Ash-Containing Cements, Concretes and Mortars; NUWEE: Rivne, Ukraine, 2022; 419p. (In Ukrainian) [Google Scholar]
- EN 12390-1:2021; Testing Hardened Concrete—Part 1: Shape, Dimensions and Other Requirements for Specimens and Moulds. CEN: Brussels, Belgium, 2021.
- Wilińska, I.; Pacewska, B. Influence of selected activating methods on hydration processes of mixtures containing high and very high amount of fly ash—A review. J. Therm. Anal. Calorim. 2018, 133, 823–843. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X. Synergistic Effects of Nano-Silica and Fly Ash on the Mechanical Properties and Durability of Internal-Cured Concrete Incorporating Artificial Shale Ceramsite. J. Build. Eng. 2023, 66, 105905. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Z.; Lu, K.; Wu, L. A review on mixture design methods for self-compacting concrete. Constr. Build. Mater. 2015, 84, 387–398. [Google Scholar] [CrossRef]
- Ghosh, R.S. Proportioning of Fly Ash Cement Concrete Mixes. Can. J. Civ. Eng. 1976, 3, 68–82. [Google Scholar] [CrossRef]
- Babu, K.G.; Rao, G.S.N. Efficiency of fly ash in concrete. Cem. Concr. Compos. 1993, 15, 223–229. [Google Scholar] [CrossRef]
- Biswas, R.; Baboo, R. Efficiency Concepts and Models that Evaluates the Strength of Concretes Containing Different Supplementary Cementitious Materials. Civ. Eng. J. 2019, 5, 18–32. [Google Scholar] [CrossRef]
- Dvorkin, L.; Dvorkin, O.; Ribakov, Y. Mathematical Experiments Planning in Concrete Technology; Nova Science Publishers, Inc.: New York, NY, USA, 2012; 173p. [Google Scholar]
- EN 12350-2:2009; Testing Fresh Concrete—Part 2: Slump-Test. CEN: Brussels, Belgium, 2009.
- Neville, A.M. Properties of Concrete, 5th ed.; Longman: London, UK, 2011; 846p. [Google Scholar]
- Liao, W.; Sun, X.; Kumar, A.; Sun, H.; Ma, H. Hydration of Binary Portland Cement Blends Containing Silica Fume: A Decoupling Method to Estimate Degrees of Hydration and Pozzolanic Reaction. Front. Mater. 2019, 6, 78. [Google Scholar] [CrossRef]


| Consumption, kg/m3 | Binder/Water | Compressive Strength, MPa | Criterion L | |||||
|---|---|---|---|---|---|---|---|---|
| Cement (C) | Ash (A) | After Steaming fcm′ | 28 Days after Steaming fcm″ | After 28 Days of Normal Curing fcm‴ | fcm′ C | fcm″ C | fcm‴ C | |
| 150 | - | 0.89 | 4.4 | 6.4 | 7.8 | 0.029 | 0.043 | 0.052 |
| 150 | 50 | 1.15 | 9.7 | 11.6 | 11.4 | 0.065 | 0.077 | 0.076 |
| 150 | 75 | 1.28 | 11.6 | 14.0 | 10.6 | 0.077 | 0.093 | 0.072 |
| 150 | 100 | 1.42 | 14.2 | 14.9 | 12.5 | 0.095 | 0.099 | 0.083 |
| 150 | 125 | 1.58 | 14.4 | 16.1 | 15.6 | 0.096 | 0.107 | 0.104 |
| 150 | 150 | 1.72 | 15.7 | 16.6 | 14.7 | 0.105 | 0.110 | 0.098 |
| 150 | 175 | 1.85 | 15.6 | 16.8 | 15.3 | 0.104 | 0.112 | 0.102 |
| 150 | 200 | 2.0 | 16.1 | 17.3 | 16.6 | 0.107 | 0.115 | 0.111 |
| Concrete Class by Compression Strength | Cement Class | Ash Consumption, kg/m3 | C/W | (C/W)m | Cement Consumption, kg/m3 | Kc.e |
|---|---|---|---|---|---|---|
| Normal curing | ||||||
| C12/15 | 32.5 | - | 1.46 | - | 293 | - |
| 150 | 1.23 | 1.46 | 246 | 0.31 | ||
| C15/20 | 32.5 | - | 1.79 | - | 357 | - |
| 150 | 1.58 | 1.79 | 317 | 0.27 | ||
| C20/25 | 42.5 | - | 1.66 | - | 331 | - |
| 150 | 1.49 | 1.66 | 298 | 0.22 | ||
| Steaming | ||||||
| C12/15 | 32.5 | - | 1.46 | - | 293 | - |
| 200 | 1.16 | 1.46 | 233 | 0.3 | ||
| C15/20 | 32.5 | - | 1.79 | - | 357 | - |
| 200 | 1.53 | 1.79 | 305 | 0.26 | ||
| C20/25 | 42.5 | - | 1.66 | - | 331 | - |
| 200 | 1.46 | 1.66 | 291 | 0.2 | ||
| Material | CaO | SiO2 | Al2O3 | Fe2O3 + FeO | MgO | Na2O + K2O | SO3 | L.O.I. * |
|---|---|---|---|---|---|---|---|---|
| Portland cement | 64.4 | 21.3 | 5.7 | 3.5 | 0.8 | 0.9 | 2.5 | 0.4 |
| Fly ash | 2.3 | 55.4 | 26.6 | 8.5 | 1.6 | 4.4 | 0.3 | 0.5 |
| Variation Factors | Factors’ Variation Levels | ||
|---|---|---|---|
| −1 | 0 | +1 | |
| X1 | 0.3 | 0.37 | 0.44 |
| X2 | 0.56 | 0.63 | 0.7 |
| X3 | 0.41 | 0.47 | 0.53 |
| X4 | 0.25 | 0.265 | 0.28 |
| X5 | 0.0 | 0.01 | 0.02 |
| Experiment Point No. | Factors Value in Coded Form | ||||
|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | |
| 1 | +1 | +1 | +1 | +1 | +1 |
| 2 | −1 | −1 | +1 | +1 | +1 |
| 3 | −1 | +1 | −1 | −1 | −1 |
| 4 | +1 | −1 | −1 | −1 | −1 |
| 5 | −1 | +1 | −1 | +1 | +1 |
| 6 | +1 | −1 | −1 | +1 | +1 |
| 7 | +1 | +1 | +1 | −1 | −1 |
| 8 | −1 | −1 | +1 | −1 | −1 |
| 9 | −1 | +1 | +1 | +1 | −1 |
| 10 | +1 | −1 | +1 | +1 | −1 |
| 11 | +1 | +1 | −1 | −1 | +1 |
| 12 | −1 | −1 | −1 | −1 | +1 |
| 13 | −1 | +1 | +1 | −1 | +1 |
| 14 | +1 | −1 | +1 | −1 | +1 |
| 15 | +1 | +1 | −1 | +1 | −1 |
| 16 | −1 | −1 | −1 | +1 | −1 |
| 17 | +1 | 0 | 0 | 0 | 0 |
| 18 | −1 | 0 | 0 | 0 | 0 |
| 19 | 0 | +1 | 0 | 0 | 0 |
| 20 | 0 | −1 | 0 | 0 | 0 |
| 21 | 0 | 0 | +1 | 0 | 0 |
| 22 | 0 | 0 | −1 | 0 | 0 |
| 23 | 0 | 0 | 0 | +1 | 0 |
| 24 | 0 | 0 | 0 | −1 | 0 |
| 25 | 0 | 0 | 0 | 0 | +1 |
| 26 | 0 | 0 | 0 | 0 | −1 |
| 27 | 0 | 0 | 0 | 0 | 0 |
| No. | Consumption of Concrete Components, kg/m3 | Compressive Strength, MPa | Criterion L, | Cementing Efficiency Coefficient Kc.e | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MS | Ash | C | W | A | SP | fcm (nc) | fcm (st) | nc | st | nc | st | |
| 1 | 114 | 151 | 138 | 132 | 1944 | 3.0 | 33.1 | 29.7 | 0.240 | 0.215 | 0.32 | 0.26 |
| 2 | 62 | 151 | 202 | 132 | 1944 | 3.0 | 13.9 | 9.3 | 0.069 | 0.046 | −0.33 | −0.43 |
| 3 | 54 | 131 | 95 | 148 | 2025 | 0.0 | 11.3 | 7.7 | 0.119 | 0.081 | 0.21 | 0.11 |
| 4 | 63 | 84 | 140 | 148 | 2025 | 0.0 | 11.7 | 5.3 | 0.084 | 0.038 | −0.02 | −0.26 |
| 5 | 60 | 146 | 107 | 165 | 1944 | 3.7 | 12.9 | 8.5 | 0.121 | 0.080 | 0.26 | 0.13 |
| 6 | 71 | 94 | 157 | 165 | 1944 | 3.7 | 20.9 | 15.7 | 0.133 | 0.100 | 0.31 | 0.12 |
| 7 | 102 | 135 | 123 | 118 | 2025 | 0.0 | 23.9 | 19.3 | 0.194 | 0.157 | 0.16 | 0.08 |
| 8 | 56 | 135 | 181 | 118 | 2025 | 0.0 | 12.3 | 8.5 | 0.068 | 0.047 | −0.36 | −0.45 |
| 9 | 78 | 189 | 138 | 132 | 1944 | 0.0 | 19.5 | 16.3 | 0.141 | 0.118 | 0.08 | 0.02 |
| 10 | 91 | 121 | 202 | 132 | 1944 | 0.0 | 19.9 | 13.9 | 0.098 | 0.069 | −0.19 | −0.33 |
| 11 | 79 | 104 | 95 | 148 | 2025 | 3.3 | 24.9 | 21.1 | 0.261 | 0.221 | 0.61 | 0.50 |
| 12 | 43 | 104 | 140 | 148 | 2025 | 3.3 | 5.7 | 0.7 | 0.041 | 0.005 | −0.24 | −0.42 |
| 13 | 70 | 169 | 123 | 118 | 2025 | 2.6 | 21.1 | 17.1 | 0.171 | 0.139 | 0.11 | 0.04 |
| 14 | 82 | 108 | 181 | 118 | 2025 | 2.6 | 29.1 | 24.3 | 0.161 | 0.134 | 0.01 | −0.10 |
| 15 | 88 | 117 | 107 | 165 | 1944 | 0.0 | 15.7 | 10.7 | 0.147 | 0.100 | 0.34 | 0.20 |
| 16 | 48 | 117 | 157 | 165 | 1944 | 0.0 | 4.1 | 0.2 | 0.026 | 0.100 | −0.30 | −0.45 |
| 17 | 86 | 114 | 143 | 140 | 1985 | 1.6 | 25.6 | 20.6 | 0.179 | 0.144 | 0.29 | 0.16 |
| 18 | 59 | 143 | 143 | 140 | 1985 | 1.6 | 15.8 | 11.6 | 0.111 | 0.081 | 0.04 | −0.07 |
| 19 | 81 | 143 | 116 | 140 | 1985 | 1.6 | 24.1 | 19.9 | 0.208 | 0.172 | 0.35 | 0.25 |
| 20 | 65 | 114 | 170 | 140 | 1985 | 1.6 | 18.5 | 13.3 | 0.109 | 0.078 | −0.03 | −0.18 |
| 21 | 82 | 145 | 161 | 125 | 1985 | 1.4 | 27.2 | 22.3 | 0.169 | 0.138 | 0.11 | 0.01 |
| 22 | 63 | 112 | 125 | 156 | 1985 | 1.7 | 19 | 13.7 | 0.152 | 0.110 | 0.35 | 0.18 |
| 23 | 77 | 136 | 151 | 148 | 1944 | 1.6 | 23.4 | 18.5 | 0.155 | 0.123 | 0.23 | 0.11 |
| 24 | 68 | 121 | 135 | 133 | 2025 | 1.5 | 23.4 | 18.5 | 0.174 | 0.137 | 0.23 | 0.11 |
| 25 | 73 | 129 | 143 | 140 | 1985 | 3.2 | 25.3 | 20.6 | 0.177 | 0.144 | 0.28 | 0.16 |
| 26 | 73 | 129 | 143 | 140 | 1985 | 0.0 | 19.9 | 15 | 0.139 | 0.105 | 0.14 | 0.02 |
| 27 | 73 | 129 | 143 | 140 | 1985 | 1.6 | 23.4 | 18.5 | 0.164 | 0.129 | 0.23 | 0.11 |
| Structure Parameters | Materials’ Consumption, kg/m3 | Compressive Strength, MPa, at 28 Days | Criterion L | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X5 | MS | Ash | C | W | ||
| Microsilica activator | |||||||||
| 0.3 | 0.70 | 0.53 | 0.02 | 63 | 148 | 128 | 122 | 22 | 0.172 |
| 0.37 | 0.70 | 0.53 | 0.02 | 78 | 133 | 128 | 122 | 30 | 0.234 |
| 0.3 | 0.70 | 0.41 | 0.02 | 48 | 112 | 99 | 153 | 15 | 0.152 |
| 0.37 | 0.70 | 0.41 | 0.02 | 60 | 103 | 99 | 153 | 19 | 0.192 |
| 0.44 | 0.70 | 0.53 | 0.02 | 93 | 119 | 128 | 122 | 33 | 0.258 |
| 0.37 | 0.63 | 0.47 | 0.02 | 62 | 107 | 140 | 138 | 23 | 0.164 |
| Without activator | |||||||||
| 0.0 | 0.47 | 0.36 | 0.0 | - | 113 | 174 | 189 | 15 | 0.086 |
| 0.0 | 0.47 | 0.36 | 0.02 | - | 113 | 174 | 164 | 20 | 0.115 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dvorkin, L.; Zhitkovsky, V.; Lapovskaya, S.; Ribakov, Y. Investigation of the Cementing Efficiency of Fly Ash Activated by Microsilica in Low-Cement Concrete. Materials 2023, 16, 6859. https://doi.org/10.3390/ma16216859
Dvorkin L, Zhitkovsky V, Lapovskaya S, Ribakov Y. Investigation of the Cementing Efficiency of Fly Ash Activated by Microsilica in Low-Cement Concrete. Materials. 2023; 16(21):6859. https://doi.org/10.3390/ma16216859
Chicago/Turabian StyleDvorkin, Leonid, Vadim Zhitkovsky, Svetlana Lapovskaya, and Yuri Ribakov. 2023. "Investigation of the Cementing Efficiency of Fly Ash Activated by Microsilica in Low-Cement Concrete" Materials 16, no. 21: 6859. https://doi.org/10.3390/ma16216859





