Experimental Study of Dynamic Tensile Strength of Steel-Fiber-Reinforced Self-Compacting Concrete Using Modified Hopkinson Bar
Abstract
:1. Introduction
2. Experimental Procedure
2.1. SFRSCC Mix Design
2.2. Basic Properties of SFRSCC
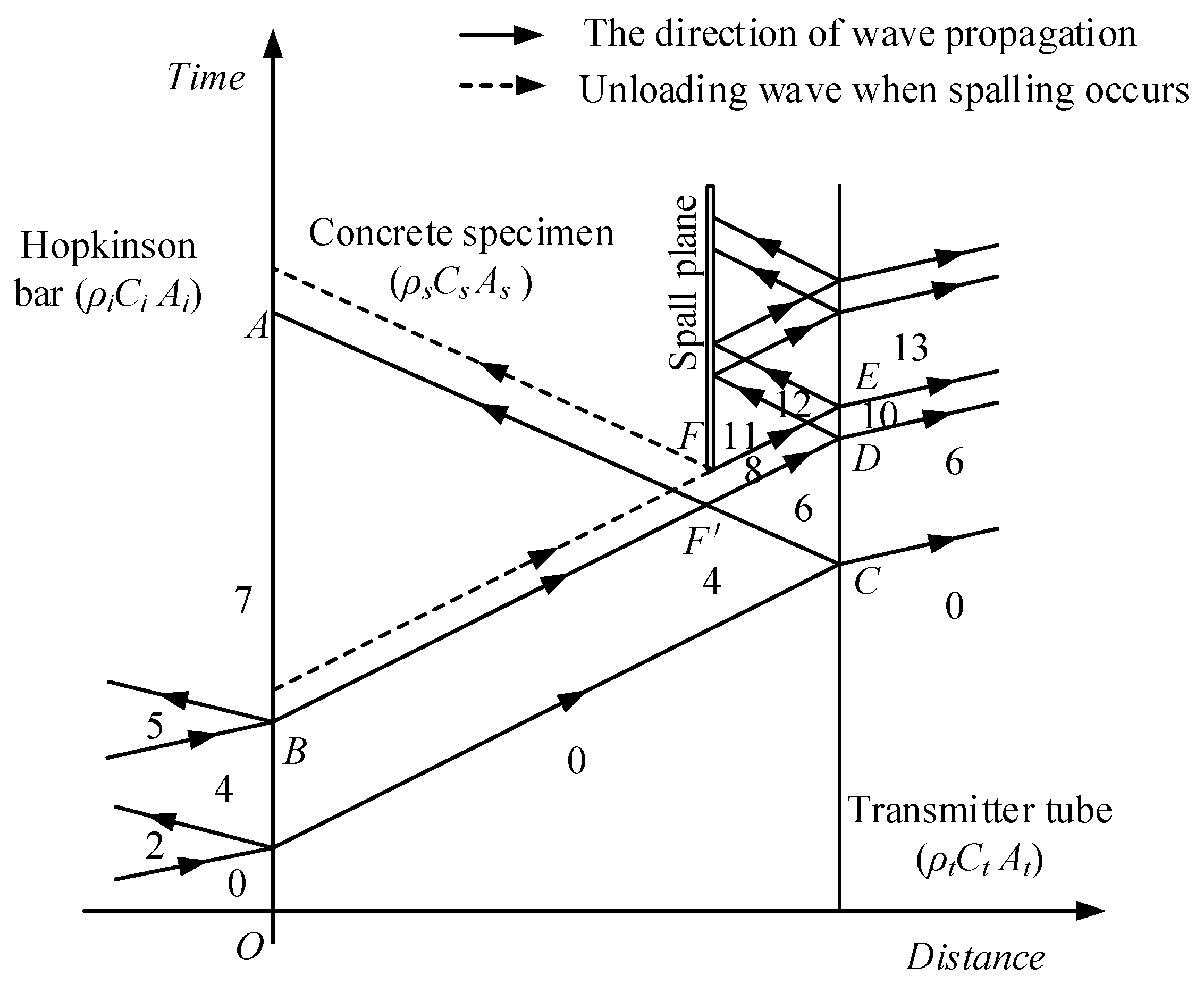
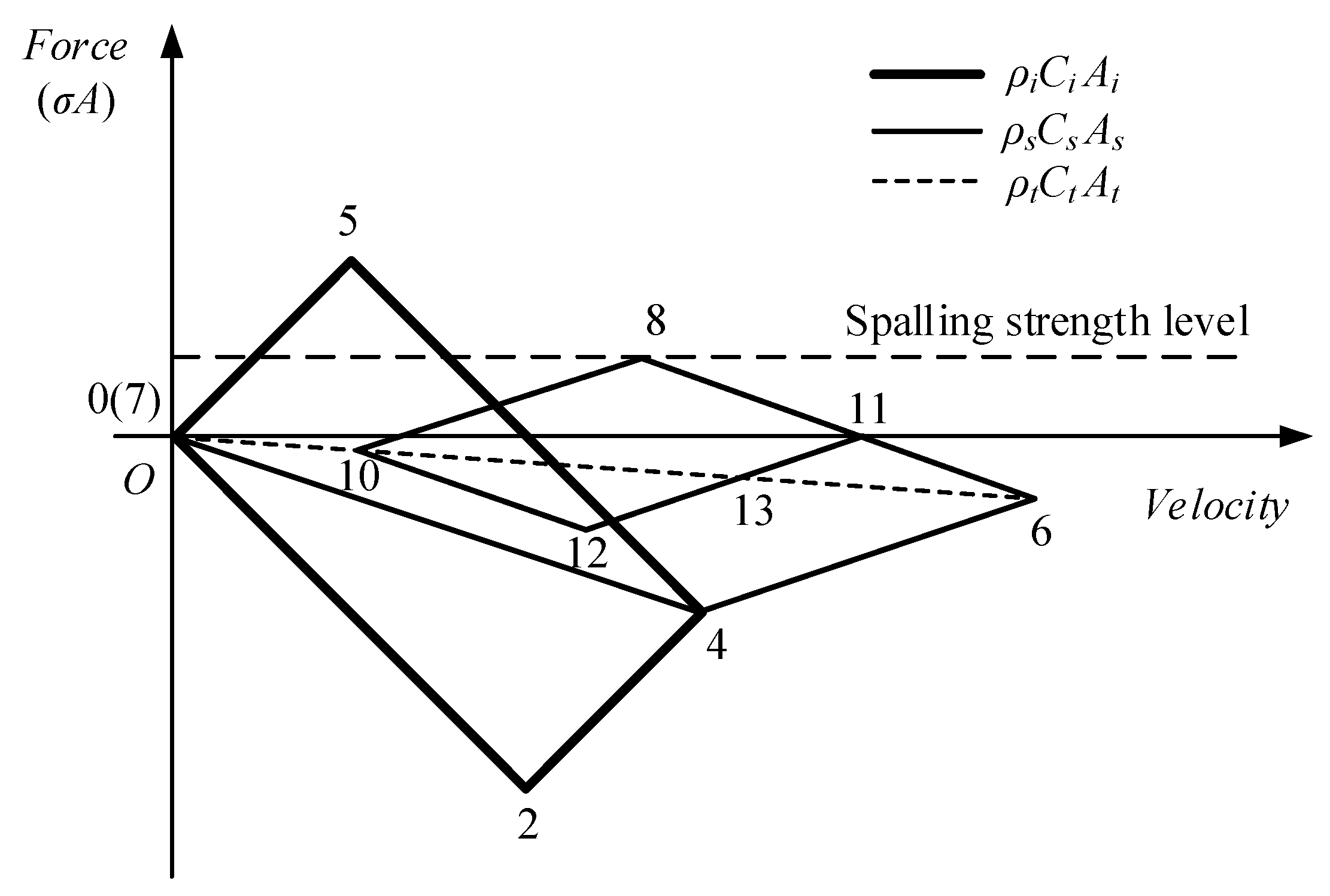
2.3. Modified Hopkinson Bar Technique
3. Results and Discussion
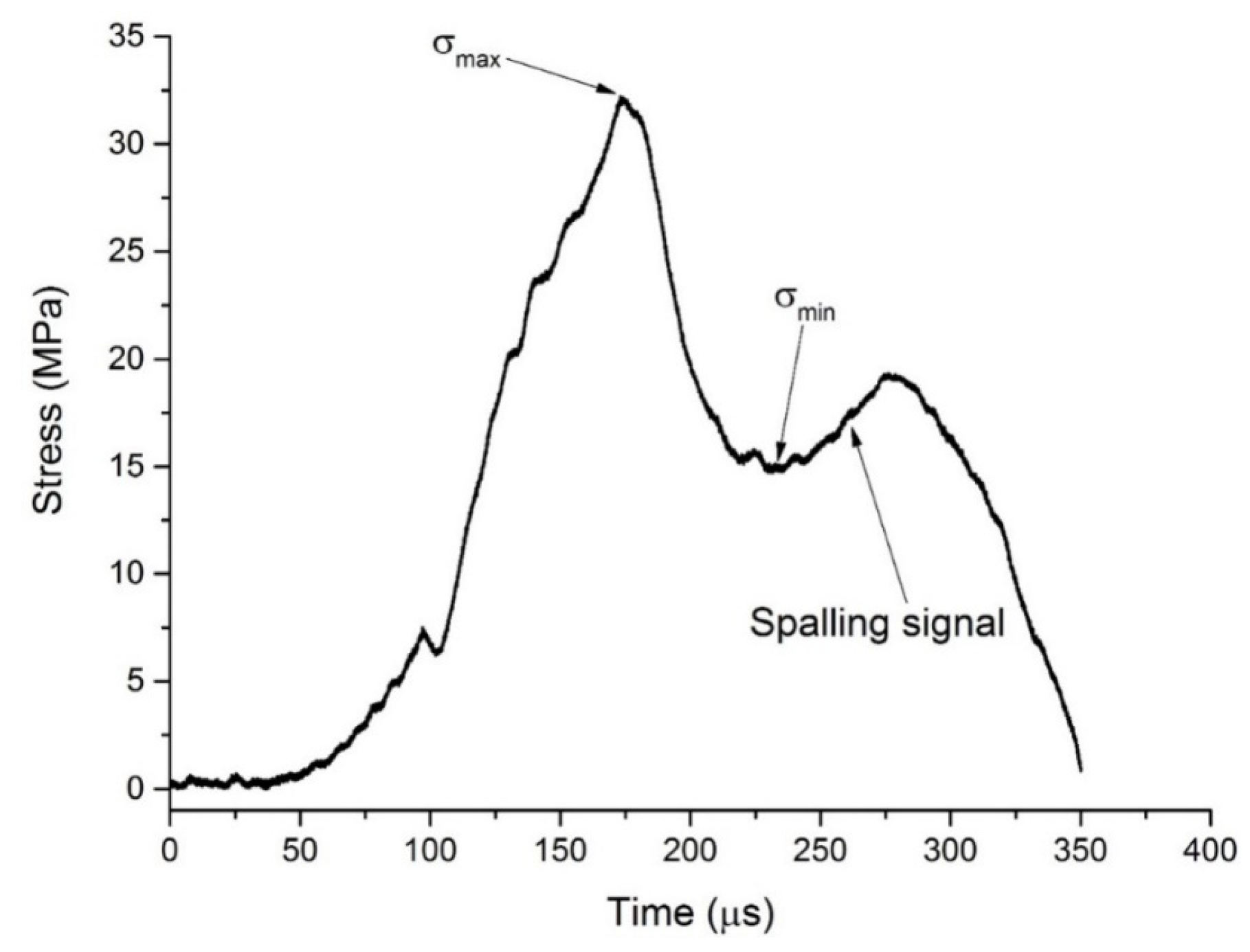
3.1. Experimental Results
3.2. Fiber-Reinforcement Effect on SFRSCC Tensile Strength
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmad, H.; Hashim, M.H.M.; Hamzah, S.H.; Bakar, A.A. Steel Fibre Reinforced Self-Compacting Concrete (SFRSC) performance in slab application: A review. AIP Conf. Proc. 2016, 1774, 030024. [Google Scholar] [CrossRef]
- Gencel, O.; Brostow, W.; Datashvili, T.; Thedford, M. Workability and Mechanical Performance of Steel Fiber-Reinforced Self-Compacting Concrete with Fly Ash. Compos. Interface 2011, 18, 169–184. [Google Scholar] [CrossRef]
- Khaloo, A.; Raisi, E.M.; Hosseini, P.; Tahsiri, H. Mechanical performance of self-compacting concrete reinforced with steel fibers. Constr. Build. Mater. 2014, 51, 179–186. [Google Scholar] [CrossRef]
- Madandoust, R.; Ranjbar, M.M.; Ghavidel, R.; Shahabi, S.F. Assessment of factors influencing mechanical properties of steel fiber reinforced self-compacting concrete. Mater. Des. 2015, 83, 284–294. [Google Scholar] [CrossRef]
- Ding, X.X.; Li, C.Y.; Han, B.; Lu, Y.Z.; Zhao, S.B. Effects of different deformed steel-fibers on preparation and fundamental properties of self-compacting SFRC. Constr. Build. Mater. 2018, 168, 471–481. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghasemi, M.R.; Mousavi, S.R. Investigating the effects of maximum aggregate size on self-compacting steel fiber reinforced concrete fracture parameters. Constr. Build. Mater. 2018, 162, 674–682. [Google Scholar] [CrossRef]
- Miao, B.; Chern, J.C.; Yang, C.A. Influences of fiber content on properties of self-compacting steel fiber reinforced concrete. J. Chin. Inst. Eng. 2003, 26, 523–530. [Google Scholar] [CrossRef]
- Yardimci, M.Y.; Baradan, B.; Tasdemir, M.A. Effect of fine to coarse aggregate ratio on the rheology and fracture energy of steel fibre reinforced self-compacting concretes. Sadhana-Acad. P. Eng. S. 2014, 39, 1447–1469. [Google Scholar] [CrossRef]
- Zarrin, O.; Khoshnoud, H.R. Experimental investigation on self-compacting concrete reinforced with steel fibers. Struct. Eng. Mech. 2016, 59, 133–151. [Google Scholar] [CrossRef]
- Kandasamy, S.; Akila, P. Experimental analysis and modeling of steel fiber reinforced SCC using central composite design. Comput. Concr. 2015, 15, 215–229. [Google Scholar] [CrossRef]
- Gulsan, M.E.; Abdulhaleem, K.N.; Kurtoglu, A.E.; Cevik, A. Size effect on strength of Fiber-Reinforced Self-Compacting Concrete (SCC) after exposure to high temperatures. Comput. Concr. 2018, 21, 681–695. [Google Scholar] [CrossRef]
- Brara, A.; Camborde, F.; Klepaczko, J.R.; Mariotti, C. Experimental and numerical study of concrete at high strain rates in tension. Mech. Mater. 2001, 33, 33–45. [Google Scholar] [CrossRef]
- Habel, K.; Gauvreau, P. Response of ultra-high performance fiber reinforced concrete (UHPFRC) to impact and static loading. Cem. Concr. Compos. 2008, 30, 938–946. [Google Scholar] [CrossRef]
- Caverzan, A.; Cadoni, E.; di Prisco, M. Dynamic Tensile Behaviour of Self Compacting Steel Fibre Reinforced Concrete. Appl. Mech. Mater. 2011, 82, 220–225. [Google Scholar] [CrossRef]
- Cadoni, E.; Caverzani, A.; di Priscoi, M. Dynamic behaviour of HPFRCC in tension. EPJ Web Conf. 2012, 26, 01014. [Google Scholar] [CrossRef]
- Zhang, X.; Ruiz, G.; Tarifa, M.; Cendon, D.; Galvez, F.; Alhazmi, W.H. Dynamic Fracture Behavior of Steel Fiber Reinforced Self-Compacting Concretes (SFRSCCs). Materials 2017, 10, 1270. [Google Scholar] [CrossRef] [PubMed]
- Lian, C.; Wang, Y.B.; Liu, S.; Hao, Y.F. Experimental Study of the Dynamic Compressive and Tensile Strengths of Fly Ash and Slag Based Alkali-Activated Concrete Reinforced With Basalt Fibers. Front. Mater. 2021, 8, 651581. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, H.; Zhang, M.Z. Experimental study on static and dynamic properties of fly ash-slag based strain hardening geopolymer composites. Cem. Concr. Compos. 2022, 129, 104481. [Google Scholar] [CrossRef]
- JGJ/T 221-2010; Chinese Industry Standard. Technical Specification for Application of Fiber Reinforced Concrete. Architecture & Building Press: Beijing, China, 2010.
- JGJ/T 221-2012; Chinese Industry Standard. Technical Specification for Application of Self-Compacting Concrete. Architecture & Building Press: Beijing, China, 2012.
- Hu, S.; Zhang, L.; Wu, H.; Wu, X. Experimental study on spalling strength of concrete. Eng. Mech. 2004, 21, 128–132. (In Chinese) [Google Scholar]
- Zhang, L.; Hu, S. A novel experimental technique to determine the spalling strength of concretes. Explos. Shock Waves 2006, 26, 537–542. (In Chinese) [Google Scholar]
- Lok, T.S.; Zhao, P.J. Impact Response of Steel Fiber-Reinforced Concrete Using a Split Hopkinson Pressure Bar. J. Mater. Civ. Eng. 2004, 16, 54–59. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, B.; Forrestal, M.J. A split Hopkinson bar technique for low-impedance materials. Exp. Mech. 1999, 39, 81–85. [Google Scholar] [CrossRef]
- Ninan, L.; Tsai, J.; Sun, C.T. Use of split Hopkinson pressure bar for testing off-axis composites. Int. J. Impact Eng. 2001, 25, 291–313. [Google Scholar] [CrossRef]
- Sun, X.; Zhao, K.; Li, Y.; Huang, R.; Ye, Z.; Zhang, Y.; Ma, J. A study of strain-rate effect and fiber reinforcement effect on dynamic behavior of steel fiber-reinforced concrete. Constr. Build. Mater. 2018, 158, 657–669. [Google Scholar] [CrossRef]
- Zain, M.F.M.; Mahmud, H.B.; Ilham, A.; Faizal, M. Prediction of splitting tensile strength of high-performance concrete. Cem. Concr. Res. 2002, 32, 1251–1258. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, S.; Chen, D.; Zhang, S.; Yu, Z.; Liu, F. Spall fracture properties of steel- fiber-reinforced concrete. Explos. Shock Waves 2009, 29, 119–124. (In Chinese) [Google Scholar]
- Bischoff, P.H.; Perry, S.H. Impact Behavior of Plain Concrete Loaded in Uniaxial Compression. J. Eng. Mech. 1995, 121, 685–693. [Google Scholar] [CrossRef]







| Specimen Type | Cement | Sand | Aggregate | Fly Ash | Water | Superplasticizer | Fibers |
|---|---|---|---|---|---|---|---|
| C40-0.5% | 427 | 724 | 862 | 107 | 171 | 2.6 | 39 |
| C40-1.0% | 427 | 721 | 856 | 107 | 171 | 2.6 | 78 |
| C40-1.5% | 427 | 714 | 849 | 107 | 171 | 2.6 | 117 |
| C40-2.0% | 427 | 708 | 843 | 107 | 171 | 2.0 | 156 |
| C60-0.5% | 494 | 714 | 831 | 49 | 148 | 3.3 | 39 |
| C60-1.0% | 494 | 696 | 810 | 49 | 148 | 4.4 | 78 |
| C60-1.5% | 494 | 678 | 789 | 49 | 148 | 5.1 | 117 |
| C60-2.0% | 494 | 658 | 778 | 49 | 148 | 3.6 | 156 |
| Mesh Size (mm) | Passing Percentage (%) |
|---|---|
| 2.36 | 98.43 |
| 4.75 | 93.42 |
| 9.5 | 44.68 |
| 16 | 2.13 |
| 19 | 0.00 |
| Test Method | Properties Tested |
|---|---|
| Slump-flow test | Filling ability, Segregation resistance |
| L-box test | Passing ability, Segregation resistance |
| Slump-flow time test | Filling ability |
| U-box test | Passing ability, Segregation resistance |
| J-ring test | Passing ability |
| SFRSCC Type | Slump-Flow Value (mm) | L-Box Test (h2/h1) | Quasi-Static Compressive Strength fc (MPa) |
|---|---|---|---|
| C40-0.5% | 795 | 0.91 | 49.8 |
| C40-1.0% | 845 | 0.91 | 43.8 |
| C40-1.5% | 750 | 0.93 | 46.6 |
| C40-2.0% | 710 | 0.90 | 48.8 |
| C60-0.5% | 755 | 0.89 | 60.1 |
| C60-1.0% | 750 | 0.93 | 69.6 |
| C60-1.5% | 760 | 0.93 | 64.9 |
| C60-2.0% | 765 | 0.94 | 66.1 |
| Fiber Volume Fraction (%) | Tensile Strength σt (MPa) | |
|---|---|---|
| C40 | C60 | |
| 0.5 | 14.3 ± 0.3 | 18.5 ± 0.6 |
| 1.0 | 17.0 ± 0.4 | 21.4 ± 0.4 |
| 1.5 | 19.8 ± 0.3 | 23.0 ± 0.5 |
| 2.0 | 23.1 ± 0.5 | 27.0 ± 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Huo, Y.; Wang, N.; Sun, Z.; Bian, L.; Huang, R. Experimental Study of Dynamic Tensile Strength of Steel-Fiber-Reinforced Self-Compacting Concrete Using Modified Hopkinson Bar. Materials 2023, 16, 5707. https://doi.org/10.3390/ma16165707
Ma J, Huo Y, Wang N, Sun Z, Bian L, Huang R. Experimental Study of Dynamic Tensile Strength of Steel-Fiber-Reinforced Self-Compacting Concrete Using Modified Hopkinson Bar. Materials. 2023; 16(16):5707. https://doi.org/10.3390/ma16165707
Chicago/Turabian StyleMa, Jian, Yifei Huo, Ning Wang, Zhang Sun, Liang Bian, and Ruiyuan Huang. 2023. "Experimental Study of Dynamic Tensile Strength of Steel-Fiber-Reinforced Self-Compacting Concrete Using Modified Hopkinson Bar" Materials 16, no. 16: 5707. https://doi.org/10.3390/ma16165707




