Analysis of Diffusion Coefficients of Iron Monoboride and Diiron Boride Coating Formed on the Surface of AISI 420 Steel by Two Different Models: Experiments and Modelling
Abstract
:1. Introduction
2. Boronizing Properties of Iron and Steel
- (i)
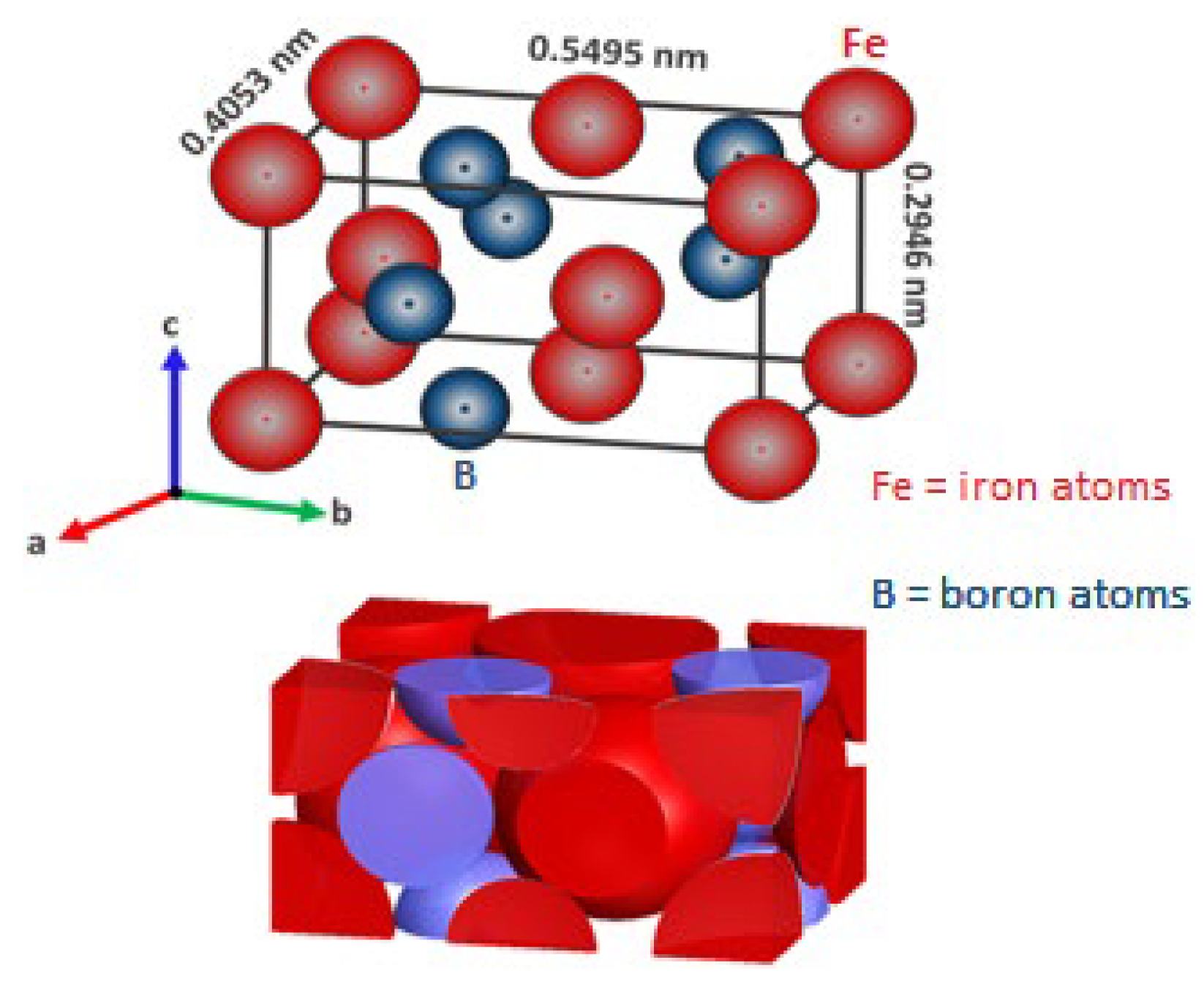
- An outer FeB layer which has an orthorhombic crystal lattice containing ~16.4% boron that is composed of 8 atoms in a cell (with four iron atoms and four boron atoms) with axial lengths: a = 405.3 × 10−12 m, b = 549.5 × 10−12 m, c = 294.6 × 10−12 m (see Figure 1).
- (ii)
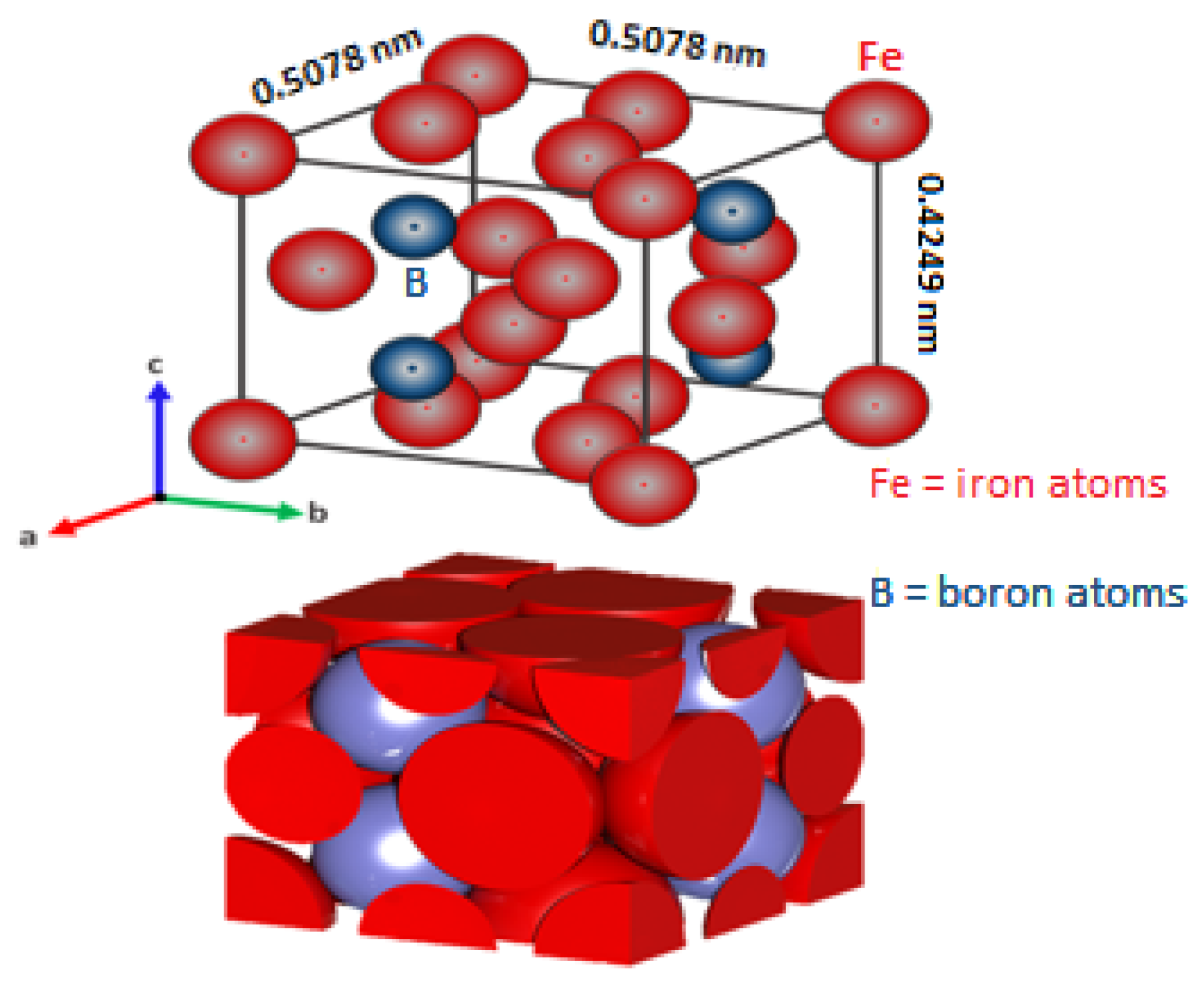
- With a microhardness range of approximately 1900–2100 Vickers Hardness, the melting point of iron monoboride is about 1663 K, Young’s modulus is about 590 × 103 MPa, the density is 6.7 × 103 kg∙m–3, its molecular mass 66.6 g∙mol−1, and the coefficient of thermal expansion is 84 × 10–9 K−1 in the temperature range of about 473–873 K. An important quality to note is that the FeB phase is chemically stable up to 1723 K in the Fe–B system [6].
3. Resources and Techniques
3.1. Resources and Experimental Method
3.2. Feature Tools
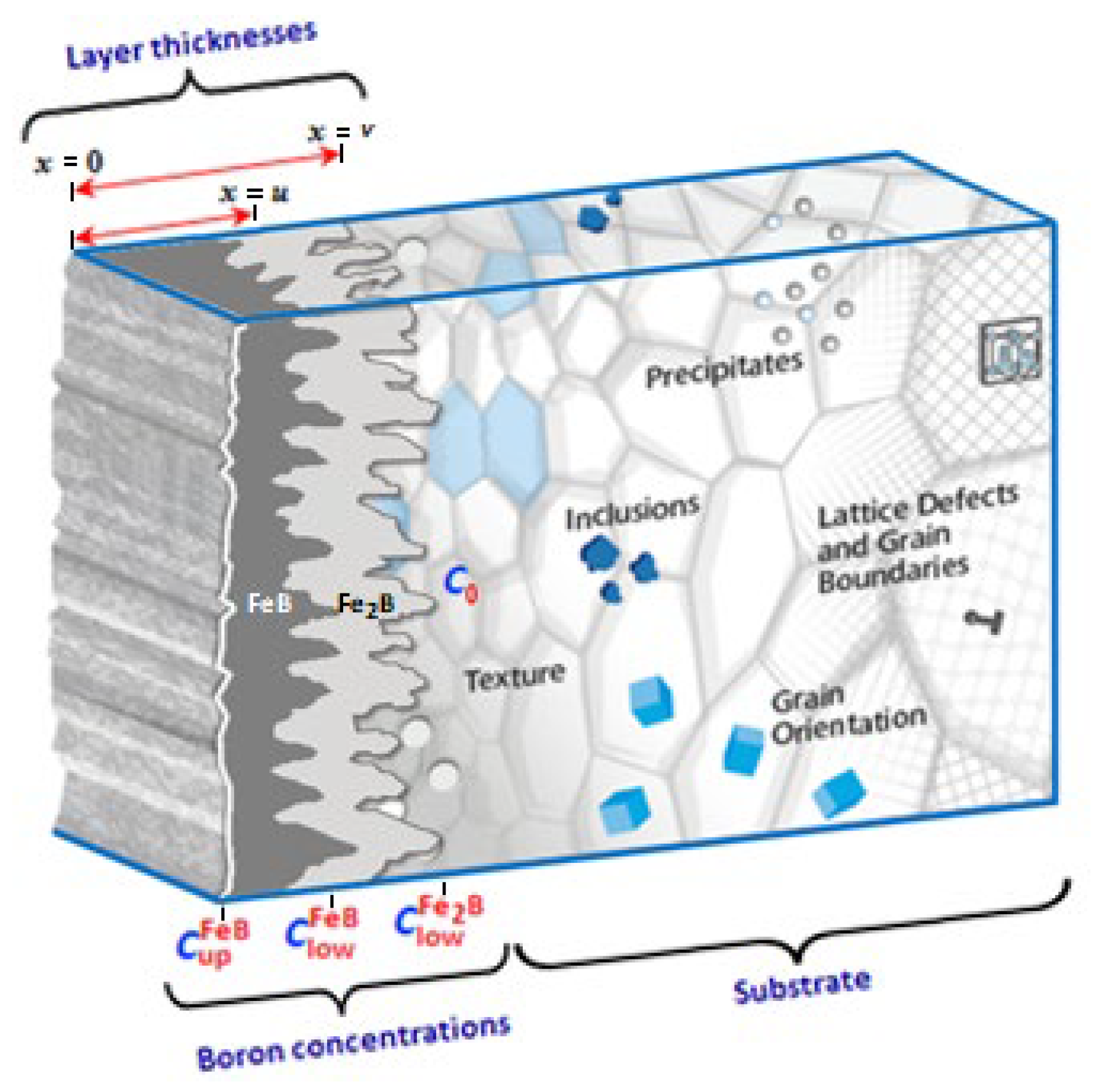
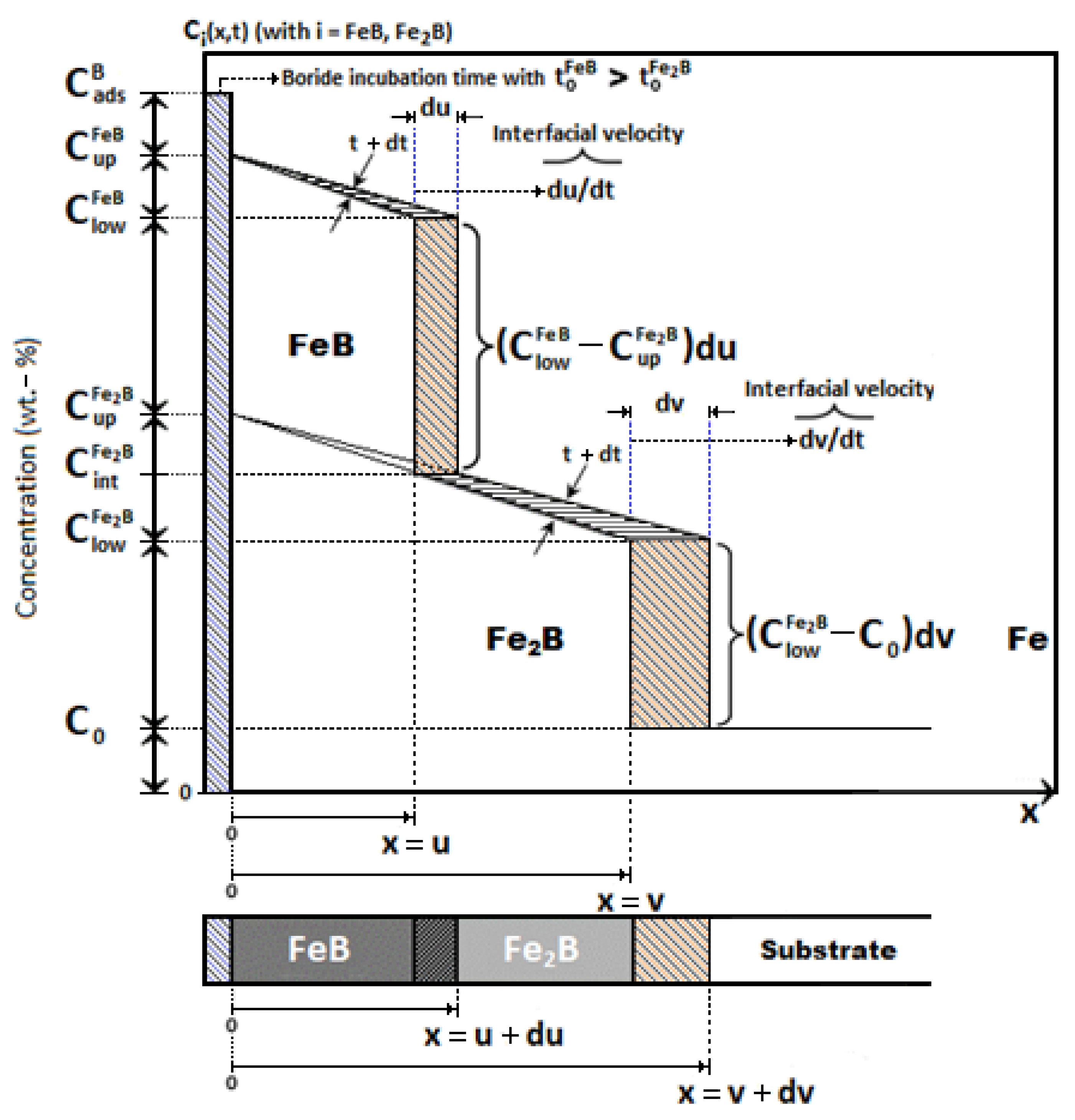
3.3. First Mathematical Model: Linear Diffusion Model without Time Dependence (Steady-State)
- After a particular incubation time, the first iron borides nucleate and form a primitive coating.
- The iron monoboride and diiron boride coatings grow as a result of perpendicular diffusion of boron atoms on the surface of the ferrous and non-ferrous alloys.
- Boron atoms obtained from the chemical reaction flow in one direction only.
- Boron concentrations at the growth interfaces (FeB/Fe2B, Fe2B/substrate) and surface remain unchanged during the process.
- The FeB and Fe2B boride layers form under conditions of thermodynamic equilibrium, i.e., constant temperature.
- The iron monoboride and diiron boride coatings follow the theoretical law of parabolic propagation.
- A planar morphology is assumed at the iron monoboride/diiron boride and diiron boride/substate growth interfaces.
3.3.1. Phase Fe2B
3.3.2. Phase FeB
3.4. Second Mathematical Model: Diffusion Model with Time Dependence
3.4.1. Phase Fe2B
3.4.2. Phase FeB
4. Results
4.1. Microscopic Inspection of the Boride Coatings Formed on the Surface of the Ferrous Alloy
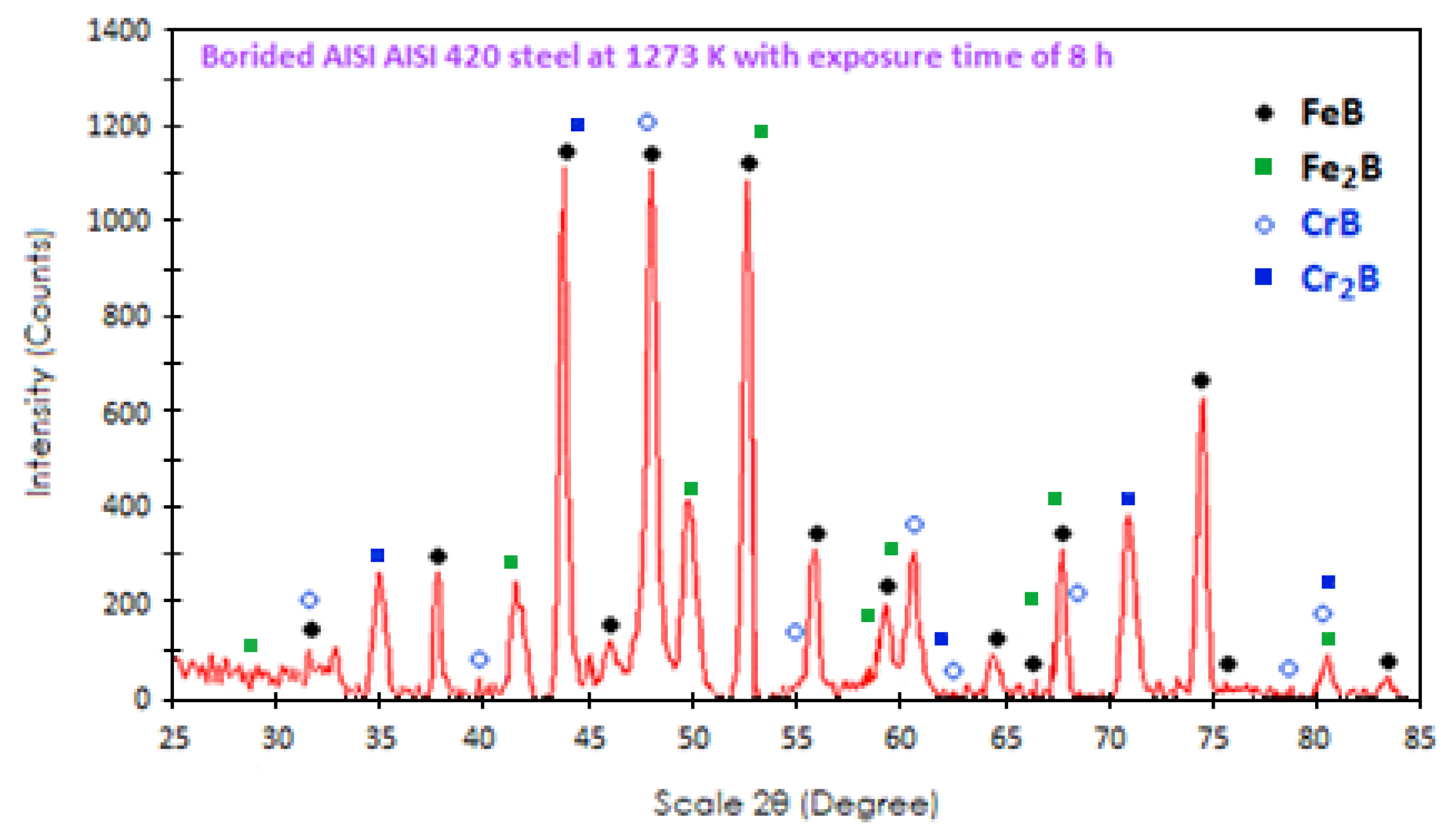
4.2. X-ray Diffraction (XRD)
4.3. Microhardness Vickers Profile
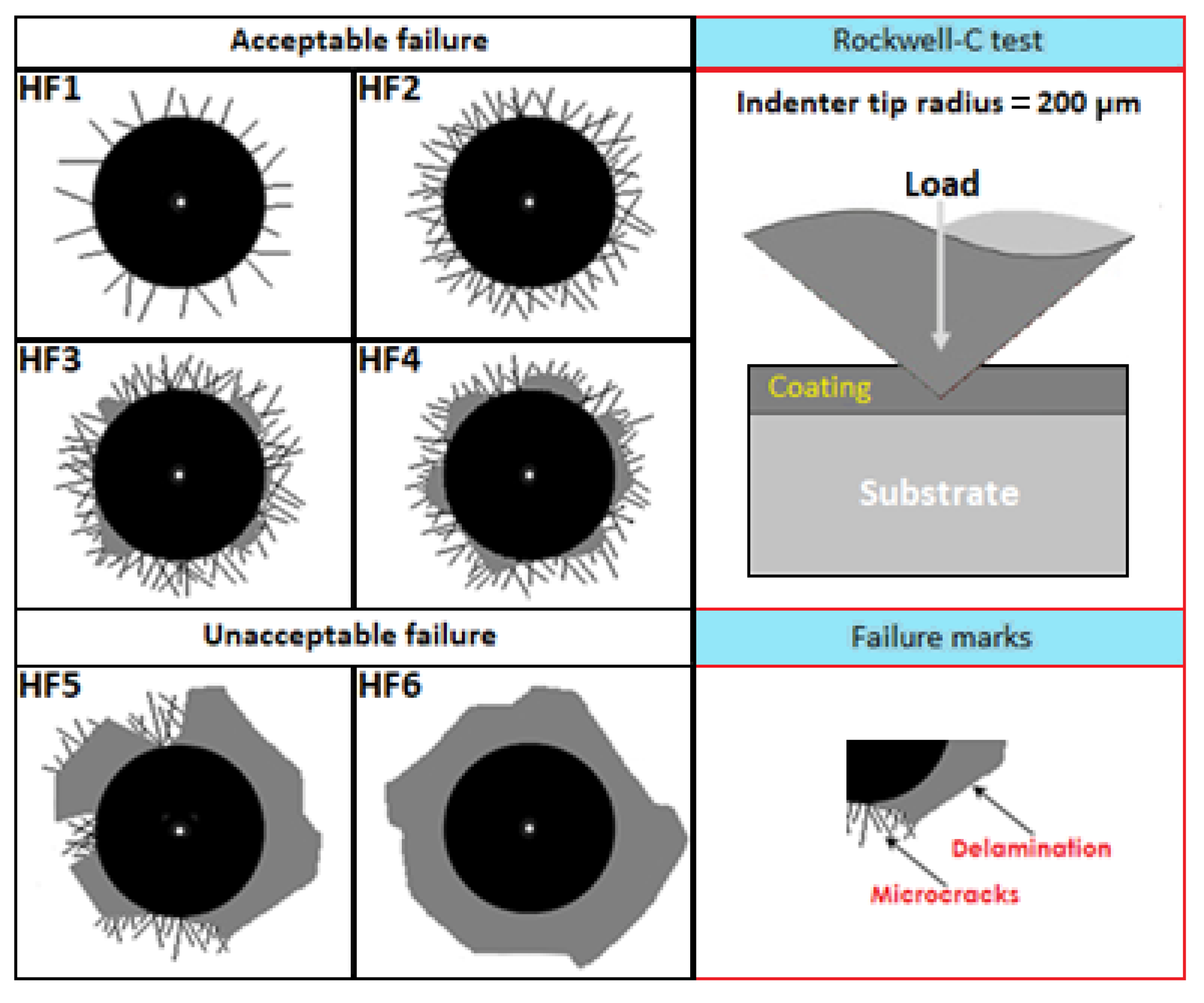
4.4. Cohesion by Daimler–Benz Rockwell-C Test
4.5. Pin-on-Disc Testing
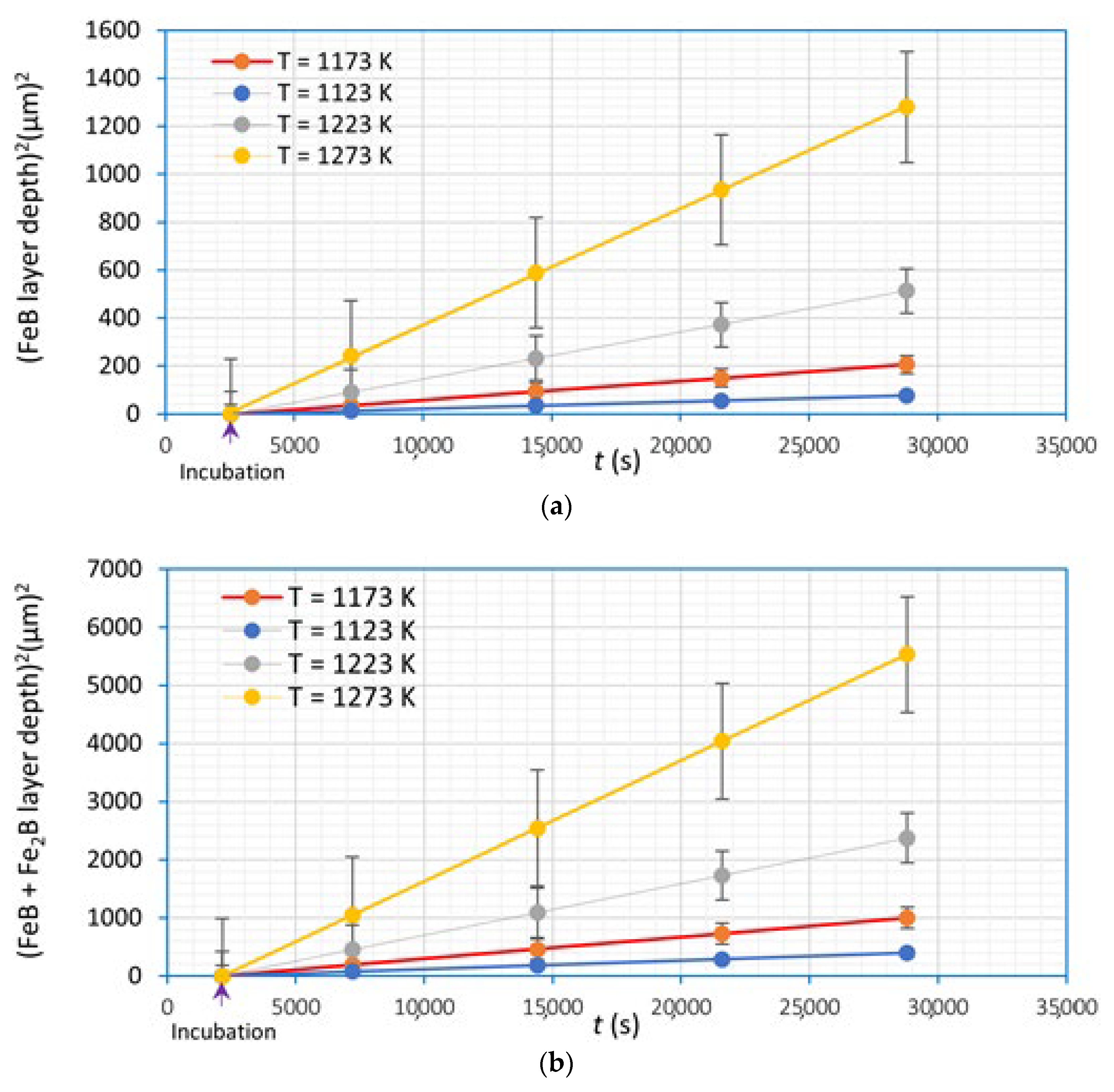
4.6. Determination of Parabolic Growth Law Constants of Boronized Coatings (Iron Monoboride and Diiron Boride)
4.6.1. Determination of Diffusion Coefficients of Boronized Coatings (Iron Monoboride and Diiron Boride) by the First Mass Transfer Model without Time Dependence
4.6.2. Determination of Diffusion Coefficients of Boronized Coatings (Iron Monoboride and Diiron Boride) by the Second Mass Transfer Model with Time Dependence
5. Discussion
5.1. Discussion of the Two Diffusion Models
5.2. Derivation of the Activation Energies of Boron in FeB and Fe2B: Comparison with the Literature
5.3. Verification of the Mathematical Models of Mass Transfer by Experimental Data
6. Conclusions
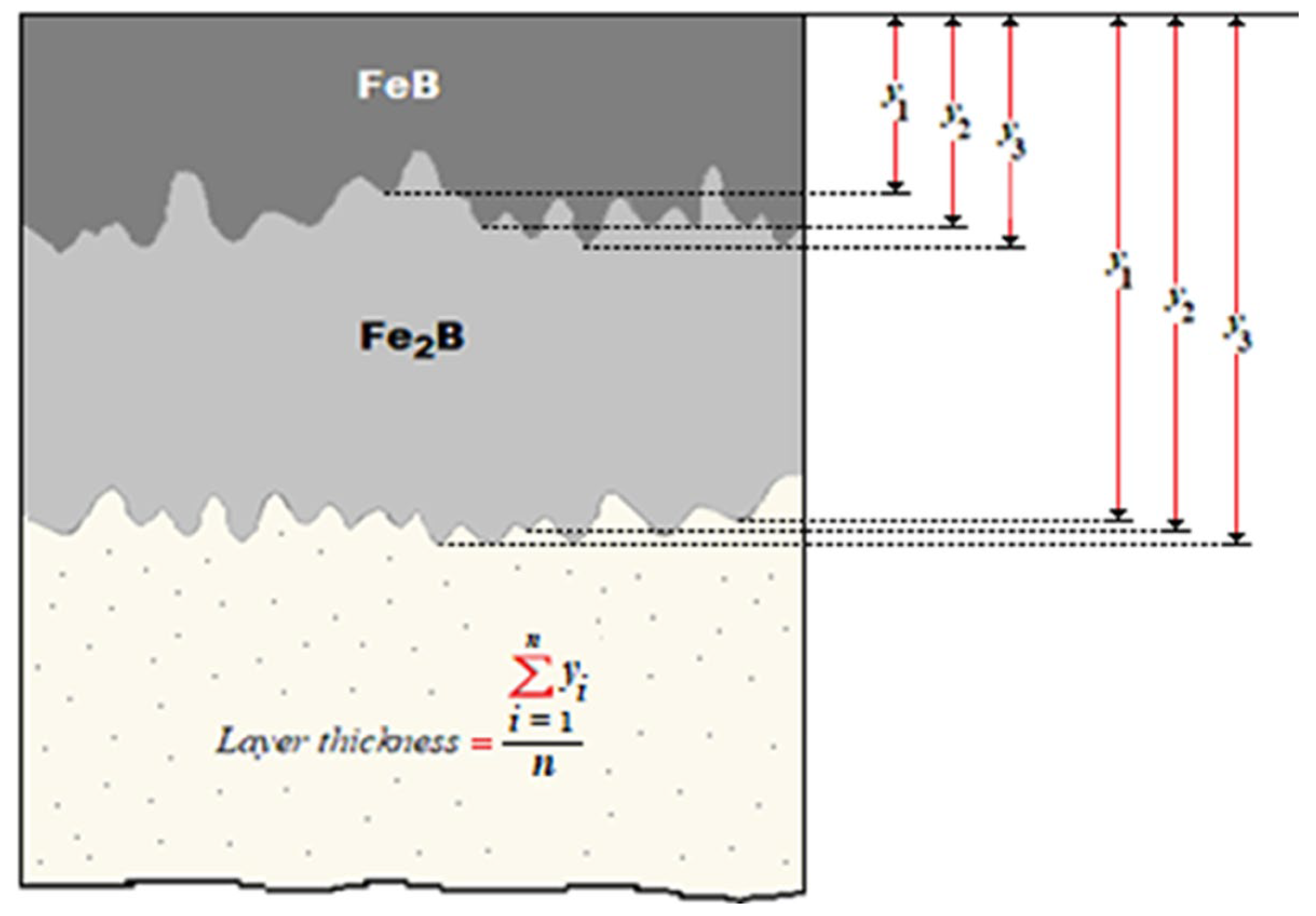
- XRD analysis verified the presence of iron monoboride, diiron boride, chromium monoboride, and chromium diiron boride phases. Scanning Electron Microscopy (SEM) images of the cross-sections of the boronized coatings showed that the growth fronts tend to be flat.
- The surface hardness profile of AISI 420 stainless steel hardened by thermochemical boronizing treatment reached elevated hardnesses from about 1767 HV0.05 to 2250 HV0.05 at 40 μm from the surface and 345 HV0.05 in the core of the untreated material.
- Based on the data obtained from the Daimler-Benz Rockwell-C indentations of the adhesion tests of the boronized coatings, it was found that the specimen hardened at a temperature of 1123 K for 2 h, exhibited adhesion quality that fell under the HF4 category, as shown in Figure 11 of the comparative patterns. This indicates that the specimen has sufficient cohesion quality. On the other hand, the sample hardened at a temperature of 1273 K for 8 h is associated with the HF5 category, meaning it does not have sufficient adhesion.
- The values of the friction coefficients for the untreated sample ranged from 0.3 to 0.7. On the other hand, for the hardened specimen at a temperature of 1273 K with 8 h of exposure time, the values ranged from 0.05 to 0.4. It is interesting how the treatment affected the range of values.
- The results of the pin-on-disc tests showed that the untreated specimen (AISI 420 stainless steel) showed greater predominantly adhesive wear. On the other hand, due to the presence of the boronized coatings (iron monoboride and diiron boride) and the dispersed carbides acting as solid lubricants, the width of the wear track was significantly reduced, improving the wear resistance considerably, as can be seen in Figure 14b. In addition, as the hardened surface (boronized surface) was sliding on a much softer surface, wear of an abrasive nature occurred.
- Very similar results were obtained for the constants and for both proposed mathematical diffusion models (model without time dependence and with time dependence); this equivalence was demonstrated through the Taylor series development of the functions that integrate Equations (27) and (29) which refer to the diffusion model with time dependence, considering only the first order of the series, which allows for reproducing the results of the model without time dependence (see Equations (14) and (21)).
- After conducting experiments on AISI 420 stainless steel, it was found that the mathematical mass transfer models used were equivalent. The activation energies for the iron monoboride and diiron boride phases formed on the surface were also estimated. The values obtained were 221.9 kJ∙mol−1 and 209.1 kJ∙mol−1. These values were compared with those found in the literature, which can be found in Table 6.
- After performing experiments for two different boronizing conditions, we verified the steady-state mass transfer model. The results obtained agree satisfactorily with the simulations (see Table 7). This shows that the model is accurate and can be relied upon for future experiments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kulka, M. Trends in Thermochemical Techniques of Boronizing. In Current Trends in Boronizing, 1st ed.; Springer: Cham, Switzerland, 2019; pp. 1–281. [Google Scholar]
- Sinha, A.K. Boriding (Boronizing) of steels. In Heat Treating, 1st ed.; ASM Heat Treating, ASM Handbook; ASM International: Russell, OH, USA, 1991; Volume 4, pp. 978–1000. [Google Scholar]
- Graf von Matuschka, A. Boronizing, 1st ed.; Carl Hanser Verlag: München, Germany, 1980; pp. 1–97. [Google Scholar]
- Davis, J.R. Surface Engineering for Corrosion and Wear Resistance, 1st ed.; ASM International: Russell, OH, USA, 2001; pp. 1–257. [Google Scholar]
- Singhal, S.C. A hard diffusion boride coating for ferrous materials. Thin Solid Films 1977, 45, 321–329. [Google Scholar] [CrossRef]
- Krukovich, M.G.; Prusakov, B.A.; Sizov, I.G. The components and phases of systems “boron–iron” and “boron–carbon–iron”. In Plasticity of Boronized Layers, 1st ed.; Springer: Cham, Switzerland, 2016; Volume 237, pp. 13–21. [Google Scholar]
- Keddam, M.; Kulka, M.; Makuch, N.; Pertek, A.; Małdzinski, L. A kinetic model for estimating the boron activation energies in the FeB and Fe2B layers during the gas–boronizing of Armco iron: Effect of boride incubation times. Appl. Surf. Sci. 2014, 298, 155–163. [Google Scholar] [CrossRef]
- Keddam, M.; Chentouf, S.M. A diffusion model for describing the player growth (FeB/Fe2B) during the iron powder–pack boronizing. Appl. Surf. Sci. 2005, 252, 393–399. [Google Scholar] [CrossRef]
- Ozdemir, O.; Usta, M.; Bindal, C.; Ucisik, A.H. Hard iron boride (Fe2B) on 99.97 wt% pure iron. Vacuum 2006, 80, 1391–1395. [Google Scholar] [CrossRef]
- Kulka, M.; Makuch, N.; Piasecki, A. Nanomechanical characterization and fracture toughness of FeB and Fe2B iron borides produced by gas boronizing of Armco iron. Surf. Coat. Technol. 2017, 325, 515–532. [Google Scholar] [CrossRef]
- Ucisik, A.H.; Bindal, C. Fracture toughness of boride formed on low–alloy steels. Surf. Coat. Technol. 1997, 94–95, 561–565. [Google Scholar] [CrossRef]
- Hernández–Sanchez, E.; Rodriguez–Castro, G.; Meneses–Amador, A.; Bravo–Bárcenas, D.; Arzate–Vazquez, I.; Martínez–Gutiérrez, H.; Romero–Romo, M.; Campos–Silva, I. Effect of the anisotropic growth on the fracture toughness measurements obtained in the Fe2B layer. Surf. Coat. Technol. 2013, 237, 292–298. [Google Scholar] [CrossRef]
- Campos–Silva, I.; Hernández–Sánchez, E.; Rodríguez–Castro, G.; Cimenoglu, H.; Nava–Sánchez, J.L.; Meneses–Amador, A.; Carrera–Espinoza, R. A study of indentation for mechanical characterization of the Fe2B layer. Surf. Coat. Technol. 2013, 232, 173–181. [Google Scholar] [CrossRef]
- Ninham, A.J.; Hutchings, I.M. On the morphology of thermochemically–produced Fe2B/Fe interfaces. J. Vac. Sci. Technol. A 1986, A4, 2827–2831. [Google Scholar] [CrossRef]
- Rodríguez –Castro, G.; Campos–Silva, I.; Martínez–Trinidad, J.; Figueroa–López, U.; Arzate–Vázquez, I.; Hernández–Sánchez, E.; Hernández–Sánchez, J. Mechanical behavior of AISI 1045 steels subjected to powder–pack boronizing. Kov. Mater. 2012, 50, 357–364. [Google Scholar]
- Palombarini, G.; Carbucicchio, M. On the morphology of thermochemically produced Fe2B/Fe interfaces. J. Mater. Sci. Lett. 1984, 3, 791–794. [Google Scholar] [CrossRef]
- Martini, C.; Palombarini, G.; Carbucicchio, M. Mechanism of thermochemical growth of iron borides on iron. J. Mater. Sci. 2004, 39, 933–937. [Google Scholar] [CrossRef]
- Tsipas, D.N.; Rus, J. Boronizing of alloy steels. J. Mater. Sci. Lett. 1987, 6, 118–120. [Google Scholar] [CrossRef]
- Brakman, C.M.; Gommers, A.W.J.; Mittemeijer, E.J. Boronizing of Fe and Fe–C, Fe–Cr, and Fe–Ni alloys; boride–layer growth kinetics. J. Mater. Res. 1989, 4, 1354–1370. [Google Scholar] [CrossRef]
- Kulka, M.; Pertek, A.; Makuch, N. The importance of carbon concentration–depth profile beneath iron borides for low–cycle fatigue strength. Mater. Sci. Eng. A 2011, 528, 8641–8650. [Google Scholar] [CrossRef]
- Kulka, M.; Makuch, N.; Pertek, A.; Piasecki, A. An alternative method of gas boronizing applied to the formation of borocarburized layer. Mater. Charact. 2012, 72, 59–67. [Google Scholar] [CrossRef]
- Campos, I.; Ramírez, G.; Figueroa, U.; Martínez, J.; Morales, O. Evaluation of boron mobility on the phases FeB, Fe2B and diffusion zone in AISI 1045 and M2 steels. Appl. Surf. Sci. 2007, 253, 3469–3475. [Google Scholar] [CrossRef]
- Yu, L.G.; Chen, X.J.; Khor, K.A.; Sundararajan, G. FeB/Fe2B phase transformation during SPS pack boronizing: Boride layer growth kinetics. Acta Mater. 2005, 53, 2361–2368. [Google Scholar] [CrossRef]
- Torres, R.; Campos, I.; Ramírez, G.; Bautista, O.; Martínez, J. Dimensional analysis in the growth kinetics of FeB and Fe2B layers during the boronizing process. Int. J. Microstruct. Mater. Prop. 2007, 2, 73–83. [Google Scholar]
- Dybkov, V.I. Basics of formation of iron boride coatings. J. Miner. Met. Mater. Eng. 2016, 2, 30–46. [Google Scholar] [CrossRef]
- Doñu Ruiz, M.A.; López Perrusquia, N.; Sánchez Huerta, D.; Torres San Miguel, C.R.; Urriolagoitia Calderón, G.M.; Cerillo Moreno, E.A.; Cortes Suarez, J.V. Growth kinetics of boride coatings formed at the surface AISI M2 during dehydrated paste pack boronizing. Thin Solid Films 2015, 596, 147–154. [Google Scholar] [CrossRef]
- Campos–Silva, I.; Ortiz–Domínguez, M.; Bravo–Bárcenas, O.; Doñu–Ruiz, M.A.; Bravo–Bárcenas, D.; TapiaQuintero, C.; Jiménez–Reyes, M.Y. Formation and kinetics of FeB/Fe2B layers and diffusion zone at the surface of AISI 316 boronized steels. Surf. Coat. Technol. 2010, 205, 403–412. [Google Scholar] [CrossRef]
- Abdellah, Z.N.; Keddam, M. Estimation of the boron diffusion coefficients in the FeB and Fe2B layers during the pack–boronizing of a high–alloy steel. Mater. Technol. 2014, 48, 237–242. [Google Scholar]
- Keddam, M.; Kulka, M. Simulation of the growth kinetics of FeB and Fe2B layers on AISI D2 steel by the integral method. Phys. Met. Metallogr. 2018, 119, 842–851. [Google Scholar] [CrossRef]
- Zong, X.; Xia, R.; Zhang, Y.; Zhang, Y.; Zhu, Q. Boriding kinetics and mechanical properties of X65Cr14 martensitic stainless steel by pack method. J. Phys. Conf. Ser. 2022, 2368, 1–7. [Google Scholar] [CrossRef]
- Azeem, M.M.; Wang, Q.; Zhang, Y.; Liu, S.; Zubair, M. Effect of Grain Boundary on Diffusion of P in Alpha–Fe: A Molecular Dynamics Study. Front. Phys. 2019, 7, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Momma, K.; Izumi, F. VESTA 3 for three–dimensional visualization of crystal, volumetric and morphology data. J. Appl. Cryst. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Crystallography Open Database. Available online: http://www.crystallography.net/ (accessed on 26 May 2023).
- Campos–Silva, I.; Ortiz–Domínguez, M.; Keddam, M.; López–Perrusquia, N.; Carmona–Vargas, A.; Elías–Espinosa, M. Kinetics of the formation of Fe2B layers in gray cast iron: Effects of boron concentration and boride incubation time. Appl. Surf. Sci. 2009, 255, 9290–9295. [Google Scholar] [CrossRef]
- Dearnley, P.A.; Bell, T. Engineering the surface with boron based materials. Surf. Eng. 1985, 1, 203–217. [Google Scholar] [CrossRef]
- Ortiz–Domínguez, M.; Gómez–Vargas, O.A.; Barcenas–Castañeda, M.; Castellanos–Escamilla, V.A. Comparison and analysis of diffusion models: Growth kinetics of diiron boride layers on ASTM A283 steel. Materials 2022, 15, 8420. [Google Scholar] [CrossRef]
- Zhong, J.; Qin, W.; Wang, X.; Medvedovski, E.; Szpunar, J.A.; Guan, K. Mechanism of texture formation in iron boride coatings on low–carbon steel. Metall. Mater. Trans. A 2019, 50, 58–62. [Google Scholar] [CrossRef]
- Orihel, P.; Drienovský, M.; Gabalcová, Z.; Jurˇci, P.; Keddam, M. Characterization and boron diffusion kinetics on the surface–hardened layers of royalloy steel. Coatings 2023, 13, 113. [Google Scholar] [CrossRef]
- Makuch, N.; Kulka, M.; Keddam, M.; Piasecki, A. Growth kinetics, microstructure evolution, and some mechanical properties of boride layers produced on X165CrV12 tool steel. Materials 2023, 16, 26. [Google Scholar] [CrossRef] [PubMed]
- Ortiz Domínguez, M.; Keddam, M.; Gómez Vargas, O.A.; Ares de Parga, G.; Zuno Silva, J. Bilayer growth kinetics and tribological characterization of boronized AISI M2 steel. Mater. Test. 2022, 64, 473–489. [Google Scholar] [CrossRef]
- Delai, O.; Xia, C.; Shiqiang, L. Growth kinetics of the FeB/Fe2B boride layer on the surface of 4Cr5MoSiV1 steel: Experiments and modelling. J. Mater. Res. Technol. 2021, 11, 1272–1280. [Google Scholar] [CrossRef]
- Okamoto, H. B–Fe (boron–iron). J. Phase Equilibria Diffus. 2004, 25, 297–298. 26. [Google Scholar] [CrossRef]
- Hunger, H.J.; Trute, G. Boronizing to produce wear–resistant surface layers. Heat Treat. Met. 1994, 2, 31–39. [Google Scholar]
- Davis, J.R. Metals Handbook Desk Edition, 2nd ed.; ASM International Handbook Committee: Russell, OH, USA, 1998; pp. 1–2571. [Google Scholar]
- ASTM E3–11; Standard Guide for Preparation of Metallographic Specimens. American Society for Metals: Russell, OH, USA, 2017.
- Verein Deutscher Ingenieure Normen. VDI 3198; VDI–Verlag Düsseldorf: Düsseldorf, Germany, 1991. [Google Scholar]
- Ortiz–Domínguez, M.; Gómez–Vargas, O.A.; Keddam, M.; Arenas–Flores, A.; García–Serrano, J. Kinetics of boron diffusion and characterization of Fe2B layers on AISI 9840 steel. Prot. Met. Phys. Chem. Surf. 2017, 53, 534–547. [Google Scholar] [CrossRef]
- Campos–Silva, I.; Bravo–Bárcenas, D.; Meneses–Amador, A.; Ortiz–Dominguez, M.; Cimenoglu, H.; Figueroa–López, U.; Andraca–Adame, J. Growth kinetics and mechanical properties of boride layers formed at the surface of the ASTM F–75 biomedical alloy. Surf. Coat. Technol. 2013, 237, 402–414. [Google Scholar] [CrossRef]
- Ortiz Domínguez, M. Contribución de la modelación matemática en el tratamiento termoquímico de borurización. Ph.D. Thesis, National Polytechnic Institute (IPN), Ciudad de México, México, 16 January 2013. [Google Scholar]
- Keddam, M.; Abdellah, Z.N.; Kulka, M. Determination of the diffusion coefficients of boron in the FeB and Fe2B layers formed on AISI D2 steel. Acta Phys. Pol. A 2015, 128, 740–745. [Google Scholar] [CrossRef]
- Glicksman, M.E. Diffusion in Solids: Field Theory, Solid–State Principles, and Applications, 1st ed.; Jon Wiley & Sons: New York, NY, USA, 2000; pp. 1–472. [Google Scholar]
- Shewmon, P.G. Diffusion in Solids, 2nd ed.; MacGraww Hill Book Company: Warrendale, PA, USA, 1989; pp. 1–243. [Google Scholar]
- Rodríguez–Castro, G.; Campos–Silva, I.; Martínez–Trinidad, J.; Figueroa–López, U.; Meléndez–Morales, D.; Vargas–Hernández, J. Effect of Boriding on the Mechanical Properties of AISI 1045 Steel. Adv. Mater. Res. 2009, 65, 63–68. [Google Scholar]
- Ortiz–Domínguez, M.; Keddam, M.; Elias–Espinosa, M.; Ramírez–Cardona, M.; Arenas–Flores, A.; Zuno–Silva, J.; Cervantes–Sodi, F.; Cardoso–Legorreta, E. Characterization and boronizing kinetics of AISI T1 steel. Metall. Res. Technol. 2019, 116, 1–11. [Google Scholar] [CrossRef]
- Keddam, M.; Chegroune, R.; Kulka, M.; Panfil, D.; Ulker, S.; Taktak, S. Characterization and diffusion kinetics of the plasma paste boronized AISI 440C Steel. Trans. Indian Inst. Met. 2017, 70, 1377–1385. [Google Scholar] [CrossRef]
- Ayvaz, S.I.; Aydin, I. Effect of the microwave heating on diffusion kinetics and mechanical properties of borides in AISI 316L. Trans. Indian Inst. Met. 2020, 73, 2635–2644. [Google Scholar] [CrossRef]
- Kayali, Y.; Taktak, S. Characterization and Rockwell–C adhesion properties of chromium–based boronized steels. J. Adhes. Sci. Technol. 2015, 29, 2065–2075. [Google Scholar] [CrossRef]
- VillaVelázquez–Mendoza, C.I.; Rodríguez–Mendoza, J.L.; Ibarra–Galván, V.; Hodgkins, R.P.; López–Valdivieso, A.; Serra–to–Palacios, L.L.; Leal–Cruz, A.L.; Ibarra–Junquera, V. Effect of substrate roughness, time and temperature on the processing of iron boride coatings: Experimental and statistical approaches. Int. J. Surf. Sci. Eng. 2014, 8, 71–91. [Google Scholar] [CrossRef]
- Dybkov, V.I.; Goncharuk, L.V.; Khoruzha, V.G.; Meleshevich, K.A.; Samelyuk, A.V.; Sidorko, V.R. Diffusional growth kinetics of boride layers on iron–chromium alloys. Solid State Phenom. 2008, 138, 181–188. [Google Scholar]
- Bondar, A. Boron–chromium–iron. In Iron Systems, Part 1, 1st ed.; Effenberg, G., IIyenko, S., Eds.; Springer–Verlag Berlin Heidelberg: Stuttgart, Germany, 2008; Volume 11D1, pp. 320–343. [Google Scholar]
- Angkurarach, L.; Juijerm, P. Effects of direct current field on powder–packed boronizing process on martensitic stainless steel AISI 420. Arch. Metall. Mater. 2012, 57, 799–804. [Google Scholar] [CrossRef]
- Turkoglu, T.; Ay, I. Investigation of mechanical, kinetic and corrosion properties of boronized AISI 304, AISI 420 and AISI 430. Surf. Eng. 2021, 37, 1020–1031. [Google Scholar] [CrossRef]
- Gunes, I. Investigation of tribological properties and characterization of boronized AISI 420 and AISI 5120 Steels. Trans. Indian Inst. Met. 2014, 67, 359–365. [Google Scholar] [CrossRef]
- Kayali, Y. Investigation of the diffusion kinetics of boronized stainless steels. Phys. Met. Metallogr. 2013, 114, 1061–1068. [Google Scholar] [CrossRef]
- Vidakis, N.; Antoniadis, A.; Bilalis, N. The VDI 3198 indentation test evaluation of a reliable qualitative control for layered compounds. J. Mater. Process. Technol. 2003, 143–144, 481–485. [Google Scholar] [CrossRef]
- Taktak, S. Some mechanical properties of boronized AISI H13 and 304 steels. Mater. Des. 2007, 28, 1836–1843. [Google Scholar] [CrossRef]
- Kayali, Y.; Büyüksaǧis, A.; Yalçin, Y. Corrosion and wear behaviors of boronized AISI 316L stainless steel. Met. Mater. Int. 2013, 19, 1053–1061. [Google Scholar] [CrossRef] [Green Version]
- Arteaga–Hernandez, L.A.; Cuao–Moreu, C.A.; Gonzalez–Rivera, C.E.; Alvarez–Vera, M.; Ortega–Saenz, J.A.; Hernandez–Rodriguez, M.A.L. Study of boronizing surface treatment in the tribological behavior of an AISI 316L stainless steel. Wear 2021, 477, 203825. [Google Scholar] [CrossRef]
- Flores–Rentería, M.A.; Ortiz–Domínguez, M.; Keddam, M.; Damián–Mejía, O.; Elias–Espinosa, M.; Flores–González, M.A.; Medina–Moreno, S.A.; Cruz–Avilés, A.; Villanueva–Ibañez, M. A Simple kinetic model for the growth of Fe2B layers on AISI 1026 steel during the powder–pack boronizing. High Temp. Mater. Process. 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Pascal: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007; pp. 1–1235. [Google Scholar]
- Ferraro, G. The Rise and Development of the Theory of Series up to the Early 1820s, 1st ed.; Springer: New York, NY, USA, 2008; pp. 1–392. [Google Scholar]
- Kayali, Y.; Mertgenç, E. Investigation of diffusion kinetic values of boronized AISI 303 steel by pack boronizing. Prot. Met. Phys. Chem. Surf. 2020, 56, 151–155. [Google Scholar]
- Juijerm, P. Diffusion kinetics of different boronizing processes on martensitic stainless steel AISI 420. Kov. Mater. 2014, 52, 231–236. [Google Scholar] [CrossRef] [Green Version]
- Campos–Silva, I.; Hernández–Ramirez, E.J.; Contreras–Hernández, A.; Rosales–Lopez, J.L.; Valdez–Zayas, E.; Mejía–Caballero, I.; Martínez–Trinidad, J. Pulsed–DC powder–pack Boronizing: Growth Kinet. Boride Layers AISI 316l Stainl. Steel Inconel 718 Superalloy. Surf. Coat. Technol. 2021, 421, 127404. [Google Scholar] [CrossRef]
- Topuz, P.; Çiçek, B.; Akar, O. Kinetic investigation of AISI 304 stainless steel boronized in indirect heated fluidized bed furnace. J. Min. Metall. Sect. B Metall. 2016, 52, 63–68. [Google Scholar] [CrossRef]
- Anantha, K.H.; Örnek, C.; Ejnermark, S.; Medvedeva, A.; Sjöström, J.; Pan, J. Correlative Microstructure Analysis and In Situ Corrosion Study of AISI 420 Martensitic Stainless Steel for Plastic Molding Applications. J. Electrochem. Soc. 2017, 164, 1–10. [Google Scholar] [CrossRef]








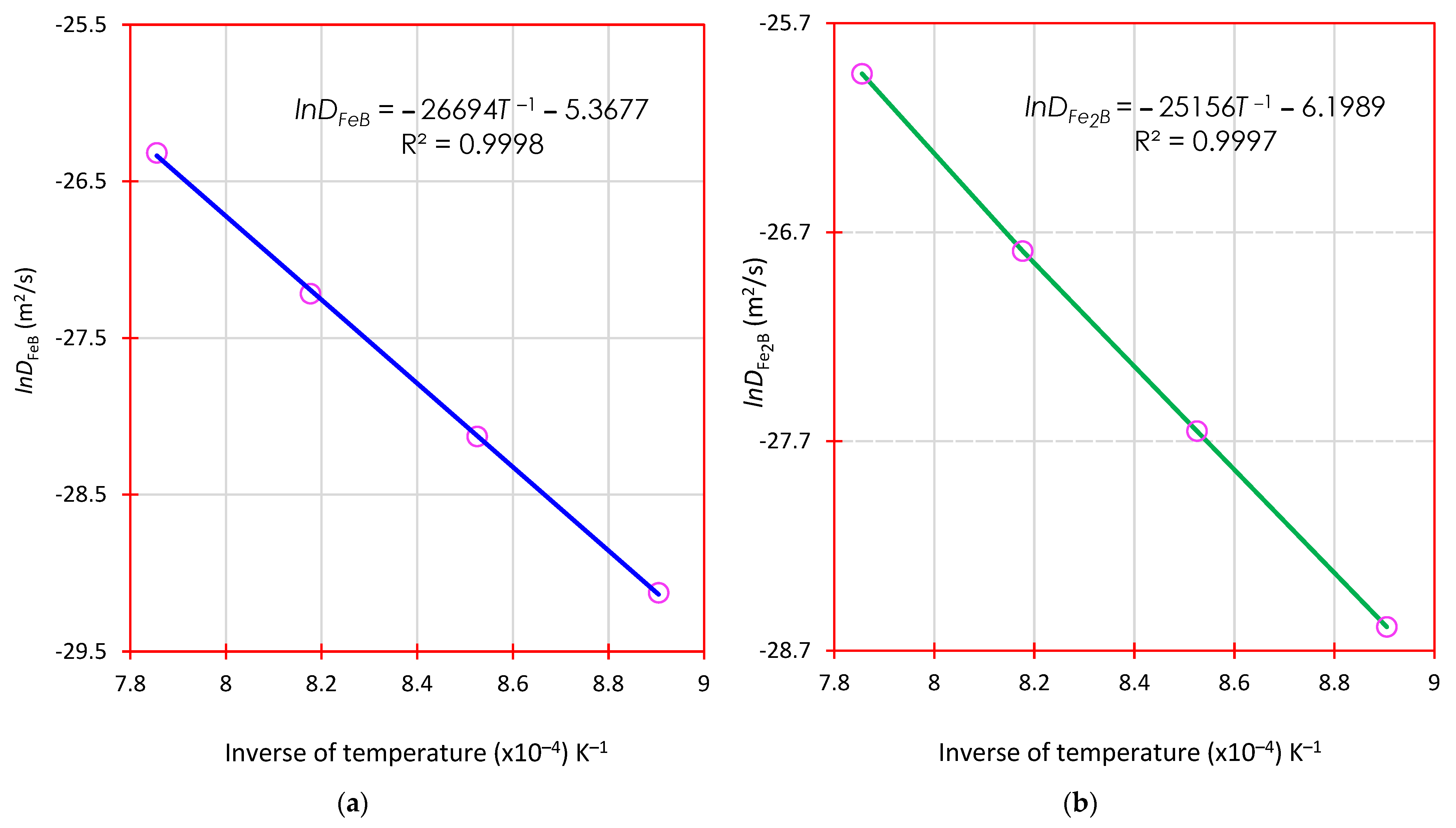
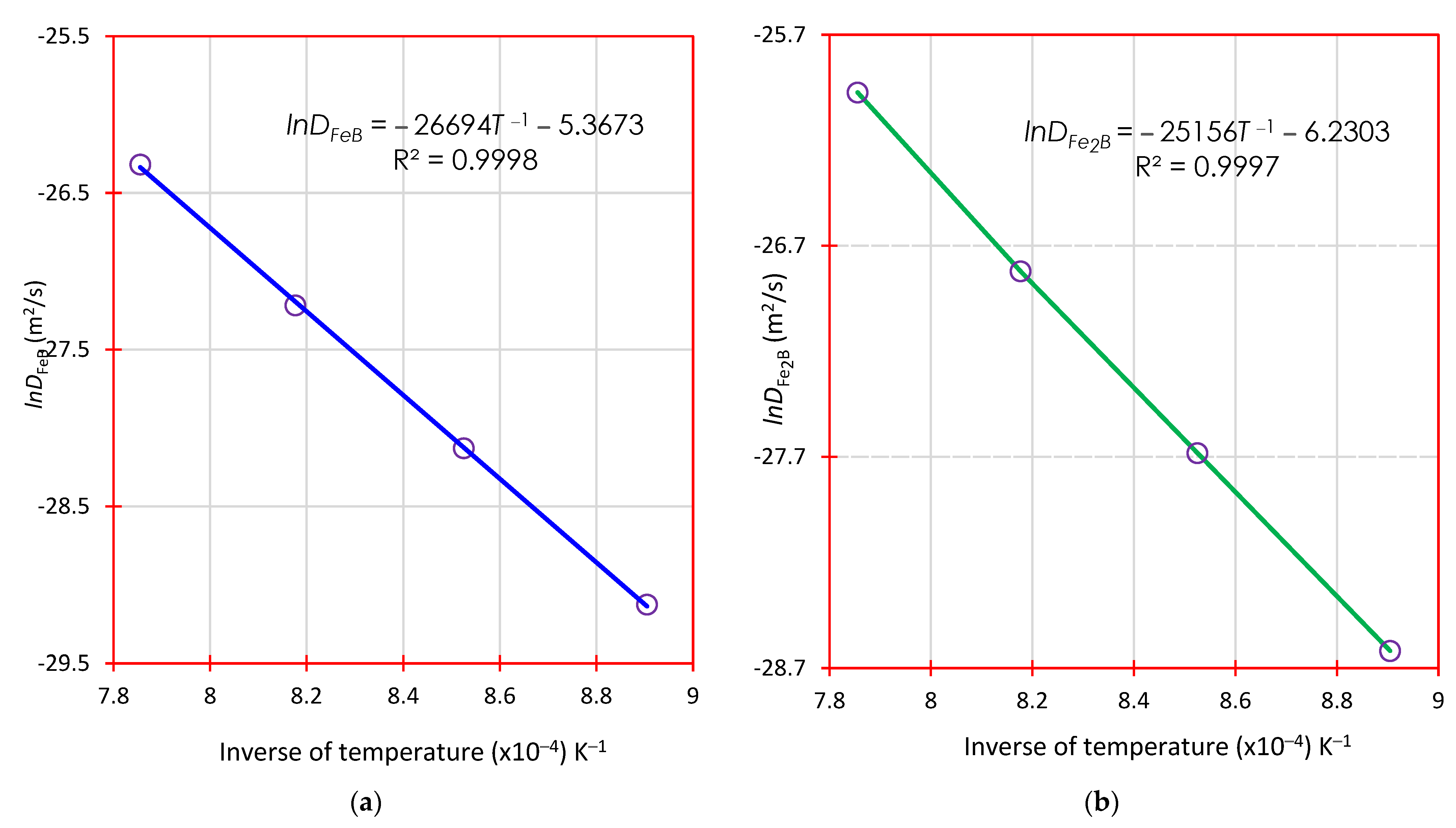

| Experimental Temperature T (K) | Experimental Constant (µm/s1/2) | Incubation Time (s) | Experimental Constant (µm/s1/2) | Incubation Time (s) |
|---|---|---|---|---|
| 1123 | 0.05 | 2528 | 0.12 | 2124 |
| 1173 | 0.08 | 2539 | 0.19 | 2135 |
| 1223 | 0.14 | 2535 | 0.29 | 2128 |
| 1273 | 0.22 | 2536 | 0.45 | 2136 |
| Experimental Temperature T (K) | Constant (without Units) | Experimental Constant (µm/s1/2) | Constant (without Units) | Experimental Constant (µm/s1/2) |
|---|---|---|---|---|
| 1123 | 3.2 × 10–3 | 0.05 | 9.6 × 10–3 | 0.12 |
| 1173 | 0.08 | 0.19 | ||
| 1223 | 0.14 | 0.29 | ||
| 1273 | 0.22 | 0.45 |
| Experimental Temperature T (K) | Boron Diffusivity in FeB (m2/s) | Boron Diffusivity in Fe2B (m2/s) |
|---|---|---|
| 1123 | 2.2 × 10−13 | 3.8 × 10−13 |
| 1173 | 6.1 × 10−13 | 9.8 × 10−13 |
| 1223 | 1.5 × 10−12 | 2.310−12 |
| 1273 | 3.7 × 10−12 | 5.4 × 10−12 |
| Experimental Temperature T (K) | Constant (without Units) | Experimental Constant (µm/s1/2) | Constant (without Units) | Experimental Constant (µm/s1/2) |
|---|---|---|---|---|
| 1123 | 3.2 × 10–3 | 0.05 | 9.8 × 10–3 | 0.12 |
| 1173 | 0.08 | 0.19 | ||
| 1223 | 0.14 | 0.29 | ||
| 1273 | 0.22 | 0.45 |
| Experimental Temperature T (K) | Boron Diffusivity in FeB (m2s) | Boron Diffusivity in Fe2B (m2s) |
|---|---|---|
| 1123 | 2.2 × 10−13 | 3.7 × 10−13 |
| 1173 | 6.1 × 10−13 | 9.5 × 10−13 |
| 1223 | 1.5 × 10−12 | 2.2 × 10−12 |
| 1273 | 3.7 × 10−12 | 5.2 × 10−12 |
| Substrate | Thermochemical Treatment | Activation Energies (kJ∙mol−1) | Temperature Interval of Investigation (K) | Growth Law | Refs. |
|---|---|---|---|---|---|
| AISI 4040 C | Plasma-paste | (FeB + Fe2B) 134.6 | 973–1073 | Parabolic | [55] |
| AISI 316L | Powder with microwave heating | (FeB + Fe2B) 244.1 | 1073–1223 | Parabolic | [56] |
| AISI 303 | Powder | (FeB + Fe2B) 236.5 | 1123–1223 | Parabolic | [72] |
| AISI 420 | Powder | (FeB + Fe2B) 206.2 | 1123–1223 | Parabolic | [64] |
| AISI 420 | Salt-bath | (FeB + Fe2B) 233.5 | 1123–1223 | Parabolic | [73] |
| AISI 420 | Powder | (FeB + Fe2B) 185.2 | 1123–1223 | Parabolic | [73] |
| AISI 420 | Powder | (FeB + Fe2B) 242.1 | 1123–1273 | Parabolic | [62] |
| AISI 430 | Powder | (FeB + Fe2B) 151.4 | 1123–1273 | Parabolic | [62] |
| AISI 316L | Pulsed-DC powder-pack boronizing | (FeB) 162, (Fe2B) 171 | 1123–1223 | Bilayer model | [74] |
| AISI 304 | Powder with indirect heating in fluidized bed | (FeB + Fe2B) 244 | 1123–1323 | Parabolic | [75] |
| AISI 420 | Powder | (FeB) 221.9, (Fe2B) 209.1 | 1123–1273 | Parabolic | This work |
| Boronizing Conditions | Experimental Layer Thickness (µm) | Simulated Layer Thickness (µm) Equation (9) | Experimental Layer Thickness (µm) | Simulated Layer Thickness (µm) Equation (10) |
|---|---|---|---|---|
| 1273 K for 5.5 h | 24.76 ± 8 | 28.5 | 53.9 ± 15 | 59.9 |
| 1323 K for 5.5 h | 38.02 ± 9 | 42.4 | 79.3 ± 23 | 87.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortiz-Domínguez, M.; Morales-Robles, Á.J.; Gómez-Vargas, O.A.; de Jesús Cruz-Victoria, T. Analysis of Diffusion Coefficients of Iron Monoboride and Diiron Boride Coating Formed on the Surface of AISI 420 Steel by Two Different Models: Experiments and Modelling. Materials 2023, 16, 4801. https://doi.org/10.3390/ma16134801
Ortiz-Domínguez M, Morales-Robles ÁJ, Gómez-Vargas OA, de Jesús Cruz-Victoria T. Analysis of Diffusion Coefficients of Iron Monoboride and Diiron Boride Coating Formed on the Surface of AISI 420 Steel by Two Different Models: Experiments and Modelling. Materials. 2023; 16(13):4801. https://doi.org/10.3390/ma16134801
Chicago/Turabian StyleOrtiz-Domínguez, Martín, Ángel Jesús Morales-Robles, Oscar Armando Gómez-Vargas, and Teresita de Jesús Cruz-Victoria. 2023. "Analysis of Diffusion Coefficients of Iron Monoboride and Diiron Boride Coating Formed on the Surface of AISI 420 Steel by Two Different Models: Experiments and Modelling" Materials 16, no. 13: 4801. https://doi.org/10.3390/ma16134801






