Experimental Investigation on the Vertical Ductility of Rectangular CFST Columns Loaded Axially
Abstract
:1. Introduction
- Structural design analysis;
- Comparison of the ductility of structural elements.
2. Ductility of CFST Columns—State-Of-The-Art
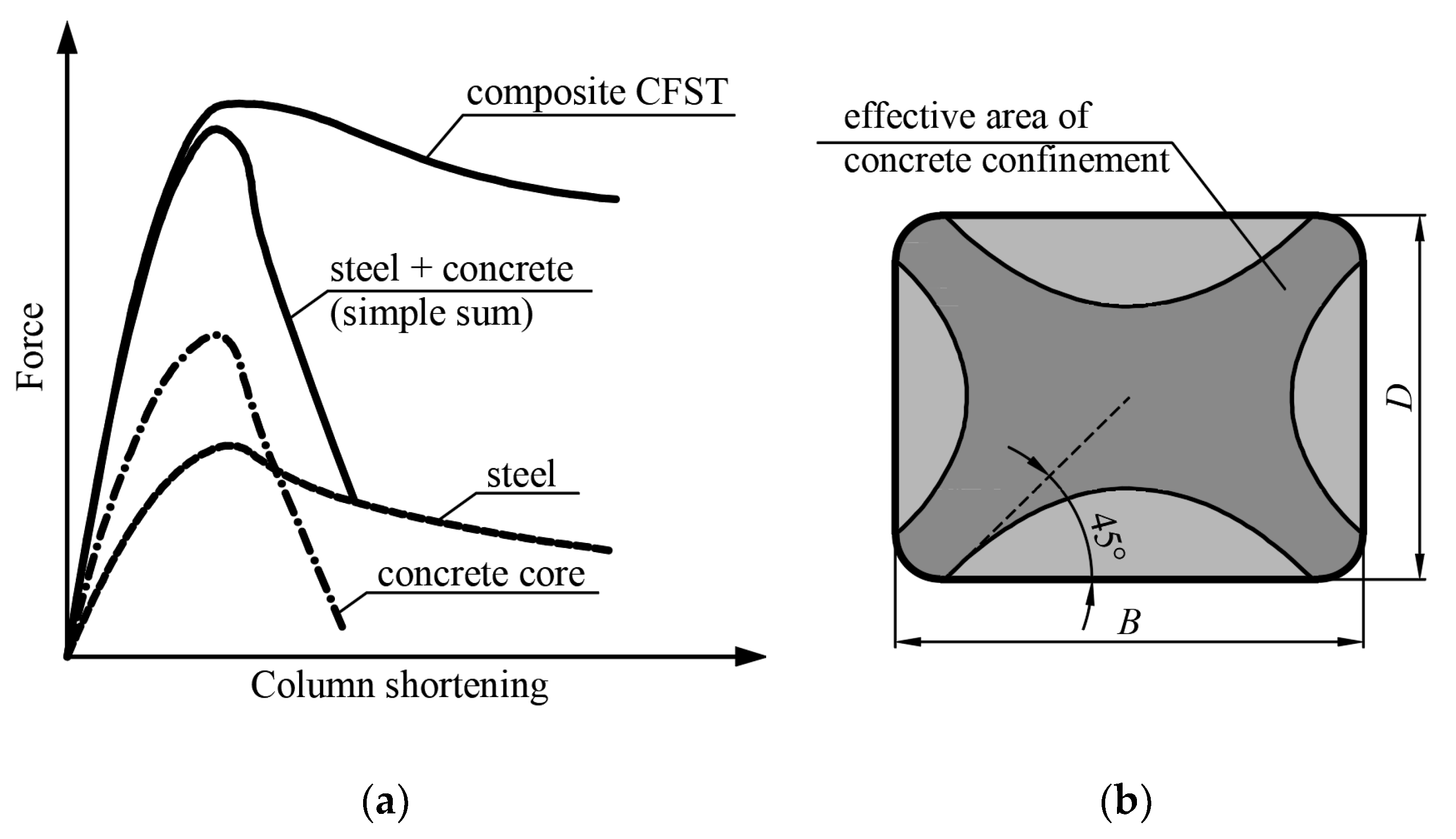
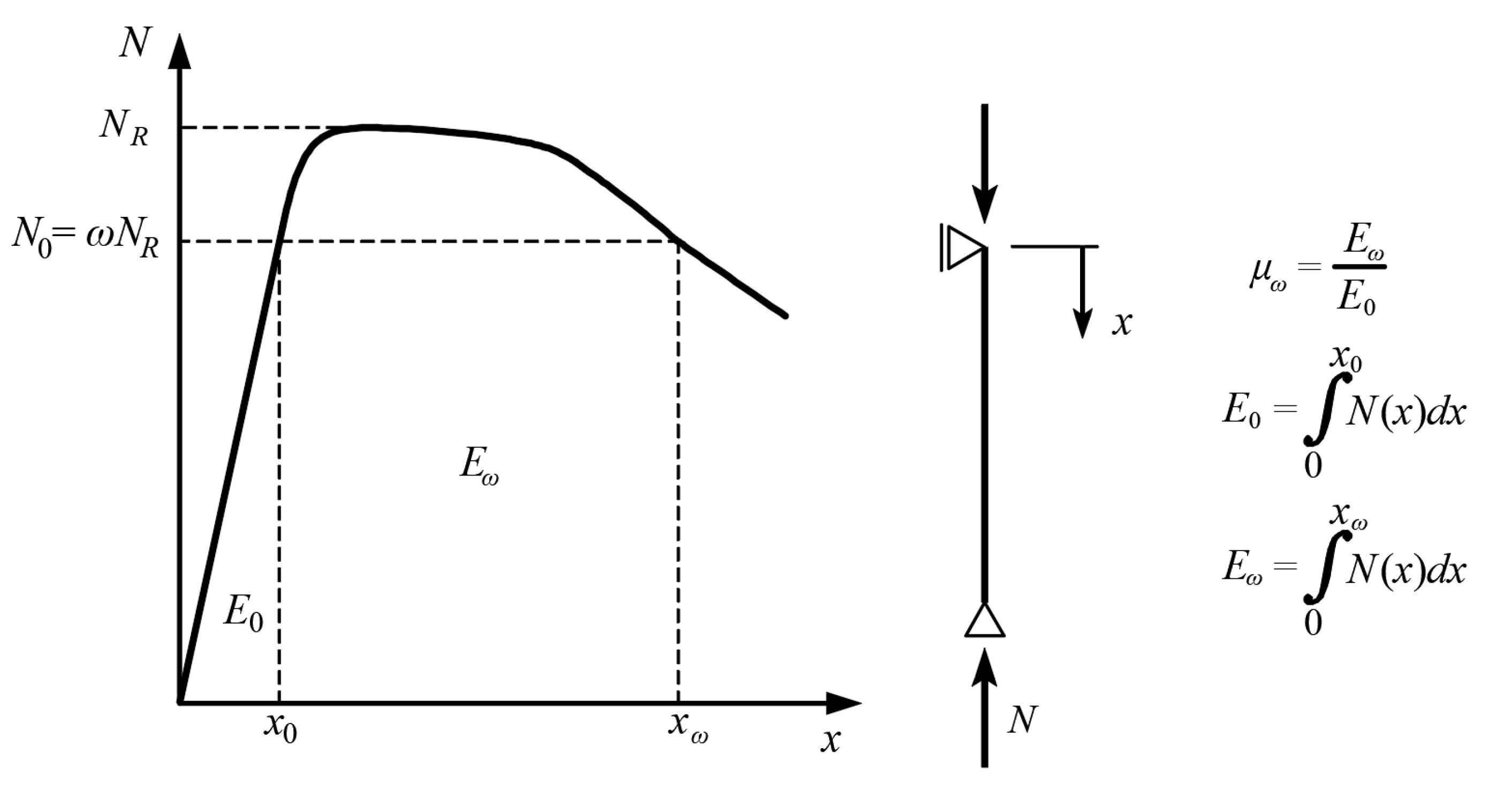
3. Proposal for the Vertical Ductility Assessment of Columns
4. Experimental Research—Methodology
5. Results of the Experimental Research and Discussion
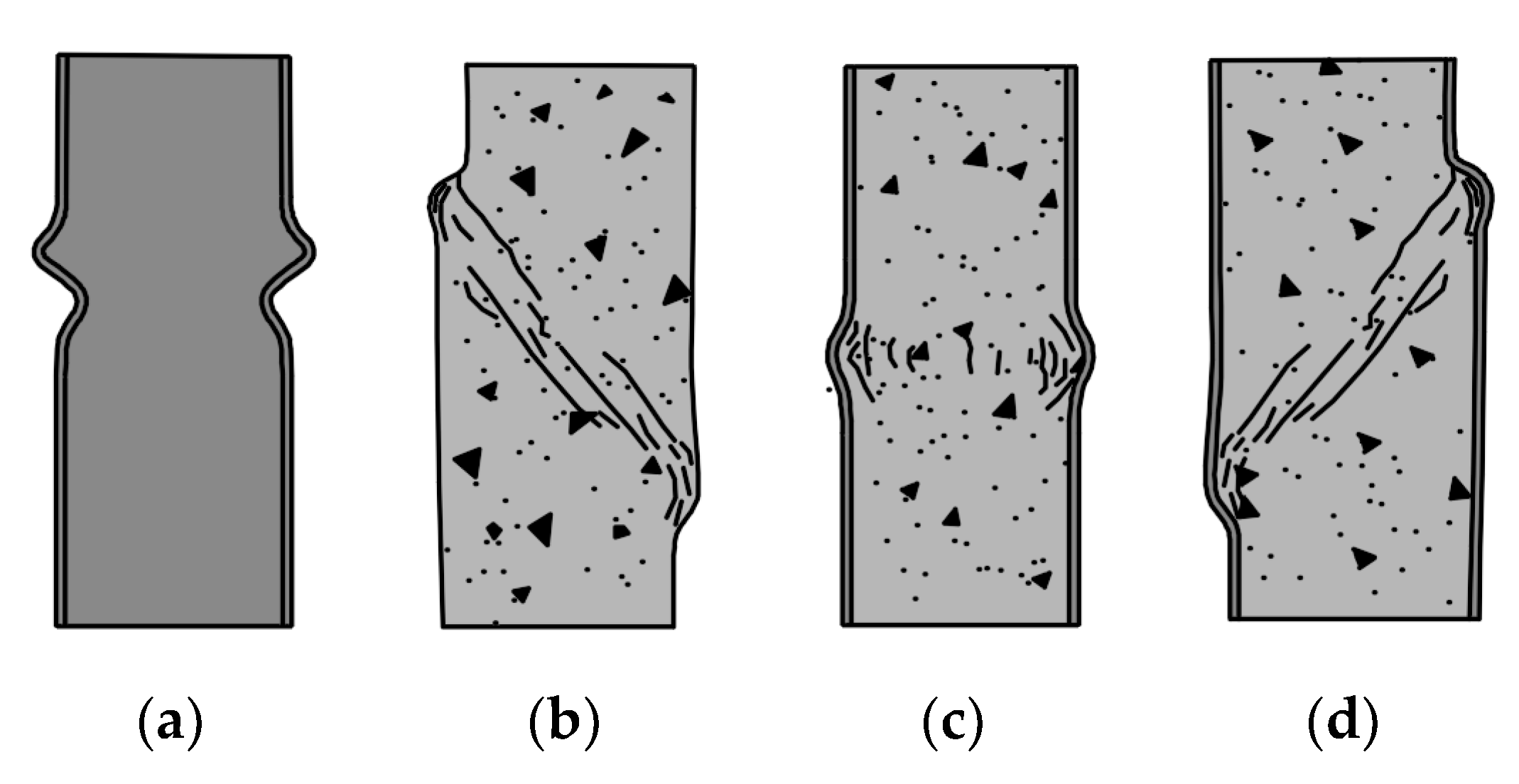
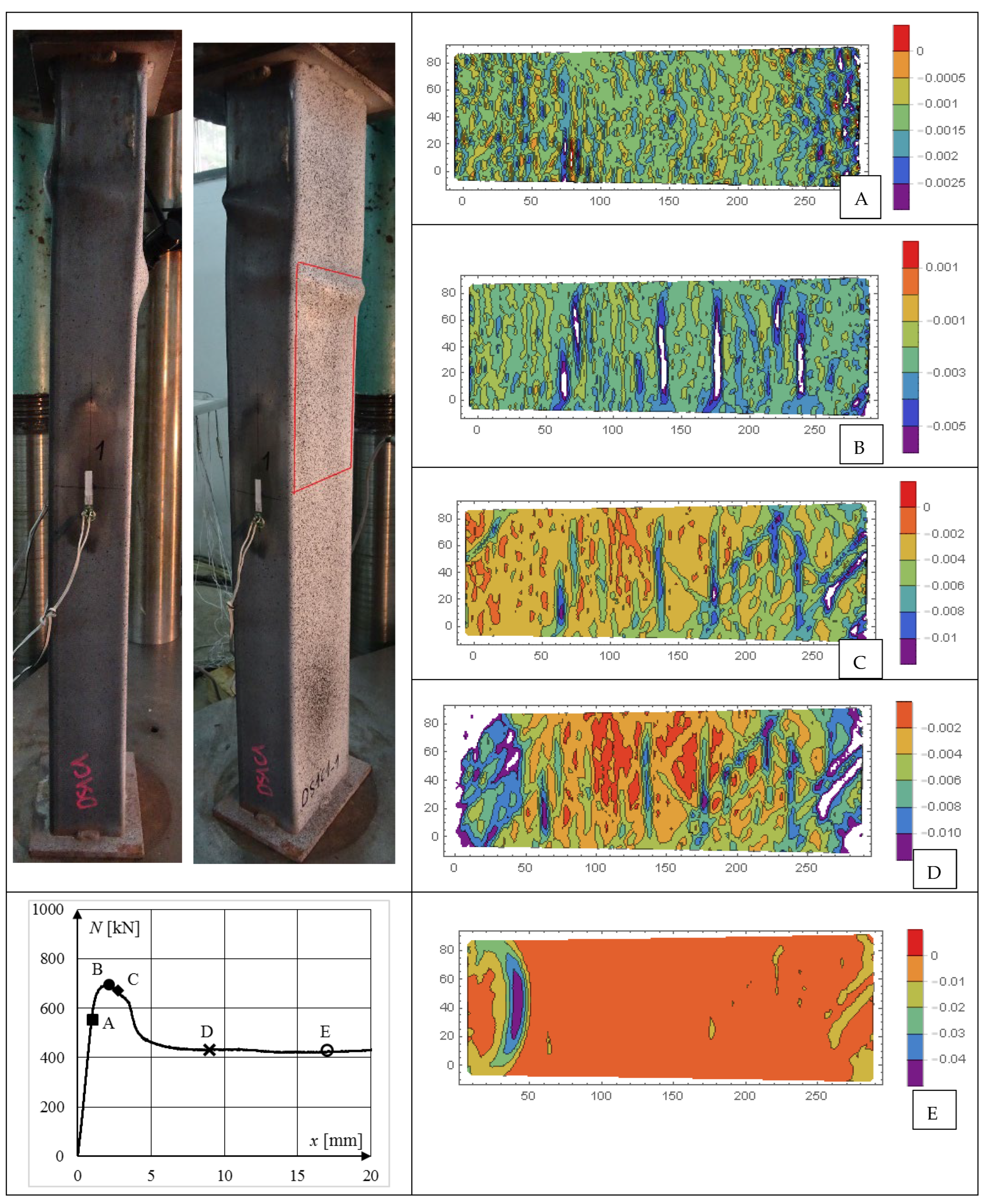
5.1. Failure Modes
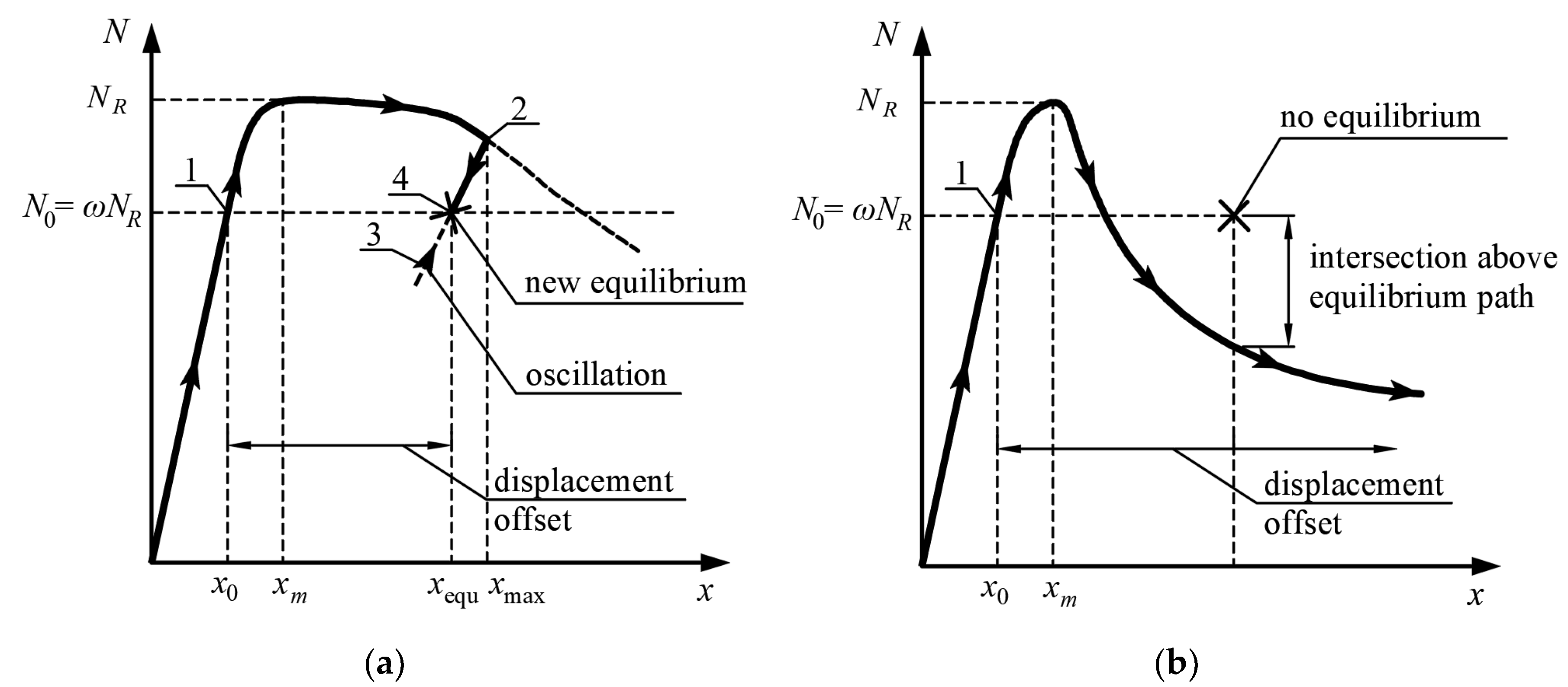
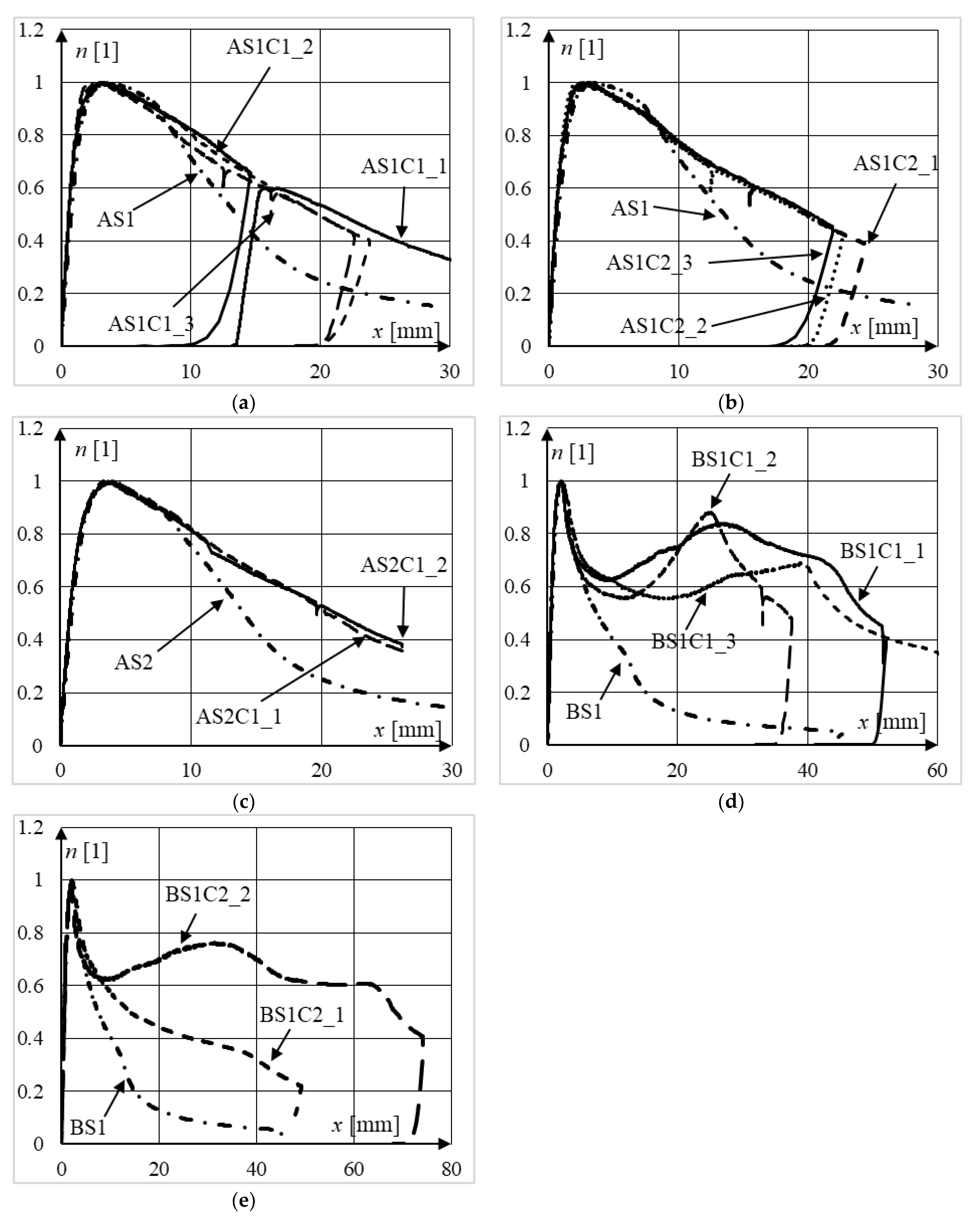
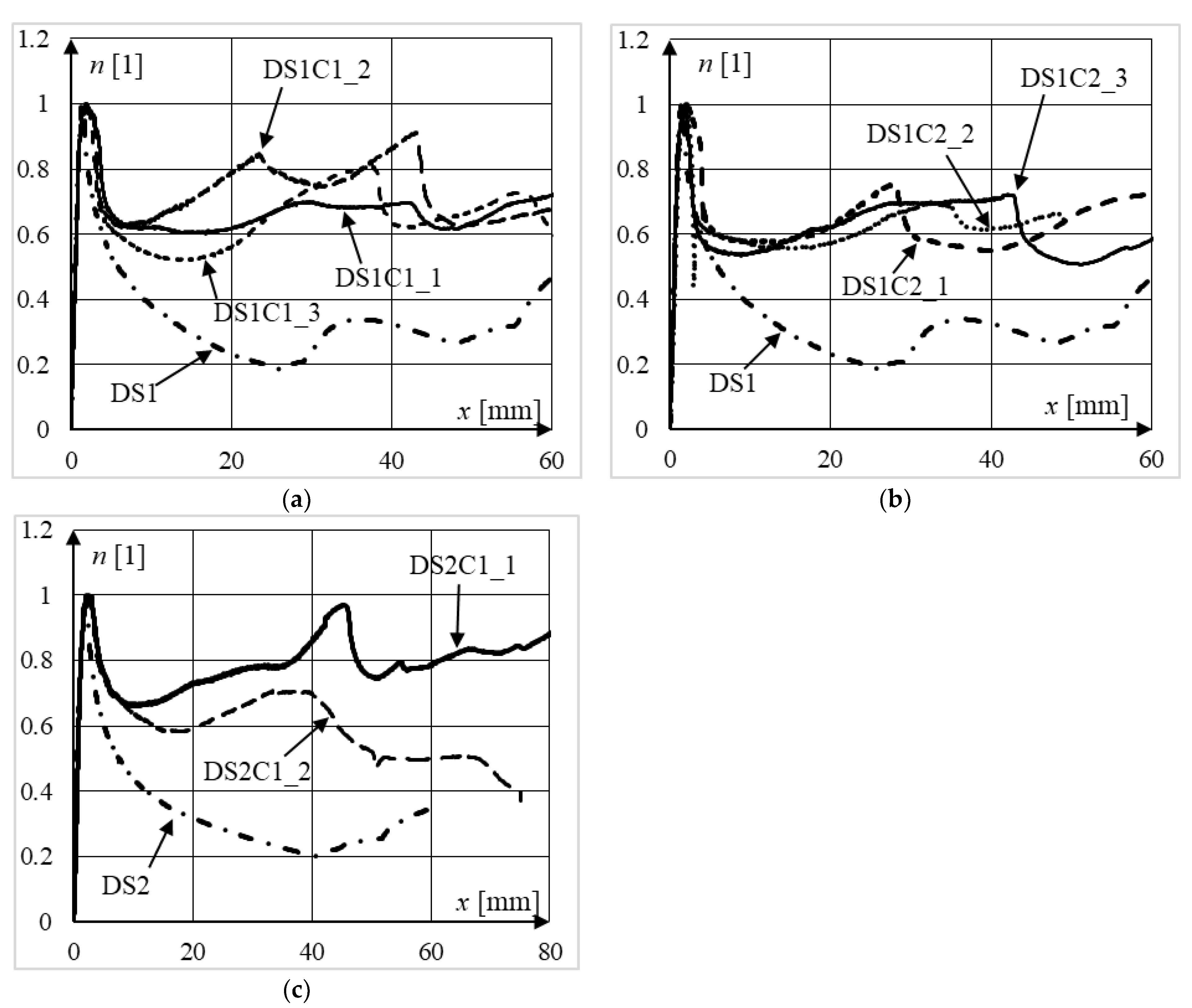
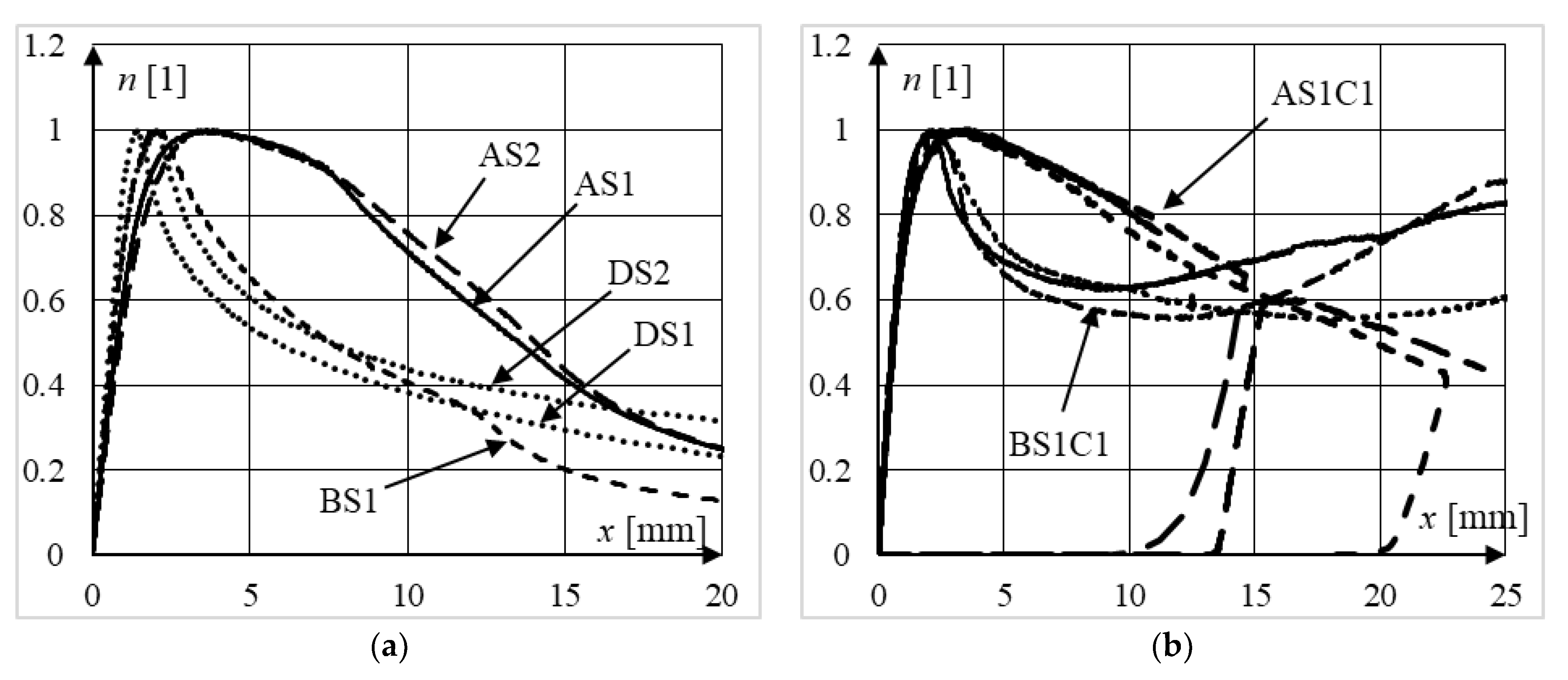
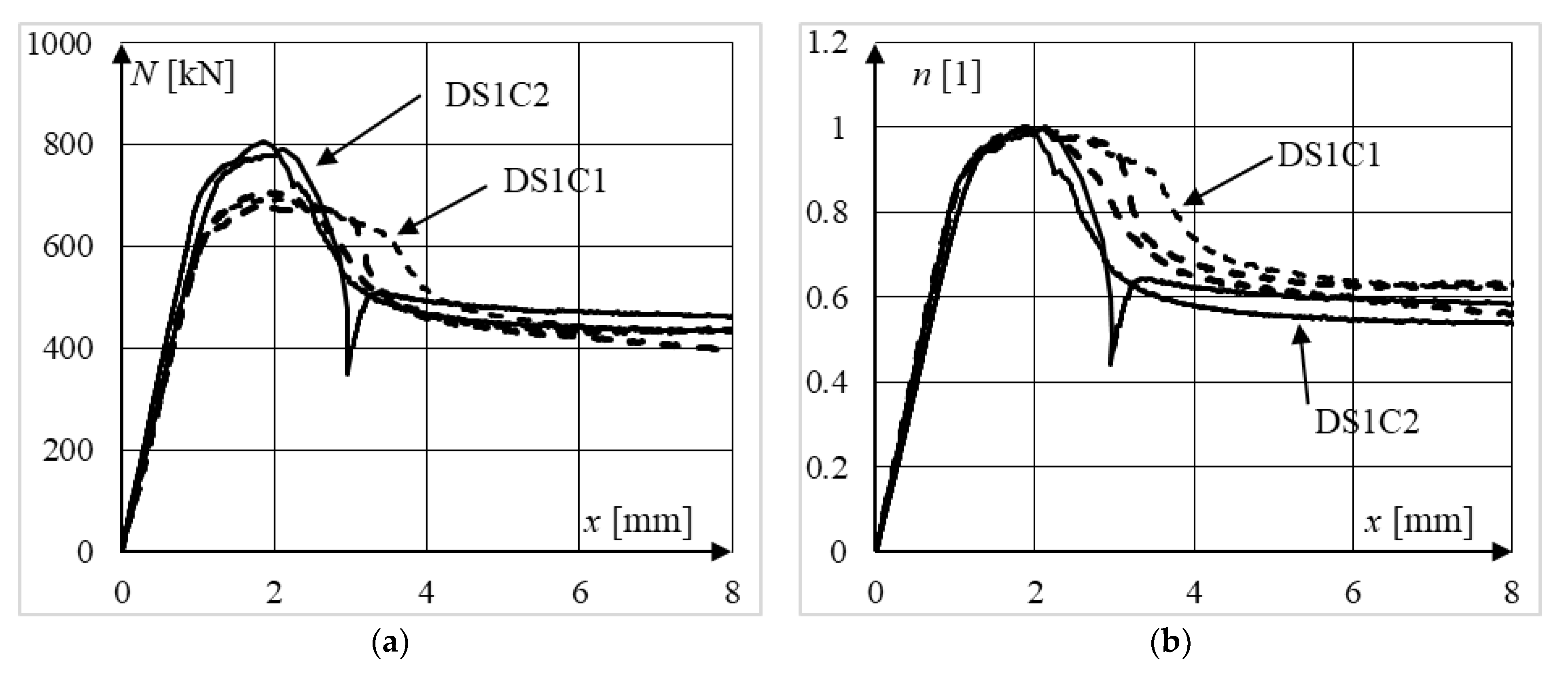
5.2. Qualitative Analysis of Equilibrium Paths
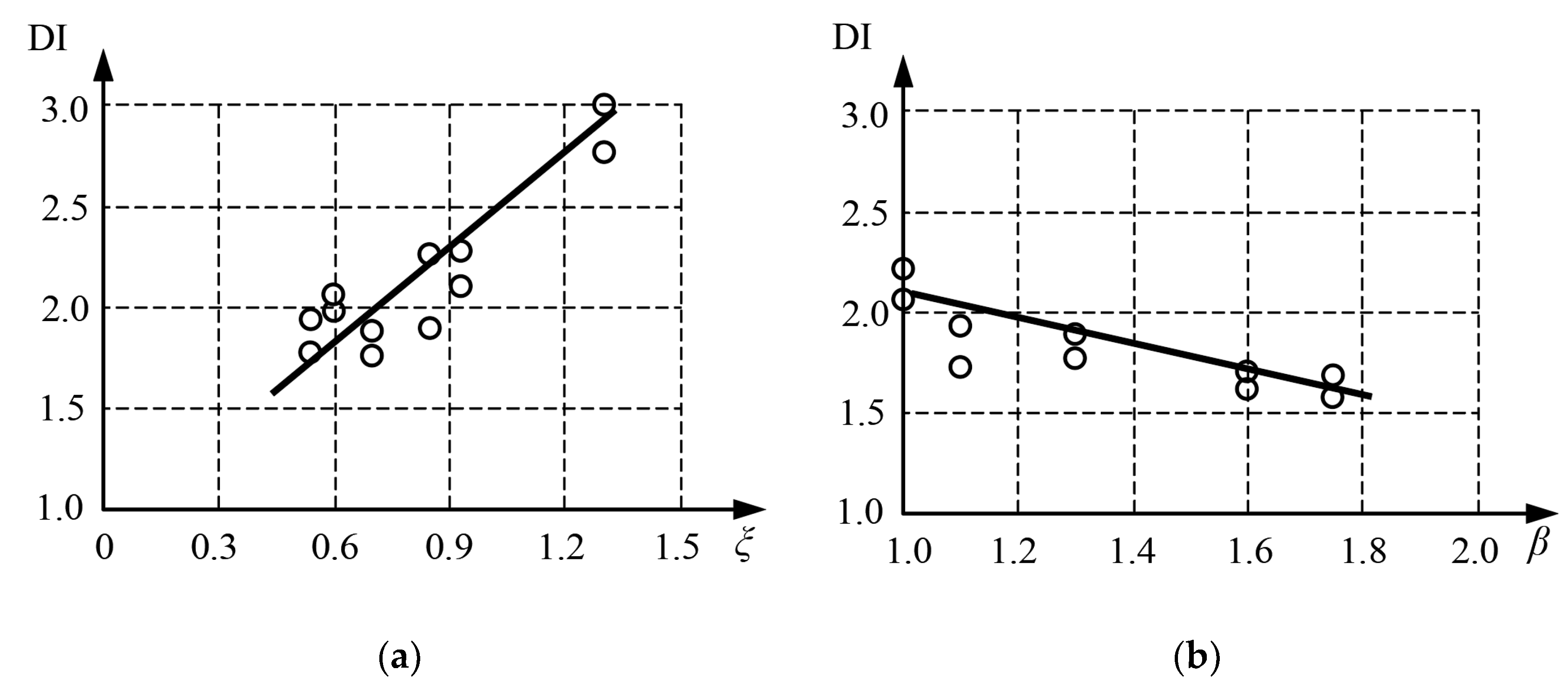
5.3. Quantitative Analysis of Equilibrium Paths
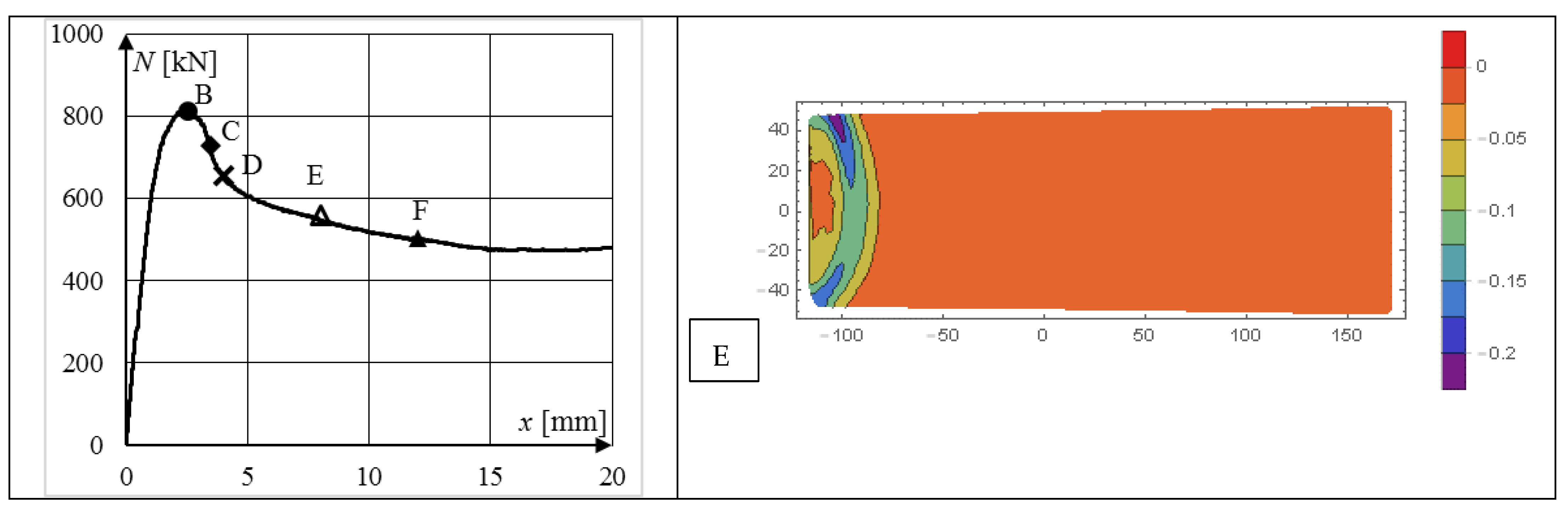
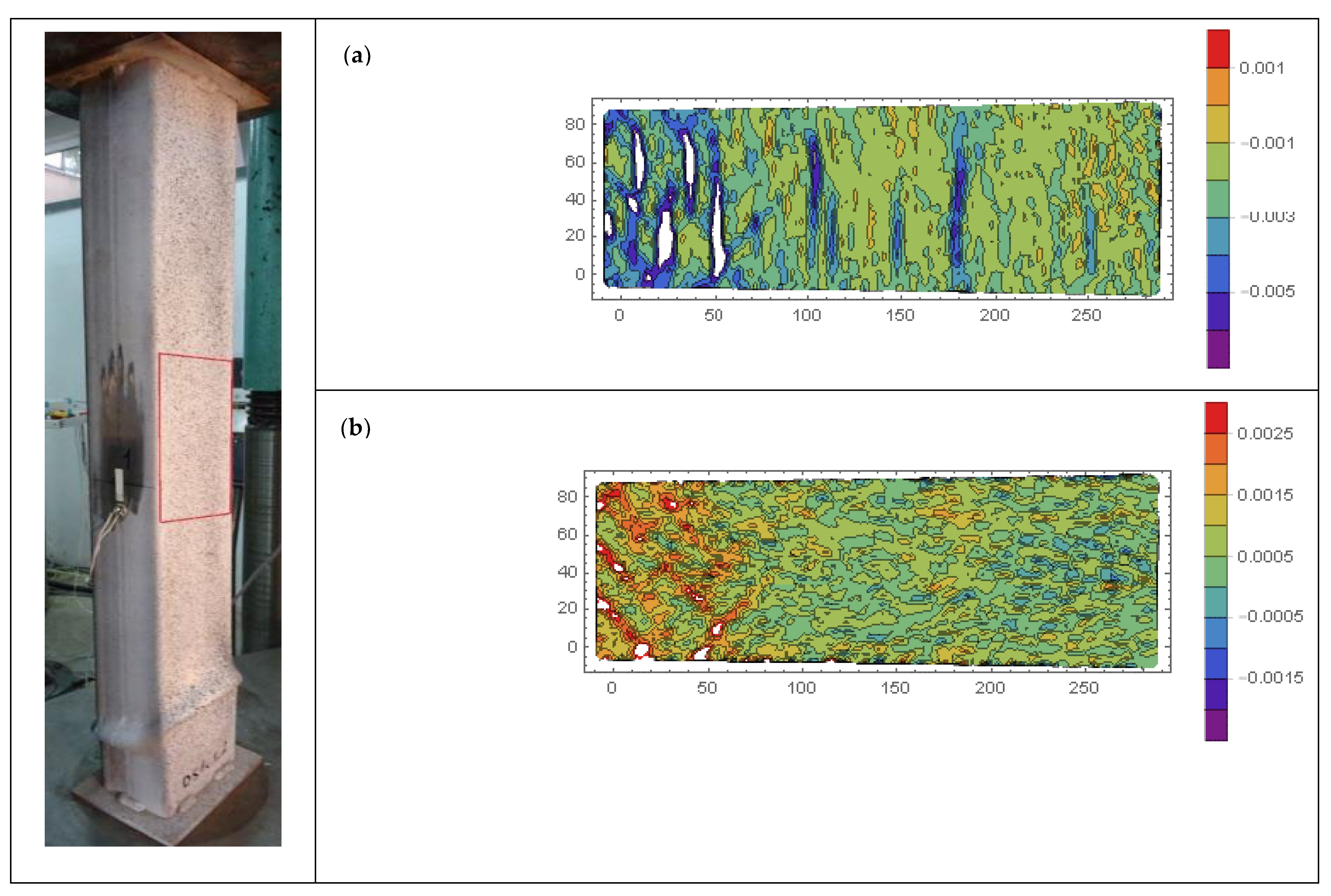
5.4. Digital Image Correlation—Results
6. Conclusions
- The concrete core failure consisted of crushing the concrete in the plastic hinge on the side of the cross-section with high compressive stresses. In elements with large D/t ratios, the additional formation of diagonal yield zones in the other cross-sections of the columns occurred.
- The higher strength concrete filling had no significant influence on the ductility of slender test elements.
- The increase in the wall thickness had a positive effect on the ductility of slender specimens.
- For elements that underwent the local failure mode:
- In shear and sliding failure mode, the concrete core failure consists of the formation of diagonal or horizontal yield zones along the height of the column, causing stress concentrations in the steel jacket, and in the weakest yield zone, shear solid wedge movements along a shear frictional surface develop. In elephant foot failure mode, the concrete core failure consists of crushing the concrete in the weakest cross-section of the column.
- Symmetrical elephant foot failure mode yielded higher vertical ductility in comparison to shear and sliding failure modes.
- The use of higher-grade steel increased the vertical ductility of the tested columns.
- The use of stronger concrete caused a decrease in the ductility of the test specimens.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kiakojouri, F.; Sheidaii, M.R.; De Biagi, V.; Chiaia, B. Progressive collapse of structures: A discussion on annotated nomenclature. Structures 2021, 29, 1417–1423. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Wu, Y. Mechanical behavior of steel-reinforced concrete-filled steel tubular (SRCFST) columns under uniaxial compressive loading. Thin Walled Struct. 2015, 97, 1–10. [Google Scholar] [CrossRef]
- Le Hoang, A.; Fehling, E. Numerical study of circular steel tube confined concrete (STCC) stub columns. J. Constr. Steel Res. 2017, 136, 238–255. [Google Scholar] [CrossRef]
- Jiang, Y.; Silva, A.; Castro, J.M.; Monteiro, R. Experimental Assessment of the Behaviour of Rubberized Concrete Filled Steel Tube Members. In Proceedings of the V International Conference on Behavior of Steel Structures in Seismic Areas, Shanghai, China, 15 July 2015. [Google Scholar]
- Lin, S.Q.; Zhao, Y.G. Ultimate Stress of the Steel Tube in Circular CFT Stub Columns Subjected to Axial Compression. Int. J. Eng. Technol. 2018, 10, 315–319. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, R., Jr.; Yamamoto, Y. Simulation of Failure Localization and Buckling Behavior of Steel-tube Confined Concrete Columns using Coupled RBSM-Shell FEM Analysis. In Proceedings of the Computational Engineering Conference JSCES, Maastricht, The Netherlands, 12 June 2018. [Google Scholar]
- Liew, J.R.; Xiong, D.X. Ultra-high strength concrete filled composite columns for multi-storey building construction. Adv. Struct. Eng. 2012, 15, 1487–1503. [Google Scholar] [CrossRef]
- Portolés, J.M.; Serra, E.; Romero, M.L. Influence of ultra-high strength infill in slender concrete-filled steel tubular columns. J. Constr. Steel Res. 2013, 86, 107–114. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Uy, B.; Aslani, F.; Hou, C. Behaviour and design of spiral-welded stainless steel tubes subjected to axial compression. J. Constr. Steel Res. 2019, 154, 67–83. [Google Scholar] [CrossRef]
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Grzeszykowski, B.; Szmigiera, E. Ductility assessment of two-chord composite steel-concrete battened columns. Struct. Infrastruct. Eng. 2017, 13, 1414–1424. [Google Scholar] [CrossRef]
- Kitada, T. Ultimate strength and ductility of state-of-the-art concrete-filled steel bridge piers in Japan. Eng. Struct. 1998, 20, 347–354. [Google Scholar] [CrossRef]
- Schneider, S.P. Axially loaded concrete-filled steel tubes. J. Struct. Eng. 1998, 124, 1125–1138. [Google Scholar] [CrossRef]
- Feng, P.; Cheng, S.; Bai, Y.; Ye, L. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression. Compos. Struct. 2015, 123, 312–324. [Google Scholar] [CrossRef]
- Abdulraheem, M.S. Experimental investigation of fire effects on ductility and stiffness of reinforced reactive powder concrete columns under axial compression. J. Build. Eng. 2018, 20, 750–761. [Google Scholar] [CrossRef]
- Hadi, M.N.S.; Khan, Q.S.; Sheikh, M.N. Axial and flexural behavior of unreinforced and FRP bar reinforced circular concrete filled FRP tube columns. Constr. Build. Mater. 2016, 122, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Al-Nimry, H.S.; Al-Rabadi, R.A. Axial–Flexural Interaction in FRP-Wrapped RC Columns. Int. J. Concr. Struct. Mater. 2019, 13, 53. [Google Scholar] [CrossRef]
- GangaRao, H.V.; Taly, N.; Vijay, P.V. Reinforced Concrete Design with FRP Composites; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Kusumawardaningsih, Y.; Hadi, M.N.S. Comparative behaviour of hollow columns confined with FRP composites. Compos. Struct. 2010, 93, 198–205. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Q.; Jiang, H.; Pan, X. Analysis and Design of Elliptical Concrete-Filled Thin-Walled Steel Stub Columns Under Axial Compression. Int. J. Steel Struct. 2018, 18, 365–380. [Google Scholar] [CrossRef]
- Szmigiera, E. Dwugałęziowe Słupy Stalowo-Betonowe; Budownictwo; Prace Naukowe Politechniki Warszawskiej: Warsaw, Poland, 2012. [Google Scholar]
- He, A.; Wang, F.; Zhao, O. Experimental and numerical studies of concrete-filled high-chromium stainless steel tube (CFHSST) stub columns. Thin Walled Struct. 2019, 144, 106273. [Google Scholar] [CrossRef]
- Gao, B.; Wang, J.; Shen, Q.; Wang, C.; Yu, Z. Eccentric compression tests and design of welded steel tube strengthened RC stub columns with high-strength grout. J. Build. Eng. 2021, 35, 102072. [Google Scholar] [CrossRef]
- Ghanbari-Ghazijahani, T.; Nabati, A.; Azandariani, M.G.; Fanaie, N. Crushing of steel tubes with different infills under partial axial loading. Thin Walled Struct. 2020, 149, 106614. [Google Scholar] [CrossRef]
- Zhao, X.L.; Hancock, G.J. Tests to determine plate slenderness limits for cold-formed rectangular hollow sections of grade C450. Steel Constr. 1991, 25, 2–16. [Google Scholar]
- Yang, H.; Lam, D.; Gardner, L. Testing and analysis of concrete-filled elliptical hollow sections. Eng. Struct. 2008, 30, 3771–3781. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Shen, Q. Numerical modelling and design recommendation of axially-loaded thin-walled RCFST slender column. Thin Walled Struct. 2019, 135, 210–226. [Google Scholar] [CrossRef]
- İpek, S.; Erdoğan, A.; Güneyisi, E.M. Compressive behavior of concrete-filled double skin steel tubular short columns with the elliptical hollow section. J. Build. Eng. 2021, 38, 102200. [Google Scholar] [CrossRef]
- Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing. Bull. N. Z. Natl. Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
- Gardner, N.J.; Jacobson, E.R. Structural behavior of concrete filled steel tubes. J. Proc. 1967, 64, 404–413. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, E. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Ho, J.; Lam, J.; Kwan, A. Effectiveness of adding confinement for ductility improvement of high-strength concrete columns. Eng. Struct. 2010, 32, 714–725. [Google Scholar] [CrossRef]
- Knowles, R.B.; Park, R. Strength of concrete filled steel columns. J. Struct. Div. 1969, 95, 2565–2587. [Google Scholar] [CrossRef]
- Knowles, R.B.; Park, R. Axial load design for concrete filled steel tubes. J. Struct. Div. 1970, 96, 2125–2153. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Chan, T.M. Experimental investigation on octagonal concrete filled steel stub columns under uniaxial compression. J. Constr. Steel Res. 2018, 147, 457–467. [Google Scholar] [CrossRef]
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Patel, V.I.; Hassanein, M.F.; Thai, H.T.; Al Abadi, H.; Elchalakani, M.; Bai, Y. Ultra-high strength circular short CFST columns: Axisymmetric analysis, behaviour and design. Eng. Struct. 2019, 179, 268–283. [Google Scholar] [CrossRef]
- Han, L.H. Tests on stub columns of concrete-filled RHS sections. J. Constr. Steel Res. 2002, 58, 353–372. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, S.L.; Fu, B.; Tong, G.S.; Tong, J.Z.; Jing, T. Behavior and design of concrete-filled narrow rectangular steel tubular (CFNRST) stub columns under axial compression. J. Build. Eng. 2021, 37, 102166. [Google Scholar] [CrossRef]
- EN-1994-1-1:2004; Eurocode 4: Design of Composite Steel and Concrete Structures-Part 1-1: General Rules and Rules for Buildings; European Union: Brussels, Belgium, 2004.
- Yang, C.; Yu, Z.X.; Sun, Y.P.; Zhao, L.; Zhao, H. Axial residual capacity of circular concrete-filled steel tube stub columns considering local buckling. Adv. Steel Constr. 2018, 14, 496–513. [Google Scholar]
- Lundberg, J.E. The reliability of composite columns and beam columns. Univ. Minn. 1993, 1867. [Google Scholar]
- Dai, X.H.; Lam, D.; Jamaluddin, N.; Ye, J. Numerical analysis of slender elliptical concrete filled columns under axial compression. Thin Walled Struct. 2014, 77, 26–35. [Google Scholar] [CrossRef]
- An, Y.F.; Han, L.H.; Zhao, X.L. Behaviour and design calculations on very slender thin-walled CFST columns. Thin Walled Struct. 2012, 53, 161–175. [Google Scholar] [CrossRef]
- Phan, D.H.H.; Patel, V.I.; Liang, Q.Q.; Al Abadi, H.; Thai, H.T. Numerical investigations of circular double-skin steel tubular slender beam-columns filled with ultra-high-strength concrete. Eng. Struct. 2022, 254, 113814. [Google Scholar] [CrossRef]
- Patel, V.I.; Liang, Q.Q.; Hadi, M.N. Nonlinear analysis of circular high strength concrete-filled stainless steel tubular slender beam-columns. Eng. Struct. 2017, 130, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite element modeling of confined concrete-I: Drucker–Prager type plasticity model. Eng. Struct. 2010, 32, 665–679. [Google Scholar] [CrossRef]
- Yu, T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite element modeling of confined concrete-II: Plastic-damage model. Eng. Struct. 2010, 32, 680–691. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Z.B.; Yu, Q. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Constr. Steel Res. 2013, 89, 121–131. [Google Scholar] [CrossRef]
- Azad, S.K.; Uy, B. Effect of concrete infill on local buckling capacity of circular tubes. J. Constr. Steel Res. 2020, 165, 105899. [Google Scholar] [CrossRef]
- Zarringol, M.; Thai, H.T.; Ngo, T.; Patel, V. Behaviour and design calculations of rectangular CFST beam-columns with slender sections. Eng. Struct. 2020, 222, 111142. [Google Scholar] [CrossRef]
- Zarringol, M.; Thai, H.T.; Thai, S.; Patel, V. Application of ANN to the design of CFST columns. Structures 2020, 28, 2203–2220. [Google Scholar] [CrossRef]
- Zarringol, M.; Thai, H.-T.; Naser, M. Application of machine learning models for designing CFCFST columns. J. Constr. Steel Res. 2021, 185, 106856. [Google Scholar] [CrossRef]
- Zarringol, M.; Thai, H.T. Prediction of the load-shortening curve of CFST columns using ANN-based models. J. Build. Eng. 2022, 51, 104279. [Google Scholar] [CrossRef]
- Aramis, Version 6.1; User Manual-Software; GOM mbH: Braunschweig, Germany, 2009.
- Tabbara, M.; Karam, G. Parametric Investigation of the Effects of Localization and Slenderness on the Stress–Strain Response and Confinement Efficiency in FRP-Wrapped Concrete Cylinders. Appl. Sci. 2020, 10, 3432. [Google Scholar] [CrossRef]



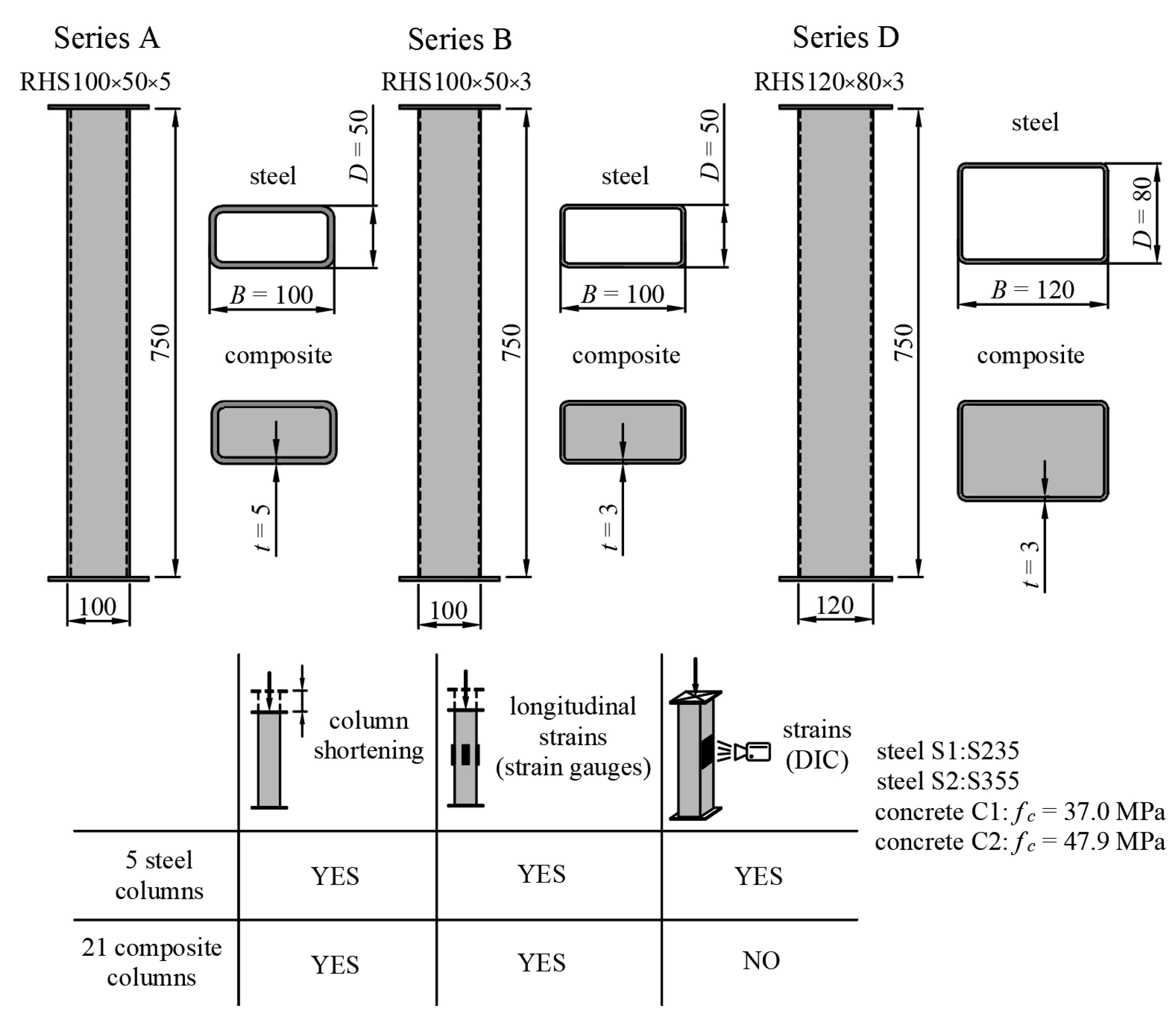








| Series | Steel Cross-Section | Steel Grade | Yield Strength fy (MPa) | Concrete Strength fc (MPa) | D/t/L/D | ξ | Quantity | |
|---|---|---|---|---|---|---|---|---|
| DS1 | RHS 120 × 80 × 3 | S235 | 317.0 | - | 26.7/9.4 | 0.29 | - | 1 |
| DS1C1 | S235 | 317.0 | 37.0 | 0.32 | 1.16 | 3 | ||
| DS1C2 | S235 | 317.0 | 47.9 | 0.34 | 0.90 | 3 | ||
| DS2 | S355 | 414.0 | - | 0.33 | - | 1 | ||
| DS2C1 | S355 | 414.0 | 37.0 | 0.35 | 1.51 | 2 | ||
| AS1 | RHS 100 × 50 × 5 | S235 | 408.3 | - | 10.0/15 | 0.54 | - | 1 |
| AS1C1 | S235 | 408.3 | 37.0 | 0.56 | 4.12 | 3 | ||
| AS1C2 | S235 | 408.3 | 47.9 | 0.57 | 3.18 | 3 | ||
| AS2 | S355 | 426.2 | - | 0.55 | - | 1 | ||
| AS2C1 | S355 | 426.2 | 37.0 | 0.57 | 4.30 | 2 | ||
| BS1 | RHS 100 × 50 × 3 | S235 | 357.4 | - | 16.7/15 | 0.48 | - | 1 |
| BS1C1 | S235 | 357.4 | 37.0 | 0.53 | 1.97 | 3 | ||
| BS1C2 | S235 | 357.4 | 47.9 | 0.54 | 1.52 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzeszykowski, B.; Szmigiera, E.D. Experimental Investigation on the Vertical Ductility of Rectangular CFST Columns Loaded Axially. Materials 2022, 15, 2231. https://doi.org/10.3390/ma15062231
Grzeszykowski B, Szmigiera ED. Experimental Investigation on the Vertical Ductility of Rectangular CFST Columns Loaded Axially. Materials. 2022; 15(6):2231. https://doi.org/10.3390/ma15062231
Chicago/Turabian StyleGrzeszykowski, Bartosz, and Elżbieta Danuta Szmigiera. 2022. "Experimental Investigation on the Vertical Ductility of Rectangular CFST Columns Loaded Axially" Materials 15, no. 6: 2231. https://doi.org/10.3390/ma15062231






