Variation of Durability and Strength Parameters of Pumice Based Mixtures
Abstract
:1. Introduction
2. Research Significance
3. Materials and Experimental Investigation
3.1. Mixture Design
3.2. Slump and Air Content
3.3. Compressive Strength
3.4. Diffusion Coefficient Calculation
4. Diffusion Coefficient Analysis
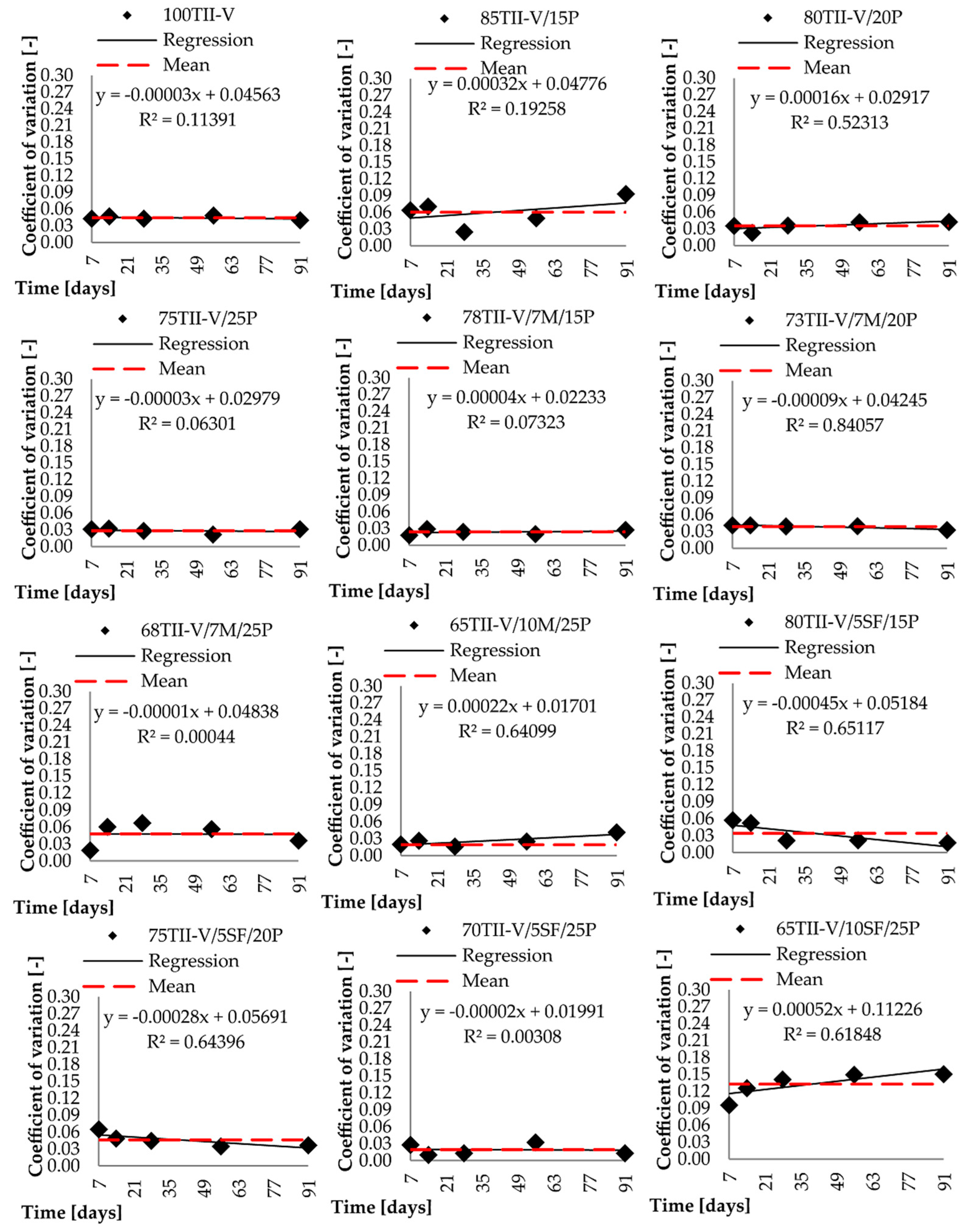
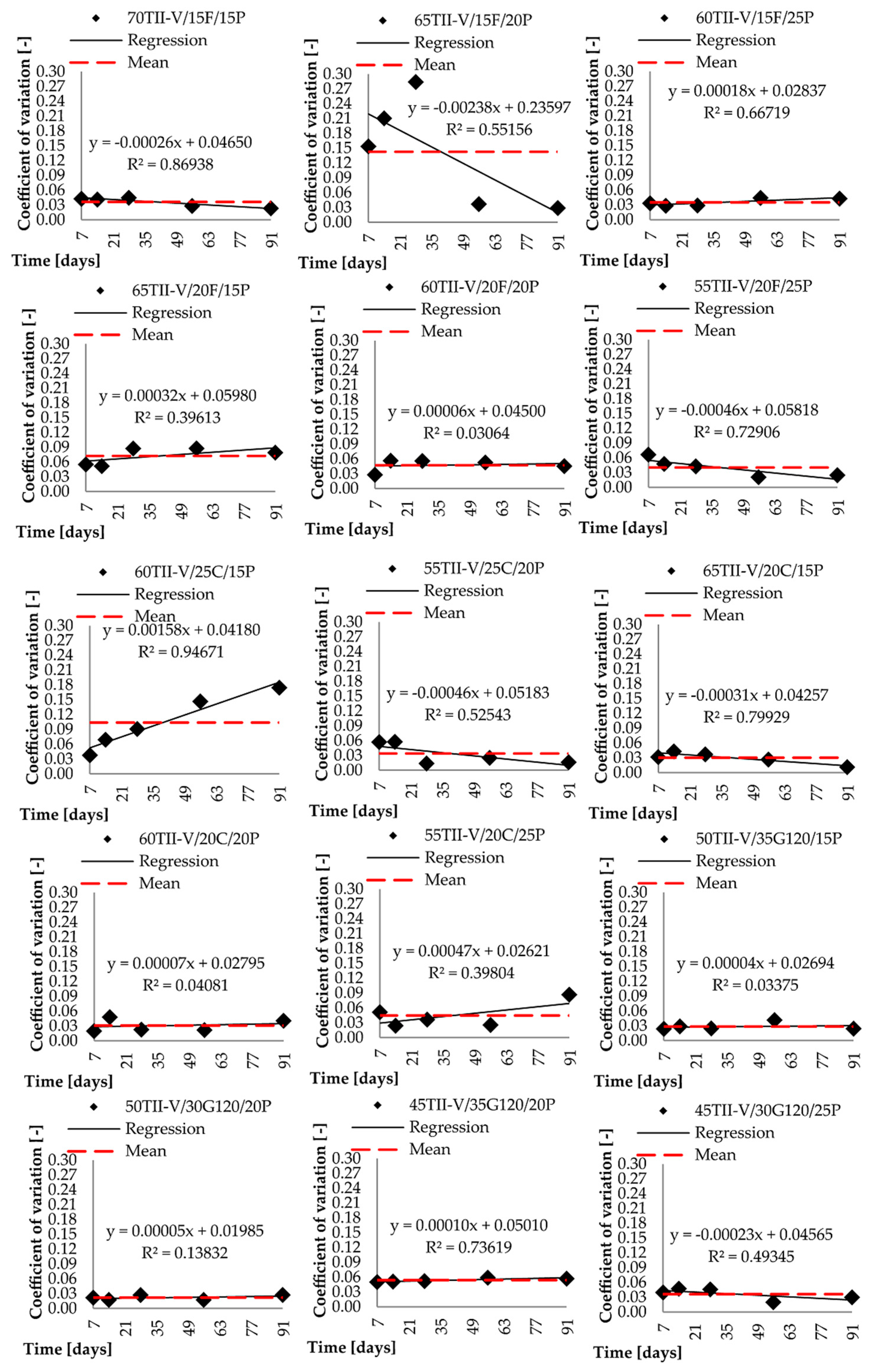
5. Coefficient of Variation Analysis
5.1. Mean Model
5.2. Trend Line Model
5.3. Statistical Evaluation
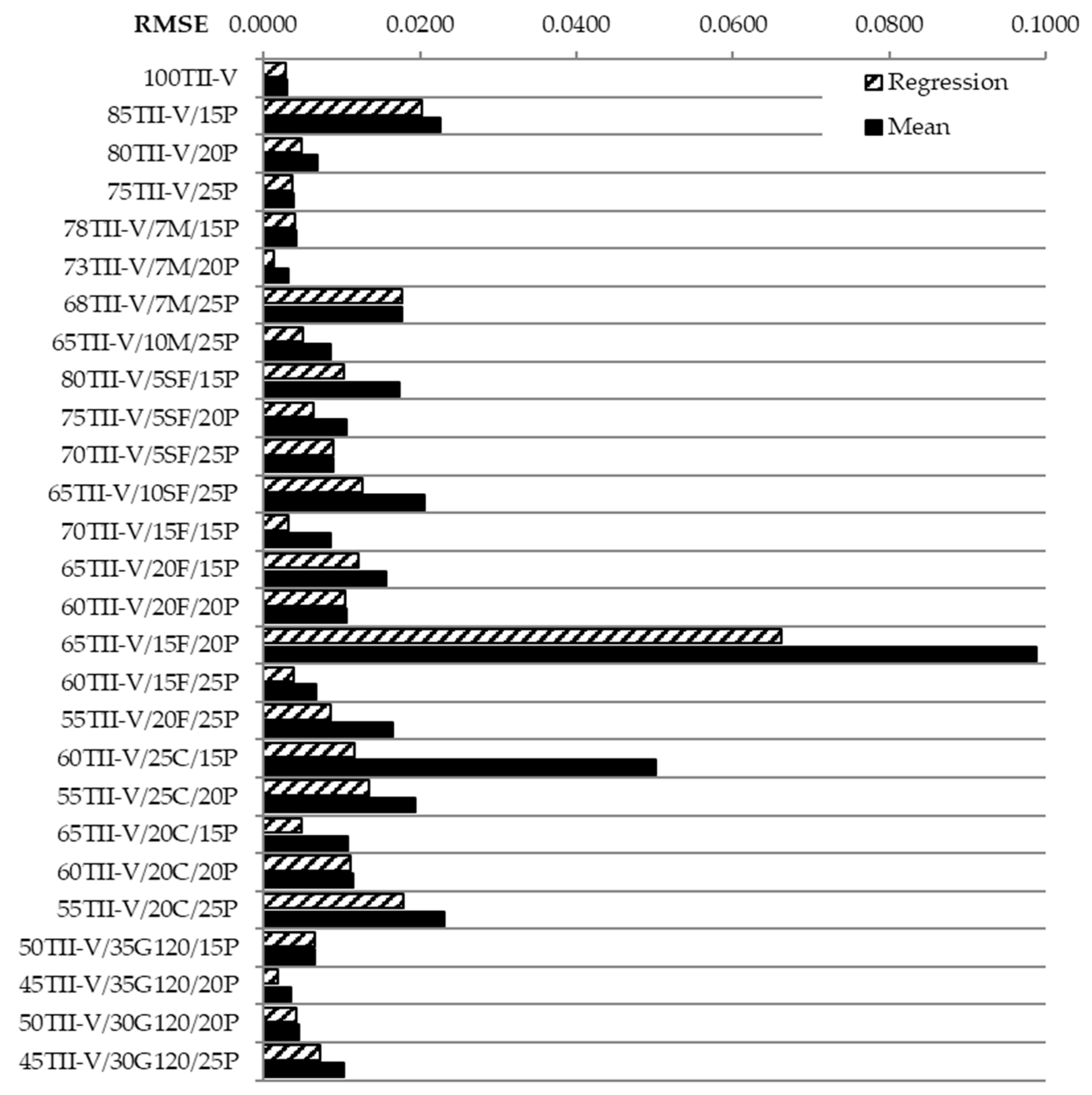
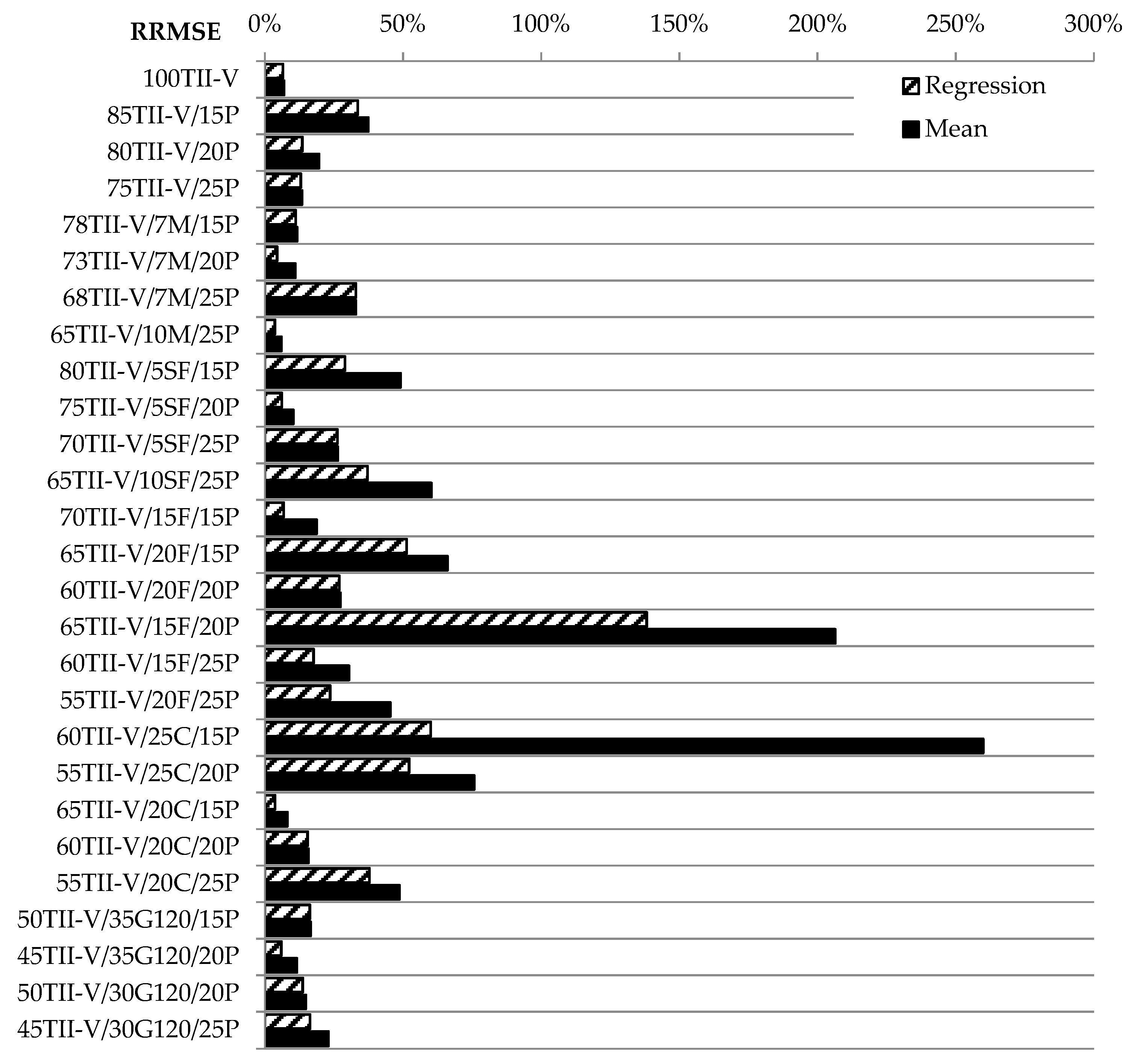
6. RMSE Analysis
7. Diffusion Coefficient Time-Dependent Variation Model
8. Discussion
8.1. Diffusion Coefficient
8.2. Compressive Strength
9. Conclusions
- Based on the RRMSE results, seven mixtures are recommended for the mean value of variation coefficient, and 10 mixtures are recommended for the linear regression of variation coefficient (see Table 3).
- For the other 10 mixtures, the recommendation of the selection of methods was considered unreliable.
- The diffusion coefficient results of Class F and Class C-based mixtures show that there is a significant effect of the amount of SCM on the values of diffusion coefficients, and there is also a very high value of diffusion coefficients at early ages of hardening.
- Analysis results of the time parameter of compressive strength have confirmed that 56 days and 91 days are more appropriate compared to 28 days strength.
- The comparison of the results between the groups of binary and ternary mixtures showed that the best performance for the matured concrete (at the age of 91 days) was observed in the group of Class F-based mixtures blended with pumice.
- In summary, this research will lead a pathway for the practical application of pumice materials in future bridge deck slabs based on their effectiveness of replacement and interaction with other cementitious materials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goodier, C.I. Development of self-compacting concrete. Proc. Inst. Civ. Eng. Struct. Build. 2003, 156, 405–414. [Google Scholar] [CrossRef]
- Hornakova, M.; Konecny, P.; Lehner, P.; Katzer, J. Durability of structural lightweight waste aggregate concrete—Electrical resistivity. MATEC Web Conf. 2020, 310, 00015. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Z.; Gao, Q.; Liu, C. A new mixture design methodology based on the Packing Density Theory for high performance concrete in bridge engineering. Constr. Build. Mater. 2018, 182, 80–93. [Google Scholar] [CrossRef]
- Lehner, P.; Ghosh, P.; Konečný, P. Statistical analysis of time dependent variation of diffusion coefficient for various binary and ternary based concrete mixtures. Constr. Build. Mater. 2018, 183, 75–87. [Google Scholar] [CrossRef]
- Thomas, M.D.A.; Bamforth, P.B. Modelling chloride diffusion in concrete effect of fly ash and slag. Cem. Concr. Res. 1999, 29, 487–495. [Google Scholar] [CrossRef]
- Seddik Meddah, M. Durability performance and engineering properties of shale and volcanic ashes concretes. Constr. Build. Mater. 2015, 79, 73–82. [Google Scholar] [CrossRef]
- Hrabova, K.; Teply, B.; Vymazal, T. Sustainability assessment of concrete mixes. IOP Conf. Ser. Earth Environ. Sci. 2020, 444, 012021. [Google Scholar] [CrossRef]
- Novák, D.; Vořechovský, M.; Teplý, B. FReET: Software for the statistical and reliability analysis of engineering problems and FReET-D: Degradation module. Adv. Eng. Softw. 2014. [Google Scholar] [CrossRef]
- Nguyen, N.L.; Jang, G.W.; Choi, S.; Kim, J.; Kim, Y.Y. Analysis of thin-walled beam-shell structures for concept modeling based on higher-order beam theory. Comput. Struct. 2018, 195, 16–33. [Google Scholar] [CrossRef]
- Bentz, D.P.; Garboczi, E.J.; Lu, Y.; Martys, N.; Sakulich, A.R.; Weiss, W.J. Modeling of the influence of transverse cracking on chloride penetration into concrete. Cem. Concr. Compos. 2013, 38, 65–74. [Google Scholar] [CrossRef]
- Sykora, M.; Markova, J.; Holicky, M. Assessment of deteriorating reinforced concrete road bridges. Reliab. Risk Saf. 2009. [Google Scholar] [CrossRef]
- Zhou, Y.; Gencturk, B.; Willam, K.; Attar, A. Carbonation-induced and chloride-induced corrosion in reinforced concrete structures. J. Mater. Civ. Eng. 2015, 27, 04014245. [Google Scholar] [CrossRef]
- Bertolini, L.; Elsener, B.; Pedeferri, P.; Polder, R. Corrosion of Steel in Concrete: Prevention, Diagnosis, Repair; Wiley: Hoboken, NJ, USA, 2005; ISBN 9783527603374. [Google Scholar]
- Costa, A.; Appleton, J. Chloride penetration into concrete in marine environment-Part II: Prediction of long term chloride penetration. Mater. Struct. 1999, 32, 354–359. [Google Scholar] [CrossRef]
- Loreto, G.; di Benedetti, M.; de Luca, A.; Nanni, A. Assessment of reinforced concrete structures in marine environment: A case study. Corros. Rev. 2019, 37, 57–69. [Google Scholar] [CrossRef]
- Andrew, R.M. Global CO2 emissions from cement production. Earth Syst. Sci. Data 2018. [Google Scholar] [CrossRef] [Green Version]
- Latawiec, R.; Woyciechowski, P.; Kowalski, K. Sustainable concrete performance—CO2-emission. Environments 2018, 5, 27. [Google Scholar] [CrossRef] [Green Version]
- Tran, Q.; Ghosh, P. Influence of pumice on mechanical properties and durability of high performance concrete. Constr. Build. Mater. 2020, 249, 118741. [Google Scholar] [CrossRef]
- Hossain, K.M.A.; Lachemi, M. Performance of volcanic ash and pumice based blended cement concrete in mixed sulfate environment. Cem. Concr. Res. 2006, 36, 1123–1133. [Google Scholar] [CrossRef]
- Anwar Hossain, K.M. Properties of volcanic pumice based cement and lightweight concrete. Cem. Concr. Res. 2004, 34, 283–291. [Google Scholar] [CrossRef]
- Játiva, A.; Ruales, E.; Etxeberria, M. Volcanic ash as a sustainable binder material: An extensive review. Materials 2021, 14, 1302. [Google Scholar] [CrossRef] [PubMed]
- Hrabová, K.; Lehner, P.; Ghosh, P.; Konečný, P.; Teplý, B. Sustainability levels in compare with mechanical properties and durability of pumice high-performance concrete. Appl. Sci. 2021, 11, 4964. [Google Scholar] [CrossRef]
- Mangat, P.S.; Molloy, B.T. Prediction of long term chloride concentration in concrete. Mater. Struct. 1994, 27, 338–346. [Google Scholar] [CrossRef]
- Castaldo, P.; Palazzo, B.; Mariniello, A. Effects of the axial force eccentricity on the time-variant structural reliability of aging r.c. cross-sections subjected to chloride-induced corrosion. Eng. Struct. 2017, 130, 261–274. [Google Scholar] [CrossRef]
- Stewart, M.G.; Rosowsky, D.V. Time-dependent reliability of deteriorating reinforced concrete bridge decks. Struct. Saf. 1998, 20, 91–109. [Google Scholar] [CrossRef]
- Biondini, F.; Vergani, M. Deteriorating beam finite element for nonlinear analysis of concrete structures under corrosion. Struct. Infrastruct. Eng. 2015, 11, 519–532. [Google Scholar] [CrossRef]
- Konečný, P.; Tikalsky, P.J.; Tepke, D.G. Performance evaluation of concrete bridge deck affected by chloride ingress: Simulation-based reliability assessment and finite element modeling. Transp. Res. Rec. 2008, 2028, 3–8. [Google Scholar] [CrossRef]
- Thomas, H.R.; Zhou, Z. Minimum time-step size for diffusion problem in FEM analysis. Int. J. Numer. Methods Eng. 1997. [Google Scholar] [CrossRef]
- Teplý, B.; Vořechovská, D. Reinforcement corrosion: Limit states, reliability and modelling. J. Adv. Concr. Technol. 2012, 10, 353–362. [Google Scholar] [CrossRef]
- Tran, Q. Durability Investigation of Ultrafine Volcanic Pumice Based HPC Mixtures; California State University: Fullerton, CA, USA, 2014. [Google Scholar]
- Tikalsky, P.J.; Pustka, D.; Marek, P. Statistical variations in chloride diffusion in concrete bridges. ACI Struct. J. 2005, 102, 481–486. [Google Scholar] [CrossRef]
- Le, T.D.T.D.; Lehner, P.; Konečnỳ, P.; Konečný, P. Probabilistic modeling of chloride penetration with respect to concrete heterogeneity and epoxy-coating on the reinforcement. Materials 2019, 12, 4068. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marek, P.; Brozzetti, J.; Gustar, M.; Elishakoff, I. Probabilistic assessment of structures using Monte Carlo simulations. Appl. Mech. Rev. 2002, 55, B31–B32. [Google Scholar] [CrossRef]
- Janas, P.; Krejsa, M.; Krejsa, V. Structural reliability assessment using a direct determined probabilistic calculation. In Proceedings of the Twelfth International Conference on Civil, Structural and Environmental Engineering Computing; Civil-Comp Press: Stirlingshire, UK, 2009. [Google Scholar]
- Lu, X. Application of the Nernst-Einstein equation to concrete. Cem. Concr. Res. 1997, 27, 293–302. [Google Scholar] [CrossRef]
- Hooton, R. Life-365 service life prediction model and computer program for predicting the service life and life-cycle cost of reinforced concrete exposed to chlorides. In Life-365 User Manual; Silica Fume Association: Lovettsville, VA, USA, 2012; pp. 1–80. [Google Scholar]
- Konečný, P.; Lehner, P.; Ghosh, P.; Morávková, Z.; Tran, Q. Comparison of procedures for the evaluation of time dependent concrete diffusion coefficient model. Constr. Build. Mater. 2020, 258, 119535. [Google Scholar] [CrossRef]
- Konečný, P.; Lehner, P.; Ghosh, P.; Tran, Q. Variation of diffusion coefficient for selected binary and ternary concrete mixtures considering concrete aging effect. Key Eng. Mater. 2018, 761, 144–147. [Google Scholar] [CrossRef]
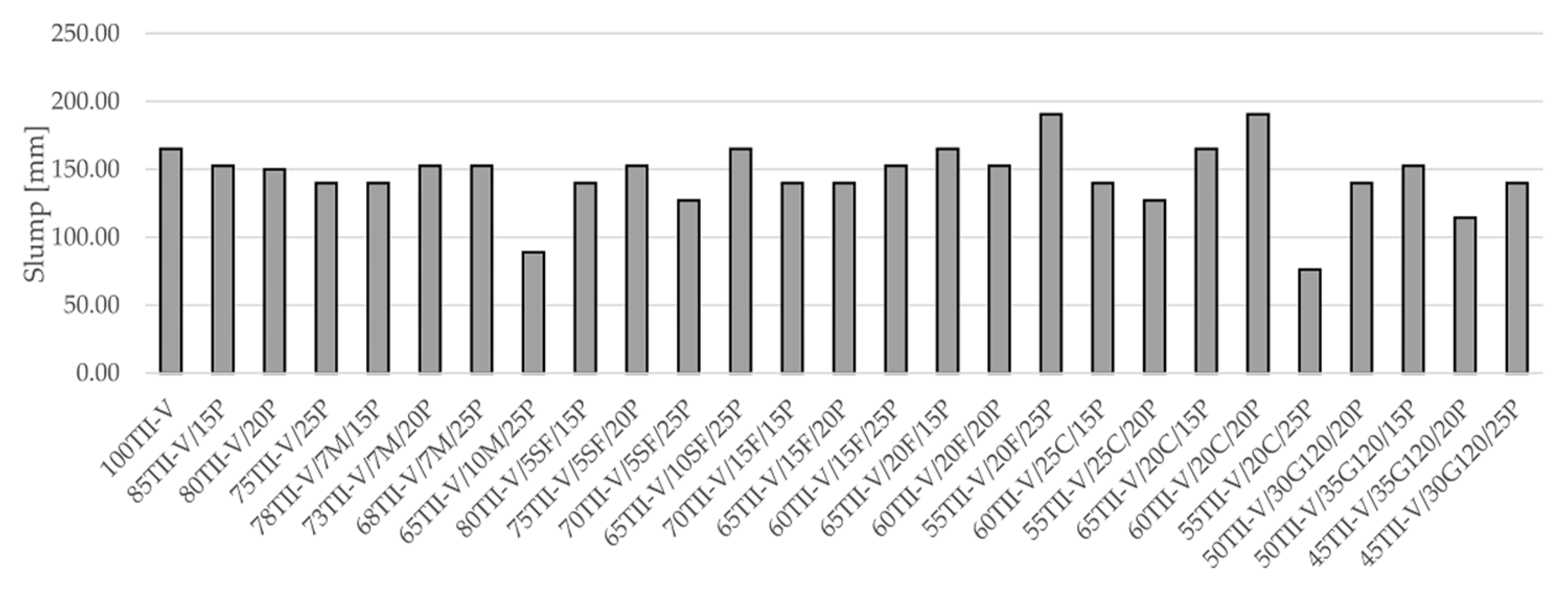

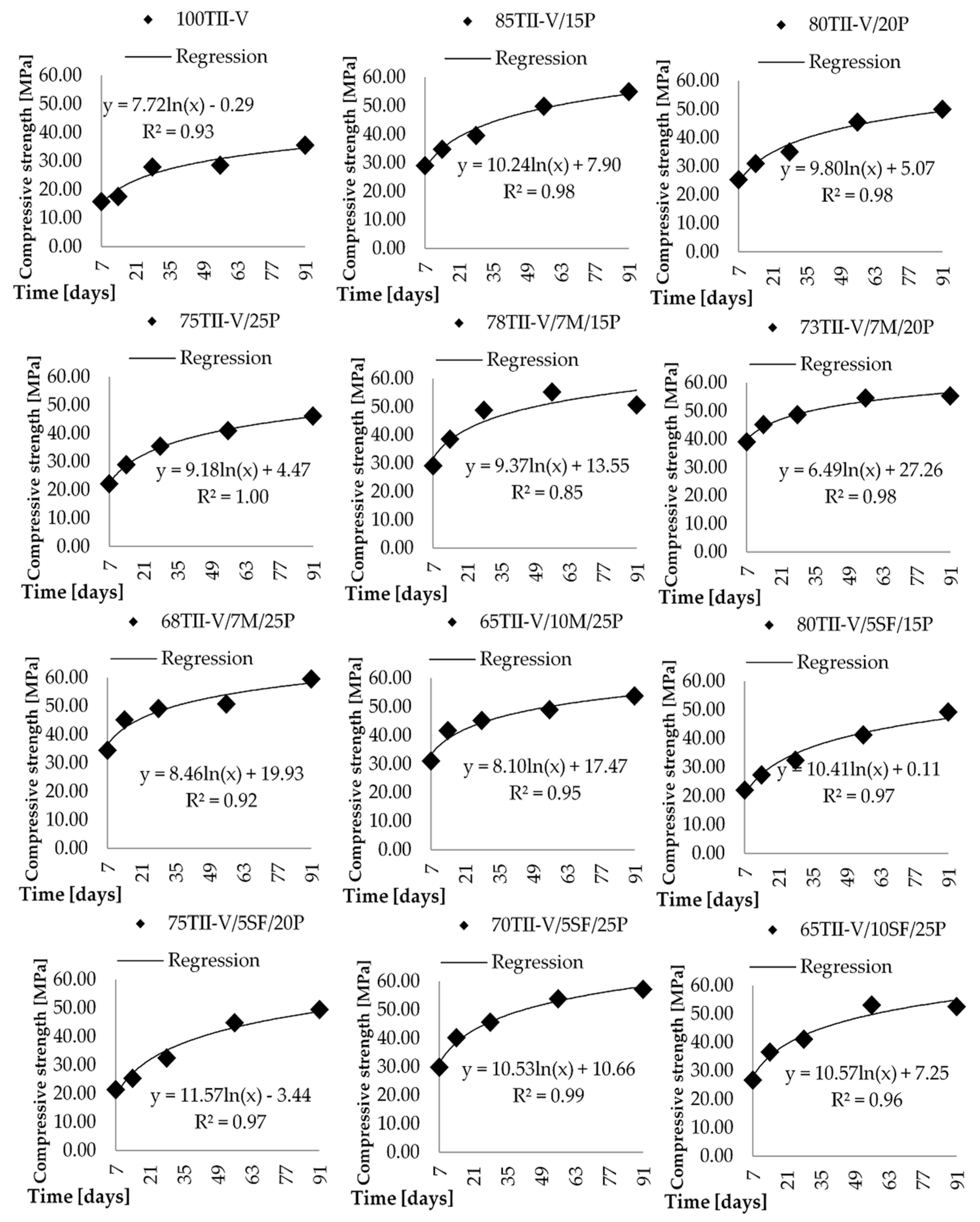
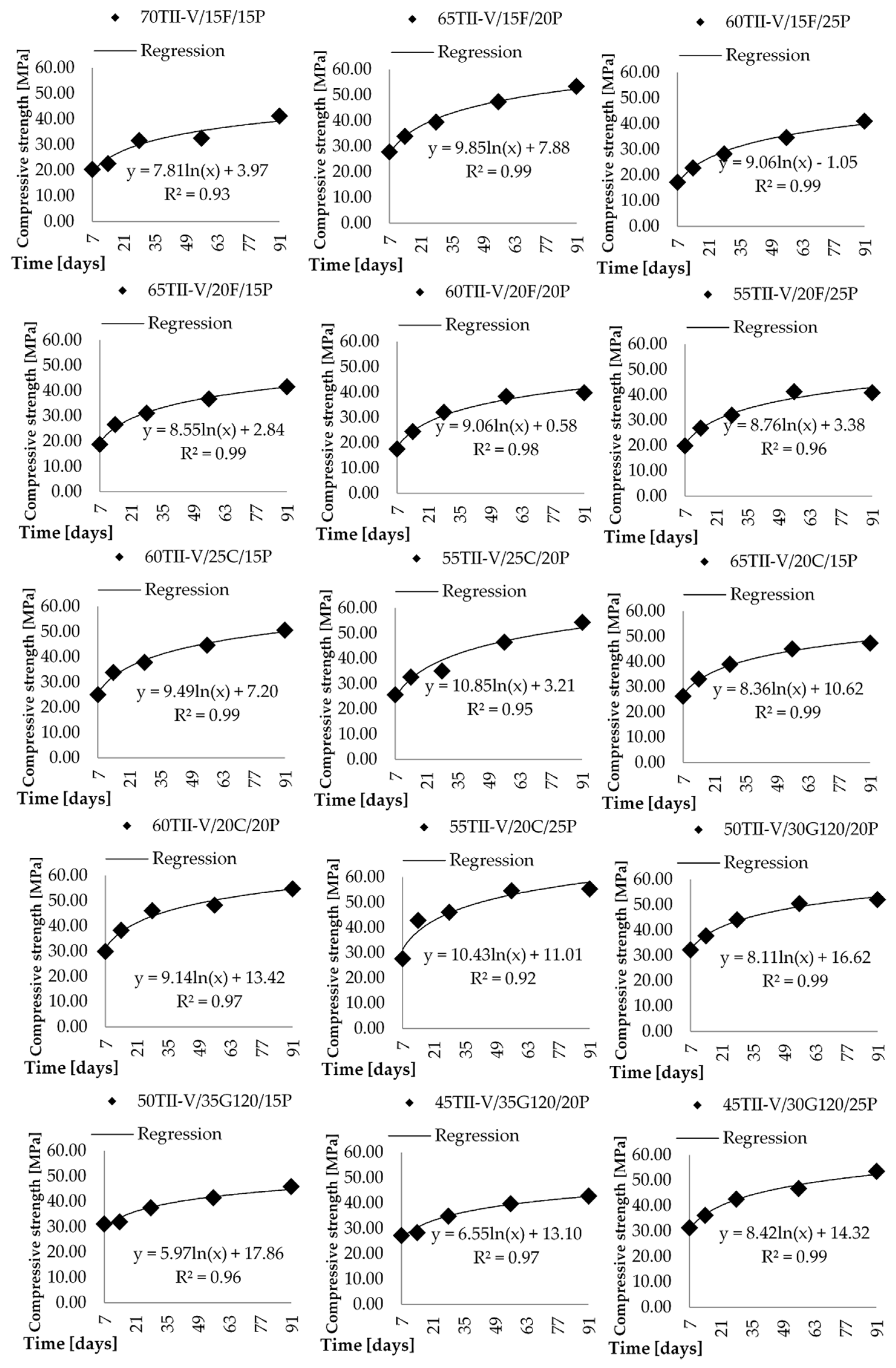

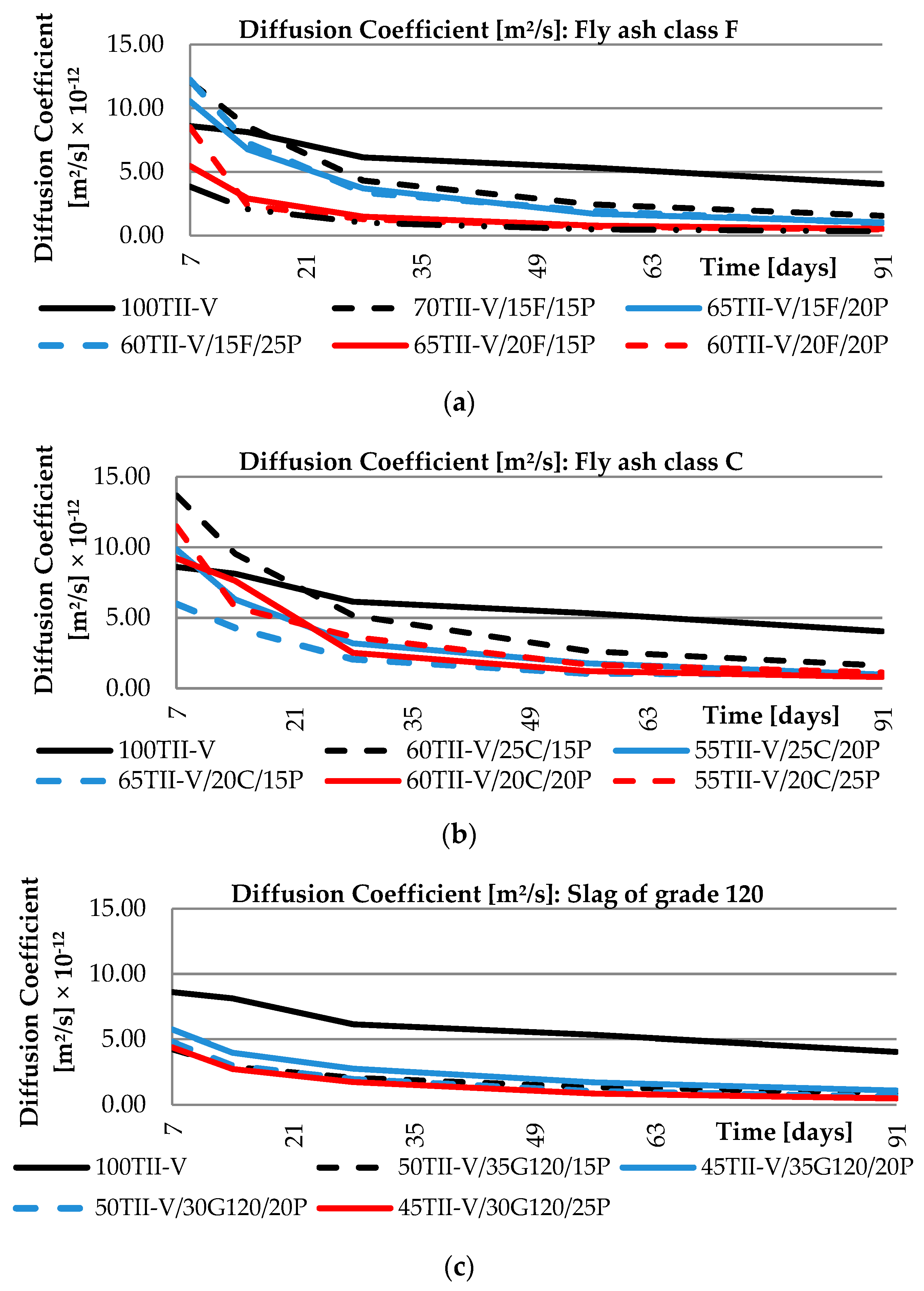
| Mix ID | Cement | Pumice | Fly Ash C | Fly Ash F | Slag G120 | Silica Fume | Metakaolin |
|---|---|---|---|---|---|---|---|
| 100TII-V | 100 | – | – | – | – | – | – |
| 85TII-V/15P | 85 | 15 | – | – | – | – | – |
| 80TII-V/20P | 80 | 20 | – | – | – | – | – |
| 75TII-V/25P | 75 | 25 | – | – | – | – | – |
| 78TII-V/7M/15P | 78 | 15 | – | – | – | – | 7 |
| 73TII-V/7M/20P | 73 | 20 | – | – | – | – | 7 |
| 68TII-V/7M/25P | 68 | 25 | – | – | – | – | 7 |
| 65TII-V/10M/25P | 65 | 25 | – | – | – | – | 10 |
| 80TII-V/5SF/15P | 80 | 15 | – | – | – | 5 | – |
| 75TII-V/5SF/20P | 75 | 20 | – | – | – | 5 | – |
| 70TII-V/5SF/25P | 70 | 25 | – | – | – | 5 | – |
| 65TII-V/10SF/25P | 65 | 25 | – | – | – | 10 | – |
| 70TII-V/15F/15P | 70 | 15 | – | 15 | – | – | – |
| 65TII-V/15F/20P | 65 | 20 | – | 15 | – | – | – |
| 60TII-V/15F/25P | 60 | 25 | – | 15 | – | – | – |
| 65TII-V/20F/15P | 65 | 15 | – | 20 | – | – | – |
| 60TII-V/20F/20P | 60 | 20 | – | 20 | – | – | – |
| 55TII-V/20F/25P | 55 | 25 | – | 20 | – | – | – |
| 60TII-V/25C/15P | 60 | 15 | 25 | – | – | – | – |
| 55TII-V/25C/20P | 55 | 20 | 25 | – | – | – | – |
| 65TII-V/20C/15P | 65 | 15 | 20 | – | – | – | – |
| 60TII-V/20C/20P | 60 | 20 | 20 | – | – | – | – |
| 55TII-V/20C/25P | 55 | 25 | 20 | – | – | – | – |
| 50TII-V/30G120/20P | 50 | 20 | – | – | 30 | – | – |
| 50TII-V/35G120/15P | 50 | 15 | – | – | 35 | – | – |
| 45TII-V/35G120/20P | 45 | 20 | – | – | 35 | – | – |
| 45TII-V/30G120/25P | 45 | 25 | – | – | 30 | – | – |
| No. | µ (m2/s) ×10−12 | cv (-) | µ (m2/s) ×10−12 | cv (-) | µ (m2/s) ×10−12 | cv (-) | µ (m2/s) ×10−12 | cv (-) | µ (m2/s) ×10−12 | cv (-) | m (-) | fc,28 (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (Days) | 7 | 14 | 28 | 56 | 91 | |||||||
| 100TII-V | 8.61 | 0.043 | 8.12 | 0.047 | 6.14 | 0.043 | 5.33 | 0.049 | 4.05 | 0.040 | 0.264 | 27.98 |
| 85TII-V/15P | 9.71 | 0.064 | 7.68 | 0.071 | 4.90 | 0.025 | 2.49 | 0.049 | 1.60 | 0.093 | 0.521 | 39.57 |
| 80TII-V/20P | 1.27 | 0.035 | 8.97 | 0.229 | 5.44 | 0.036 | 2.57 | 0.042 | 1.58 | 0.042 | 0.628 | 34.97 |
| 75TII-V/25P | 1.15 | 0.031 | 7.88 | 0.032 | 3.85 | 0.028 | 2.15 | 0.021 | 1.33 | 0.031 | 0.807 | 35.44 |
| 78TII-V/7M/15P | 5.69 | 0.018 | 2.76 | 0.029 | 1.77 | 0.024 | 1.18 | 0.020 | 8.69 | 0.027 | 0.764 | 31.60 |
| 73TII-V/7M/20P | 3.75 | 0.041 | 2.45 | 0.041 | 1.77 | 0.039 | 1.16 | 0.040 | 7.95 | 0.033 | 0.522 | 37.43 |
| 68TII-V/7M/25P | 6.08 | 0.019 | 2.29 | 0.060 | 1.71 | 0.067 | 1.19 | 0.056 | 7.61 | 0.036 | 0.532 | 34.92 |
| 65TII-V/10M/25P | 3.96 | 0.020 | 2.40 | 0.026 | 1.62 | 0.016 | 1.02 | 0.025 | 7.32 | 0.041 | 0.766 | 39.35 |
| 80TII-V/5SF/15P | 9.59 | 0.058 | 7.04 | 0.053 | 2.76 | 0.021 | 1.30 | 0.022 | 9.50 | 0.017 | 0.936 | 28.26 |
| 75TII-V/5SF/20P | 1.12 | 0.065 | 7.89 | 0.049 | 2.89 | 0.045 | 1.31 | 0.035 | 9.06 | 0.037 | 0.721 | 37.81 |
| 70TII-V/5SF/25P | 8.18 | 0.028 | 3.34 | 0.010 | 1.69 | 0.013 | 7.86 | 0.032 | 4.40 | 0.013 | 0.825 | 35.16 |
| 65TII-V/10SF/25P | 5.53 | 0.096 | 2.46 | 0.126 | 1.20 | 0.141 | 5.57 | 0.150 | 3.82 | 0.151 | 0.932 | 32.31 |
| 70TII-V/15F/15P | 1.21 | 0.043 | 8.57 | 0.042 | 4.32 | 0.045 | 2.45 | 0.029 | 1.56 | 0.023 | 1.000 | 32.40 |
| 65TII-V/15F/20P | 1.06 | 0.154 | 6.77 | 0.210 | 3.72 | 0.284 | 1.71 | 0.037 | 1.04 | 0.029 | 0.826 | 48.65 |
| 60TII-V/15F/25P | 1.22 | 0.033 | 7.28 | 0.028 | 3.39 | 0.029 | 1.92 | 0.044 | 9.83 | 0.043 | 0.537 | 48.72 |
| 65TII-V/20F/15P | 5.46 | 0.055 | 2.91 | 0.052 | 1.49 | 0.088 | 7.80 | 0.088 | 5.26 | 0.079 | 0.883 | 49.11 |
| 60TII-V/20F/20P | 8.51 | 0.028 | 2.35 | 0.056 | 1.28 | 0.055 | 6.89 | 0.053 | 4.82 | 0.045 | 0.651 | 44.05 |
| 55TII-V/20F/25P | 3.84 | 0.066 | 2.08 | 0.047 | 1.01 | 0.042 | 4.86 | 0.020 | 3.32 | 0.025 | 0.675 | 42.50 |
| 60TII-V/25C/15P | 1.37 | 0.038 | 9.55 | 0.069 | 5.17 | 0.091 | 2.64 | 0.147 | 1.62 | 0.174 | 1.000 | 45.66 |
| 55TII-V/25C/20P | 9.85 | 0.057 | 6.31 | 0.058 | 3.20 | 0.014 | 1.78 | 0.025 | 9.87 | 0.016 | 0.636 | 45.24 |
| 65TII-V/20C/15P | 5.99 | 0.032 | 4.29 | 0.043 | 2.07 | 0.037 | 1.06 | 0.027 | 1.01 | 0.012 | 1.000 | 41.16 |
| 60TII-V/20C/20P | 9.21 | 0.020 | 7.63 | 0.048 | 2.52 | 0.023 | 1.23 | 0.022 | 8.06 | 0.041 | 0.937 | 31.12 |
| 55TII-V/20C/25P | 1.15 | 0.051 | 5.76 | 0.024 | 3.65 | 0.036 | 1.68 | 0.025 | 1.13 | 0.087 | 1.000 | 32.00 |
| 50TII-V/30G120/20P | 4.79 | 0.022 | 2.99 | 0.017 | 1.95 | 0.027 | 1.00 | 0.017 | 6.06 | 0.027 | 0.968 | 32.02 |
| 50TII-V/35G120/15P | 4.25 | 0.024 | 2.89 | 0.028 | 2.06 | 0.025 | 1.33 | 0.041 | 9.22 | 0.024 | 0.793 | 38.96 |
| 45TII-V/35G120/20P | 5.75 | 0.050 | 3.99 | 0.051 | 2.77 | 0.052 | 1.71 | 0.059 | 1.08 | 0.057 | 0.986 | 46.06 |
| 45TII-V/30G120/25P | 4.40 | 0.040 | 2.73 | 0.047 | 1.73 | 0.046 | 8.55 | 0.020 | 4.81 | 0.030 | 0.818 | 46.12 |
| No. | Mean | Linear Regression | ∆RRMSE | Recommen. | |||
|---|---|---|---|---|---|---|---|
| cv.mean (-) | RRMSEmean | cv,LR (-) | R2LR | RRMSELR | |||
| 100TII-V | 0.0443 | 7% | −0.00003x + 0.04563 | 0.114 | 7% | 0% | Mean |
| 85TII-V/15P | 0.0603 | 37% | 0.00032x + 0.04776 | 0.193 | 34% | 4% | LR |
| 80TII-V/20P | 0.0356 | 20% | 0.00016x + 0.02917 | 0.523 | 14% | 6% | LR |
| 75TII-V/25P | 0.0286 | 13% | −0.00003x + 0.02979 | 0.063 | 13% | 0% | Mean |
| 78TII-V/7M/15P | 0.0238 | 12% | 0.00004x + 0.02233 | 0.073 | 11% | 0% | Mean |
| 73TII-V/7M/20P | 0.0388 | 11% | −0.00009x + 0.04245 | 0.841 | 4% | 7% | LR |
| 68TII-V/7M/25P | 0.0479 | 33% | −0.00001x + 0.04838 | 0.000 | 33% | 0% | Mean |
| 65TII-V/10M/25P | 0.0257 | 6% | 0.00022x + 0.01701 | 0.641 | 4% | 2% | LR |
| 80TII-V/5SF/15P | 0.0341 | 49% | −0.00045x + 0.05184 | 0.651 | 29% | 20% | Not reliable |
| 75TII-V/5SF/20P | 0.0460 | 10% | −0.00028x + 0.05691 | 0.644 | 6% | 4% | LR |
| 70TII-V/5SF/25P | 0.0193 | 26% | −0.00002x + 0.01991 | 0.003 | 26% | 0% | Mean |
| 65TII-V/10SF/25P | 0.1328 | 60% | 0.00052x + 0.11226 | 0.618 | 37% | 23% | Not reliable |
| 70TII-V/15F/15P | 0.0363 | 19% | −0.00026x + 0.04650 | 0.869 | 7% | 12% | Not reliable |
| 65TII-V/15F/20P | 0.1427 | 206% | −0.00238x + 0.23597 | 0.552 | 138% | 68% | Not reliable |
| 60TII-V/15F/25P | 0.0353 | 31% | 0.00018x + 0.02837 | 0.667 | 18% | 13% | Not reliable |
| 65TII-V/20F/15P | 0.0724 | 66% | 0.00032x + 0.05980 | 0.396 | 51% | 15% | Not reliable |
| 60TII-V/20F/20P | 0.0474 | 27% | 0.00006x + 0.04500 | 0.031 | 27% | 0% | Mean |
| 55TII-V/20F/25P | 0.0402 | 45% | −0.00046x + 0.05818 | 0.729 | 24% | 22% | Not reliable |
| 60TII-V/25C/15P | 0.1037 | 260% | 0.00158x + 0.04180 | 0.947 | 60% | 200% | Not reliable |
| 55TII-V/25C/20P | 0.0339 | 76% | −0.00046x + 0.05183 | 0.525 | 52% | 24% | Not reliable |
| 65TII-V/20C/15P | 0.0303 | 8% | −0.00031x + 0.04257 | 0.799 | 4% | 5% | LR |
| 60TII-V/20C/20P | 0.0309 | 16% | 0.00007x + 0.02795 | 0.041 | 15% | 0% | Mean |
| 55TII-V/20C/25P | 0.0447 | 49% | 0.00047x + 0.02621 | 0.398 | 38% | 11% | Not reliable |
| 50TII-V/30G120/20P | 0.0220 | 15% | 0.00005x + 0.01985 | 0.138 | 14% | 1% | LR |
| 50TII-V/35G120/15P | 0.0285 | 17% | 0.00004x + 0.02694 | 0.034 | 16% | 0% | Mean |
| 45TII-V/35G120/20P | 0.0539 | 12% | 0.00010x + 0.05010 | 0.736 | 6% | 6% | LR |
| 45TII-V/30G120/25P | 0.0365 | 23% | −0.00023x + 0.04565 | 0.493 | 16% | 7% | LR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehner, P.; Konečný, P.; Ghosh, P. Variation of Durability and Strength Parameters of Pumice Based Mixtures. Materials 2021, 14, 3674. https://doi.org/10.3390/ma14133674
Lehner P, Konečný P, Ghosh P. Variation of Durability and Strength Parameters of Pumice Based Mixtures. Materials. 2021; 14(13):3674. https://doi.org/10.3390/ma14133674
Chicago/Turabian StyleLehner, Petr, Petr Konečný, and Pratanu Ghosh. 2021. "Variation of Durability and Strength Parameters of Pumice Based Mixtures" Materials 14, no. 13: 3674. https://doi.org/10.3390/ma14133674







