Nanoindentation of γ-TiAl with Different Crystal Surfaces by Molecular Dynamics Simulations
Abstract
:1. Introduction
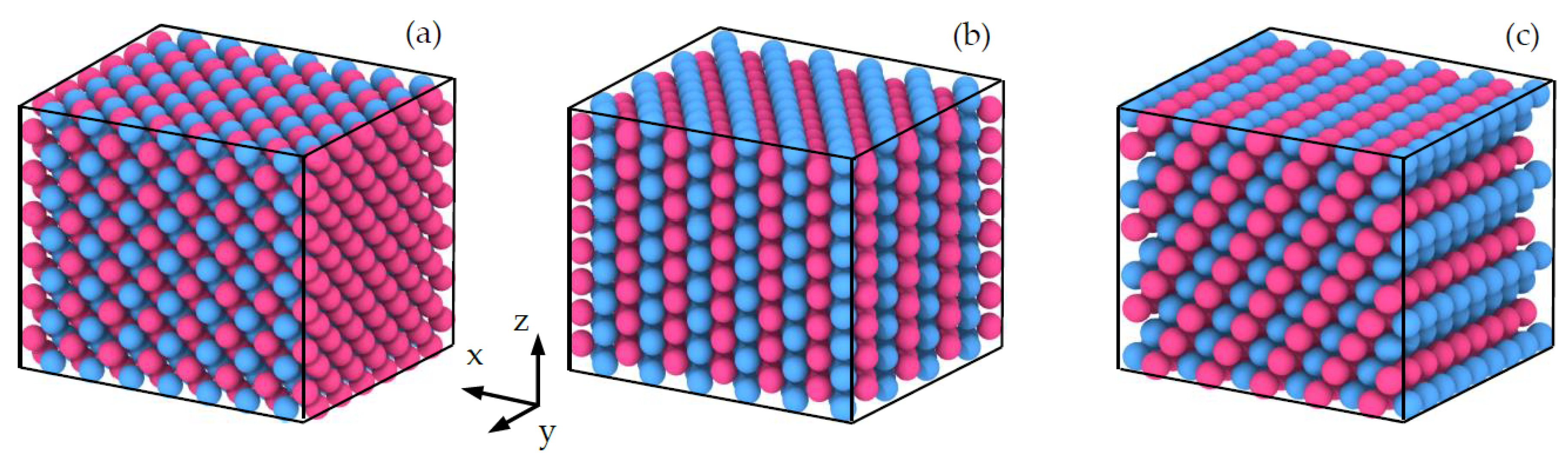
2. Materials and Methods
3. Results
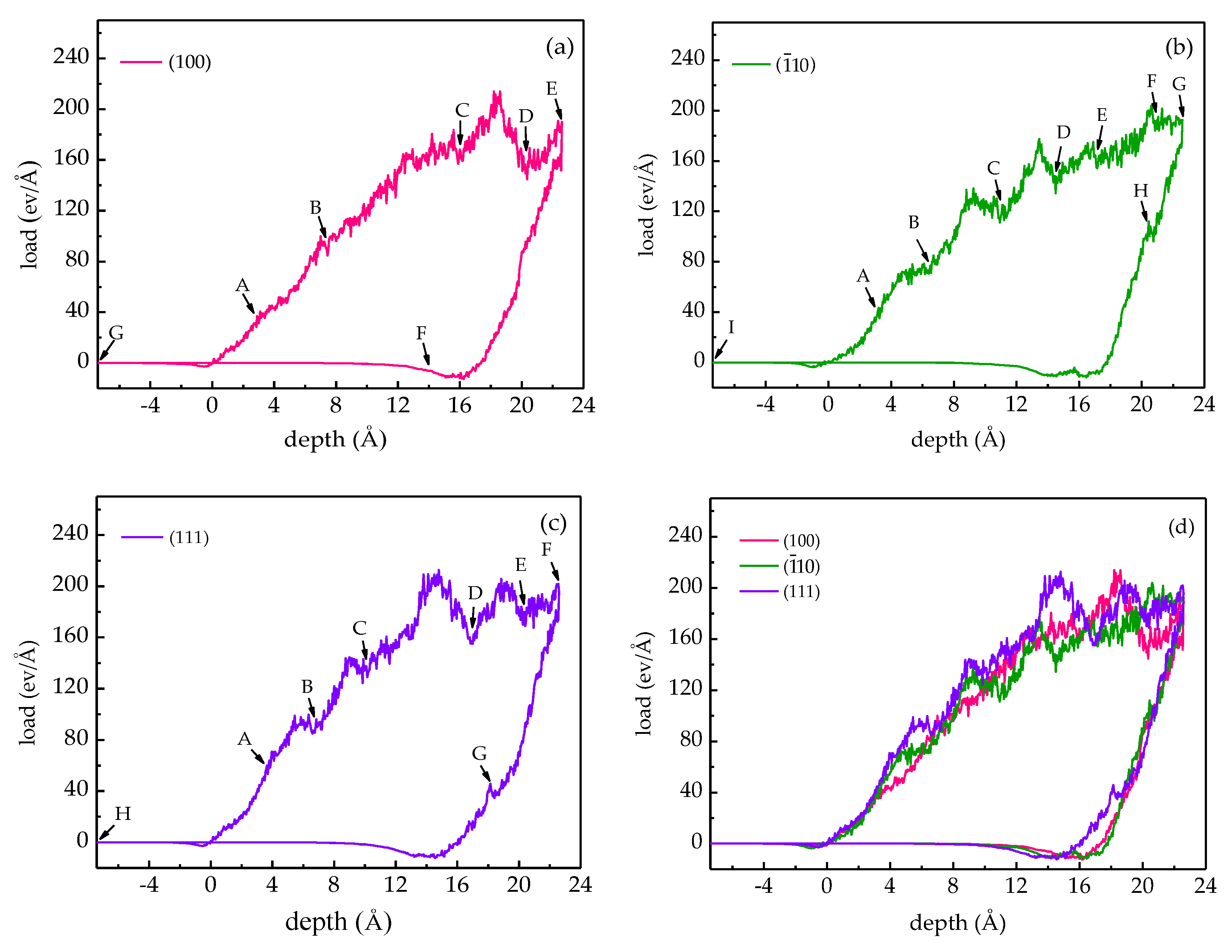
3.1. Analysis of Load-Depth Curves
3.2. Analysis of Defect Evolution
3.2.1. Analysis of Defect Evolution for the (100) Sample
3.2.2. Analysis of Defect Evolution for the () Sample
3.2.3. Analysis of Defect Evolution for the (111) Sample
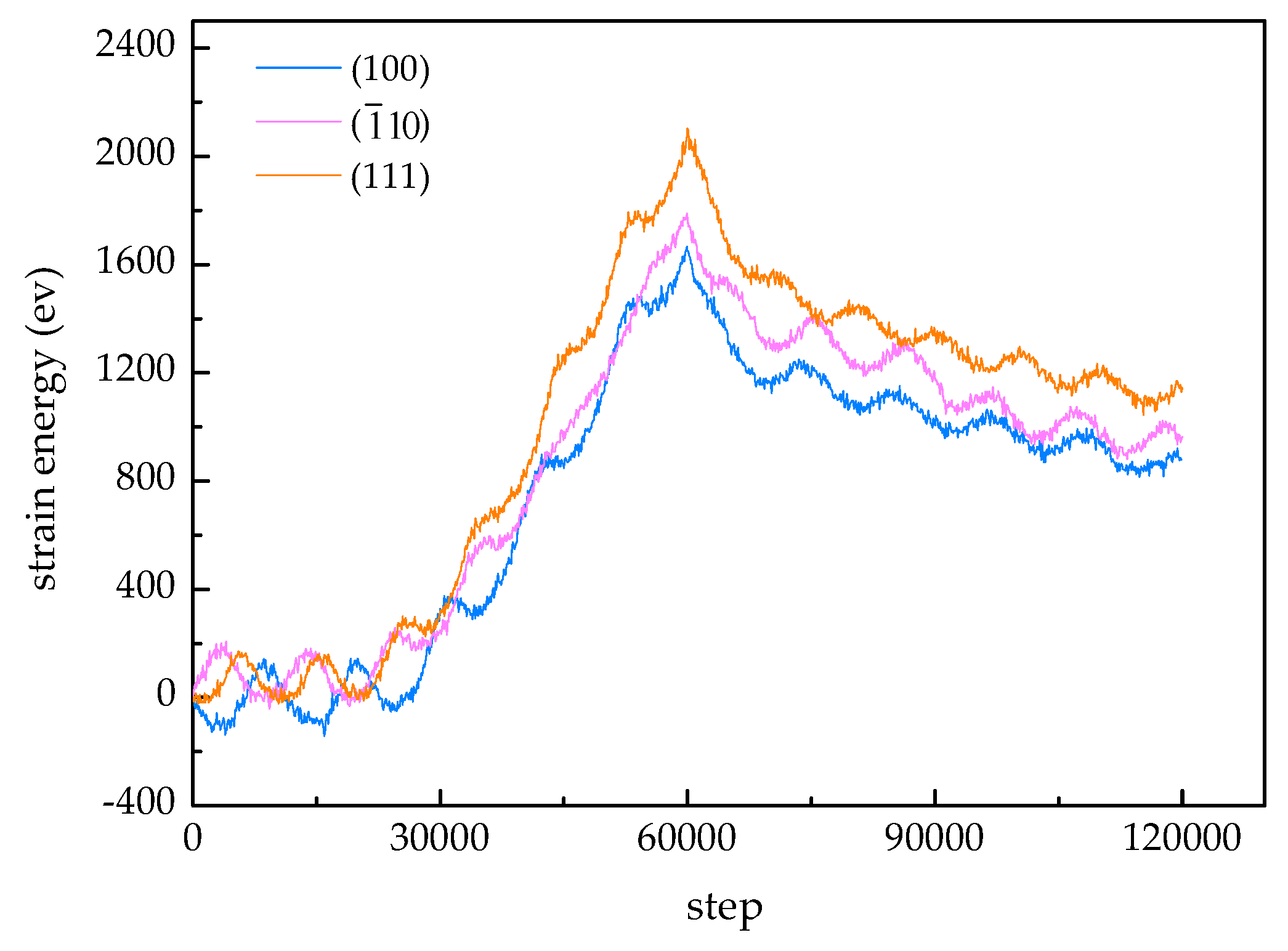
3.3. Analysis of Strain Energy for Different Samples
3.4. Calculation of Hardness and Elastic Modulus
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clemens, H.; Mayer, S. Advanced Intermetallic TiAl Alloys. Mater. Sci. Forum 2016, 879, 113–118. [Google Scholar] [CrossRef]
- Clemens, H.; Mayer, S. Design, Processing, Microstructure, Properties, and Applications of Advanced Intermetallic TiAl Alloys. Adv. Eng. Mater. 2013, 15, 191–215. [Google Scholar] [CrossRef]
- Clemens, H.; Mayer, S. Intermetallic titanium aluminides in aerospace applications-processing, microstructure and properties. Mater. High Temp. 2016, 33, 560–570. [Google Scholar] [CrossRef]
- Tezok, F.; Brahimi, M.; Paraschivoiu, I. Investigation of the physical processes underlying the ice accretion phenomena. In Proceedings of the Aiaa Aerospace Sciences Meeting & Exhibit, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Stegall, D.E.; Elmustafa, A.A. Activation volume of pure face centered cubic metals using uniaxial testing and nanoindentation equipped with high load capability. Mater. Res. Express 2016, 3, 105024. [Google Scholar] [CrossRef]
- Bigl, S.; SchoBerl, T.; Wurster, S.; Cordill, M.J.; Kiener, D. Correlative Microstructure and Topography Informed Nanoindentation of Copper Films. Surf. Coat. Technol. 2016, 308, 404–413. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, G.; Tay, S.L.; Guo, Y.; Sun, X.; Gao, W. Effects of Bi Addition on the Microstructure and Mechanical Properties of Nanocrystalline Ag Coatings. Materials 2017, 10, 932. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Chromik, R.R. Relationship between indentation plastic zone size and residual stresses in plastically deformed Fe. Mater. Sci. Eng. A 2017, 696, 1–9. [Google Scholar] [CrossRef]
- Huape, E.; Villafañe, A.M.; Soto, R.P.T.; Macias, A.H. Mechanical properties of γ-TiAl alloys on the Aluminium-Rich side by Nanoindentation. Int. J. Sci. Adv. Tech. 2015, 5, 1–6. [Google Scholar]
- Guitton, A.; Kriaa, H.; Bouzy, E.; Guyon, J.; Maloufi, N. A Dislocation-Scale Characterization of the Evolution of Deformation Microstructures around Nanoindentation Imprints in a TiAl Alloy. Materials 2018, 11, 305. [Google Scholar] [CrossRef] [PubMed]
- Han, J.K.; Li, X.; Dippenaar, R.; Liss, K.D.; Kawasaki, M. Microscopic plastic response in a bulk nano-structured TiAl intermetallic compound processed by high-pressure torsion. Mater. Sci. Eng. A 2018, 714, 84–92. [Google Scholar] [CrossRef]
- Khosravani, A.; Morsdorf, L.; Tasan, C.C.; Kalidindi, S.R. Multiresolution mechanical characterization of hierarchical materials: Spherical nanoindentation on martensitic Fe-Ni-C steels. Acta Mater. 2018, 153, 257–269. [Google Scholar] [CrossRef]
- Li, R.; Mo, C.; Liao, Y. Mechanical Properties of U-Cu Intermetallic Compound Measured by Nanoindentation. Materials 2018, 11, 2215. [Google Scholar] [CrossRef] [PubMed]
- Heng, C.; Taihua, Z.; Yi, M. Effect of Applied Stress on the Mechanical Properties of a Zr-Cu-Ag-Al Bulk Metallic Glass with Two Different Structure States. Materials 2017, 10, 711. [Google Scholar] [CrossRef]
- Ying, S.; Ma, L.; Sui, T.; Papadaki, C.; Salvati, E.; Romano Brandt, L.; Zhang, H.; Korsunsky, A.M. Nanoscale Origins of the Size Effect in the Compression Response of Single Crystal Ni-Base Superalloy Micro-Pillars. Materials 2018, 11, 561. [Google Scholar] [CrossRef] [PubMed]
- Xiong, K.; Liu, X.; Gu, J. Multiscale modeling of lattice dynamical instability in gamma-TiAl crystal. Model. Simul. Mater. Sci. Eng. 2015, 23, 045006. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K.; Farkas, D. Nanotwinned fcc metals: Strengthening versus softening mechanisms. Phys. Rev. B 2010, 82, 4196–4205. [Google Scholar] [CrossRef]
- Brostow, W.; Hagg Lobland, H.E. Materials: Introduction and Applications; John Wiley & Sons: New York, NY, USA, 2017; Chapter 15; p. 184. [Google Scholar]
- Liu, Q.; Deng, L.; Wang, X.; Li, J. Formation of stacking fault tetrahedron in single-crystal Cu during nanoindentation investigated by molecular dynamics. Comput. Mater. Sci. 2017, 131, 44–47. [Google Scholar] [CrossRef]
- Jiao, S.; Tu, W.; Zhang, P.; Zhang, W.; Qin, L.; Sun, Z.; Chen, J. Atomistic insights into the prismatic dislocation loop on Al (100) during nanoindentation investigated by molecular dynamics. Comput. Mater. Sci. 2018, 143, 384–390. [Google Scholar] [CrossRef]
- Shih-Wei, L.; Ren-Zheng, Q.; Te-Hua, F. Molecular dynamics simulations of nanoindentation and scratch in Cu grain boundaries. Beilstein J. Nanotechnol. 2017, 8, 2283–2295. [Google Scholar] [CrossRef]
- Talaei, M.S.; Nouri, N.; Ziaei-Rad, S. Grain Boundary Effects on Nanoindentation of Fe Bicrystal Using Molecular Dynamic. Mech. Mater. 2016, 102, 97–107. [Google Scholar] [CrossRef]
- Abu-Shams, M.; Shabib, I. Effect of voids on nanoindentation response of Fe-10%Cr alloys using molecular dynamics simulation. Mater. Express 2017, 7, 329–340. [Google Scholar] [CrossRef]
- Biao, Y.; Bailin, Z.; Xingjian, H.; Pengfei, H.; Zhufeng, Y. Effect of Void on Nanoindentation Process of Ni-Based Single Crystal Alloy. Acta Metall. Sin. 2016. [Google Scholar] [CrossRef]
- Dasilva, C.J.; Rino, J.P. Atomistic simulation of the deformation mechanism during nanoindentation of gamma titanium aluminide. Comput. Mater. Sci. 2012, 62, 1–5. [Google Scholar] [CrossRef]
- Xu, S.; Wan, Q.; Sha, Z.; Liu, Z. Molecular dynamics simulations of nanoindentation and wear of the γ-TiAl alloy. Comput. Mater. Sci. 2015, 110, 247–253. [Google Scholar] [CrossRef]
- Jun, T.S.; Armstrong, D.E.J.; Britton, T.B. A nanoindentation investigation of local strain rate sensitivity in dual-phase Ti alloys. J. Alloys Compd. 2016, 672, 282–291. [Google Scholar] [CrossRef] [Green Version]
- Ziegenhain, G.; Urbassek, H.M.; Hartmaier, A. Influence of crystal anisotropy on elastic deformation and onset of plasticity in nanoindentation: A simulational study. J. Appl. Phys. 2010, 107, 156. [Google Scholar] [CrossRef]
- Xiong, K.; Lu, H.; Gu, J. Atomistic simulations of the nanoindentation-induced incipient plasticity in Ni3Al crystal. Comput. Mater. Sci. 2016, 115, 214–226. [Google Scholar] [CrossRef]
- Xiong, K.; Gu, J. Understanding pop-in phenomena in FeNi3 nanoindentation. Intermetallics 2015, 67, 111–120. [Google Scholar] [CrossRef]
- Kempf, M.; Goken, M.; Vehoff, H. The mechanical properties of different lamellae and domains in PST-TiAl investigated with nanoindentations and atomic force microscopy. Mater. Sci. Eng. A 2002, 329–331, 184–189. [Google Scholar] [CrossRef]
- Zambaldi, C.; Raabe, D.; Roters, F. Plastic anisotropy of γ-TiAl revealed by axisymmetric indentation. Acta Mater. 2010, 58, 3516–3530. [Google Scholar] [CrossRef] [Green Version]
- Demidov, A.G.; Fortunato, M.E.; Colina, C.M. Update 0.2 to “pysimm: A python package for simulation of molecular systems”. Softwarex 2018, 7, 70–73. [Google Scholar] [CrossRef]
- Zope, R.R.; Mishin, Y. Interatomic potentials for atomistic simulations of the TiAl system. Phys. Rev. B 2003, 68, 366–369. [Google Scholar] [CrossRef]
- Blonski, S.; Brostow, W.; Kubát, J. Molecular-Dynamics Simulations of Stress Relaxation in Metals and Polymers. Phys. Rev. B 1994, 49, 6494. [Google Scholar] [CrossRef]
- Baowan, D.; Triampo, W.; Triampo, D. Encapsulation of TiO2 nanoparticles into single-walled carbon nanotubes. New J. Phys. 2009, 11, 093011. [Google Scholar] [CrossRef]
- Peng, P.; Liao, G.; Shi, T.; Tang, Z.; Gao, Y. Molecular dynamic simulations of nanoindentation in aluminum thin film on silicon substrate. Appl. Surf. Sci. 2010, 256, 6284–6290. [Google Scholar] [CrossRef]
- Jian, S.R.; Fang, T.H.; Chuu, D.S. Nanomechanical characterizations of InGaN thin films. Appl. Surf. Sci. 2006, 252, 3033–3042. [Google Scholar] [CrossRef]
- Liang, H.; Woo, C.H.; Huang, H.; Ngan, A.H.W.; Yu, T.X. Crystalline plasticity on copper (001), (110), and (111) surfaces during nanoindentation. Comp. Model. Eng. 2004, 6, 105–114. [Google Scholar] [CrossRef]
- Zhu, P.Z.; Hu, Y.Z.; Wang, H. Atomistic simulations of the effect of a void on nanoindentation response of nickel. Sci. China Ser. G 2010, 53, 1716–1719. [Google Scholar] [CrossRef]
- Fu, T.; Peng, X.; Chen, X.; Weng, S.; Hu, N.; Li, Q.; Wang, Z. Molecular dynamics simulation of nanoindentation on Cu/Ni nanotwinned multilayer films using a spherical indenter. Sci. Rep. 2016, 6, 35665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, T.Y.; Zheng, B.L.; Hu, M.Y.; He, P.F.; Yue, Z.F. Molecular dynamics simulation of incipient plasticity of nickel substrates of different surface orientations during nanoindentation. Mater. Sci. Technol. 2015, 31, 325–331. [Google Scholar] [CrossRef]
- Cross, G.L.W.; Schirmeisen, A.; Grütter, P.; Düring, U.T. Plasticity, healing and shakedown in sharp-asperity nanoindentation. Nat. Mater. 2006, 5, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Xiong, K.; Liu, X.; Li, C.; Gu, J. Phonon instability of Co single crystal in uniaxial tension and nanoindentation. Comput. Mater. Sci. 2015, 99, 47–56. [Google Scholar] [CrossRef]
- Kelchner, L. Dislocation Nucleation and Defect Structure during Surface Indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Alhafez, I.A.; Ruestes, C.J.; Gao, Y.; Urbassek, H.M. Nanoindentation of hcp metals: A comparative simulation study of the evolution of dislocation networks. Nanotechnology 2016, 27, 045706. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ni, Y.; Wang, H.; Mei, J. Effects of Crystalline Anisotropy and Indenter Size on Nanoindentation by Multiscale Simulation. Nanoscale Res. Lett. 2009, 5, 420–443. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Park, J.Y.; Kim, S.Y.; Jun, S.; Im, S. Atomistic simulations of incipient plasticity under Al (111) nanoindentation. Mech. Mater. 2005, 37, 1035–1048. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 20. [Google Scholar] [CrossRef]
- Belak, J.; Boercker, D.B.; Stowers, I.F. Simulation of nanometer-scale deformation of metallic and ceramic surfaces. MRS Bull. 1993, 18, 55–60. [Google Scholar] [CrossRef]
- He, Y.; Schwarz, R.B.; Migliori, A.; Whang, S.H. Elastic constants of single crystal γ-TiAl. J. Mater. Res. 1995, 10, 1187–1195. [Google Scholar] [CrossRef]
- Fu, H.; Li, D.; Peng, F.; Gao, T.; Cheng, X. Structural and elastic properties of γ-TiAl under high pressure from electronic structure calculations. J. Alloys Compd. 2009, 473, 255–261. [Google Scholar] [CrossRef]



| Parameters | σ (Å) | ϵ (10−1ev) | r0 (Å) |
|---|---|---|---|
| C-Al | 2.976 | 3.15 | 7.44 |
| C-Ti | 3.759 | 0.314 | 9.398 |
| Samples | (100) | (111) | |
|---|---|---|---|
| Hardness (GPa) | 6.42 | 6.63 | 6.91 |
| Elastic modulus (GPa) | 164.5 | 175.8 | 192.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Rui, Z.; Cao, H.; Fu, R.; Feng, R.; Yan, C. Nanoindentation of γ-TiAl with Different Crystal Surfaces by Molecular Dynamics Simulations. Materials 2019, 12, 770. https://doi.org/10.3390/ma12050770
Fan X, Rui Z, Cao H, Fu R, Feng R, Yan C. Nanoindentation of γ-TiAl with Different Crystal Surfaces by Molecular Dynamics Simulations. Materials. 2019; 12(5):770. https://doi.org/10.3390/ma12050770
Chicago/Turabian StyleFan, Xiaocui, Zhiyuan Rui, Hui Cao, Rong Fu, Ruicheng Feng, and Changfeng Yan. 2019. "Nanoindentation of γ-TiAl with Different Crystal Surfaces by Molecular Dynamics Simulations" Materials 12, no. 5: 770. https://doi.org/10.3390/ma12050770





