Dynamic Simulation of a Fe-Ga Energy Harvester Prototype Through a Preisach-Type Hysteresis Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Magneto-Mechanical Preisach Model of the Fe–Ga Rod
2.2. Finite Element Model of the Generator
2.3. Magnetostrictive Properties
2.4. Harvester Prototype Setup and Modeling
2.5. Characterization and Experimental Setups
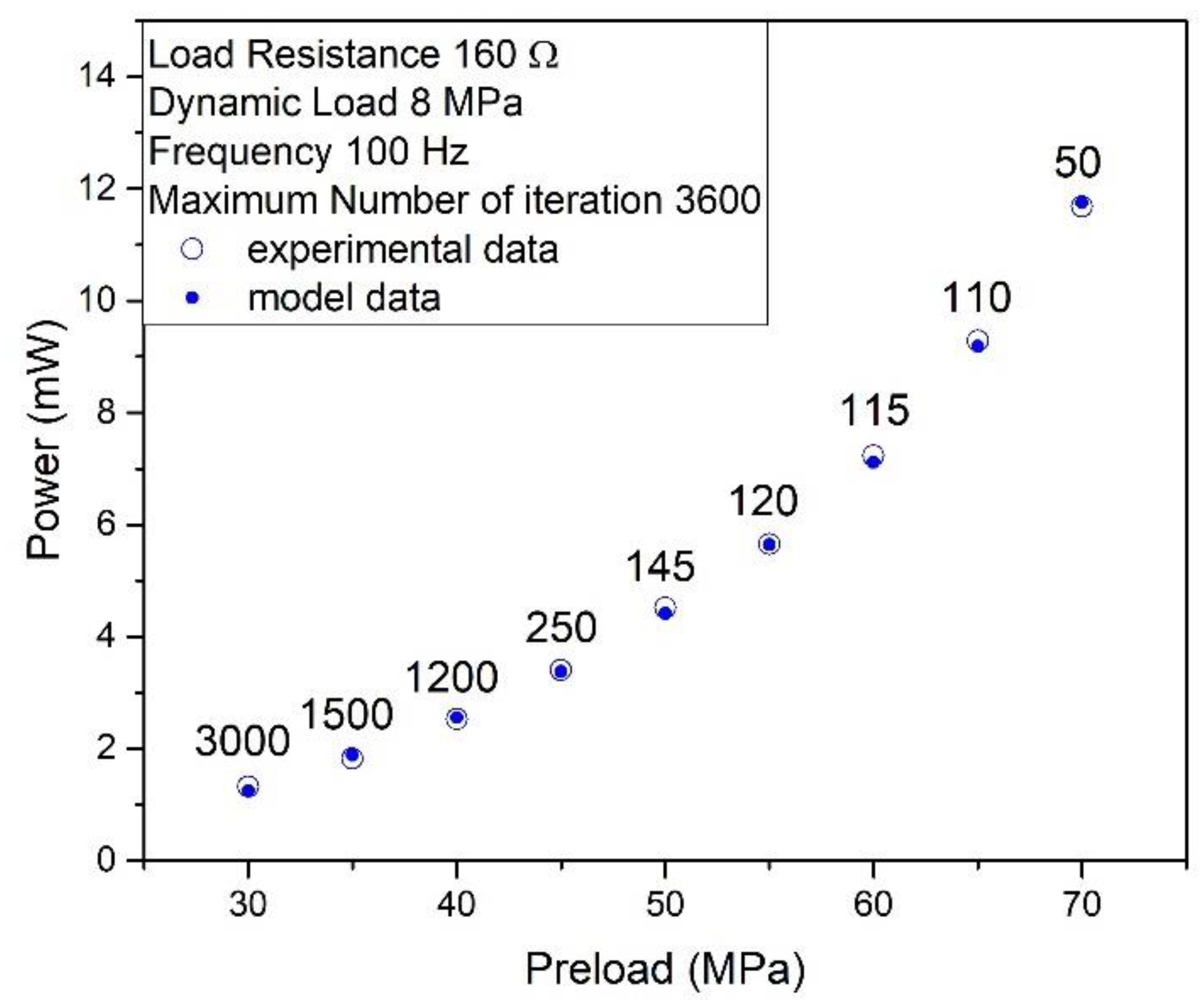
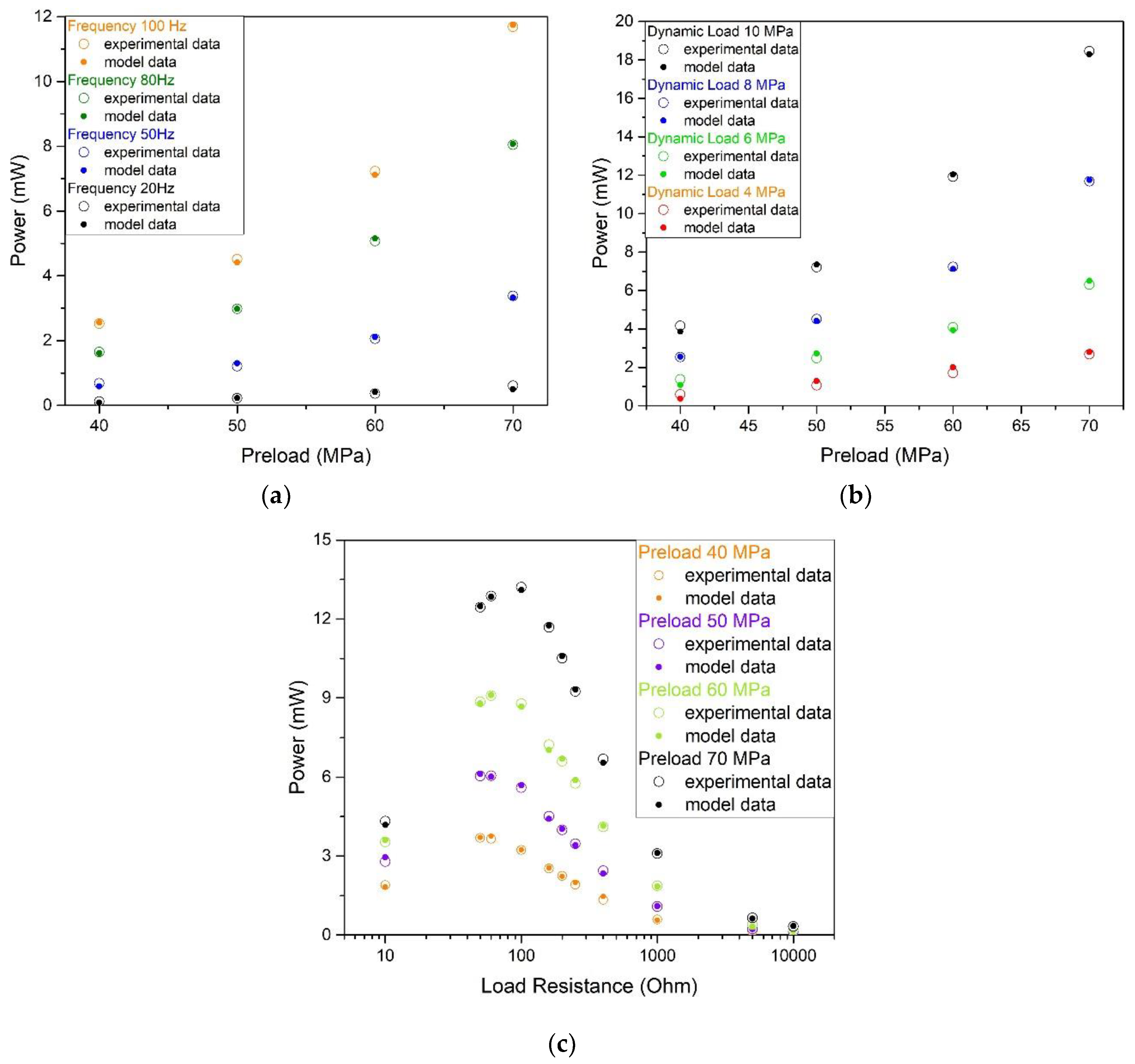
3. Results
3.1. Preliminary Results
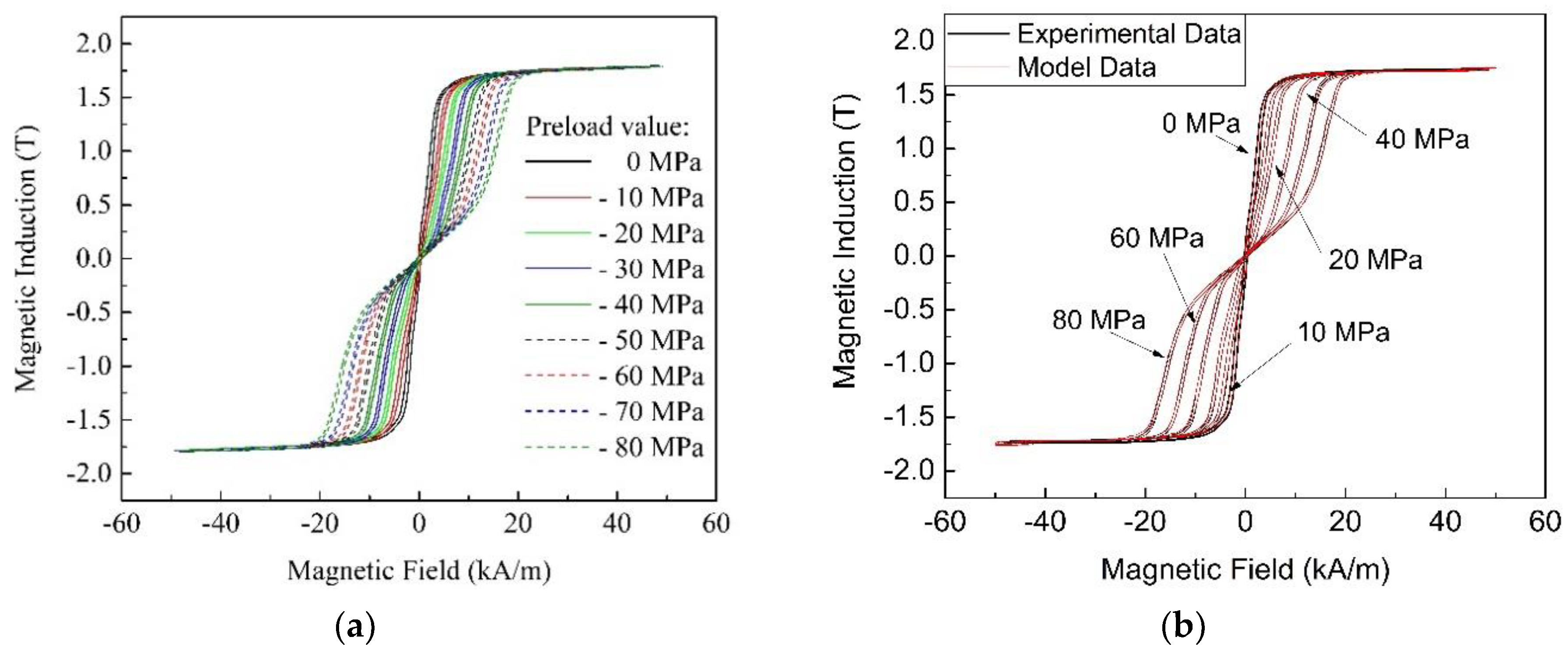
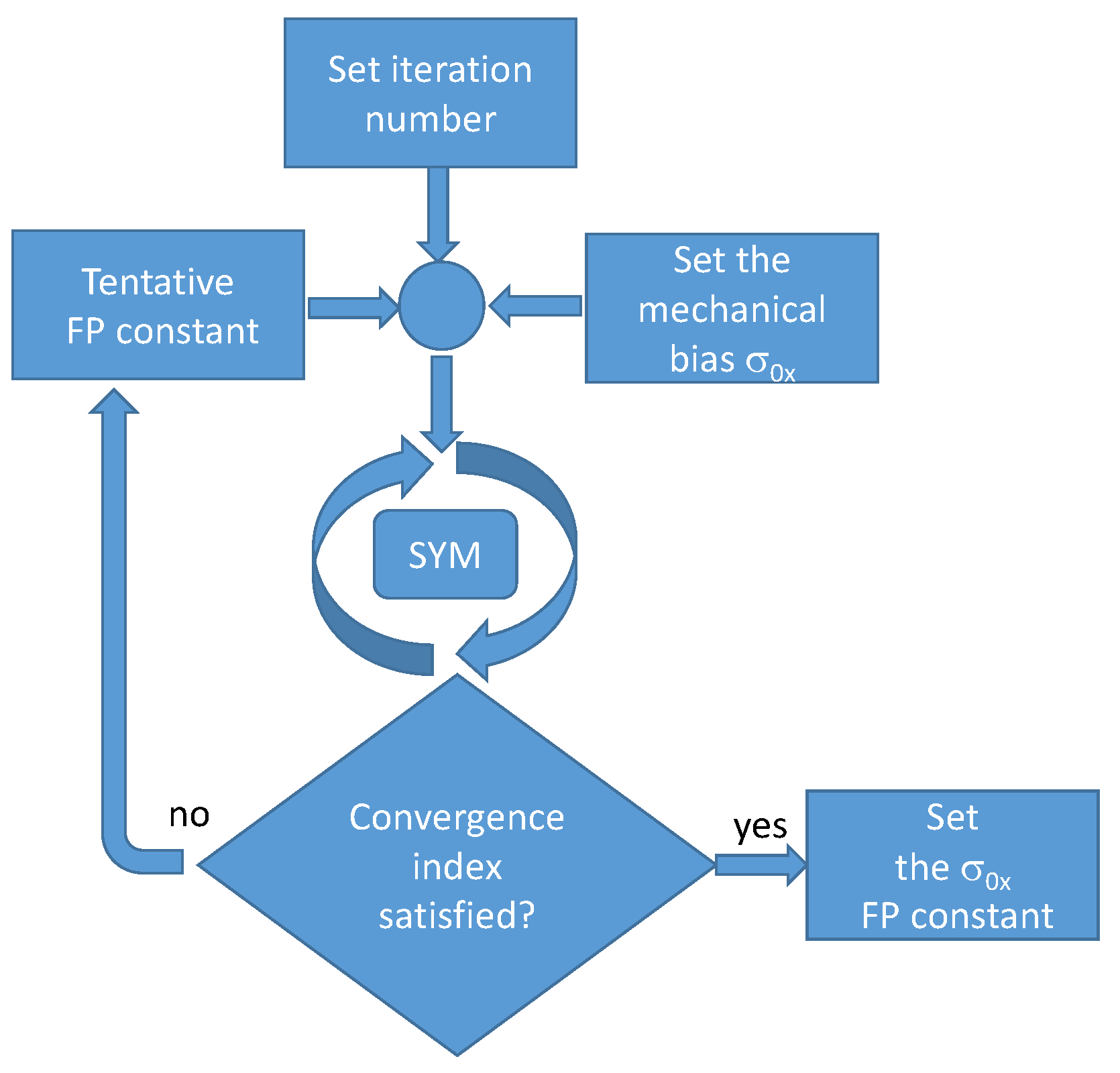
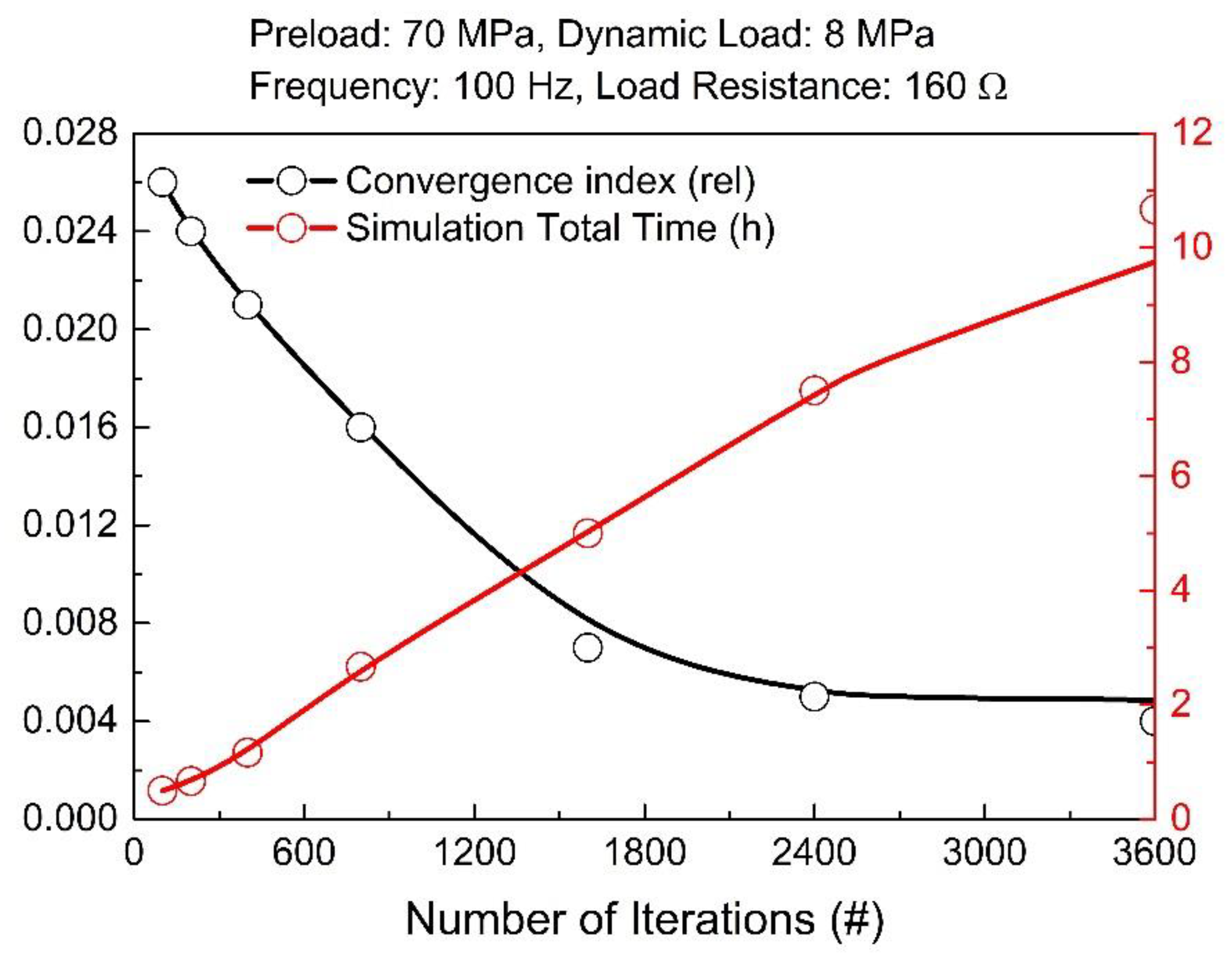
3.2. Model Tuning
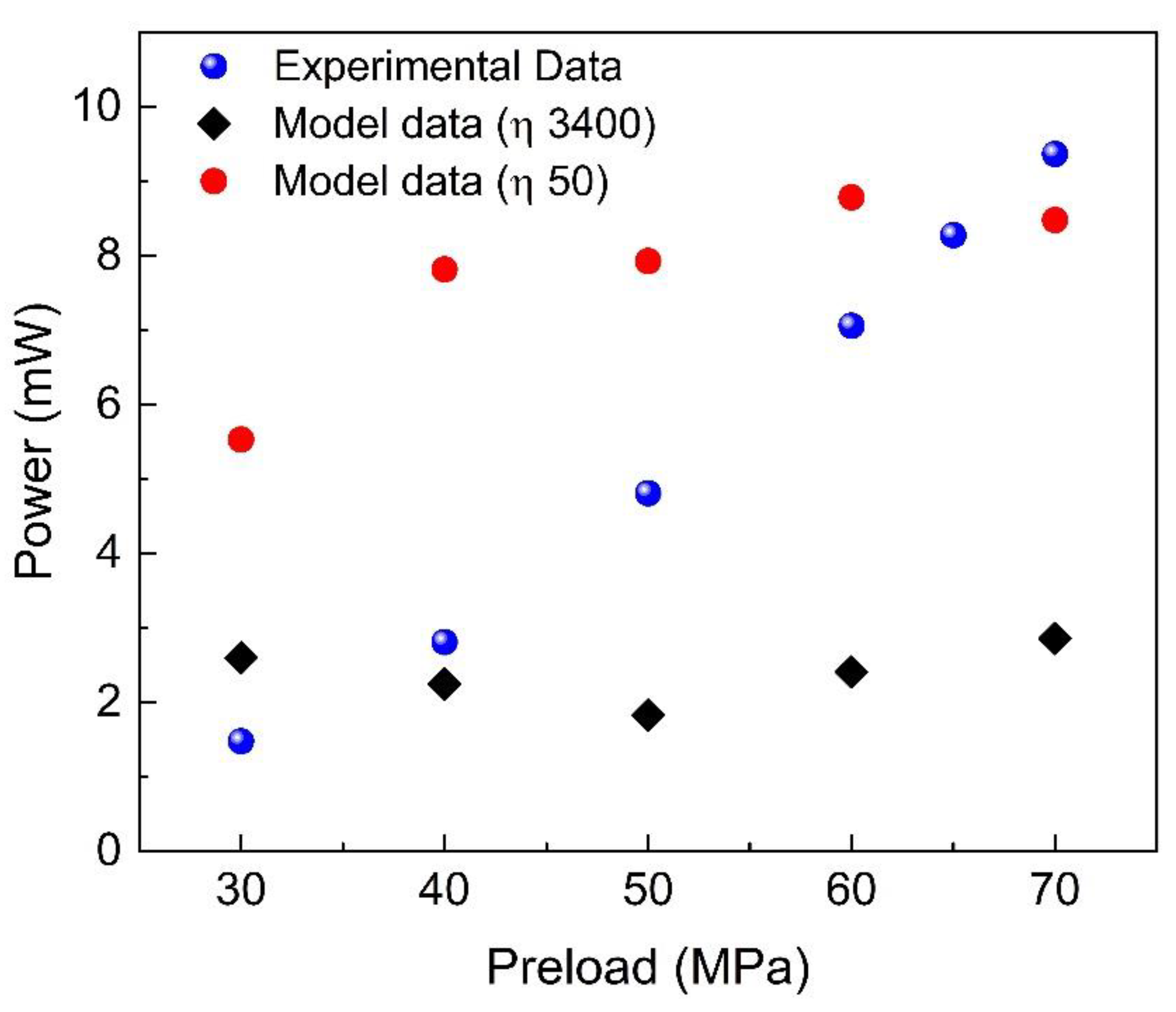
3.3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mandayam, S.; Udpa, L.; Udpa, S.S.; Sun, Y.S. A fast iterative finite element model for electrodynamic and magnetostrictive vibration adsorbers. IEEE Trans. Magn. 1994, 30, 3300–3303. [Google Scholar] [CrossRef]
- Adly, A.A.; Mayergoyz, I.D.; Bergqvist, A. Utilizing anisotropic Preisach-type models in the accurate simulation of magnetostriction. IEEE Trans. Magn. 1997, 33, 3931–3933. [Google Scholar] [CrossRef]
- Armstrong, W.D. Magnetization and magnetostriction processes in Tb (0.27−0.30) Dy (0.73−0.70) Fe (1.9−2.0). J. Appl. Phys. 1997, 81, 2321. [Google Scholar] [CrossRef]
- Gros, L.; Reyne, G.; Body, C.; Meunier, G. Strong coupling magneto mechanical methods applied to model heavy magnetostrictive actuators. IEEE Trans. Magn. 1998, 34, 3150–3153. [Google Scholar] [CrossRef]
- Stillesjö, F.; Engdahl, G.; Bergqvist, A. A design technique for magnetostrictive actuators with laminated active materials. Simul. Model. Pract. Theory 1998, 32, 2141–2143. [Google Scholar]
- Besbes, M.; Ren, Z.; Razek, A. A generalized finite element mode of magnetostriction phenomena. IEEE Trans. Magn. 2001, 37, 3324–3328. [Google Scholar] [CrossRef]
- Pèrez-Aparicio, J.L.; Sosa, H. A continuum three-dimensional, fully coupled, dynamic, non-linear finite element formulation for magnetostrictive materials. Smart Mater. Struct. 2004, 13, 493–502. [Google Scholar] [CrossRef]
- Davino, D.; Natale, C.; Pirozzi, S.; Visone, C. Rate-dependent losses modeling for magnetostrictive actuators. J. Magn. Magn. Mat. 2004, 272, e1781–e1782. [Google Scholar] [CrossRef]
- Bottauscio, O.; Chiampi, M.; Lovisolo, A.; Roccato, P.E.; Zucca, M. Dynamic modelling and experimental analysis of Terfenol-D rods for magnetostrictive actuators. J. Appl. Phys. 2008, 103, 07F121. [Google Scholar] [CrossRef]
- Bottauscio, O.; Lovisolo, A.; Roccato, P.E.; Zucca, M.; Sasso, C.; Bonin, R. Modelling and experimental analysis of magnetostrictive devices: from the material characterisation to their dynamic behaviour. IEEE Trans. Magn. 2008, 44, 3009–3012. [Google Scholar] [CrossRef]
- Stuebner, M.; Atulasimha, J.; Smith, R.C. Quantification of hysteresis and nonlinear effects on the frequency response of ferroelectric and ferromagnetic materials. Smart Mater. Struct. 2009, 18, 104019. [Google Scholar] [CrossRef]
- Kaltenbacher, M.; Meiler, M.; Ertl, M. Physical modeling and numerical computation of magnetostriction. Int. J. Comp. Math. Electr. Electron. Eng. 2009, 48, 819–832. [Google Scholar] [CrossRef]
- Graham, F.C.; Mudivarthi, C.; Datta, S.; Flatau, A.B. Modeling of a Galfenol transducer using the bidirectionally coupled magnetoelastic model. Smart Mater. Struct. 2009, 18, 104013. [Google Scholar] [CrossRef]
- Evans, P.G.; Dapino, M.J. Efficient magnetic hysteresis model for field and stress application in magnetostrictive Galfenol. J. Appl. Phys. 2010, 107, 3009–3012. [Google Scholar] [CrossRef]
- Almeida, L.A.L.; Depp, G.S.; Lima, A.M.N.; Neff, H. Modeling a magnetostrictive transducer using genetic algorithm. J. Magn. Magn. Mat. 2001, 266–230, 1262–1264. [Google Scholar] [CrossRef]
- Cao, S.C.; Wang, B.; Zheng, J.; Huang, W.; Sun, Y.; Yang, Q. Modeling dynamic hysteresis for giant magnetostrictive actuator using hybrid genetic algorithm. IEEE Trans. Magn. 2006, 42, 911–914. [Google Scholar]
- Davino, D.; Giustiniani, A.; Visone, C. Experimental properties of an efficient stress-dependent magnetostriction model. J. Appl. Phys. 2009, 105, 07D512. [Google Scholar] [CrossRef]
- Bottauscio, O.; Roccato, P.E.; Zucca, M. Modeling the dynamic behavior of magnetostrictive actuators. IEEE Trans. Magn. 2010, 46, 3022–3028. [Google Scholar] [CrossRef]
- Zucca, M.; Bottauscio, O. Hysteretic modeling of electrical micro-power generators based on Villari effect. IEEE Trans. Magn. 2012, 48, 3092. [Google Scholar] [CrossRef]
- Berbyuk, V. Vibration energy harvesting using Galfenol-based transducer. Act. Passiv. Smart Struct. Integr. Syst. 2013, 8688, 86881F. [Google Scholar]
- Rezaeealam, B. Finite element analysis of magnetostrictive vibration energy harvester. Compel Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 1757–1773. [Google Scholar] [CrossRef]
- Davino, D.; Krejčí, P.; Visone, C. Fully coupled modeling of magneto-mechanical hysteresis through thermodynamic compatibility. Smart Mater. Struct. 2013, 22, 095009. [Google Scholar] [CrossRef]
- Davino, D.; Krejčí, P.; Pimenov, A.; Rachinskii, D.; Visone, C. Analysis of an operator-differential model for magnetostrictive energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 504–519. [Google Scholar] [CrossRef] [Green Version]
- Clemente, C.S.; Mahgoub, A.; Davino, D.; Visone, C. Multiphysics circuit of a magnetostrictive energy harvesting device. J. Intell. Mater. Syst. Struct. 2017, 28, 2317–2330. [Google Scholar] [CrossRef]
- Kholmetskaa, I.; Chlebouna, J.; Krejcíˇ, P. Numerical modeling of Galfenol magnetostrictive response. Appl. Math. Comput. 2018, 319, 527–537. [Google Scholar] [CrossRef]
- Ahmed, U.; Jeronen, J.; Zucca, M.; Palumbo, S.; Rasilo, P. Finite element analysis of magnetostrictive energy harvesting concept device utilizing thermodynamic magneto-mechanical model. J. Magn. Magn. Mater. 2019, 486, 165275. [Google Scholar] [CrossRef]
- Bertotti, G.; Mayergoy, I.D. The Science of Hysteresis; Academic Press: Oxford, UK, 2006; Volume 1. [Google Scholar]
- Sablik, M.J.; Jiles, D.C. Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis. IEEE Trans. Magn. 1993, 29, 429–439. [Google Scholar] [CrossRef]
- Calkins, F.T.; Smith, R.C.; Flatau, A.B. Energy-based hysteresis model for magnetostrictive transducers. IEEE Trans. Magn. 2000, 36, 3931–3933. [Google Scholar] [CrossRef]
- Cho, C.; Hong, Y.; Jiang, C.; Chen, Y. Study of Dynamic Behavior of Magnetostrictively Patterned Flexible Micro-Wings. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Backman, G.; Lawton, B.; Morley, N.A. Magnetostrictive Energy Harvesting: Materials and Design Study. IEEE Trans. Magn. 2019, 55. [Google Scholar] [CrossRef]
- Song, Y. Finite-Element Implementation of Piezoelectric Energy Harvesting System from Vibrations of Railway Bridge. J. Energy Eng. 2018, 145, 04018076. [Google Scholar] [CrossRef]
- Zucca, M.; Mei, P.; Ferrara, E.; Fiorillo, F. Sensing dynamic forces by Fe-Ga in compression. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Palumbo, S.; Rasilo, P.; Zucca, M. Experimental investigation on a Fe-Ga close yoke vibrational harvester by matching magnetic and mechanical biases. J. Magn. Magn. Mater. 2019, 469, 354–363. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palumbo, S.; Chiampi, M.; Bottauscio, O.; Zucca, M. Dynamic Simulation of a Fe-Ga Energy Harvester Prototype Through a Preisach-Type Hysteresis Model. Materials 2019, 12, 3384. https://doi.org/10.3390/ma12203384
Palumbo S, Chiampi M, Bottauscio O, Zucca M. Dynamic Simulation of a Fe-Ga Energy Harvester Prototype Through a Preisach-Type Hysteresis Model. Materials. 2019; 12(20):3384. https://doi.org/10.3390/ma12203384
Chicago/Turabian StylePalumbo, Stefano, Mario Chiampi, Oriano Bottauscio, and Mauro Zucca. 2019. "Dynamic Simulation of a Fe-Ga Energy Harvester Prototype Through a Preisach-Type Hysteresis Model" Materials 12, no. 20: 3384. https://doi.org/10.3390/ma12203384




