Time-Dependent Density Functional Computations of the Spectrochemical Properties of Dithiolodithiole and Thiophene Electrochromic Systems
Abstract
:1. Introduction
2. Computational Details
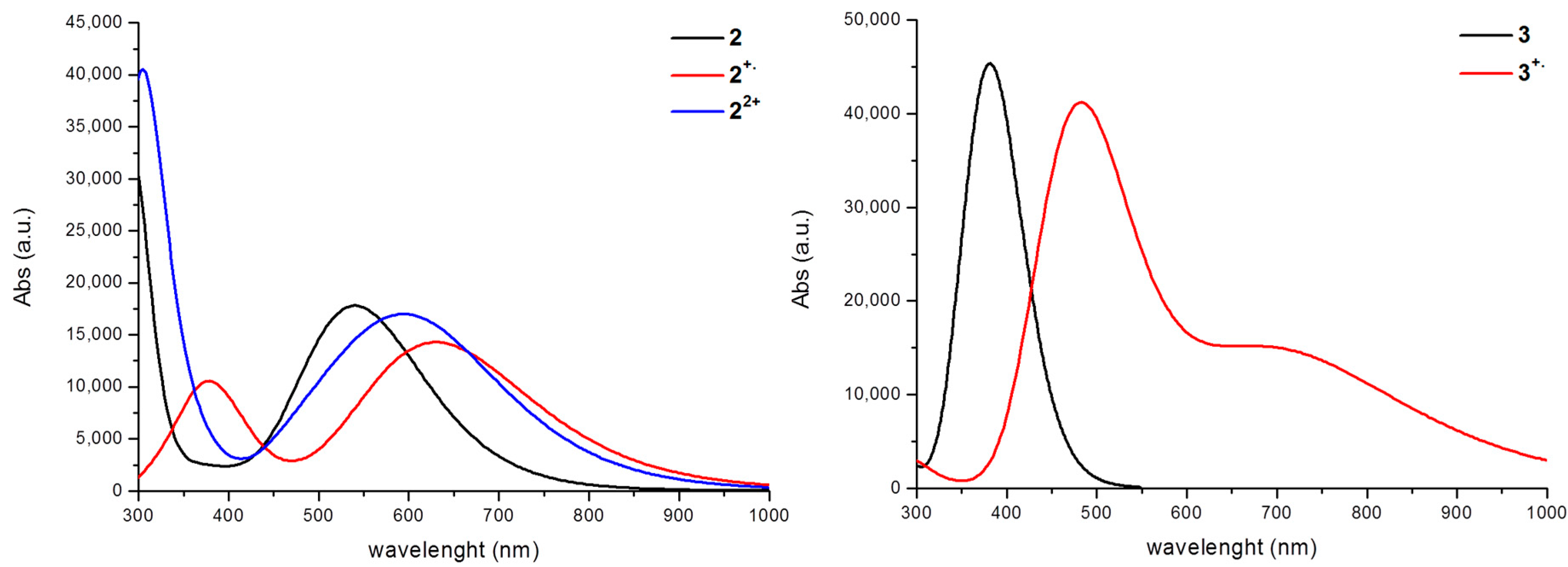
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Platt, J.R. Electrochromism, a possible change in color producible in dyes by an electric field. J. Chem. Phys. 1961, 34, 862–864. [Google Scholar] [CrossRef]
- Deb, S.K. A novel electrophotographic system. Appl. Opt. 1969, 8, 192–195. [Google Scholar] [CrossRef] [PubMed]
- Monk, P.M.S.; Mortimer, R.J.; Rosseinsky, R.D. Electrochromism and Electrochromic Devices; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rauh, R.D. Electrochromic windows: An overview. Electrochim. Acta 1999, 44, 3165–3176. [Google Scholar] [CrossRef]
- Llordes, A.; Garcia, G.; Gazquez, J.; Milliron, D.J. Tunable near-Infrared and Visible-Light Transmittance in Nanocrystal-in-Glass Composites. Nature 2013, 500, 323–326. [Google Scholar] [CrossRef] [PubMed]
- Mortimer, R.J.; Dyer, A.L.; Reynolds, J.R. Electrochromic Organic and Polymeric Materials for Display Applications. Displays 2006, 27, 2–18. [Google Scholar] [CrossRef]
- Alesanco, Y.; Viñuales, A.; Palenzuela, J.; Odriozola, I.; Cabañero, G.; Rodriguez, J.; Tena-Zaera, R. Multicolor Electrochromics: Rainbow-Like Devices. ACS Appl. Mater. Interfaces 2016, 8, 14795–14801. [Google Scholar] [CrossRef] [PubMed]
- Granqvist, C.G. Handbook of Inorganic Electrochromic Materials; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Monk, P.M.S. The Viologens: Physicochemical Properties, Synthesis, and Applications of the Salts of 4,4′-Bipyridine; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Tonar, W.L.; Byker, H.J.; Siegrist, K.E.; Anderson, J.S.; Ash, K.L. Electrochromic Layer and Devices Comprising Same. U.S. Patent 5888431 A, 30 March 1999. [Google Scholar]
- He, X.; Borau-Garcia, J.; Woo, A.Y.Y.; Trudel, S.; Baumgartner, T. Dithieno[3,2-c:2′,3′-e]-2,7-diketophosphepin: A Unique Building Block for Multifunctional π-Conjugated Materials. J. Am. Chem. Soc. 2013, 135, 1137–1147. [Google Scholar] [CrossRef] [PubMed]
- Schipper, D.J.; Moh, L.C.H.; Muller, P.; Swager, T.M. Dithiolodithiole as a Building Block for Conjugated Materials. Angew. Chem. Int. Ed. 2014, 53, 5847–5851. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B Condens. Matter Mater. Phys. 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functionals Without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 84106–84155. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Cossi, M.; Barone, V. Solvent effect on vertical electronic transitions by the polarizable continuum model. J. Chem. Phys. 2000, 112, 2427–2435. [Google Scholar] [CrossRef]
- Tomasi, J.; Menucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Fisher, C.L.; Chen, J.L.; Bashford, D.; Noodleman, L. Calculation of Redox Potentials and pKa Values of Hydrated Transition Metal Cations by a Combined Density Functional and Continuum Dielectric Theory. Inorg. Chem. 1996, 35, 4694–4702. [Google Scholar] [CrossRef]
- De Simone, B.C.; Marino, T.; Prejanò, M.; Russo, N. Can fused thiophene–pyrrole-containing rings act as possible new electrochromic dyes? A computational prediction. Theor. Chem. Acc. 2016, 135, 238. [Google Scholar] [CrossRef]
- Maltese, V.; Cospito, S.; Beneduci, A.; De Simone, B.C.; Russo, N.; Chidichimo, G.; Janssen, R.A.J. Electro-optical Properties of Neutral and Radical Ion Thienosquaraines. Chem. Eur. J. 2016, 22, 10179–10186. [Google Scholar] [CrossRef] [PubMed]
- De Simone, B.C.; Marino, T.; Russo, N. TDDFT investigation on methylviologen, 3,7-diazabenzophosphole, and helical helquat electrochromic systems. Theor. Chem. Acc. 2016, 135, 118. [Google Scholar] [CrossRef]
- Alberto, M.E.; De Simone, B.C.; Cospito, S.; Imbardelli, D.; Veltri, L.; Chidichimo, G.; Russo, N. Experimental and theoretical characterization of a new synthesized extended viologen. Chem. Phys. Lett. 2012, 552, 141–145. [Google Scholar] [CrossRef]
- De Simone, B.C.; Quartarolo, A.D.; Cospito, S.; Veltri, L.; Chidichimo, G.; Russo, N. Theoretical and experimental investigation on the near-infrared and UV–vis spectral regions of a newly synthesized triarylamine electrochromic system. Theor. Chem. Acc. 2012, 131, 1225. [Google Scholar] [CrossRef]
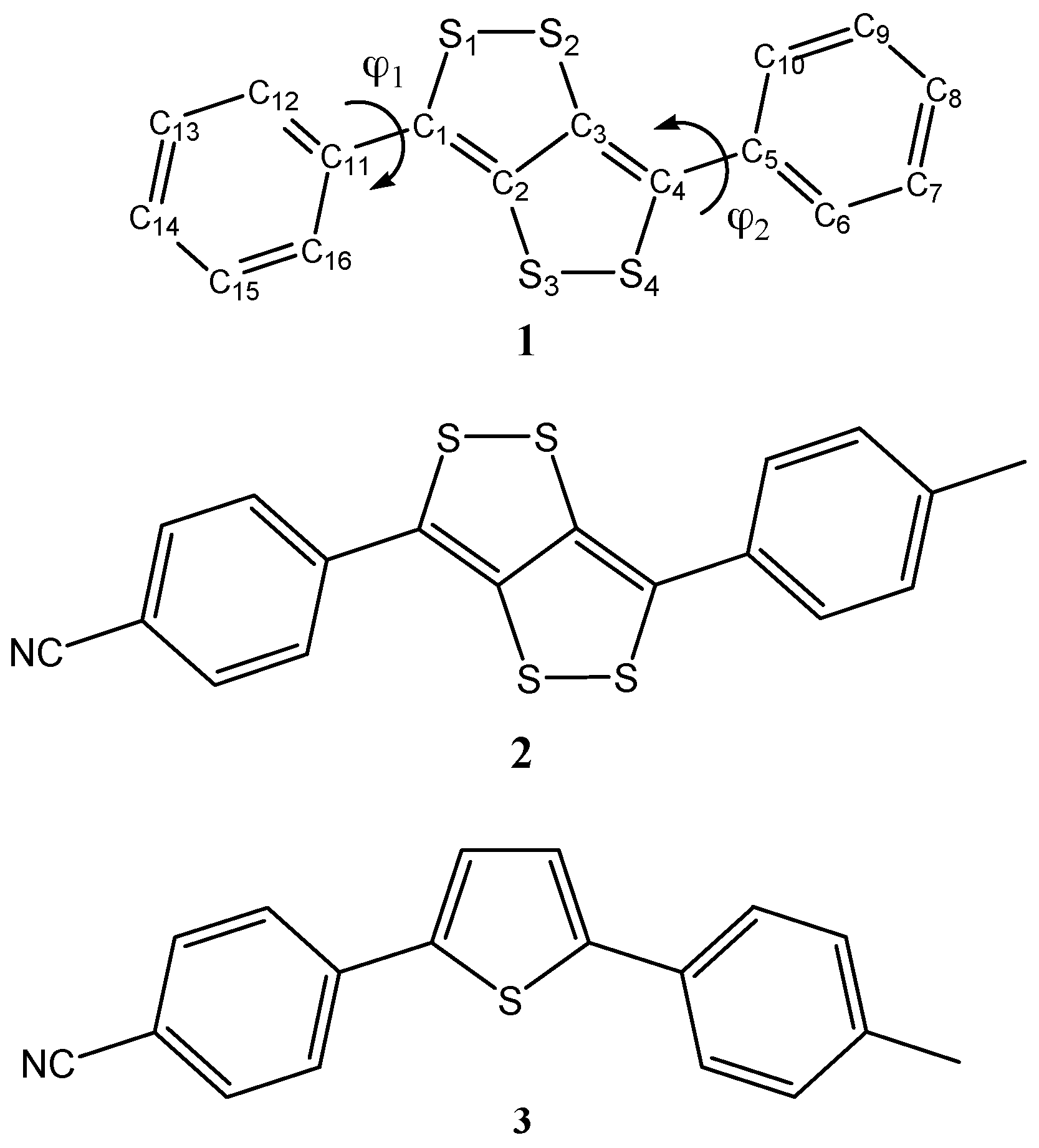
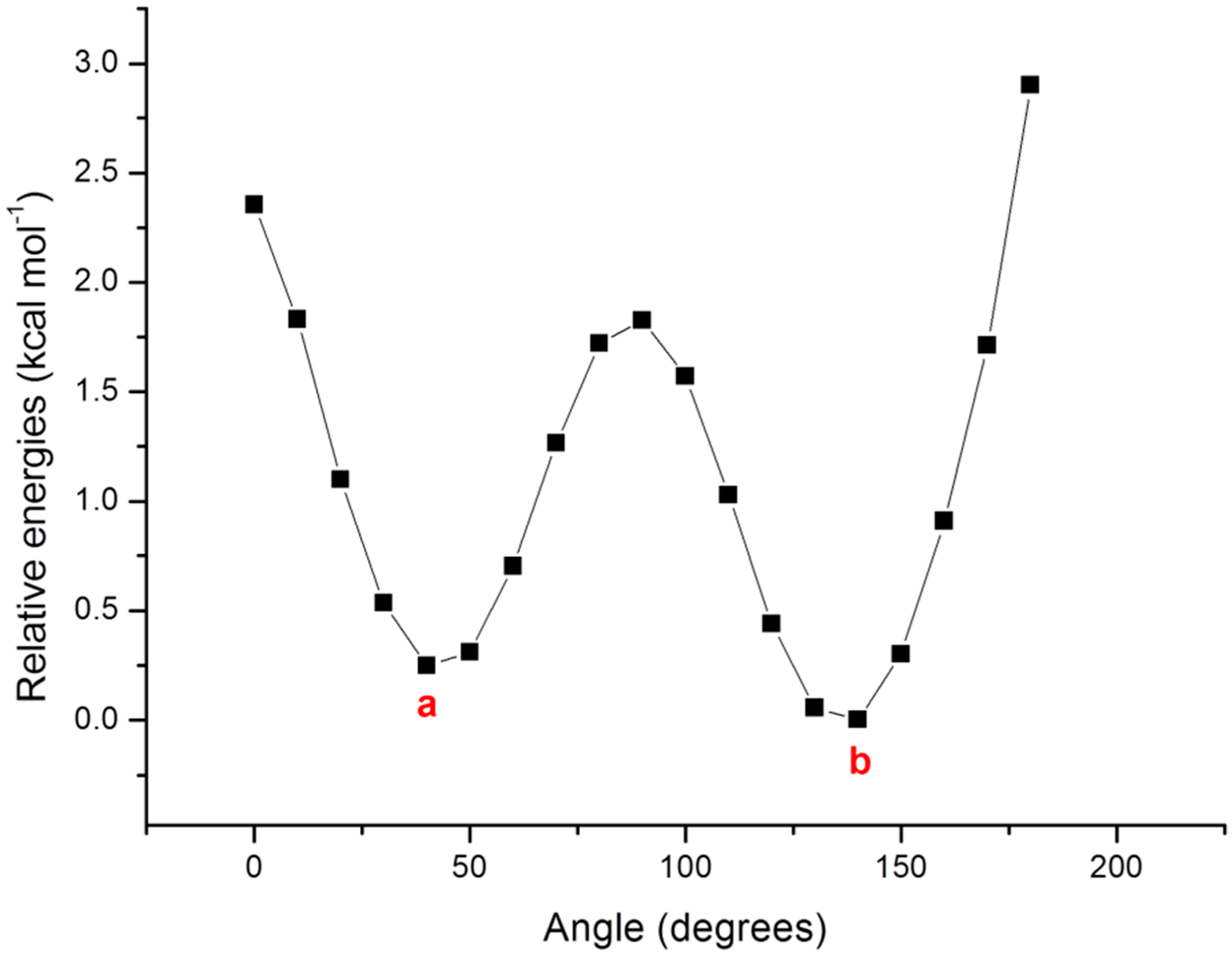
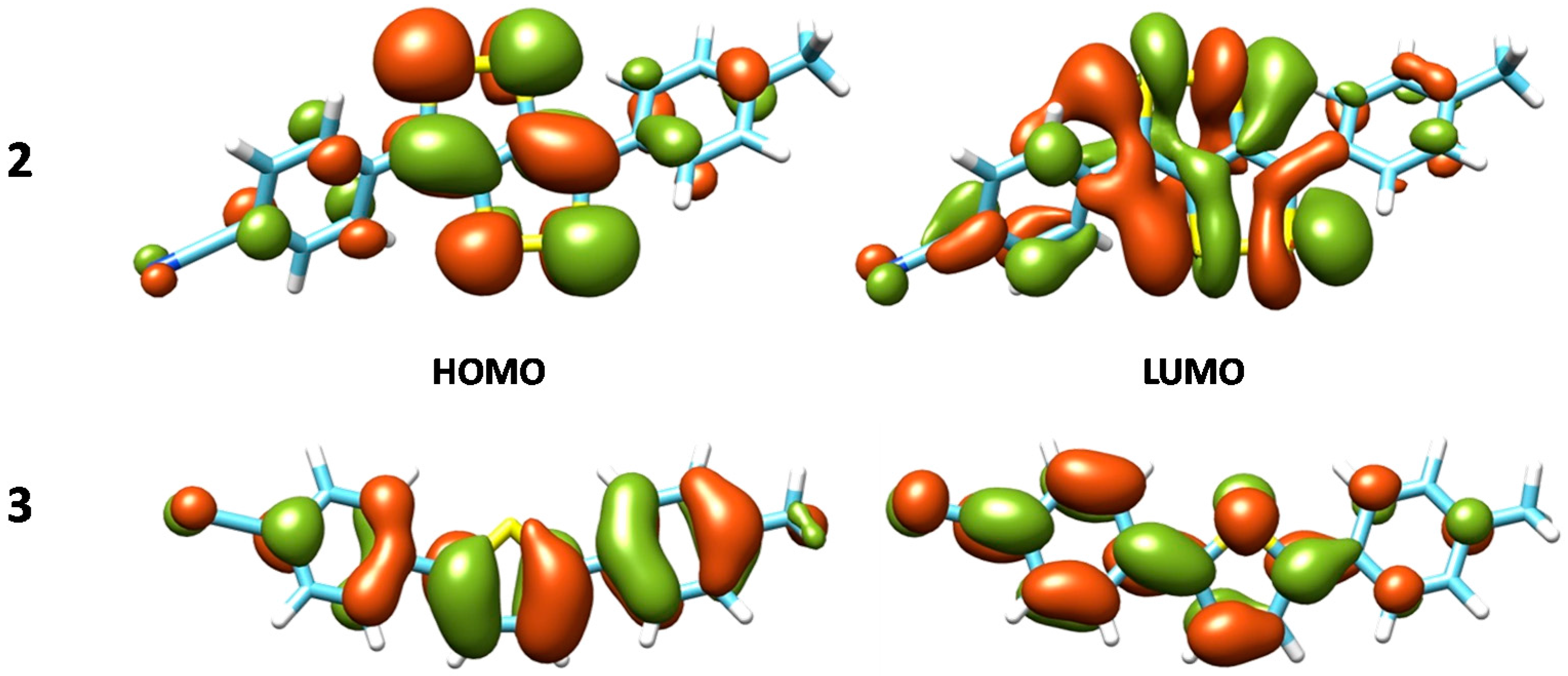
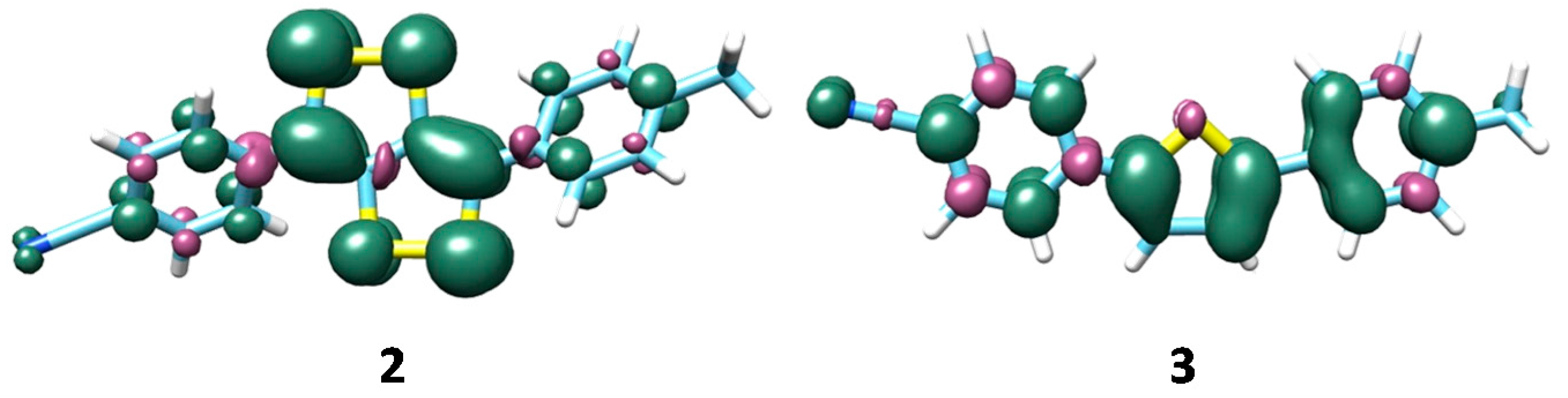
| Parameter | X-ray a | B3LYP | B3LYPD3 | M06 | PBE0 | wB97XD |
|---|---|---|---|---|---|---|
| C1-C2 | 1.365 | 1.361 | 1.359 | 1.357 | 1.359 | 1.347 |
| (1.360) | (1.359) | (1.357) | (1.358) | (1.347) | ||
| C2-C3 | 1.444 | 1.448 | 1.449 | 1.442 | 1.442 | 1.453 |
| (1.449) | (1.450) | (1.442) | (1.443) | (1.453) | ||
| C2-S3 | 1.757 | 1.786 | 1.788 | 1.774 | 1.767 | 1.773 |
| (1.787) | (1.788) | (1.775) | (1.767) | (1.773) | ||
| S3-S4 | 2.084 | 2.132 | 2.134 | 2.123 | 2.102 | 2.108 |
| (2.134) | (2.137) | (2.125) | (2.104) | (2.110) | ||
| C1-C2-S3 | 126.5 | 125.4 | 125.4 | 125.6 | 125.9 | 126.0 |
| (125.4) | (125.4) | (125.7) | (126.0) | (126.1) | ||
| C3-C2-S3 | 113.4 | 113.6 | 113.7 | 113.7 | (113.7 | 113.7 |
| (113.6) | (113.7) | (113.7) | (113.7) | (113.7) | ||
| C2-S3-S4 | 95.8 | 95.0 | 94.9 | 95.0 | 95.3 | 95.1 |
| (94.9) | (94.8) | (94.9) | (95.2) | (95.0) | ||
| C2-C3-C4 | 120.1 | 120.7 | 120.6 | 120.3 | 120.1 | 120.0 |
| (120.7) | (120.6) | (120.3) | (120.1) | (120.0) | ||
| φ1 | 154.6 | 141.3 | 136.5 | 143.3 | 143.5 | 134.7 |
| (140.7) | (136.0) | (143.1) | (143.2) | (134.3) | ||
| φ2 | 26.1 | 141.0 | 136.6 | 142.3 | 143.2 | 136.1 |
| (38.6) | (43.3) | (36.0) | (35.9) | (44.6) |
| Conformer | Theory | λtheo/nm | ΔE/eV | f |
|---|---|---|---|---|
| 1a | B3LYP | 492 | 2.52 | 0.309 |
| B3LYP_D3 | 489 | 2.53 | 0.259 | |
| M06 | 492 | 2.52 | 0.346 | |
| PBE0 | 480 | 2.58 | 0.366 | |
| wB97XD | 402 | 3.08 | 0.321 | |
| 1b | B3LYP | 480 | 2.58 | 0.405 |
| B3LYP_D3 | 474 | 2.62 | 0.369 | |
| M06 | 479 | 2.59 | 0.424 | |
| PBE0 | 471 | 2.63 | 0.380 | |
| wB97XD | 399 | 3.10 | 0.470 | |
| Exp a | 458 |
| Compound | XC | ΔE | λtheo | f | MO contribution a,b | λexp c |
|---|---|---|---|---|---|---|
| 2 | B3LYP | 2.24 | 554 | 0.412 | H→L, 96% | 517 |
| B3LYP-D3 | 2.24 | 554 | 0.354 | |||
| M06 | 2.28 | 543 | 0.405 | |||
| PBE0 | 2.31 | 537 | 0.457 | |||
| wB97XD | 2.91 | 425 | 0.460 | |||
| 2+∙ | B3LYP | 1.91 | 648 | 0.173 | H(β) c→L(β), 100% | ≈650 |
| 2.00 | 619 | 0.146 | H(α)→L(α), 91% | |||
| 3.12 | 397 | 0.130 | H-5 (β)→L (β), 92% | ≈400 | ||
| B3LYP-D3 | 1.92 | 646 | 0.164 | |||
| 2.02 | 613 | 0.144 | ||||
| 3.10 | 400 | 0.137 | ||||
| M06 | 1.94 | 640 | 0.220 | |||
| 2.00 | 620 | 0.128 | ||||
| 3.25 | 381 | 0.143 | ||||
| PBE0 | 2.00 | 619 | 0.280 | |||
| 2.02 | 606 | 0.067 | ||||
| 3.29 | 376 | 0.134 | ||||
| wB97XD | 2.25 | 551 | 0.242 | |||
| 2.55 | 550 | 0.132 | ||||
| 3.32 | 374 | 0.185 | ||||
| 22+ | B3LYP | 1.92 | 644 | 0.366 | H→L, 99% | ≈570 |
| 2.32 | 533 | 0.149 | H-2→L, 88% | |||
| B3LYP-D3 | 1.91 | 649 | 0.336 | |||
| 2.31 | 536 | 0.145 | ||||
| M06 | 2.02 | 613 | 0.371 | |||
| 2.49 | 498 | 0.154 | ||||
| PBE0 | 2.04 | 606 | 0.370 | |||
| 2.48 | 499 | 0.155 | ||||
| wB97XD | 2.43 | 509 | 0.544 | |||
| 3.02 | 411 | 0.107 | ||||
| 3 | B3LYP-D3 | 3.20 | 387 | 1.090 | H→L,99% | ≈360 |
| M06 | 3.25 | 381 | 1.120 | |||
| 3+∙ | B3LYP-D3 | 1.68 | 738 | 0.163 | H(β)→L(β), 100% | |
| 1.75 | 709 | 0.157 | H(β)→L(β), 100% | |||
| 2.59 | 478 | 1.033 | H(α)→L(α), 100% | |||
| M06 | 1.72 | 721 | 0.278 | |||
| 2.57 | 483 | 0.966 |
| Compd. | EoxI/V | EoxII/V | ||
|---|---|---|---|---|
| Computed | Experimental | Computed | Experimental | |
| 2 | 0.31 | 0.13 | 0.88 | 0.71 |
| 3 | 0.85 | ≈1.00 | - | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Simone, B.C.; Mazzone, G.; Marino, T.; Russo, N.; Toscano, M. Time-Dependent Density Functional Computations of the Spectrochemical Properties of Dithiolodithiole and Thiophene Electrochromic Systems. Materials 2017, 10, 981. https://doi.org/10.3390/ma10090981
De Simone BC, Mazzone G, Marino T, Russo N, Toscano M. Time-Dependent Density Functional Computations of the Spectrochemical Properties of Dithiolodithiole and Thiophene Electrochromic Systems. Materials. 2017; 10(9):981. https://doi.org/10.3390/ma10090981
Chicago/Turabian StyleDe Simone, Bruna Clara, Gloria Mazzone, Tiziana Marino, Nino Russo, and Marirosa Toscano. 2017. "Time-Dependent Density Functional Computations of the Spectrochemical Properties of Dithiolodithiole and Thiophene Electrochromic Systems" Materials 10, no. 9: 981. https://doi.org/10.3390/ma10090981







