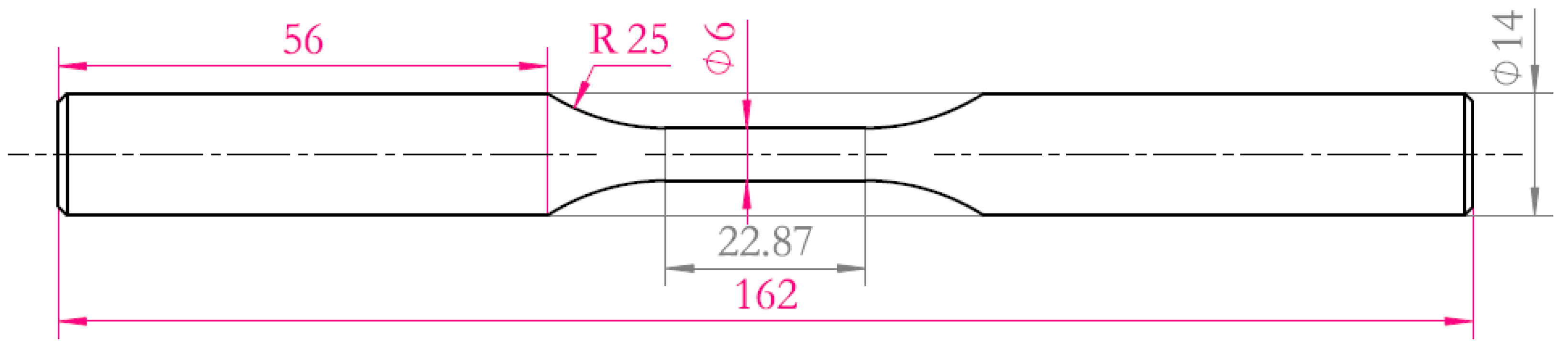
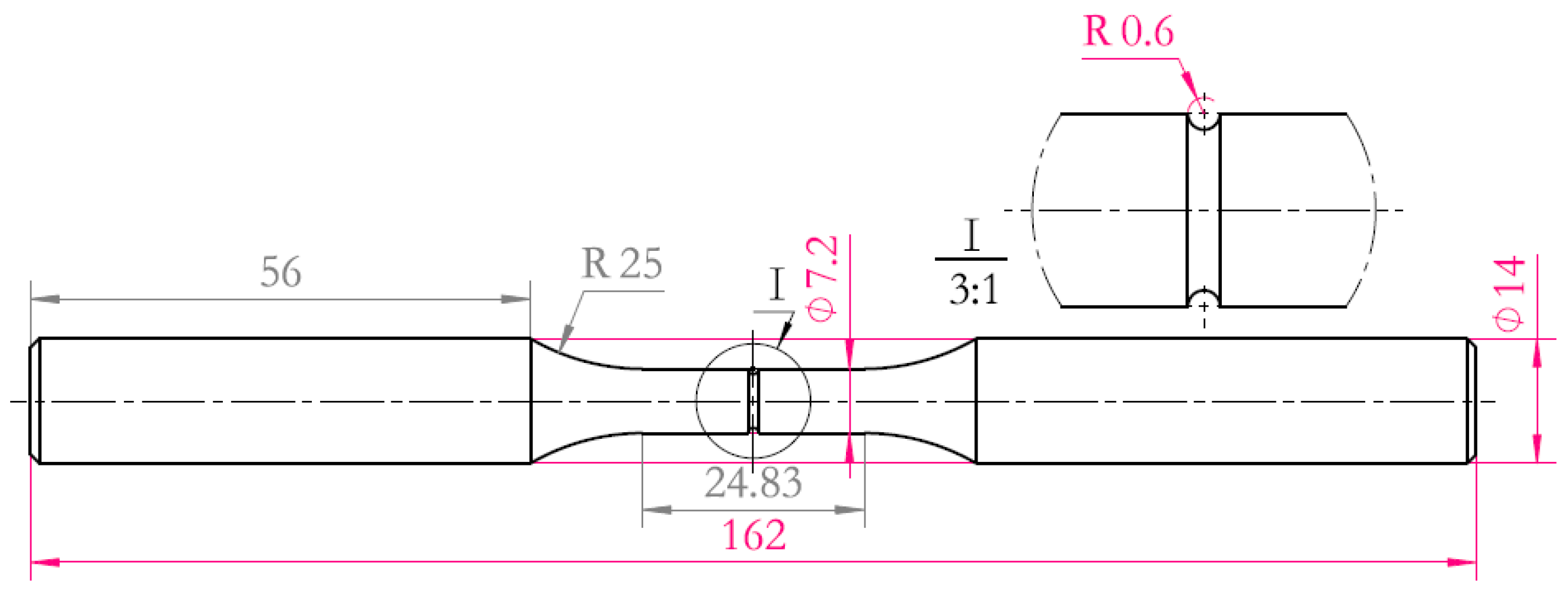
3.2. S–N Curves
The S–N curve is a basic curve for characterizing the fatigue properties of the material. According to the experimental data from
Table 3,
Table 4,
Table 5 and
Table 6, the S–N curves of the smooth specimen and the notched specimen can be fitted. The S–N curve has a variety of forms of expression. The three-parameter S–N curve model can be used to describe the stress-life relationship of the long-life region. This study selected the classical three-parameter power function S–N curve model [
7].
Where
is the maximum stress,
N is the fatigue life,
is the theoretical fatigue limit,
H and
C are the material constant. A double weighted least square method is used for fitting.
From the data in
Table 3 and
Table 5, the parameters of the smooth specimen were obtained,
= 613.1649 MPa, H = 0.9665, C = 1.9333 × 10
7, and the S–N curve equation of the smooth specimen was obtained
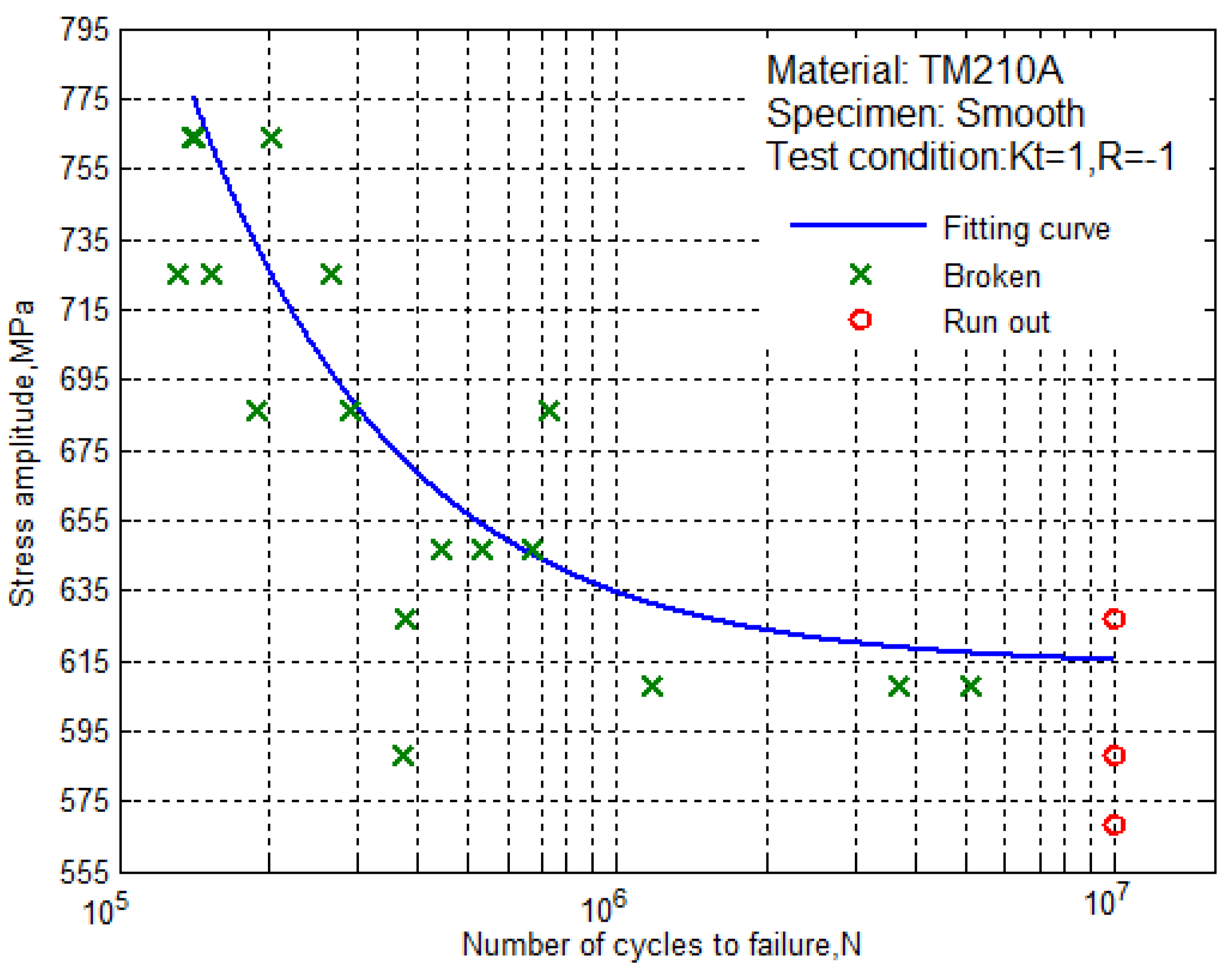
According to the fitting equation, we can draw the S–N curve of the smooth specimens of the ultra-high strength maraging steel TM210A with a 50% survival rate, as shown in
Figure 4. It can be seen that the fatigue limit of the smooth specimen was not more than 615 MPa.
From the data in
Table 4 and
Table 6, the parameters of the notched specimen were obtained,
= 350.8066MPa, H = 2.0649, C = 1.7488 × 10
7, and the S–N curve equation of the notched specimen was obtained
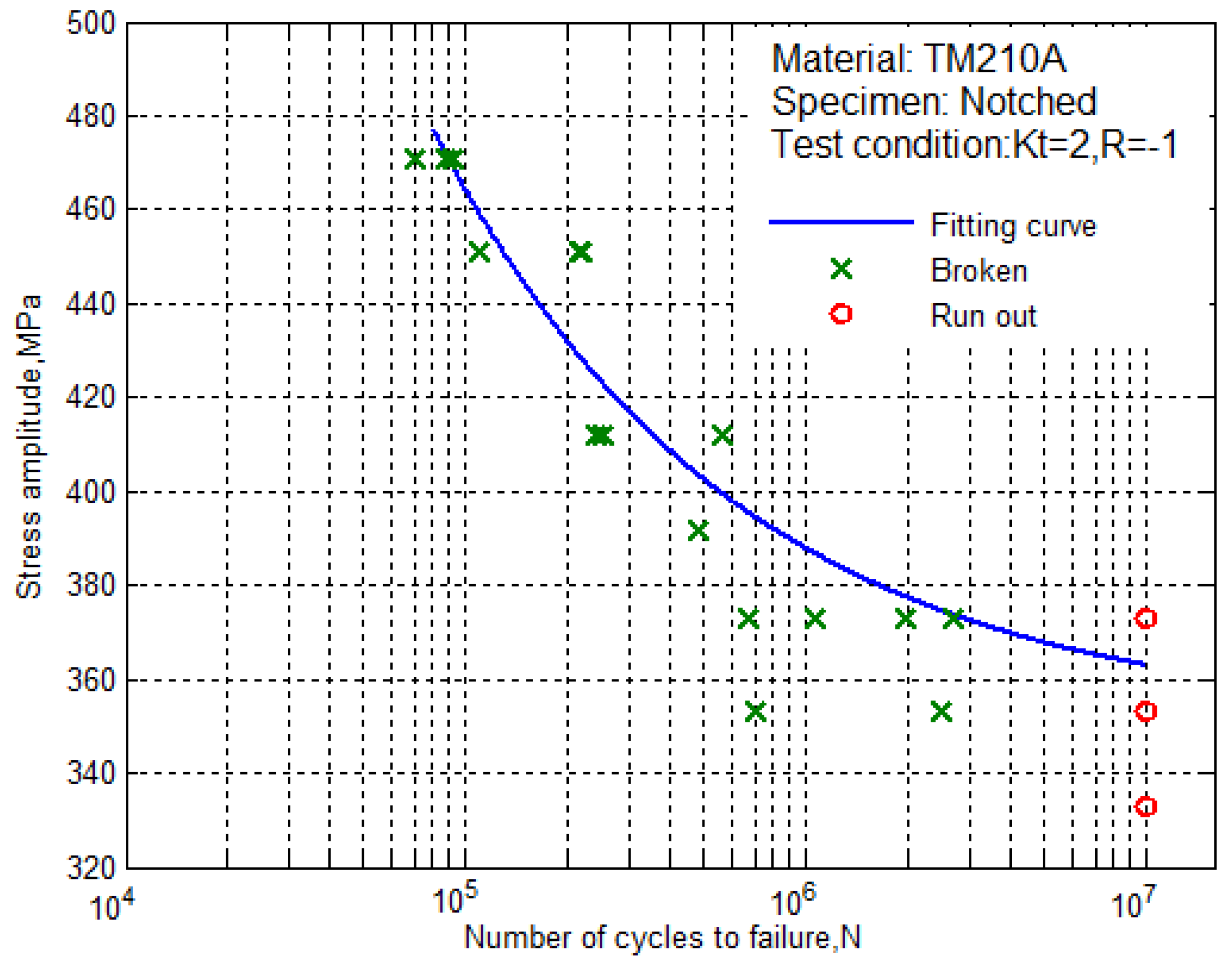
According to the fitting equation, we can draw the S–N curve of the notched specimens of the ultra-high strength maraging steel TM210A with a 50% survival rate, as shown in
Figure 5. It can be seen that the fatigue limit of the notched specimen was not more than 365 MPa.
From
Figure 4 to
Figure 5, it can be seen that the S–N curves of the smooth specimens and the notched specimens of the ultra-high strength maraging steel TM210A decreased with the decrease of the stress level, and the fatigue life was prolonged. The fatigue stress-life data contained two parts. Part 1: the data of the test was from initiation to before the fatigue limit, which corresponded to the fracture of the specimen due to the crack initiation-expansion (cross symbols). Part 2: the data of the test was at lower stress levels, in which the specimen did not break (circular symbols).
For a more intuitive process,
Figure 6 and
Figure 7 show the fatigue lift graphs for smooth and notched specimens at
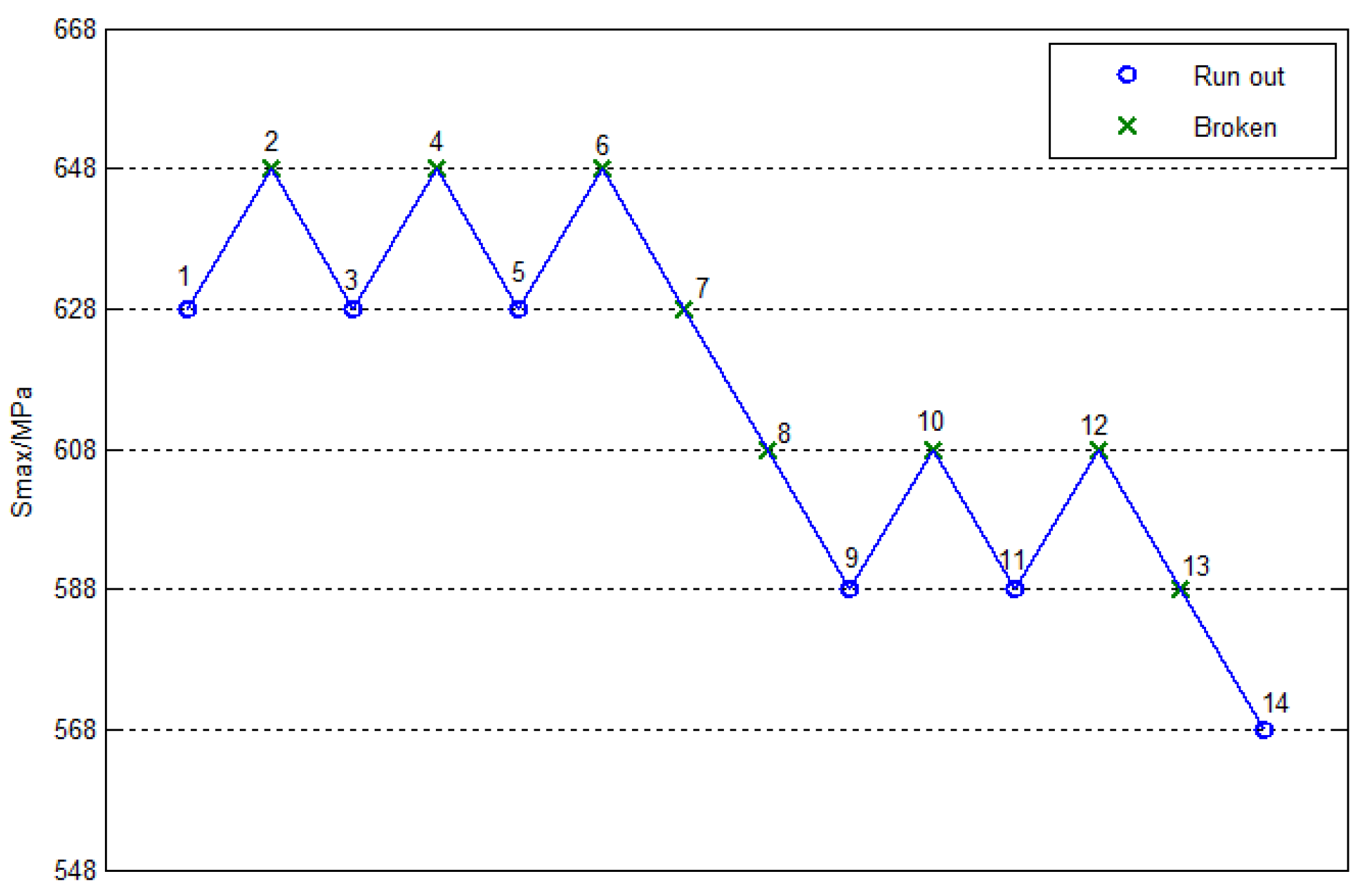
cycles, respectively. Only five stress levels were considered in the analysis of the smooth specimen, as shown in
Figure 6, where the beginning stress was 628MPa, the step stress was 20MPa, and the number of the effective specimen was 14. Only four stress levels were considered in the analysis of the notched specimen, as shown in
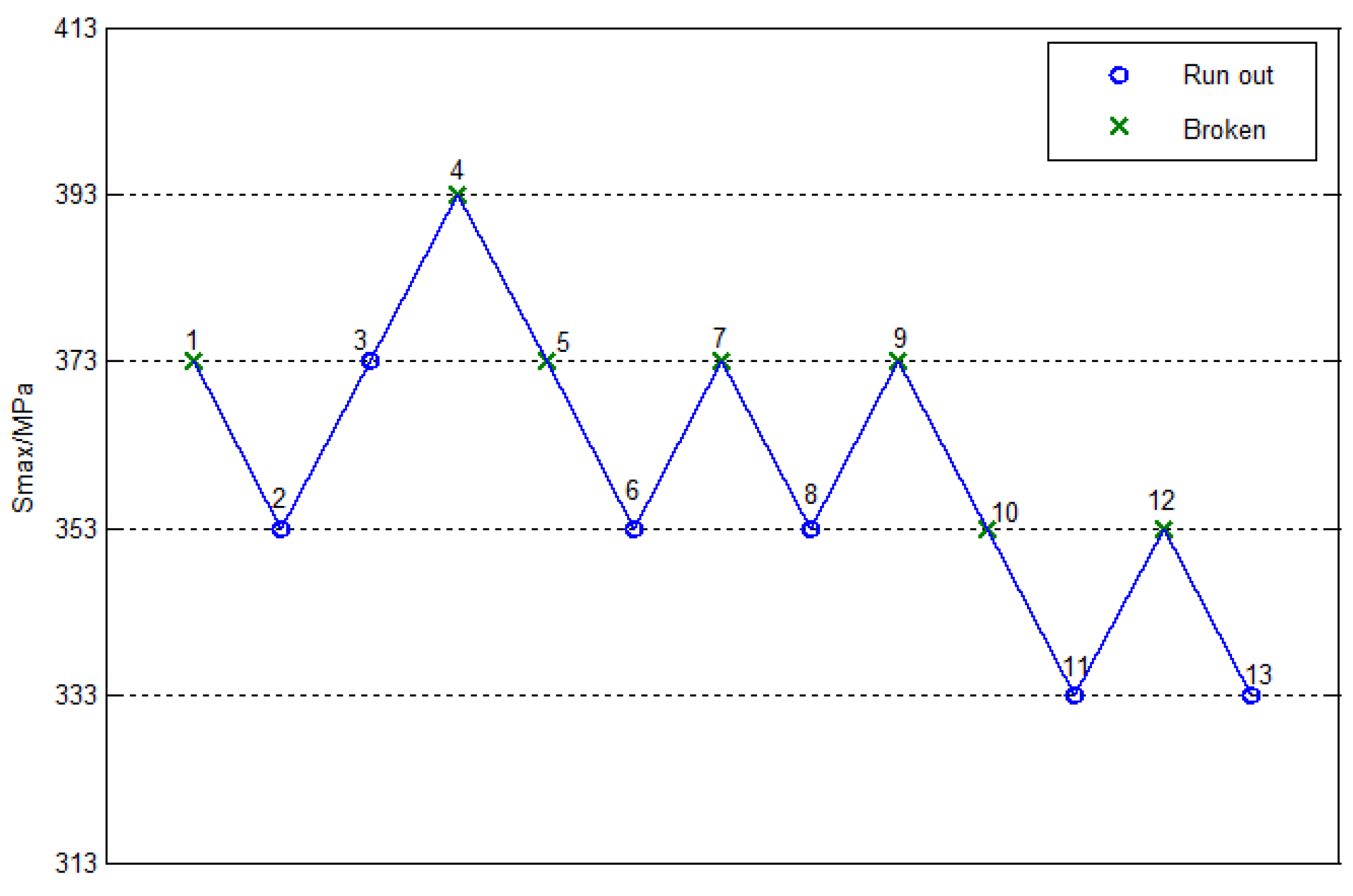
Figure 7, where the stress began at 373 MPa, the step stress was 20 MPa, and the number of the effective specimen was 13.
According to the statistical theory
where
is the mean fatigue limit,
k is the number of matched pairs,
n is the number of effective specimens,
l is the number of the stress levels,
is the
i-th pair fatigue limit in the matched pair,
is the
j-th level stress value of the stress levels, and
is the number of the effective specimen in the
j-th level stress level, whether the specimen is broken or not.
Therefore, the fatigue limit of the smooth specimen was 615MPa.The ratio of the fatigue limit to tensile strength was 0.29. The fatigue limit of the notched specimen was 363MPa. Besides this, the fatigue limit of the notched specimen was reduced by about 41% compared with the smooth specimen.
3.3. Fractography
The fracture micrographs of the smooth specimens and notched specimens of the ultra-high strength maraging steel TM210A were observed by scanning electron microscopy, as shown in
Figure 8 and
Figure 9, respectively. It can be seen that the fractures were composed of the crack initiation area, the crack propagation area, and the instantaneous fracture area, whether it was a smooth or notched specimen.
As shown in
Figure 8, the crack initiation of the smooth specimen was at the surface of the specimen. In the vicinity of the crack initiation, the crack occurred in a quasi-cleavable way, with a distinct river pattern. The crack propagation area had obvious fatigue striations, and there were some relatively large step shapes. The instantaneous fracture area was a rough dimple.
As shown in
Figure 9, the crack initiation of the notched specimen was at the front end of the annular circumference notch with a large stress concentration, in a distinct river pattern. The crack propagation area had obvious fatigue striations, and there were obvious tear edges. The instantaneous fracture area was a rough dimple.
3.4. Fatigue Notch Sensitivity Index
The theoretical elastic stress concentration factor
Kt relates the local stress ahead of the notch tip to far-field loading, and is defined as the ratio of the maximum local stress σ
max to the nominal stress S. Under fatigue loading conditions, the elastic stress concentration factor is replaced by the so-called fatigue notch factor:
In general, fatigue experiments suggest that notches produce a less stress-concentrating effect than predicted by theoretical elastic analysis, such that we find
Kf ‹
Kt; Kf →
Kt for large notch-root radii and for higher strength materials. The degree of agreement between theoretical predictions of elastic stress concentration and actual effects is often measured by the so-called notch sensitivity index, which is defined as [
8]
The fatigue limits of the smooth specimen and the notched specimen of the TM210A were 615 MPa and 363 MPa, respectively. The theoretical elastic stress concentration factor Kt was 2, and, therefore, the fatigue notch sensitivity index qf was 0.69.