A Piezoresponse Force Microscopy Study of CaxBa1−xNb2O6 Single Crystals
Abstract
:1. Introduction
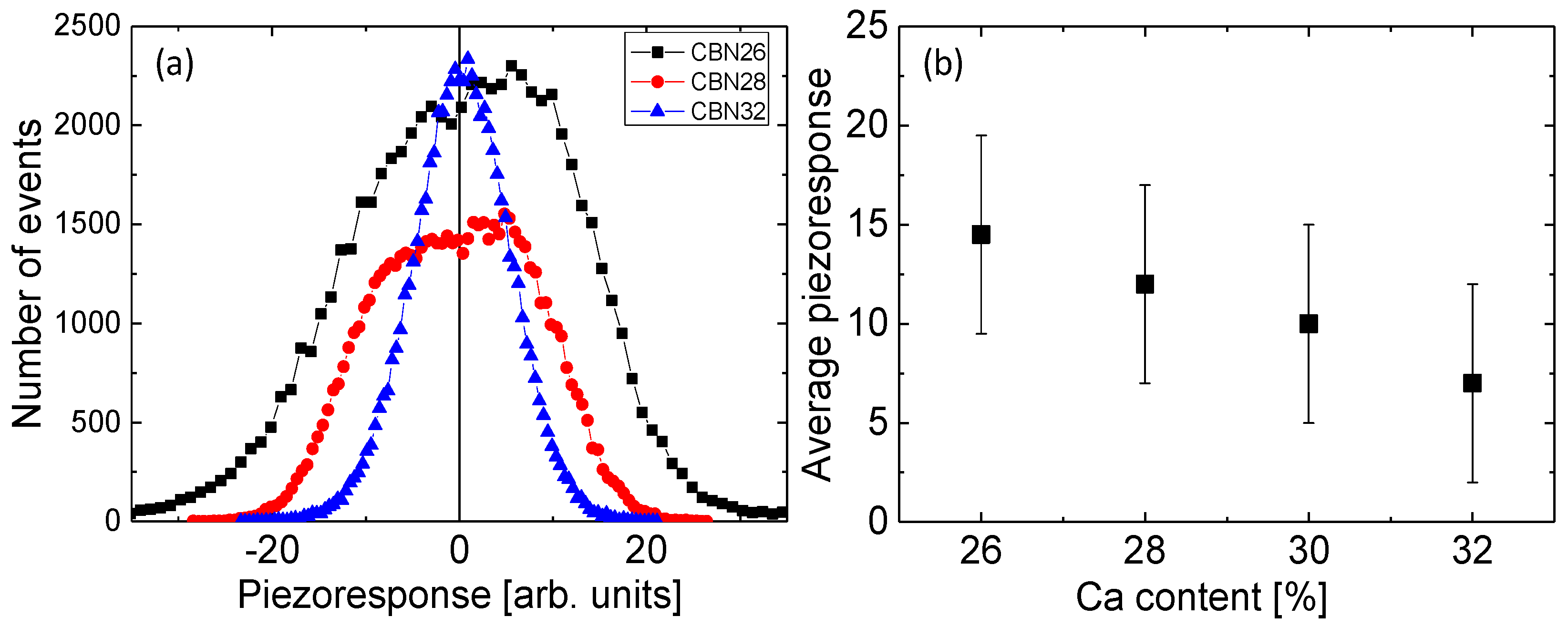
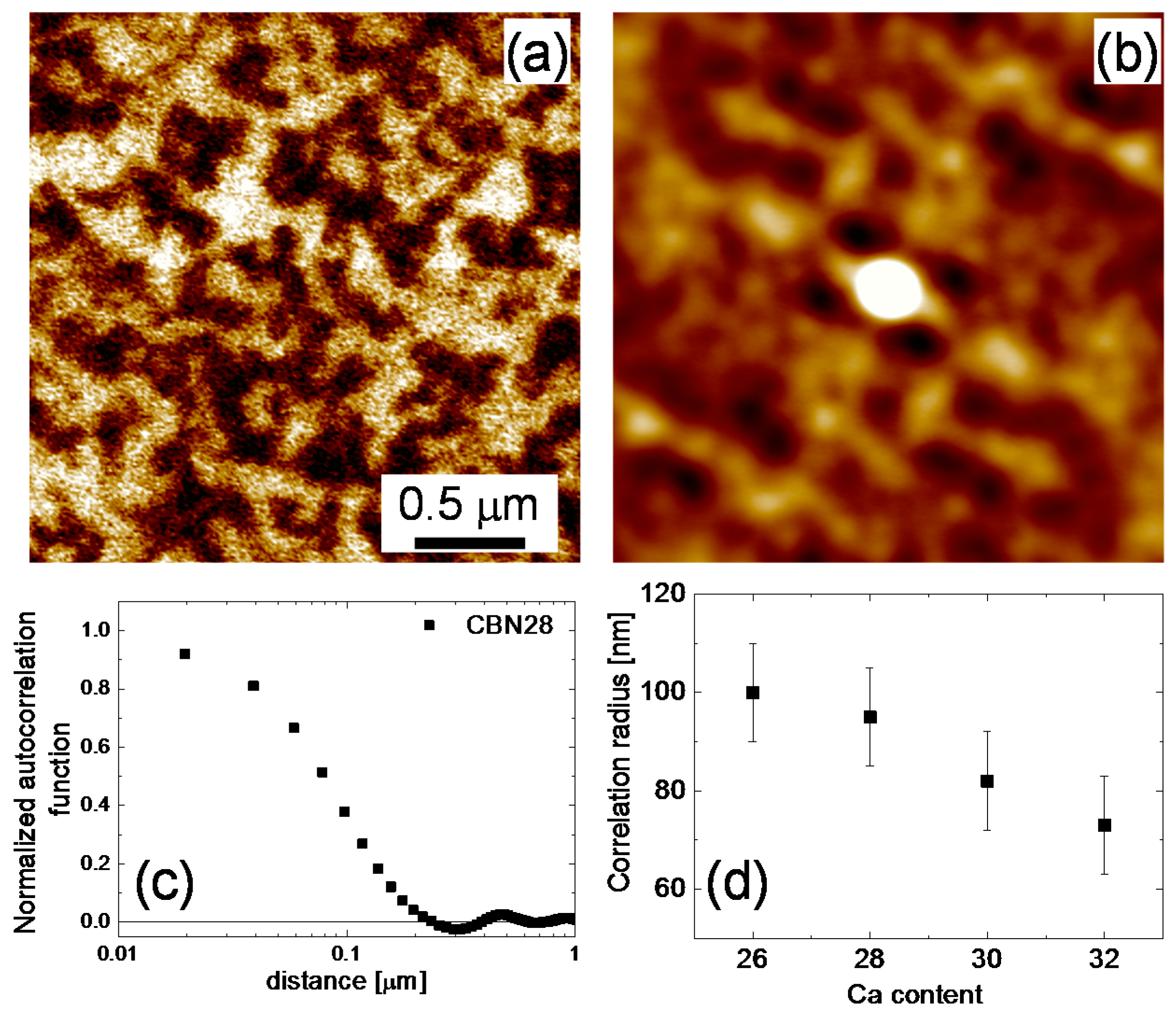
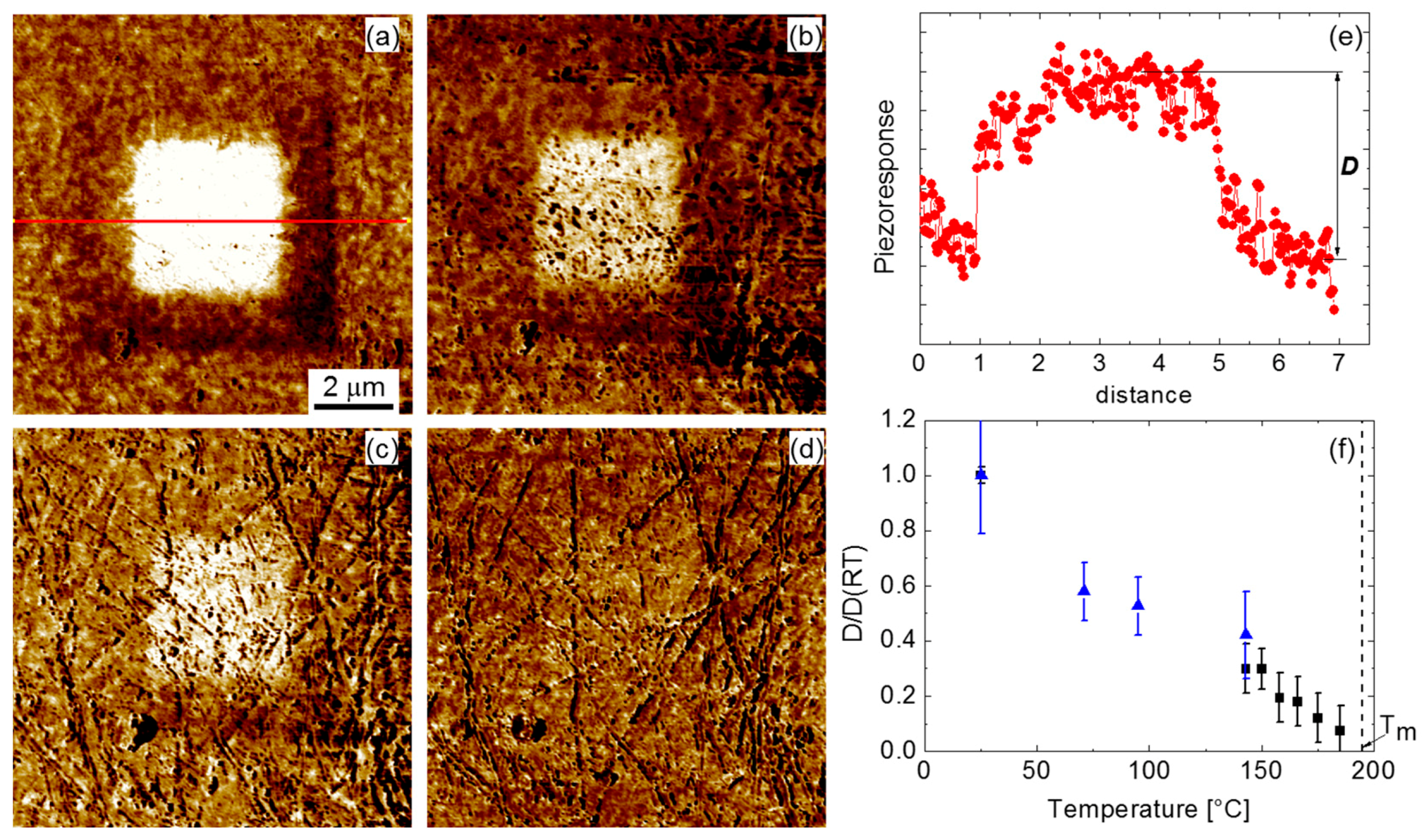
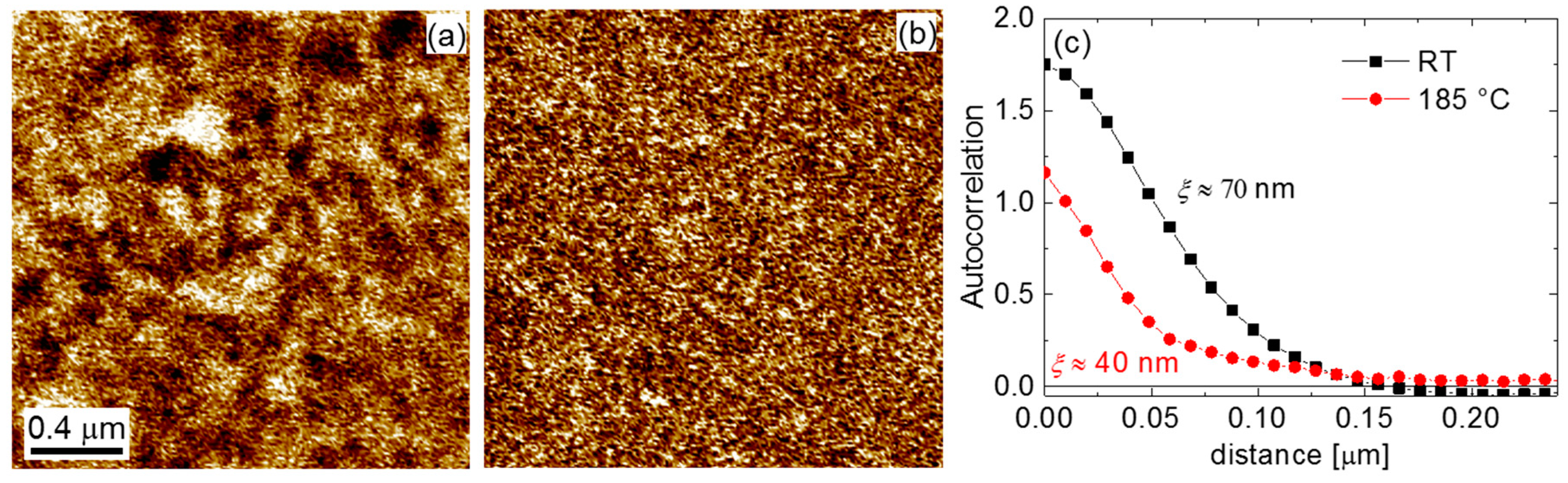
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shvartsman, V.V.; Lupascu, D.C. Lead-free relaxor ferroelectrics. J. Am. Ceram. Soc. 2012, 95, 1–26. [Google Scholar] [CrossRef]
- Xu, Y. Ferroelectric Materials and Their Applications; Elsevier: Amsterdam, The Netherlands, 1991; ISBN 978-0-444-88354-4. [Google Scholar]
- Francombe, M.H. The relation between structure and ferroelectricity in lead barium and barium strontium niobates. Acta Crystallogr. 1960, 13, 131–140. [Google Scholar] [CrossRef]
- Neurgaonkar, R.R.; Cory, W.K.; Oliver, J.R. Growth and applications of ferroelectric tungsten bronze family crystals. Ferroelectrics 1983, 51, 3–8. [Google Scholar] [CrossRef]
- David, S.; Granzow, T.; Tunyagi, A.; Wöhlecke, M.; Woike, T.; Betzler, K.; Ulex, M.; Imlau, M.; Pankrath, R. Composition dependence of the phase transition temperature in SrxBa1−xNb2O6. Phys. Status Solidi A 2004, 201, R49–R52. [Google Scholar] [CrossRef]
- Kleemann, W. The relaxor enigma—Charge disorder and random fields in ferroelectrics. J. Mater. Sci. 2006, 41, 129–136. [Google Scholar] [CrossRef]
- Qi, Y.J.; Lu, C.J.; Zhu, J.; Chen, X.B.; Song, H.L.; Zhang, H.J.; Xu, X.G. Ferroelectric and dielectric properties of Ca0.28Ba0.72Nb2O6 single crystals of tungsten bronzes structure. Appl. Phys. Lett. 2005, 87, 082904. [Google Scholar] [CrossRef]
- Burianek, M.; Joschko, B.; Kerkamm, I.; Schoenbeck, T.; Klimm, D.; Muehlberg, M. Crystal growth and characterization of CaxBa1−xNb2O6 (CBN) in the composition range of 0.22 ≤ x ≤ 0.35. J. Cryst. Growth 2007, 299, 413–417. [Google Scholar] [CrossRef]
- Pandey, C.S.; Schreuer, J.; Burianek, M.; Mühlberg, M. Anomalous elastic behavior of relaxor ferroelectric Ca0.28Ba0.72Nb2O6 single crystals. Phys. Rev. B 2011, 84, 174102. [Google Scholar] [CrossRef]
- Suzuki, K.; Matsumoto, K.; Dec, J.; Łukasiewicz, T.; Kleemann, W.; Kojima, S. Critical slowing down and elastic anomaly of uniaxial ferroelectric Ca0.28Ba0.72Nb2O6 crystals with tungsten bronze structure. Phys. Rev. B 2014, 90, 064110. [Google Scholar] [CrossRef]
- Pandey, C.S.; Schreuer, J.; Burianek, M.; Mühlberg, M. Relaxor behavior of CaxBa1−xNb2O6 (0.18 ≤ x ≤ 0.35) tuned by Ca/Ba ratio and investigated by resonant ultrasound spectroscopy. Phys. Rev. B 2013, 87, 094101. [Google Scholar] [CrossRef]
- Malyshkina, O.V.; Lisitsin, V.S.; Dec, J.; Łukasiewicz, T. Pyroelectric and dielectric properties of calcium barium niobate single crystals. Phys. Solid State 2014, 56, 1824–1827. [Google Scholar] [CrossRef]
- Song, H.; Zhang, H.; Jiang, Q.; Xu, X.; Lu, C.; Hu, X.; Wang, J.; Jiang, M. Growth, dielectric, ferroelectric and optical properties of Ca0.28Ba0.72Nb2O6 single crystals. J. Cryst. Growth 2006, 290, 431–435. [Google Scholar] [CrossRef]
- Heine, U.; Voelker, U.; Betzler, K.; Burianek, M.; Muehlberg, M. The ferroelectric phase transition of calcium barium niobate: Experimental evidence of Smolenskii’s model for diffuse phase transitions? New J. Phys. 2009, 11, 083021. [Google Scholar] [CrossRef]
- Smolensky, G. Ferroelectrics with diffuse phase transition. Ferroelectrics 1984, 53, 129–135. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Dkhil, B.; Kholkin, A.L. Mesoscale domains and nature of the relaxor state by piezoresponse force microscopy. Annu. Rev. Mater. Res. 2013, 43, 423–449. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Kleemann, W.; Łukasiewicz, T.; Dec, J. Nanopolar structure in SrxBa1−xNb2O6 single crystals tuned by the Sr/Ba ratio and investigated by piezoelectric force microscopy. Phys. Rev. B 2008, 77, 054105. [Google Scholar] [CrossRef]
- Lehnen, P.; Kleemann, W.; Woike, T.; Pankrath, R. Ferroelectric nanodomains in the uniaxial relaxor system Sr0.61−xBa0.39Nb2O6:Cex3+. Phys. Rev. B 2001, 64, 224109. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Dec, J.; Miga, S.; Łukasiewicz, T.; Kleemann, W. Ferroelectric domains in SrxBa1−xNb2O6 single crystals (0.4 ≤ x ≤ 0.75). Ferroelectrics 2008, 376, 1–8. [Google Scholar] [CrossRef]
- Łukasiewicz, T.; Swirkowicz, M.A.; Dec, J.; Hofman, W.; Szyrski, W. Strontium–barium niobate single crystals, growth and ferroelectric properties. J. Cryst. Growth 2008, 310, 1464–1469. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shvartsman, V.V.; Gobeljic, D.; Dec, J.; Lupascu, D.C. A Piezoresponse Force Microscopy Study of CaxBa1−xNb2O6 Single Crystals. Materials 2017, 10, 1032. https://doi.org/10.3390/ma10091032
Shvartsman VV, Gobeljic D, Dec J, Lupascu DC. A Piezoresponse Force Microscopy Study of CaxBa1−xNb2O6 Single Crystals. Materials. 2017; 10(9):1032. https://doi.org/10.3390/ma10091032
Chicago/Turabian StyleShvartsman, Vladimir V., Danka Gobeljic, Jan Dec, and Doru C. Lupascu. 2017. "A Piezoresponse Force Microscopy Study of CaxBa1−xNb2O6 Single Crystals" Materials 10, no. 9: 1032. https://doi.org/10.3390/ma10091032
APA StyleShvartsman, V. V., Gobeljic, D., Dec, J., & Lupascu, D. C. (2017). A Piezoresponse Force Microscopy Study of CaxBa1−xNb2O6 Single Crystals. Materials, 10(9), 1032. https://doi.org/10.3390/ma10091032





