Design of Waveguide Bars for Transmitting a Pure Shear Horizontal Wave to Monitor High Temperature Components
Abstract
:1. Introduction
2. Selection of a Guided Wave Source
3. Structural Design of Waveguide Bars
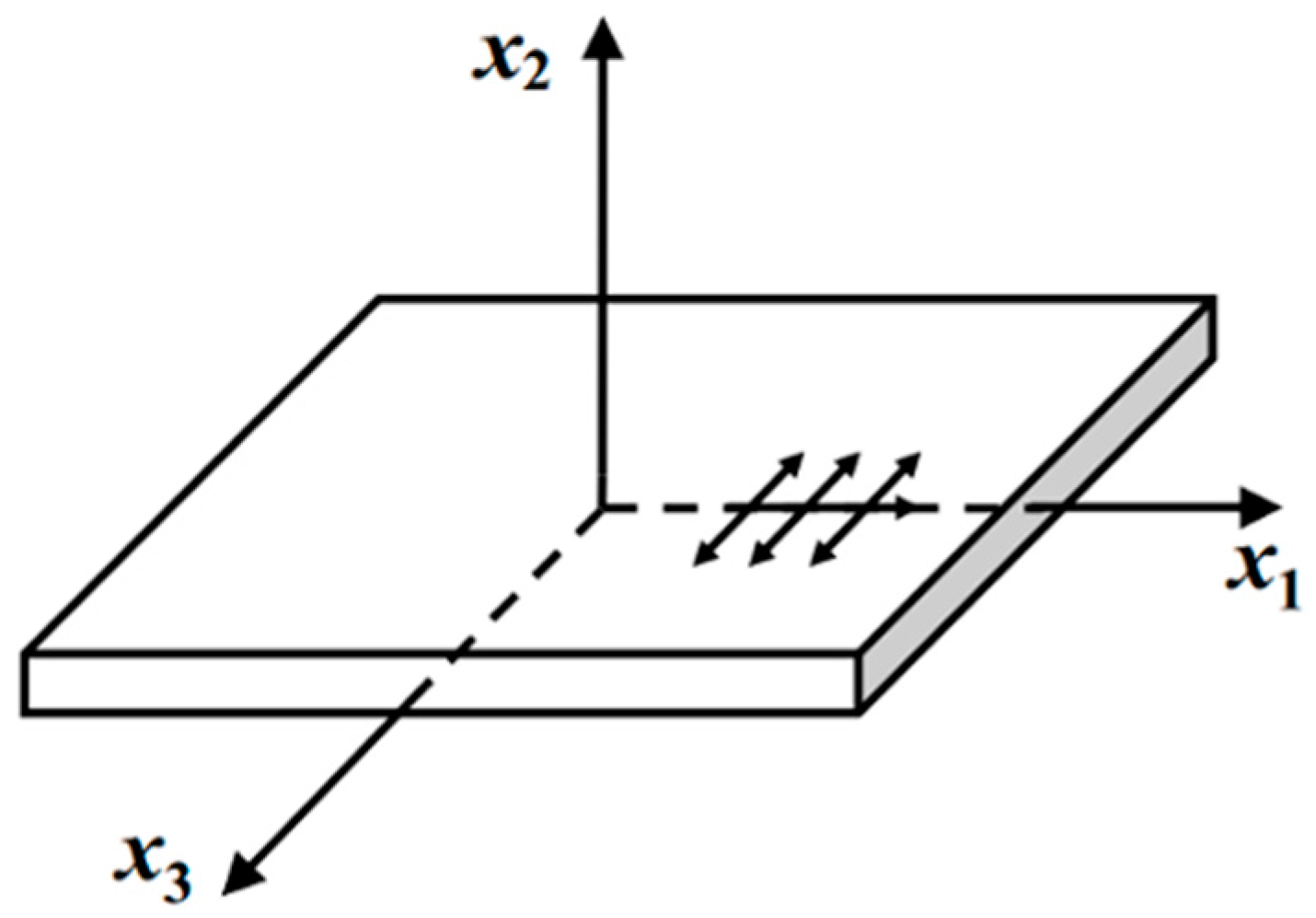
3.1. Theoretical Analyses
3.2. Calculating the Thickness
3.3. Calculating the Width
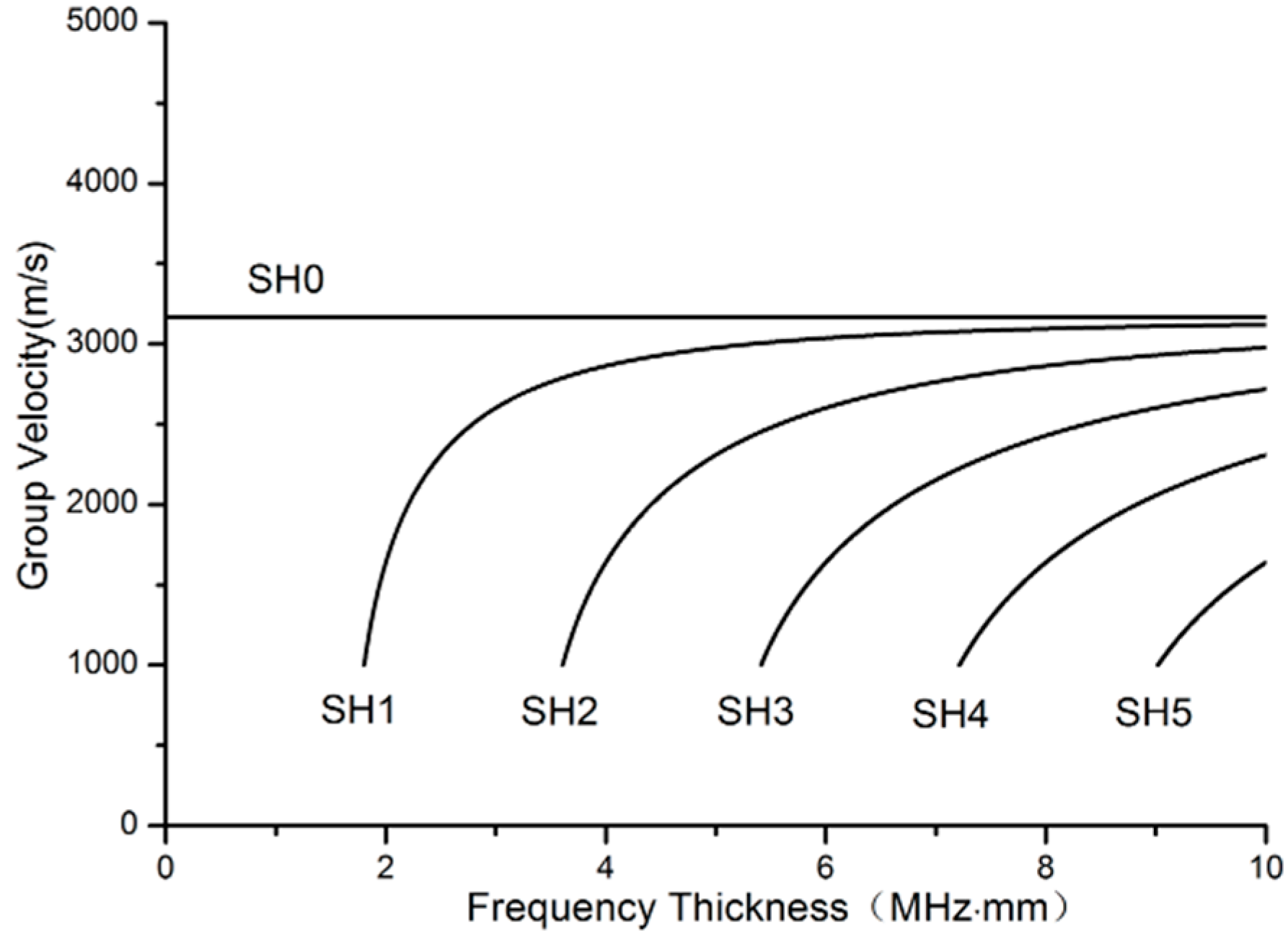
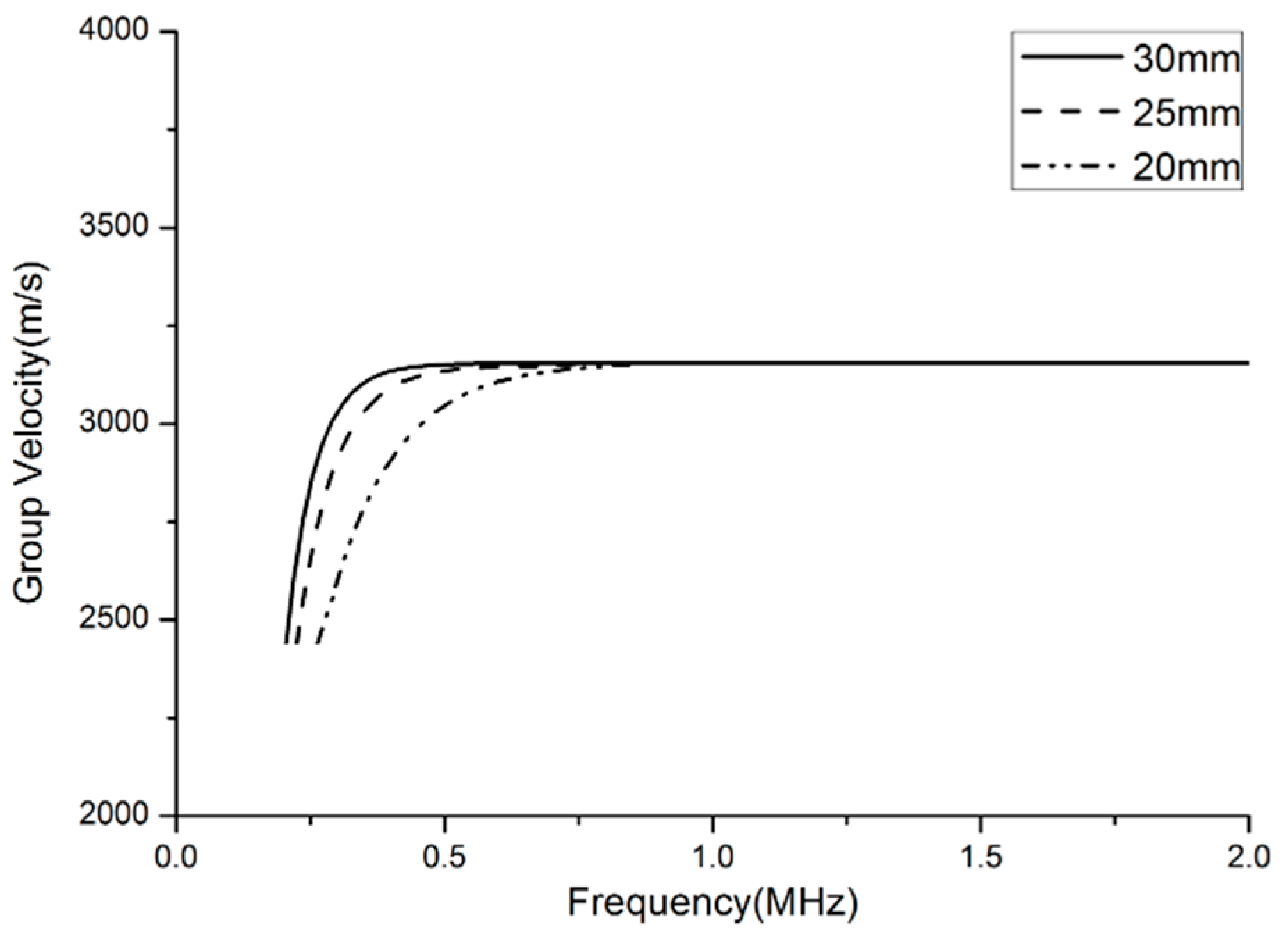
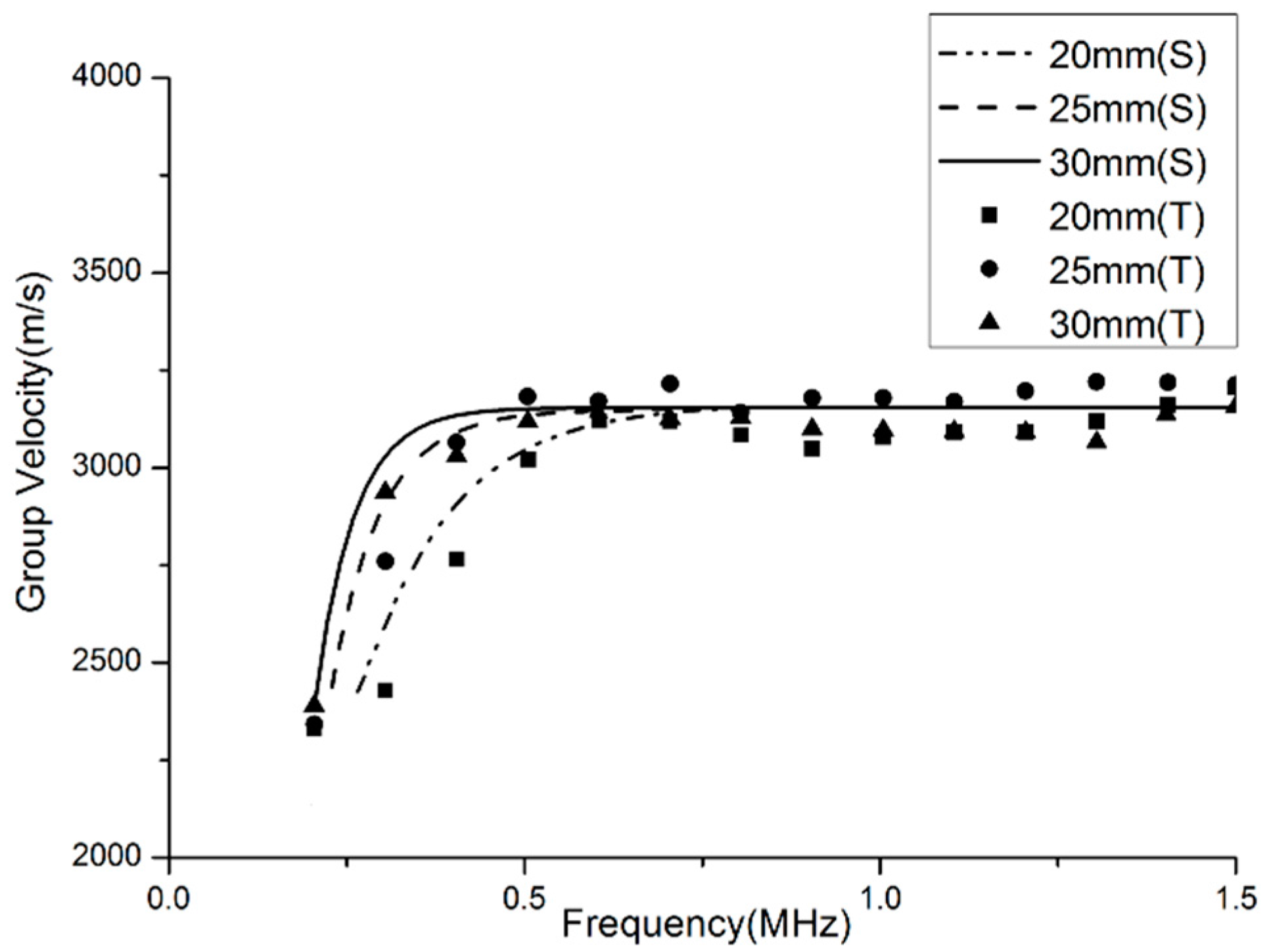
3.4. Frequency Dependence
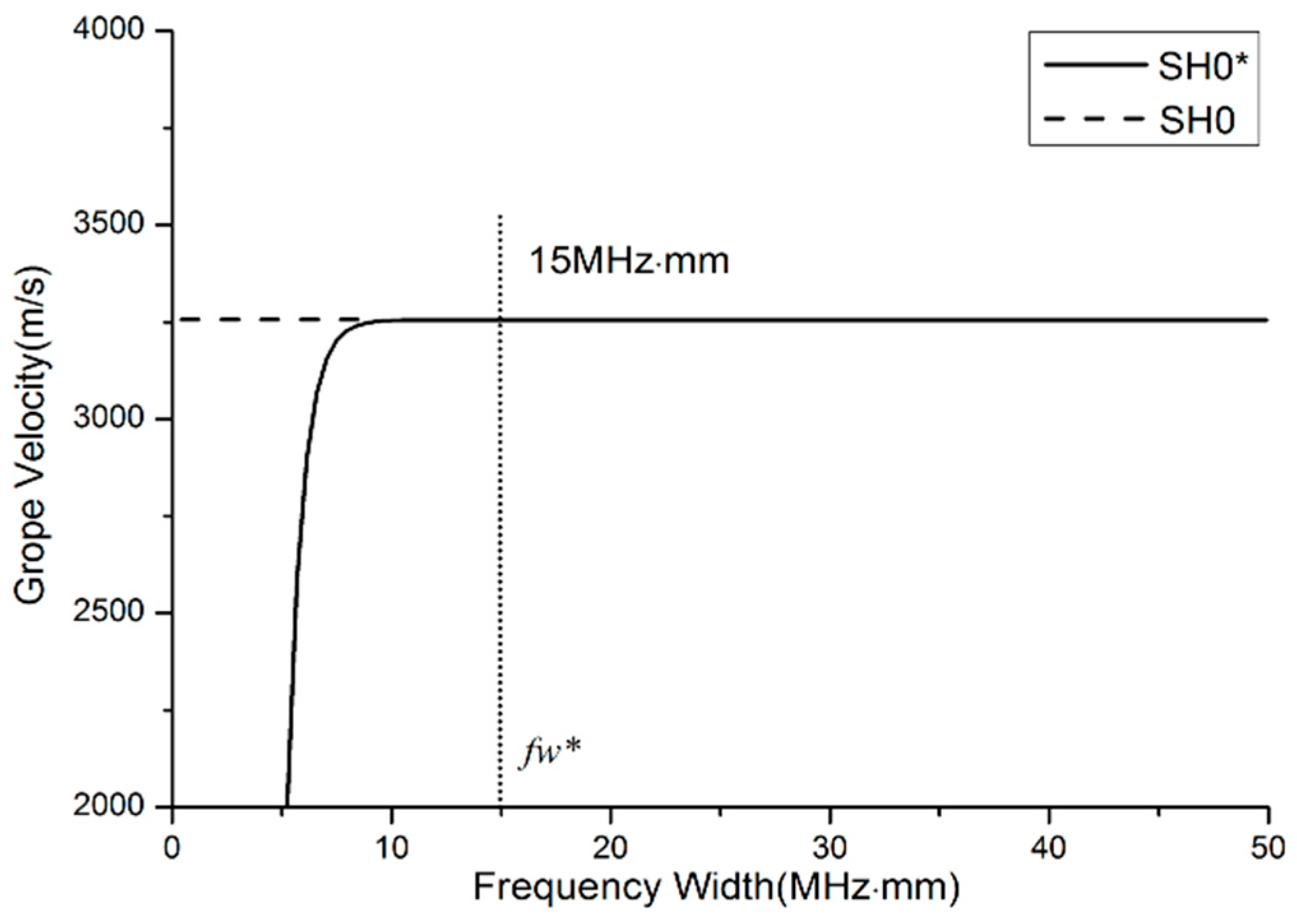
3.5. Structural Design Criteria
4. Room Temperature Experimental Verification
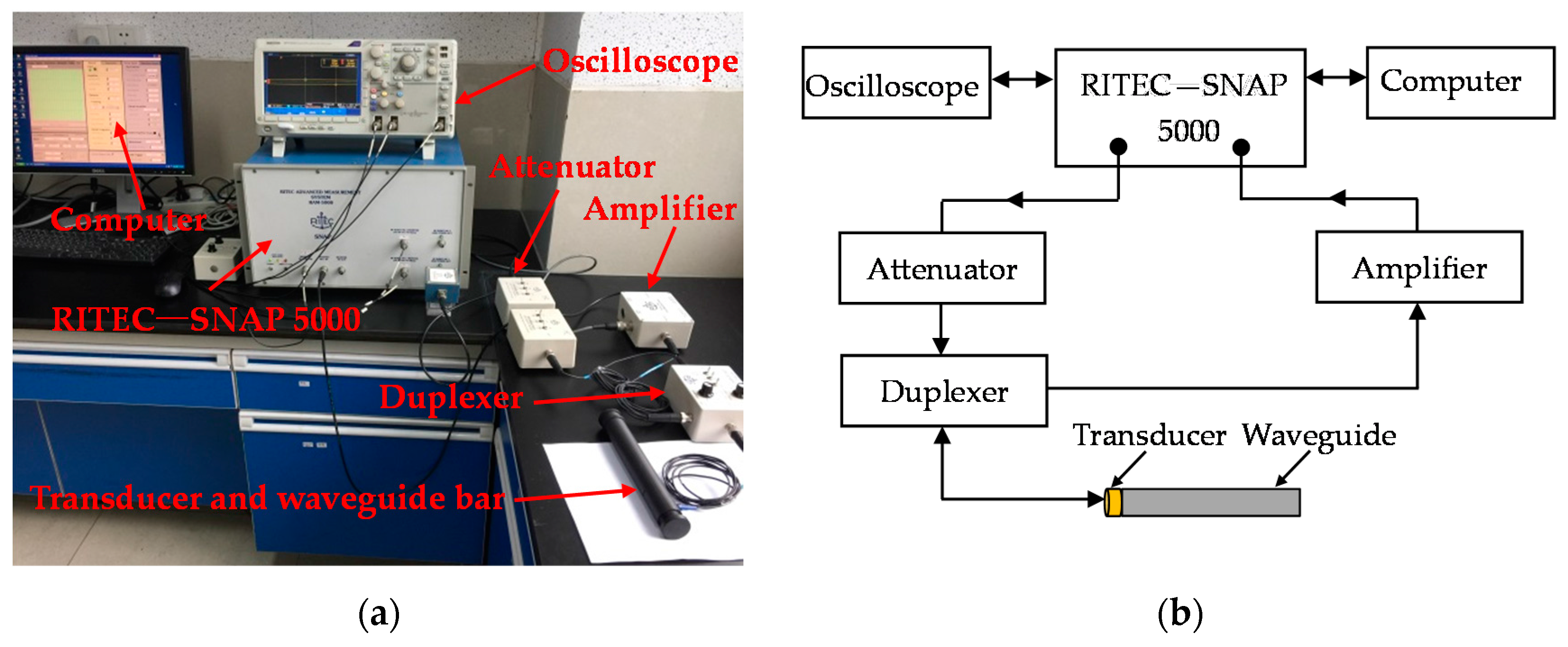
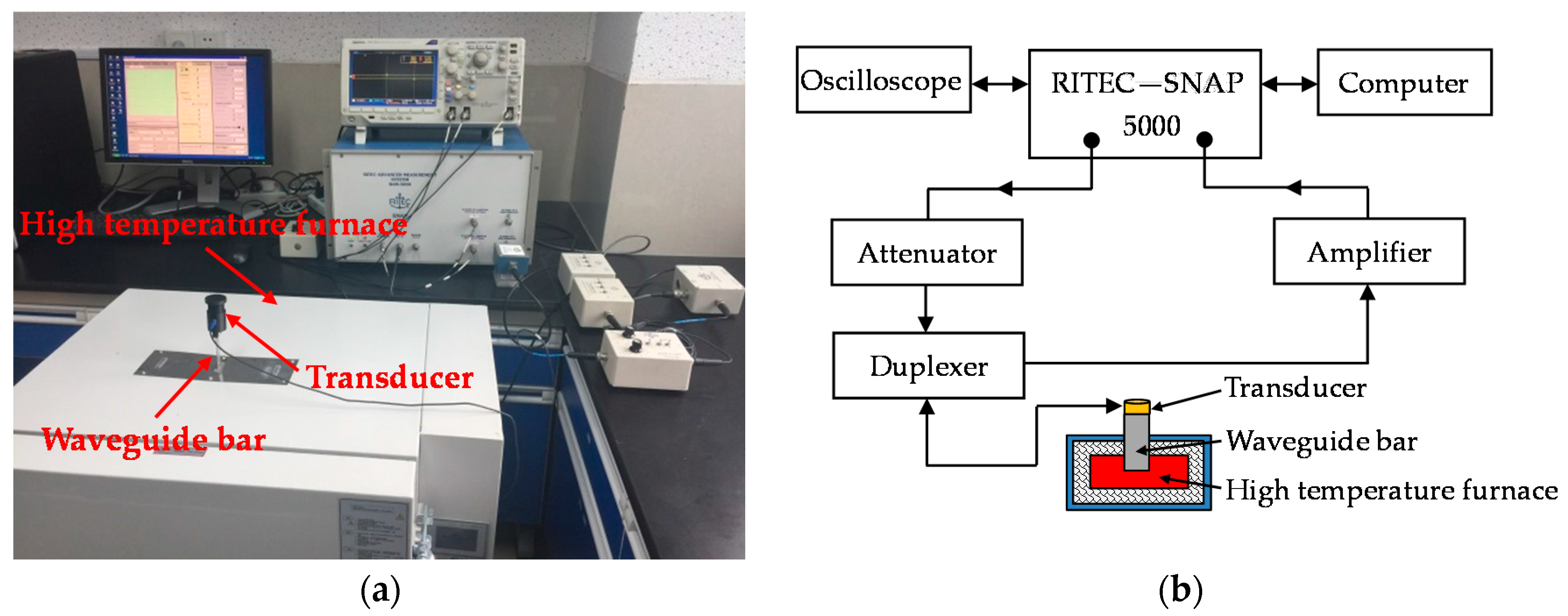
4.1. Experimental System
4.2. Verification of Thickness
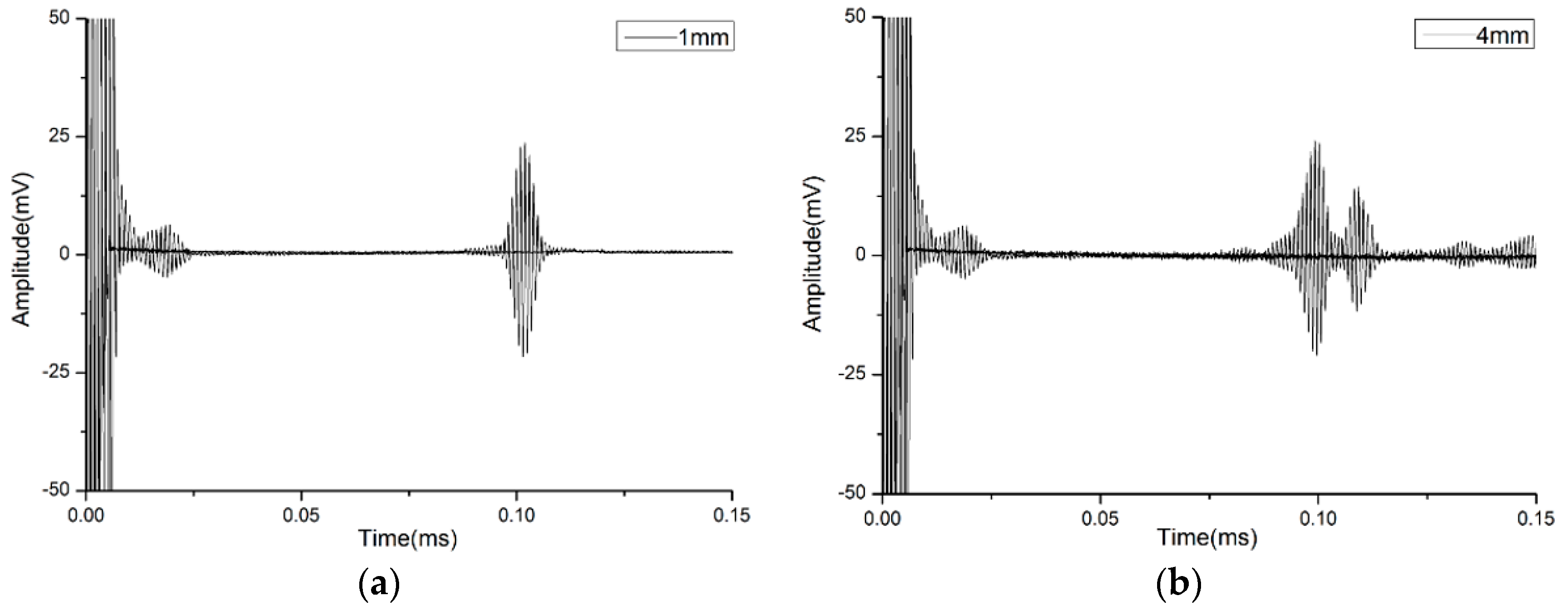
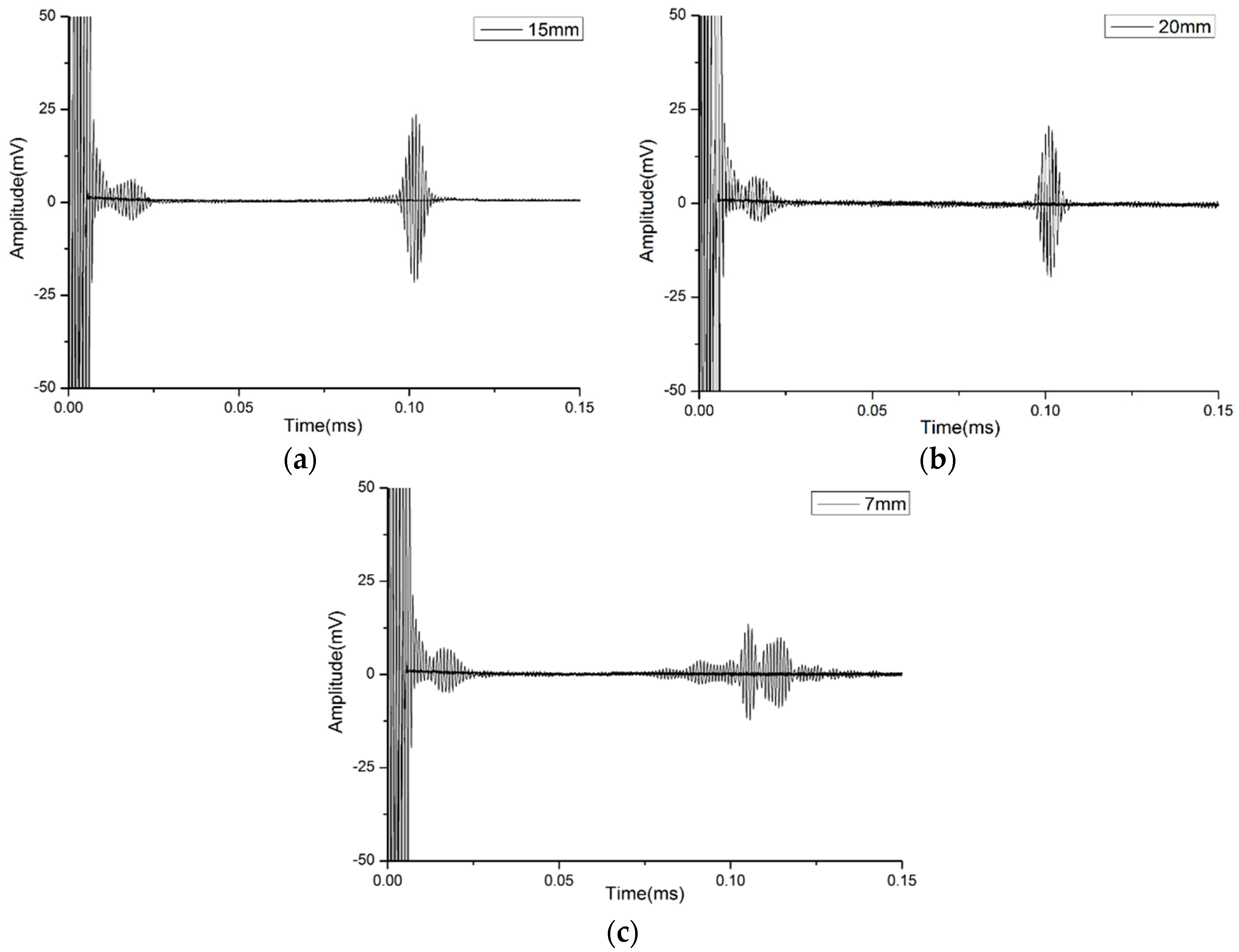
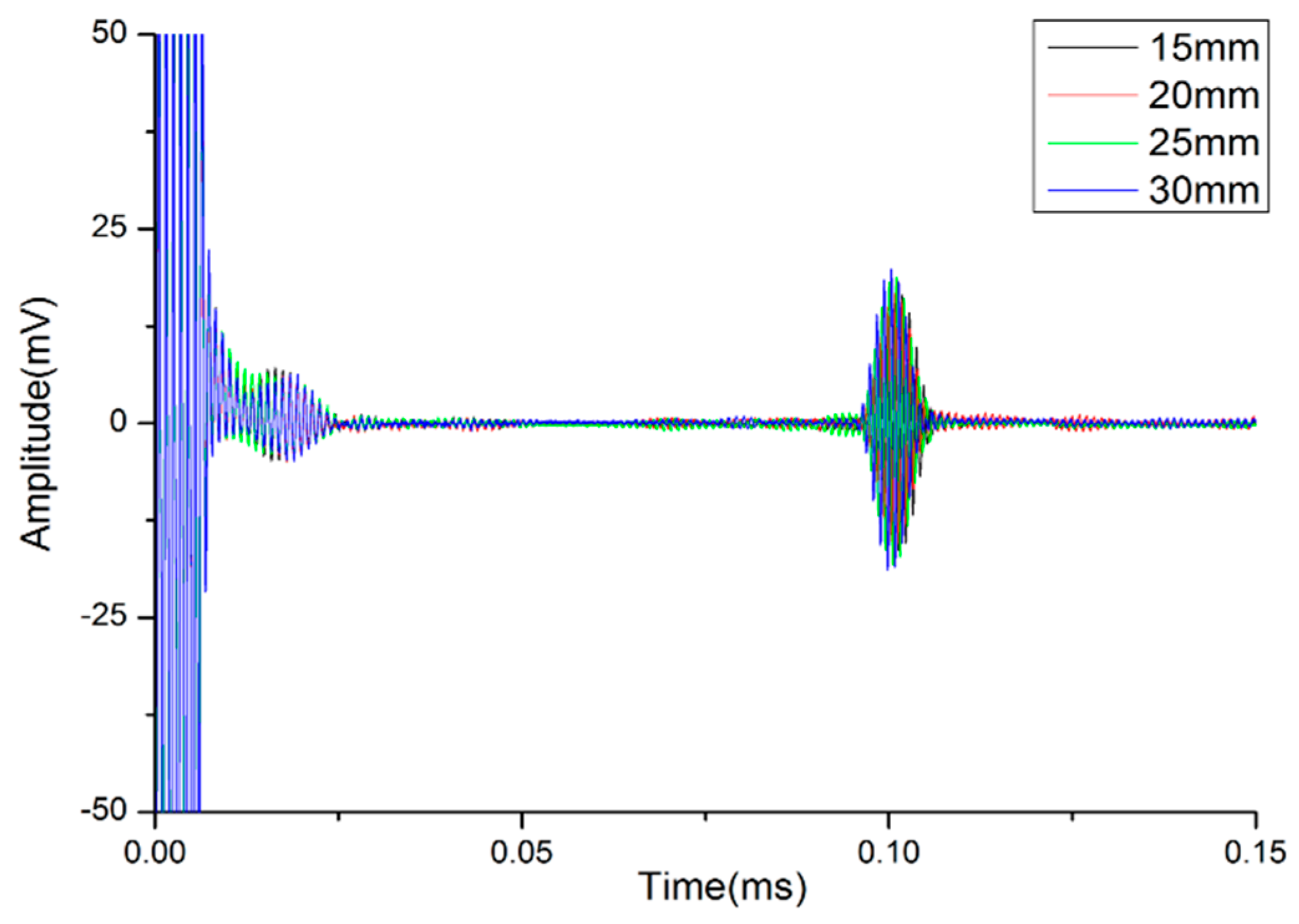
4.3. Verification of Width
4.4. Verification of the Frequency Dependence
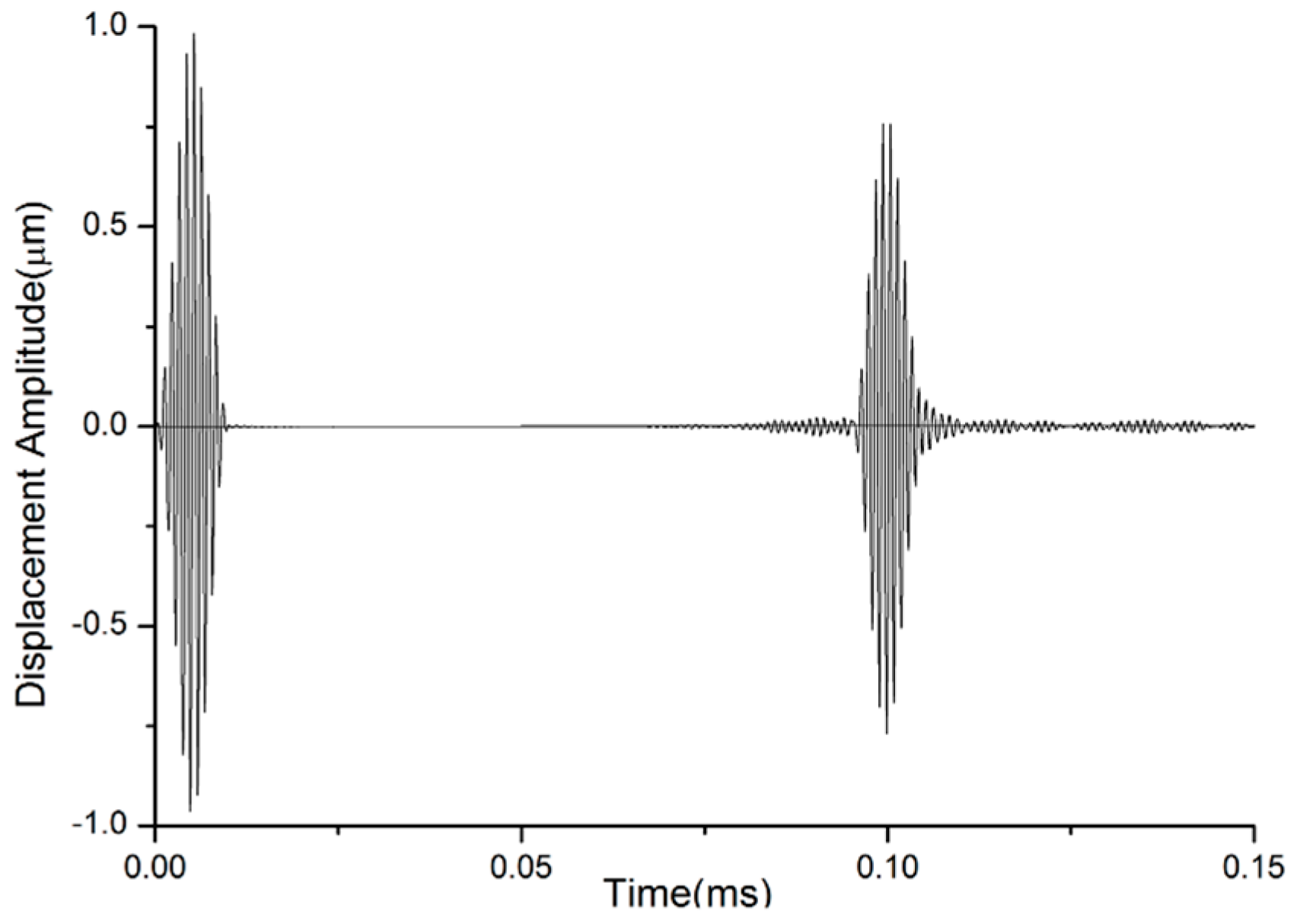
4.5. Propagating Characteristics of Designed Waveguide Bars
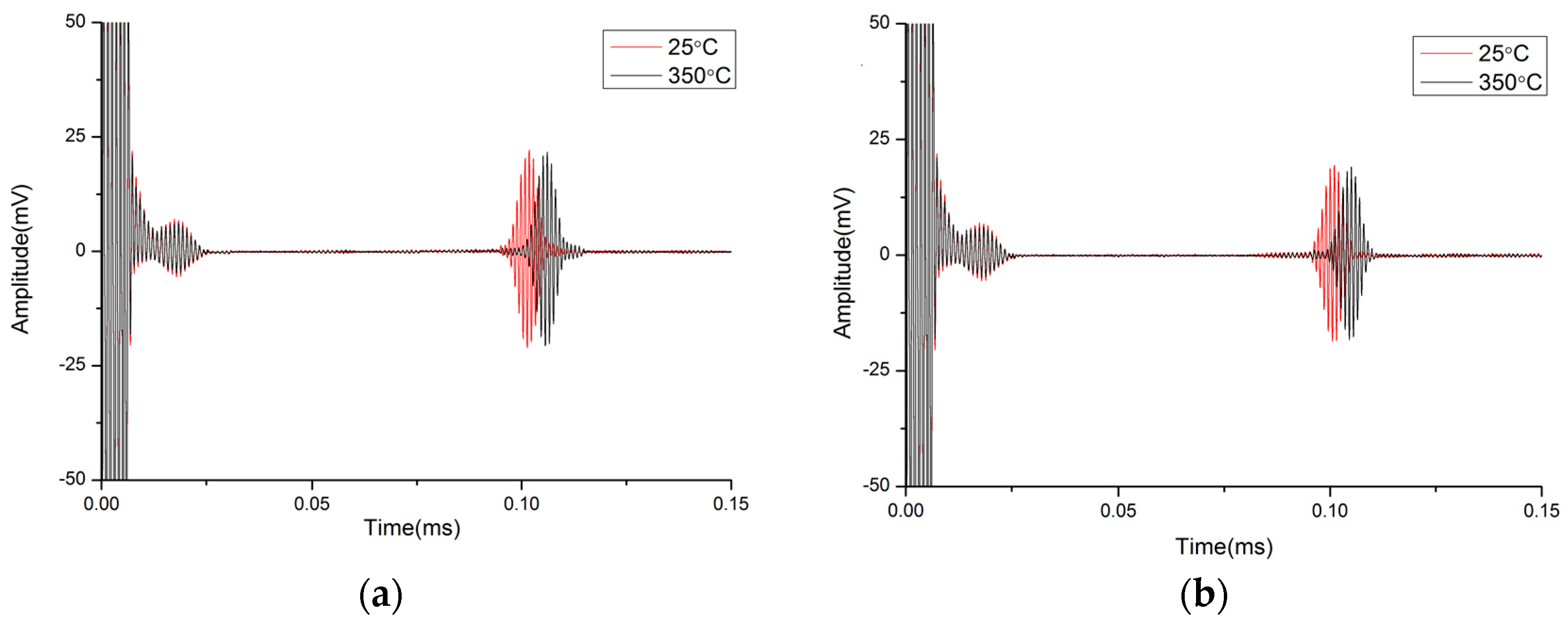
5. High Temperature Experimental Validation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yuan, S.F.; Lai, X.S.; Zhao, X.; Xu, X.; Zhang, L. Distributed structural health monitoring system based on smart wireless sensor and multi-agent technology. Smart Mater. Struct. 2006, 15, 1–8. [Google Scholar] [CrossRef]
- Zhang, H.C.; Jia, J.H.; Wang, N.; Hu, X.Y.; Tu, S.T.; Zhou, S.P.; Wang, Z.D. Development of on-line monitoring systems for high temperature components in power plants. Sensors 2013, 13, 15504–15512. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.H.; Hu, X.Y.; An, Z.L.; Xuan, F.Z.; Tu, S.T. Design and verification of a sensing device for deformation measurement of high temperature pipes. J. Press. Vessel Technol. 2011, 133, 041601. [Google Scholar] [CrossRef]
- Qiu, L.; Yuan, S.F.; Chang, F.K.; Bao, Q.; Mei, H. On-line updating Gaussian mixture model for aircraft wing spar damage evaluation under time-varying boundary condition. Smart Mater. Struct. 2014, 23, 125001. [Google Scholar] [CrossRef]
- Li, F.C.; Liu, Z.Q.; Sun, X.W.; Li, H.; Meng, G. Propagation of guided waves in pressure vessel. Wave Motion 2015, 52, 216–228. [Google Scholar] [CrossRef]
- Ni, J.; Zhou, S.P.; Zhang, P.G.; Li, Y. Effect of pipe bend configuration on guided waves-based defects detection: An experimental study. J. Press. Vessel Technol. 2016, 138, 021203. [Google Scholar] [CrossRef]
- Cegla, F.B.; Cawley, P.; Allin, J.; Davies, J. High-temperature (>500 °C) wall thickness monitoring using dry-coupled ultrasonic waveguide transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 156–166. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.H.; Hu, X.Y.; Wang, N.; Tu, S.T. Test verification of an extensometer for deformation measurement of high temperature straight pipes. Measurement 2012, 45, 1933–1936. [Google Scholar] [CrossRef]
- Hu, X.Y.; Jia, J.H.; Wang, N.; Xia, X.M.; Wang, Z.D.; Tu, S.T. Design and test of an extensometer for strain monitoring of high temperature pipelines. J. Press. Vessel Technol. 2012, 134, 044501. [Google Scholar] [CrossRef]
- Li, Y.H. High Performance BS-PT Based Transducers for High-Temperature Structural Health Monitoring Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2015. [Google Scholar]
- Hou, R.; Hutson, D.; Kirk, K.J. Development of sputtered AIN thin-film ultrasonic transducers for durable high-temperature applications. Insight 2013, 55, 302–307. [Google Scholar] [CrossRef]
- Sinding, K.; Searfass, C.; Malarich, N.; Reinhardt, B.; Tittmann, B.R. High temperature ultrasonic transducers for the generation of guided waves for nondestructive evaluation of pipes. AIP Conf. Proc. 2014, 1581, 302–307. [Google Scholar]
- Fuse, N.; Kaneshige, K.; Watanabe, H. Development of thickness measurement system for hot steel with laser-ultrasonic wave technology. Mater. Trans. 2014, 55, 1011–1016. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, Z.; Zhou, J. Application of laser ultrasonic method for on-line monitoring of friction stir spot welding process. Appl. Opt. 2015, 54, 7483. [Google Scholar] [CrossRef] [PubMed]
- Kogia, M.; Gan, T.H.; Balachandran, W.; Livadas, M.; Kappatos, V.; Szabo, I.; Mohimi, A.; Round, A. High temperature shear horizontal electromagnetic acoustic transducer for guided wave inspection. Sensors 2016, 16, 582. [Google Scholar] [CrossRef] [PubMed]
- Burrows, S.E.; Fan, Y.; Dixon, S. High temperature thickness measurements of stainless steel and low carbon steel using electromagnetic acoustic transducers. NDT E Int. 2014, 68, 73–77. [Google Scholar] [CrossRef]
- Vinogradov, S.; Duffer, C.; Light, G. Magnetostrictive sensing probes for guided wave testing of high temperature pipes. Mater. Eval. 2014, 72, 803–811. [Google Scholar]
- Vasile, C.F.; Thompson, R.B. Excitation of horizontally polarized shear elastic waves by electromagnetic transducers with periodic permanent magnets. J. Appl. Phys. 1979, 50, 2583–2588. [Google Scholar] [CrossRef]
- Thompson, R.B. Generation of horizontally polarized shear waves in ferromagnetic materials using magnetostrictively coupled meander-coil electromagnetic transducers. Appl. Phys. Lett. 1979, 34, 175–177. [Google Scholar] [CrossRef]
- Köhler, B.; Gaul, T.; Lieske, U.; Schubert, F. Shear horizontal piezoelectric fiber patch transducers (SH-PFP) for guided elastic wave applications. NDT E Int. 2016, 82, 1–12. [Google Scholar] [CrossRef]
- Lynnworth, L.C. Marginally Dispersive Ultrasonic Waveguides. U.S. Patent 005159838A, 3 November 1992. [Google Scholar]
- Lynnworth, L.C.; Liu, Y. Ultrasonic Path Bundle and Systems. U.S. Patent 005962790A, 5 October 1999. [Google Scholar]
- Jen, C.K.; Legoux, J.G. Clad Ultrasonic Waveguides with Reduced Trailing Echoes. U.S. Patent 005828274A, 27 October 1998. [Google Scholar]
- Heijnsdijk, A.M.; Van Klooster, J.M. Ultrasonic Waveguide. U.S. Patent 6400648B1, 4 July 2002. [Google Scholar]
- Cawley, P.; Cegla, F.B. Ultrasonic Nondestructive Testing. U.S. Patent 2016/0109414Al, 21 April 2016. [Google Scholar]
- Kwon, Y.E.; Jeon, H.J.; Kim, H.W.; Kim, Y.Y. Waveguide tapering for beam-width control in a waveguide transducer. Ultrasonics 2014, 54, 953–960. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Ogilvy, J.A.; Temple, J.A.G. Diffraction of elastic waves by cracks: Application to time-of-flight inspection. Ultrasonics 1983, 21, 259–269. [Google Scholar] [CrossRef]
- Vanniamparambil, P.A.; Carmi, R.; Khan, F.; Cuadra, J.; Bartoli, I.; Kontsos, A. An active—Passive acoustics approach for bond-line condition monitoring in aerospace skin stiffener panels. Aerosp. Sci. Technol. 2015, 43, 289–300. [Google Scholar] [CrossRef]
- Khan, F.; Rajaram, S.; Vanniamparambil, P.A.; Bolhassani, M.; Hamid, A.; Kontsos, A.; Bartoli, I. Multi-sensing NDT for damage assessment of concrete masonry walls. Struct. Control Health Monit. 2015, 22, 449–462. [Google Scholar] [CrossRef]




| Elastic Modulus | Poisson’s Ratio | Material Density |
|---|---|---|
| E = 211 Gpa | R = 0.286 | d = 7800 kg/m3 |
| Number | Width/mm | Thickness/mm | Length/mm |
|---|---|---|---|
| 1 | 20 | 1 | 150 |
| 2 | 25 | 1 | 150 |
| 3 | 30 | 1 | 150 |
| Number | Width/mm | Thickness/mm | Length/mm |
|---|---|---|---|
| No. 1 | 15 | 1 | 150 |
| No. 2 | 15 | 4 | 150 |
| No. 3 | 7 | 1 | 150 |
| No. 4 | 20 | 1 | 150 |
| No. 5 | 25 | 1 | 150 |
| No. 6 | 30 | 1 | 150 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Wang, Q.; Liao, Z.; Tu, Y.; Tu, S.-T. Design of Waveguide Bars for Transmitting a Pure Shear Horizontal Wave to Monitor High Temperature Components. Materials 2017, 10, 1027. https://doi.org/10.3390/ma10091027
Jia J, Wang Q, Liao Z, Tu Y, Tu S-T. Design of Waveguide Bars for Transmitting a Pure Shear Horizontal Wave to Monitor High Temperature Components. Materials. 2017; 10(9):1027. https://doi.org/10.3390/ma10091027
Chicago/Turabian StyleJia, Jiuhong, Qiyue Wang, Zuoyu Liao, Yun Tu, and Shan-Tung Tu. 2017. "Design of Waveguide Bars for Transmitting a Pure Shear Horizontal Wave to Monitor High Temperature Components" Materials 10, no. 9: 1027. https://doi.org/10.3390/ma10091027




