Effect of Fly-Ash Cenospheres on Properties of Clay-Ceramic Syntactic Foams
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Processing
2.3. Composition
2.4. Characterisation
3. Results and Discussion
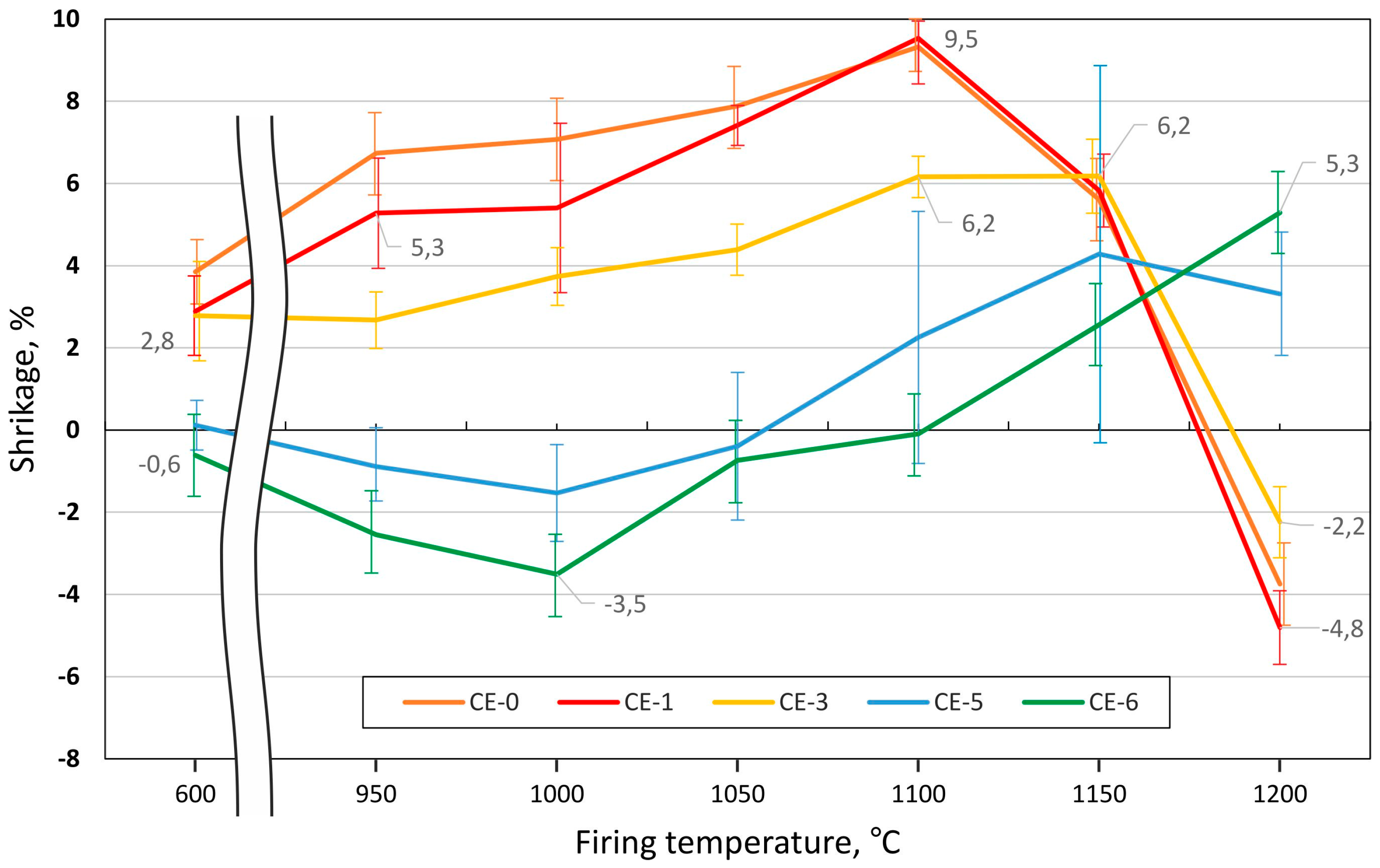
3.1. Appearance of Samples, Shrinkage
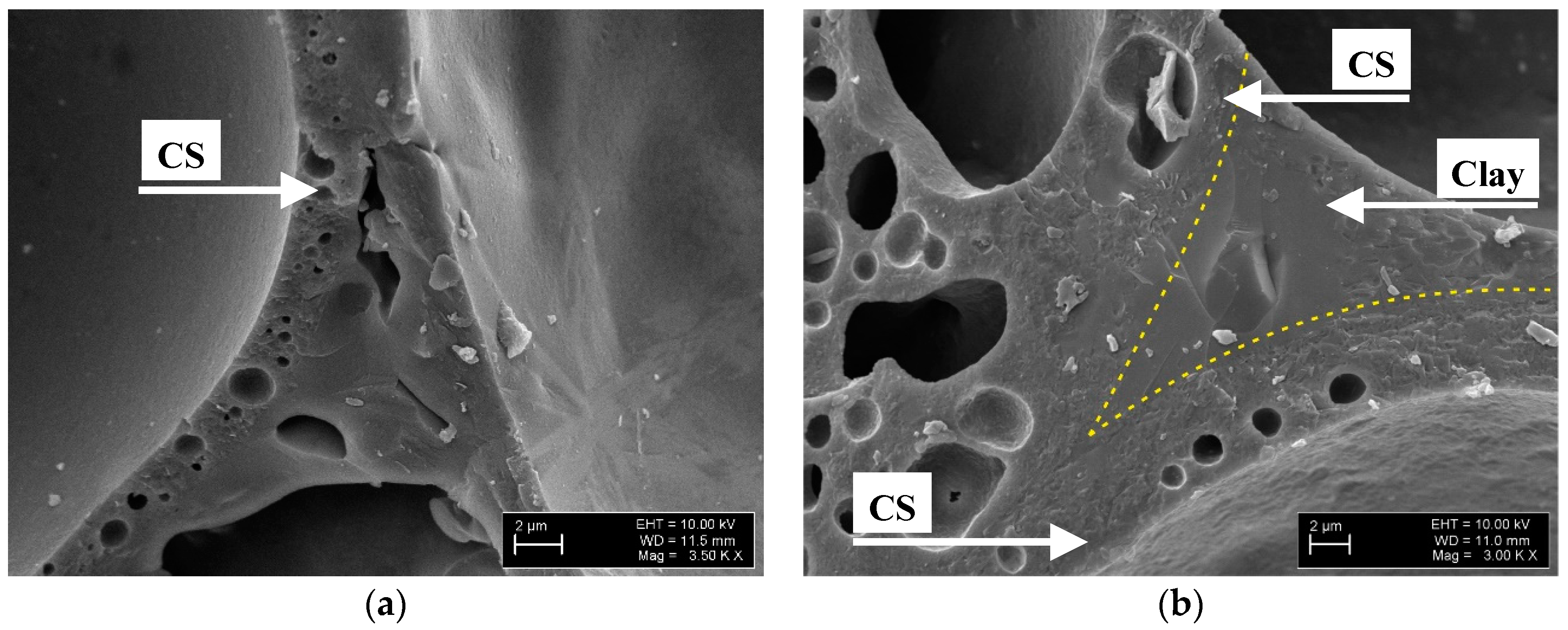
3.2. Microstructure
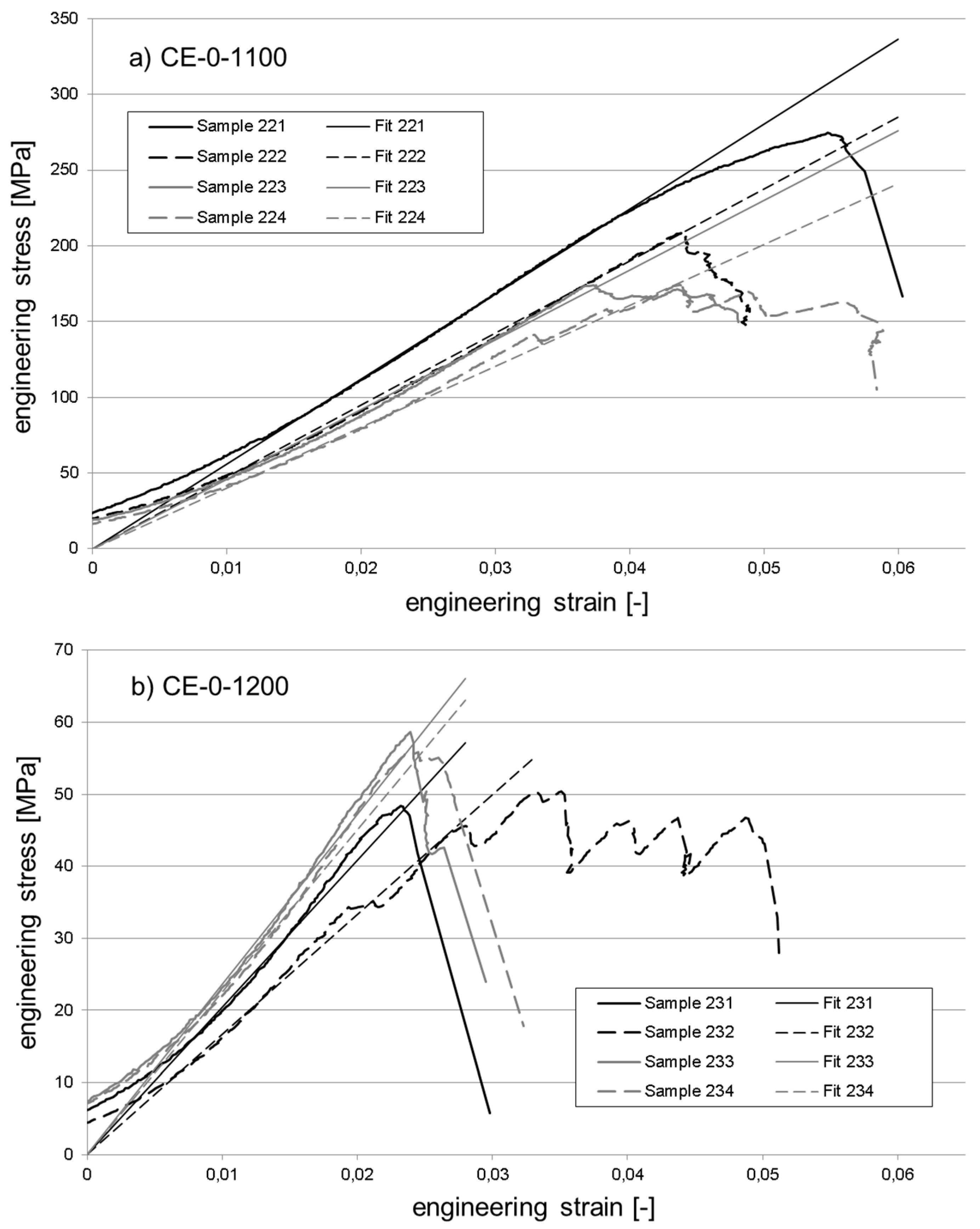
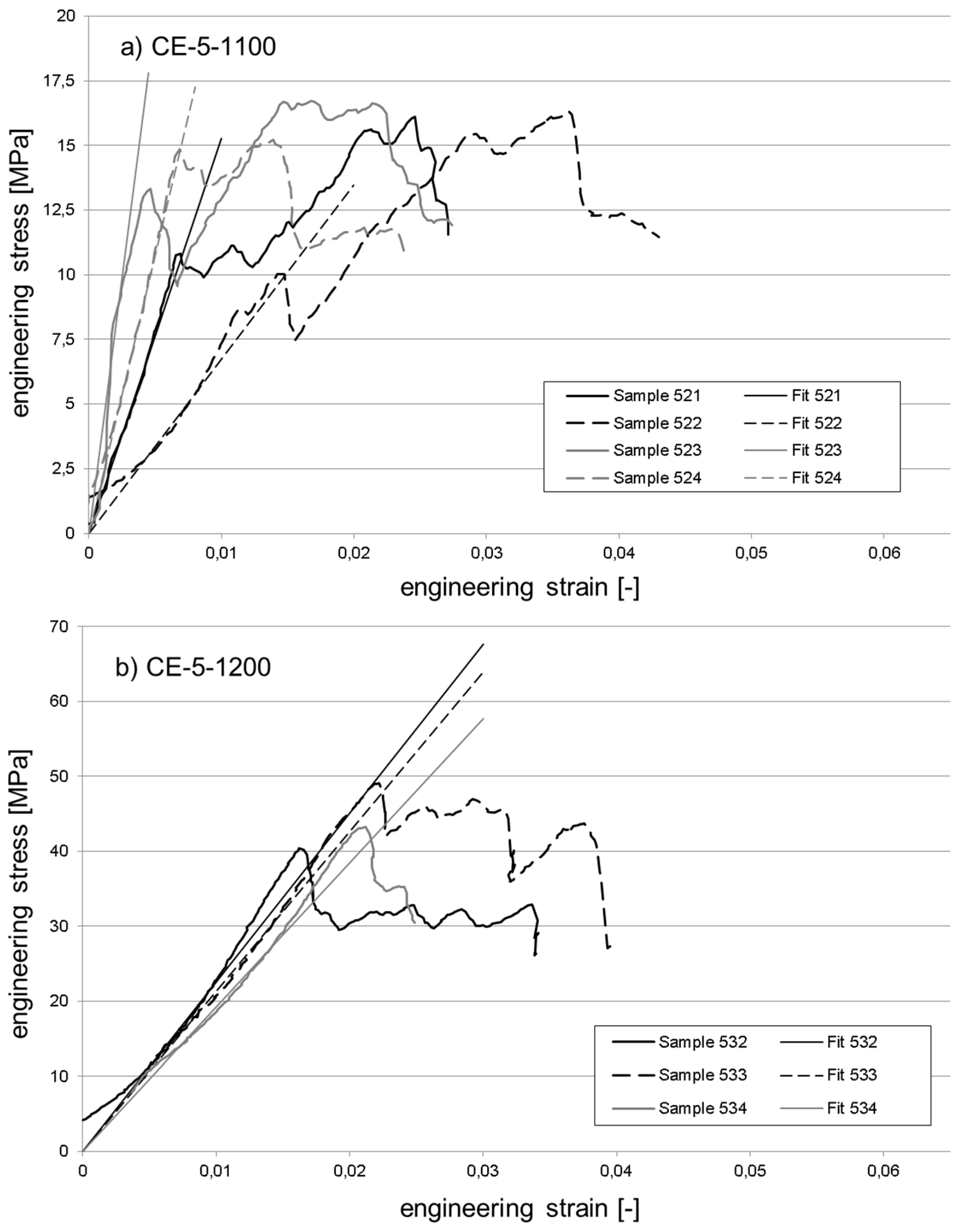
3.3. Syntactic Foam Properties
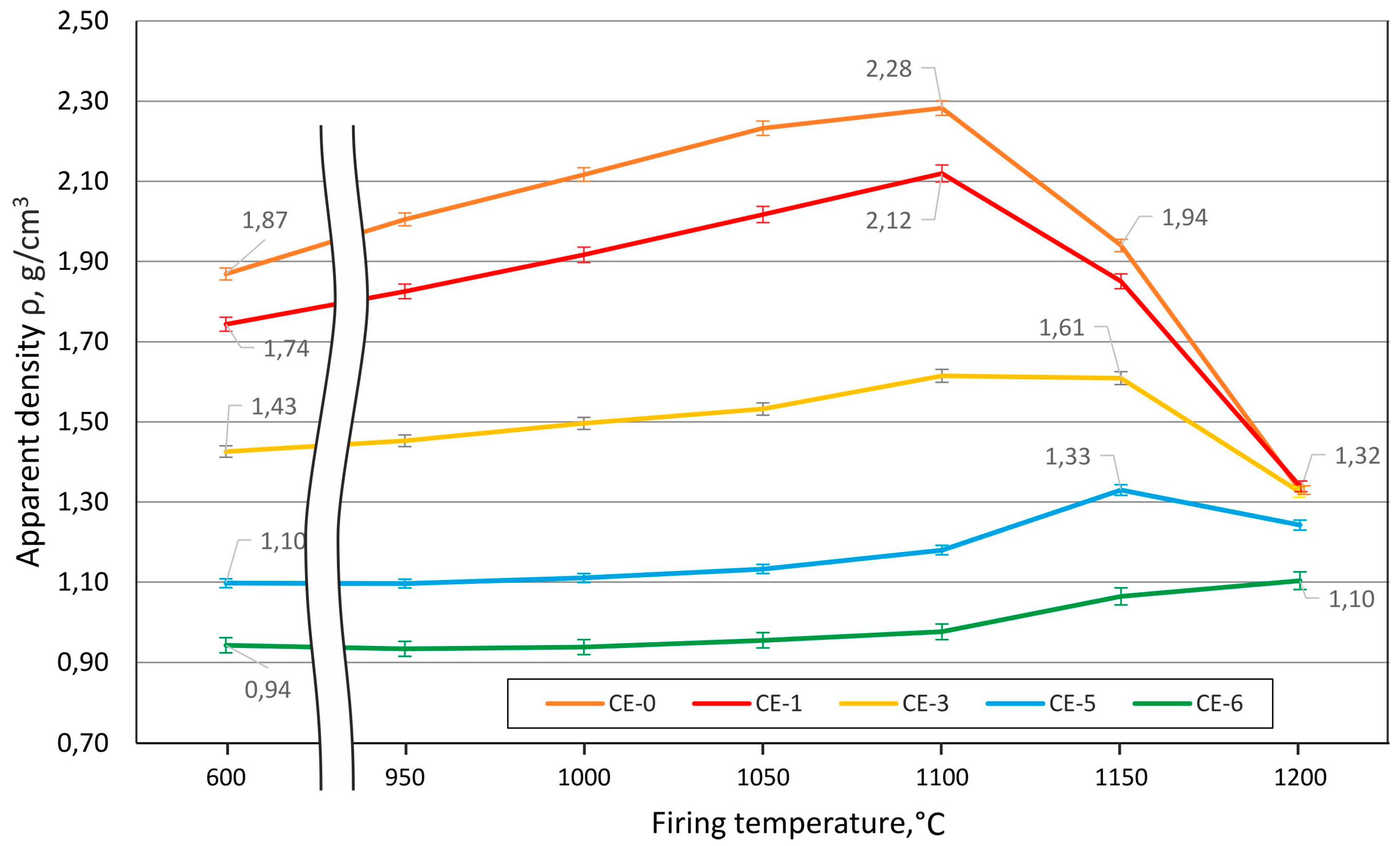
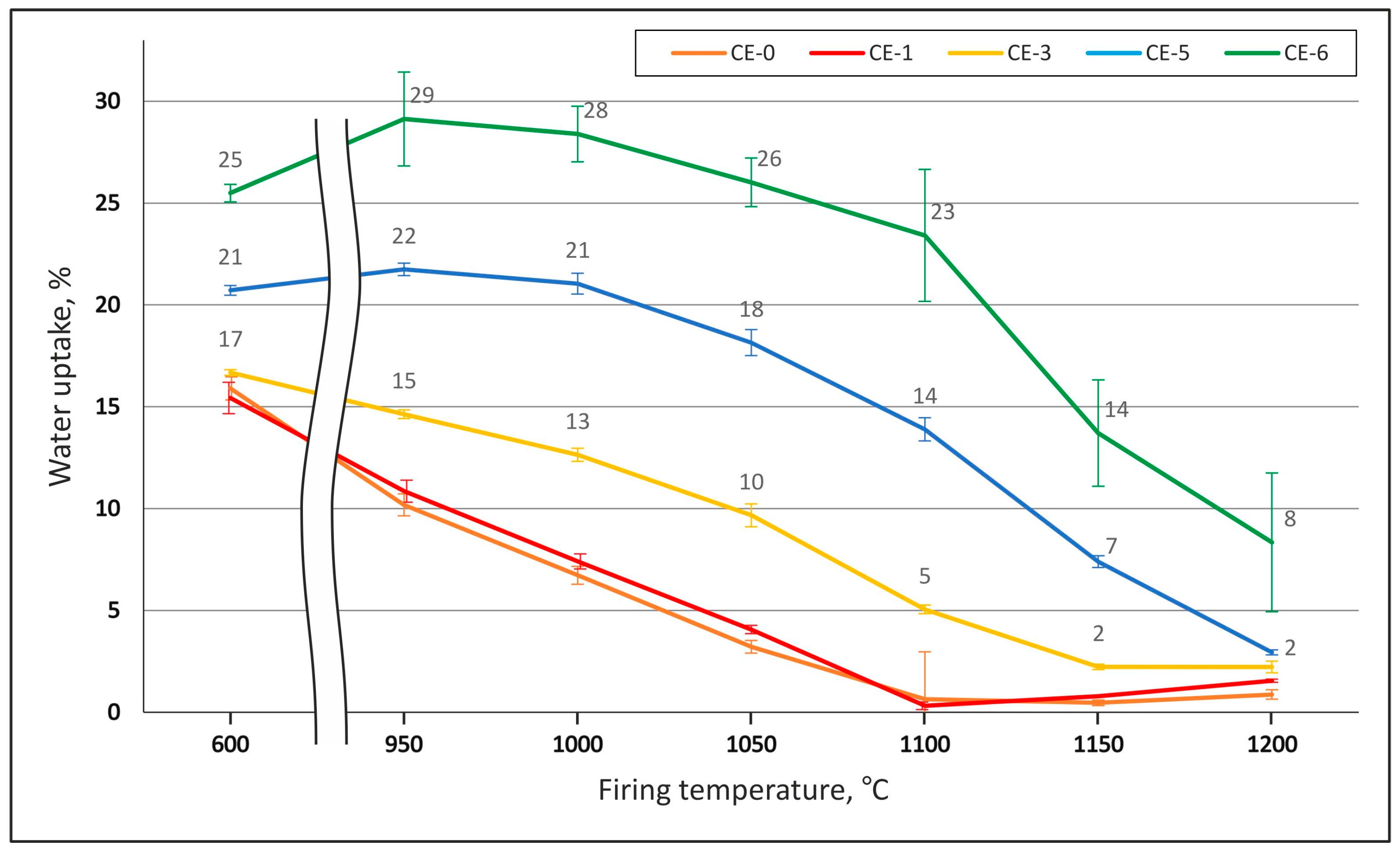
3.3.1. Density and Open vs. Closed Porosity Levels
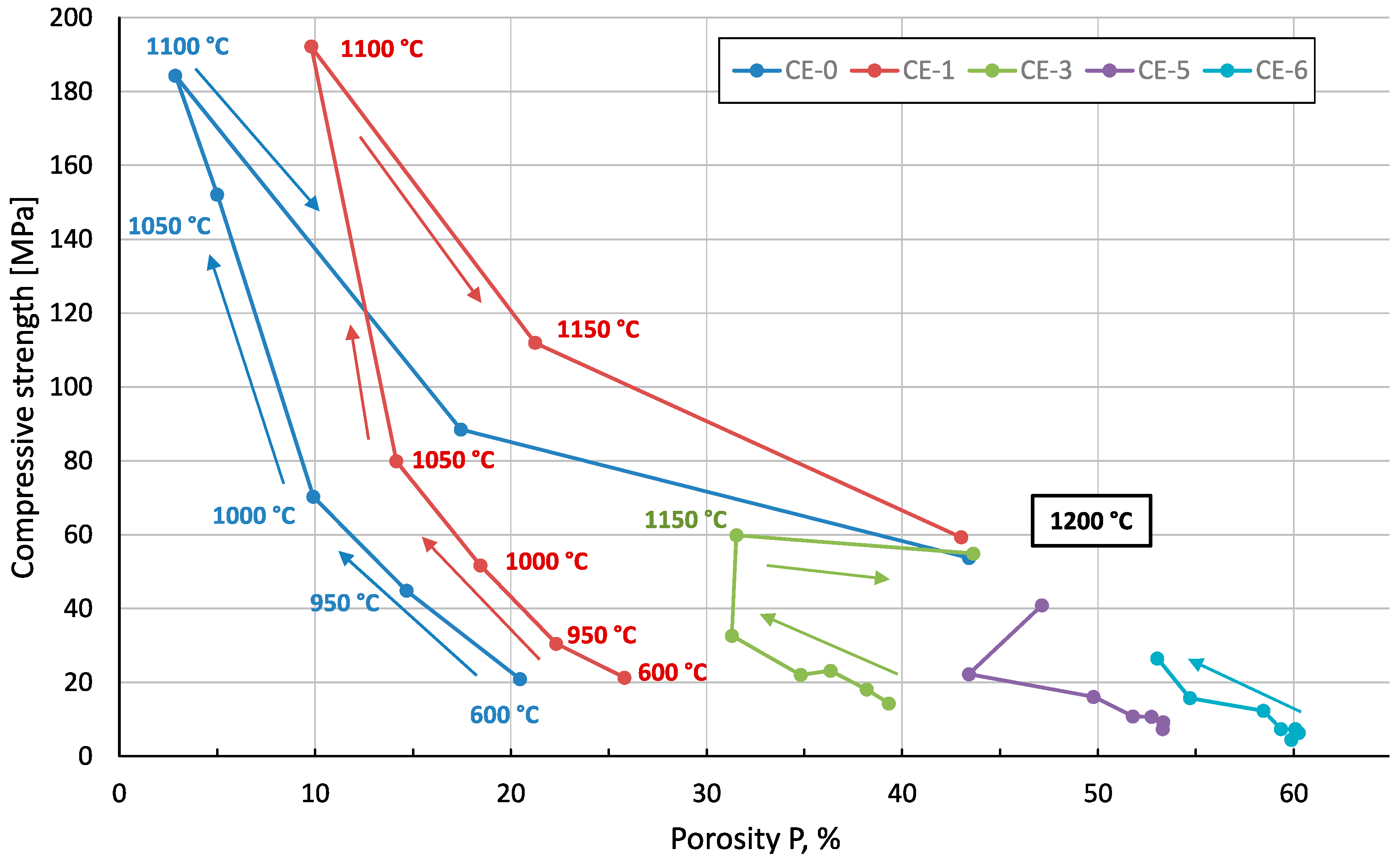
3.3.2. Density and Porosity Levels vs. Compressive Strength
4. Conclusions
- Formation of improved interfaces between cenospheres and matrix and specifically between cenospheres (in this case via the matrix), with the increase of interface area as the main aspect.
- Reduction of internal kerf radii and thus of local stress concentration, with the elimination of potential failure initiation sites as a consequence.
- Formation of mullite crystals originating from the cenospheres and growing into the matrix, with the possible formation of a full mullite framework within the matrix, and as a result strengthening of (a) the cenosphere-matrix interface and (b, potentially) the matrix itself.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Anshits, N.; Mikhailova, O.A.; Salanov, A.N.; Anshits, A.G. Chemical composition and structure of the shell of fly ash non-perforated cenospheres produced from the combustion of the Kuznetsk coal (Russia). Fuel 2010, 89, 1849–1862. [Google Scholar] [CrossRef]
- Ahmaruzzaman, M. A review on the utilization of fly ash. Prog. Energy Combust. Sci. 2010, 36, 327–363. [Google Scholar]
- Deepthi, M.V.; Sharma, M.; Sailaja, R.R.N.; Anantha, P.; Sampathkumaran, P.; Seetharamu, S. Mechanical and thermal characteristics of high density polyethylene–fly cenosphere composites. Mater. Des. 2010, 31, 2051–2060. [Google Scholar] [CrossRef]
- Jha, N.; Mondal, D.P.; Goel, M.D.; Majumdar, J.D.; Das, S.; Modi, O.P. Titanium cenosphere syntactic foam with coarser cenosphere fabricated by powder metallurgy at lower compaction load. Trans. Nonferr. Met. Soc. China 2014, 24, 89–99. [Google Scholar] [CrossRef]
- Bharath Kumar, B.R.; Doddamani, M.; Zeltmann, S.E.; Gupta, N.; Ramesh, M.R.; Ramakrishna, S. Processing of cenosphere/HDPE syntactic foams using an industrial scale polymer injection molding machine. Mater. Des. 2016, 92, 414–423. [Google Scholar]
- Mondal, D.P.; Das, S.; Ramakrishnan, N.; Uday Bhasker, K. Cenosphere filled aluminum syntactic foam made through stir-casting technique. Compos. Part A Appl. Sci. Manuf. 2009, 40, 279–288. [Google Scholar] [CrossRef]
- Wu, G.H.; Dou, Z.Y.; Sun, D.L.; Jiang, L.T.; Ding, B.S.; He, B.F. Compression behaviors of cenosphere—Pure aluminum syntactic foams. Scr. Mater. 2007, 56, 221–224. [Google Scholar]
- Mondal, D.P.; Datta Majumder, J.; Jha, N.; Badkul, A.; Das, S.; Patel, A.; Gupta, G. Titanium-cenosphere syntactic foam made through powder metallurgy route. Mater. Des. 2012, 34, 82–89. [Google Scholar]
- Sanders, W.S.; Gibson, L.J. Mechanics of BCC and FCC hollow-sphere foams. Mater. Sci. Eng. A 2003, 352, 150–161. [Google Scholar] [CrossRef]
- Sanders, W.S.; Gibson, L.J. Mechanics of hollow sphere foams. Mater. Sci. Eng. A 2003, 347, 70–85. [Google Scholar]
- Gupta, N.; Zeltmann, S.E.; Shunmugasamy, V.C.; Pinisetty, D. Applications of polymer matrix syntactic foams. JOM 2013, 66, 245–254. [Google Scholar] [CrossRef]
- Gupta, N.; Maharsia, R. Enhancement of energy absorption in syntactic foams by nanoclay incorporation for sandwich core applications. Appl. Compos. Mater. 2005, 12, 247–261. [Google Scholar] [CrossRef]
- Porfiri, M.; Gupta, N. Effect of volume fraction and wall thickness on the elastic properties of hollow particle filled composites. Compos. Part B Eng. 2009, 40, 166–173. [Google Scholar] [CrossRef]
- Luong, D.; Lehmhus, D.; Gupta, N.; Weise, J.; Bayoumi, M. Structure and compressive properties of invar-cenosphere syntactic foams. Materials 2016, 9, 115. [Google Scholar] [CrossRef]
- Luong, D.D.; Gupta, N.; Daoud, A.; Rohatgi, P.K. High strain rate compressive characterization of aluminum alloy/fly ash cenosphere composites. JOM 2011, 63, 53–56. [Google Scholar]
- Rohatgi, P.K. Thermal expansion of aluminum-fly ash cenosphere composites synthesized by pressure infiltration technique. J. Compos. Mater. 2005, 40, 1163–1174. [Google Scholar] [CrossRef]
- Luong, D.D.; Gupta, N.; Rohatgi, P.K. The high strain rate compressive response of Mg-Al alloy/fly Ash cenosphere composites. JOM 2011, 63, 48–52. [Google Scholar]
- Shishkin, A.; Mironovs, V.; Zemchenkov, V.; Antonov, M.; Hussainova, I. Hybrid syntactic foams of metal—Fly ash cenosphere–clay. Key Eng. Mater. 2016, 674, 35–40. [Google Scholar] [CrossRef]
- Shao, Y.; Jia, D.; Zhou, Y.; Liu, B. Novel method for fabrication of silicon nitride/silicon oxynitride composite ceramic foams using fly ash cenosphere as a pore-forming agent. J. Am. Ceram. Soc. 2008, 91, 3781–3785. [Google Scholar] [CrossRef]
- Wang, C.; Liu, J.; Du, H.; Guo, A. Effect of fly ash cenospheres on the microstructure and properties of silica-based composites. Ceram. Int. 2012, 38, 4395–4400. [Google Scholar] [CrossRef]
- Shao, Y.; Jia, D.; Liu, B. Characterization of porous silicon nitride ceramics by pressureless sintering using fly ash cenosphere as a pore-forming agent. J. Eur. Ceram. Soc. 2009, 29, 1529–1534. [Google Scholar] [CrossRef]
- Baronins, J.; Setina, J.; Sahmenko, G.; Lagzdina, S.; Shishkin, A. Pore distribution and water uptake in a cenosphere-cement paste composite material. IOP Conf. Ser. Mater. Sci. Eng. 2015, 96, 12011. [Google Scholar] [CrossRef]
- Sutcu, M.; Akkurt, S. Utilization of recycled paper processing residues and clay of different sources for the production of porous anorthite ceramics. J. Eur. Ceram. Soc. 2010, 30, 1785–1793. [Google Scholar] [CrossRef]
- Shishkin, A.; Laksa, A.; Shidlovska, V.; Timermane, Z.; Aguedal, H.; Mironovs, V.; Ozolins, J. Illite clay ceramic hollow sphere—Obtaining and properties. Key Eng. Mater. 2016, 721, 316–321. [Google Scholar] [CrossRef]
- Shishkin, A.; Drozdova, M.; Kozlov, V.; Hussainova, I.; Lehmhus, D. Vibration-assisted sputter coating of cenospheres: A new approach for realizing Cu-Based metal matrix syntactic foams. Metals 2017, 7, 16. [Google Scholar] [CrossRef]
- Polykov, A.; Mironovs, V.; Shishkin, A.; Baronins, J. Preparation of Coal-Water Slurries Using a High—Speed Mixer—Disperser. In Proceedings of the 4th International Scientific Conference on Civil Engineering ’13, Jelgava, Latvia, 16–17 May 2013; pp. 77–81. [Google Scholar]
- Sartorius Marketing Weighing Technology. Part 1: Density. In Manual of Weighing Applications; Sartorius: Göttingen, Germany, 1999.
- Ardakani, A.; Yazdani, M. The relation between particle density and static elastic moduli of lightweight expanded clay aggregates. Appl. Clay Sci. 2014, 93–94, 28–34. [Google Scholar] [CrossRef]
- Chandra, S.; Berntsson, L. Lightweight Aggregate Concrete: Science, Technology, and Applications, 1st ed.; William Andrew: Norwick, NY, USA, 2002. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Peroni, L.; Scapin, M.; Avalle, M.; Weise, J.; Lehmhus, D.; Baumeister, J.; Busse, M. Syntactic iron foams—On deformation mechanisms and strain-rate dependence of compressive properties. Adv. Eng. Mater. 2012, 14, 909–918. [Google Scholar] [CrossRef]
- Luong, D.D.; Shunmugasamy, V.C.; Gupta, N.; Lehmhus, D.; Weise, J.; Baumeister, J. FQuasi-static and high strain rates compressive response of iron and Invar matrix syntactic foams. Mater. Des. 2015, 66, 516–531. [Google Scholar] [CrossRef]






| Nr | Comp. | wt % | g·cm−3 | CE-0 | CE-1 | CE-3 | CE-5 | CE-6 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vol % | wt % | vol % | wt % | vol % | wt % | vol % | wt % | vol % | wt % | ||||
| 1 | Clay | - | 2.2 1 | 100.0 | 84.4 | 90.0 | 81.4 | 70.0 | 73.8 | 50.0 | 63.2 | 40.0 | 56.1 |
| 2 | CS | - | 0.74 1 | 0 | 0 | 10.0 | 3.0 | 30.0 | 10.6 | 50.0 | 21.2 | 60.0 | 28.3 |
| 3 | NaOH 6M | 14 | 1.22 2 | - | 11.8 | - | 11.8 | - | 11.8 | - | 11.8 | - | 11.8 |
| 4 | Zusoplast G 72 | 2 | 1.10 2 | - | 1.69 | - | 1.69 | - | 1.69 | - | 1.69 | - | 1.69 |
| 5 | Surfactant | 2 | 1.03 2 | - | 1.69 | - | 1.69 | - | 1.69 | - | 1.69 | - | 1.69 |
| 6 | Dolaflux B 11 | 0.5 | 0.80 3 | - | 0.42 | - | 0.42 | - | 0.42 | - | 0.42 | - | 0.42 |
| Designation | CE-0-1100 | CE-0-1200 | CE-5-1100 | CE-5-1200 | |
|---|---|---|---|---|---|
| CS Content (vol %) | 0 | 0 | 50 | 50 | |
| Firing Temp. (°C) | 1100 | 1200 | 1100 | 1200 | |
| Tangent Modulus (MPa) | no. of samples | 4 | 4 | 4 | 3 |
| min. value | 4019.2 | 1664.2 | 673.4 | 1109,8 | |
| max. value | 5611.4 | 2359.2 | 3957.1 | 2254,5 | |
| average | 4744.9 | 2079.9 | 2078.7 | 1855 | |
| standard deviation | 657.9 | 306.7 | 1392.2 | 515,4 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rugele, K.; Lehmhus, D.; Hussainova, I.; Peculevica, J.; Lisnanskis, M.; Shishkin, A. Effect of Fly-Ash Cenospheres on Properties of Clay-Ceramic Syntactic Foams. Materials 2017, 10, 828. https://doi.org/10.3390/ma10070828
Rugele K, Lehmhus D, Hussainova I, Peculevica J, Lisnanskis M, Shishkin A. Effect of Fly-Ash Cenospheres on Properties of Clay-Ceramic Syntactic Foams. Materials. 2017; 10(7):828. https://doi.org/10.3390/ma10070828
Chicago/Turabian StyleRugele, Kristine, Dirk Lehmhus, Irina Hussainova, Julite Peculevica, Marks Lisnanskis, and Andrei Shishkin. 2017. "Effect of Fly-Ash Cenospheres on Properties of Clay-Ceramic Syntactic Foams" Materials 10, no. 7: 828. https://doi.org/10.3390/ma10070828
APA StyleRugele, K., Lehmhus, D., Hussainova, I., Peculevica, J., Lisnanskis, M., & Shishkin, A. (2017). Effect of Fly-Ash Cenospheres on Properties of Clay-Ceramic Syntactic Foams. Materials, 10(7), 828. https://doi.org/10.3390/ma10070828









