1. Introduction
With improved fatigue and impact performance [
1,
2,
3], metal matrix composites (MMCs) have in the recent past been used toward reducing weights of structural components and parts. For instance, Al-matrix composites with ceramic TiC reinforcing particles exhibit excellent mechanical strength with improved fatigue resistance and creep resistance [
4,
5,
6,
7] and have been used in automobile industry. A detailed review for literature of fatigue of reinforced composites and recent applications may be found in LLorca [
8].
The fatigue behavior of MMCs is known to be mainly responsible for fracture and failure of structural components and parts made of such materials. Toward effectively assessing structural reliability and safety under complex service conditions, rational and realistic modeling of the fatigue failure behavior for MMCs is accordingly essential and has attracted intensive interest in both theoretical and experimental studies.
In the past decades, numerous investigations into fracture and failure of MMCs have been carried out from various standpoints. Details may be found in the survey articles [
9,
10,
11,
12]. Certain representative results for MMCs are as follows. Quast et al. [
13] investigated the out-of-phase thermomechanical fatigue behavior of Ultra SCS-6/Ti-24Al-17Nb-xMo (at.%) MMCs; the fatigue behavior of two 2009/SiC/15p-T4 DRA (discontinuously reinforced aluminum) composites in the very high cycle fatigue was investigated by Huang et al. [
14]; Ni et al. [
15] studied residual stresses and high cycle fatigue properties of friction stir welded SiCp/AA2009 composites; fatigue failure mechanisms of microsphere Al2O3-Al particulate MMCs were determined from examination of the fracture surfaces and the crack profiles by Park et al. [
16]; Sivananth et al. [
7] evaluated the load bearing behavior of titanium carbide reinforced aluminum matrix composites and their suitability for automotive application; Feng et al. [
17] determined the relationship between the applied stress and fatigue life of a SiC fiber-reinforced titanium matrix composite and examined the fracture surfaces to study the fatigue damage and fracture failure mechanisms using SEM; and the creep–fatigue behavior of aluminum alloy-based MMC has been modeled using an idealized plane strain model [
18]. Moreover, many other related studies may be found in [
19,
20,
21,
22,
23,
24,
25].
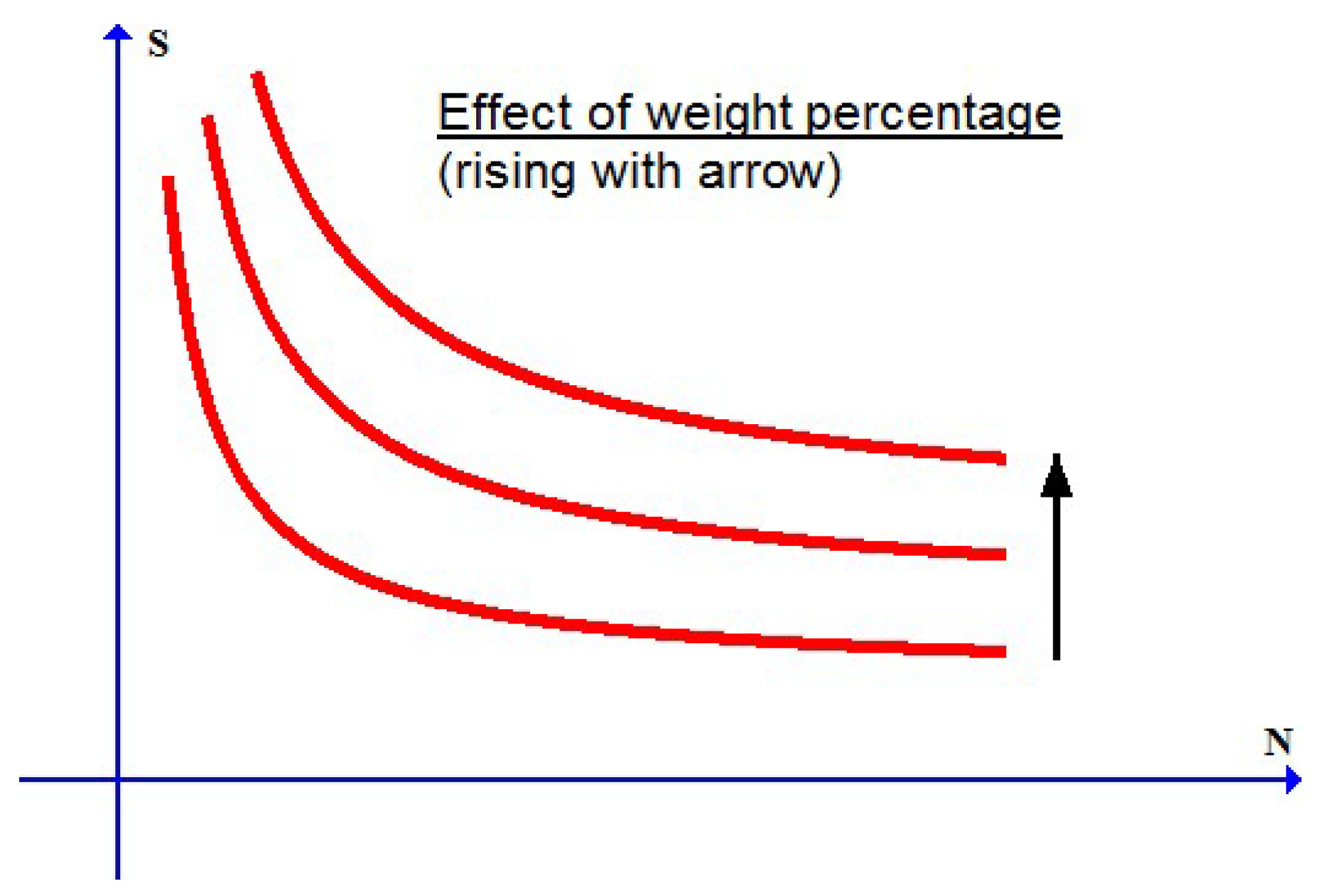
According to usual approaches, however, issues in a few respects have been left outstanding. First, augmented constitutive structures with additional damage-like variables should be assumed from different standpoints [
9,
10,
11,
12] and, second, various ad hoc criteria for fracture and failure, etc. should be introduced on an empirical basis [
9,
10,
11,
12]. Third, because of disparate failure features under low and high cycle conditions, such as the complicated duplex effect, etc., as will be explained in
Section 2, the low and high cycle fatigue failure effects have to be treated, separately, and it does not appear that a unified simulation of both effects is currently available. In particular, fatigue failure effects of MMCs should be simulated individually for various cases of the weight percentage of reinforcing particles.
In a most recent study [
26,
27], it has been demonstrated that a new, direct approach may be proposed toward modeling fatigue, fracture and failure effects of metals, etc. Toward this objective, the central idea is to establish new elastoplasticity models into which the fatigue failure behavior is incorporated as inherent constitutive features. With such new models, it has been shown [
26,
27] that the usual notion of yielding becomes irrelevant with a gradual, smooth transition from the elastic to the plastic state in a more realistic sense. As a result, the fatigue failure behavior may be automatically derived as a direct consequence of certain simple asymptotic properties of the strength quantities incorporated.
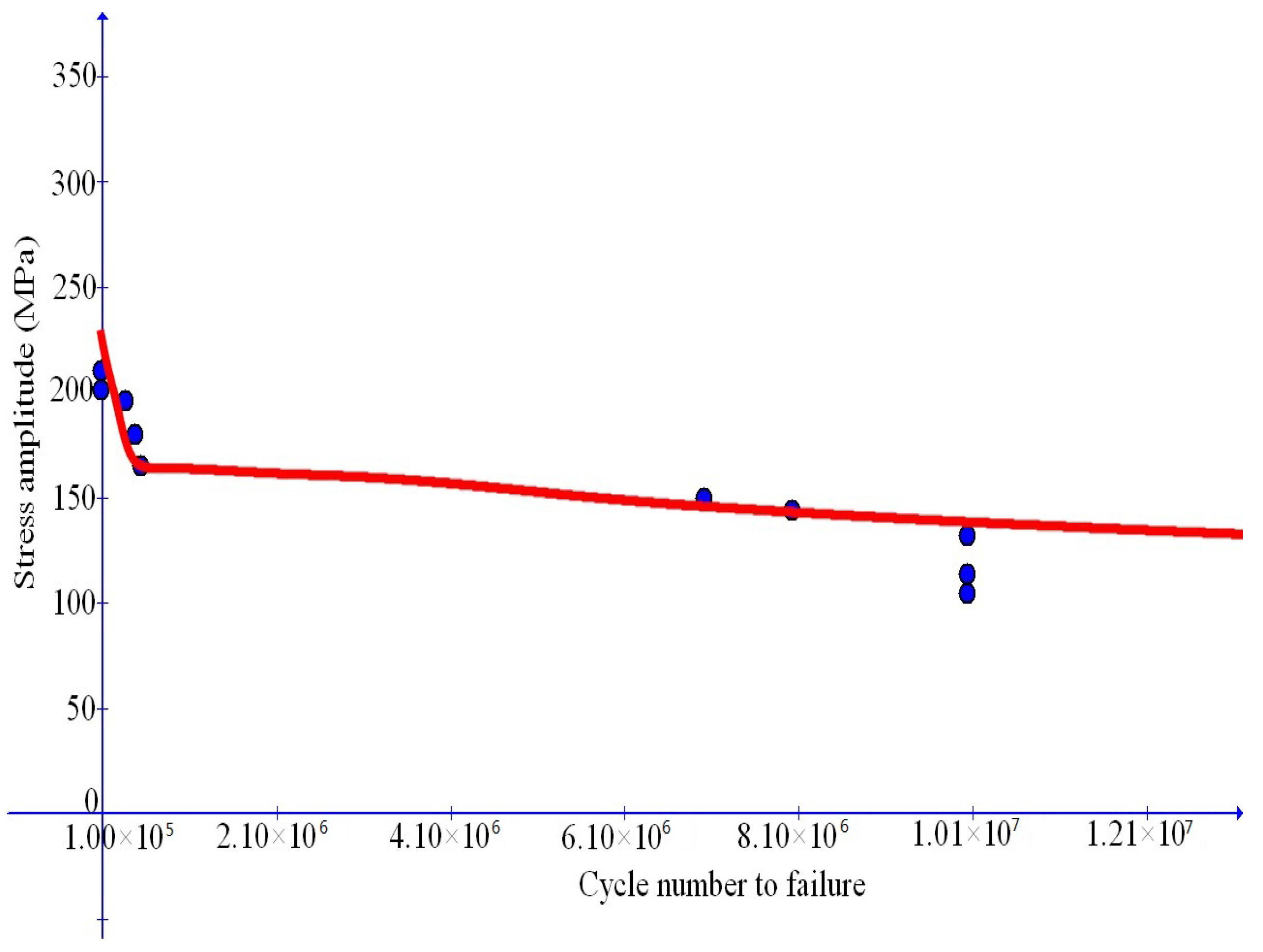
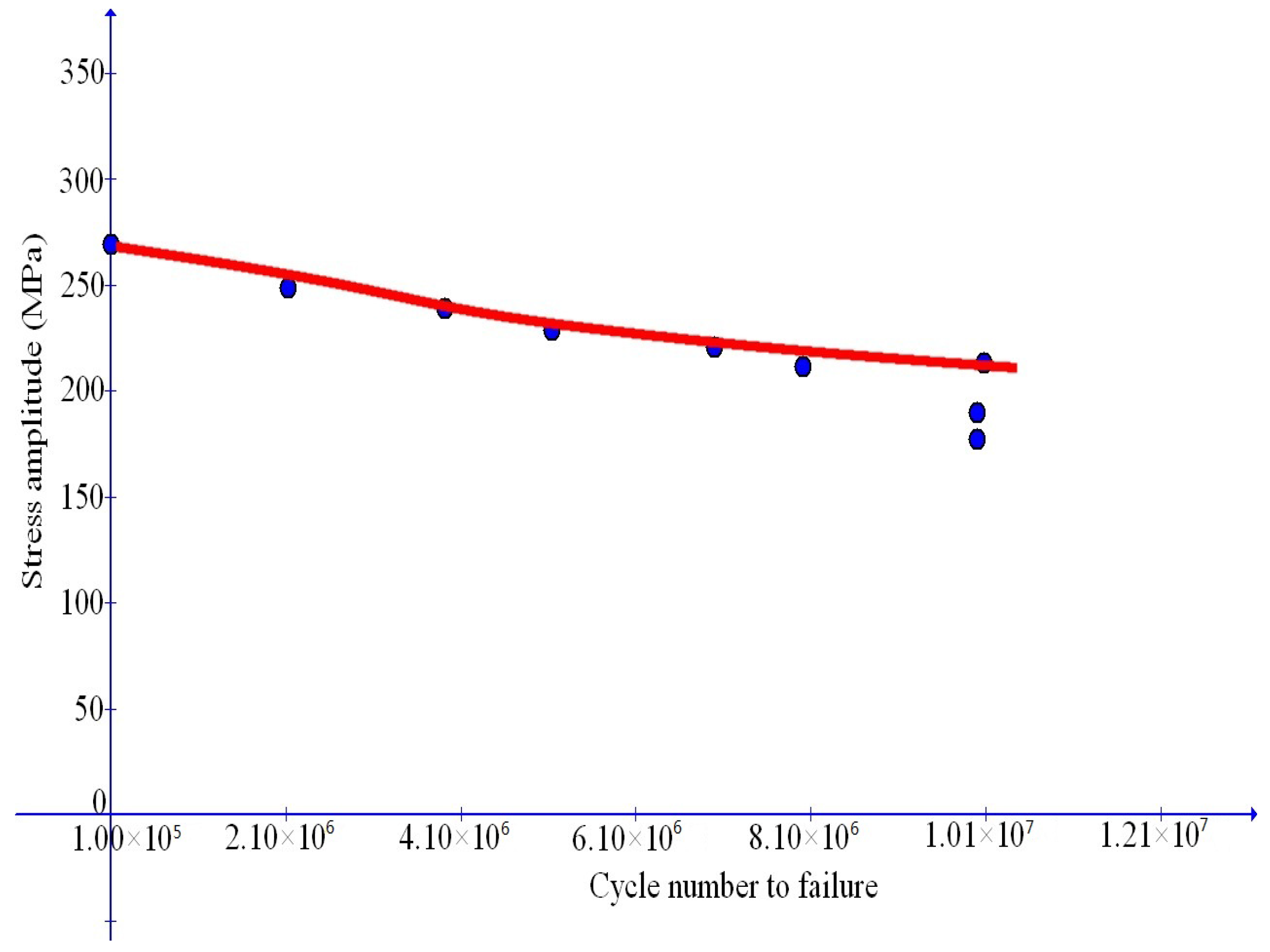
In this article, new elastoplastic -flow constitutive equations at finite deformations in the general framework of the most recent study above will be proposed for the purpose of simulating the fatigue failure behavior for MMCs. A new, direct approach will be established in a two-fold sense of unification. Namely, both low and high cycle fatigue failure behaviors of MMCs may be simultaneously simulated for various cases of the weight percentage of reinforcing particles. Novel results will be presented in four respects. First, both the yield condition and the loading–unloading conditions in a usual sense need not be involved but may be automatically incorporated into inherent features of the proposed constitutive equations; second, low-to-high cycle fatigue behaviors may be directly represented by a simple condition for asymptotic loss of the material strength, without involving any additional damage-like variables; third, both high and low cycle fatigue failure effects need not be separately treated but may be automatically derived as model predictions with a unified criterion for critical failure states, without assuming any ad hoc failure criteria; and, finally, explicit expressions for each incorporated model parameter changing with the weight percentage of reinforcing particles may be obtainable directly from appropriate test data. Numerical examples will be presented for medium-to-high cycle fatigue effects and for complicated duplex effects from low to high cycle fatigue failure effects and will be compared with test data.
The main content of this contribution is arranged as follows. In
Section 2, certain main concepts on the fatigue failure for MMCs are introduced for the purpose of motivating the succeeding development and, in
Section 3, a new elastoplastic
-flow model will be proposed in the aforementioned novel sense; thermodynamic consistency of this new model will be demonstrated in explicit, identical sense in
Section 4; in
Section 5, a failure criterion in unified form will be derived from the proposed model; predictions of the proposed model under uniaxial cyclic loadings up to failure will be then studied and numerical examples will be presented and compared with test data in
Section 6; and, finally, some remarks will be given in
Section 7.
3. Innovative Elastoplastic -Flow Model for MMCs
Consider an elastoplastic body undergoing finite deformations. Let
F and
L be the deformation gradient and the velocity gradient and, moreover, let
,
W and
D be the Kirchhoff stress, the vorticity tensor and the stretching tensor, namely,
where
and
J are the Cauchy stress (true stress) and the volumetric ratio, respectively.
In the past decades, various formulations of finite elastoplastic deformations have been developed (cf., e.g., [
28]). In what follows, we direct attention to the self-consistent objective Eulerian rate-type formulation [
29,
30,
31,
32,
33] based on the following additive separation of the strechting
D:
with the elastic part and the plastic part . These two parts should be formulated by two Eulerian objective rate equations and will be given in two steps below, separately.
3.1. Elastic Rate Equation
A Eulerian elastic rate equation is given at the first step in the following self-consistent sense: prior to the initial yielding with
, it is exactly integrable to really deliver a finite hyperelastic relation. For MMCs with small elastic strain, by extending the rate form of the well-known Hooke’s law, a self-consistent elastic rate formulation may be given below [
29,
30,
31,
32,
33]:
In the above,
and
G are the Poisson ratio and the shear modulus and, moreover,
is the co-rotational logarithmic rate of the Kirchhoff stress
below:
with the logarithmic spin
where
, ⋯,
and
, ⋯,
are the
n distinct eigenvalues of the left Cauchy–Green tensor
and the corresponding eigenprojections of
B, respectively. Details may be found in [
34].
3.2. New Flow Rule
A flow rule for the plastic part
is given at the next step. To this end, the normality flow rule of the following form is used (cf., e.g., [
35,
36]):
where the plastic indicator
, the yield function
f, and the loading factor
are explained and given below.
According to the classical theory of elastoplasticity, the plastic indicator
in Equation (
5) is assumed to be given by the idealized approximation below: no plastic deformation would be induced prior to yielding, whereas plastic deformation would be induced only in the case when yielding is attained and maintained. Specifically,
for the unloading case and
for the loading case (refer to, e.g., [
35] for details).
As explained in [
26,
37], each usual elastoplasticity model with the plastic indicator
prescribed above could not simulate fatigue failure effects under cyclic loading conditions. This may particularly be the case for the so-called high cycle fatigue failure with the stress amplitude far below the initial yield limit. Instead of assuming the above plastic indicator
in a sense of idealized approximation, a new plastic indicator
may be introduced in a more realistic sense below. Namely, the plastic deformation may be induced at any stress level with a continuously changing plastic indicator
, which becomes close to 0 for the stress point staying far away from the yield surface
and close to 1 for the stress point staying in the vicinity of the yield surface
.
With the above idea in mind, we may introduce a more realistic plastic indicator
as follows:
where
,
,
and
are positive material parameters, the
is the deviatoric part of
, and the
q is known as the stress limit and will be given in Equation (
9) later on. The meanings of these parameters will be explained slightly later.
With the new plastic indicator
given in Equation (
6), a new flow rule may be given as follows [
26,
37,
38,
39]:
In the above, the
f is the von Mises function of the form:
with the stress limit of the form below [
39]:
In the above,
,
, and
are positive material parameters and the
is the plastic work prescribed by
In addition, the loading factor
in the flow rule Equation (
7) is given by
with
3.3. New -Flow Model
The new
-flow model is obtained by combining Equations (
1) and (
2) and Equations (
7)–(
13), as given below:
where the plastic indicator
and the stress limit
q are given by Equations (
6) and (
9), respectively.
The new elastoplastic
-flow model proposed above is fully free in a sense without involving the yield condition as well as the loading–unloading conditions. The new model gives rise to plastic flow at any non-zero stress level whenever
. Whenever the stress reaches such a level that the yield limit in classical sense is met, plastic strain will become dominant. Otherwise, it may be negligibly small for a stress level within the yield limit. Consequences implied by the new model may be found in [
26,
27,
37].
As explained in [
26,
27,
37], fatigue failure effects may be automatically incorporated as inherent constitutive features of the new model. Here, the essential point lies in the fact that, from a phenomenological standpoint, the physical essence of material failure would be just loss of the stress-bearing capacity attendant with fully developed plastic flow. The conditions expressing this fact have been presented in [
26] in a general constitutive framework. The plastic indicator
and the stress limit
q given in Equations (
6) and (
9) are just particular forms meeting these general conditions.
In the above, the plastic factor
ensures accumulation of the plastic work at any stress level and, accordingly, it plays an essential role in characterizing the fatigue failure under both low and high cycle conditions. As such, the new elastoplastic model established can automatically simulate fatigue failure behavior without any additional variables and related equations and conditions. In fact, a unified criterion for critical failure states will be derived as a direct consequence, as will be shown in
Section 5. Detail in this respect may be found in [
26,
27] and in
Section 5.
It should be pointed out that the stress limit
q given in Equation (
9) is taken from the previous study [
37], whereas the plastic indicator
given in Equation (
6) is new and includes the following form:
as a particular case with
. The above form has been used (cf., [
39]) in simulating certain aspects of the fatigue failure for metals. The new plastic indicator as given in Equation (
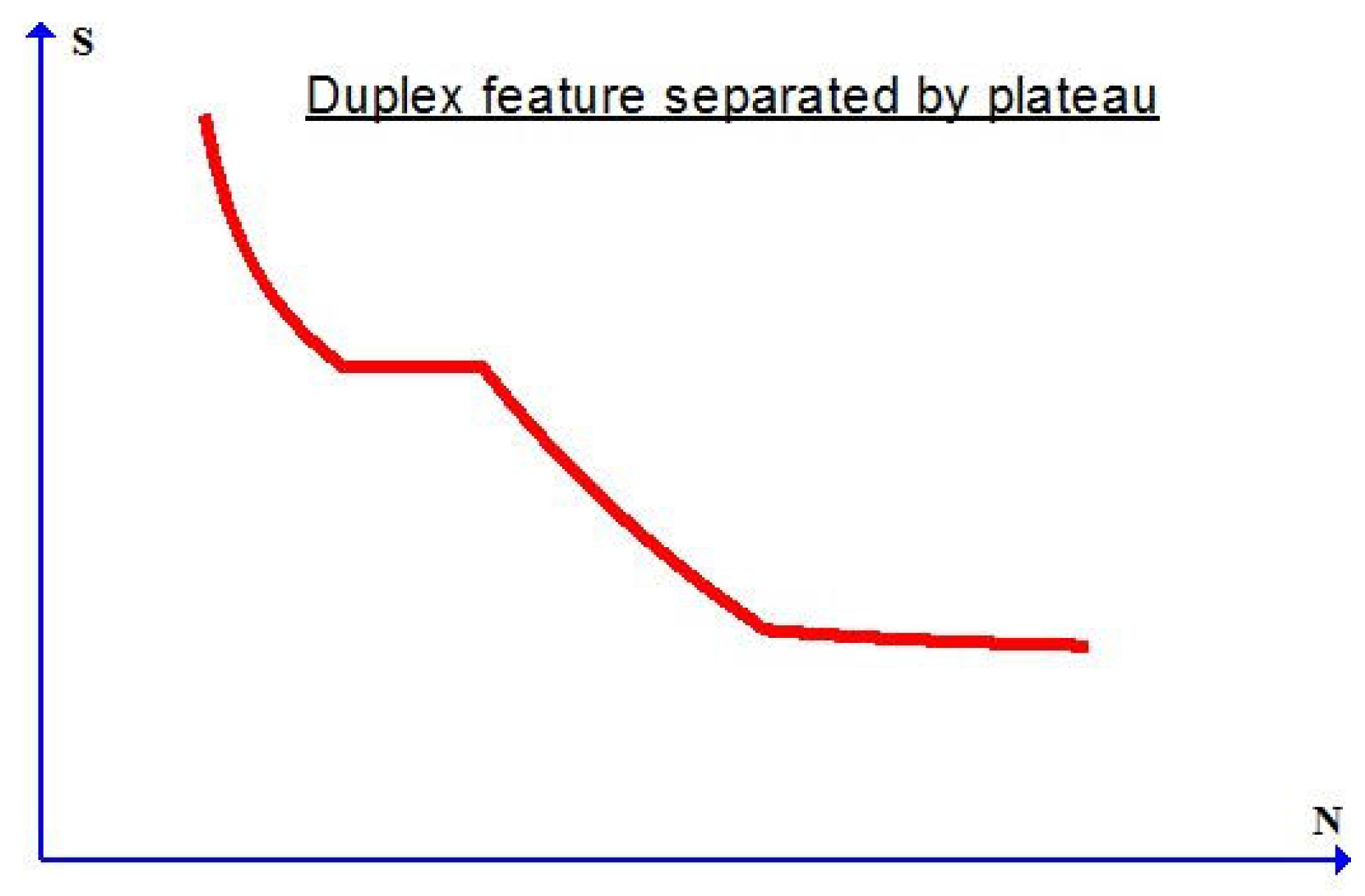
6) is essential for a unified simulation of low-to-high cycle fatigue failure effects with the duplex feature indicated in
Figure 2.
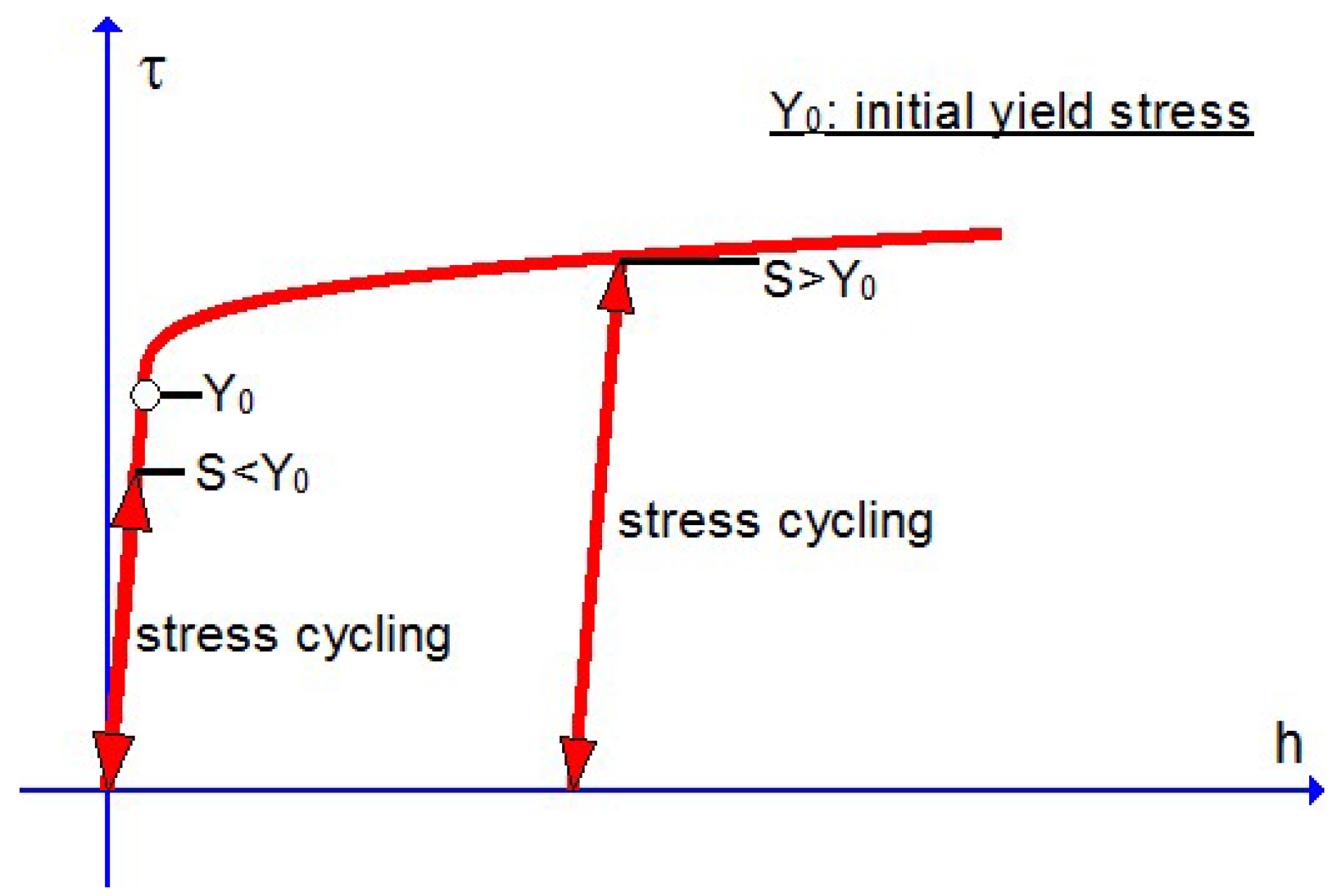
As indicated in the last subsection, fatigue effects under cyclic loadings could not be simulated by the usual
-flow model with the classical plastic indicator taking values 0 or 1, but may be automatically simulated by the new
-flow model with a new plastic indicator. Toward highlighting this difference, the responses of the usual and the new model under the uniaxial stress cycling from 0 to
S and then back to 0 are shown in
Figure 3,
Figure 4 and
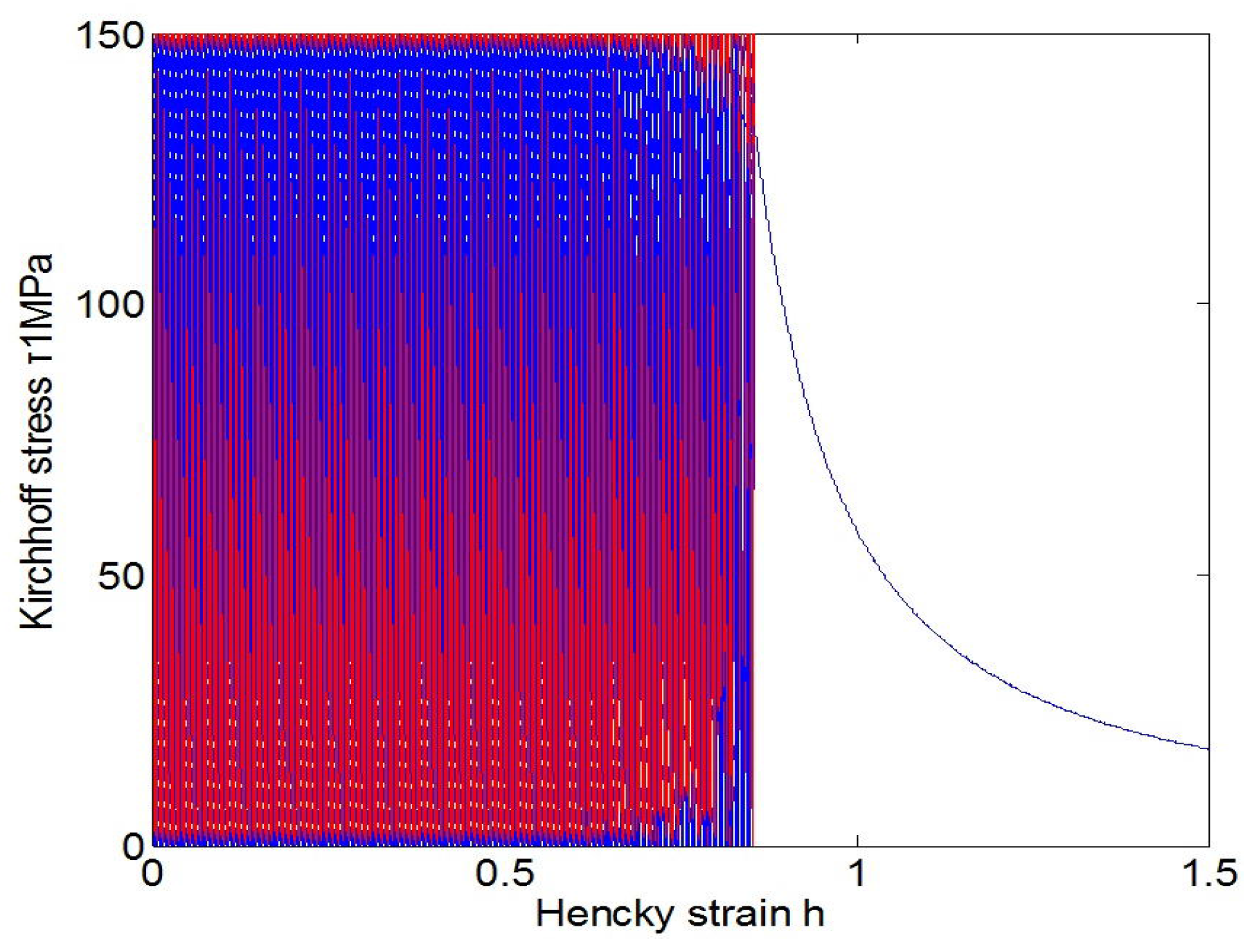
Figure 5, separately. Under the stress cycling at issue, the usual model with the classical plastic indicator could predict no fatigue effects, let alone the eventual failure, whereas the new model may automatically predict the ratcheting effect up to the eventual failure, with no assumed failure criteria associated with any additional damage-like variables.
3.4. Physical Meanings of the Material Parameters
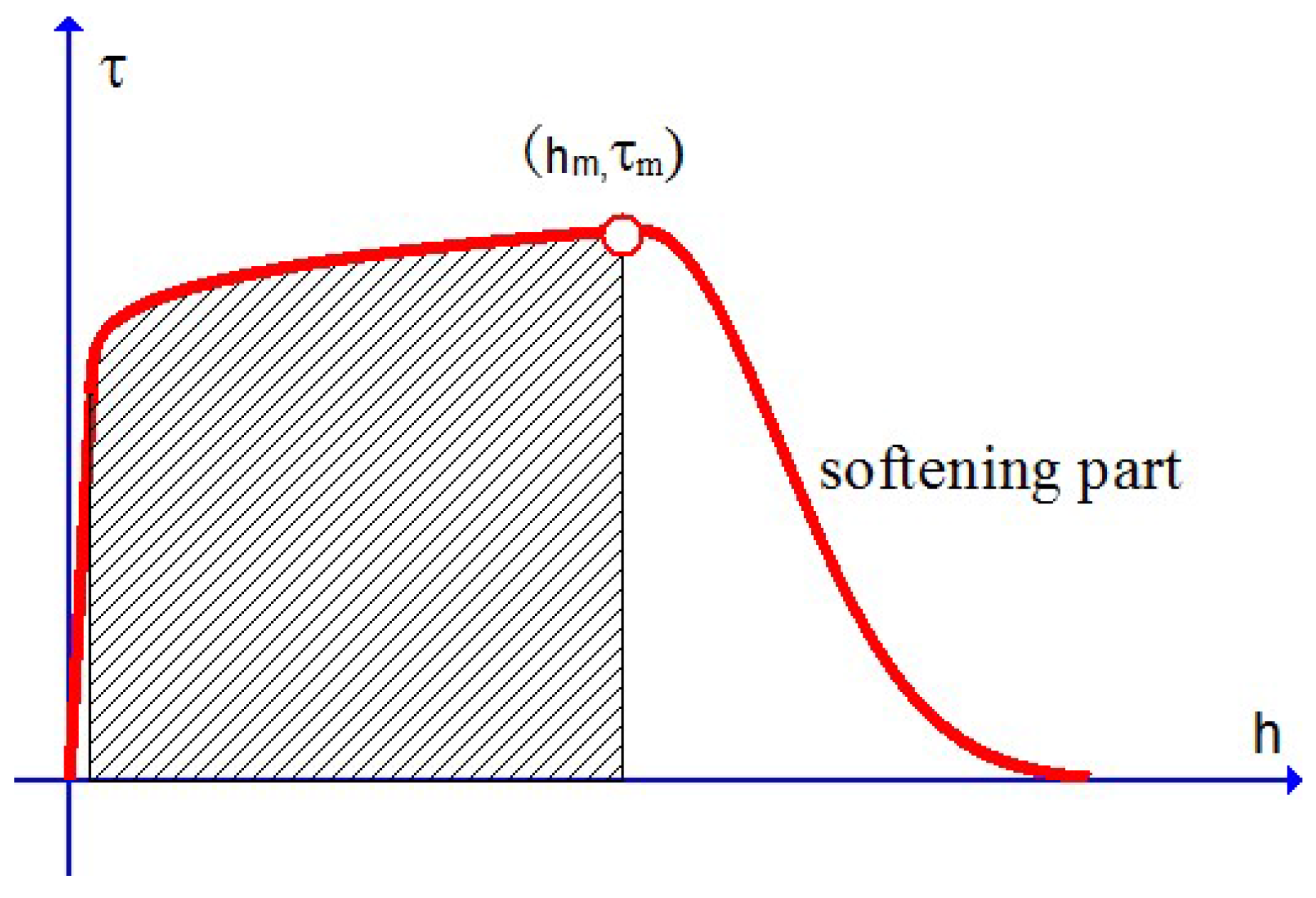
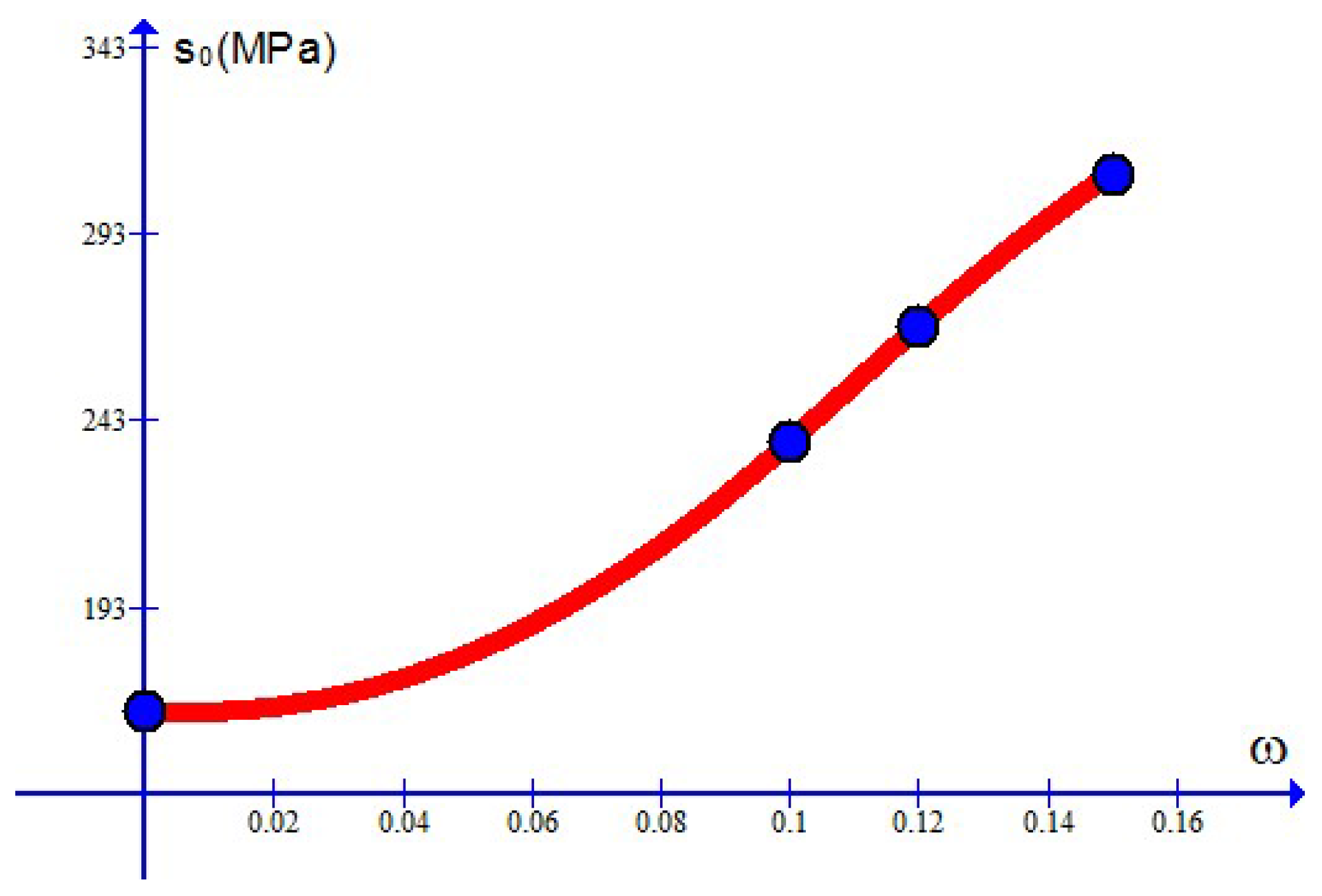
The main feature of the stress limit
q given by Equation (
9) is as follows: for a fairly large
, the stress limit
q actually yield a constant value,
, before the plastic work
reaches a critical value slightly greater than
. After the plastic work
reaches the critical value
, the stress limit goes rapidly down to vanish with softening effect up to eventual failure. The dimensionless parameter
is referred to as the softening index of the following property: the greater the
is, the more rapidly the stress limit
q goes down to vanish. All these three parameters may be evaluated with a uniaxial tensile curve with softening effect, as illustrated in
Figure 6.
The parameter
in the plastic indicator Equation (
6) is referred to as the plastic index, which specifies the magnitude of plastic strain induced at each stress level. The parameters
and
in Equation (
6) control the magnitude of plastic strain as the stress amplitude is above or below
. On the other side, the parameter
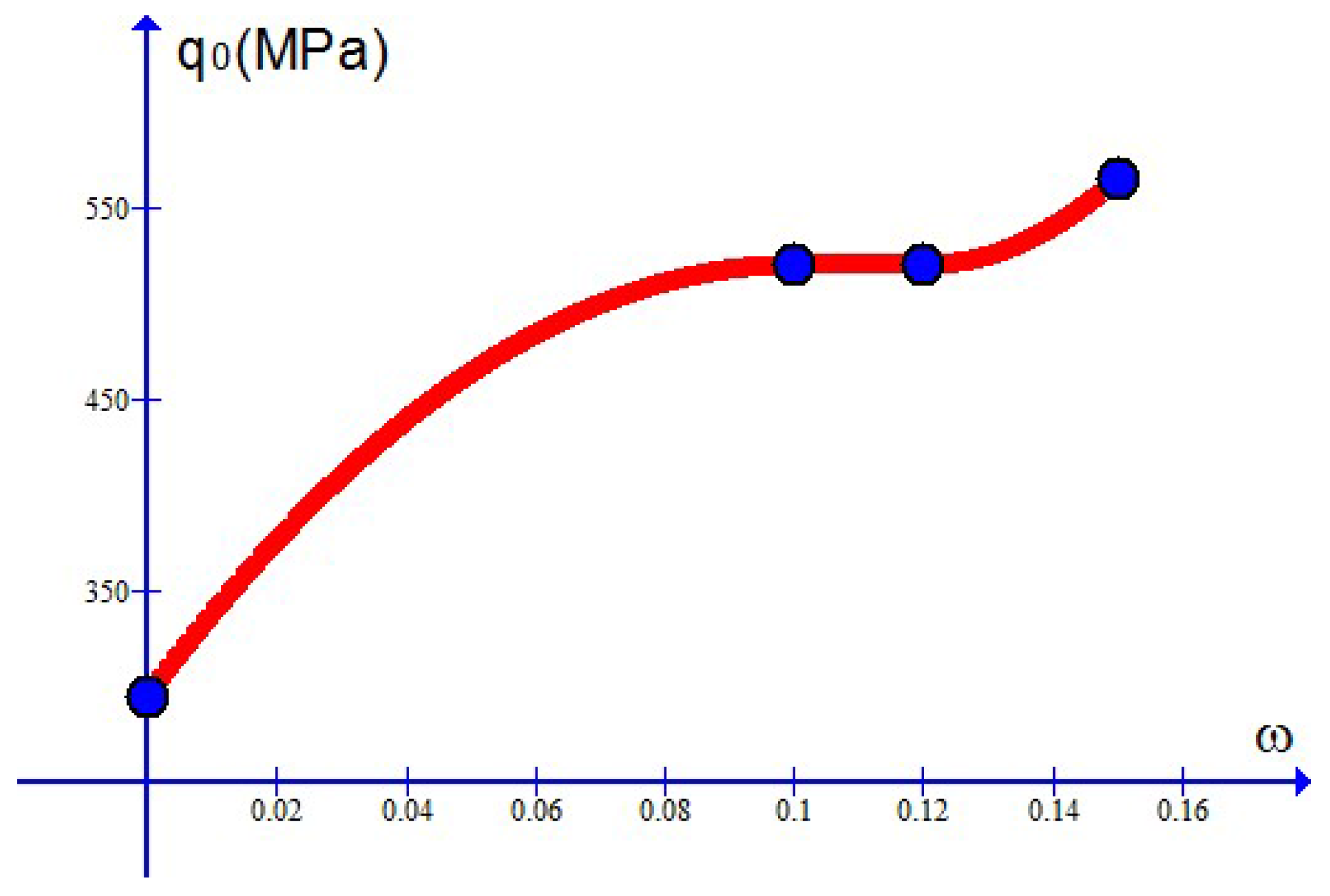
represents stress level at which the pleteau part in
Figure 2 locates and is called the plateau stress. In addition, the parameter
controls the slope of the plateau part and is referred to as the transition index.
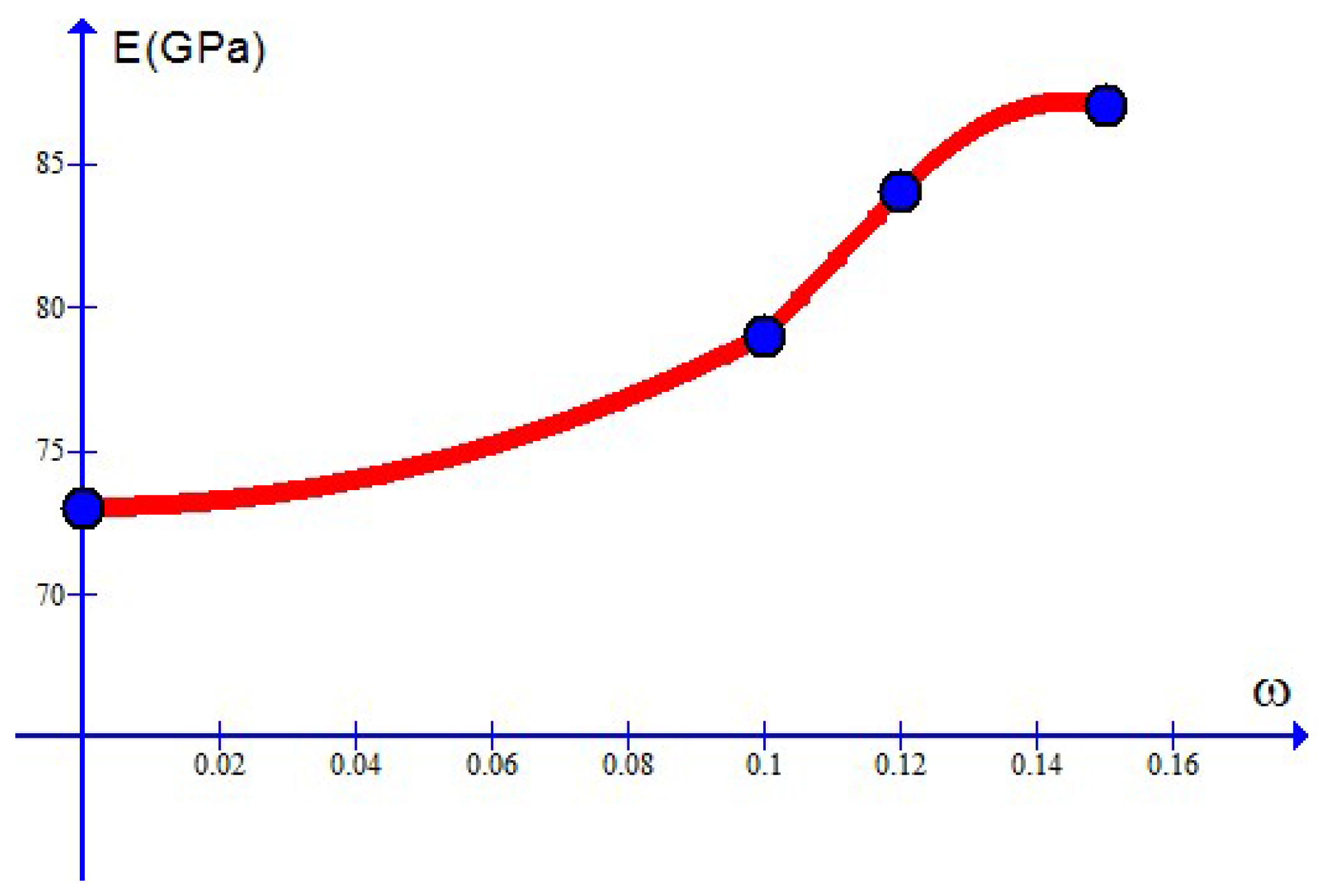
In what follows, it will be demonstrated that the fatigue failure behavior of MMCs with the main features indicated in the last section may be in a unified manner simulated by the new
-flow model by finding out suitable values of the above material parameters and the elastic constants
and
. Toward this objective, it should be noted that each parameter introduced will rely on the weight percentage of reinforcing particles. Let this weight percentage be designated by
. Then,
As will be shown in
Section 6, the above parameters changing with the weight percentage
may be determined from suitable test data by means of direct procedures.
4. Thermodynamic Consistency of the New Model
Since fatigue failure effects are always associated with strong dissipation, it may be essential that a constitutive model simulating such effects should be placed on the rigorous thermodynamic ground, in order to guarantee the physical reality and reasonableness. On account of this, in this section, we are going to demonstrate that the new model proposed in the last section identically meets the universal restrictions imposed by the thermodynamic laws. To this end, following the main procedures in [
33,
38], we demonstrate that the specific entropy function and the free energy function, here denoted
and
, may be presented in explicit forms, so that the second law with non-negative intrinsic dissipation, viz., the Clausius–Duhem inequality below [
33,
38]:
is fulfilled for any given forms of the constitutive quantities incorporated in the proposed model. In the above,
is the absolute temperature,
is the heat flux vector and
J is the deformation Jacobian.
With a positive function
monotonically increasing with increasing plastic work
, i.e.,
we construct the following forms of the specific entropy and the Helmholtz free energy:
where the temperature-dependent quantity
represents the specific heat capacity and the
is the complementary elastic strain-energy function of quadratic form below:
with Young’s modulus
(here, both
E and
G are allowed to be temperature-dependent in a broad sense). Then, it follows from Equations (
1), (
2), (
7), (
10) and Equations (
18)–(
21) that the intrinsic dissipation
is given by
Thus, from the above and the fact that the heat flux
should be opposed to the temperature gradient, namely,
we deduce that the Clausius–Duhem inequality Equation (
18) is identically fulfilled.
Thus, we come to the conclusion that the proposed model is thermodynamically consistent for any given forms of the plastic indicator and the stress limit q.
5. Unified Criterion for Critical Failure States
The main objective of this section is to derive a unified criterion for fatigue failure effects from the new model proposed. Toward the above objective, we reformulate the loading factor
(cf., Equation (
11)) in terms of the strain rate (stretching)
D, as given by Equations (
11)–(
13), in an other form in terms of the stress rate
. With
, this will be done as follows.
First, from Equations (
7) and (
8) and Equations (
10)–(
13) with
we deduce
and
where the
and
are given by Equations (
12) and (
13) and, moreover, the
is given by
Then, we obtain
Now, it becomes clear that, for each non-vanishing stress rate, the plastic work
may grow at an infinite rate whenever the denominator in Equation (
28) becomes vanishing, namely,
As the plastic work invariably accumulates, the above condition will be satisfied and a critical failure state is reached. Immediately following such a state, the plastic work
will exceed the critical value
and the stress limit
q (cf., Equation (
9)) will go rapidly down to vanish with further development of plastic flow. Then, eventual failure follows.
It may be worthwhile to note that the criterion Equation (
29) is derived in a broad sense for every process of multi-axial deformations. With the above understanding, the usually known fatigue failure effect under cyclic loading conditions becomes evident. Indeed, according to the new model proposed, plastic strain will be induced at every non-vanishing stress level, albeit very small, and, accordingly, the plastic work
will constantly grow as a loading cycle repeats itself. As such, the criterion Equation (
29) will be met and a critical failure state in the foregoing will be reached, thus leading to eventual failure.
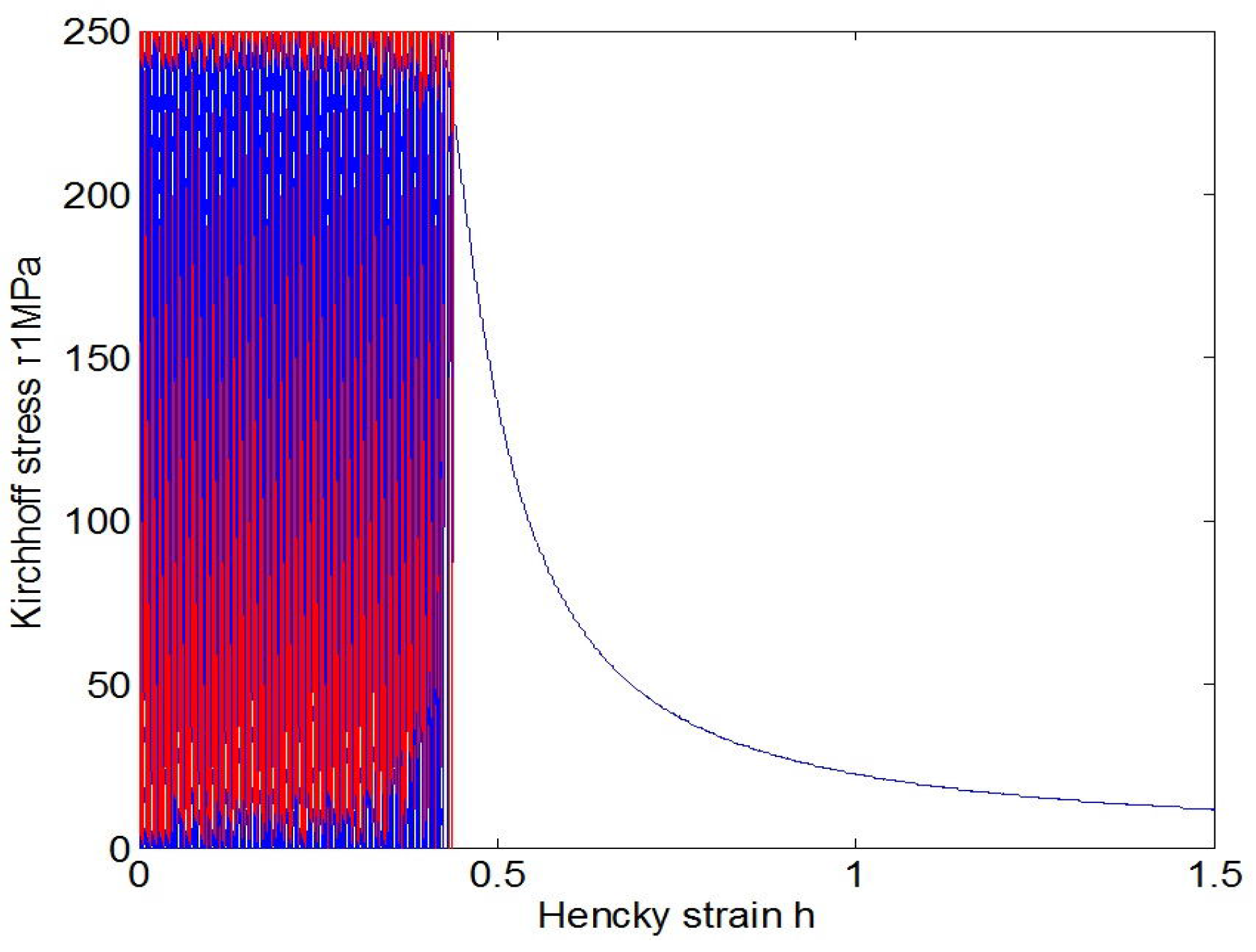
The above facts are evidenced in
Figure 4 and
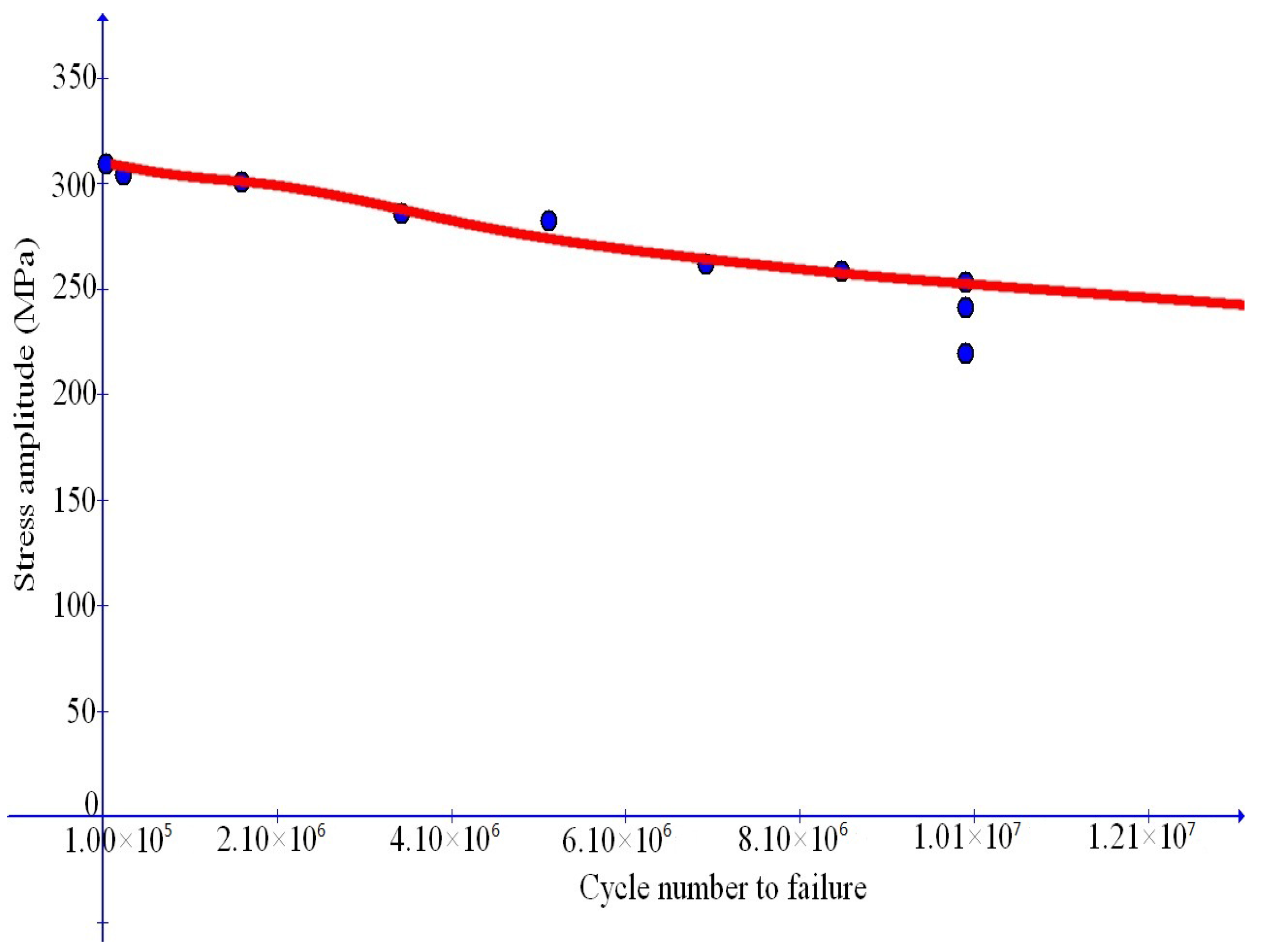
Figure 5. Under the stress cycling in these figures, the critical failure states are reached after 4032 cycles for the stress amplitude 250 MPa and after 40,746 cycles for the stress amplitude 150 MPa, separately, and then the eventual failure follows in both cases of low and high cycle fatigue .
A direct, unified approach toward simulating fatigue failure effects may be established based on the proposed new model with the unified criterion Equation (
29). In particular, low and high cycle fatigue failure effects may be simultaneously simulated, as will be shown in the numerical examples given in the next section.
7. Conclusions
In the previous sections, new elastoplastic -flow equations have been proposed for the purpose of achieving a direct, unified simulation of fatigue failure effects for MMCs. A unified criterion for critical failure states has been derived as model prediction, which is applicable to all cases of multiaxial fatigue failure. Numerical examples for model validation have been presented separately for medium-to-high cycle fatigue failure effects and for low-to-high cycle fatigue failure effects with complex duplex feature. It has been demonstrated that simulation results are in good agreement with experimental data.
As indicated in
Section 4, the new approach proposed is applicable for simulating fatigue failure effects in a broad case of general multi-axial deformations. Here, simulation results are given for the uniaxial case and compared with test data under uniaxial cyclic loadings. Further study will be needed to compare model predictions with test data for fatigue failure effects under various types of multi-axial cyclic and non-cyclic loadings and to treat deformation modes with rotational effects, such as simple shear and torsion, etc. In particular, non-uniform deformations and stresses need be treated for fatigue failure effects displaying in realistic components made of MMCs. For such realistic problems, it is expected that finite element modeling should be used together with the new model proposed here.
Moreover, it may be of interest to simulate fatigue failure effects for fiber-reinforced composite materials and for polymeric solids. Initial anisotropies need be treated for the former, while appreciable rate-dependent effects should be considered for the latter. It is expected that, in conjunction with the previous work for initially anisotropic elastoplastic solids [
33] and for rate-dependent elastoplastic models of soft solids [
38], the approach proposed here may be extended to study these further aspects. Results will be reported elsewhere.