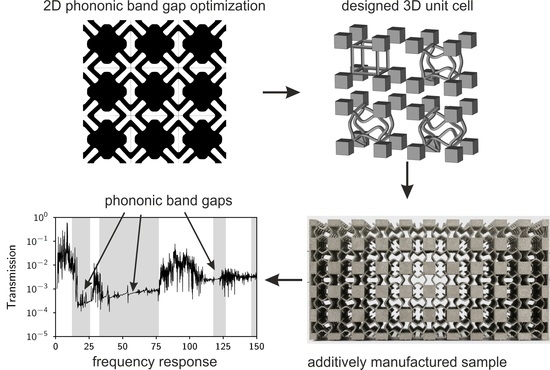
Design and Additive Manufacturing of 3D Phononic Band Gap Structures Based on Gradient Based Optimization
Abstract
:1. Introduction
2. Methods
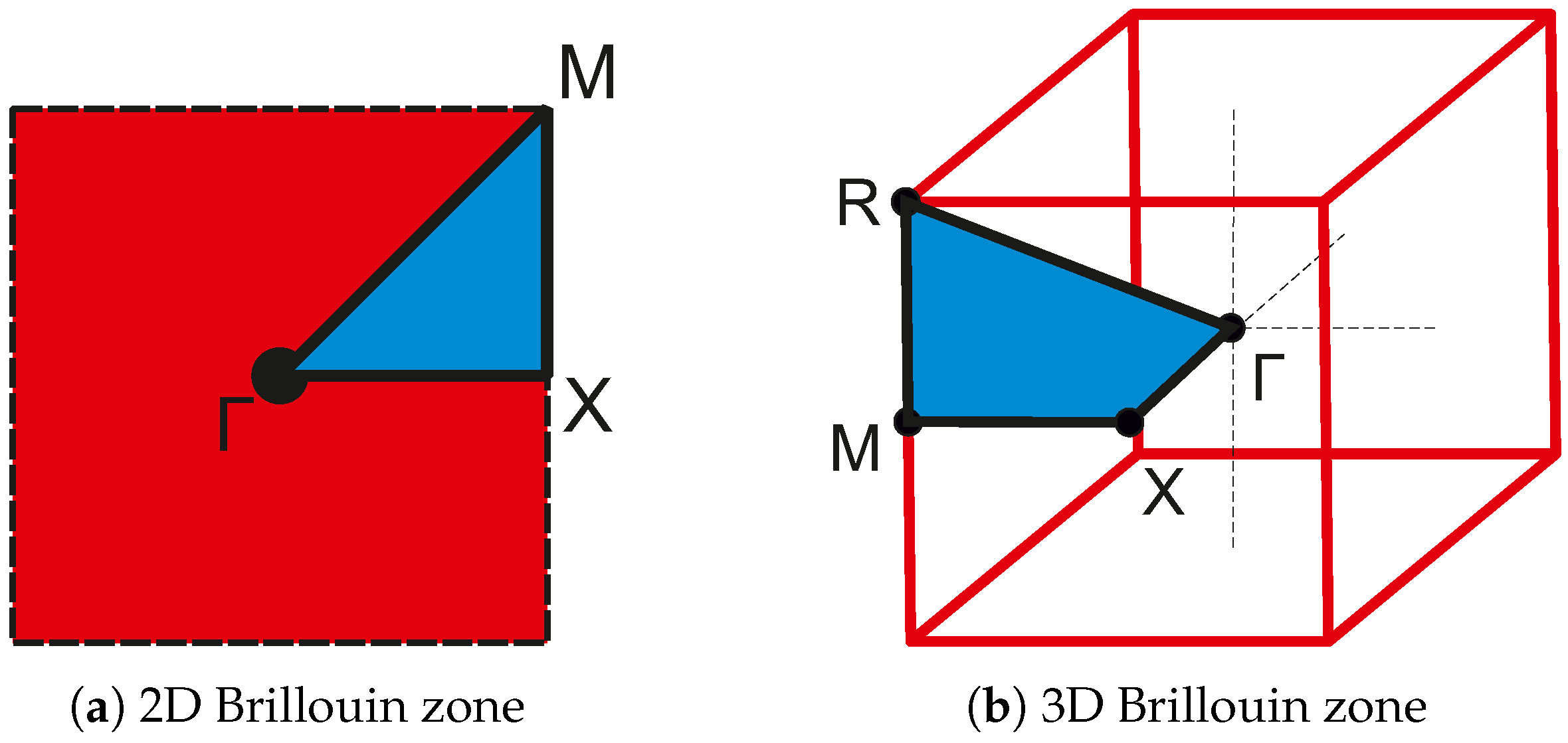
2.1. Dispersion Relation
2.2. Gradient Based Structural Optimization
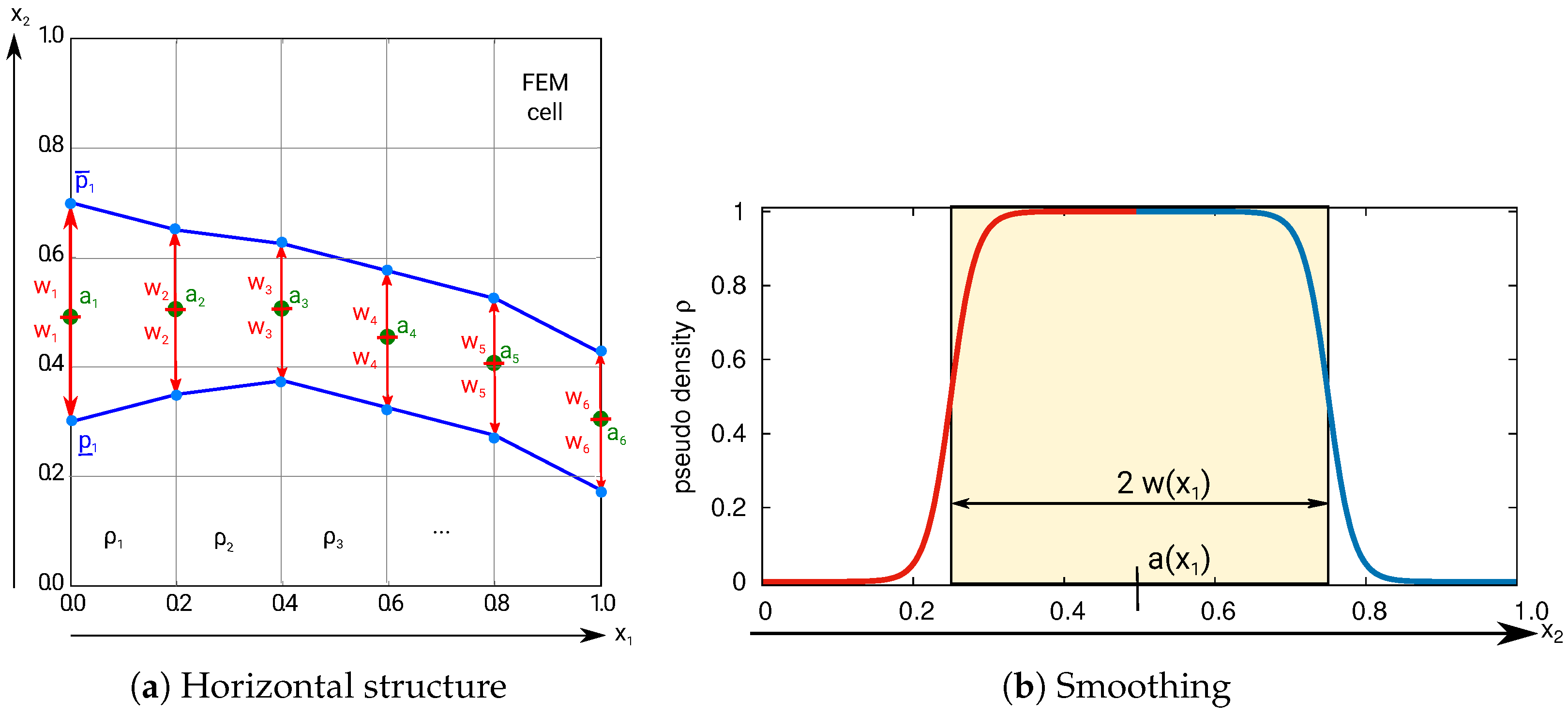
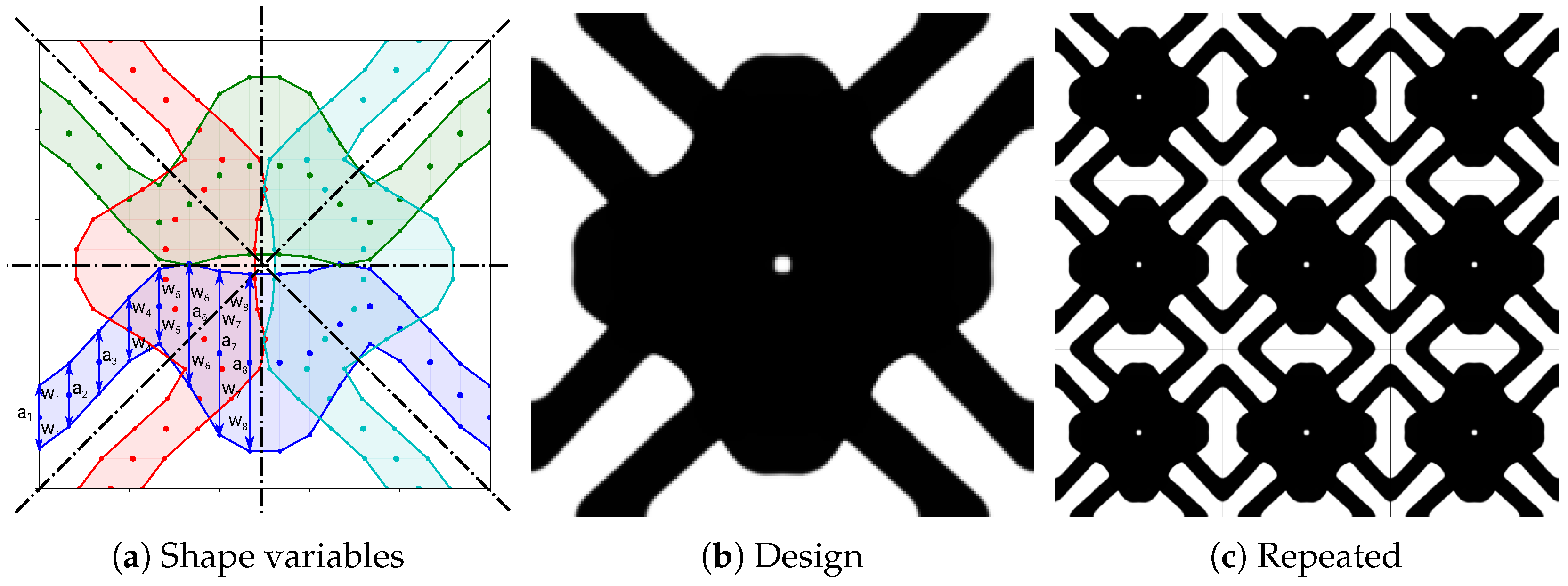
2.2.1. Shape Mapping
2.2.2. PBG Problem Formulation
2.3. Sample Fabrication and Measurement Setup
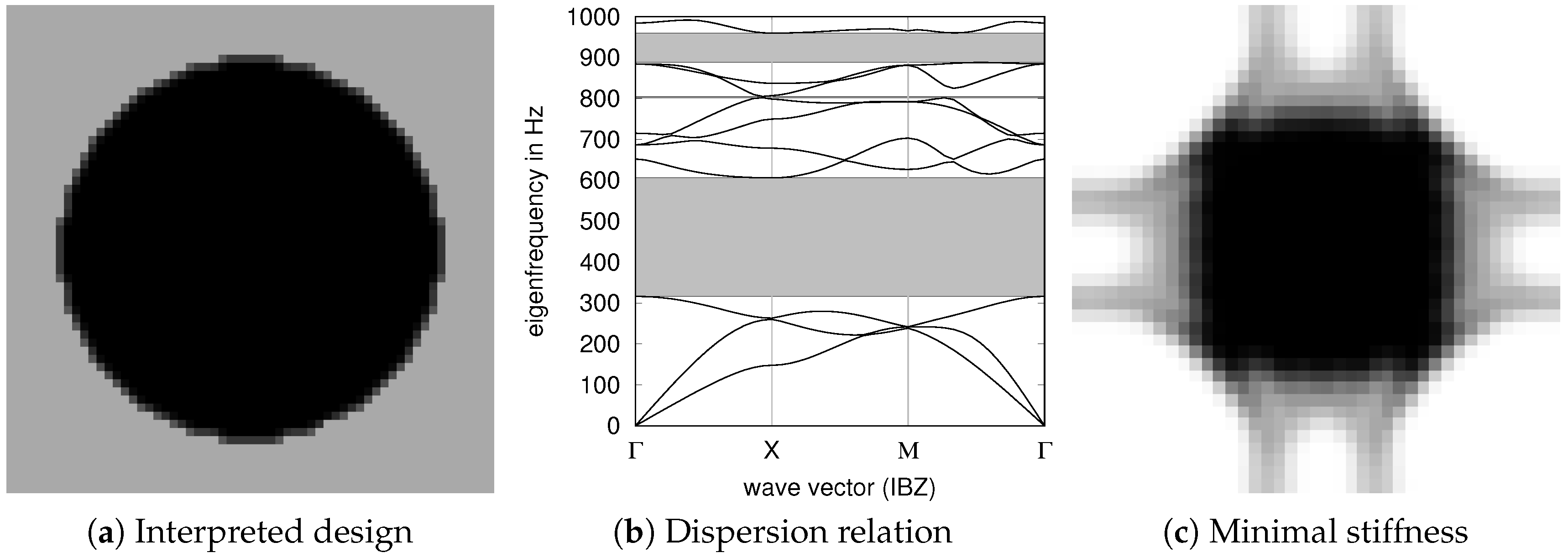
3. Results
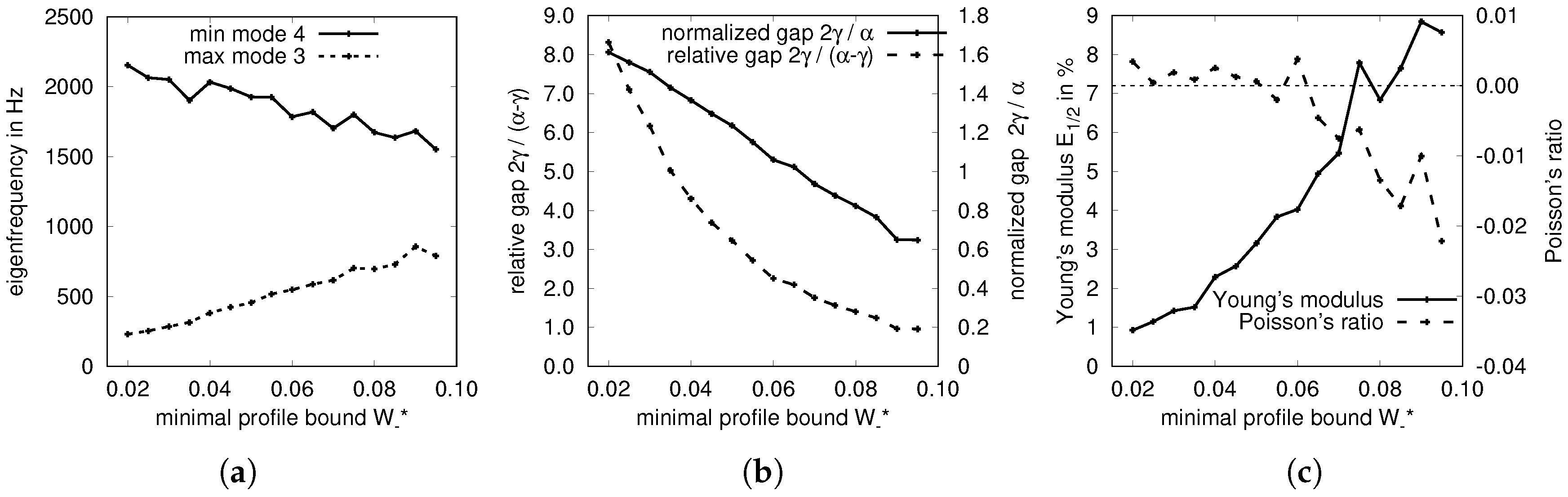
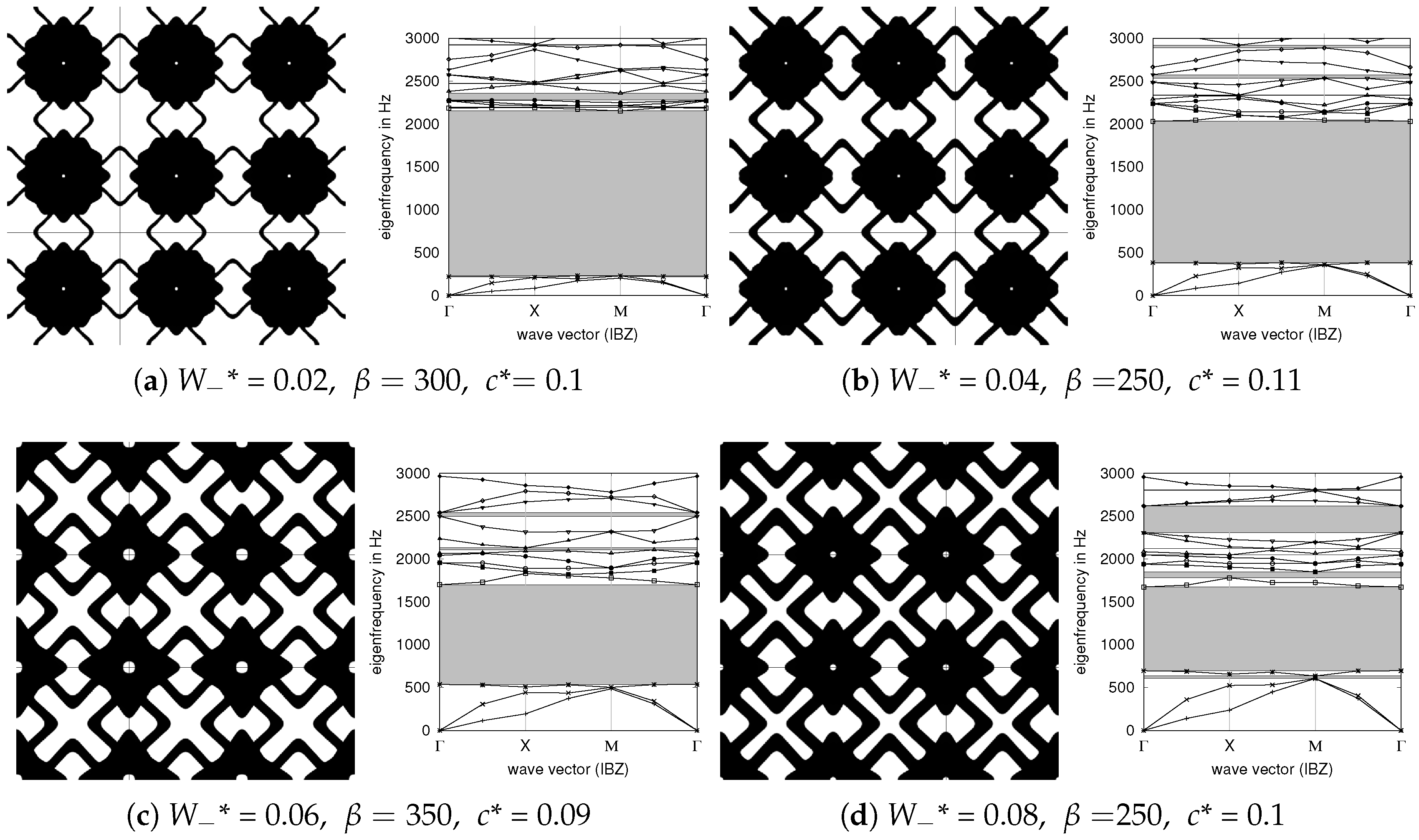
3.1. Optimized Unit Cells
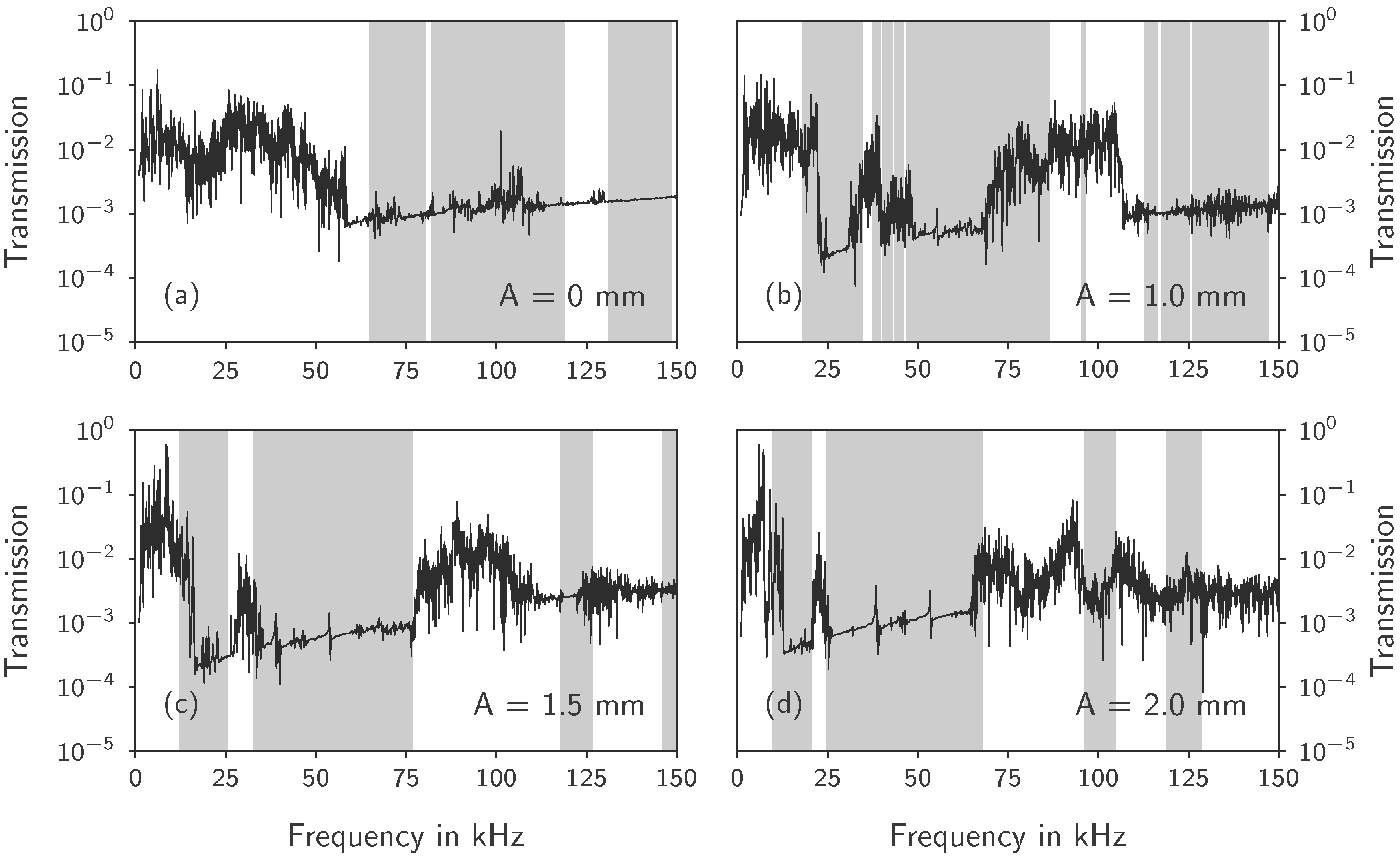
3.2. Transmission Measurements
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kushwaha, M.S. The phononic crystals: An unending quest for tailoring acoustics. Mod. Phys. Lett. B 2016, 30, 1630004. [Google Scholar] [CrossRef]
- Lu, M.H.; Feng, L.; Chen, Y.F. Phononic crystals and acoustic metamaterials. Mater. Today 2009, 12, 34–42. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Sala, R.; Sancho, J.; Sánchez, J.V.; Gómez, V.; Llinares, J.; Meseguer, F. Sound attenuation by sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Montero de Espinosa, F.R.; Jiménez, E.; Torres, M. Ultrasonic Band Gap in a Periodic Two-Dimensional Composite. Phys. Rev. Lett. 1998, 80, 1208–1211. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, L.; Phani, A.S. Local resonance bandgaps in periodic media: Theory and experiment. J. Acoust. Soc. Am. 2013, 134, 1950. [Google Scholar] [CrossRef] [PubMed]
- Croënne, C.; Lee, E.J.S.; Hu, H.; Page, J.H. Band gaps in phononic crystals: Generation mechanisms and interaction effects. AIP Adv. 2011, 1, 041401. [Google Scholar] [CrossRef]
- Diaz, A.; Haddow, A.; Ma, L. Design of band-gap grid structures. Struct. Multidiscip. Optim. 2005, 29, 418–431. [Google Scholar] [CrossRef]
- Oh, J.H.; Seung, H.M.; Kim, Y.Y. Adjoining of negative stiffness and negative density bands in an elastic metamaterial. Appl. Phys. Lett. 2016, 108, 093501. [Google Scholar] [CrossRef]
- Tee, K.F.; Spadoni, A.; Scarpa, F.; Ruzzene, M. Wave Propagation in Auxetic Tetrachiral Honeycombs. J. Vib. Acoust. 2010, 132, 031007. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M.; Gonella, S.; Scarpa, F. Phononic properties of hexagonal chiral lattices. Wave Motion 2009, 46, 435–450. [Google Scholar] [CrossRef]
- Ruzzene, M.; Scarpa, F. Directional and band-gap behavior of periodic auxetic lattices. Phys. Status Solidi B 2005, 242, 665–680. [Google Scholar] [CrossRef]
- Mukherjee, S.; Scarpa, F.; Gopalakrishnan, S. Phononic band gap design in honeycomb lattice with combinations of auxetic and conventional core. Smart Mater. Struct. 2016, 25, 054011. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, H.; Wang, L. Acoustic band gaps of three-dimensional periodic polymer cellular solids with cubic symmetry. J. Appl. Phys. 2013, 114, 043521. [Google Scholar] [CrossRef]
- Lucklum, F.; Vellekoop, M.J. Realization of Complex 3-D Phononic Crystals With Wide Complete Acoustic Band Gaps. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 796–797. [Google Scholar] [CrossRef] [PubMed]
- Trainiti, G.; Rimoli, J.J.; Ruzzene, M. Wave propagation in periodically undulated beams and plates. Int. J. Solids Struct. 2015, 75-76, 260–276. [Google Scholar] [CrossRef]
- Taniker, S.; Yilmaz, C. Design, analysis and experimental investigation of three-dimensional structures with inertial amplification induced vibration stop bands. Int. J. Solids Struct. 2015, 72, 88–97. [Google Scholar] [CrossRef]
- Körner, C.; Liebold-Ribeiro, Y. A systematic approach to identify cellular auxetic materials. Smart Mater. Struct. 2015, 24, 025013. [Google Scholar] [CrossRef]
- Warmuth, F.; Körner, C. Phononic Band Gaps in 2D Quadratic and 3D Cubic Cellular Structures. Materials 2015, 8, 8327–8337. [Google Scholar] [CrossRef] [PubMed]
- Warmuth, F.; Wormser, M.; Körner, C. Single phase 3D phononic band gap material. Sci. Rep. 2017, 7, 3843. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, O.; Jensen, J.S. Systematic design of phononic band-gap materials and structures by topology optimization. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2003, 361, 1001–1019. [Google Scholar] [CrossRef] [PubMed]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Multidiscip. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Method and Applications, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Halkjær, S.; Sigmund, O.; Jensen, J.S. Maximizing band gaps in plate structures. Struct. Multidiscip. Optim. 2006, 32, 263–275. [Google Scholar] [CrossRef]
- Hussein, M.I.; Hamza, K.; Hulbert, G.M.; Saitou, K. Optimal synthesis of 2D phononic crystals for broadband frequency isolation. Waves Random Complex Media 2007, 17, 491–510. [Google Scholar] [CrossRef]
- Bilal, O.R.; Hussein, M.I. Ultrawide phononic band gap for combined in-plane and out-of-plane waves. Phys. Rev. E 2011, 84, 065701. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.W.; Wang, Y.S.; Zhang, C. Topology Optimization of Chiral Phoxonic Crystals With Simultaneously Large Phononic and Photonic Bandgaps. IEEE Photonics J. 2017, 9, 1–16. [Google Scholar] [CrossRef]
- Andreassen, E.; Jensen, J.S. Topology optimization of periodic microstructures for enhanced dynamic properties of viscoelastic composite materials. Struct. Multidiscip. Optim. 2014, 49, 695–705. [Google Scholar] [CrossRef]
- Laude, V. Phononic Crystals: Artificial Crystals for Sonic, Acoustic, and Elastic Waves, 1st ed.; De Gruyter Studies in Mathematical Physics; De Gruyter: Berlin, Germany; Boston, MA, USA, 2015; pp. 1–56. [Google Scholar]
- Deymier, P.A. Acoustic Metamaterials and Phononic Crystals; Springer: Berlin/Heidelberg, Germany, 2013; pp. 329–372. [Google Scholar]
- Sigmund, O. A new class of extremal composites. J. Mech. Phys. Solids 2000, 48, 397–428. [Google Scholar] [CrossRef]
- Guest, J.; Prévost, J.; Belytschko, T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Methods Eng. 2004, 61, 238–254. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Wein, F.; Stingl, M. A Combined Parametric Shape Optimization and Ersatz Material Approach. Struct. Multidiscip. Optim. 2017, accepted. [Google Scholar] [CrossRef]
- Norato, J.; Bell, B.; Tortorelli, D. A geometry projection method for continuum-based topology optimization with discrete elements. Comput. Methods Appl. Mech. Eng. 2015, 293, 306–327. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, J.; Guo, X. Lagrangian Description Based Topology Optimization: A Revival of Shape Optimization. J. Appl. Mech. 2016, 83, 041010. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM J. Optim. 2002, 12, 979–1006. [Google Scholar] [CrossRef]
- Körner, C. Additive manufacturing of metallic components by selective electron beam melting—A review. Int. Mater. Rev. 2016, 61, 361–377. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Heinl, P.; Singer, R.; Körner, C. Auxetic cellular structures through selective electron-beam melting. Phys. Stat. Solidi B 2010, 247, 269–272. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting. Acta Mater. 2012, 60, 3370–3379. [Google Scholar] [CrossRef]
- Warmuth, F.; Osmanlic, F.; Adler, L.; Lodes, M.A.; Körner, C. Fabrication and characterisation of a fully auxetic 3D lattice structure via selective electron beam melting. Smart Mater. Struct. 2017, 26, 025013. [Google Scholar] [CrossRef]
- Adler, L.; Warmuth, F.; Lodes, M.A.; Osmanlic, F.; Körner, C. The effect of a negative Poisson’s ratio on thermal stresses in cellular metallic structures. Smart Mater. Struct. 2016, 25, 115038. [Google Scholar] [CrossRef]
- Wormser, M.; Warmuth, F.; Körner, C. Evolution of full phononic band gaps in periodic cellular structures. Appl. Phys. A 2017, accepted. [Google Scholar]

| Parameter | Struts | Cubes |
|---|---|---|
| Current I | 5 | 12 |
| Voltage V | 60 | 60 |
| Scan speed | 1.5 m | 10 m |
| Line energy | 0.2 J | 0.072 J |
| Line offset | - | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wormser, M.; Wein, F.; Stingl, M.; Körner, C. Design and Additive Manufacturing of 3D Phononic Band Gap Structures Based on Gradient Based Optimization. Materials 2017, 10, 1125. https://doi.org/10.3390/ma10101125
Wormser M, Wein F, Stingl M, Körner C. Design and Additive Manufacturing of 3D Phononic Band Gap Structures Based on Gradient Based Optimization. Materials. 2017; 10(10):1125. https://doi.org/10.3390/ma10101125
Chicago/Turabian StyleWormser, Maximilian, Fabian Wein, Michael Stingl, and Carolin Körner. 2017. "Design and Additive Manufacturing of 3D Phononic Band Gap Structures Based on Gradient Based Optimization" Materials 10, no. 10: 1125. https://doi.org/10.3390/ma10101125