1. Introduction
A wireless rechargeable sensor network (WRSN) [
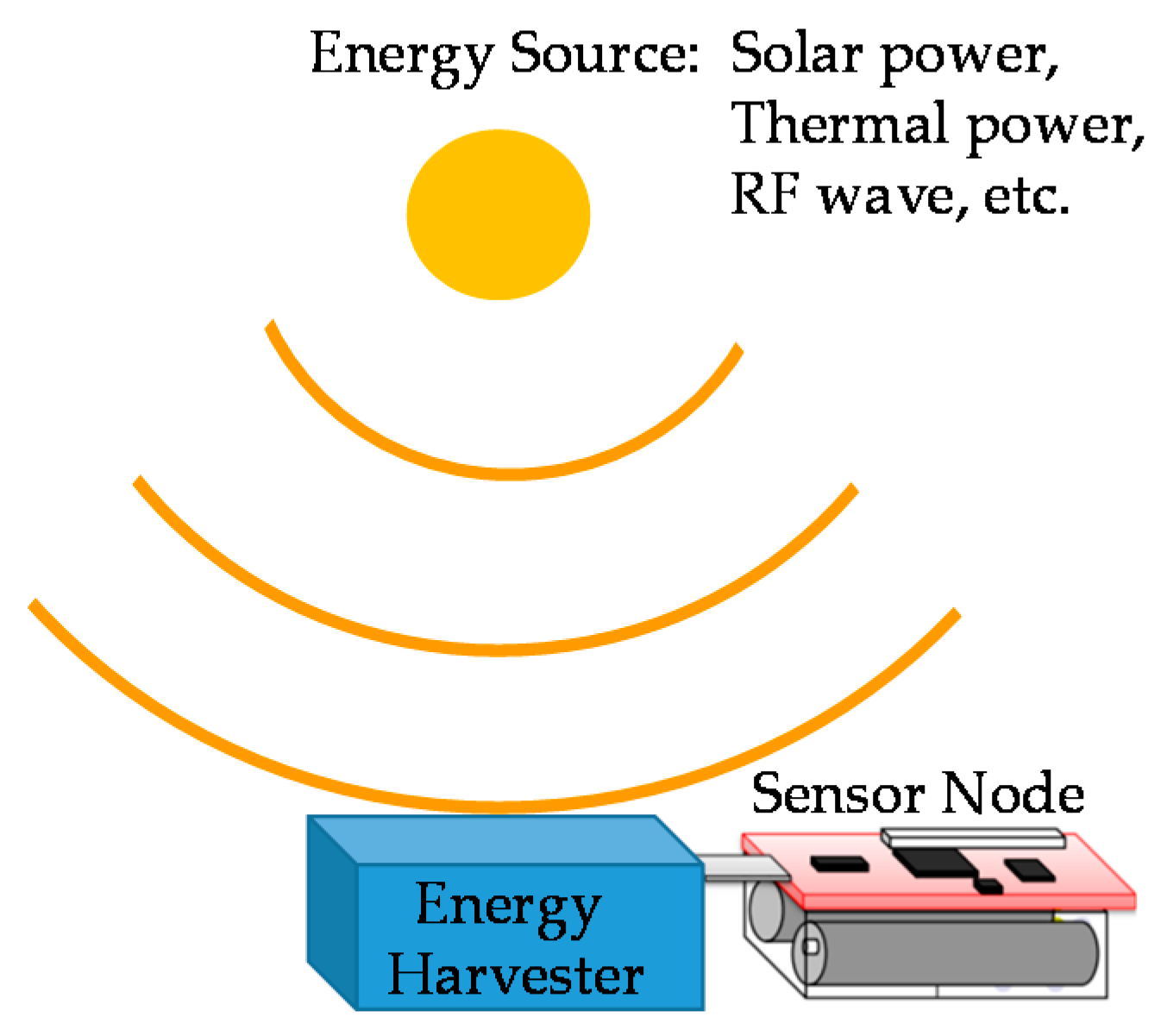
1] consists of many rechargeable sensor nodes and one or more sink nodes. Sensor nodes are powered by batteries and can sense physical phenomena (e.g., temperature, humidity, atmospheric pressure, light intensity, and electromagnetic field strength) and forward the sensed data to the sink node(s) via multi-hop wireless communications. WRSNs are sustainable since they utilize energy harvesting technologies to replenish the batteries of sensor nodes. The replenishing is achieved by equipping every sensor node with an energy harvester to harvest energy from different sources [
2,
3], such as solar power, thermal power, radio frequency (RF) waves, or air flow, as shown in
Figure 1. Many recent studies [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13] focus on the WRSNs due to their sustainability. Some other studies [
14,
15,
16,
17,
18,
19,
20] investigate battery-less or battery-free wireless sensor networks (WSNs) in which sensor nodes are powered by capacitors storing energy harvested through wireless power transmission (WPT), especially microwave power transmission (MPT). Without loss of generality, such WSNs are regarded as WRSNs in this paper.
Energy harvesting technologies are generally divided into two classes: (1) charger-based energy harvesting and (2) ambient energy harvesting. The former technology deploys specific devices, called chargers, to emit energy, and utilizes harvesters to capture the energy. The latter technology applies ambient energy harvesting devices to capture energy from the ambient environment. Typical devices include solar panels, thermoelectric generators, and ambient RF harvesters to capture energies from TV, Wi-Fi, and 3G/4G stations. It is more difficult for the latter to control the amount of harvested energy due to the unstable nature of ambient energy sources (ESs). This is problematic if sensor nodes have to meet specific energy requirements. Therefore, this paper pays attention to WRSNs using charger-based energy harvesting technologies. It practically focuses on indoor WRSNs using the RF wireless energy harvesting technology.
The deployment of “RF wireless chargers” (or “chargers” for short) is challenging, since every harvester needs to be covered by at least one charger and the charging space of chargers is usually limited. For example, the effective charging distance is 3–5 m and the effective charging angle is 30°–45° between the Powercast TX91501-3W-ID charger (Powercast Corp., Pittsburgh, PA, USA) [
21] and the Powercast P2110-EVAL-02 harvester (Powercast Corp.) [
22]. It is also a cost-consuming task, as wireless chargers are expensive. For example, the Powercast TX91501-3W-ID charger currently costs about 1,000 US dollars. This motivated the authors to study the wireless charger deployment optimization (WCDO) problem defined below. Given a set of WRSN sensor nodes equipped with harvesters, the WCDO addresses how to deploy as few as possible chargers to cover all sensor nodes for satisfying their energy requirements to make the WRSN sustainable. To the best of our knowledge, no research has addressed the same problem up to now.
This paper proposes two algorithms for solving the WCDO problem. It is assumed that wireless chargers are equipped with directional antennas whose charging space is modeled as a cone and charging efficiency complies with the Friis free space transmission equation [
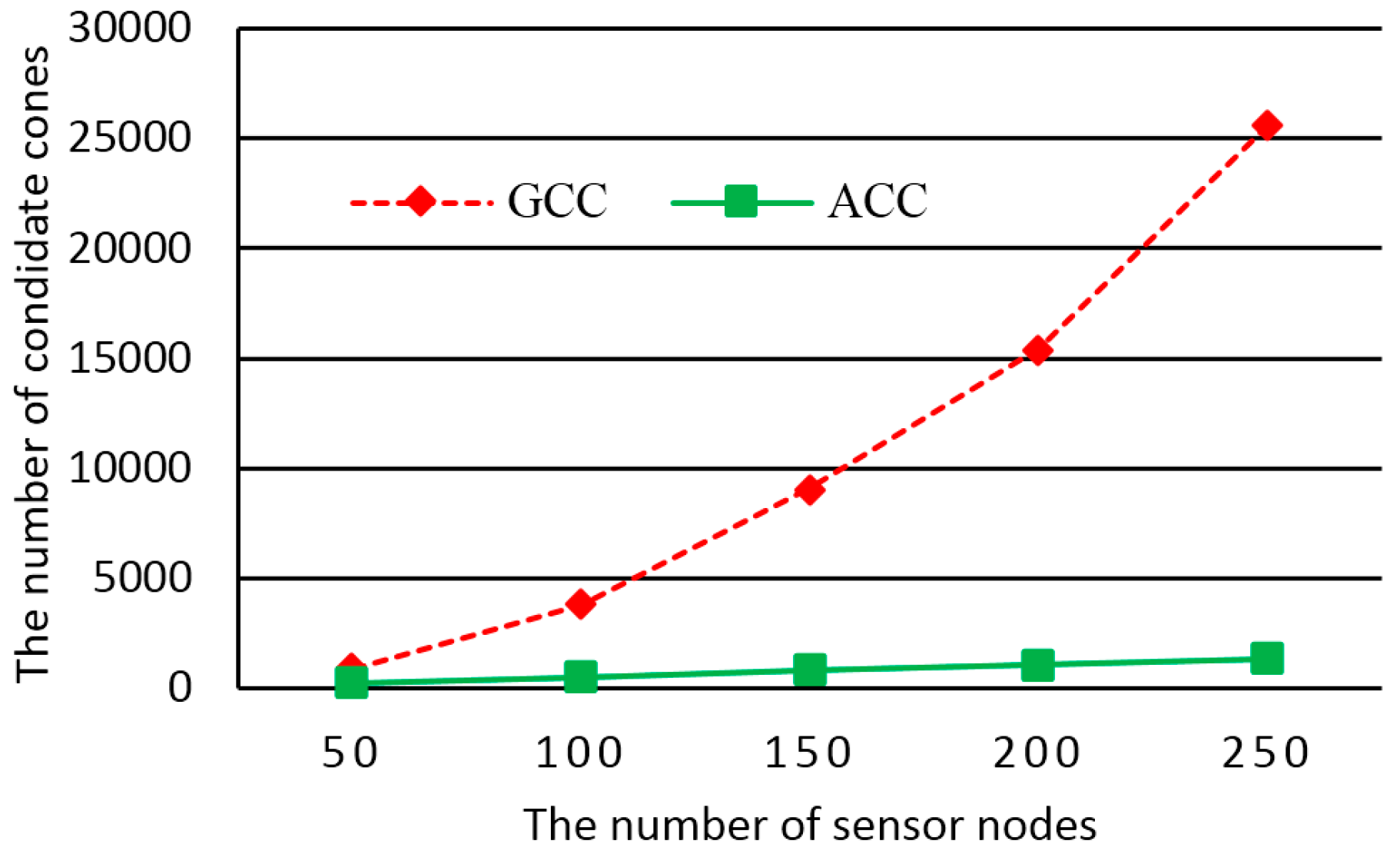
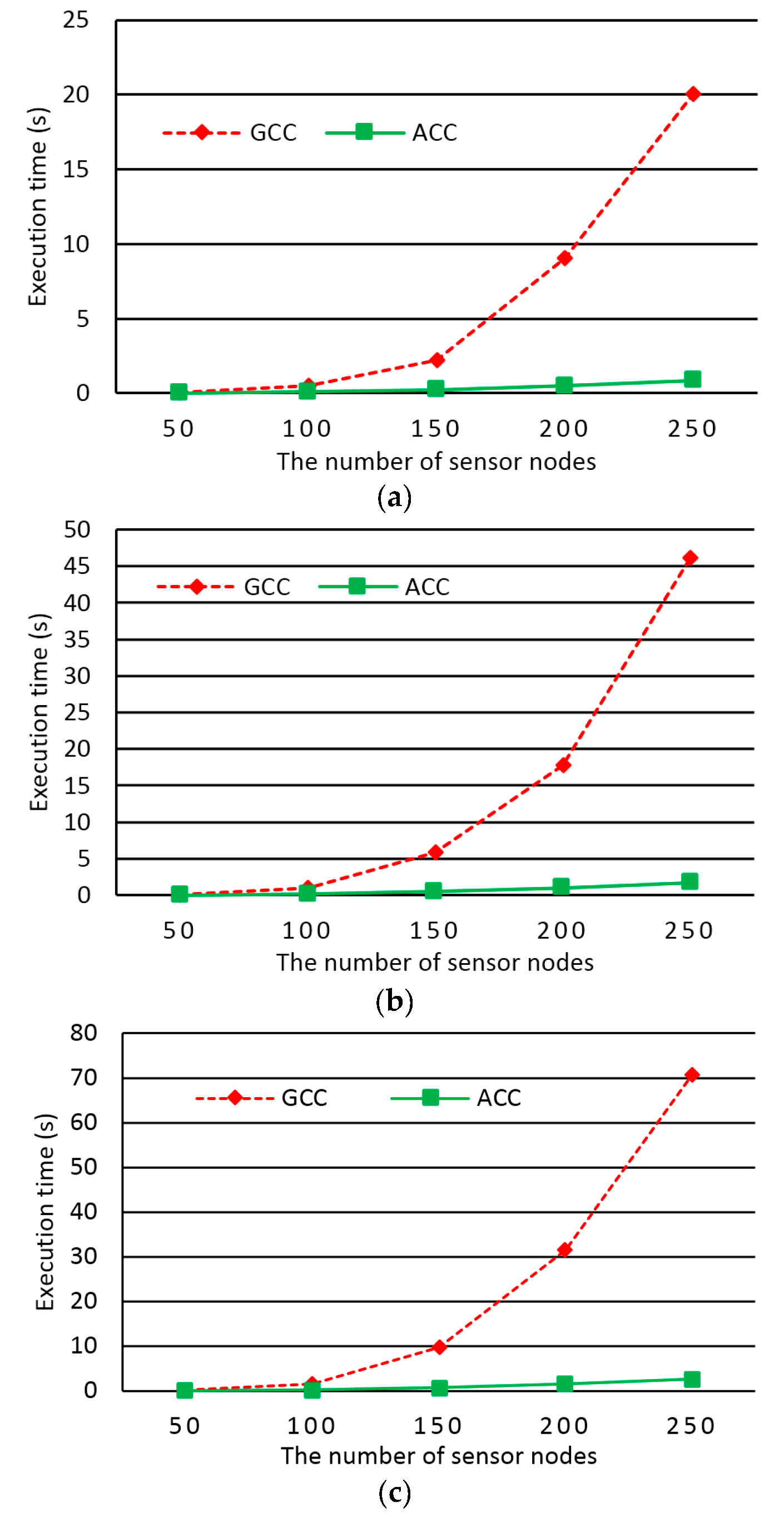
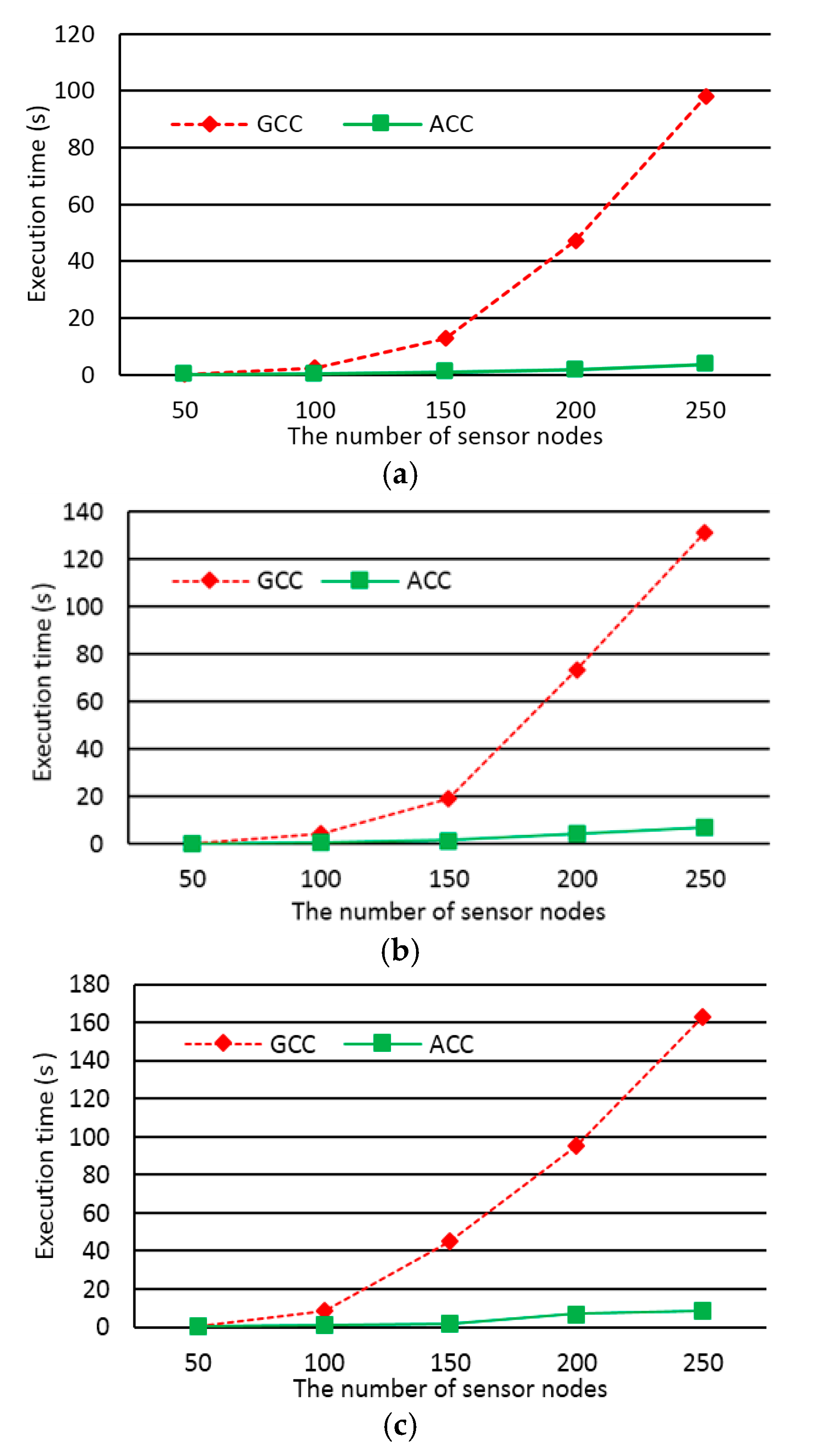
23]. It is also assumed that chargers are deployed on grid points at a specific height and the sensor nodes equipped with wireless harvesters are distributed beneath the chargers on the floor or object surfaces. The proposed algorithms are the greedy cone covering (GCC) algorithm and the adaptive cone covering (ACC) algorithm. Both algorithms treat chargers as cones. The GCC (respectively, ACC) algorithm greedily (respectively, adaptively) generates candidate cones that can cover as many as possible sensor nodes. The two algorithms then greedily select the fewest number of candidate cones, each of which corresponds to the deployment of a charger, to derive approximate solutions to the WCDO problem. We perform extensive experiments to justify our assumptions. We also conduct comprehensive simulations and do analyses for the algorithms to compare them in terms of the time complexity, the number of chargers deployed, and the execution time.
The remainder of the paper is organized as follows: some related studies are reviewed in
Section 2.
Section 3 presents the modeling and the problem definition. In
Section 4, the two proposed algorithms to solve the problem are described.
Section 5 shows algorithm time complexity analyses and grid point separation analyses for deploying chargers. Experiments about the charging efficiency and results of algorithm simulations are described in
Section 6. Finally,
Section 7 concludes the paper.
2. Related Work
In this section, we review the research results [
3,
4,
5,
6,
7,
8,
13,
14,
15,
16,
17] most related to our work. Kim et al. [
3] investigated various ambient energy-harvesting technologies using different power sources, such as solar power, thermal power, piezoelectric power, and wireless RF power, in the aspect of their applicability for self-sustainable wireless sensor platforms. They stated that although ambient RF energy has low power density values of 0.2 nW/cm
2–1 μW/cm
2 and low radio frequency-direct current (RF-DC) conversion values of 10%–30%, a larger amount of total available power can be harvested by utilizing high gain antennas. Some antennas designed by the authors were shown [
3]. For example, a folded dual-bad antenna at 915 MHz and 2.45 GHz was designed to harvest RF power from cellular and WiFi sources with power densities about 1 μW/cm
2. Moreover, a folded dipole antenna was designed to harvest RF power from a two-way radio at the UHF band (464 and 468 MHz). They also implemented a prototype of an embedded microcontroller-enabled sensor platform successfully powered by an ambient UHF digital TV signal (512–566 MHz) from a broadcasting antenna that is 6.3 km away.
Fu et al. [
4] proposed a moving and stopping plan for mobile chargers to guarantee that the time to charge all given stationary sensor nodes is minimized. An optimal solution using linear programming for the plan is proposed; however, the computational complexity of the solution is very high. Therefore, a heuristic solution discretizing the charging power on a two-dimension space was proposed to reduce the time complexity. The heuristic solution has been proved to have a bounded approximation ratio.
He et al. [
5] proposed two types of energy provisioning problems for WRSNs: point provisioning and path provisioning. The former addresses how to use the least number of chargers to ensure that a static sensor node placed in any position of the network will receive a sufficient recharge rate to ensure WRSN sustainability. The latter addresses the same problem for mobile sensor nodes under the assumption that sensor nodes can harvest excess energy in power-rich areas and store the energy for later use in power-deficient areas. The authors utilized the triangular deployment of chargers to solve the two problems. They also proposed a modified Friis free space transmission equation adjusted for short distance transmission for evaluating the deployment. The original Friis equation and the modified version are shown below in Equations (1) and (2), respectively:
In Equations (1) and (2),
and
denote the power and the antenna gain of the transmitter (i.e., charger), respectively, and
and
denote the power and the antenna gain of the receiver (i.e., harvester), respectively. Furthermore, λ is the wave length, and
D is the distance between the antennas of the charger and the harvester. η is the rectifier efficiency,
is polarization loss, and β is a parameter to adjust the original Friis equation for short distance transmission.
Dai et al. [
6] stated that if the constraints of sensor node speed and battery capacity are considered, the sustainable operation of sensor nodes may not be guaranteed. It proposed the concept of quality of energy provisioning (QoEP) to characterize the expected portion of time that a sensor node can sustain operation by taking into account node speed and battery capacity. The upper and lower bounds of QoEP in 1D and 2D sensor node mobility cases are derived.
Xu et al. [
7] considered the scheduling problem of arranging multiple mobile chargers to collaboratively charge sensor nodes with the goal of minimizing the total traveling distance of all chargers. This can be formulated as finding multiple travelling salesperson problem (TSP) closed tours covering all sensor nodes such that the total length of the tours is minimized. The authors proposed a 2-approximation algorithm to solve the problem under the assumption that the energy consumption rates of all sensor nodes are fixed.
Liang et al. [
8] considered a scheduling problem similar to that addresses by Xu et al. in [
6]. The problem is how to use the minimum number of mobile chargers to charge sensor nodes so that none of sensor nodes runs out of energy, subject to the energy capacity of mobile chargers. The authors designed a 5-approximation algorithm to find multiple closed tours. Afterwards, by bounding the total distance of each tour, the authors designed another approximation algorithm invoking the 5-approximation algorithm to provide approximate solutions to the problem.
Ye et al. [
9] introduced a new metric, the charging utility, to measure the charging quality of the charger with the considerations of both the fairness of charging sensor nodes and the number of sensor nodes charged by mobile chargers traveling along closed tours. It is assumed that each mobile charger can only travel a limited length per tour, due to its limited energy capacity. The authors formulated an optimization problem of scheduling a mobile charger to charge sensor nodes, with an objective of maximizing the charging utility, subject to the total traveling distance of the mobile charger per tour and the deadline of each sensor node to be charged. An approximation algorithm with a guaranteed approximation ratio was proposed to solve the problem.
Maehara et al. [
14] proposed a WPT scheme called multi-point carrier shift diversity (MPCSD), in which the center frequency of the carrier of each power transmitting point (or transmitter) is slightly shifted with a predefined amount to create artificial fading. Suppose there are
N different transmitters, the carrier frequency
of the
nth transmitter is defined in Equation (3), shown below:
In Equation (3),
is the center frequency,
B is the channel bandwidth, and
n = 1, …,
N. The proposed scheme is shown to be capable of mitigating power attenuation caused by the path loss effect and the standing-wave effect created by multipath and interference between multiple power transmitters so that the coverage of energy supply field is improved. Maehara et al. [
15] investigated the energy transmission coverage of the MPCSD scheme through theoretical discussions and practical experiments. It is shown that the MPCSD scheme can achieve 100% of coverage in an indoor environment for the sensor node duty factor of 1/100 (i.e., the sensor node is in the transmitting mode for the duration of 10 ms per second).
Imoto et al. [
16] conducted experiments in an IEEE 802.11g-based wireless local area network (WLAN) in which an ES transmits microwave power to a sensor station (SS) using the carrier sense multiple access with collision avoidance (CSMA/CA) protocol to transmit data to an access point (AP). They derived the following two requirements for coexistence of MPT and the WLAN wireless data transmission (WDT). First, MPT and WDT should not proceed simultaneously. Therefore, the ES should share the timing information of MPT with the SS so that the SS attempts to transmit data frames only when the ES does not transmit microwave power. Second, the ES should not transmit microwave power to the SS when the AP broadcasts beacon frames so that the SS is not disassociated from the AP. This can also prevent data throughput degradation due to WLAN automatic data rate selection.
Yamashita et al. [
17] assumed the same environment as assumed by Imoto et al. [
16] and designed and implemented a scheduling scheme to solve the disassociation problem and the throughput degradation problem caused by the coexistence of MPT and WDT. In the scheduling scheme, the SS goes to the active mode to transmit data towards and to receive delivery traffic indication map (DTIM) beacons from the AP periodically. It goes to the power-saving (sleep) mode for most of the time to save energy. As long as the SS is in the sleep mode, the ES can transmit microwave power. On the basis of link budget analysis, the authors also clarified the maximum distance between the EC and the SS to conclude that the scheduling scheme can be applied to a closed space or room.
Yoshida et al. [
18] designed an aerospace WSN that allow the coexistence of high-power MPT and WDT. The aerospace WSN is used in the aircraft application of the reusable vehicle test (RVT) or space capsule for health and safety monitoring inside the RVT. The WSN is based on the time-division operation and the frequency-division operation. The former operation uses a control function to schedule MPT and WDT so that MPT is not activated when WDT is activated. The latter operation applies different frequency bands for WPT and WDT to avoid the interference between them. Through a practical experiment lasting 120 min, it is shown that the aerospace WSN can achieve sustainable balance between harvested power and consumed power.
3. Modeling and Problem Definition
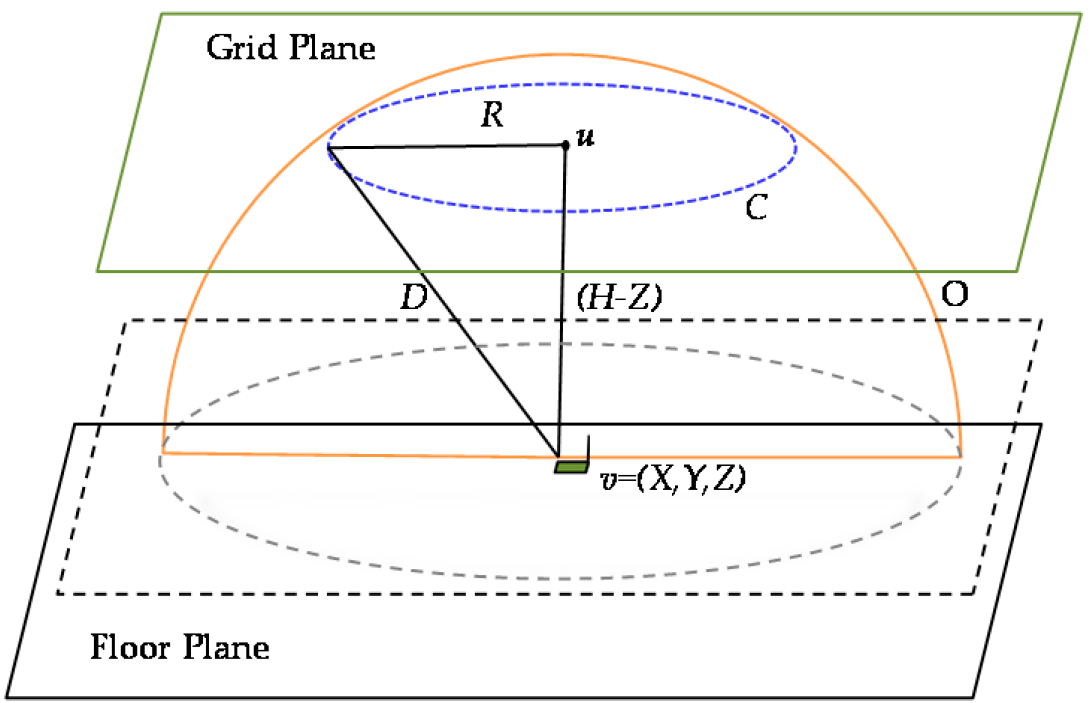
Sensor nodes in the WRSN are assumed to be distributed in a cuboid with the length
L, width
W and height
H; they have different energy requirements and can be located on the floor plane or object surfaces. The energy requirements and locations are summed to be known in advance and fixed. Wireless chargers equipped with directional antennas are assumed to be deployed at grid points on the grid plane or the deployment plane that is with height
H and parallel to the floor plane
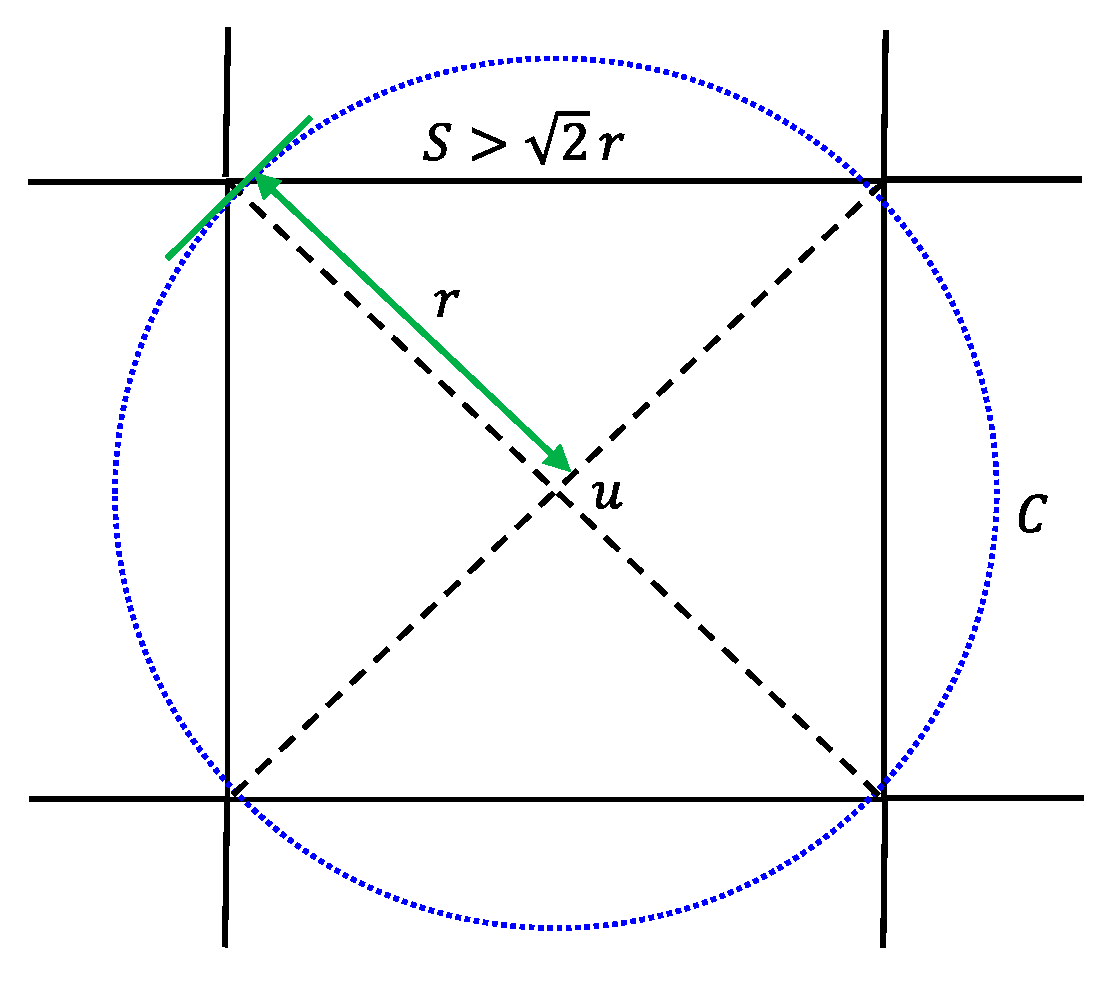
. Moreover, the grid points are with the separation
S; that is, the nearest grid points are of the distance
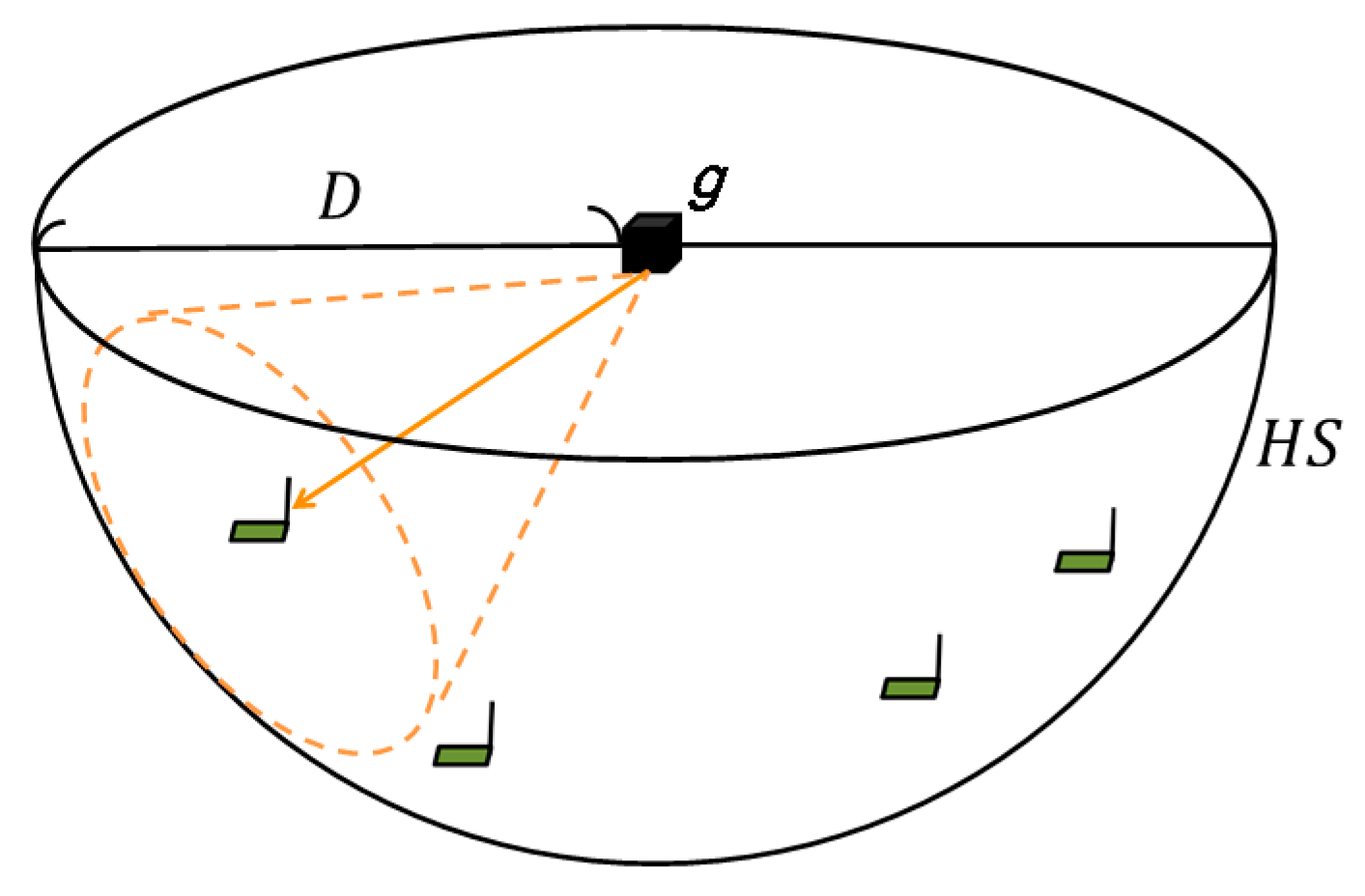
S. Please refer to
Figure 2 for the illustration of the distribution of sensor nodes and the deployment of wireless chargers. Note that we assume no more than
Q,
Q ≥ 1, chargers can be deployed at a same grid point.
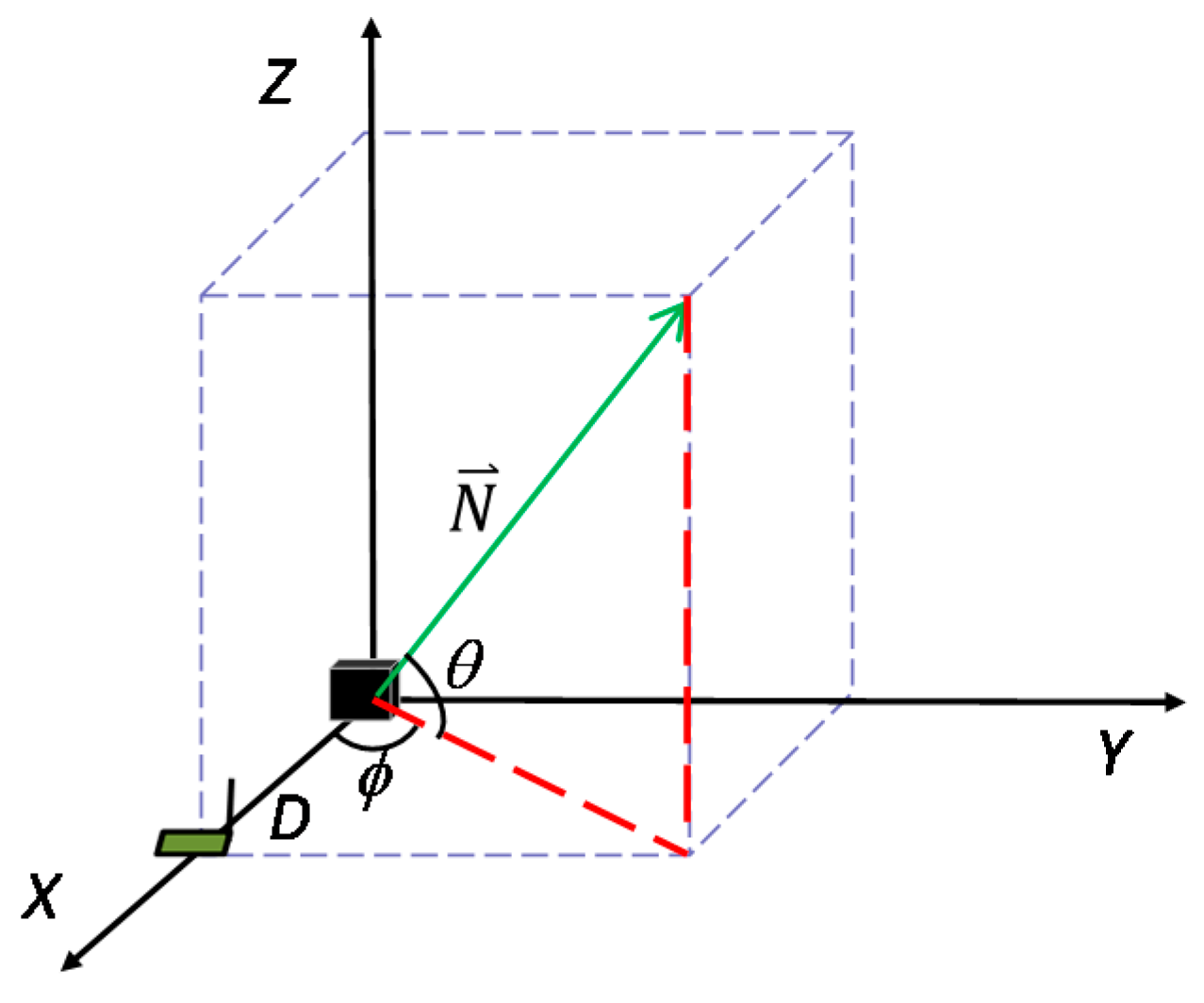
The effective charging space of wireless chargers is modeled as a cone, called a charger cone. Note that the two terms “charger” and “cone” are used interchangeably later in this paper. The modeling is based on the fact that direction antennas usually have specific beamwidth due to vertical and horizontal polarization. For example, the direction antenna of the Powercast TX91501-3W-ID charger has 60° beamwidth in both the horizontal direction and the vertical direction. As shown in
Figure 3, every charger cone is characterized by an apex
X, a normal vector
whose direction is parallel to the symmetrical axis of the cone, an effective charging distance (i.e., the cone generatrix length)
D, and an effective charging angle (i.e., the opening angle)
A. When a sensor node is within the charger cone of a charger, we assume the sensor node can be charged effectively by the charger; otherwise, the sensor node cannot be charged effectively. Note that the point
E is regarded as an extreme point within the charger cone, where the distance between
E and
X is
D and the angle between the normal vector
and the vector going from
X to
E is
A/2.
The famous Friis transmission equation [
23], shown in Equation (1), is used to model the energy received by the harvester. By the equation, we can see that the received energy
is inversely proportional to
D2, that is,
, where α is a constant and
D is the distance between the charger and the harvester. This paper utilizes a more general empirical model
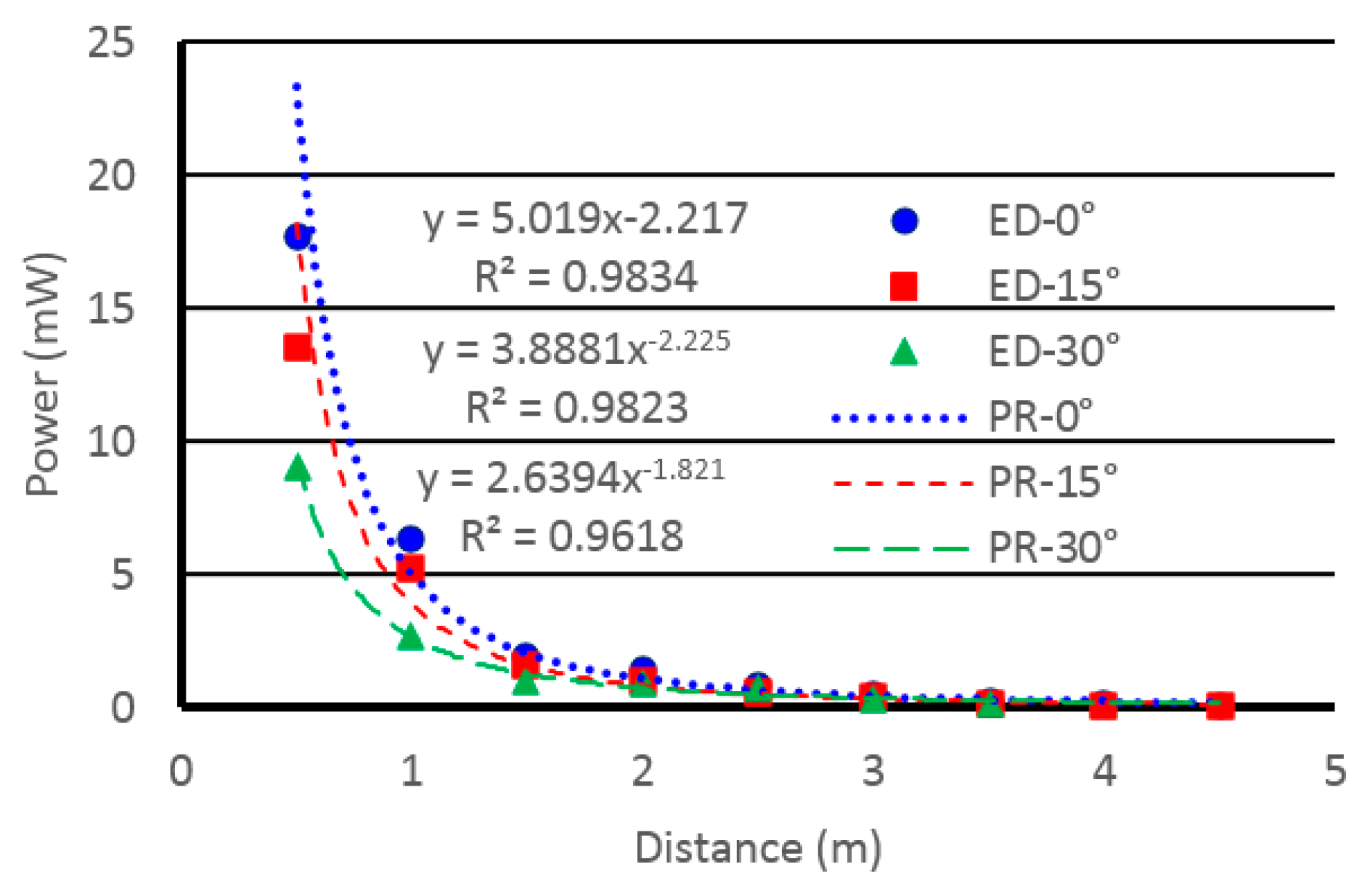
, where β > 0, to estimate the energy received by the harvester. Later in
Section 5, we will show how to apply the power regression analysis to derive appropriate α and β values for the model to fit experimental data accurately.
With all the assumptions mentioned above, the WCDO problem deals with how to deploy the minimum number of wireless chargers to cover all sensor nodes and fulfil their energy demands. To be more precise, given a set of sensor nodes distributed in a cuboid and a set of grid points, the WCDO problem addresses how to deploy as few as possible chargers at grid points to charge sensor nodes to make them sustainable under the assumption that the effective charging space of chargers is a cone. A special case of the WCDO problem in which every charger’s charging space is a half sphere (instead of a cone) and every sensor node needs to be covered by only one charger can be solved by the reduction to the NP-hard set covering (SC) problem [
24]. It is believed the WCDO problem is also NP-hard. Nevertheless, the NP-hardness of the WCDO problem has not yet proven.
4. Proposed Algorithms
Two algorithms, namely the GCC algorithm and the ACC algorithm, are proposed to solve the WCDO problem efficiently. The algorithms have different time complexity and achieve different approximate solutions to the WCDO problem. The details of the two algorithms are described below.
For a WSRN with
n sensor nodes and with chargers being deployed on some of
m grid points, the set of sensor nodes is denoted by
and the set of grid points is denoted by
, where
,
S is the separation of grid points, and
L,
W and
H are the length, width, and height of the sensor node deployment cuboid, respectively. Note that we assume each sensor node
in
has energy requirement
in
. There are two forms of energy requirements: coverage requirement and power requirement. For the coverage requirement,
is a positive integer 1, 2,…, indicating sensor node
needs the coverage of
chargers to fulfill its energy demand. For the power requirement,
is of the unit mW, indicating
needs to capture
mW of power to make itself sustainable. The coverage requirement is actually about extreme cases. Specifically, a node’s coverage requirement can be derived by calculating the ratio of the node’s power requirement over the power harvested by the extreme point
E, as indicated in
Figure 3.
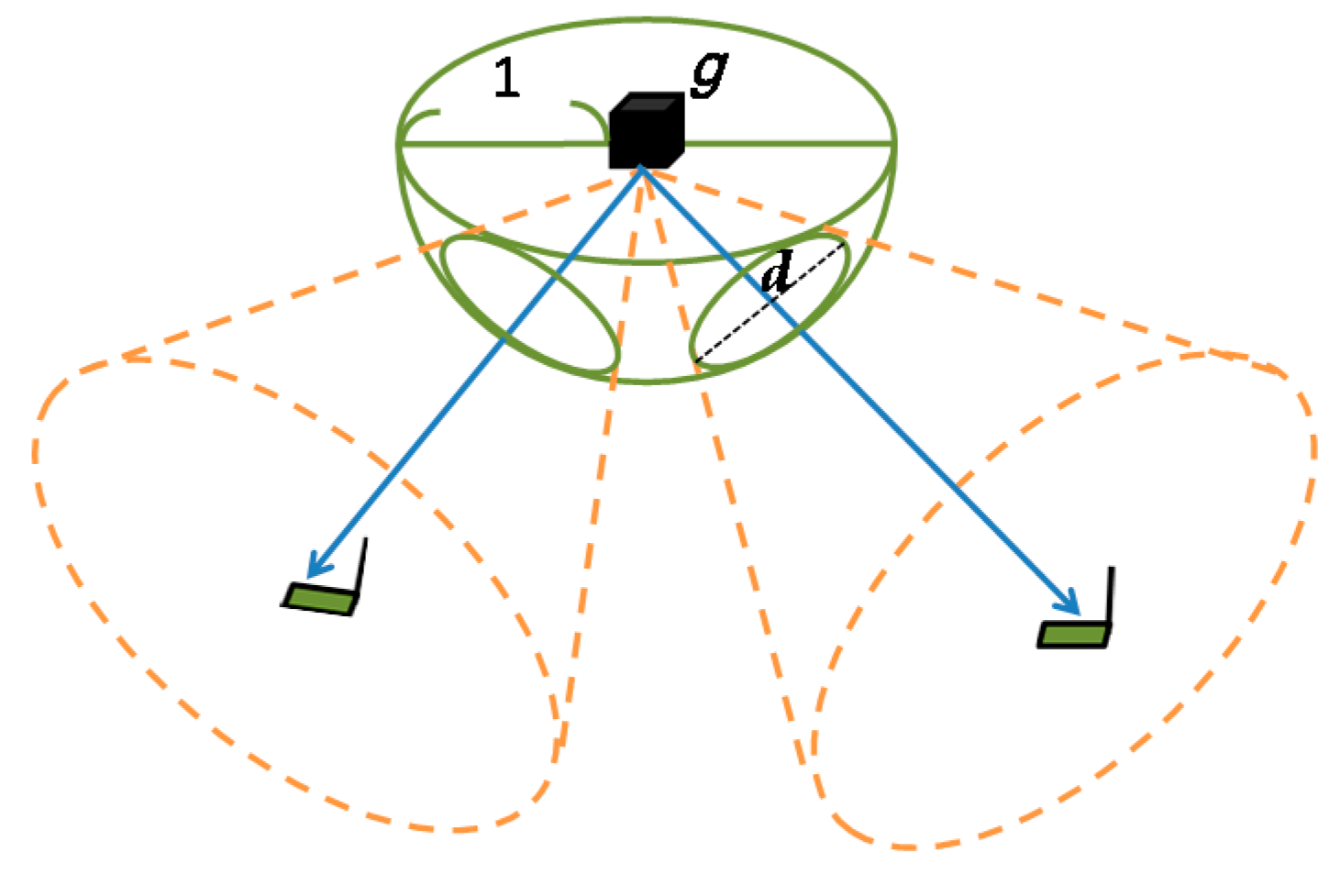
Both algorithms have two phases. The first one is the cone generation phase to generate candidate cones to be selected; the second one is the cone selection phase to select some candidate cones for deploying chargers. In the first phase, the algorithms generate cones by taking every grid point as the apex of cones. As shown in
Figure 4, for every grid point, the algorithms first generate a half sphere (
HS) centered at the point and calculate the sensor set (
SS) of sensor nodes covered by
HS (i.e., within
HS). Afterwards, the first algorithm generates candidate cones on a node-pair-by-node-pair basis (i.e., for every pair of nodes in
SS), while the second algorithm, on a node-by-node basis (i.e., for every node in
SS). For generating better candidate cones, the algorithms greedily adjust cones so that every single cone can cover as many as sensor nodes or can charge sensor nodes more efficiently.
In the second phase, both algorithms first unmark all sensor nodes. Note that a sensor node is unmarked if its energy requirement is not satisfied; otherwise, it will be marked. The algorithms then run iteration by iteration, and greedily select the qualified cone covering most unmarked sensor nodes, where a cone is said to be qualified if it takes a grid point as its apex and is totally taken by no more than Q selected cones as their apex. A selected cone corresponds to a deployed charger. For every newly selected cone, the algorithms marks every sensor node whose energy requirement is satisfied by the cone. And the algorithms continue until all sensor nodes are marked. In this way, the WCDO problem can be solved near-optimally.
The pseudo code of the GCC algorithm is shown in
Figure 5. In the code,
stands for a vector going from grid point
to sensor node
, and
Cone(
) stands for a cone which takes
as the apex, takes
as the symmetrical axis (or the
direction), and has an effective charging distance
D and an effective charging angle
A. Also note that
stands for the number of unmarked sensor nodes in
NS covered by
Cone (
). Moreover,
stands for the angle between the two vectors
and
.
In the GCC algorithm, for every grid point , a lower half sphere HS is obtained with as the center and D as the radius. If HS covers only one sensor node , then the algorithm generates one candidate cone taking the vector going from to as the direction. However, if HS covers k, k > 1, sensor nodes , then the algorithm generates k unit vectors going from to . Afterwards, the GCC algorithm compares the opening angle A with the angle B (i.e., ) between any two vectors associated with the two distinct sensor nodes and . There are three cases for the comparison: B = A, B > A, and B < A.
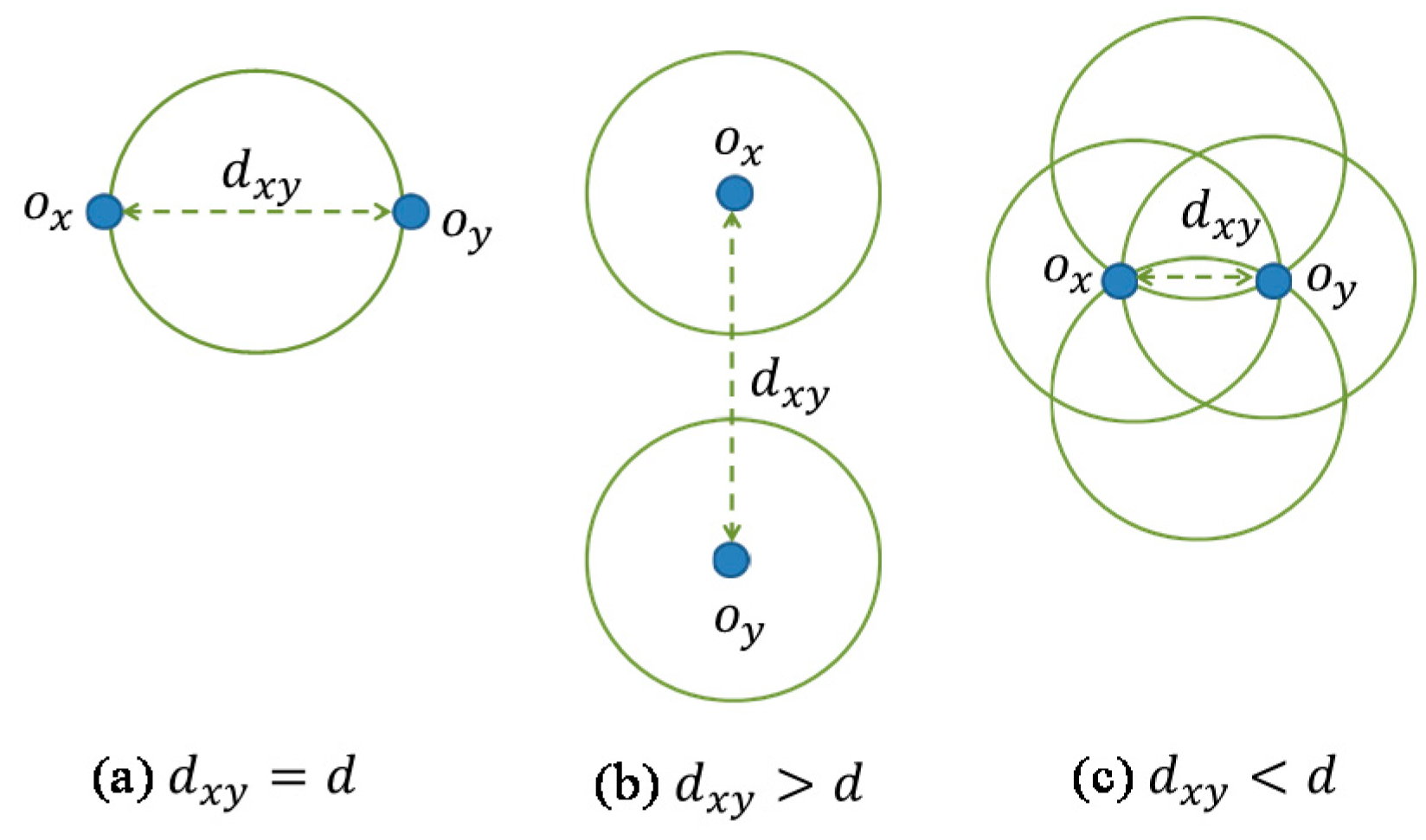
The GCC algorithm performs the aforementioned angle comparison by projecting every vector and every cone onto the surface of a unit sphere centered at grid point
. As shown in
Figure 6, the projection of a vector is a point, while the projection of a cone is a circle of diameter
d. Referring to
Figure 7a–c, for any pair of distinct sensor nodes
, let
ox and
oy be the projection points of
and
on the unit sphere
O centered at grid point
, and let
dxy be the Euclidean distance between the two points. There are three cases of the relationship between
dxy and
d, which correspond to the three relationship cases of
A and
B. The three cases are elaborated below. Case (a)
dxy =
d. This case corresponds to the case of
B =
A. For such a case, one candidate cone is generated. Note that
ox and
oy should be on the diameter of the projection circle of the cone. Case (b)
>
d. This case corresponds to the case of
B >
A. For such a case, two candidate cones taking
and
as directions are generated. Case (c)
<
d. This case corresponds to the case of
B <
A. For such a case, four candidate cones are generated. For two of the cones,
ox and
oy should be on the arcs of the projection circles (at the top and at the bottom) of the cones. For another cone,
ox should be on the projection circle (on the right), and the line
should go through the center of the circle. For yet another cone,
oy should be on the projection circle (on the left), and the line
should go through the center of the circle. Note that for Case (c), the GCC algorithm generates four candidate cones to cover sensor nodes
. In practice, it greedily adjusts the cones to the extreme limitation with the purpose that the cones may at the same time cover as many as possible other sensor nodes.
After generating candidate cones, the GCC algorithm greedily selects the qualified cone covering the most unmarked sensor nodes to deploy a charger. Note that if a sensor node’s energy demand is met by the chargers already deployed, it is marked; otherwise, it is unmarked. In this way, chargers are deployed iteration by iteration until all sensor nodes are marked. Also note that we use function
to estimate the energy provision between the charger
c and the sensor node
. Corresponding to the coverage requirement,
returns 0 or 1, indicating the cone or the charger
c can or cannot cover the sensor node
si. Corresponding to the power requirement,
returns the power (in the unit of mW) received by
si from the energy emitted by charger
c. As will be shown in
Section 5, the received power can be calculated by interpolating power regression expressions derived from practical experimental data.
The pseudo code of the ACC algorithm is shown in
Figure 8. Like the GCC algorithm, the ACC algorithm first derives, for every grid point
, a lower half sphere
HS centered at
with the radius
D. If
HS covers only one sensor node
, then the algorithm generates one candidate cone taking the vector going from
to
as the direction. If
HS covers
k,
k > 1, sensor nodes
, then the algorithm generates
k unit vectors
going from
to
. The ACC algorithm constructs candidate cones on a node by node basis. In practice, the ACC algorithm initially constructs a candidate cone
Cone(
) to cover sensor node
for 1 ≤
x ≤
k. Besides covering node
, the ACC algorithm adaptively and greedily adjusts
so that
Cone(
) can cover as many as possible other sensor nodes. This is achieved by adjusting the direction of
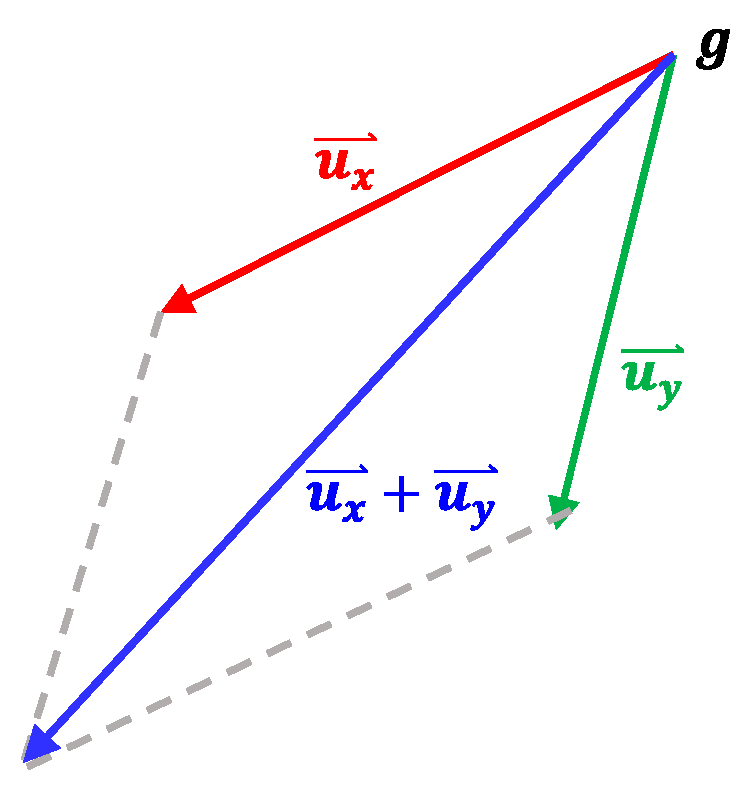
by composing
and
for every vector
, where 1 ≤
y ≤
k and
x ≠
y (
Figure 9). The direction adjustment (Lines 12–14) proceeds on a node-by-node basis. Certainly, the direction adjustment should guarantee that the number of sensor nodes covered by
Cone(
) is increasing and that the sensor node
is still covered by
Cone(
) whatever the adjusted
is.
In the GCC and the ACC algorithms, stands for the set of unmarked sensor nodes with unsatisfied energy requirement. For most cases, the two algorithm stop and return CS* and , with is empty. For such cases, the cones in CS* can be used to deploy chargers to satisfy the energy requirements of all sensor nodes. On the contrary, when the algorithms terminate and return a non-empty set of , they should re-run by setting , and the re-running should proceed until is empty. The re-running is to satisfy the pending energy requirements of unmarked nodes. When is empty, the requirements of all sensor nodes are satisfied and all the cones ever reported in CS* by running and re-running the algorithms are the final selected cones for deploying chargers. However, the re-running algorithms will report an error if it finds that no available grid point exists, where an available grid point is a grid point that no more than Q selected cones take as their apex. For such an error condition, we may need to decrease S, the separation of grid points, to increase the total number of grid points for more possible locations for deploying chargers to satisfy sensor nodes’ energy requirements.