One-Dimensional Modelling of Marine Current Turbine Runaway Behaviour
Abstract
:1. Introduction
2. Modelling
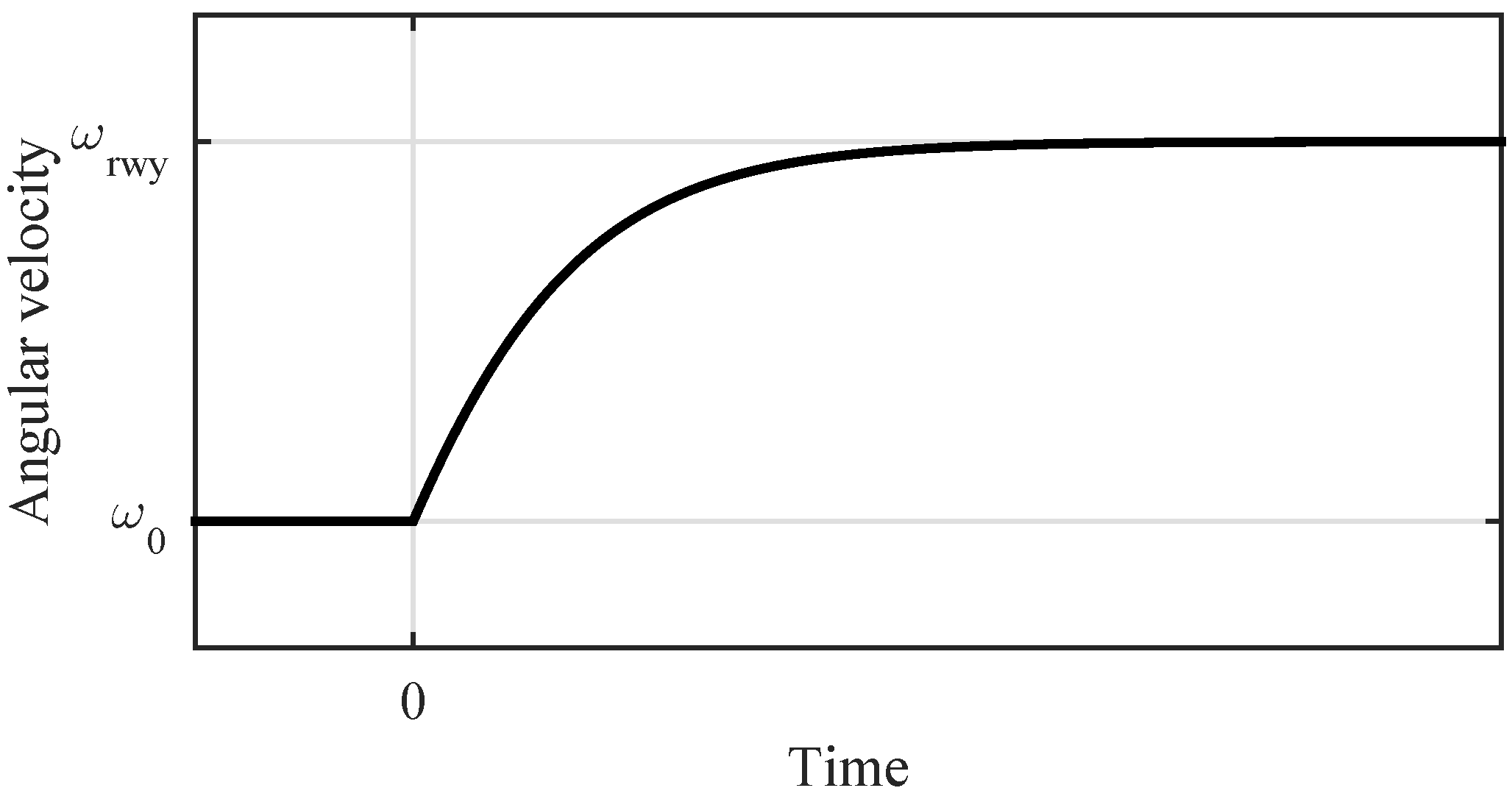
2.1. Analytical Model
2.2. Numerical Model
3. Measurements
3.1. The Söderfors Test Site
3.2. Performance of Measurements
3.3. Turbine Reference Measurements
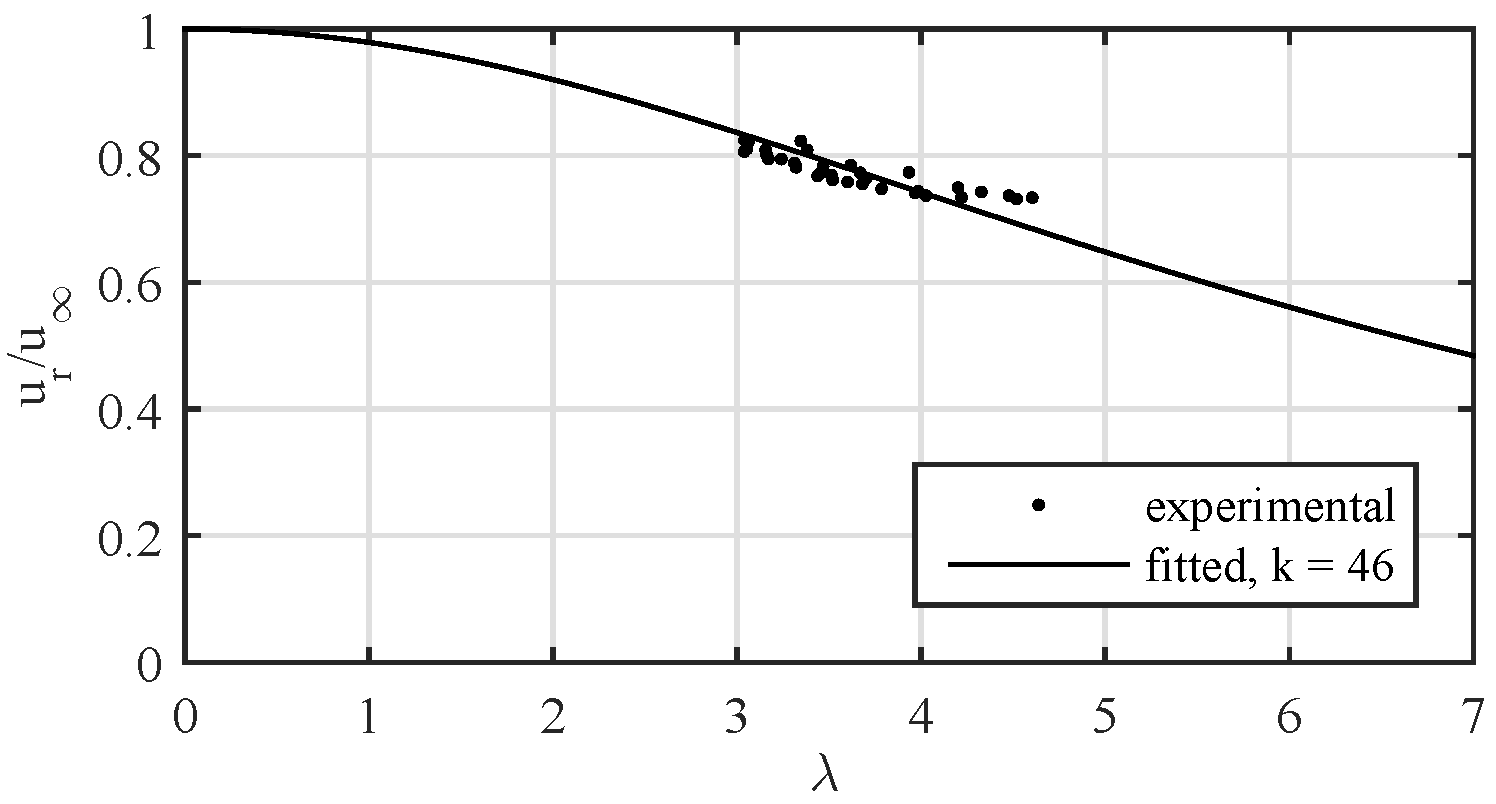
3.4. Wake Speed
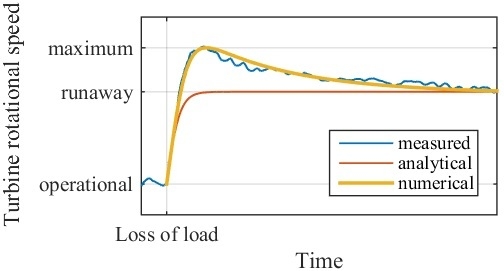
3.5. Runaway
- (a)
- Nominal rotational speed, i.e., load disconnect during operation at or near the optimum power coefficient C. This was assumed to be the most likely scenario, a fault occurring during normal operation of the turbine.
- (b)
- Zero rotational speed, where the turbine was allowed to self-start. This was taken as the worst possible scenario, since when starting from 0, there is no wake at all behind the turbine, and the runaway speed overshoot is likely to be the highest under these circumstances.
- (c)
- Rotational speed below nominal speed, but not 0. This would be a not unlikely operational scenario in case of unusually high water speeds, when it could be desirable to operate at lower than peak C.
- (d)
- Rotational speed above nominal speed, but not runaway speed. While not a highly likely operational case, it was deemed useful for completeness.
4. Implementation and Evaluation
4.1. Calibration
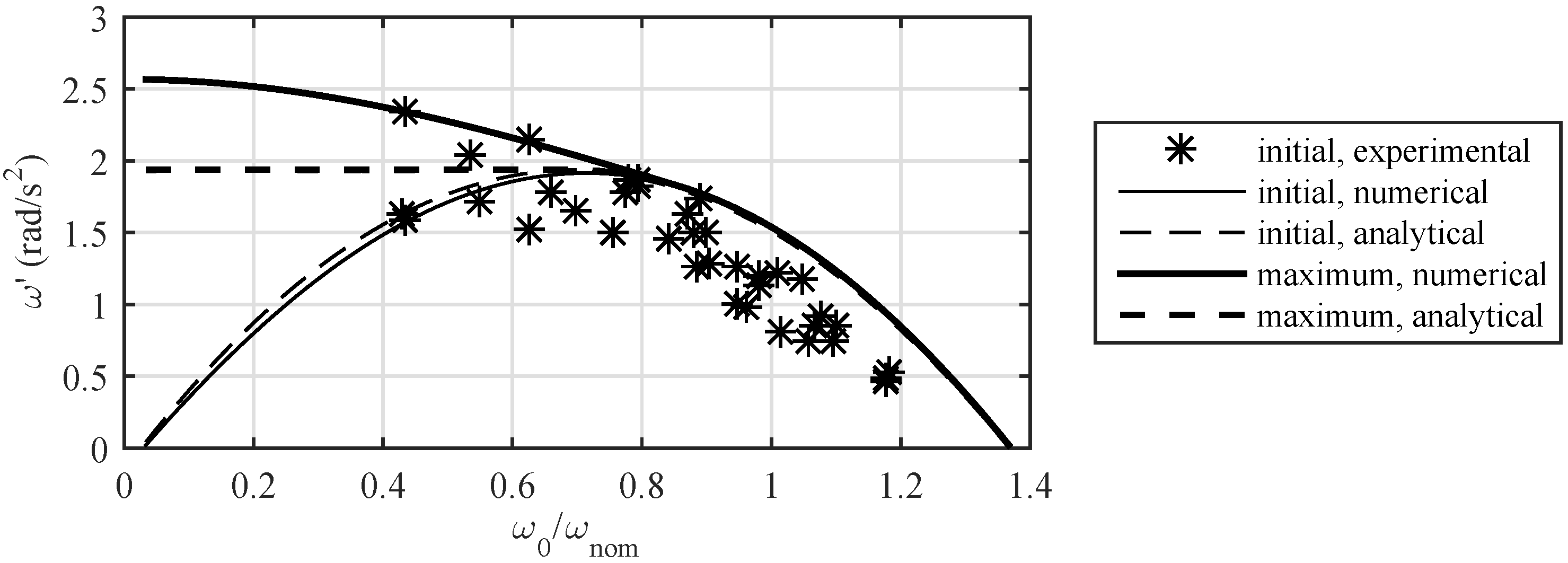
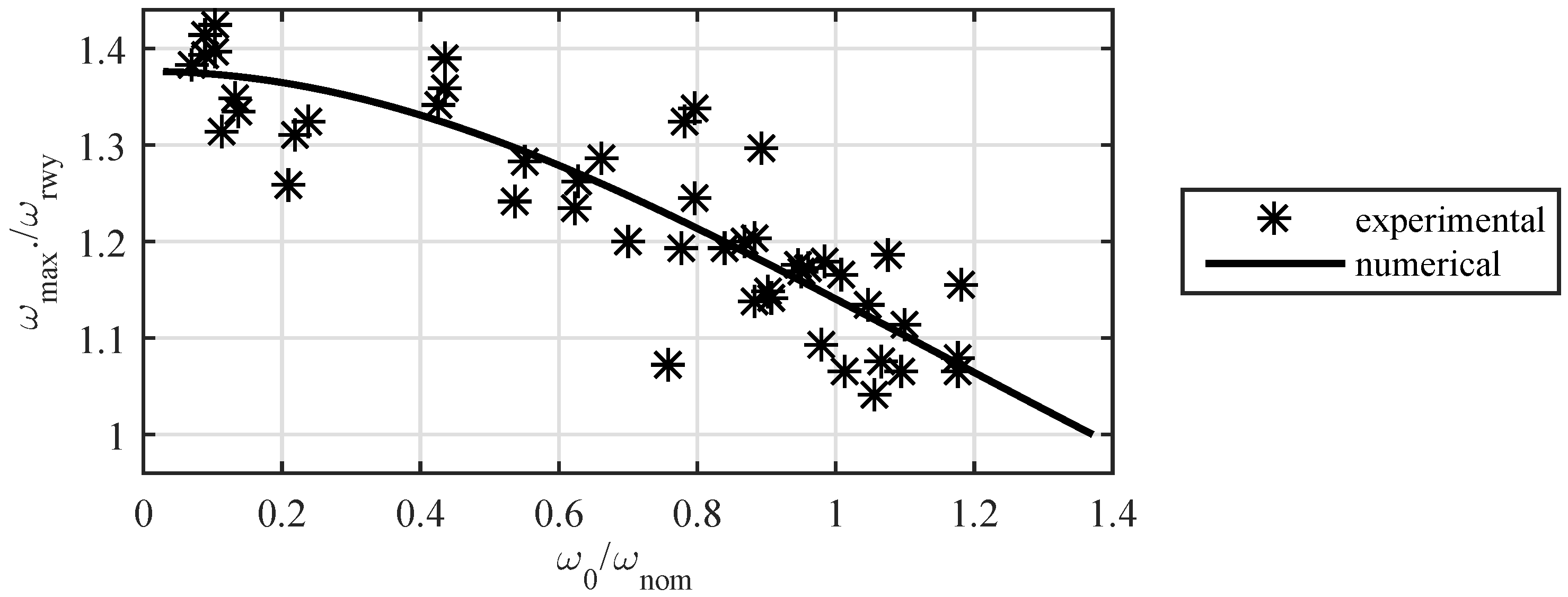
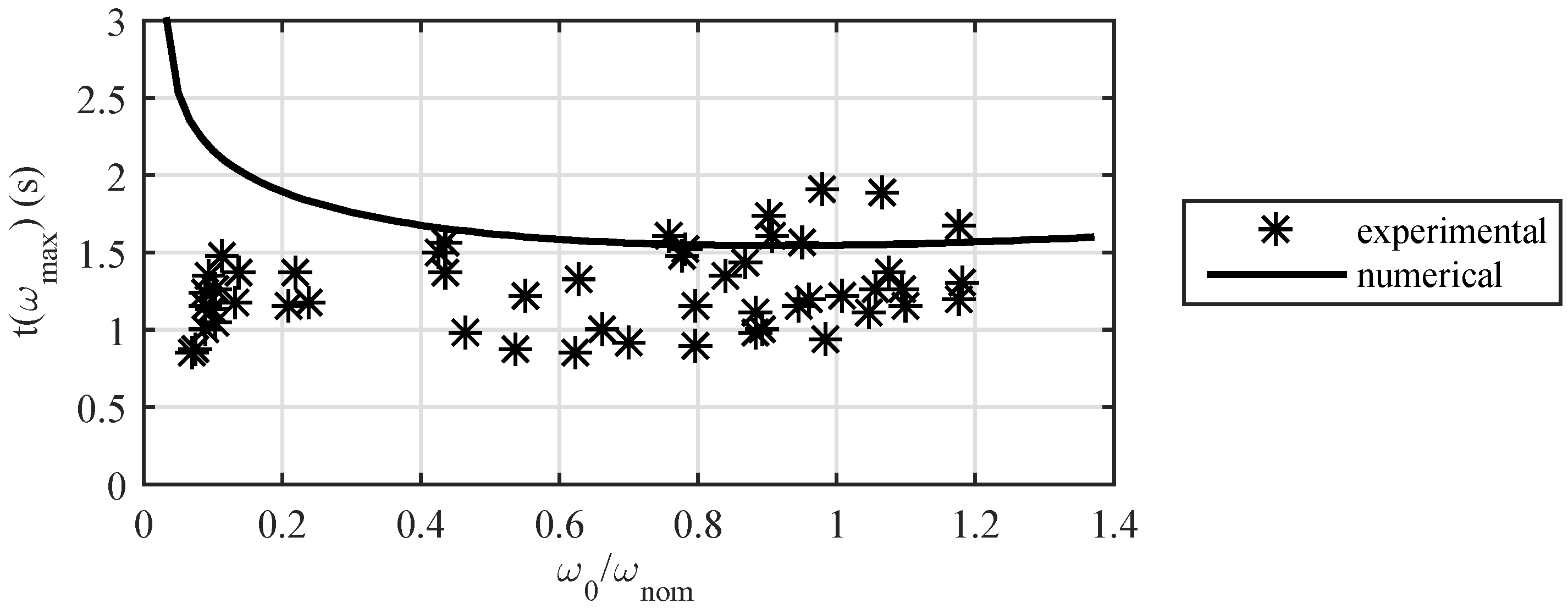
4.2. Comparison with Measured Data
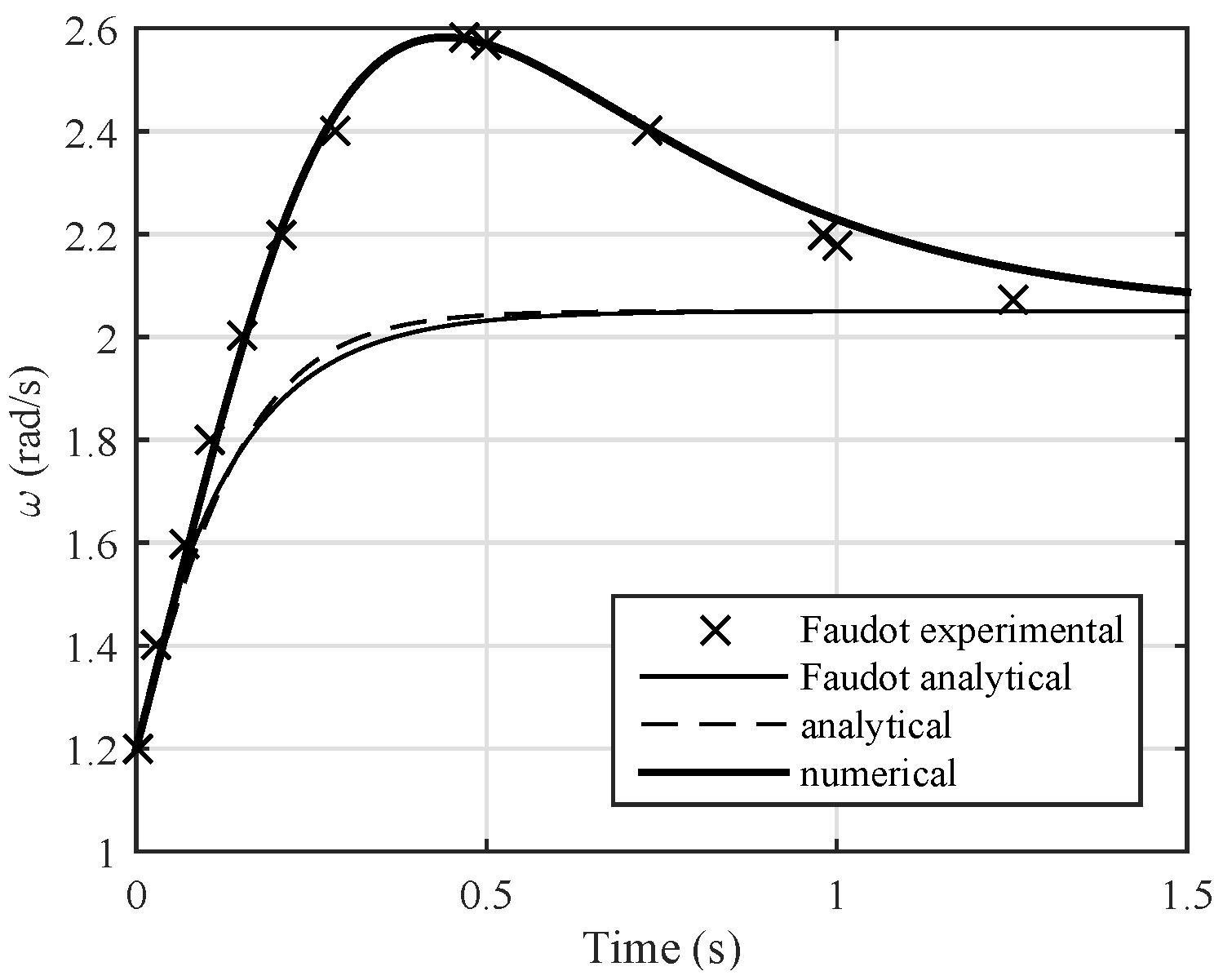
4.3. Comparison with Published Results
4.4. Application to Wind Power Turbine
4.5. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| rad/s | Angular velocity of turbine | |
| rad/s | Initial angular velocity | |
| rad/s | Peak angular velocity | |
| rad/s | Operational angular velocity | |
| rad/s | Runaway angular velocity | |
| rad/s | Nominal angular velocity | |
| u | m/s | Flow speed |
| u | m/s | Freestream flow speed |
| u | m/s | Flow speed seen by turbine |
| u | m/s | u in steady operation |
| u | m/s | Flow speed in the far wake |
| u | m/s | u when turbine is at |
| u | m/s | u when turbine is at |
| u | m/s | Flow speed at turbine runner |
| k | kg·m | Constant associated with hydrodynamic driving torque |
| k | kg·m | Constant associated with hydrodynamic torque loss |
| k | N·m | Torque loss constant |
| k | - | Steady speed constant |
| k | - | Operational volume size constant |
| t | s | Time at which occurs |
| s | Time between zero-crossings | |
| f | s | Electric frequency |
| E | J | Energy |
| E | J | Kinetic energy of operational volume |
| E | J | Rotational energy of rotating system |
| Q | N·m | Torque |
| Q | N·m | Hydrodynamic torque contribution |
| Q | N·m | Constant torque loss |
| Q | N·m | Torque due to connected load |
| Q | N·m | Torque due to iron losses in stator |
| P | W | Power |
| P | W | Power dissipated in load |
| P | W | Copper losses in generator windings |
| P | W | Power delivered by turbine in steady operation |
| P | W | Electric power |
| C | - | Power coefficient |
| J | kg·m | Inertia of rotating system |
| R | m | Turbine radius |
| D | m | Turbine diameter |
| m | Turbine cross-sectional area | |
| V | m | Operational volume |
| kg/m | Mass density of flow | |
| - | Tip speed ratio | |
| C | - | Constant of integration |
References
- Faudot, C.; Dahlhaug, O.G.; Holst, M.A. Tidal Turbine Blades in Runaway Situation: Experimental and Numerical Approaches. In Proceedings of the 10th European Wave and Tidal Energy Conference (EWTEC13), Aalborg, Denmark, 2–5 September 2013.
- Winter, A.I. Differences in Fundamental Design Drivers for Wind and Tidal Turbines. In Proceedings of the OCEANS 2011 IEEE-Spain, Santander, Spain, 6–9 June 2011; pp. 1–10.
- Hosseinimanesh, H.; Devals, C.; Nennemann, B.; Guibault, F. Comparison of steady and unsteady simulation methodologies for predicting no-load speed in Francis turbines. Int. J. Fluid Mach. Syst. 2015, 8, 155–168. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2nd ed.; Wiley: Chichester, UK, 2009. [Google Scholar]
- Eriksson, S.; Bernhoff, H. Loss evaluation and design optimisation for direct driven permanent magnet synchronous generators for wind power. Appl. Energy 2011, 88, 265–271. [Google Scholar] [CrossRef]
- Yuen, K.; Lundin, S.; Grabbe, M.; Lalander, E.; Goude, A.; Leijon, M. The Söderfors Project: Construction of an Experimental Hydrokinetic Power Station. In Proceedings of the 9th European Wave and Tidal Energy Conference (EWTEC11), Southampton, UK, 5–9 September 2011; pp. 1–5.
- Lundin, S.; Forslund, J.; Carpman, N.; Grabbe, M.; Yuen, K.; Apelfröjd, S.; Goude, A.; Leijon, M. The Söderfors Project: Experimental Hydrokinetic Power Station Deployment and First Results. In Proceedings of the 10th European Wave and Tidal Energy Conference (EWTEC13), Aalborg, Denmark, 2–5 September 2013.
- Kjellin, J.; Bülow, F.; Eriksson, S.; Deglaire, P.; Leijon, M.; Bernhoff, H. Power coefficient measurement on a 12 kW straight bladed vertical axis wind turbine. Renew. Energy 2011, 36, 3050–3053. [Google Scholar] [CrossRef]
- Deglaire, P.; Eriksson, S.; Kjellin, J.; Bernhoff, H. Experimental Results from a 12 kW Vertical Axis Wind Turbine with a Direct Driven PM Synchronous Generator. In Proceedings of the European Wind Energy Conference & Exhibition (EWEC 2007), Milan, Italy, 7–10 May 2007.




| Parameter | Value | |
|---|---|---|
| Turbine runner | Number of blades | 5 |
| Hydrofoil | NACA0021 | |
| Blade chord length | 0.18 m | |
| Blade height | 3.5 m | |
| Diameter | 6.0 m | |
| Generator | Number of poles | 112 |
| Nominal frequency | 14 s | |
| Winding resistance | 0.324 Ω/phase | |
| Iron loss torque | 110 N·m | |
| Rotating system | Mass moment of inertia | 3 000 kg·m |
| Mechanical torque loss | 350 N·m | |
| Nominal operation | Water flow speed | 1.4 m/s |
| Rotational speed | 15 rpm | |
| Angular velocity | 1.57 rad/s | |
| Output power | 7.5 kW | |
| Quantity | Value | |
|---|---|---|
| Freestream flow speed u | 1.42 m/s | |
| With load connected | Power P | 7 340 W |
| Angular velocity | 1.55 rad/s | |
| Without load (runaway) | Angular velocity | 2.15 rad/s |
| Cases | Unit | Note | (a) | (b) | (c) | (d) | |
|---|---|---|---|---|---|---|---|
| Modelling conditions | Initial angular velocity | rad/s | - | 0.052 | 1.21 | 1.49 | 1.85 |
| Normalized | - | - | 0.033 | 0.773 | 0.947 | 1.18 | |
| Freestream speed u | m/s | - | 1.43 | 1.41 | 1.41 | 1.40 | |
| Results | Initial acceleration | rad/s | Experimental | 0.281 | 1.77 | 1.01 | 0.528 |
| rad/s | Analytical | 0.045 | 1.90 | 1.63 | 0.894 | ||
| rad/s | Numerical | 0.024 | 1.87 | 1.60 | 0.801 | ||
| Peak angular velocity | rad/s | Experimental | 2.98 | 2.61 | 2.47 | 2.30 | |
| rad/s | Numerical | 2.98 | 2.60 | 2.47 | 2.25 | ||
| Relative runaway speed | - | Experimental | 1.38 | 1.21 | 1.15 | 1.07 | |
| Overshoot | - | Numerical | 1.38 | 1.21 | 1.14 | 1.05 | |
| Time of peak angular velocity | s | Experimental | 2.04 | 1.47 | 1.63 | 1.43 | |
| From release t | s | Numerical | 3.00 | 1.57 | 1.56 | 1.60 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lundin, S.; Goude, A.; Leijon, M. One-Dimensional Modelling of Marine Current Turbine Runaway Behaviour. Energies 2016, 9, 309. https://doi.org/10.3390/en9050309
Lundin S, Goude A, Leijon M. One-Dimensional Modelling of Marine Current Turbine Runaway Behaviour. Energies. 2016; 9(5):309. https://doi.org/10.3390/en9050309
Chicago/Turabian StyleLundin, Staffan, Anders Goude, and Mats Leijon. 2016. "One-Dimensional Modelling of Marine Current Turbine Runaway Behaviour" Energies 9, no. 5: 309. https://doi.org/10.3390/en9050309