1. Introduction
Load flow studies are essential for power system operators and planners, and accurate real-time load flow analysis is the basis of advanced application of modern EMS, such as optimal power flow, voltage control and so on. However, with the rapid increase in renewable energy (primarily wind and solar energy) which has strong volatility and intermittency, deterministic load flow (DLF) analysis cannot reflect the uncertainties of a power system properly. Therefore, the uncertainty of modern power grid needs to be qualified to analyze its influence on the power system.
Uncertainty quantification (UQ) [
1] is the science of quantitative characterization and reduction of uncertainties in applications. It tries to determine how likely certain outcomes are if some aspects of the system are not exactly known. Probabilistic load flow (PLF) evaluation is an efficacious UQ tool to tackle the uncertainties in power systems and obtain the statistical quantities of random output variables. Traditional PLF methods can be classified into four categories: simulation methods, approximate techniques, analytical methods and heuristic procedures.
The Monte Carlo method (MCM) [
2] is the most straightforward among simulation methods, but it requires DLF calculations at numerous sampling nodes even though some improvements have been proposed (such as Latin Hypercube [
3] and Quasi-Monte Carlo [
4] samplings). Approximate techniques provide approximate description of the statistical quantities of random output variables, and they include the point estimate method (PEM) [
5], first-order second-moment method (FOSM) [
6], non-parametric density estimate method [
7], state variable method (such as polynomial transformation [
3] and unscented transformation [
8]). However, the accuracy of an approximate technique worsens as the order of estimated statistical quantities becomes higher. Analytical methods include the FFT method [
9], the cumulants method (based on Gram-Charlier [
10,
11] Cornish Fisher [
12] and Legendre [
13] expansion)
etc.; they have a high calculation speed but require some algorithm simplifications which might introduce large errors. Heuristic methods mainly refer to the fuzzy logic method [
14]; it can handle the uncertain variables without statistical information (such as probability distribution function (PDF) and cumulative distribution function (CDF)).
A spectral method based on generalized polynomial chaos (gPC) expansion [
15,
16,
17,
18,
19,
20,
21] has become one of the most widely adopted UQ methods nowadays, which is efficient at uncertainty reduction and quantitative characterization for complex stochastic systems. The gPC-based methods represent system uncertain variables by truncated gPC series expansions, and gPC coefficients are computed by a stochastic collocation (SC) [
18,
19,
20,
21] or stochastic Galerkin (SG) approach [
18,
20]. The SC method is non-intrusive, and it solves a set of decoupled equations by repeatedly calling an existing deterministic solver at sampling nodes and obtaining gPC coefficients by post processing. It is easy to apply but has inferior accuracy due to “aliasing errors” [
16]. The intrusive SG method forms coupled deterministic equations by Galerkin projection and computes gPC coefficients directly. By ensuring the residue of the Galerkin system equations to be orthogonal to the linear space spanned by gPC basis functions, SG method offers the optimal accuracy with the least number of equations among all the gPC-based methods [
16]. However, the derived Galerkin system equations are usually coupled and high dimensioned, which makes them cumbersome to solve or even unsolvable.
In this paper, a spectral method based on the high-precision SG method was presented to solve PLF, and the cumbersome SG method is modified by utilizing the P-Q decoupling properties of load flow. Thus the proposed method can achieve high calculation speed and accuracy.
This paper is organized as follows: the basic ideas of gPC expansion and the PLF Galerkin system equations constructed by Galerkin projection are introduced in
Section 2.
Section 3 presents the modified SG method to solve the coupled equations of the PLF Galerkin system, while detailed derivations are given in
Appendix.
Section 4 studies the performances of the proposed method. Finally,
Section 5 concludes this paper.
2. PLF Model Based on gPC Expansion
2.1. gPC Expansion of Stochastic Variables
Define
as the univariate gPC polynomial of random variable
, index
as the polynomial order. Taking
as the set of D-variate gPC basis functions of muti-dimensional random variable
, the order of
equals
,
can be defined as follows:
The inner product of a random function is defined as:
where
denotes the inner product, and
denotes the PDF of variable
. Set
, where
is the Kronecker delta function. The orthogonal property of
is as follows:
According to UQ theory [
15,
16,
17], any R-valued random variable defined on a probability space
can be well approximated by a truncated gPC series. Thus
can be approximated by an order-P gPC series. In Equation (7), which contains K gPC basis functions,
denotes the gPC coefficient.
Replacing the index vector
by a scalar
:
,
,
, Equation (7) can be rewritten as:
With
, the mean and variance of
can be approximated by:
Similarly, other statistical quantities of can also be approximated by applying their definitions directly to the gPC approximation.
Generally in the modern power grid, the uncertain factors (such as fluctuations of wind speeds and loads,
etc.) are mutually dependent, and the impactions of their correlations are significant and cannot be ignored. Setting the PDF of D-dimensioned random variable
as
, and constructing the gPC basis function
according to
can achieve the optimal approximation convergence rate; the detailed procedure can be seen in [
16,
17]. The typical correspondence between the type of gPC basis function and their underlying random variables
is shown in
Table 1.
There are two ways to choose the gPC model. First, if all the random variables are the same type, we can directly choose the gPC basis, and
Table 1 shows some common conditions. Second, if the types of random variables are different or not common, we can directly construct the gPC basis. The two methods have been studied deeply in [
16,
17] and will not be elaborated on here. In this paper, in order to facilitate the following study and description, inverse transformation method and Cholescky decomposition [
22,
23] are used to transform various correlated random inputs into independent Gaussian random variables.
2.2. Construct Galerkin System of PLF Based on gPC
The original non-linear load flow equations for a power system can be expressed as:
The uncertainties of the power system can be depicted by random variables
; random inputs such as Gaussian distributed power loads and Weibull distributed wind speeds are expressed as
,
and
. Wind power generation can be derived by applying the wind speed in the power curve
of a wind turbine generator (see Equation (31)). Therefore, the P-order gPC series of
and
can be pre-calculated, and their gPC coefficients
,
are treated as known constants:
The unknown random outputs can also be expressed as:
Therefore, the following main task is to calculate the gPC coefficients
,
by SG method. Apply Equations (12) and (13) in load flow Equation (11) to obtain the PLF model, which is also called the residual PLF equations in the SG method. Express the residual equations in a vector-matrix form:
where
,
, vector
contains the active power balance equations of PQ and PV buses, vector
contains the reactive power balance equations of PQ buses. Define the matrices of coefficients
,
as follows:
Galerkin projection ensures residual Equation (14) to be orthogonal to the linear space spanned by gPC basis functions
forming a
dimensional PLF Galerkin system with
,
as follows:
The inner product in the right hand of Equation (16) is actually multivariate stochastic integration. Numerical quadrature such as Gaussian quadrature can be used to effectively evaluate the integral by a weighted sum of function values at specified grid points, that is:
where
and
are the quadrature nodes and weights that constructed by the cubature rule.
Among all the cubature rules, the tensor product rule is used to construct a full-grid point
and its corresponding weights
[
24], and the number of quadrature nodes equals
which increases exponentially with the dimensionality
of the integral. Thus, improved methods are proposed, such as a nested grid (with
) [
17], testing nodes (with
) [
20] and sparse grid [
16,
25]. The details of these cubature rules for constructing quadrature nodes are out of the scope of this paper. This paper applies the widely used sparse-grid technique, and software for generating sparse grids is available online [
26]. The sparse-grid technique uses a subset of the points from the tensor product rule and rescales the weight values appropriately; it can significantly decrease the computation expense especially when the dimensionality D is much larger than 1:
Set
, we can derive a constant matrix
by calculating the value of gPC basis function
at N sets of quadrature nodes:
Set
,
and
are the
elements in the vectors
and
respectively. Approximating Equation (16) by Gaussian quadrature, the PLF Galerkin system can be obtained:
Reshape matrices
and
into vectors:
where
reshape the
matrix whose elements are taken column-wise from matrix
.
3. Solve the PLF Galerkin System in a Decoupled Manner
Starting from an initial guess of
and
are computed by using the Newton iteration method to solve the Galerkin system Equation (20):
Superscript
means the
iteration, set
and Jacobian matrix
has the following structure:
Set
,
, and if
, the
element in the submatrix
can be calculated as follows, and more detailed derivation of
is given in the
Appendix.
At each iteration,
in
need to be evaluated at N quadrature nodes, and their sum needs to be calculated for each element in
. Therefore, the Newton’s iteration of SG is very expensive. Even if the power system is small and
is sparse, it can still be unsolvable. For example,
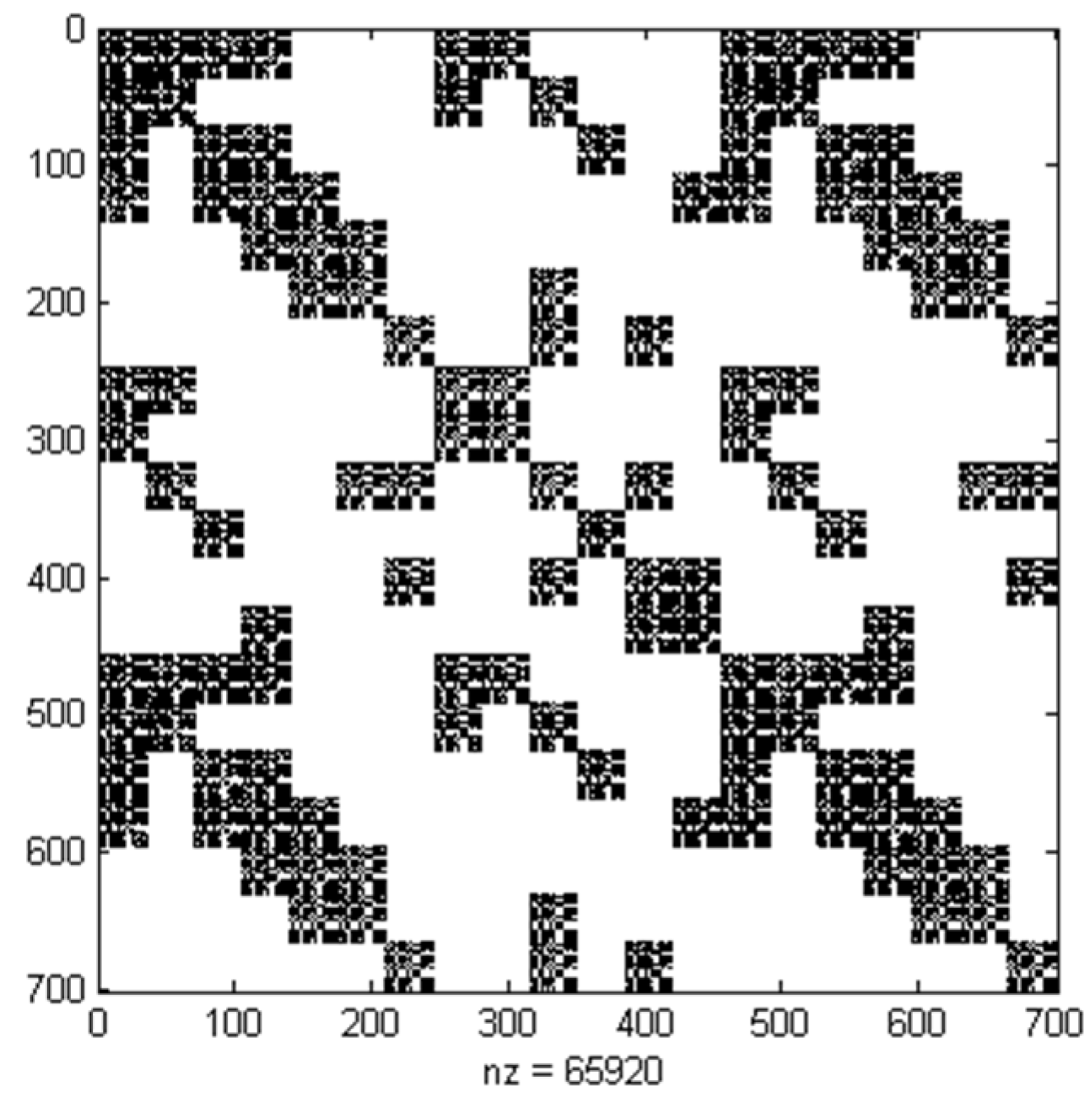
Figure 1 shows the structure of
in the IEEE 14-bus test system; if
,
,
, there will be 124 sub-blocks and 65,920 non-zeros in
and
calculation times are needed to renew
if L iterations are used.
Utilizing the P-Q decoupled characteristic in power flow calculation, this paper forms constant Jacobian matrices
and
to avoid the regeneration of Jacobian, the calculation speed will be significantly improved.
,
are the constant Jacobian matrices in the traditional P-Q fast decoupled load flow method [
27], which only contains network admittances:
Applying Equation (24) in the derivation of
above,
changed into two constant matrices
,
which only need to be calculated once (see the
Appendix).
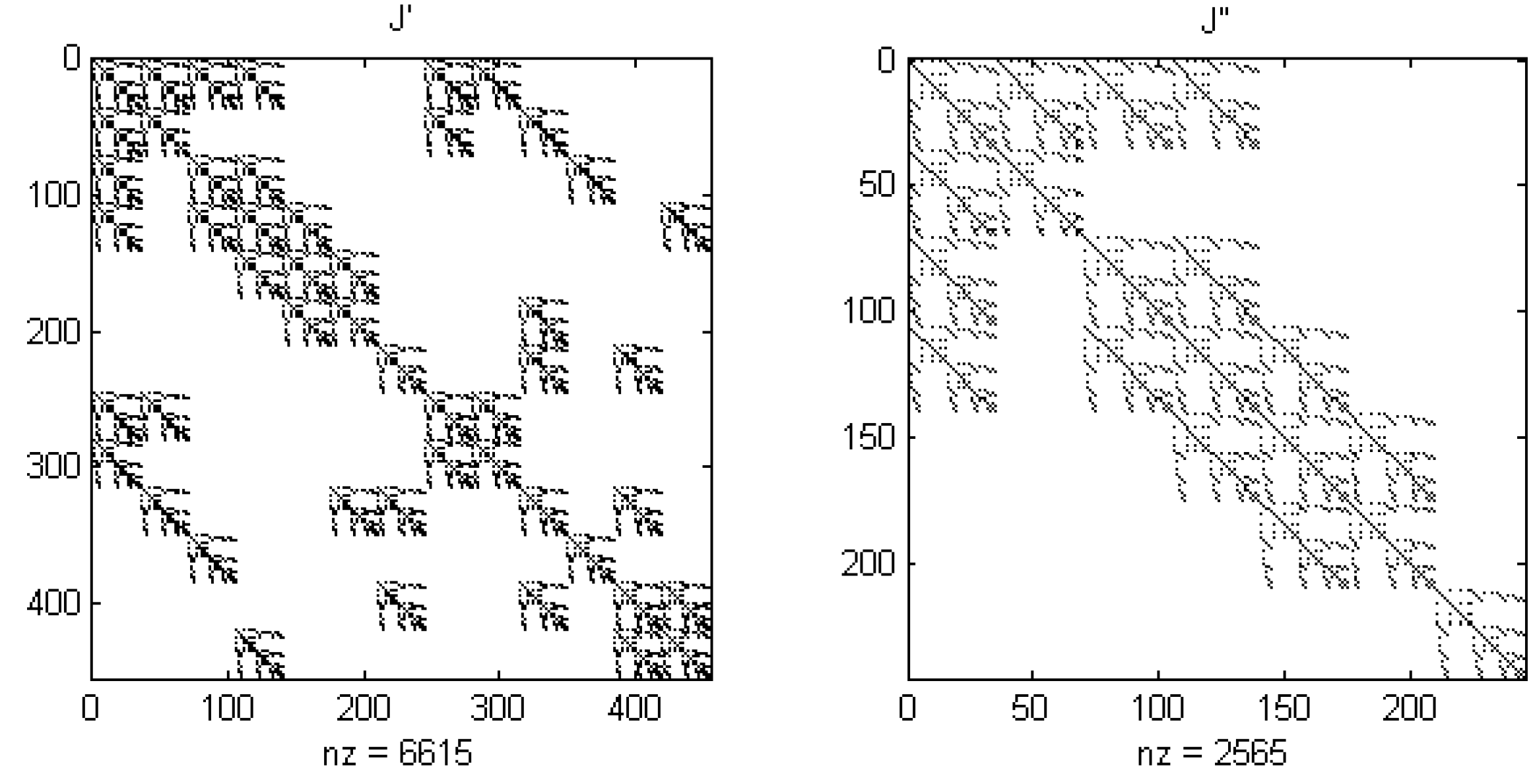
Figure 2 shows the structure of matrices
and
after the matrix
in
Figure 1 is decoupled; there will be 6615 and 2565 nonzeros in
and
, and
calculation times are needed, which is far less than before.
For ease of expression, N constant matrices
are constructed at N quadrature nodes:
Thus
and
can be expressed as:
,
can be computed directly by Newton iteration method:
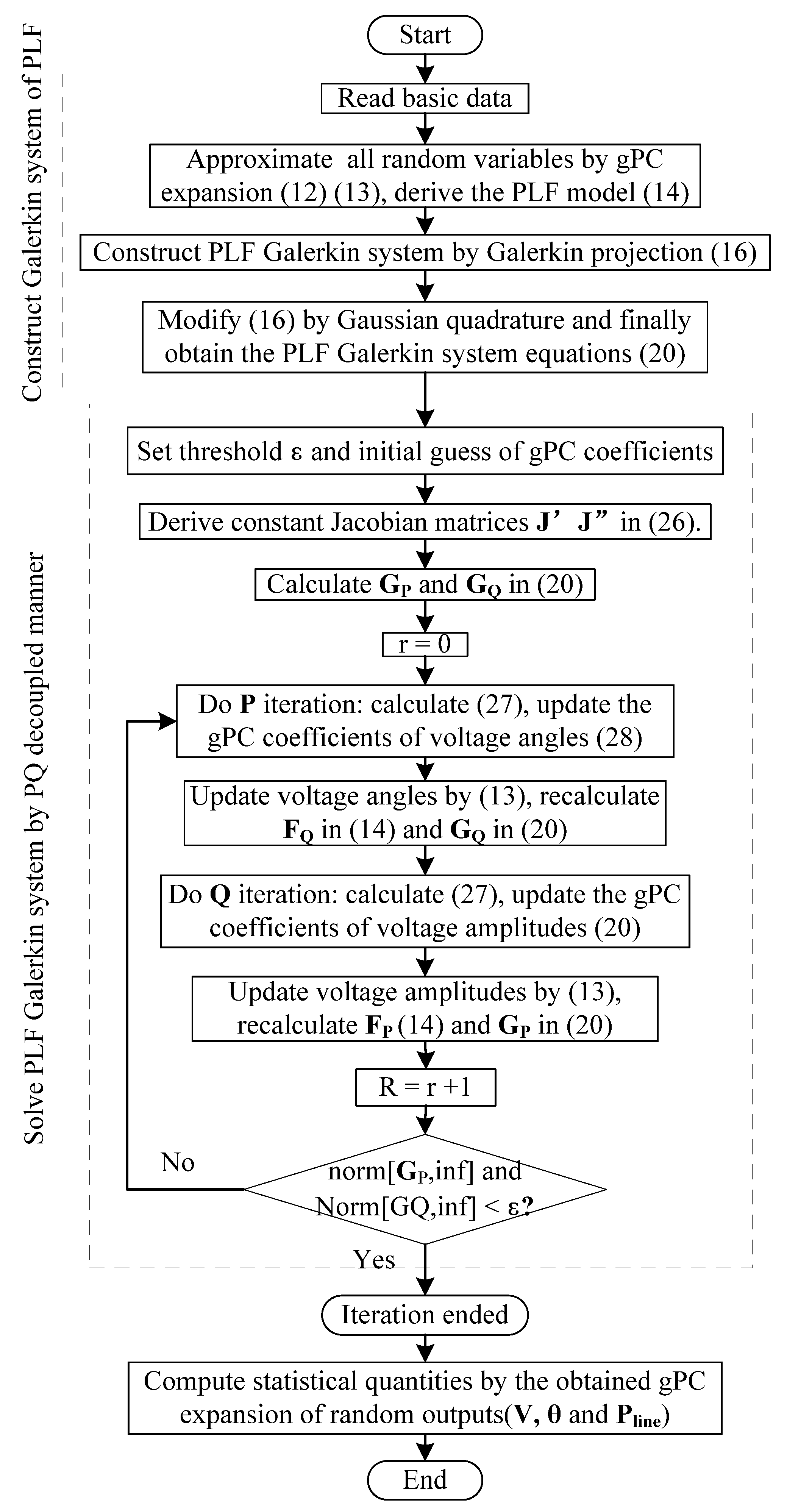
The proposed PLF method (referred to as SG-PLF method) only needs to compute deterministic PLF Galerkin system Equation (20) and construct constant Jacobian matrices Equation (26) at limited quadrature nodes, then solve Equation (20) by the Newton iteration method only once to reach high accuracy. The flow chart of the SG-PLF method is depicted by
Figure 3, which consists of two parts.
Firstly, based on the system basic data and PDF of input random variables, we form the PLF model Equation (14) based on gPC expansion of random variables and transform it into Equation (16) by Galerkin projection, then further approximate Equation (16) by Gaussian quadrature, and finally obtain the PLF Galerkin system Equation (20). Secondly, we solve the Galerkin system for coefficients directly by a Newton iteration method, and the gPC expansion of random output variables can be derived easily.
4. Comparison with other PLF Methods
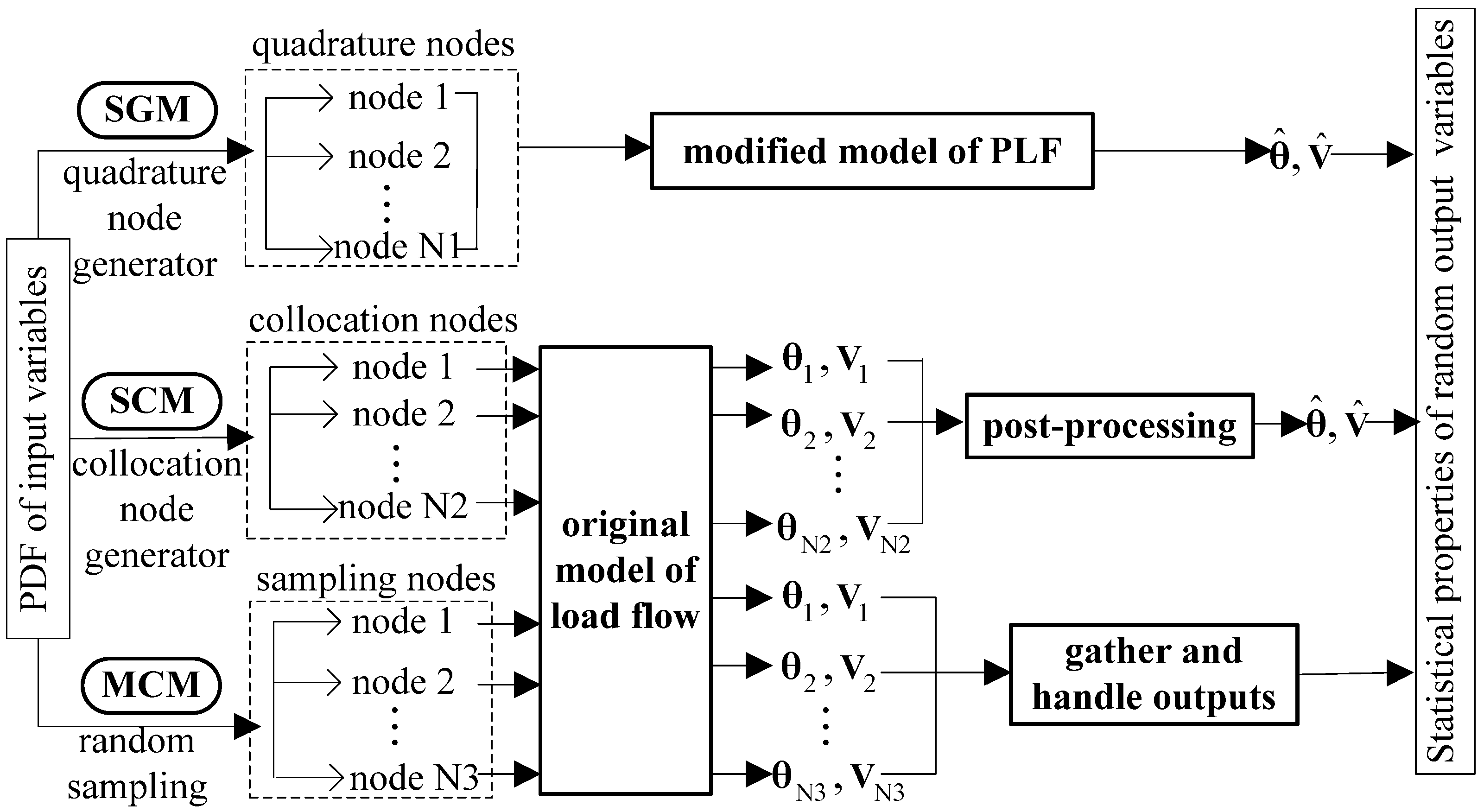
This section compares the calculation procedures of MCM, SC method (SCM) and the proposed modified SG method (SGM); see
Figure 4.
MCM and SCM are both non-intrusive methods, they both start from the original load flow Equation (11) without using gPC approximation
a priori, and compute the deterministic solutions at a set of nodes. The main difference of MCM and SCM lies in how to select the nodes. MCM draws sampling nodes randomly according to the PDF of
and is uncertainty-dimension independent; the MCM may be the only choice when the number of random variables to be dealt with is too high (in ultra-high-dimensional problem). However, SCM constructs collocation nodes with a nodes generator which uses cubature rules such as tensor product, nested grid or sparse grid techniques. After repeatedly simulating deterministic load flow equations, MCM provides the statistical information by gathering and handling the resulting outputs, whereas SCM reconstructs the gPC coefficients in a post-processing step such as numerical integration. For example, SCM constructs
collocation nodes
and weights
of random output variable
(in Equation (8)), and then the gPC coefficients can be computed by:
The SGM is an intrusive method as it directly computes the gPC coefficients by simulating a larger-size coupled PLF only once. With gPC approximation, it starts from the residual function Equation (14). The proposed SG-PLF method constructs nodes by sparse grid technique and modified the SGM by utilizing the P-Q decoupling properties of power system, which can avoid the heavy computation burden of forming Jacobian matrix in each iteration.
Figure 5 shows a detailed illustration of the modified calculation model of the proposed SG-PLF method.
If the original load flow Equation (11) are solved by P-Q fast decouple method, and the time cost of solving is then the total time cost by MCM is where is much larger than and If the node generators in SCM and SGM are both using the sparse grid technique, where set the time for constructing nodes is and the time cost of post-processing is Thus, the total time cost of SCM is In SGM, the times needed for constructing constant Jacobian matrices are and for solving the modified model are so the total time required for SGM is .
The dimension of modified PLF model in SGM is times the size of the original PLF model, and the equations need to be solved in SCM is times the size of the original PLF model. can be ignored, and is slightly larger than , so there are no significant difference between the total computational time of SCM and SGM , this can be verified in the following case study.
In conclusion, on the one hand, since is much larger than and , MCM needs numerous deterministic load flow calculations to obtain accurate results, the SG-PLF method has a distinct speed advantage over MCM. On the other hand, SCM only requires no errors at each collocation node and will introduce aliasing errors caused by the introduction of the nodal sets, whereas the SG-PLF method ensures that the residue of the PLF Equation (14) is orthogonal to the linear space spanned by the gPC basis functions, as in Equation (16). In this sense, the accuracy of SGM is optimal.
Therefore, the proposed SG-PLF method has accuracy advantage over the non-intrusive SCM and speed advantage over the MCM.
5. Case study
5.1. Verification Index
In order to evaluate the computational accuracy and efficiency of SG-PLF method, a series of PLF studies are carried out on the modified IEEE14-bus and IEEE 118-bus test systems. The base case data of these two test systems are available in [
28]. Two types of input random variables are considered in this case study, load and wind power included. Relative error
(RE) [
5] and average root mean square (ARMS) [
12] error
are computed using the MCM results of 30,000 trials as reference. RE is defined as:
The ARMS is defined as:
where
refers to the type of random output variables (
,
and
etc.),
may refer to the mean
and standard deviation
denotes the result calculated by MCM and is taken as the reference value,
is the result obtained by SG-PLF method.
and
are the average and maximum values of
Choosing T sampling nodes of variable
arbitrarily:
,
and
are the outputs of the SG-PLF method and MCM at the
node
.
5.2. IEEE 14-Bus Test System
The case considered in this section is the IEEE 14-bus test system which is modified to include wind generation. The uncertainties of forecasted loads are modeled as normal distribution with
5% to
, whose means equal the base case data. The load correlation matrix between bus 4 and bus 5 is
. Two wind farms are located at bus 13 and bus 14, and their wind speed correlation matrix is
:
The wind power is mainly affected by wind speed distribution, power curve and control strategy of wind turbine generator. The wind speed is assumed to follow the Weibull distribution with scale parameter as 10.7 and shape parameter as 3.97. The wind speed is transformed into wind power according to the power curve of wind turbine generator
[
3]: the cut-in, rated and cut-off speeds are
respectively, and the rated power
is 0.7 p.u. The wind turbine generator is controlled by constant power factor strategy.
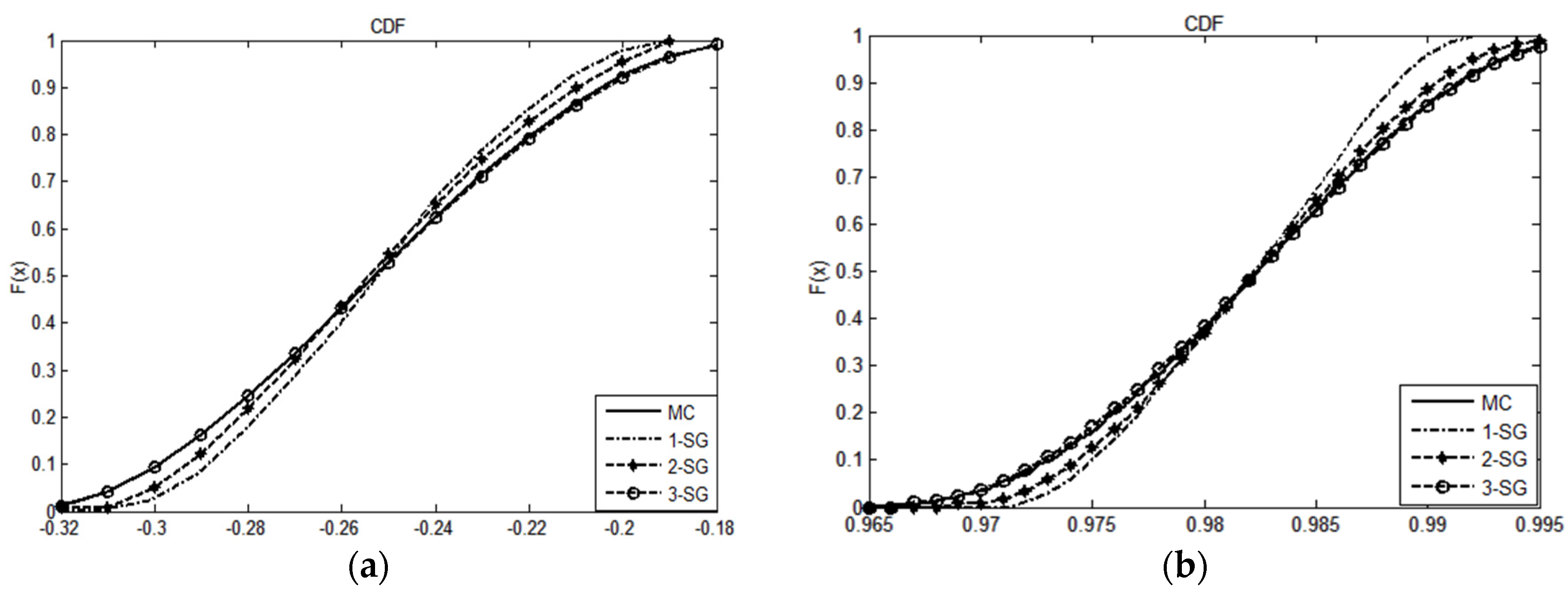
5.2.1. Impact of the gPC Expansion Order
Figure 6 shows the CDFs obtained by SG-PLF method under different gPC expansion order P (defined in Equation (7)). The results shows that the order-3 SG-PLF method provides good fitting to the CDF obtained by MCM, gives an intuitive confirmation that the order-3 SG-PLF method has the ability to well handle over the PLF problem as almost the same accuracy as the MCM.
Furthermore, the resulted
and
under different order P are shown in
Table 2, which verified the good computing performance of the order-3 SG-PLF method.
Therefore, the gPC expansion order P can affect the calculation performance of the proposed method: when P is too low, the gPC expansion approximation Equation (8) will induce large truncation error; when P is too high, the number of quadrature nodes N will increase significantly, so it will lead to increasing of calculation but no progress in computation accuracy, because all the high order gPC coefficients in gPC expansion approximation Equation (8) will be zeros. In this paper, the expansion order is chosen by numerical experiments, but direct methods to determine the order are to be further studied in our future work.
To further investigate the calculation efficiency of using the SGM to solve PLF, the calculation time and nodes number N of SGM, SCM and MCM are compared in
Table 3, in which, the gPC-based SCM and SGM both construct the nodes according to the sparse grid technique, and the time cost with different P are compared.
Figure 7 shows the PDFs and CDFs of the buses whose power injection have large fluctuations, and the results corresponding to the order-3 SG-PLF method are almost not visible because they coincide with those of MCM.
From the results above, the order-3 SG-PLF method can maintain high accuracy with feasible computation expense. This conclusion is further confirmed by comparing the ARMS results of the order-3 SG-PLF method in
Table 4. Thus in the following study, the order-3 SG-PLF method is used for PLF investigation and verification.
Take the frequency table of
as an example, set the results of MCM as the reference, and further compare the calculation accuracy of order-3 SCM and order-3 SGM, shown in
Table 5:
In this section, the results above show that:
(1) the MCM can achieve the highest accuracy, but it needs the longest calculation time; and
(2) although the computational speed of SGM is slightly slower than SCM, the intrusive SGM has obvious precision advantage than SCM (which is also analyzed in
Section 4).
Therefore, through comprehensive consideration of calculation speed and accuracy, the proposed SG-PLF method is the optimal among three methods.
5.2.2. Impact of the Fluctuation of Power Injection
In order to appraise how the variation level of uncertain variable impacts on the calculation performance of the proposed order-3 SG-PLF method,
Table 6 shows the
and
of proposed method under different load fluctuations at bus 4 (set the ratio of
to
is from 10% to 40%).
From the results, it can be inferred that the variance level of power injection has no discernible effect on the calculation accuracy of the proposed method.
5.2.3. Impact of Wind Speed Correlation
Choose the statistical moments of active line power (mean and standard deviation ) as the research objects in this section. The uncertain wind powers of two wind farms are directly injected into both the end of lines 13–14, while lines 1–2 have no direct connection to wind power.
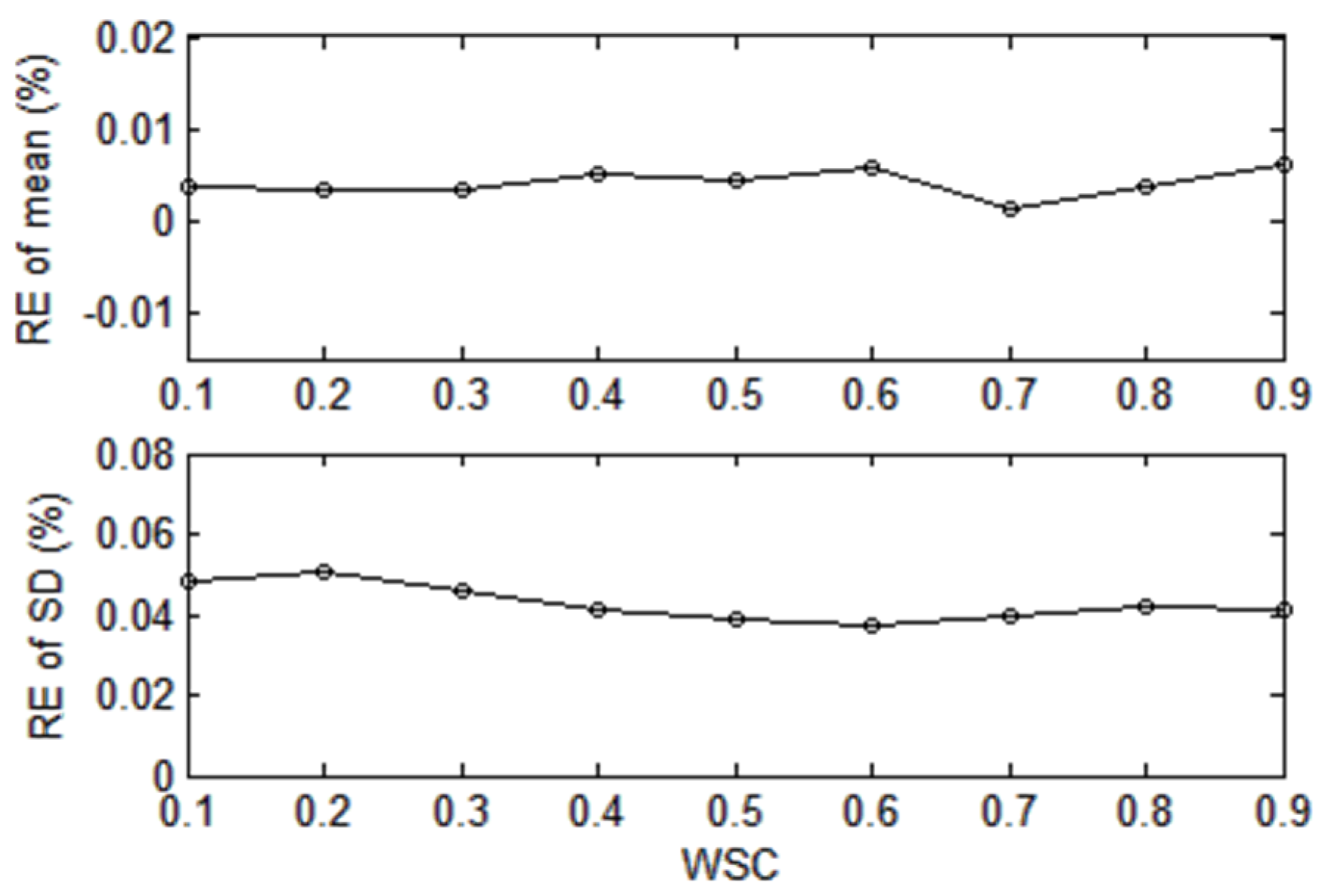
Under different wind speed correlations (WSC) between two wind farms,
Figure 8 and
Figure 9 present the calculated mean and standard deviation (SD) values of the REs of all buses and illustrate how the calculation accuracy of the proposed 3-order SG-PLF method will change with the WSC growing from 0.1 to 0.9. The results show that WSC has a minor effect on the calculation accuracy of the proposed method.
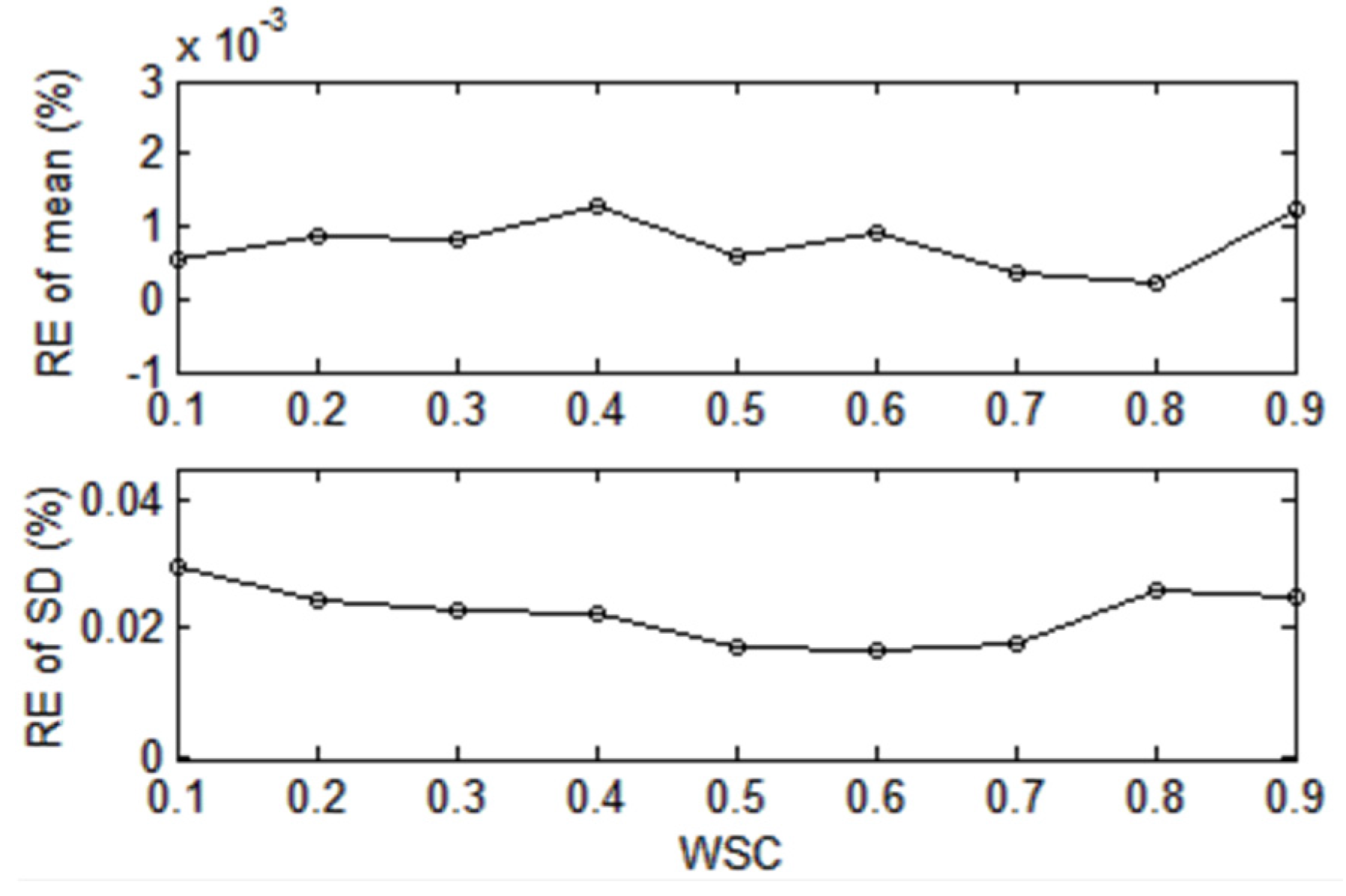
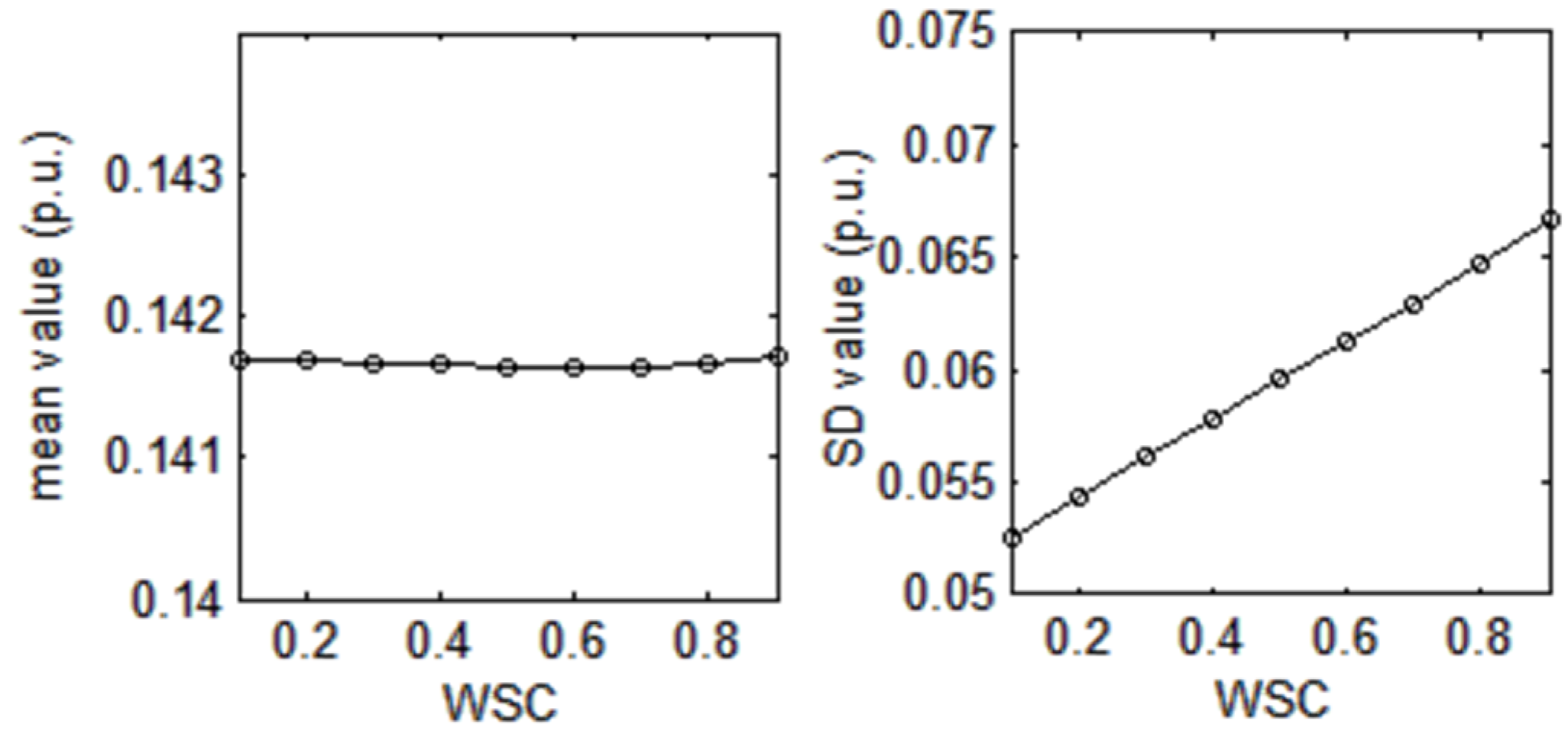
Figure 10 and
Figure 11 present the values of
and
with WSC growing from 0.1 to 0.9. Results show that, at different sites, the WSC has different impact on system condition.
remains basically unchanged but
is proportional to WSC, while
are all proportional to WSC.
5.3. IEEE 118-Bus Test System
In this section, PLF problem is solved for the IEEE 118-bus test system with the purpose of assessing how an increase in the uncertainty level (dimension and variance of random variables) would affect the performance of proposed method. From bus 24 to bus 27, each bus is connected to a wind farm, the rated power of each wind turbine generator
is 0.2 p.u. The random active loads at bus 60, bus 78, bus 79 and bus 82 are assumed to follow Gaussian distribution. The variance of the random loads are larger than the previous case, with
is 10% to
. The correlation matrices of wind speeds and loads are in Equation (33). Other parameters of wind farms are consistent with the previous case.
To solve this case, the calculation time of MCM is 16.436 s while the order-3 SG-PLF method only takes 3.306 s. The RE and ARMS results of the proposed method are shown in
Table 7, where the maximum RE values of
and
appeared at bus 26 and bus 49.
Figure 12 shows the resulting CDFs and PDFs of
and
which proved the calculation accuracy of the proposed order-3 SG-PLF method again. Therefore, when the variance and dimension of uncertain variables rise, the proposed method can maintain high accuracy whilst providing significant computational savings.
Based on all of the previous simulation results, the details of some influencing factors on the performance of the proposed SG-PLF method are summarized in
Table 8, where
denotes increase,
means decrease,
presents minor impact.
6. Conclusions
An intrusive spectral method was proposed in this paper to solve the PLF problem, and simulations in IEEE 14-bus and 118-bus test systems demonstrate its accuracy, efficiency and practicability. The main characteristics of the proposed method are as follows:
High accuracy. The accuracy of proposed method mainly depends on the gPC expansion approximation Equation (7); by properly choosing the type of gPC basis function and the expansion order P, the proposed methods can offer the optimal accuracy with the least number of equations among all the gPC-based methods.
Low computation burden. By fully utilizing the P-Q decoupling properties of load flow, the proposed method formed two constant Jacobian matrices in Newton’s iterations, which reduces the computation cost significantly.
Comprehensibility of the results. The gPC expansion can efficiently handle various random variables and form a functional relationship between the system random inputs and outputs, which is also known as the uncertainty propagation in UQ theory. Thus it can efficiently illustrate the effect of the random inputs on the outputs in PLF problem.
Since the future operating conditions of power system involve more uncertainty due to the growing penetration of distributed generation and renewable energy sources, the proposed method may be increasingly desirable. We believe that it would encourage more interest in UQ research for power systems, with more sophisticated uncertainties and less expenditures of calculation time and resources.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant 50907034, and in part by the National Key Basic Research Program of China (973 Program) under Grant 2012CB215203. The work of Y. Sun was supported by the China Scholarship Council for a one-year sabbatical study in the Galvin Center at the Illinois Institute of Technology, Chicago, IL, USA.
Author Contributions
Yingyun Sun proposed the research topic, modified the calculation model and revised the paper. Rui Mao designed the original model, performed the simulation, analyzed the data and wrote the draft of the paper. Zuyi Li and Wei Tian polished the manuscript and corrected spelling and grammar mistakes. All authors contributed to the writing of the manuscript, and have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Jacobian matrices in PQ decoupled method |
| Nonlinear active, reactive load flow equations |
| Vector-matrix form of |
| PLF Galerkin system derived from |
| Index of bus |
| Constant Jacobian matrices in SG-PLF |
| Number of PQ and PV bus |
| Active and reactive powers injected to bus |
| The gPC expansion coefficient of |
| Active power line flow |
| Number of Newton’s iterations |
| PQ and PV bus sets |
| Wind speed of wind farm |
| Bus voltage angle and amplitude |
| Vector-matrix form of |
| The gPC expansion coefficient of |
| Vector-matrix form of |
| Kronecker product operator |
Appendix
Applying the gPC expansion of
and
(see Equation (13)) in the derivation of Jacobian matrix
:
From the above derivation, we can see that the elements in Jacobian
are complex and need to be renewed during each iteration,
are the constant Jacobian matrices in a traditional P-Q fast decoupled load flow method [
18], and the partial derivatives in
above can be rewritten as follows:
For
:
For
:
Applying
in the derivation of
above,
changed into two constant Jacobian matrices
and
, which is shown as follows:
References
- Lin, G.; Engel, D.W.; Esliner, P.W. Survey and Evaluate Uncertainty Quantification Methodologies. PNNL-20914 Rep. Richland. 2012. Available online: http://web.stanford.edu/group/uq/events/UQLS_stanford/Iaccarino.pdf (accessed on 1 March 2016).
- Borkowska, B. Probabilistic load flow. IEEE Trans. Power Appl. Syst. 1974, PAS-93, 752–759. [Google Scholar] [CrossRef]
- Cai, D.F.; Shi, D.Y.; Chen, J. Probabilistic load flow computation with polynomial normal transformation and Latin hypercube sampling. Gener. Transm. Distrib. 2013, 7, 474–482. [Google Scholar] [CrossRef]
- Cui, T.; Franchetti, F. A Quasi-Monte Carlo Approach for Radial Distribution System Probabilistic Load Flow. In Proceeding of the Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–6.
- Morales, M.J.; Pérez-Ruiz, J. Point Estimate Schemes to Solve the Probabilistic Power Flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
- Dopazo, J.F.; Klitin, O.A.; Sasson, M.A. Stochastic load flows. IEEE Trans. Power Appl. Syst. 1975, 94, 752–759. [Google Scholar] [CrossRef]
- Soleimanpour, N.; Mohammadi, M. Probabilistic load flow by using nonparametric density estimators. IEEE Trans. Power Syst. 2013, 28, 3747–3755. [Google Scholar] [CrossRef]
- Morteza, A.; Mahmud, F. Probabilistic Load Flow in Correlated Uncertain Environment Using Unscented Transformation. IEEE Trans. Power Syst. 2012, 27, 2233–2241. [Google Scholar]
- Kolba, D.; Parks, W. A prime factor FFT algorithm using high-speed convolution. IEEE Trans. Acoust. Speech Signal 1977, 25, 281–294. [Google Scholar] [CrossRef]
- Zhang, P.; Lee, S.T. Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion. IEEE Trans. Power Syst. 2004, 19, 676–682. [Google Scholar] [CrossRef]
- Fan, M.; Vittal, V. Probabilistic Power Flow Studies for Transmission Systems with Photovoltaic Generation Using Cumulants, IEEE Trans. Power Syst. 2012, 27, 2251–2261. [Google Scholar] [CrossRef]
- Usaola, J. Probabilistic load flow with correlated wind power injections. Electr. Power Syst. Res. 2010, 80, 528–536. [Google Scholar] [CrossRef]
- Ruiz-Rodriguez, F.; Hernandez, J.; Jurado, F. Harmonic modelling of PV systems for probabilistic harmonic load flow studies. Int. J. Circuit Theory Appl. 2015, 43, 1541–1565. [Google Scholar] [CrossRef]
- Alireza, S.; Mehdi, E. A possibilistic-probabilistic tool for evaluating the impact of stochastic renewable and controllable power generation on energy losses in distribution networks-a case study. Renew. Sustain. Energy 2011, 15, 794–800. [Google Scholar]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Maitre, L.; Knio, O.; Omar, M. Spectral Methods for Uncertainty Quantification; Springer Netherlands: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Pulch, R. Stochastic Collocation and Stochastic Galerkin Methods for Linear Differential Algebraic Equations. Available online: http://www.imacm.uni-wuppertal.de/fileadmin/imacm/preprints/2012/imacm_12_31.pdf (accessed on 1 March 2016).
- Xiu, D.; Hesthaven, J.S. High-order collocation methods for differential equations with random inputs. SIAM J. Sci. Comput. 2005, 27, 1118–1139. [Google Scholar] [CrossRef]
- Zhang, Z.; El-Moselhy, T.A.; Elfadel, I.M.; Daniel, L. Stochastic testing method for transistor-level uncertainty quantification based on generalized polynomial chaos. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2013, 32, 1533–1545. [Google Scholar] [CrossRef]
- Tang, J.J.; Ni, F.; Ponci, F.; Monti, A. Dimension-adaptive sparse grid interpolation for uncertainty quantification in modern power systems: Probabilistic power flow. IEEE Trans. Power Syst. 2015, 31, 907–919. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.Y.; Yan, W.; Yu, J.; Zhao, X. Probabilistic Optimal Power Flow Considering Correlations of Wind Speeds Following Different Distributions. IEEE Trans Power Syst. 2014, 29, 1847–1854. [Google Scholar] [CrossRef]
- Aien, M.; Firuzabad, M.F. Probabilistic optimal power flow in correlated hybrid Wind–Photovoltaic power systems. IEEE Trans. Power Syst. 2014, 5, 130–138. [Google Scholar] [CrossRef]
- Smolyak, S.A. Quadrature and interpolation formulas for tensor products of certain classes of functions. Soviet Math. 1963, 4, 240–243. [Google Scholar]
- Gerstner, T.; Griebel, M. Numerical integration using sparse grids. Numer. Algorithms. 1998, 18, 209–232. [Google Scholar] [CrossRef]
- MATLAB Source Codes. Available online: http://people.sc.fsu.edu/~jburkardt/m_src/m_src.html (accessed on 15 October 2011).
- Stott, B.; Alsac, O. Fast decoupled load flow. IEEE Trans. Power App. Syst. 1974, PAS-93, 859–869. [Google Scholar] [CrossRef]
- Power Systems Test Case Archive. Available online: http://www.ee.washington.edu/research/pstca (accessed on 1 March 2016).
Figure 1.
Structure of Jacobian matrix for an IEEE 14-bus test system with D = 4 before decoupling.
Figure 1.
Structure of Jacobian matrix for an IEEE 14-bus test system with D = 4 before decoupling.
Figure 2.
Structure of Jacobian matrix for IEEE 14-bus test system with D = 4 after decoupling.
Figure 2.
Structure of Jacobian matrix for IEEE 14-bus test system with D = 4 after decoupling.
Figure 3.
Flow chart of the proposed SG-PLF method.
Figure 3.
Flow chart of the proposed SG-PLF method.
Figure 4.
Calculation procedure of PLF by SGM, SCM and MCM.
Figure 4.
Calculation procedure of PLF by SGM, SCM and MCM.
Figure 5.
Modified calculation model of SG-PLF.
Figure 5.
Modified calculation model of SG-PLF.
Figure 6.
CDFs of and under 1–3 order in IEEE-14 system: (a) ; (b) .
Figure 6.
CDFs of and under 1–3 order in IEEE-14 system: (a) ; (b) .
Figure 7.
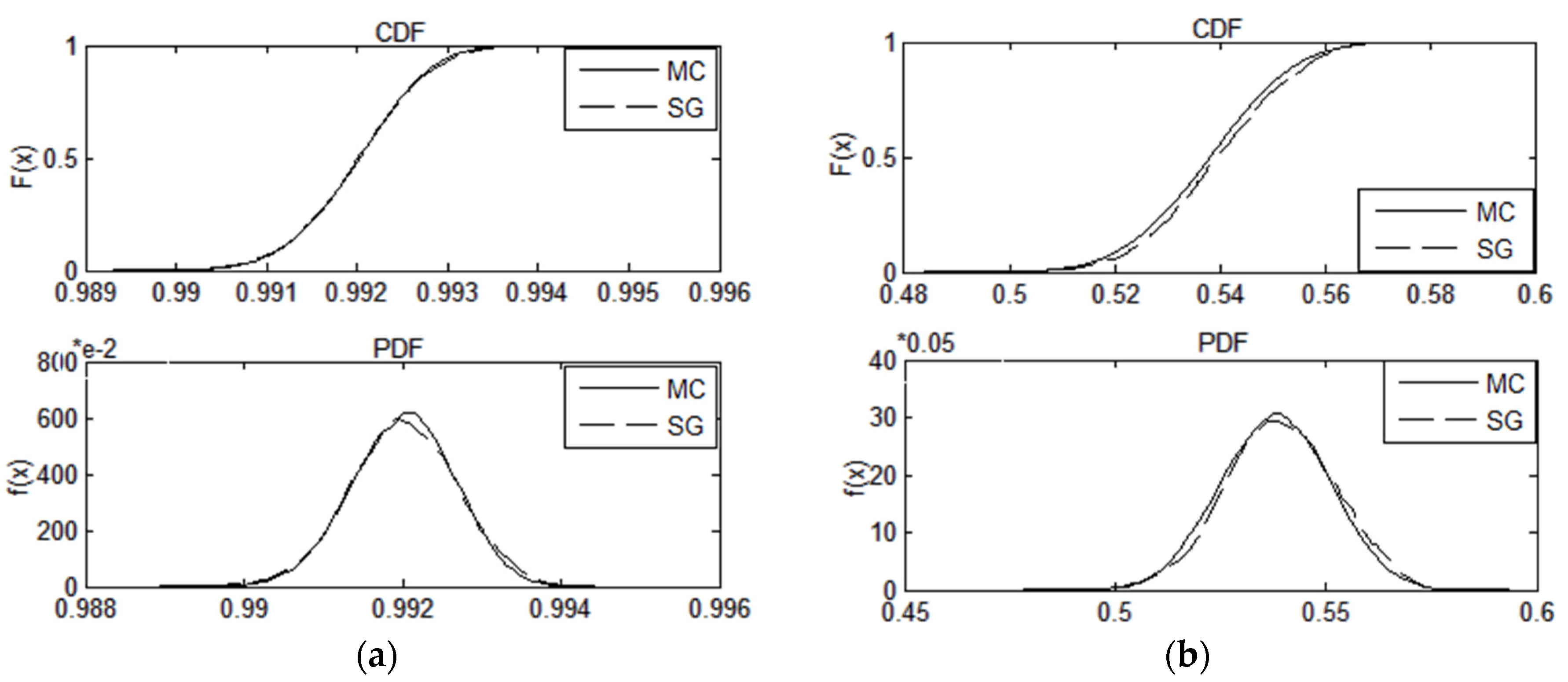
PDFs and CDFs of θ, V at the bus which has large fluctuation: (a) θ14(rad); (b) V4(p.u.).
Figure 7.
PDFs and CDFs of θ, V at the bus which has large fluctuation: (a) θ14(rad); (b) V4(p.u.).
Figure 8.
of 3-order SG-PLF method under different WSC.
Figure 8.
of 3-order SG-PLF method under different WSC.
Figure 9.
of 3-order SG-PLF method under different WSC.
Figure 9.
of 3-order SG-PLF method under different WSC.
Figure 10.
of 3-order SG-PLF under different WSC.
Figure 10.
of 3-order SG-PLF under different WSC.
Figure 11.
of 3-order SG-PLF under different WSC.
Figure 11.
of 3-order SG-PLF under different WSC.
Figure 12.
CDFs and PDFs of and in IEEE-118 system: (a) (p.u.); (b) (rad).
Figure 12.
CDFs and PDFs of and in IEEE-118 system: (a) (p.u.); (b) (rad).
Table 1.
Correspondence of gPC and their underlying random variables.
Table 1.
Correspondence of gPC and their underlying random variables.
| Variable Type | gPC Basis Function |
|---|
| Continuous | Gaussian | Hermite-gPC |
| Gamma | Lauguerre-gPC |
| Beta | Jacobi-gPC |
| Uniform | Legendre-gPC |
| Discrete | Binomial | Krawtchouk-gPC |
| Poisson | Charlier-gPC |
| Negative binomial | Meixner-gPC |
| Hypergeometric | Hahn-gPC |
Table 2.
Mean and maximum of ER of SG-PLF under 1-3 order.
Table 2.
Mean and maximum of ER of SG-PLF under 1-3 order.
| Order-P | | |
|---|
| s = μ | s = σ | s = μ | s = σ |
|---|
| 1 | 8.38 × 10−2 | 6.34 | 9.16 × 10−2 | 8.17 |
| 2 | 2.14 × 10−2 | 3.88 | 1.07 × 10−2 | 8.06 |
| 3 | 8.69 × 10−4 | 0.332 | 1.13 × 10−3 | 2.32 |
| 1 | 1.01 | 7.90 | 2.50 | 10.3 |
| 2 | 0.745 | 6.02 | 1.33 | 8.65 |
| 3 | 7.78 × 10−2 | 0.582 | 0.139 | 0.920 |
Table 3.
Computation time comparison.
Table 3.
Computation time comparison.
| Method | Expansion Order P | MCM |
|---|
| 1 | 2 | 3 |
|---|
| SCM | SGM | SCM | SGM | SCM | SGM |
|---|
| Time/s | 0.011 | 0.011 | 0.053 | 0.099 | 0.188 | 0.298 | 13.326 |
| Nodes (N) | 9 | 41 | 145 | 30,000 |
Table 4.
Mean and maximum of ARMS of order-3 SG-PLF method.
Table 4.
Mean and maximum of ARMS of order-3 SG-PLF method.
| ARMS | | |
|---|
| Mean | 1.60 × 10−4 | 1.24 × 10−5 |
| Maximum | 3.13 × 10−4 | 2.14 × 10−5 |
Table 5.
The frequency table of different methods.
Table 5.
The frequency table of different methods.
| Distribution Interval of | Probability/100% |
|---|
| MCM | SGM | SCM |
|---|
| [1.0122,1.0146) | 0.96 | 0.96 | 0.95 |
| [1.0146,1.0169) | 3.76 | 3.64 | 3.36 |
| [1.0169,1.0193) | 7.68 | 7.79 | 8.17 |
| [1.0193,1.0216) | 12.08 | 11.88 | 11.35 |
| [1.0216,1.0240) | 15.12 | 15.54 | 15.69 |
| [1.0240,1.0263) | 16.64 | 16.43 | 16.16 |
| [1.0263,1.0287) | 15.28 | 15.31 | 15.52 |
| [1.0287,1.0311) | 15.12 | 15.10 | 15.03 |
| [1.0311,1.0334) | 8.56 | 8.69 | 8.97 |
| [[1.0334,1.0358] | 5.04 | 5.01 | 4.80 |
Table 6.
Mean and maximum of RE of order-3 SG-PLF with different load variance.
Table 6.
Mean and maximum of RE of order-3 SG-PLF with different load variance.
| Ratio | | |
|---|
| s = μ | s = σ | s = μ | s = σ |
|---|
| 10% | 2.76 × 10−3 | 0.899 | 1.15 × 10−2 | 4.44 |
| 20% | 2.21 × 10−3 | 0.618 | 8.78 × 10−3 | 4.55 |
| 30% | 2.65 × 10−3 | 0.422 | 1.37 × 10−2 | 4.58 |
| 40% | 2.83 × 10−3 | 0.369 | 1.12 × 10−2 | 4.23 |
| 10% | 0.316 | 2.48 | 0.737 | 3.11 |
| 20% | 0.182 | 2.13 | 0.265 | 3.19 |
| 30% | 0.264 | 1.27 | 0.771 | 2.55 |
| 40% | 0.498 | 1.75 | 0.653 | 1.41 |
Table 7.
Mean and maximum ERs and ARMSs of 3-order SG-PLF.
Table 7.
Mean and maximum ERs and ARMSs of 3-order SG-PLF.
| x | | | | |
|---|
| μ | σ | μ | σ |
|---|
| 1.74 × 10−3 | 0.91 | 8.01 × 10−3 | 1.56 | 2.09 × 10−6 | 3.40 × 10−5 |
| 0.313 | 2.15 | 0.962 | 7.54 | 1.56 × 10−5 | 6.11 × 10−5 |
Table 8.
Summary on the factors influencing the performance of the proposed SG-PLF method.
Table 8.
Summary on the factors influencing the performance of the proposed SG-PLF method.
| Impacting Factor | Accuracy | Speed |
|---|
| Expansion order (P) | | |
| Efficiency of node generator | | |
| Dimension of random inputs | | |
| Dimension of random outputs | | |
| Variance of random inputs | | |
| WSC | | |
| Size of test system | | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).