A Review of Modeling Bioelectrochemical Systems: Engineering and Statistical Aspects
Abstract
:1. Introduction
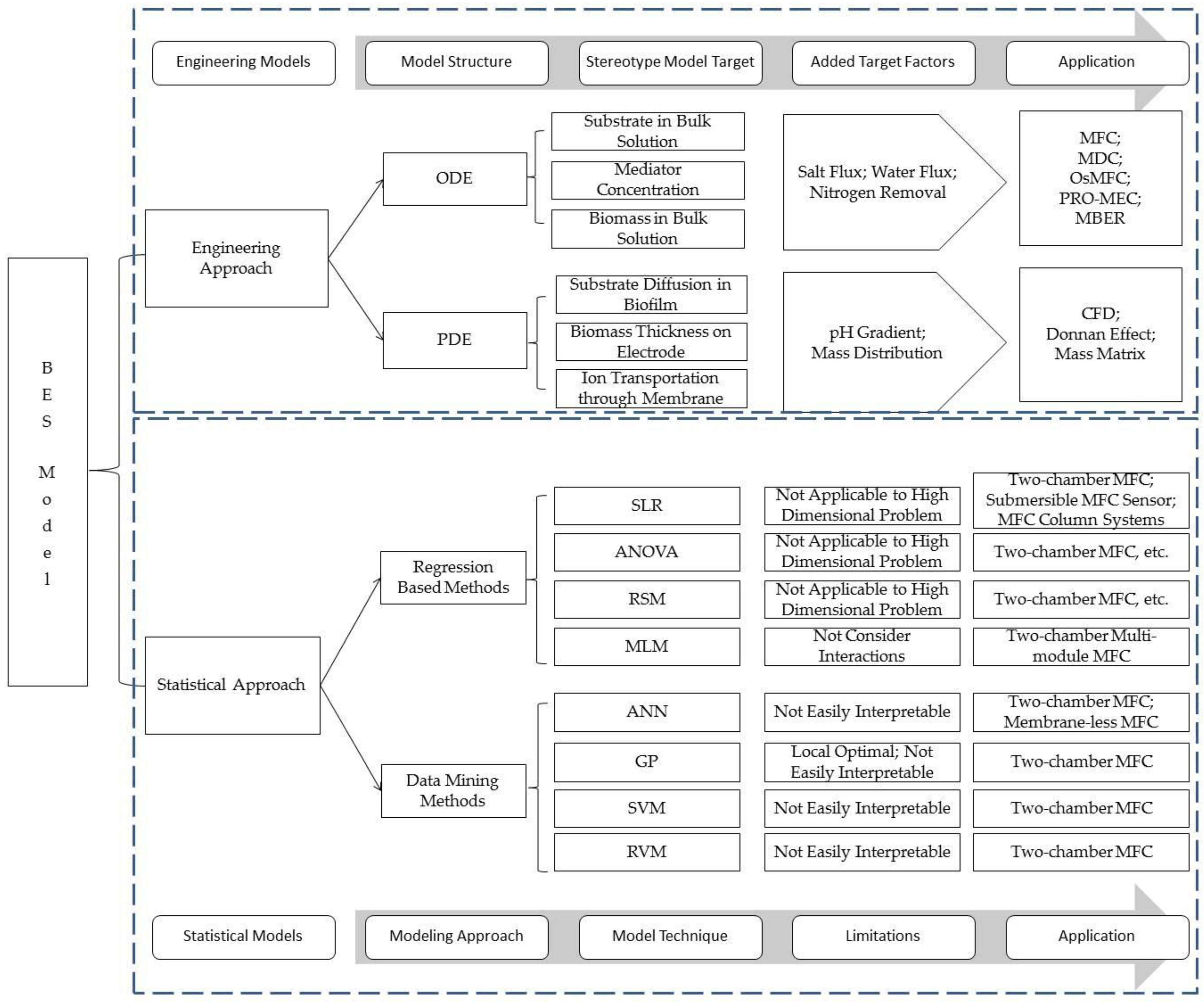
2. Engineering Models
2.1. Overview
2.2. Ordinary Differential Equations
2.2.1. Introduction of Ordinary Differential Equations
2.2.2. Ordinary Differential Equation Stereotypes in Bioelectrochemical Systems
2.2.3. Applications of Ordinary Differential Equation Stereotypes
2.2.4. Advantages and Limitations
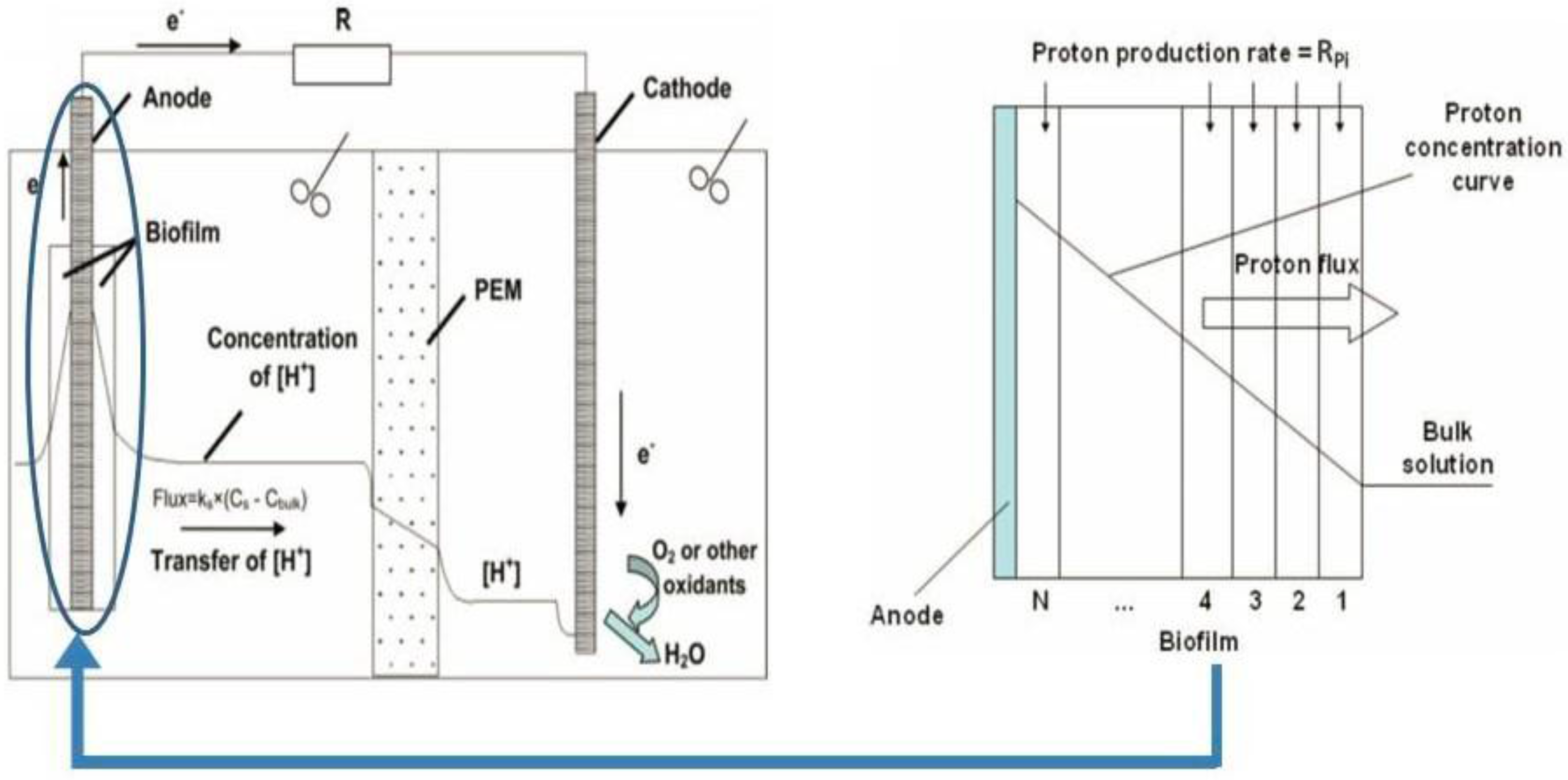
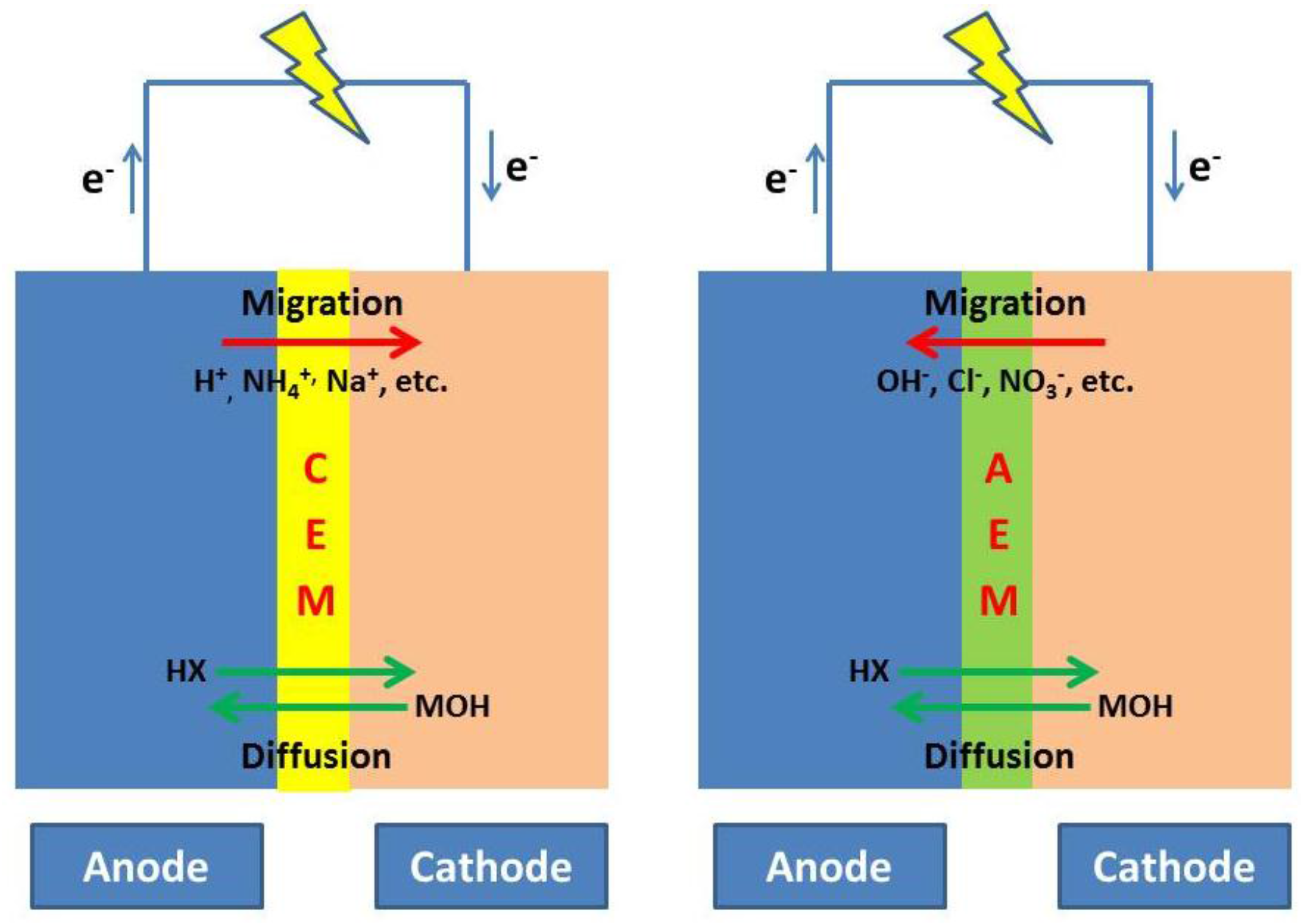
2.3. Partial Differential Equations
2.3.1. Introduction of Partial Differential Equations
2.3.2. Partial Differential Equation Stereotypes in Bioelectrochemical Systems
2.3.3. Applications of Partial Differential Equation Stereotypes
2.3.4. Advantages and Limitations
2.4. Model Adjustment and Validation
2.4.1. Sensitivity Analysis of Model Parameters
2.4.2. Model Validation
3. Statistical Modeling
3.1. Overview
3.2. Data Generation
3.3. Linear Regression
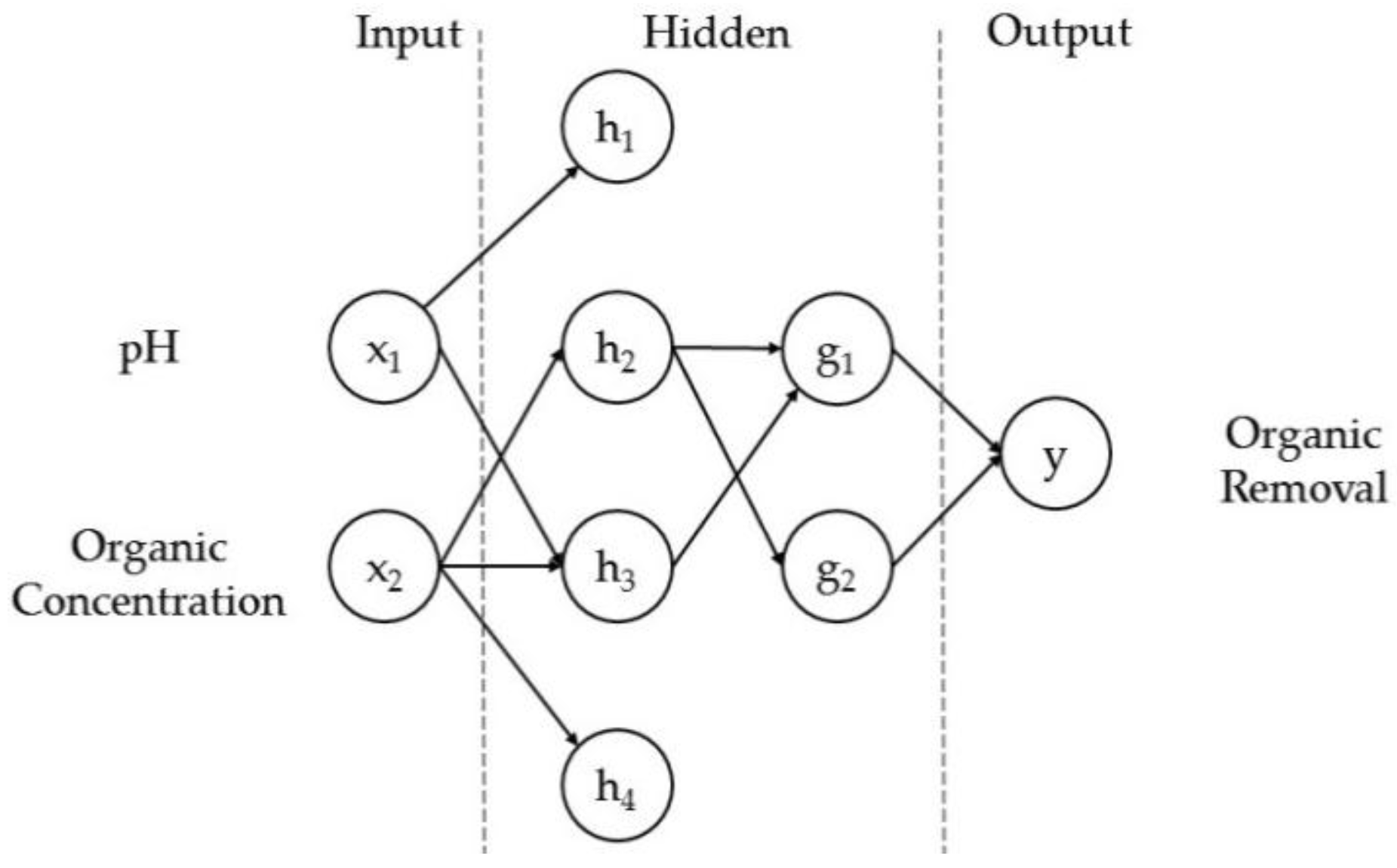
3.4. Data Mining Methods
3.5. Model Diagnostic
3.6. Variable Selection
4. Perspective
4.1. Variable Selection
4.2. Modeling with Functional Data
4.3. Data Fusion
4.4. Hybrid Models
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, W.; Yu, H.; He, Z. Towards sustainable wastewater treatment by using microbial fuel cells-centered technologies. Energy Environ. Sci. 2013, 7, 911–924. [Google Scholar] [CrossRef]
- Pant, D.; Singh, A.; Van Bogaert, G.; Olsen, S.I.; Nigam, P.S.; Diels, L.; Vanbroekhoven, K. Bioelectrochemical systems (BES) for sustainable energy production and product recovery from organic wastes and industrial wastewaters. RSC Adv. 2012, 2, 1248–1263. [Google Scholar] [CrossRef]
- Wang, H.; Luo, H.; Fallgren, P.H.; Jin, S.; Ren, Z.J. Bioelectrochemical system platform for sustainable environmental remediation and energy generation. Biotechnol. Adv. 2015, 33, 317–334. [Google Scholar] [CrossRef] [PubMed]
- Mohanakrishna, G.; Srikanth, S.; Pant, D. Bioelectrochemical Systems (BES) for Microbial Electroremediation: An Advanced Wastewater Treatment Technology. In Applied Environmental Biotechnology: Present Scenario and Future Trends; Springer: New Delhi, India, 2015; pp. 145–167. [Google Scholar]
- McCarty, P.L.; Bae, J.; Kim, J. Domestic wastewater treatment as a net energy producer—Can this be achieved? Environ. Sci. Technol. 2011, 45, 7100–7106. [Google Scholar] [CrossRef] [PubMed]
- Logan, B. Food and Light Bulbs. Environ. Sci. Technol. Lett. 2014, 1, 442. [Google Scholar] [CrossRef]
- Wang, H.; Park, J.D.; Ren, Z.J. Practical energy harvesting for microbial fuel cells: A review. Environ. Sci. Technol. 2015, 49, 3267–3277. [Google Scholar] [CrossRef] [PubMed]
- Logan, B.E.; Hamelers, B.; Rozendal, R.; Schröder, U.; Keller, J.; Freguia, S.; Aelterman, P.; Verstraete, W.; Rabaey, K. Microbial fuel cells: Methodology and Technology. Environ. Sci. Technol. 2006, 40, 5181–5192. [Google Scholar] [CrossRef] [PubMed]
- Kelly, P.T.; He, Z. Nutrients removal and recovery in bioelectrochemical systems: A review. Bioresour. Technol. 2014, 153, 351–360. [Google Scholar] [CrossRef] [PubMed]
- Oon, Y.-L.; Ong, S.-A.; Ho, L.-N.; Wong, Y.-S.; Dahalan, F.A.; Oon, Y.-S.; Lehl, H.K.; Thung, W.-E. Synergistic effect of up-flow constructed wetland and microbial fuel cell for simultaneous wastewater treatment and energy recovery. Bioresour. Technol. 2016, 203, 190–197. [Google Scholar] [CrossRef] [PubMed]
- Santoro, C.; Soavi, F.; Serov, A.; Arbizzani, C.; Atanassov, P. Self-powered supercapacitive microbial fuel cell: The ultimate way of boosting and harvesting power. Biosens. Bioelectron. 2016, 78, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, U.; Jin, W.; Pervez, A.; Bhatti, Z.A.; Tariq, M.; Shaheen, S.; Iqbal, A.; Mahmood, Q. Anaerobic microbial fuel cell treating combined industrial wastewater: Correlation of electricity generation with pollutants. Bioresour. Technol. 2016, 200, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Qin, M.; Molitor, H.; Brazil, B.; Novak, J.T.; He, Z. Recovery of nitrogen and water from landfill leachate by a microbial electrolysis cell-forward osmosis system. Bioresour. Technol. 2015, 200, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Escapa, A.; Mateos, R.; Martínez, E.; Blanes, J. Microbial electrolysis cells: An emerging technology for wastewater treatment and energy recovery. From laboratory to pilot plant and beyond. Renew. Sustain. Energy Rev. 2016, 55, 942–956. [Google Scholar] [CrossRef]
- Rosenbaum, M.; He, Z.; Angenent, L.T. Light energy to bioelectricity: Photosynthetic microbial fuel cells. Curr. Opin. Biotechnol. 2010, 21, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Ge, Z.; Grimaud, J.; Hurst, J.; He, Z. Long-term performance of liter-scale microbial fuel cells treating primary effluent installed in a municipal wastewater treatment facility. Environ. Sci. Technol. 2013, 47, 4941–4948. [Google Scholar] [CrossRef] [PubMed]
- Zhi, W.; Ge, Z.; He, Z.; Zhang, H. Methods for understanding microbial community structures and functions in microbial fuel cells: A review. Bioresour. Technol. 2014, 171, 461–468. [Google Scholar] [CrossRef] [PubMed]
- Logan, B.E. Scaling up microbial fuel cells and other bioelectrochemical systems. Appl. Microbiol. Biotechnol. 2010, 85, 1665–1671. [Google Scholar] [CrossRef] [PubMed]
- Ortiz-Martínez, V.M.; Salar-García, M.J.; De Los Ríos, A.P.; Hernández-Fernández, F.J.; Egea, J.A.; Lozano, L.J. Developments in microbial fuel cell modeling. Chem. Eng. J. 2015, 271, 50–60. [Google Scholar] [CrossRef]
- Song, H.-L.; Zhu, Y.; Li, J. Electron transfer mechanisms, characteristics and applications of biological cathode microbial fuel cells—A mini review. Arab. J. Chem. 2015. [Google Scholar] [CrossRef]
- He, Z.; Kan, J.; Mansfeld, F.; Angenent, L.T.; Nealson, K.H. Self-Sustained Phototrophic Microbial Fuel Cells Based on the Synergistic Cooperation between Photosynthetic Microorganisms and Heterotrophic Bacteria. Environ. Sci. Technol. 2009, 43, 1648–1654. [Google Scholar] [CrossRef] [PubMed]
- Pendyala, B.; Chaganti, S.R.; Lalman, J.A.; Heath, D.D. Optimizing the performance of microbial fuel cells fed a combination of different synthetic organic fractions in municipal solid waste. Waste Manag. 2016. [Google Scholar] [CrossRef] [PubMed]
- Recio-Garrido, D.; Perrier, M.; Tartakovsky, B. Modeling, optimization and control of bioelectrochemical systems. Chem. Eng. J. 2016, 289, 180–190. [Google Scholar] [CrossRef]
- Ki, D.; Popat, S.C.; Torres, C.I. Reduced overpotentials in microbial electrolysis cells through improved design, operation, and electrochemical characterization. Chem. Eng. J. 2016, 287, 181–188. [Google Scholar] [CrossRef]
- Choi, S. Microscale microbial fuel cells: Advances and challenges. Biosens. Bioelectron. 2015, 69, 8–25. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Abu-Reesh, I.; He, Z. Development of Bioelectrochemical Systems to Promote Sustainable Agriculture. Agriculture 2015, 5, 367–388. [Google Scholar] [CrossRef]
- Rozendal, R.A.; Hamelers, H.V.; Rabaey, K.; Keller, J.; Buisman, C.J. Towards practical implementation of bioelectrochemical wastewater treatment. Trends Biotechnol. 2008, 26, 450–459. [Google Scholar] [CrossRef] [PubMed]
- Sleutels, T.H.; Ter Heijne, A.; Buisman, C.J.; Hamelers, H.V. Bioelectrochemical systems: An outlook for practical applications. ChemSusChem 2012, 5, 1012–1019. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Mu, Z.; Yang, H.; Wang, Y.; Mu, Y.; Yu, H. Electron acceptors for energy generation in microbial fuel cells fed with wastewaters: A mini-review. Chemosphere 2015, 140, 12–17. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Li, H.; Gu, T. A state of the art review on microbial fuel cells: A promising technology for wastewater treatment and bioenergy. Biotechnol. Adv. 2007, 25, 464–482. [Google Scholar] [CrossRef] [PubMed]
- Pant, D.; Van Bogaert, G.; Diels, L.; Vanbroekhoven, K. A review of the substrates used in microbial fuel cells (MFCs) for sustainable energy production. Bioresour. Technol. 2010, 101, 1533–1543. [Google Scholar] [CrossRef] [PubMed]
- Liew, K.B.; Daud, W.R.W.; Ghasemi, M.; Leong, J.X.; Su Lim, S.; Ismail, M. Non-Pt catalyst as oxygen reduction reaction in microbial fuel cells: A review. Int. J. Hydrog. Energy 2014, 39, 4870–4883. [Google Scholar] [CrossRef]
- Janicek, A.; Fan, Y.; Liu, H. Design of microbial fuel cells for practical application: A review and analysis of scale-up studies. Biofuels 2014, 5, 79–92. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, S.; Logan, B.E. Production of electricity from acetate or butyrate using a single-chamber microbial fuel cell. Environ. Sci. Technol. 2005, 39, 658–662. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.R.; Rodríguez, J.; Hawkes, F.R.; Dinsdale, R.M.; Guwy, A.J.; Premier, G.C. Increasing power recovery and organic removal efficiency using extended longitudinal tubular microbial fuel cell (MFC) reactors. Energy Environ. Sci. 2011, 4, 459–465. [Google Scholar] [CrossRef]
- Aelterman, P.; Versichele, M.; Marzorati, M.; Boon, N.; Verstraete, W. Loading rate and external resistance control the electricity generation of microbial fuel cells with different three-dimensional anodes. Bioresour. Technol. 2008, 99, 8895–8902. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.R.; Cheng, S.; Oh, S.-E.; Logan, B.E. Power generation using different cation, anion, and ultrafiltration membranes in microbial fuel cells. Environ. Sci. Technol. 2007, 41, 1004–1009. [Google Scholar] [CrossRef] [PubMed]
- Marcus, A.K.; Torres, C.I.; Rittmann, B.E. Conduction-based modeling of the biofilm anode of a microbial fuel cell. Biotechnol. Bioeng. 2007, 98, 1171–1182. [Google Scholar] [CrossRef] [PubMed]
- Picioreanu, C.; Head, I.M.; Katuri, K.P.; Van Loosdrecht, M.C.; Scott, K. A computational model for biofilm-based microbial fuel cells. Water Res. 2007, 41, 2921–2940. [Google Scholar] [CrossRef] [PubMed]
- Picioreanu, C.; Katuri, K.P.; van Loosdrecht, M.C.M.; Head, I.M.; Scott, K. Modelling microbial fuel cells with suspended cells and added electron transfer mediator. J. Appl. Electrochem. 2009, 40, 151–162. [Google Scholar] [CrossRef]
- Picioreanu, C.; Van Loosdrecht, M.; Katuri, K.P.; Scott, K.; Head, I. Mathematical model for microbial fuel cells with anodic biofilms and anaerobic digestion. Water Sci. Technol. 2008, 965–971. [Google Scholar] [CrossRef] [PubMed]
- Logan, B.E.; Regan, J.M. Electricity-producing bacterial communities in microbial fuel cells. Trends Microbiol. 2006, 14, 512–518. [Google Scholar] [CrossRef] [PubMed]
- Mohan, S.V.; Velvizhi, G.; Modestra, J.A.; Srikanth, S. Microbial fuel cell: Critical factors regulating bio-catalyzed electrochemical process and recent advancements. Renew. Sustain. Energy Rev. 2014, 40, 779–797. [Google Scholar] [CrossRef]
- Zhang, L.; Deshusses, M. Application of the finite difference method to model pH and substrate concentration in a double-chamber microbial fuel cell. Environ. Technol. 2014, 35, 1064–1076. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.; Wu, Y.; Cao, D.; Zhao, L.; Sun, Q. Electricity generation and modeling of microbial fuel cell from continuous beer brewery wastewater. Bioresour. Technol. 2009, 100, 4171–4175. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Li, X.; Li, B.; Wang, L. Design and modeling of an underwater energy harvesting system. In Proceedings of the International Congress on Analytical Sciences (ICAS 2011), Kyoto, Japan, 22–26 May 2011.
- Pinto, R.; Tartakovsky, B.; Srinivasan, B. Optimizing energy productivity of microbial electrochemical cells. J. Process Control 2012, 22, 1079–1086. [Google Scholar] [CrossRef]
- Bender, E.A. An Introduction to Mathematical Modeling; John Wiley & Sons: New York, NY, USA, 1978. [Google Scholar]
- Joseph, V.R.; Melkote, S.N. Statistical adjustments to engineering models. J. Qual. Technol. 2009, 41, 362–375. [Google Scholar]
- Joseph, V.R.; Yan, H. Engineering-Driven Statistical Adjustment and Calibration. Technometrics 2015, 57, 257–267. [Google Scholar] [CrossRef]
- Thomann, R.V. Deterministic and statistical models of chemical fate in aquatic systems. In Applied Mathematical Ecology; Springer: Berlin, Germany, 1989; pp. 322–351. [Google Scholar]
- Scholz, G.; Scholz, F. First-order differential equations in chemistry. ChemTexts 2015, 1, 1–12. [Google Scholar] [CrossRef]
- Zwillinger, D. Handbook of Differential Equations; Academic Press: Orlando, FL, USA, 1998. [Google Scholar]
- Pinto, R.P.; Srinivasan, B.; Manuel, M.F.; Tartakovsky, B. A two-population bio-electrochemical model of a microbial fuel cell. Bioresour. Technol. 2010, 101, 5256–5265. [Google Scholar] [CrossRef] [PubMed]
- Tebbutt, P. Basic Mathematics for Chemists; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Escapa, A.; Gil-Carrera, L.; García, V.; Morán, A. Performance of a continuous flow microbial electrolysis cell (MEC) fed with domestic wastewater. Bioresour. Technol. 2012, 117, 55–62. [Google Scholar] [CrossRef] [PubMed]
- De Los Angeles Fernandez, M.; de Los Angeles Sanroman, M.; Marks, S.; Makinia, J.; Del Campo, A.G.; Rodrigo, M.; Fernandez, F.J. A grey box model of glucose fermentation and syntrophic oxidation in microbial fuel cells. Bioresour. Technol. 2015, 200, 396–404. [Google Scholar] [CrossRef] [PubMed]
- Rimboud, M.; Desmond-Le Quemener, E.; Erable, B.; Bouchez, T.; Bergel, A. Multi-system Nernst-Michaelis-Menten model applied to bioanodes formed from sewage sludge. Bioresour. Technol. 2015, 195, 162–169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torres, C.I.; Marcus, A.K.; Lee, H.-S.; Parameswaran, P.; Krajmalnik-Brown, R.; Rittmann, B.E. A kinetic perspective on extracellular electron transfer by anode-respiring bacteria. FEMS Microbiol. Rev. 2010, 34, 3–17. [Google Scholar] [CrossRef] [PubMed]
- Kano, K.; Ikeda, T. Fundamentals and Practices of Mediated Bioelectrocatalysis. Anal. Sci. 2000, 16, 1013–1021. [Google Scholar] [CrossRef]
- Holcman, D.; Yuste, R. The new nanophysiology: Regulation of ionic flow in neuronal subcompartments. Nat. Rev. Neurosci. 2015, 16, 685–692. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.R.; Premier, G.C.; Hawkes, F.R.; Dinsdale, R.M.; Guwy, A.J. Development of a tubular microbial fuel cell (MFC) employing a membrane electrode assembly cathode. J. Power Sources 2009, 187, 393–399. [Google Scholar] [CrossRef]
- Harnisch, F.; Warmbier, R.; Schneider, R.; Schröder, U. Modeling the ion transfer and polarization of ion exchange membranes in bioelectrochemical systems. Bioelectrochemistry 2009, 75, 136–141. [Google Scholar] [CrossRef] [PubMed]
- Walz, D.; Teissié, J.; Milazzo, G. Bioelectrochemistry of Membranes; Birkhäuser Verlag: Basel, Switzerland, 2012. [Google Scholar]
- Xiao, L.; Ge, Z.; Kelly, P.; Zhang, F.; He, Z. Evaluation of normalized energy recovery (NER) in microbial fuel cells affected by reactor dimensions and substrates. Bioresour. Technol. 2014, 157, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Zhang, J.; Shi, X. Performance Improvement of a Microbial Fuel Cell Based on Model Predictive Control. Int. J. Electrochem. Sci. 2015, 10, 737–748. [Google Scholar]
- Ki, D.; Park, J.; Lee, J.; Yoo, K. Microbial diversity and population dynamics of activated sludge microbial communities participating in electricity generation in microbial fuel cells. Water. Sci. Technol. 2008, 58, 2195–2201. [Google Scholar] [CrossRef] [PubMed]
- Teschl, G. Ordinary Differential Equations and Dynamical Systems; American Mathematical Society: Providence, RL, USA, 2012. [Google Scholar]
- Pinto, R.; Srinivasan, B.; Escapa, A.; Tartakovsky, B. Multi-population model of a microbial electrolysis cell. Environ. Sci. Technol. 2011, 45, 5039–5046. [Google Scholar] [CrossRef] [PubMed]
- Yahya, A.M.; Hussain, M.A.; Wahab, A.; Khairi, A. Modeling, optimization, and control of microbial electrolysis cells in a fed-batch reactor for production of renewable biohydrogen gas. Int. J. Energy Res. 2015, 39, 557–572. [Google Scholar] [CrossRef]
- Li, J.; Rosenberger, G.; He, Z. Integrated experimental investigation and mathematical modeling of a membrane bioelectrochemical reactor with an external membrane module. Chem. Eng. J. 2016, 287, 321–328. [Google Scholar] [CrossRef]
- Picioreanu, C.; Kreft, J.U.; Van Loosdrecht, M.C.M. Particle-Based Multidimensional Multispecies Biofilm Model. Appl. Environ. Microbiol. 2004, 70, 3024–3040. [Google Scholar] [CrossRef] [PubMed]
- Ping, Q.; Zhang, C.; Chen, X.; Zhang, B.; Huang, Z.; He, Z. Mathematical model of dynamic behavior of microbial desalination cells for simultaneous wastewater treatment and water desalination. Environ. Sci. Technol. 2014, 48, 13010–13019. [Google Scholar] [CrossRef] [PubMed]
- Ping, Q.; Huang, Z.; Dosoretz, C.; He, Z. Integrated experimental investigation and mathematical modeling of brackish water desalination and wastewater treatment in microbial desalination cells. Water. Res. 2015, 77, 13–23. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Brastad, K.S.; He, Z. Integrating forward osmosis into microbial fuel cells for wastewater treatment, water extraction and bioelectricity generation. Environ. Sci. Technol. 2011, 45, 6690–6696. [Google Scholar] [CrossRef] [PubMed]
- Qin, M.; Ping, Q.; Lu, Y.; Abu-Reesh, I.M.; He, Z. Understanding electricity generation in osmotic microbial fuel cells through integrated experimental investigation and mathematical modeling. Bioresour. Technol. 2015, 195, 194–201. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Lu, Y.; Abu-Reesh, I.M.; He, Z. Bioelectrochemical production of hydrogen in an innovative pressure-retarded osmosis/microbial electrolysis cell system: experiments and modeling. Biotechnol. Biofuels 2015, 8. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ge, Z.; He, Z. Advancing membrane bioelectrochemical reactor (MBER) with hollow-fiber membranes installed in the cathode compartment. J. Chem. Technol. Biotechnol. 2014, 89, 1330–1336. [Google Scholar] [CrossRef]
- Pimentel, G.A.; Wouwer, A.V.; Harmand, J.; Rapaport, A. Design, analysis and validation of a simple dynamic model of a submerged membrane bioreactor. Water Res. 2015, 70, 97–108. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; He, Z. Development of a dynamic mathematical model for membrane bioelectrochemical reactors with different configurations. Environ. Sci. Pollut. Res. 2015, 23, 3897–3906. [Google Scholar] [CrossRef] [PubMed]
- Kazemi, M.; Biria, D.; Rismani-Yazdi, H. Modelling bio-electrosynthesis in a reverse microbial fuel cell to produce acetate from CO2 and H2O. Phys. Chem. Chem. Phys. 2015, 17, 12561–12574. [Google Scholar] [CrossRef] [PubMed]
- Rabaey, K. Bioelectrochemical Systems: From Extracellular Electron Transfer to Biotechnological Application; International Water Association Publishing: London, UK, 2009. [Google Scholar]
- Zeng, Y.; Choo, Y.F.; Kim, B.-H.; Wu, P. Modelling and simulation of two-chamber microbial fuel cell. J. Power Sources 2010, 195, 79–89. [Google Scholar] [CrossRef]
- Merkey, B.V.; Chopp, D.L. The performance of a microbial fuel cell depends strongly on anode geometry: A multidimensional modeling study. Bull. Math. Biol. 2012, 74, 834–857. [Google Scholar] [CrossRef] [PubMed]
- Dykstra, J.; Biesheuvel, P.; Bruning, H.; Ter Heijne, A. Theory of ion transport with fast acid-base equilibrations in bioelectrochemical systems. Phys. Rev. E 2014, 90. [Google Scholar] [CrossRef] [PubMed]
- Missner, A.; Kügler, P.; Saparov, S.M.; Sommer, K.; Mathai, J.C.; Zeidel, M.L.; Pohl, P. Carbon dioxide transport through membranes. J. Biol. Chem. 2008, 283, 25340–25347. [Google Scholar] [CrossRef] [PubMed]
- Galama, A.; Post, J.; Stuart, M.C.; Biesheuvel, P. Validity of the Boltzmann equation to describe Donnan equilibrium at the membrane–solution interface. J. Membr. Sci. 2013, 442, 131–139. [Google Scholar] [CrossRef]
- Wiedemann, E.; Heintz, A.; Lichtenthaler, R. Sorption isotherms of vanadium with H3O+ ions in cation exchange membranes. J. Membr. Sci. 1998, 141, 207–213. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, B.; Bai, B.; Zhao, T. A transient electrochemical model incorporating the Donnan effect for all-vanadium redox flow batteries. J. Power Sources 2015, 299, 202–211. [Google Scholar] [CrossRef]
- Leung, A. Systems of Nonlinear Partial Differential Equations: Applications to Biology and Engineering; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Picioreanu, C.; Van Loosdrecht, M.C.; Curtis, T.P.; Scott, K. Model based evaluation of the effect of pH and electrode geometry on microbial fuel cell performance. Bioelectrochemistry 2010, 78, 8–24. [Google Scholar] [CrossRef] [PubMed]
- McCarty, P.; Rittmann, B. Environmental Biotechnology: Principles and Applications; McGraw-Hill Education: Boston, MA, USA, 2001. [Google Scholar]
- Cheng, S.; Liu, H.; Logan, B.E. Increased performance of single-chamber microbial fuel cells using an improved cathode structure. Electrochem. Commun. 2006, 8, 489–494. [Google Scholar] [CrossRef]
- Sirinutsomboon, B. Modeling of a membraneless single-chamber microbial fuel cell with molasses as an energy source. Int. J. Renew. Energy Environ. Eng. 2014, 5, 1–9. [Google Scholar] [CrossRef]
- Hang, H.; Guo, Y.; Liu, J.; Bai, L.; Xia, J.; Guo, M.; Hui, M. Computational fluid dynamics modeling of an inverted frustoconical shaking bioreactor for mammalian cell suspension culture. Biotechnol. Bioprocess Eng. 2011, 16, 567–575. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Kim, B.; Yu, J. Computational fluid dynamics analysis in microbial fuel cells with different anode configurations. Water Sci. Technol. 2014, 69, 1447–1452. [Google Scholar] [CrossRef] [PubMed]
- Korth, B.; Rosa, L.F.; Harnisch, F.; Picioreanu, C. A framework for modeling electroactive microbial biofilms performing direct electron transfer. Bioelectrochemistry 2015, 106, 194–206. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-T.; Shaw, C.K.; Hu, T.-Y. Optimization of flow in microbial fuel cells: An investigation into promoting micro-mixer efficiency with obstacle. Tamkang J. Sci. Eng. 2011, 14, 25–31. [Google Scholar]
- Cord-Ruwisch, R.; Law, Y.; Cheng, K.Y. Ammonium as a sustainable proton shuttle in bioelectrochemical systems. Bioresour. Technol. 2011, 102, 9691–9696. [Google Scholar] [CrossRef] [PubMed]
- Maurer, M.; Schwegler, P.; Larsen, T. Nutrients in urine: Energetic aspects of removal and recovery. Nutr. Remov. Recovery 2003, 48, 37–46. [Google Scholar]
- Ewing, R.E.; Wang, H. A summary of numerical methods for time-dependent advection-dominated partial differential equations. J. Comput. Appl. Math. 2001, 128, 423–445. [Google Scholar] [CrossRef]
- Prieto, D.; Asensio, M.; Ferragut, L.; Cascón, J. Sensitivity analysis and parameter adjustment in a simplified physical wildland fire model. Adv. Eng. Softw. 2015, 90, 98–106. [Google Scholar] [CrossRef]
- Kauschinger, B.; Kabitzsch, K.; Schroeder, S. Adjustment of Uncertain Parameters in Thermal Models of Machine Tools. In Thermo-Energetic Design of Machine Tools; Springer International Publishing: Cham, Switzerland, 2015; pp. 145–157. [Google Scholar]
- Hu, J.; Wang, Y.; Cheng, A.; Zhong, Z. Sensitivity analysis in quantified interval constraint satisfaction problems. J. Mech. Des. 2015, 137. [Google Scholar] [CrossRef]
- Rasi, M.; Rajendran, L.; Subbiah, A. Analytical expression of transient current-potential for redox enzymatic homogenous system. Sens. Actuators B 2015, 208, 128–136. [Google Scholar] [CrossRef]
- Yang, J.; Xu, M.; Zhang, X.; Hu, Q.; Sommerfeld, M.; Chen, Y. Life-cycle analysis on biodiesel production from microalgae: Water footprint and nutrients balance. Bioresour. Technol. 2011, 102, 159–165. [Google Scholar] [CrossRef] [PubMed]
- Power, M. The predictive validation of ecological and environmental models. Ecol. Model. 1993, 68, 33–50. [Google Scholar] [CrossRef]
- Bühlmann, P.; Hothorn, T. Boosting algorithms: Regularization, prediction and model fitting. Stat. Sci. 2007, 22, 477–505. [Google Scholar] [CrossRef]
- Manohar, A.K.; Bretschger, O.; Nealson, K.H.; Mansfeld, F. The use of electrochemical impedance spectroscopy (EIS) in the evaluation of the electrochemical properties of a microbial fuel cell. Bioelectrochemistry 2008, 72, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Ramasamy, R.P.; Gadhamshetty, V.; Nadeau, L.J.; Johnson, G.R. Impedance spectroscopy as a tool for non-intrusive detection of extracellular mediators in microbial fuel cells. Biotechnol. Bioeng. 2009, 104, 882–891. [Google Scholar] [CrossRef] [PubMed]
- Sekar, N.; Ramasamy, R.P. Electrochemical Impedance Spectroscopy for Microbial Fuel Cell Characterization. J. Microb. Biochem. Technol. 2013. [Google Scholar] [CrossRef]
- Rabaey, K.; Boon, N.; Siciliano, S.D.; Verhaege, M.; Verstraete, W. Biofuel cells select for microbial consortia that self-mediate electron transfer. Appl. Environ. Microbiol. 2004, 70, 5373–5382. [Google Scholar] [CrossRef] [PubMed]
- Adelaja, O.; Keshavarz, T.; Kyazze, G. The effect of salinity, redox mediators and temperature on anaerobic biodegradation of petroleum hydrocarbons in microbial fuel cells. J. Hazard. Mater. 2015, 283, 211–217. [Google Scholar] [CrossRef] [PubMed]
- Min, B.; Angelidaki, I. Innovative microbial fuel cell for electricity production from anaerobic reactors. J. Power Sources 2008, 180, 641–647. [Google Scholar] [CrossRef]
- Zhang, Y.; Angelidaki, I. A simple and rapid method for monitoring dissolved oxygen in water with a submersible microbial fuel cell (SBMFC). Biosens. Bioelectron. 2012, 38, 189–194. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Angelidaki, I. Recovery of ammonia and sulfate from waste streams and bioenergy production via bipolar bioelectrodialysis. Water Res. 2015, 85, 177–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Min, B.; Poulsen, F.W.; Thygesen, A.; Angelidaki, I. Electric power generation by a submersible microbial fuel cell equipped with a membrane electrode assembly. Bioresour. Technol. 2012, 118, 412–417. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Liu, L.; Gao, B.; Yang, F. Integration of bio-electrochemical cell in membrane bioreactor for membrane cathode fouling reduction through electricity generation. J. Membr. Sci. 2013, 430, 196–202. [Google Scholar] [CrossRef]
- Liu, R.; Huang, X.; Sun, Y.F.; Qian, Y. Hydrodynamic effect on sludge accumulation over membrane surfaces in a submerged membrane bioreactor. Process Biochem. 2003, 39, 157–163. [Google Scholar] [CrossRef]
- Xiao, L.; Young, E.B.; Berges, J.A.; He, Z. Integrated photo-bioelectrochemical system for contaminants removal and bioenergy production. Environ. Sci. Technol. 2012, 46, 11459–11466. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Young, E.B.; Grothjan, J.J.; Lyon, S.; Zhang, H.; He, Z. Wastewater treatment and microbial communities in an integrated photo-bioelectrochemical system affected by different wastewater algal inocula. Algal Res. 2015, 12, 446–454. [Google Scholar] [CrossRef]
- Luo, H.; Jenkins, P.E.; Ren, Z. Concurrent desalination and hydrogen generation using microbial electrolysis and desalination cells. Environ. Sci. Technol. 2010, 45, 340–344. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.J.; Chu, Y.; Hahn, J. Model simplification procedure for signal transduction pathway models: An application to IL-6 signaling. Chem. Eng. Sci. 2010, 65, 1964–1975. [Google Scholar] [CrossRef]
- Dopico, D.; Zhu, Y.; Sandu, A.; Sandu, C. Direct and Adjoint Sensitivity Analysis of Ordinary Differential Equation Multibody Formulations. J. Comput. Nonlinear Dyn. 2015, 10. [Google Scholar] [CrossRef]
- Madani, S.; Gheshlaghi, R.; Mahdavi, M.A.; Sobhani, M.; Elkamel, A. Optimization of the performance of a double-chamber microbial fuel cell through factorial design of experiments and response surface methodology. Fuel 2015, 150, 434–440. [Google Scholar] [CrossRef]
- Al-Shehri, A. Statistical optimization of pentachlorophenol biodegradation and electricity generation simultaneously in mediator–less air cathode microbial fuel cell. J. Environ. Appl. Biores. 2015, 3, 6–15. [Google Scholar]
- Sajana, T.K.; Ghangrekar, M.M.; Mitra, A. Effect of operating parameters on the performance of sediment microbial fuel cell treating aquaculture water. Aquac. Eng. 2014, 61, 17–26. [Google Scholar] [CrossRef]
- Fang, F.; Zang, G.-L.; Sun, M.; Yu, H.-Q. Optimizing multi-variables of microbial fuel cell for electricity generation with an integrated modeling and experimental approach. Appl. Enery 2013, 110, 98–103. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Vossoughi, M.; Alemzadeh, I. An efficient approach to cathode operational parameters optimization for microbial fuel cell using response surface methodology. J. Environ. Health Sci. Eng. 2014, 12. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Angelidaki, I. Submersible microbial fuel cell sensor for monitoring microbial activity and BOD in groundwater: Focusing on impact of anodic biofilm on sensor applicability. Biotechnol. Bioeng. 2011, 108, 2339–2347. [Google Scholar] [CrossRef] [PubMed]
- Al-Shehri, A.N.; Ghanem, K.M.; Al-Garni, S.M. Statistical Optimization of Medium Components to Enhance Bioelectricity Generation in Microbial Fuel Cell. Arab. J. Sci. Eng. 2012, 38, 21–27. [Google Scholar] [CrossRef]
- Jia, Q.; Wei, L.; Han, H.; Shen, J. Factors that influence the performance of two-chamber microbial fuel cell. Int. J. Hydrog. Energy 2014, 39, 13687–13693. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, J.; Yan, Y.; Feng, L. Enhanced production of short-chain fatty acid by co-fermentation of waste activated sludge and kitchen waste under alkaline conditions and its application to microbial fuel cells. Appl. Enery 2013, 102, 1197–1204. [Google Scholar] [CrossRef]
- Zhang, F.; Ge, Z.; Grimaud, J.; Hurst, J.; He, Z. In situ investigation of tubular microbial fuel cells deployed in an aeration tank at a municipal wastewater treatment plant. Bioresour. Technol. 2013, 136, 316–321. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.; Wu, L.; Zhang, F.; He, Z. Energy extraction from a large-scale microbial fuel cell system treating municipal wastewater. J. Power Sources 2015, 297, 260–264. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics Springer: Berlin, Germany, 2001. [Google Scholar]
- Esfandyari, M.; Fanaei, M.A.; Gheshlaghi, R.; Mahdavi, M.A. Neural network and neuro-fuzzy modeling to investigate the power density and Columbic efficiency of microbial fuel cell. J. Taiwan Inst. Chem. Eng. 2015, 58, 84–91. [Google Scholar] [CrossRef]
- Garg, A.; Vijayaraghavan, V.; Mahapatra, S.S.; Tai, K.; Wong, C.H. Performance evaluation of microbial fuel cell by artificial intelligence methods. Expert Syst. Appl. 2014, 41, 1389–1399. [Google Scholar] [CrossRef]
- Tront, J.M.; Fortner, J.D.; Plotze, M.; Hughes, J.B.; Puzrin, A.M. Microbial fuel cell biosensor for in situ assessment of microbial activity. Biosens. Bioelectron. 2008, 24, 586–590. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, J.; Samimi, A. Steady state electric power generation in up-flow microbial fuel cell using the estimated time span method for bacteria growth domestic wastewater. Biomass Bioenergy 2012, 45, 65–76. [Google Scholar] [CrossRef]
- Rozendal, R.A.; Hamelers, H.V.; Buisman, C.J. Effects of membrane cation transport on pH and microbial fuel cell performance. Environ. Sci. Technol. 2006, 40, 5206–5211. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Luo, S.; Jin, R.; He, Z. Multitask Lasso Model for Investigating Multimodule Design Factors, Operational Factors, and Covariates in Tubular Microbial Fuel Cells. ACS Sustain. Chem. Eng. 2015, 3, 3231–3238. [Google Scholar] [CrossRef]
- Wei, L.; Yuan, Z.; Cui, M.; Han, H.; Shen, J. Study on electricity-generation characteristic of two-chambered microbial fuel cell in continuous flow mode. Int. J. Hydrog. Energy 2012, 37, 1067–1073. [Google Scholar] [CrossRef]
- Tardast, A.; Rahimnejad, M.; Najafpour, G.; Ghoreyshi, A.; Premier, G.C.; Bakeri, G.; Oh, S.-E. Use of artificial neural network for the prediction of bioelectricity production in a membrane less microbial fuel cell. Fuel 2014, 117, 697–703. [Google Scholar] [CrossRef]
- Oh, S.; Min, B.; Logan, B.E. Cathode performance as a factor in electricity generation in microbial fuel cells. Environ. Sci. Technol. 2004, 38, 4900–4904. [Google Scholar] [CrossRef] [PubMed]
- Gil, G.-C.; Chang, I.-S.; Kim, B.H.; Kim, M.; Jang, J.-K.; Park, H.S.; Kim, H.J. Operational parameters affecting the performannce of a mediator-less microbial fuel cell. Biosens. Bioelectron. 2003, 18, 327–334. [Google Scholar] [CrossRef]
- Zhang, F.; Jacobson, K.S.; Torres, P.; He, Z. Effects of anolyte recirculation rates and catholytes on electricity generation in a litre-scale upflow microbial fuel cell. Energy Environ. Sci. 2010, 3, 1347–1352. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, S.; Logan, B.E. Power generation in fed-batch microbial fuel cells as a function of ionic strength, temperature, and reactor configuration. Environ. Sci. Technol. 2005, 39, 5488–5493. [Google Scholar] [CrossRef] [PubMed]
- Chae, K.J.; Choi, M.J.; Lee, J.W.; Kim, K.Y.; Kim, I.S. Effect of different substrates on the performance, bacterial diversity, and bacterial viability in microbial fuel cells. Bioresour. Technol. 2009, 100, 3518–3525. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.E.; Logan, B.E. Proton exchange membrane and electrode surface areas as factors that affect power generation in microbial fuel cells. Appl. Microbiol. Biotechnol. 2006, 70, 162–169. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, O.; Tan, Z.; Kharkwal, S.; Ng, H.Y. Effect of increasing anodic NaCl concentration on microbial fuel cell performance. Bioresour. Technol. 2012, 112, 336–340. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.J.; Hamada, M.S. Experiments: Planning, Analysis, and Optimization; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Tartakovsky, B.; Guiot, S.R. A comparison of air and hydrogen peroxide oxygenated microbial fuel cell reactors. Biotechnol. Progress 2006, 22, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Plackett, R.L.; Burman, J.P. The design of optimum multifactorial experiments. Biometrika 1946, 33, 305–325. [Google Scholar] [CrossRef]
- Fang, K.-T.; Lin, D.K. Ch. 4. Uniform experimental designs and their applications in industry. Handb. Stat. 2003, 22, 131–170. [Google Scholar]
- Albert, D.B.; Martens, C.S. Determination of low-molecular-weight organic acid concentrations in seawater and pore-water samples via HPLC. Mar. Chem. 1997, 56, 27–37. [Google Scholar] [CrossRef]
- Doyon, G.; Gaudreau, G.; St-Gelais, D.; Beaulieu, Y.; Randall, C. Simultaneous HPLC determination of organic acids, sugars and alcohols. Can. Inst. Food Sci. Technol. J. 1991, 24, 87–94. [Google Scholar] [CrossRef]
- Guo, W.; Luo, S.; He, Z.; Feng, X. 13C pathway analysis of biofilm metabolism of Shewanella oneidensis MR-1. RSC Adv. 2015, 5, 39840–39843. [Google Scholar] [CrossRef]
- Luo, S.; Guo, W.; Nealson, K.H.; Feng, X.; He, Z. 13C pathway analysis for the role of formate in electricity generation by Shewanella Oneidensis MR-1 using lactate in microbial fuel cells. Sci. Rep. 2016. [Google Scholar] [CrossRef] [PubMed]
- Chang, I.S.; Moon, H.; Jang, J.K.; Kim, B.H. Improvement of a microbial fuel cell performance as a BOD sensor using respiratory inhibitors. Biosens. Bioelectron. 2005, 20, 1856–1859. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Casillas, H.A.; Cocke, D.L.; Gomes, J.A.; Morkovsky, P.; Parga, J.; Peterson, E. Electrocoagulation mechanism for COD removal. Sep. Purif. Technol. 2007, 56, 204–211. [Google Scholar] [CrossRef]
- Yabur, R.; Bashan, Y.; Hernández-Carmona, G. Alginate from the macroalgae Sargassum sinicola as a novel source for microbial immobilization material in wastewater treatment and plant growth promotion. J. Appl. Phycol. 2007, 19, 43–53. [Google Scholar] [CrossRef]
- Ge, Z.; Li, J.; Xiao, L.; Tong, Y.; He, Z. Recovery of electrical energy in microbial fuel cells. Environ. Sci. Technol. Lett. 2014, 1, 137–141. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.; Neter, J. Applied Linear Statistical Models; McGraw-Hill/Irwin: Boston, MA, USA, 2004. [Google Scholar]
- Kalogirou, S.A. Artificial neural networks in renewable energy systems applications: A review. Renew. Sustain. Energy Rev. 2001, 5, 373–401. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Platt, J.C. A Fast Algorithm for Training Support Vector Machines; Report MSR-TR-98–14; Microsoft Research: Redmond, WA, USA, 1998. [Google Scholar]
- Grendar, M. Is the p-value a good measure of evidence? Asymptotic consistency criteria. Stat. Probab. Lett. 2012, 82, 1116–1119. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models; Chicago/Irwin: Boston, MA, USA, 1996. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, L.; Zheng, Y.; Zhou, S.; Yuan, Y.; Yuan, H.; Chen, Y. Scalable microbial fuel cell (MFC) stack for continuous real wastewater treatment. Bioresour. Technol. 2012, 106, 82–88. [Google Scholar] [CrossRef] [PubMed]
- Woodward, L.; Tartakovsky, B.; Perrier, M.; Srinivasan, B. Maximizing power production in a stack of microbial fuel cells using multiunit optimization method. Biotechnol. Progress 2009, 25, 676–682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hastie, T.; Tibshirani, R. Varying-coefficient models. J. R. Stat. Soc. Ser. B Methodol. 1993, 55, 757–796. [Google Scholar]
- Jin, R.; Deng, X. Ensemble modeling for data fusion in manufacturing process scale-up. IIE Trans. 2015, 47, 203–214. [Google Scholar] [CrossRef]



| Methods | Data Generation | Systems | Major Conclusions | References |
|---|---|---|---|---|
| SLR | OFAT | Submersible MFC | Current density increased with increase of microorganisms concentration before saturation | [130] |
| SLR | OFAT | MFC biosensor | Current density increased with increase of acetate concentration before saturation | [139] |
| SLR | OFAT | Two-chamber MFC | Voltage increased with increase of organic loading rate and flow rate at neutral pH | [140] |
| SLR | OFAT | Two-chamber MFC | Mainly cation species were responsible for the transport of positive charge | [141] |
| ANOVA, RSM | FD, CCD | Two-chamber MFC | The interaction effect was significant | [125] |
| ANOVA, RSM | FD | Two-chamber MFC | Two-factor and three-factor interaction effects were less significant | [127] |
| MLM | FD with covariates | Two-chamber MFC | Cathode moisture was significant on energy recovery but insignificant on organic removal efficiency | [142] |
| ANOVA, RSM | CCD | Two-chamber MFC | Quadratic effects can be significant, but interaction effects were not significant | [129] |
| ANOVA, RSM | CCD | Mediator-less single-chamber MFC | Interaction and quadratic effects can be significant | [126] |
| ANOVA, RSM | CCD | Two-chamber MFC | All the linear, square and interaction effects were significant | [132] |
| ANOVA, RSM | CCD | Membrane-less MFC | Interaction and quadratic effects can be significant | [133] |
| ANOVA | PBD | Submersible MFC | Temperature, initial pH, and conductivity were significant | [130] |
| ANOVA, RSM | PBD | Two-chamber MFC | Glucose, NaHCO3 and KCl were significant | [131] |
| GP, ANN, SVM | [143] | Two-chamber MFC | GP performed best among the three models | [138] |
| ANN | Controlled Experiment | Membrane-less MFC | R2 value can be as high as 0.99 | [144] |
| RVM | UD | Two-chamber MFC | RVM performed better than SVM | [128] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Sun, H.; Ping, Q.; Jin, R.; He, Z. A Review of Modeling Bioelectrochemical Systems: Engineering and Statistical Aspects. Energies 2016, 9, 111. https://doi.org/10.3390/en9020111
Luo S, Sun H, Ping Q, Jin R, He Z. A Review of Modeling Bioelectrochemical Systems: Engineering and Statistical Aspects. Energies. 2016; 9(2):111. https://doi.org/10.3390/en9020111
Chicago/Turabian StyleLuo, Shuai, Hongyue Sun, Qingyun Ping, Ran Jin, and Zhen He. 2016. "A Review of Modeling Bioelectrochemical Systems: Engineering and Statistical Aspects" Energies 9, no. 2: 111. https://doi.org/10.3390/en9020111
APA StyleLuo, S., Sun, H., Ping, Q., Jin, R., & He, Z. (2016). A Review of Modeling Bioelectrochemical Systems: Engineering and Statistical Aspects. Energies, 9(2), 111. https://doi.org/10.3390/en9020111






