1. Introduction
Inductive Power Transfer (IPT) is receiving wide interest in wireless charging of electric vehicles (EVs), due to advantages such as: opportunity charging; battery volume reduction; safety; visual appeal due to removal of cord; and relieving the user from handling a bulky and heavy charging chord [
1]. An IPT system consists of two coils: a primary coil placed on the surface, connected to a power supply; and a secondary coil, placed underneath the vehicle, connected to the load. Since power transfer takes place due to the mutual coupling of coils, an optimum coupling between both coils is required for an efficient power transfer. This requires the vehicle to be parked in a specific position [
2,
3]. However, while parking the vehicle over the primary coil, certain misalignments could always occur. Due to misalignments, coils could deviate from the optimal coupling scenario. Moreover, the parameters of the system could vary due to reasons such as: fluctuation in supply voltage; and variation of load due to varying state of the charge of the battery pack. These issues can lead to the deviation of output voltage and current from the desired operating points.
A suitably designed closed-loop controller is consistently needed, in order to improve tolerance to misalignments and parameter variations. Recent papers mainly present steady-state models and experiments [
4,
5]. Steady-state models cannot accurately predict the dynamic behavior of a system; therefore, they cannot be used as a tool for controller and physical system design.
For the design of control loops, dynamic analysis of the IPT system is essential [
6]. An IPT system is a typical higher-order resonant circuit, and consists of one slow moving pole, due to the output filter (rectifier + capacitor) and fast moving poles, and due to the resonant tank elements. This causes a difference in frequency between the resonant network and the filter network. This relegates the usage of modelling techniques typically used for PWM DC/DC converters [
7]. Therefore, in due course of time, various specialized techniques have been developed for dynamic analysis of such resonant systems. Some of the popular techniques include: Generalized state-space averaging (GSSA) method [
7], sampled data modelling (SDM) technique [
8], extended describing function (EDF) method [
9], and general unified phasor transformation (GUPT) [
10]. While each method has its own advantages and limitations, it is not the intention of this paper to compare them. The aim of the paper merely is to derive an accurate simplified small-signal model of SS compensated IPT system using the EDF method. The derived model will be used to design a voltage control loop.
The EDF method has been preferred over other methods due to its reputation of generating highly accurate mathematical model of resonant converters. The EDF technique was first introduced by Yang et al. in 1991 [
11]. The most recent work and advancement on the EDF method has been presented in [
12,
13]. This modeling technique works on the basic principle of first harmonic approximation of state variables. This in turn provides a set of modulation functions that relate the state variables with the input and control variables, which are both in time-domain and frequency-domain [
13]. The EDF method is highly accurate but requires higher order representation and therefore more complex formulation effort. For instance, a small signal model of SS compensated IPT system has been derived in [
14,
15,
16,
17] which is the ninth order system.
In [
18], authors derived a simplified mathematical model of SS compensated IPT system. The derived model is a fifth order system as compared to the ninth order model derived by others. However, only simulation results were presented and the paper lacks experimental verification. As a follow-up to that paper, the authors present the detailed analysis of the derived model in this paper. Detailed analysis includes verification of small signal model using AC sweep method and verification of designed controller for its robustness using experimental results. Targeted application is static charging of EVs. For this type of application, the IPT system usually has single secondary coil drawing power from the single primary coil. Due to the coupled nature of the circuit, primary side control has been preferred to avoid secondary side DC-DC converter and associated losses with it. An experimental setup of a 3.6 kW wireless charger has been built in the lab to operate at a nominal switching frequency of 40 kHz. Frequency was selected based on DSP module and switching elements available in the lab at the time. However, the idea presented in the paper is applicable to the entire power and frequency of interest related to IPT system for EV battery charging.
2. Equivalent Circuit Derivation for an SS Compensated IPT System
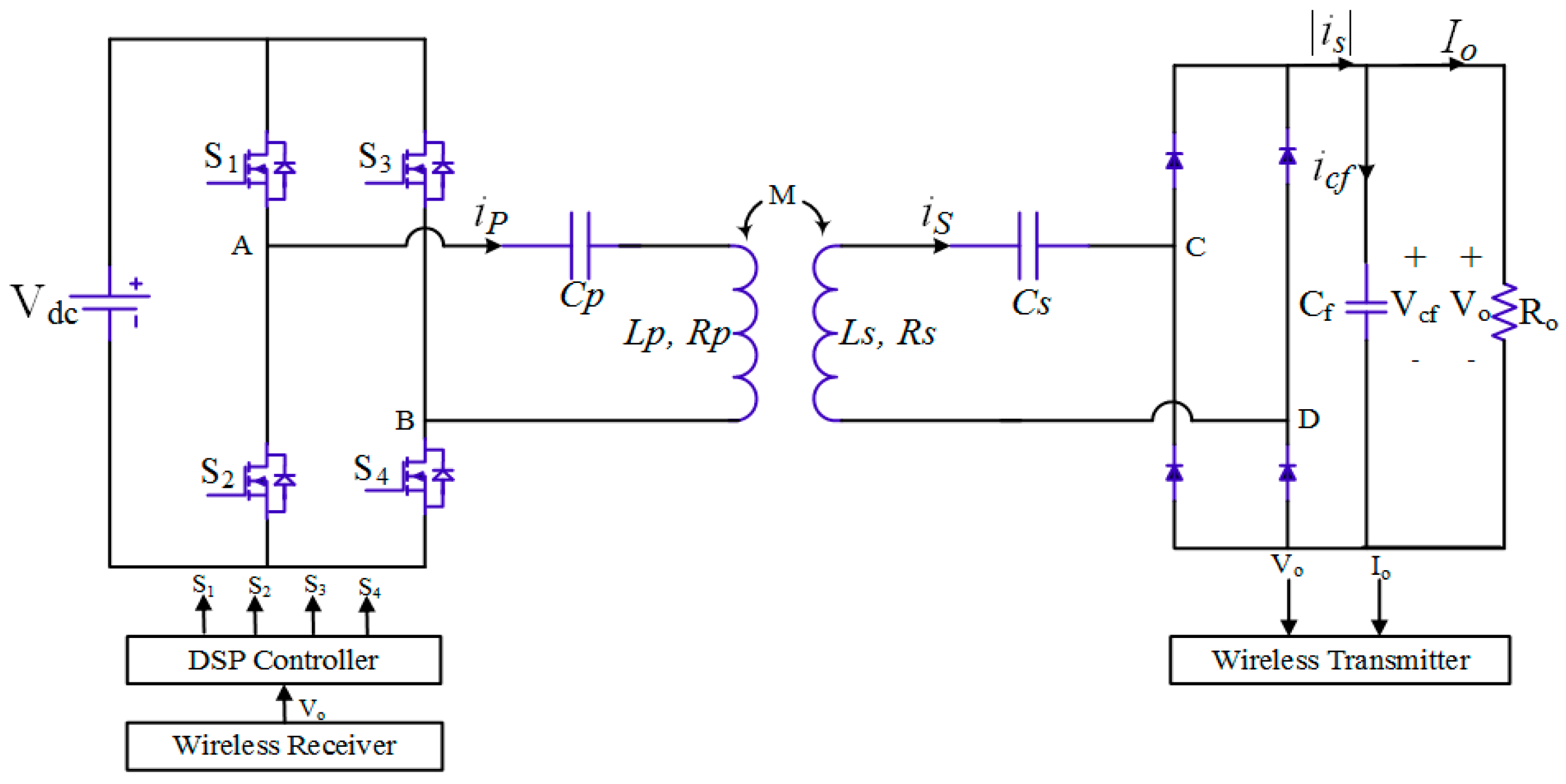
A typical SS compensated IPT system under the primary side control is shown in
Figure 1. An H-Bridge inverter in the primary side converts the DC input into high frequency voltage/current for the resonant tank. A diode bridge rectifier on the secondary side converts the high frequency voltage/current back to the DC value required by the load resistance
Ro.
Figure 1 will be referred to as the ‘full model’ of SS compensated IPT system in this paper from now on. To simplify the derivation of the small-signal model, first a reduced dynamic model is obtained from the full model. From the reduced dynamic model a small signal model has been derived. This two-step derivation reduces the complexity and computation effort required, for applying EDF for the derivation of the small-signal model. The following discussion entails the derivation of the reduced dynamic model as follows:
It is assumed that the secondary coil is resonating at the switching frequency
and the primary coil resonating at the resonant frequency
.
should be less than
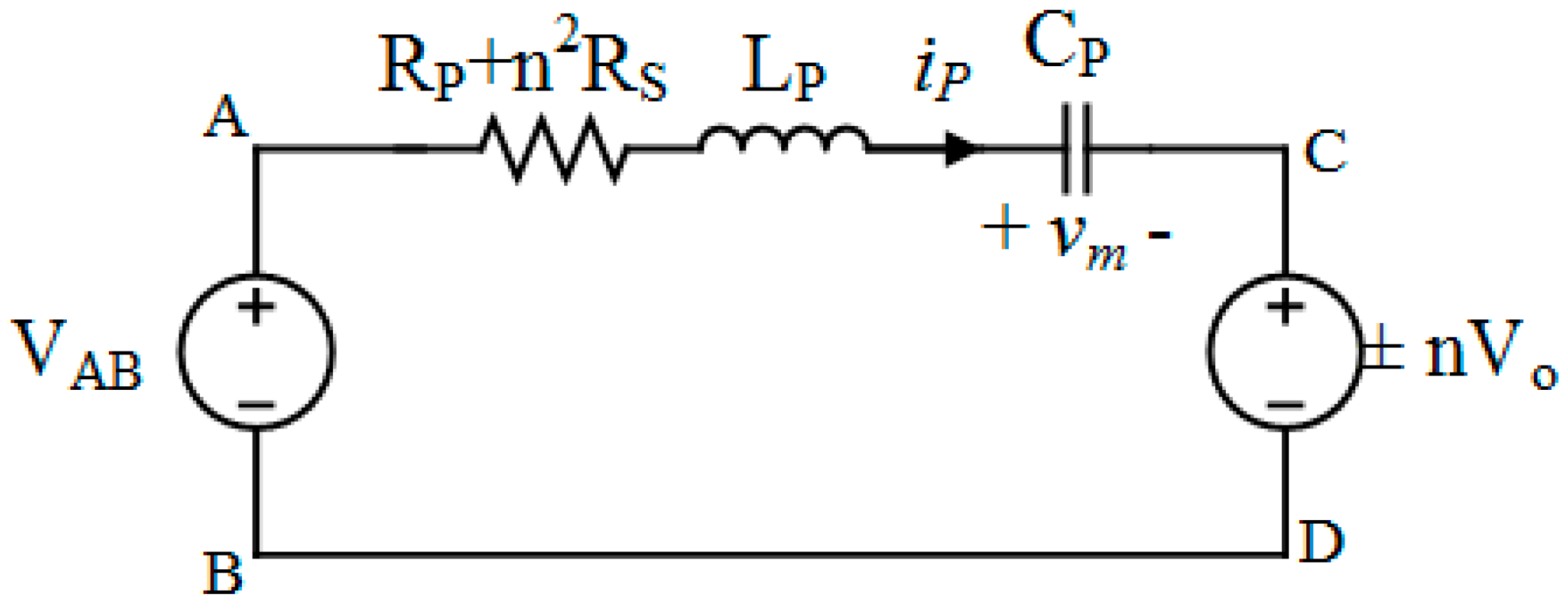
to maintain ZVS in H-bridge inverter. Under this assumption, equivalent circuit of
Figure 1 can be redrawn as in
Figure 2.
Applying Kirchhoff’s voltage Law (KVL) to circuit shown in
Figure 2:
Applying Kirchhoff’s current law (KCL) to the rectifier network of
Figure 1:
Output equation is given by:
Equations (1)–(4) gives the ‘reduced dynamic model’ of the SS compensated IPT system. Here, . Meaning of symbols used are given in Nomenclature section.
3. Small-Signal Modeling
The equivalent circuit shown in
Figure 2 is a greater simplification over the equivalent circuit derived in [
14,
15,
16,
17]. This is similar to the equivalent circuit of a series-loaded resonant DC/DC converter. Since,
and
are almost sinusoidal (due to filtering provided by resonant circuit) they can be approximated to their fundamental component using harmonic approximation. Hence,
V
AB can be modelled using the fundamental component of the inverter output waveform since in EDF only the first harmonic component is of prime importance [
12]. There are mainly three narrow frequency-range control techniques used for the control of resonant converters, namely asymmetrical duty cycle (ADC), asymmetrical clamped mode (ACM), and symmetrical clamped mode (SCM) control. It has been shown in [
19,
20,
21] that only ACM control has the best performance in terms of the least losses in the inverter switches as compared to other two control strategies and has the lowest switching frequency for obtaining ZVS under all load conditions. Therefore, ACM control has been considered in this paper for the inverter control.
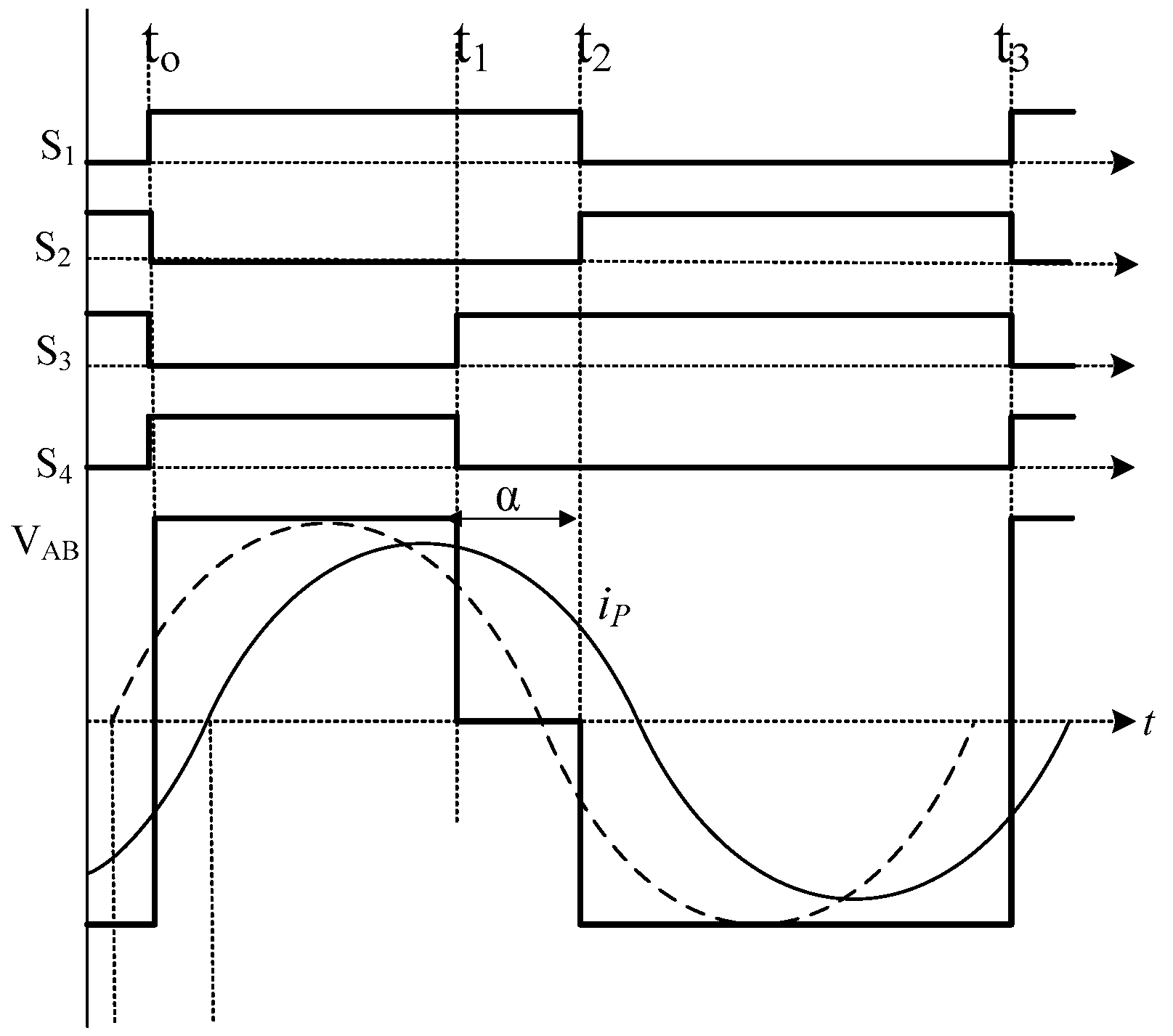
Figure 3 shows a typical switching logic and the inverter output voltage for ACM control.
V
AB in term of duty cycle
d (
is given by Equation (7).
Using EDF non-linear terms
is written as function of
and
. Hence,
Put Equations (5)–(8) in Equations (1) and (2), and by equating the coefficients of DC, sine, and cosine terms respectively, one can get:
Equations (10)–(14) give the large-signal model of the SS compensated IPT system in terms of the state variables. It contains both the steady-state model and the small-signal model. One can observe from the large signal model that it is constructed of five state variables as opposed to the nine variables used in [
14,
15,
16,
17]. The operating point is determined by {
} and have been mentioned in
Appendix A. The state variable vector and control/input variables vector can be expressed as:
The small-signal model can be derived by introducing ac perturbation, represented by ‘~’ in input variables vector and state variables resulting in:
Separating perturbations from the DC and very small signals gives the small-signal model of SS topology:
4. Verification of Small-Signal Model and Design of Control Loops
A prototype of the SS compensated IPT system was built in the lab.
Table 1 gives the parameters of the experimental setup. Using theories presented in [
19,
20,
21], and depending on availability of capacitors in the market,
fS was calculated to be 41.426 kHz for ensuring ZVS for any variation of α, and the primary coil was tuned to a resonant frequency of 39.031 kHz.
The controller was designed based on fixed frequency and variable duty ratio control. Some of the latest work, presented in the literature, related to the controller design for an IPT system can be read in [
22,
23,
24,
25]. Following subsection discusses a step by step procedure for derivation of a voltage controller.
4.1. Bode Plot of Open-Loop System
Transfer function of output variable to the control variable (i.e., plant) can be obtained using Equation (20).
Here, G
P(s) represents plant transfer function,
.
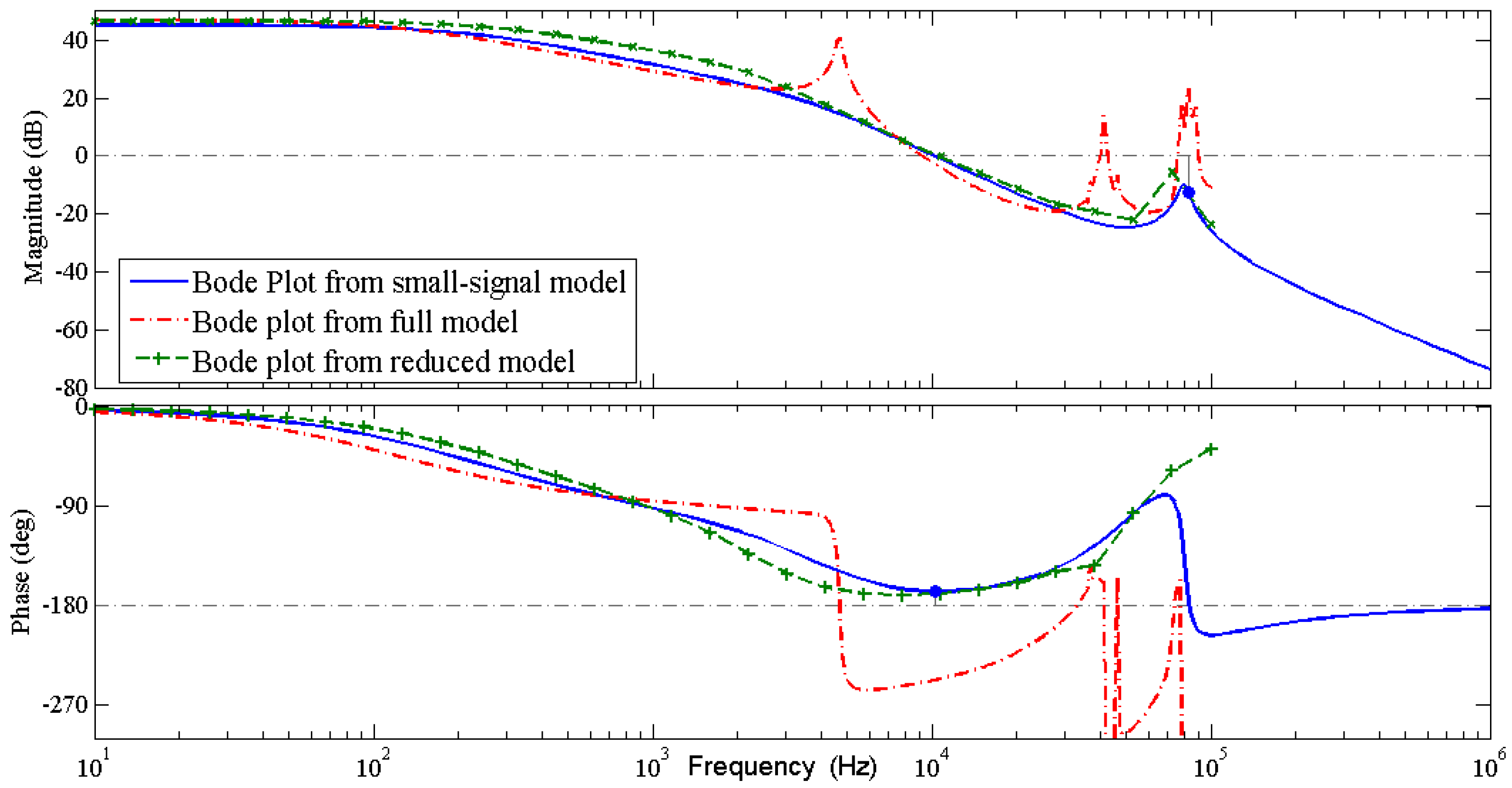
Figure 4 compares the open loop Bode plot obtained from small-signal model, reduced dynamic model and full model of the SS compensated IPT system. The Bode plot of the full model and the reduced dynamic model in open loop have been obtained by simulating these models in PLECS 3.7.5 and applying an AC sweep for a few discrete points.
In
Figure 4, one can observe that the AC sweep result for the reduced dynamic model closely follows the Bode plot of the small-signal model. Both models have the phase margin of 12° at the crossover frequency of 10.2 kHz. The gain cross-over frequency lies to the left of the phase crossover frequency which indicates a stable open-loop system. The gain crossover frequency of the full model is also near to 10 kHz but the phase crossover frequency is less than the gain crossover frequency which makes the actual system unstable for small disturbances in the duty cycle, load, and input DC voltage. The Bode plot of full model closely follows the small-signal model up to 4 kHz frequency. Here the aim is to design the control loop for output voltage control which is DC. As a rule of thumb, the bandwidth of the closed-loop system is selected 5 to 10 times the highest frequency being controlled. Therefore, the derived small-signal model is useful for the design of voltage control loop.
4.2. Derivation of Closed-Loop Voltage Controller
The design of voltage loop, shown in
Figure 5, involves defining the voltage loop quantitatively and should meet the design criteria of phase margin (PM) and bandwidth (BW) or crossover frequency,
fc.
Here, Gc(s) is the transfer function of PI regulator. Voltage loop transfer function (LTF) is then given by, LTF(s) = Gc(s) GP(s). The following steps were followed in deriving the transfer function of the controller:
1. Select phase margin, cross-over frequency, and type of controller:
A bandwidth (
fc) of 40 Hz is selected. The phase margin (PM) of 85° is chosen to provide adequate damping to the closed-loop system for a sudden change in duty cycle. Since the slope of the open loop plant is 0 dB/dec at the selected crossover frequency, therefore, a simple PI regulator is sufficient to regulate the output voltage. The transfer function of the PI controller is given by Equation (21):
2. Calculate the needed Phase boost:
From the Bode plot of the open loop plant
GP(s):
and
. Therefore, PI controller has to present a phase lead of
and a gain of 45 dB. Here,
The required phase boost at crossover frequency is given by Equation (23):
3. Calculate the time constant,
:
∴
= 4.182 × 10
−4.
4. Calculate the controller gain at the crossover frequency:
At the desired crossover frequency the
LTF should cross 0 dB line, i.e.,
∴
KPI = 0.00054.
Therefore PI controller becomes:
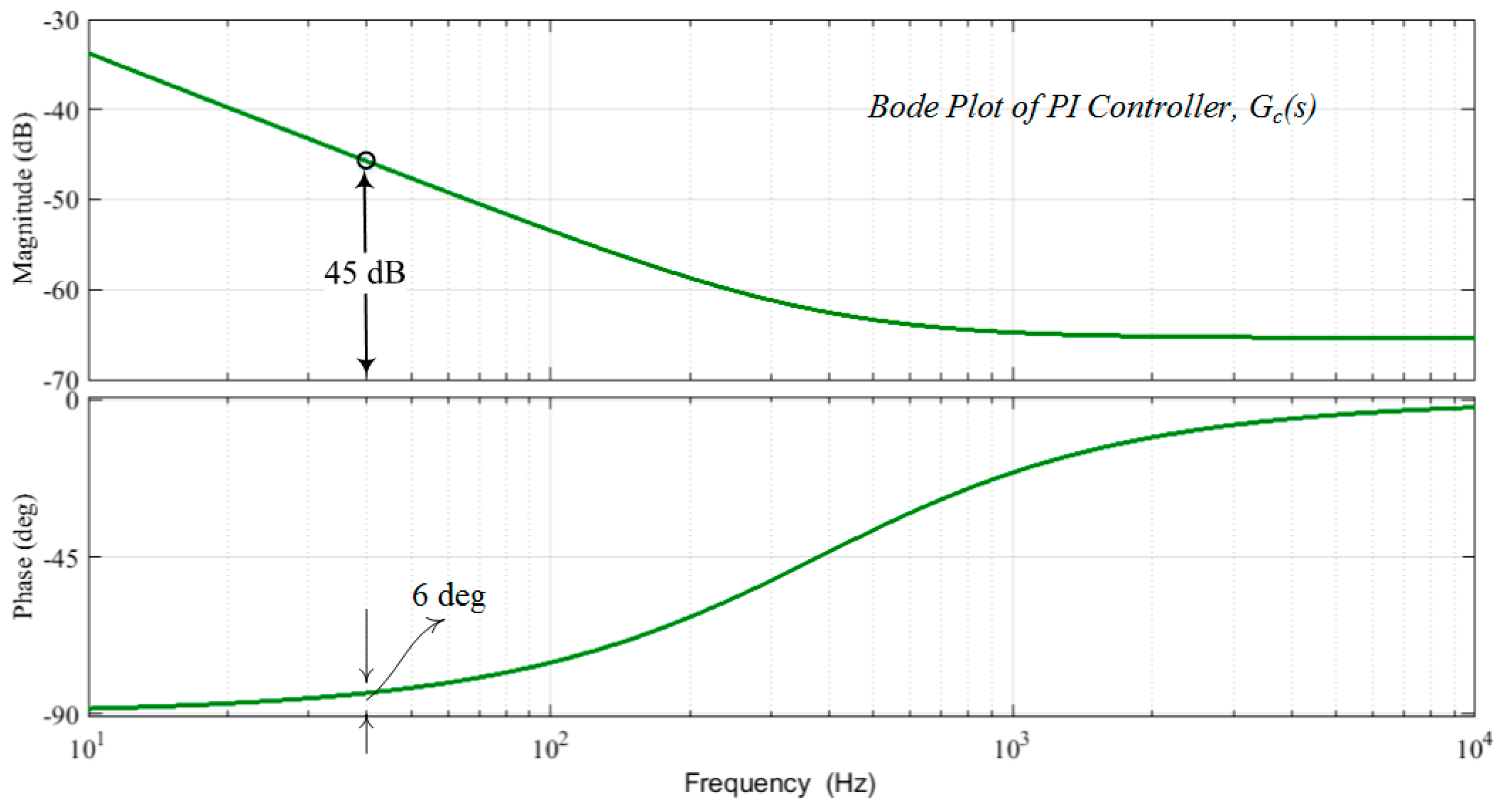
Figure 6 shows the Bode diagram of the designed PI controller.
From
Figure 6, one can observe that at 40 Hz, the phase boost provided by the PI controller is 6°. Moreover, a gain of –45 dB provided by the PI controller will make the gain of LTF zero at 40 Hz, i.e., crossover frequency of 40 Hz is achieved.
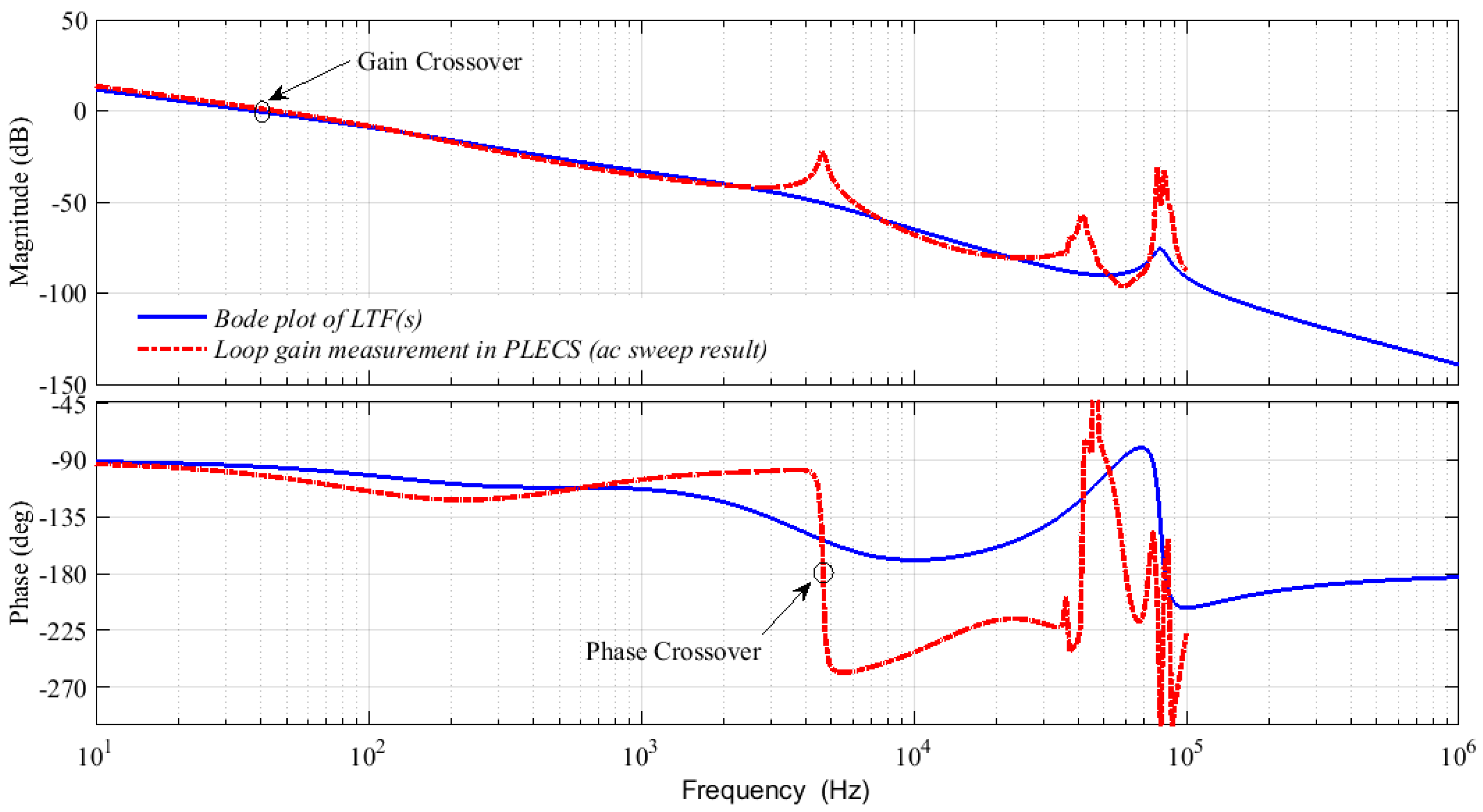
Figure 7 shows the Bode plot of the loop gain obtained using the small-signal model (i.e., LTF(s)) as well as the loop gain obtained using the ac sweep of full model simulated in PLECS 3.7.5.
From
Figure 7, one can observe that the gain crossover frequency of 40 Hz and PM of 85° has been achieved for the derived small-signal model as well as for the full model (precisely 87° in ac sweep). Moreover, for the closed-loop system, the location of gain cross-over frequency is to the left of the phase crossover frequency for both the derived model as well as the full model. Therefore, the closed loop system is stable.
5. Simulation and Experimental Results
In this section, simulation results and experimental results for the closed-loop voltage control have been compared for different cases. Designed controller was implemented on the IPT system whose parameters have been mentioned in
Table 1. Simulation results have been obtained from PLECS3.7.5 standalone. For experimental results, the closed-loop voltage controller was implemented in real-time using dSPACE
® ControlDesk 5.3. LEM sensor LV20-P was used to sense the output voltage. A 63800 series (63804) programmable AC/DC electronic load from Chroma system solutions was used as the DC load. XR Series power supplies from Magna-Power Electronics were used as the programmable DC power supply. The inverter was built using full-bridge MOSFET power module (APTM120H29FG) from Microsemi (Aliso Viejo, CA, USA). For the rectifier, low loss fast recovery diode module from IXYS (Milpitas, CA, USA) (DSEI2X101-06A) was used. To build the coils, Litz wire Type II 8 AWG 5 × 5 × 42/32 has been used. Outer diameter of both the primary and secondary coil is 47 cm. The inner diameter of primary coil is 22 cm whereas inner diameter of secondary coil is 36 cm. The experimental setup is shown in
Figure 8. Different test cases are discussed below.
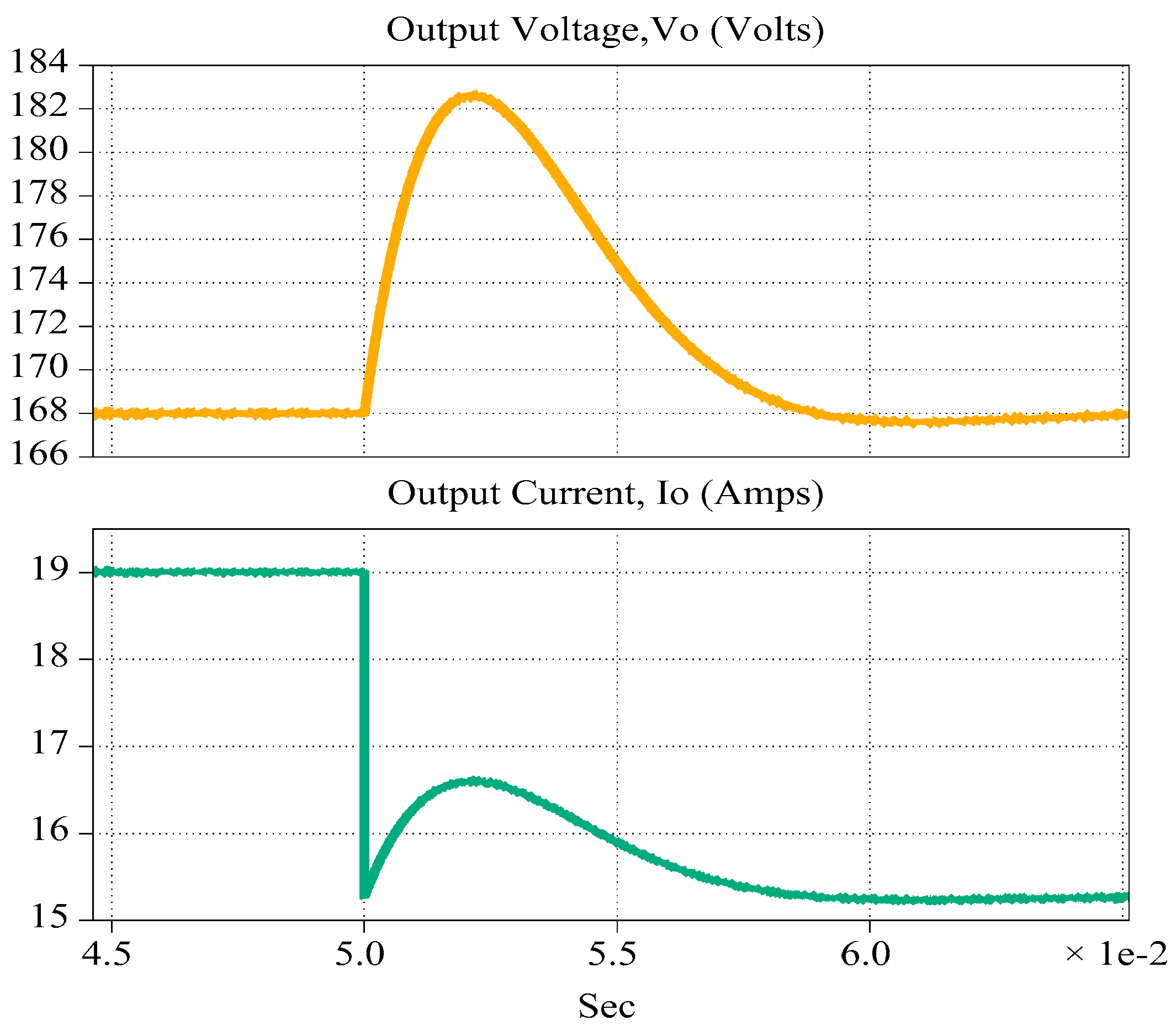
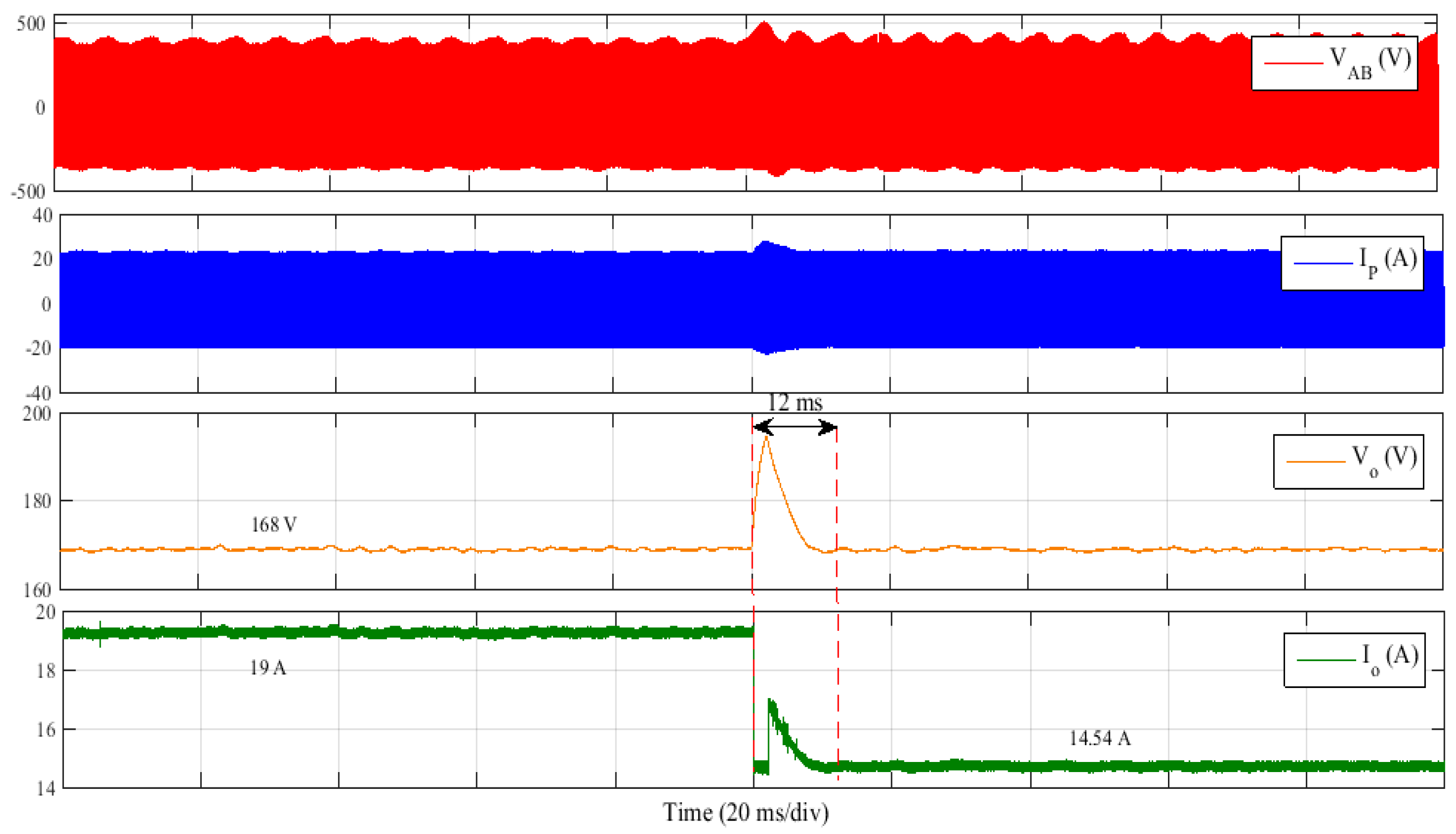
Case I—Change in load at fixed reference voltage:
To test the dynamic performance of the designed controller, a step change in the DC load was performed at the fixed reference voltage. For this purpose, the reference voltage was set at 168 V and load was stepped down from 8.84 Ω (3192.76 W) to 11.56 Ω (2441.5 W).
Figure 9 shows the transient performance of simulated results, while experimental results are shown in
Figure 10. From the results, it can be observed that when the step increase in load is applied, output voltage overshoots and the controller takes corrective action to bring it back to 168 V in about 12 ms in experimental result and 11 ms in simulation result. Voltage overshoot in simulation and experimental results is 9% and 13% respectively.
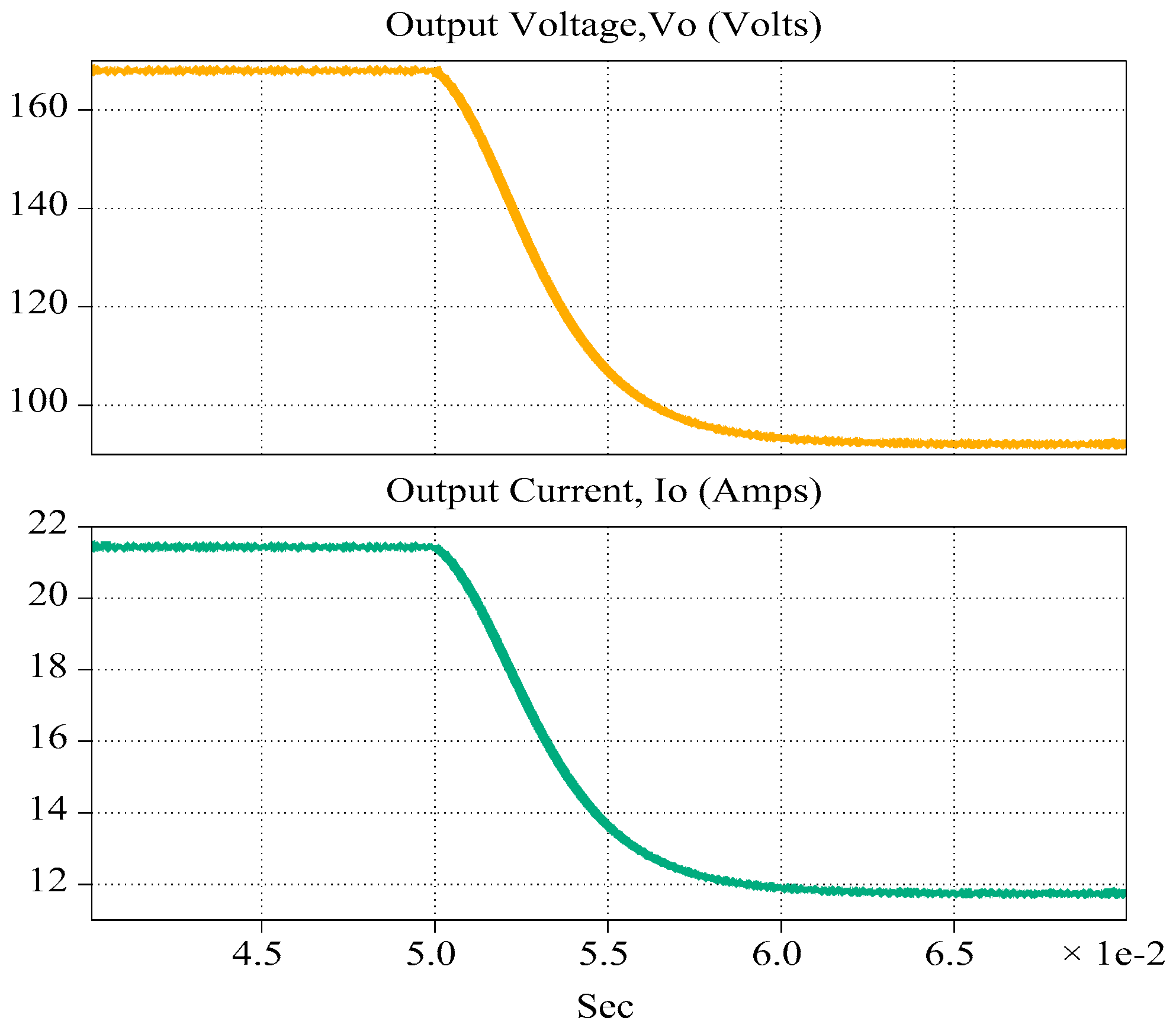
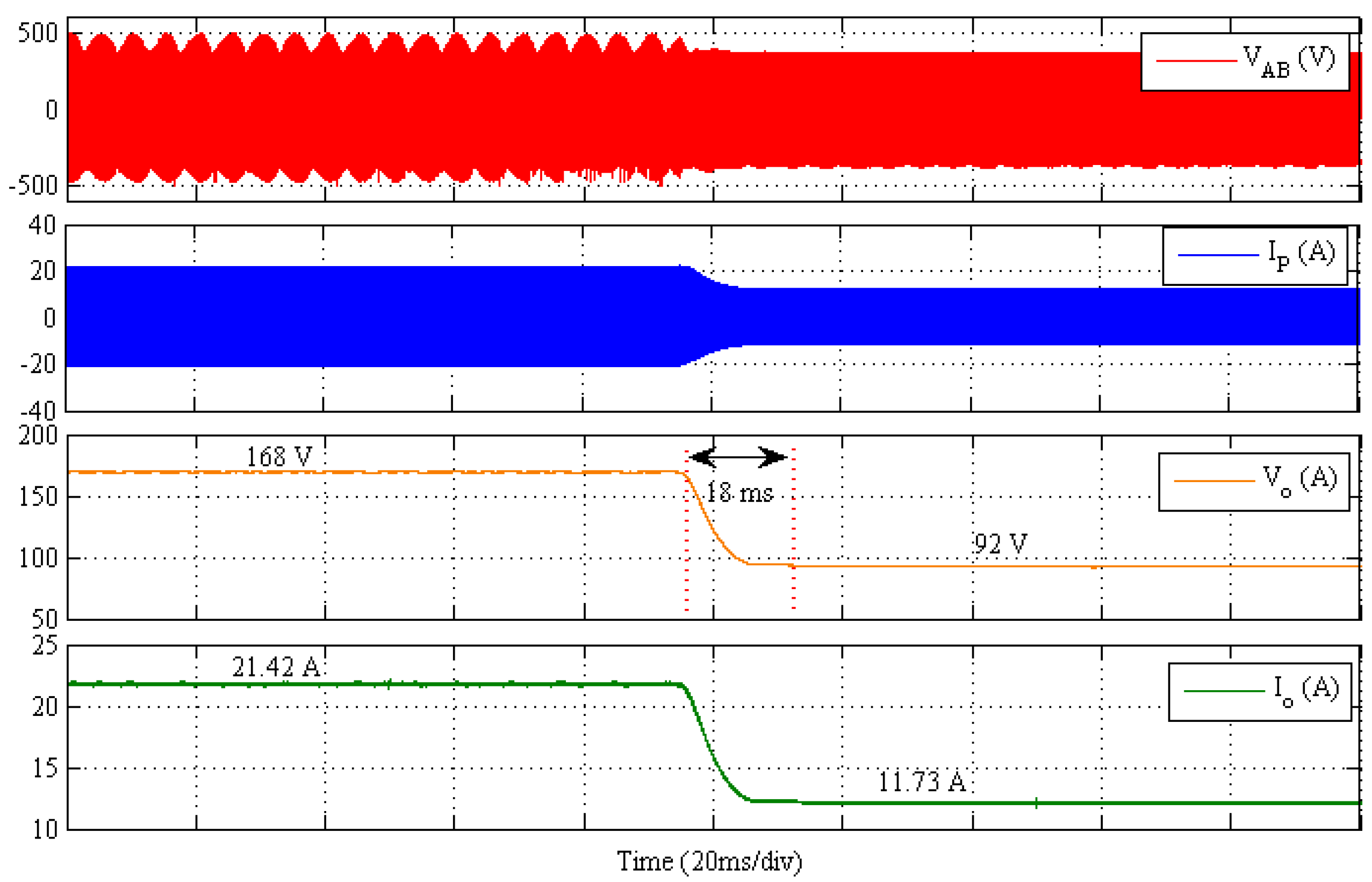
Case II—Change in reference voltage at fixed load:
Reference voltage was stepped down from 168 V (rated Voltage) to 92 V at 7.84 Ω load resistance.
Figure 11 shows the transient performance of simulated results, while experimental results are shown in
Figure 12.
From the results, it can be observed that the controller takes approximately 14 ms to reach steady state for the simulation and 18 ms for the experimental results. No transient undershoot/overshoot occurs due to damping provided by the high PM (85°) of controller.
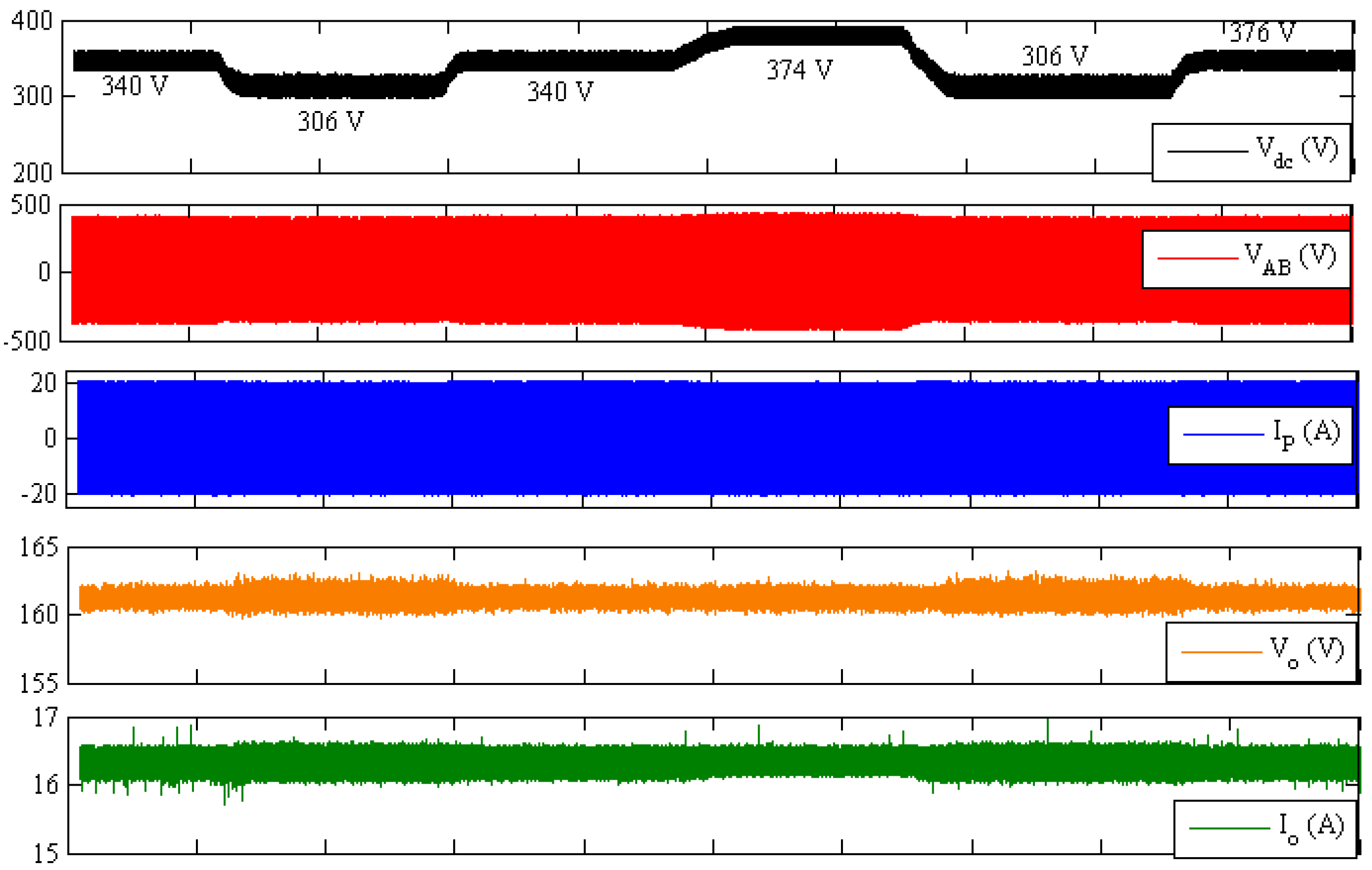
Case III—Tracking performance of controller for variation in DC input voltage:
To test the robustness of the designed controller for the variations in DC input voltage, the reference voltage was kept 160 V at 10 Ω load and ±10% variation in DC input voltage (340 V) was introduced manually. Results obtained are shown in
Figure 13.
From
Figure 13, it can be seen that the controller keeps the output voltage fixed at a reference voltage in spite of variations in the DC input voltage. Since the load is fixed, the output current also remains constant.
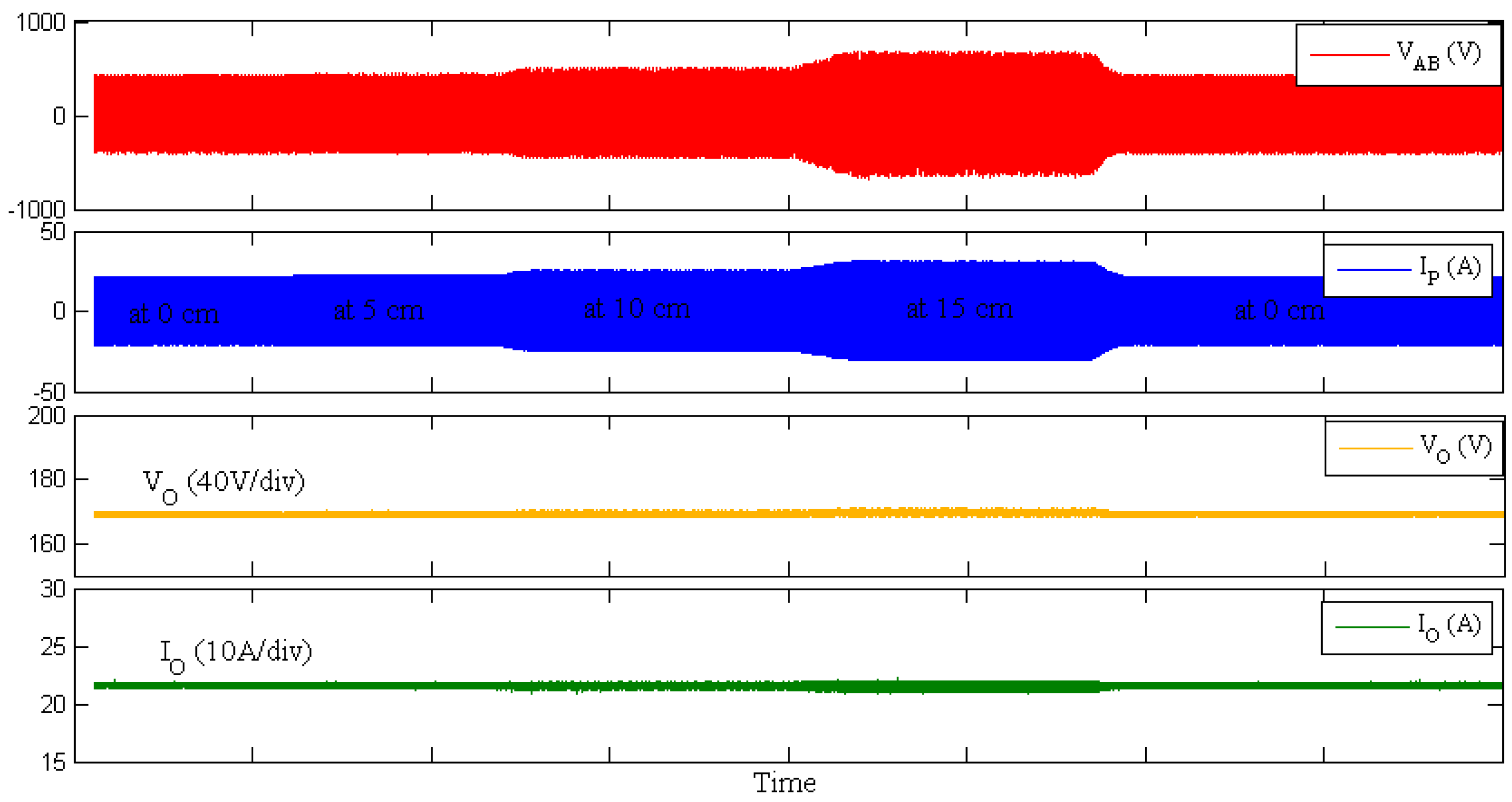
Case IV—Tracking performance of controller for variation in mutual coupling:
To test the controller performance during variation in mutual coupling between the primary and secondary coils, alignment of secondary with respect to primary was varied manually in the sequence [0 cm–5 cm–10 cm–15 cm–0 cm]. The reference voltage and the load was kept 168 V and 7.84 Ω respectively. Results obtained are shown in
Figure 14.
From
Figure 14, one can observe that the output voltage remains fixed in spite of the variation in the mutual inductance between the primary and the secondary coil.
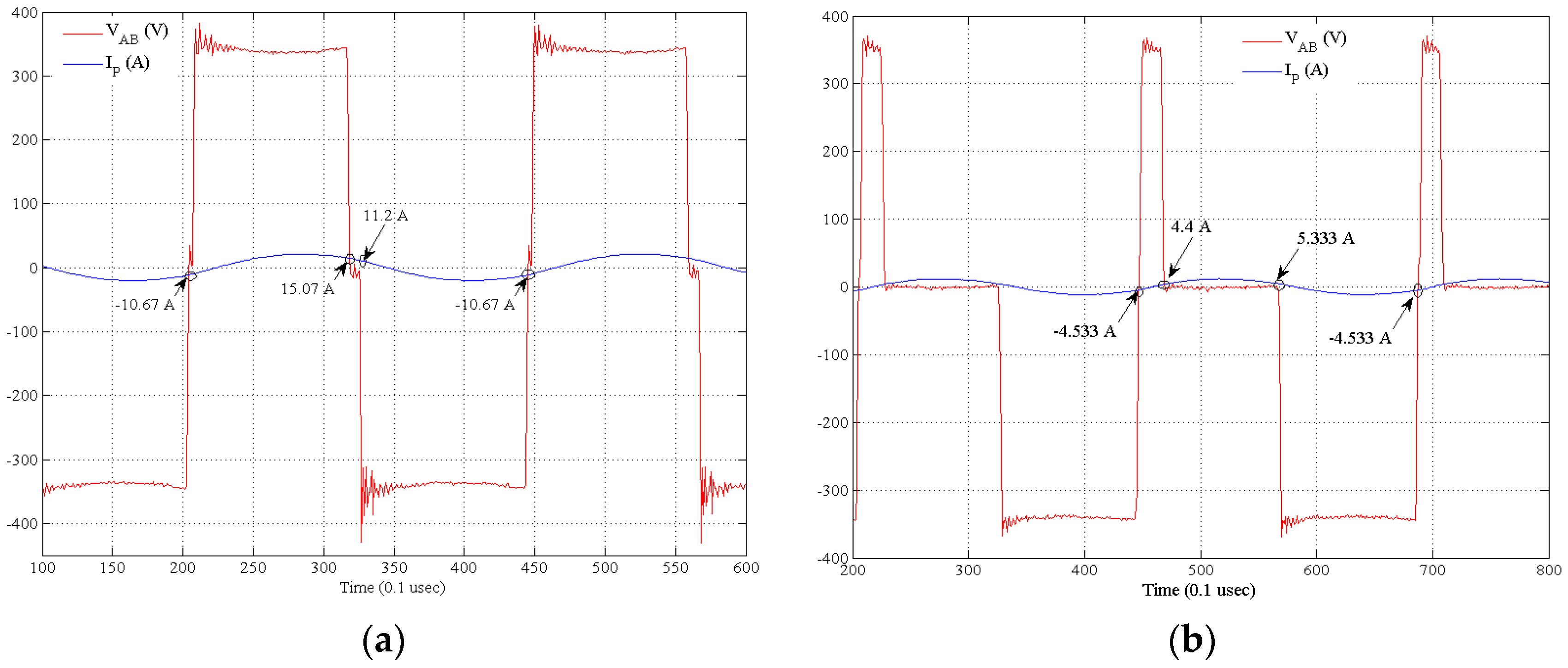
6. Verification of ZVS in INVERTER Switches
To verify for the ZVS in the inverter switches, the method described in [
21] has been used. According to [
19], polarity of current at four switching instance (
t0,
t1,
t2,
t3) shown in
Figure 3 should be according to the Equation (27) for the switches to operate under ZVS condition.
Figure 15a shows the primary voltage and the primary current waveform for 168 V, 7.84 Ω load, (i.e., 3.6 kW) output.
Figure 15b shows the primary voltage and primary current for 92 V, 7.84 Ω, (i.e., 1.08 kW).
From
Figure 15, one can observe that current full fills the ZVS condition defined by Equation (27) for the rated load (3.6 kW) condition, as well as, for the partial load (1.08 kW) condition.
Table 2 gives the DC to DC efficiency for all the cases discussed previously.
It should be noted that, although inverter output voltage is asymmetric, the inverter output is being applied to a series resonant tank which acts as sharply tuned band pass filter. The primary capacitor will block the DC component from flowing into primary coil inductor. Therefore, primary current and hence the secondary current will be almost sinusoidal. This can be observed in experimental result as shown in
Figure 15 that the primary current is sinusoidal.
7. Conclusions
In this paper, a simplified small-signal model of an SS compensated IPT system has been presented. To derive the small signal model, a reduced dynamic model was first derived considering the ZVS in the inverter switches. Although the ZVS has been considered, a fairly accurate mathematical model can also be derived for the zero current switching (ZCS) conditions. AC sweep results show that the frequency response of the derived small-signal model follows the frequency response of the actual full model with proximity in low-frequency region. Therefore, a derived model can be used for the design of voltage control loop. From the derived model an output voltage controller was designed. The voltage controller was implemented on a 3.6 kW IPT system built in the lab. The IPT system was designed for the frequency and voltage level depending on the equipment’s (load, power supply) ratings available in the lab. However, the idea presented in this paper applies to the standard defined by SAE J2954.
A PI controller was designed using the derived small-signal model. Although the controller was designed considering 0.8 duty cycle operation at 7.84 Ω load resistance, it shows good tracking capability for different tests conditions such as: different load resistance; change in DC input voltage; change in reference voltage; and change in coupling coefficient. Therefore, it can be said that the derived controller is very robust against parameter variations. Results obtained show that the derived small signal-model is useful for the design of control loops.