Analytical Modeling of Static Eccentricities in Axial Flux Permanent-Magnet Machines with Concentrated Windings
Abstract
:1. Introduction
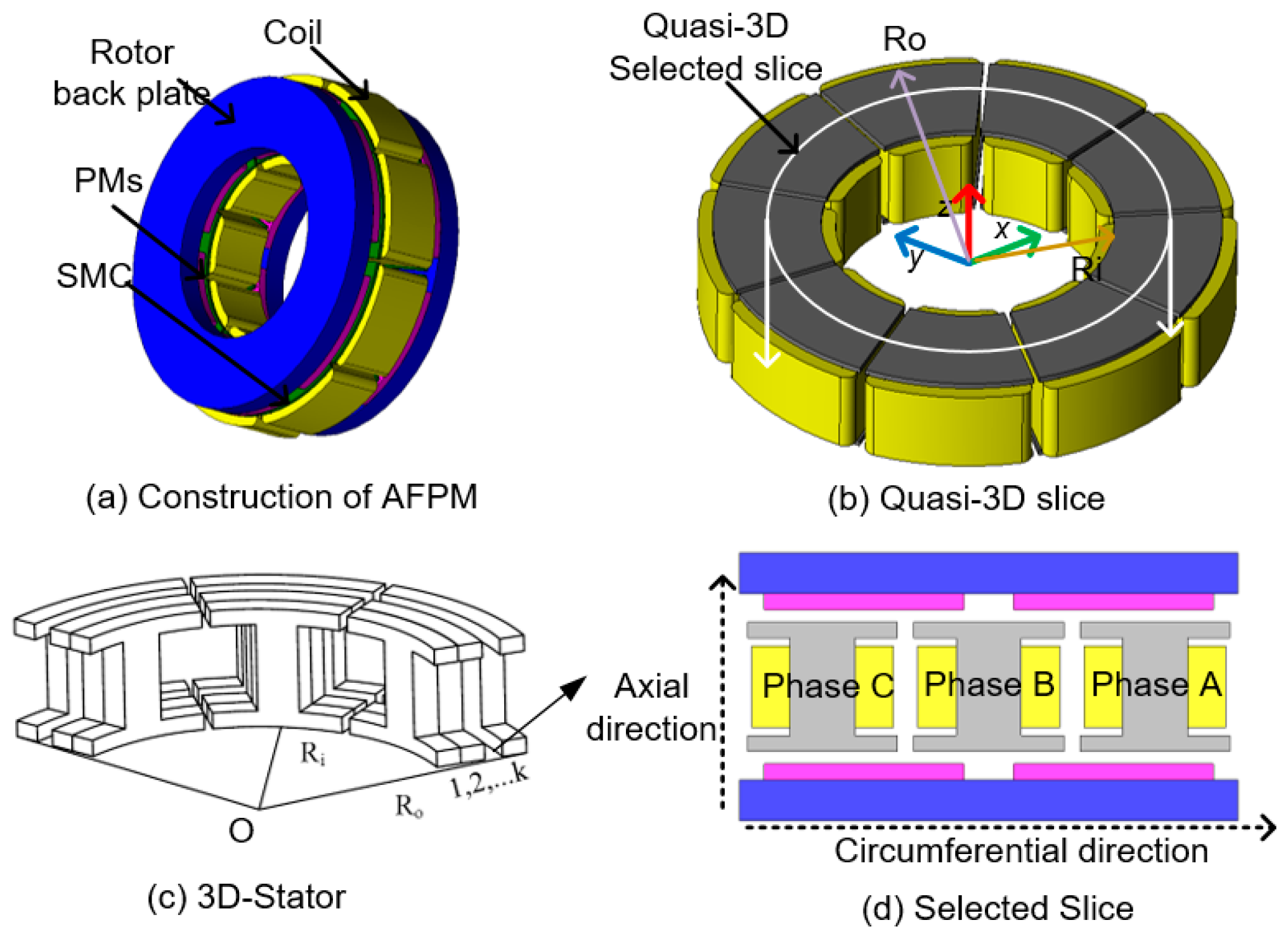
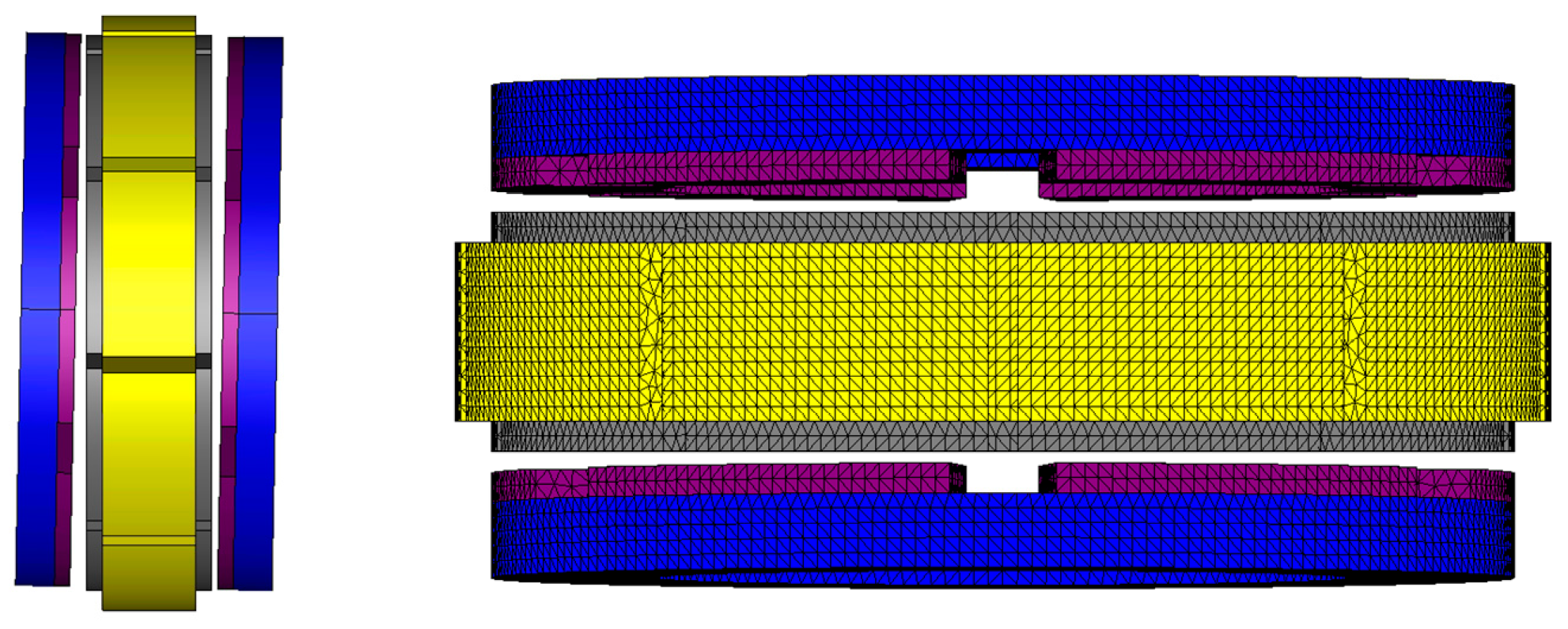
2. Description of the Prototype Axial Flux Permanent Magnet Machine
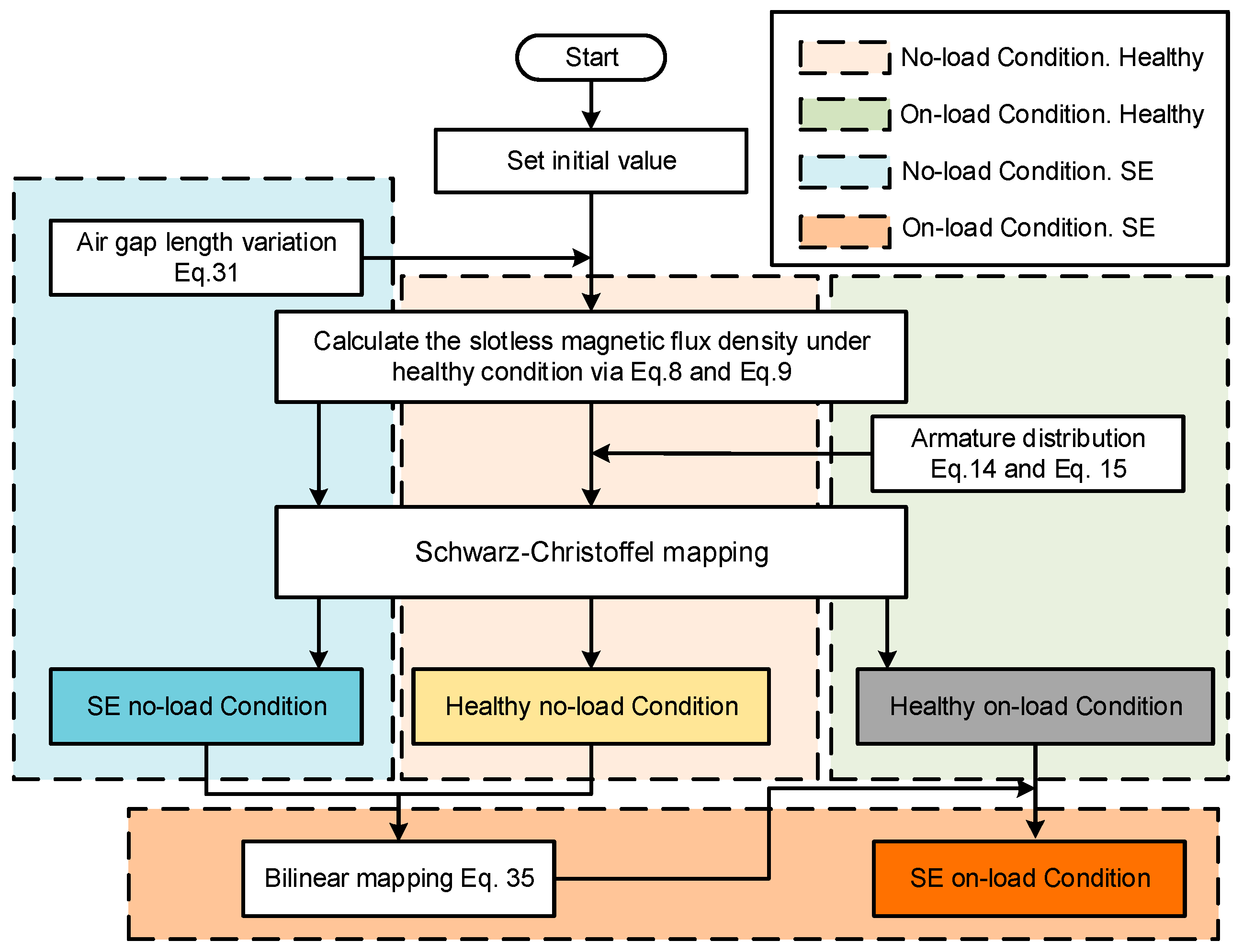
3. Calculation of the Magnetic Field
- (1)
- The magnetic material has a uniform magnetization and the relative recoil permeability μr is constant and has a value close to unity such as in NdFeB materials.
- (2)
- For the computation of armature reaction field, the magnet regions are regarded as free space.
- (3)
- Magnetic saturation is absent and the rotor iron cores have infinite magnetic permeability.
- (4)
- Eddy current effects are neglected, which avoids the need for the complex eddy current field formulation.
3.1. Model of Permanent Magnets (PMs)
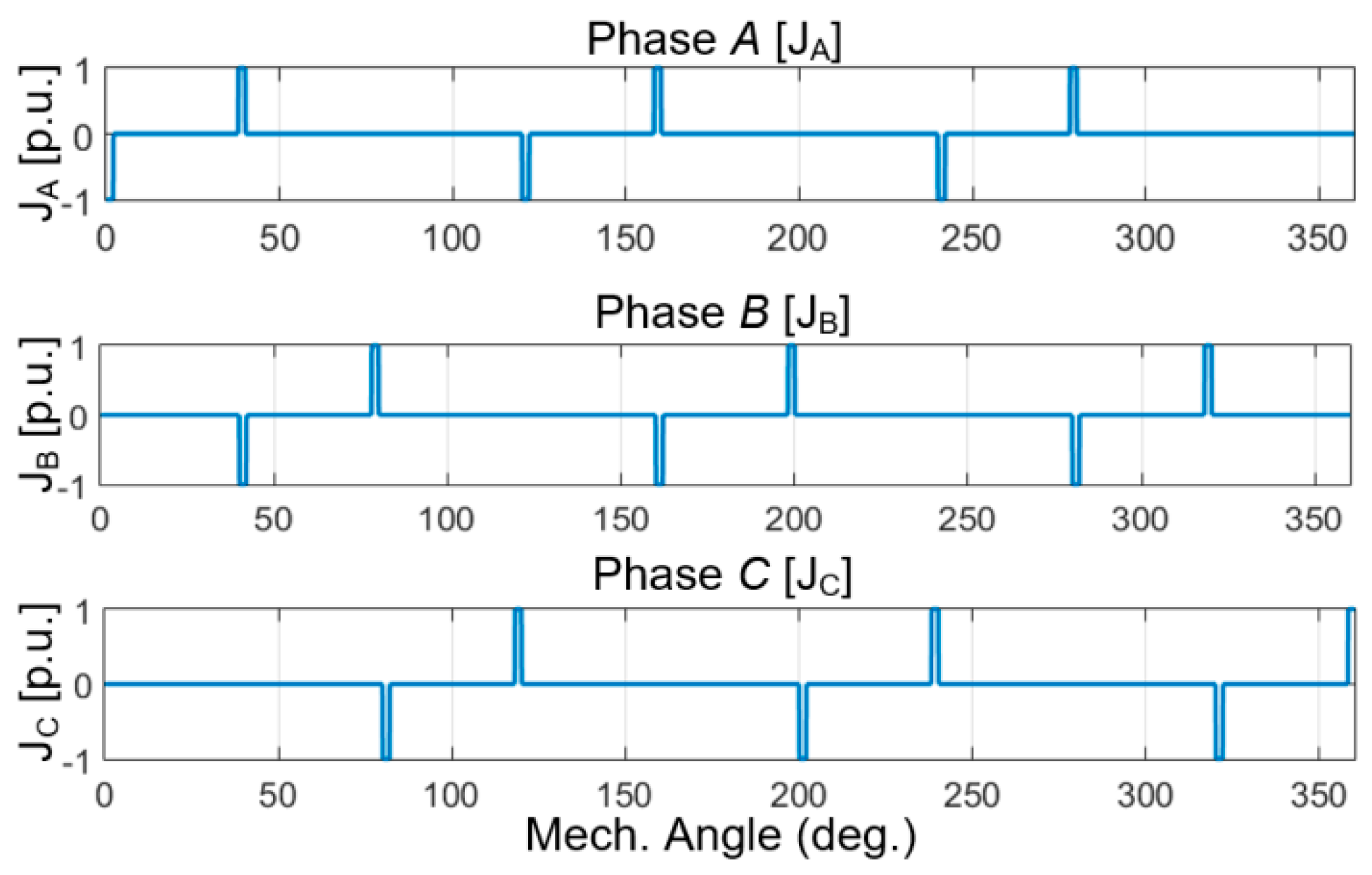
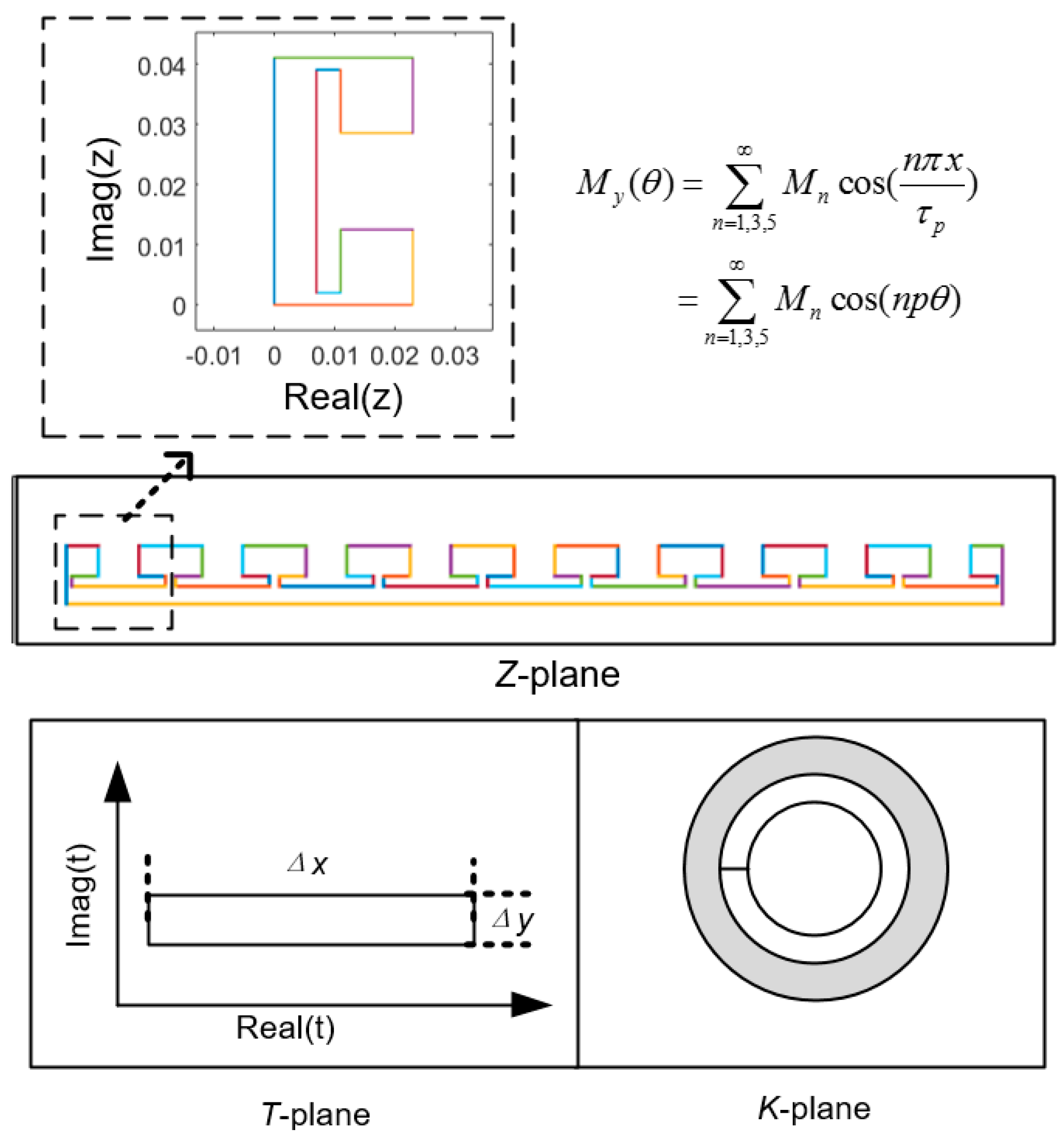
3.2. Model of Armature Reaction Current
3.3. Model of Stator Slotting
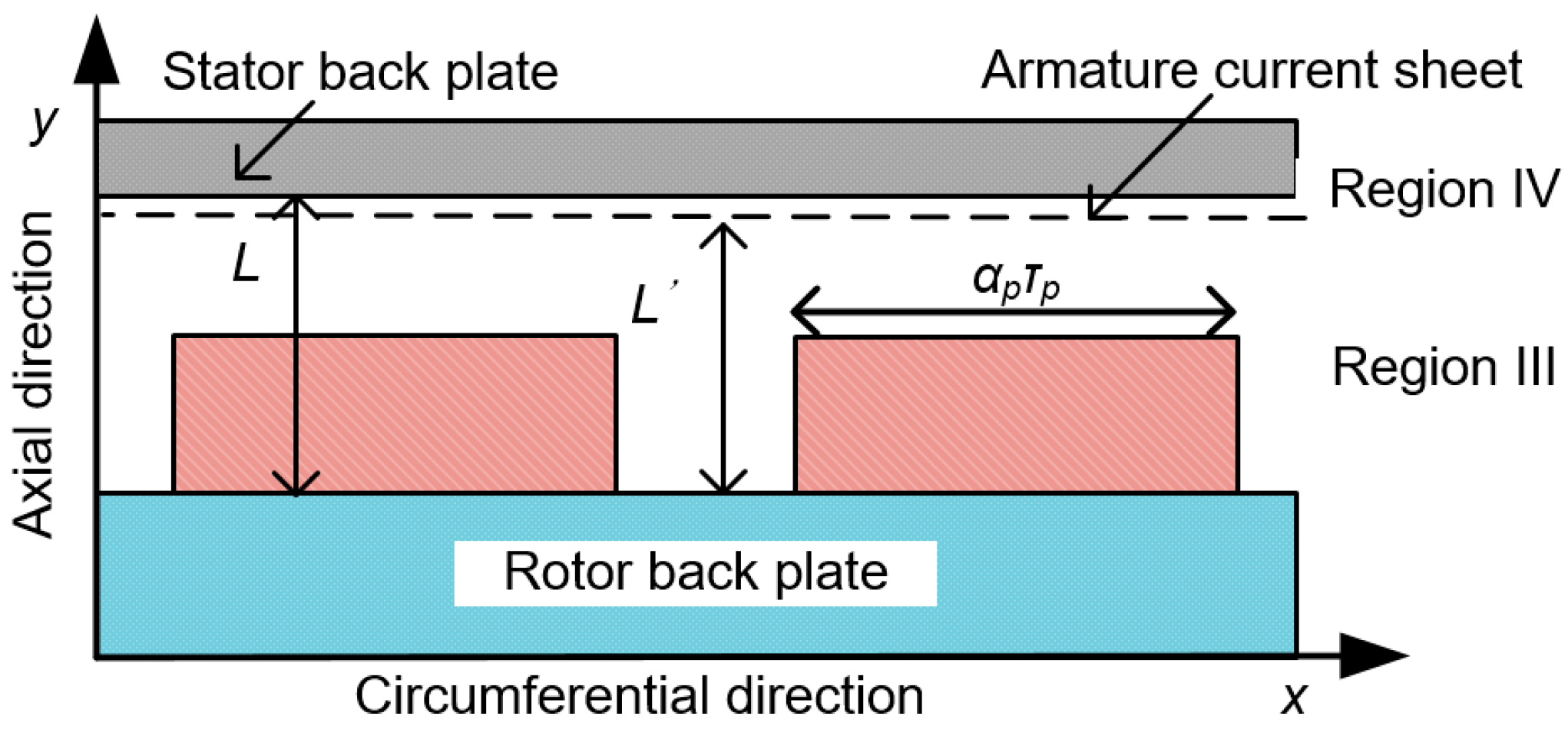
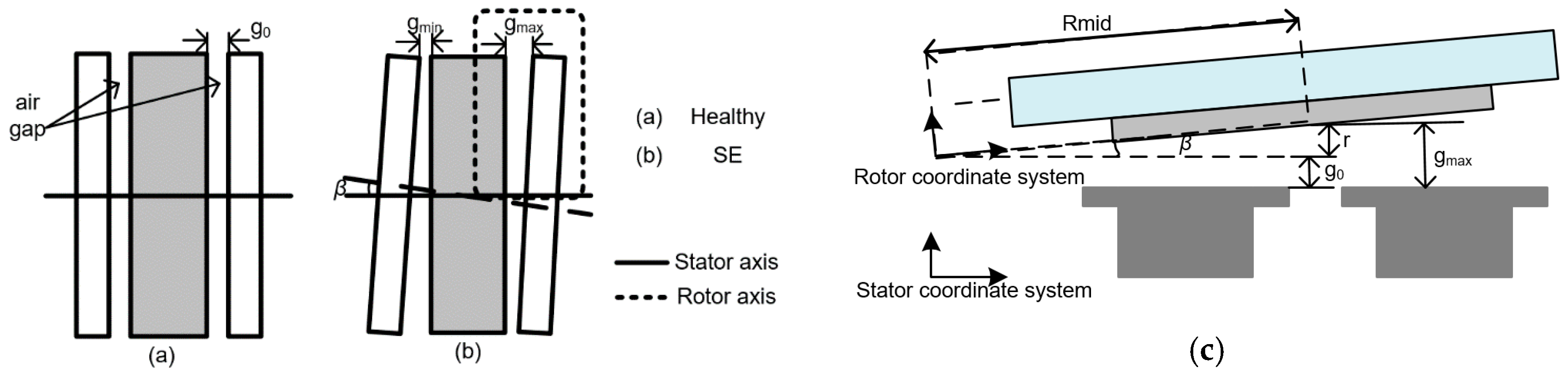
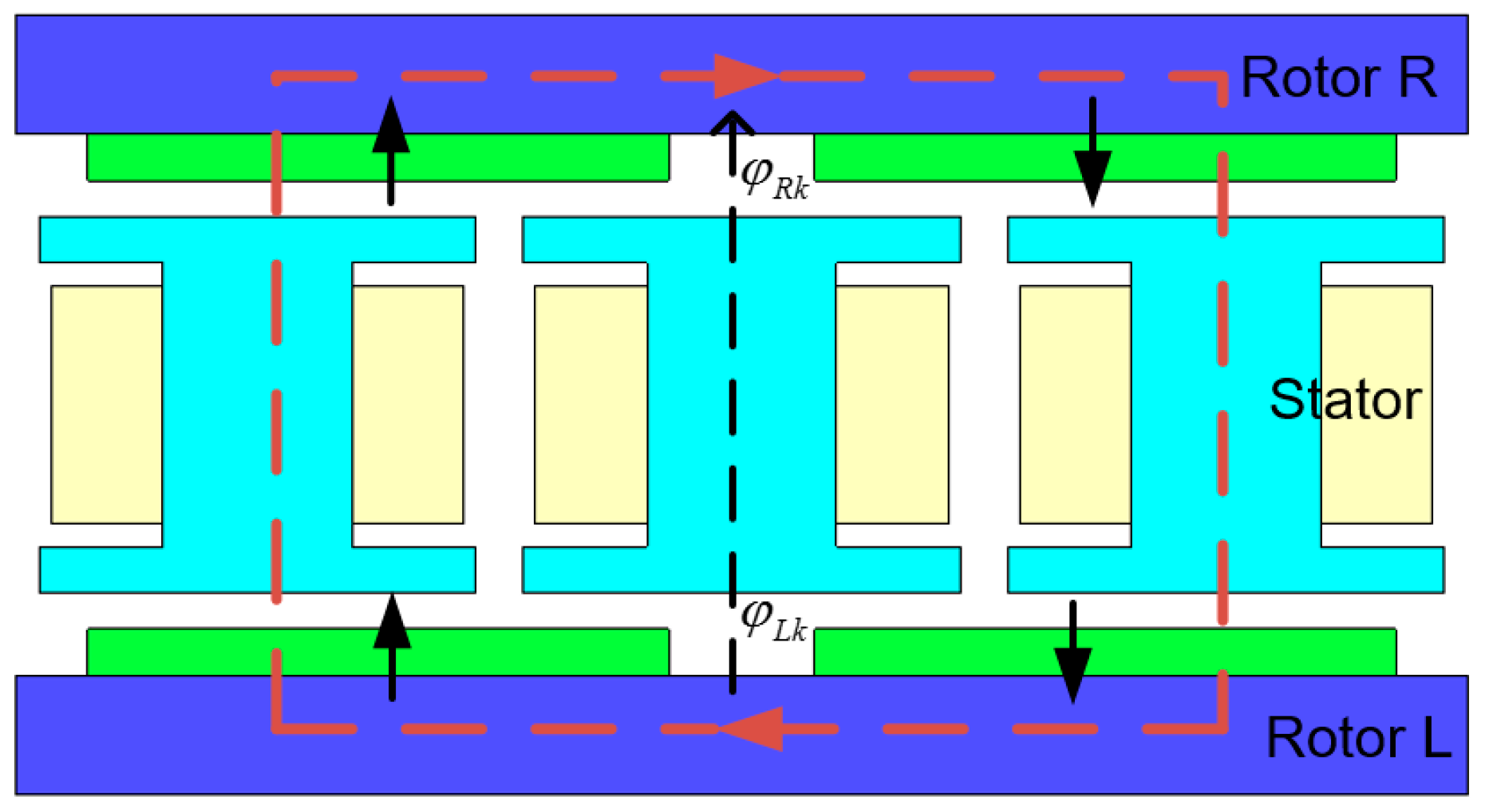
3.4. Model of Static Eccentricity
3.5. Bilinear Mapping
4. Simulation Verification
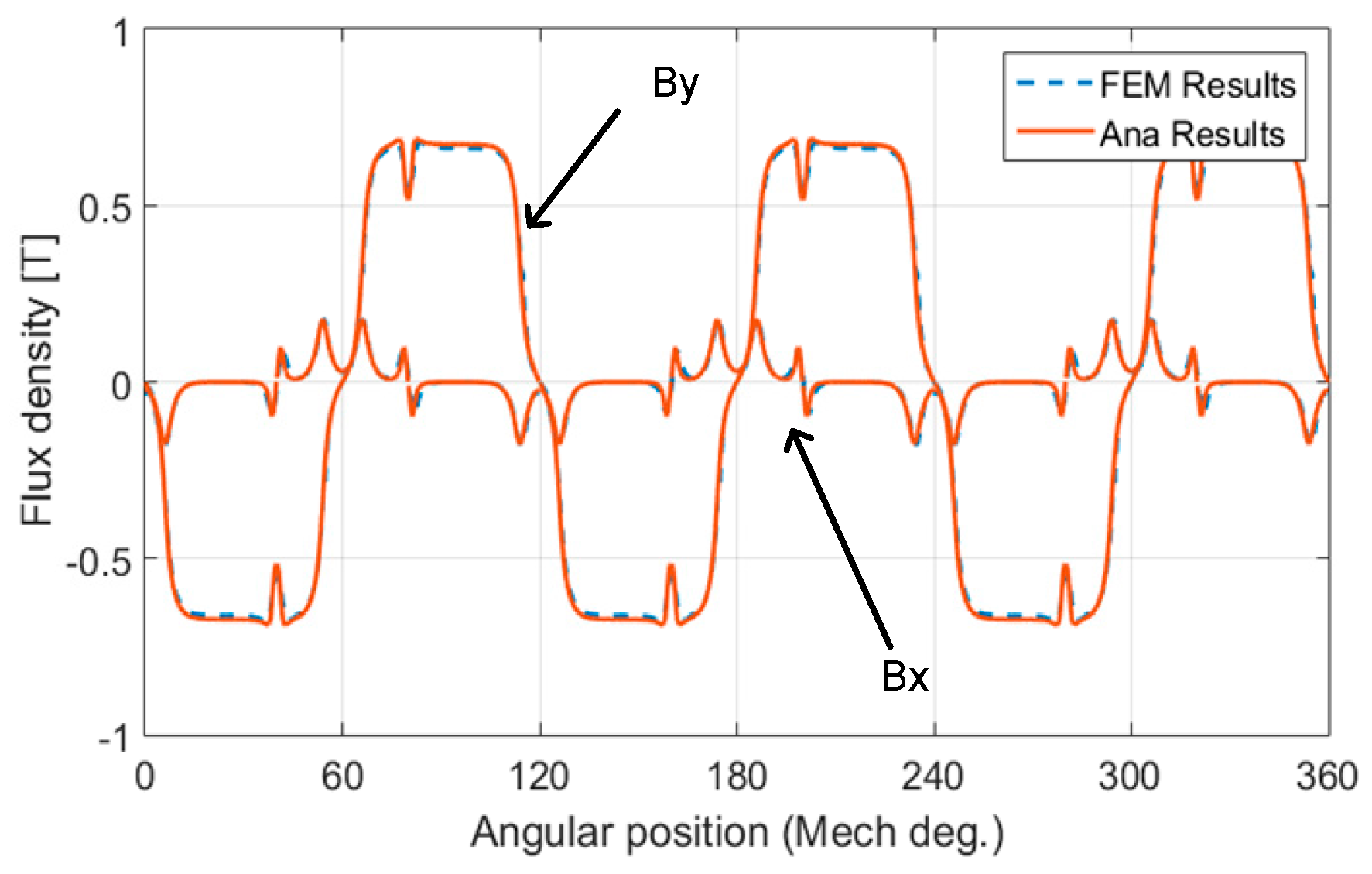
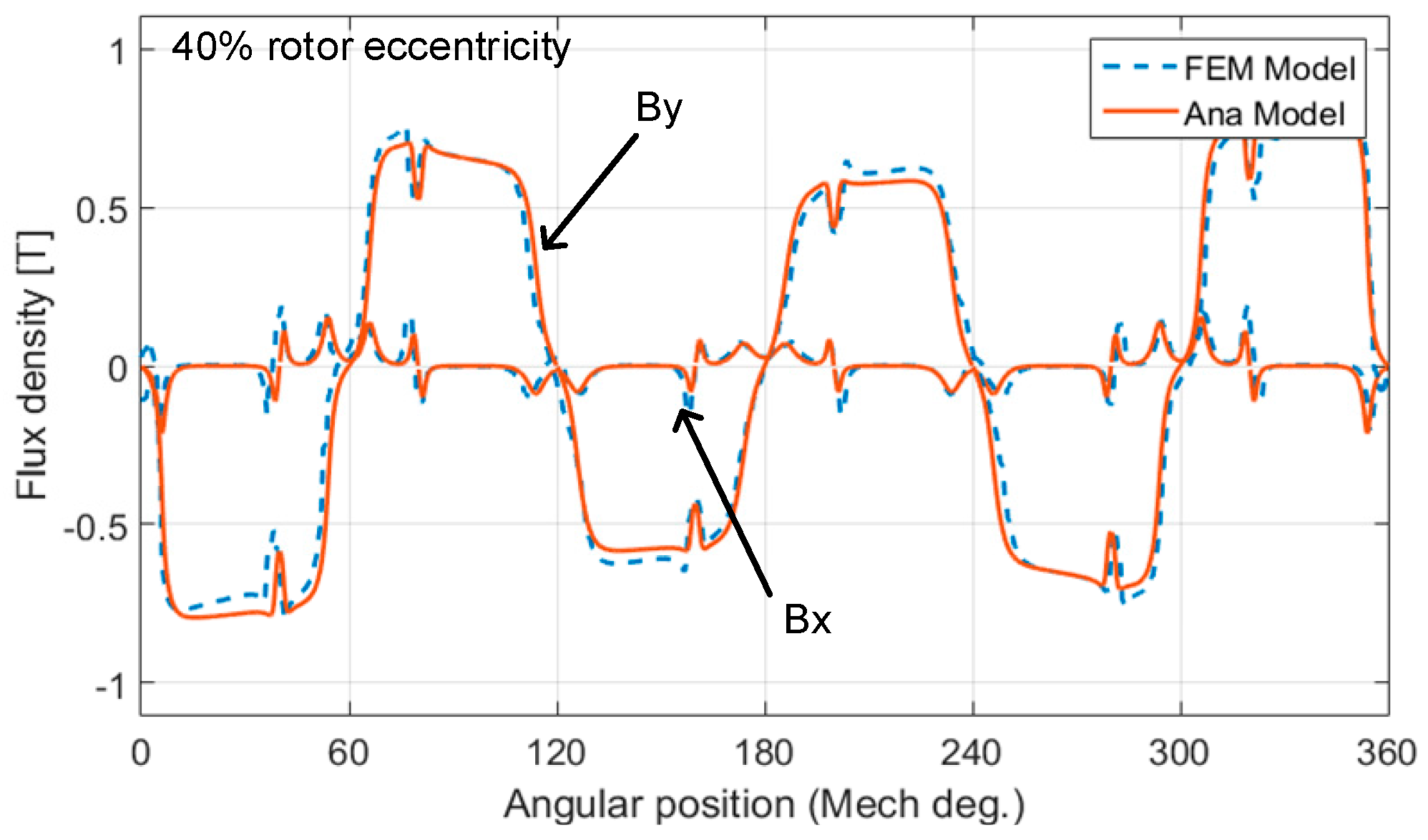
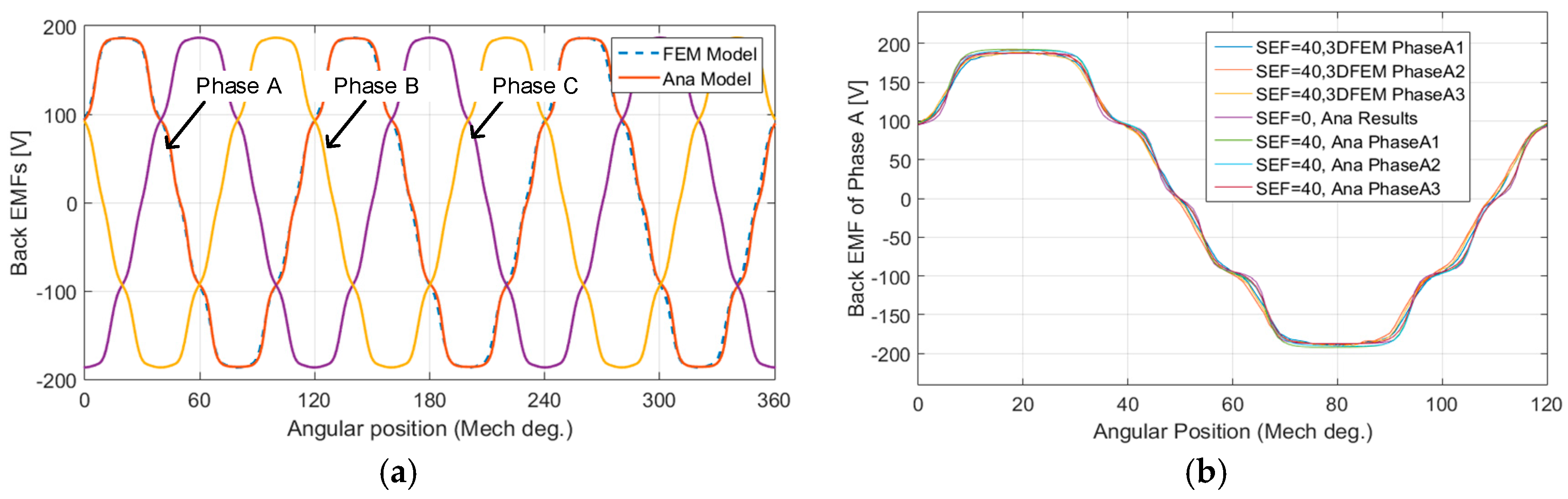
4.1. Air Gap Flux under Healthy Condition
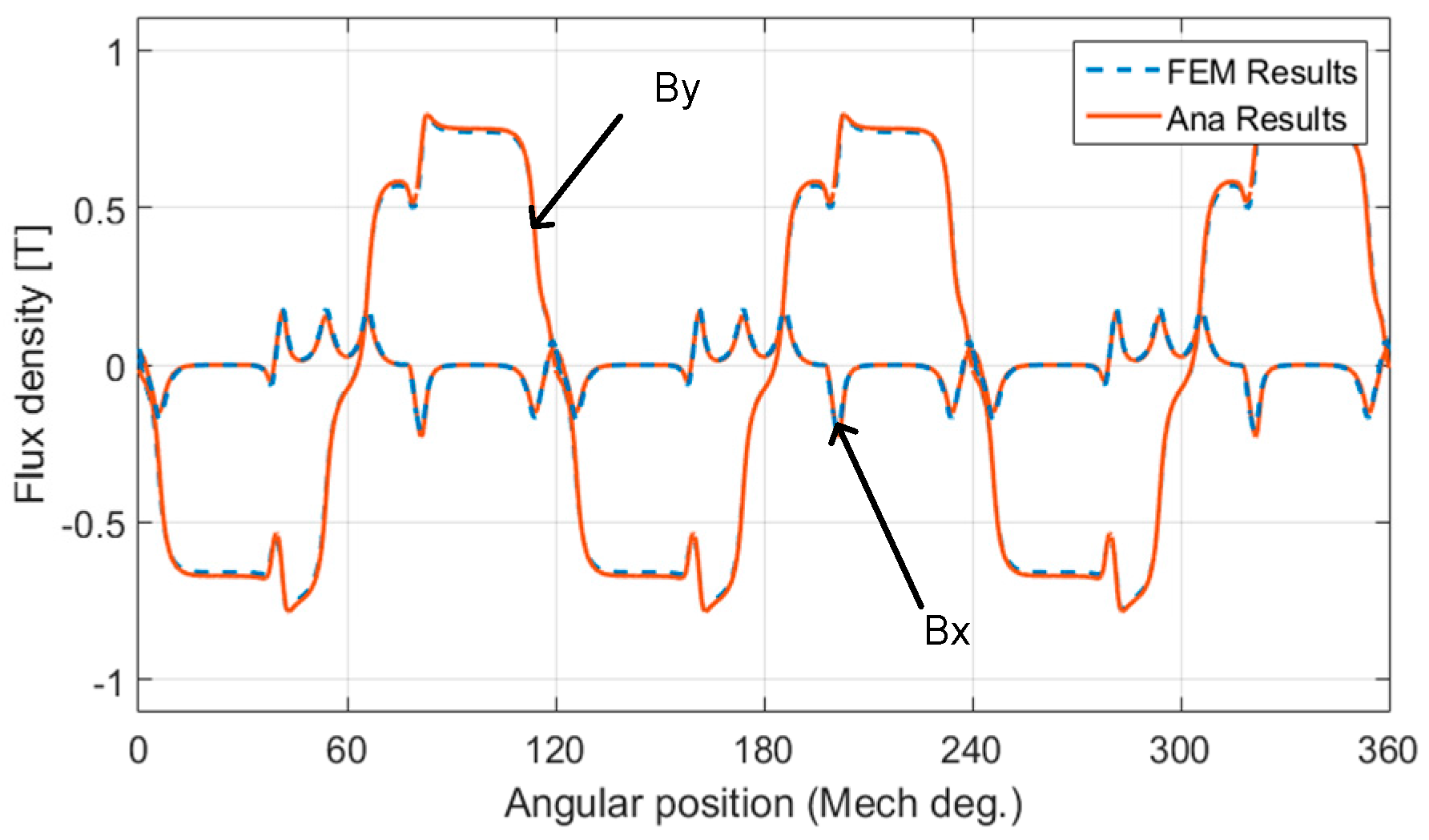
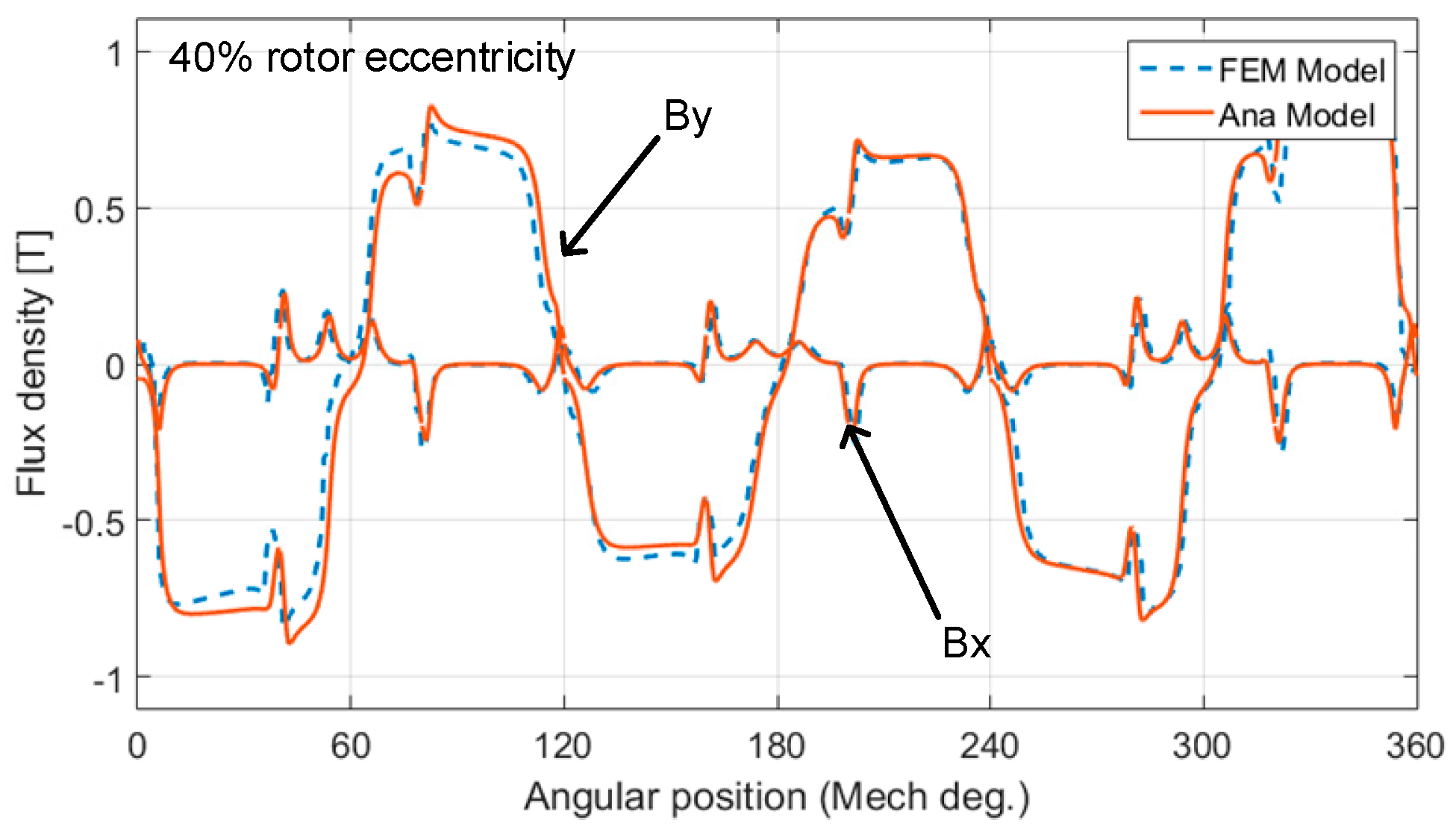
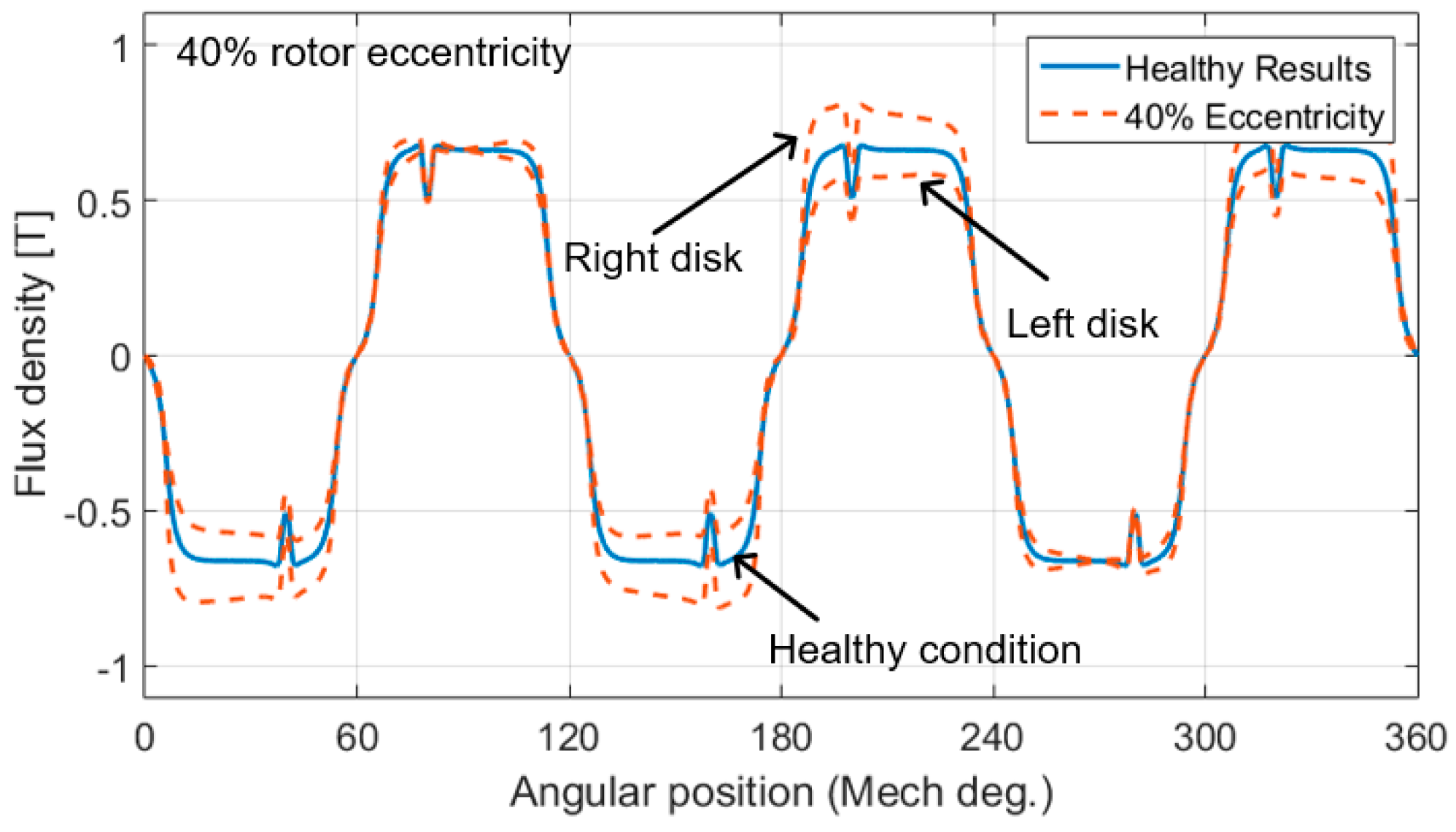
4.2. Air Gap Flux Density under SE Condition
5. Results and Discussion
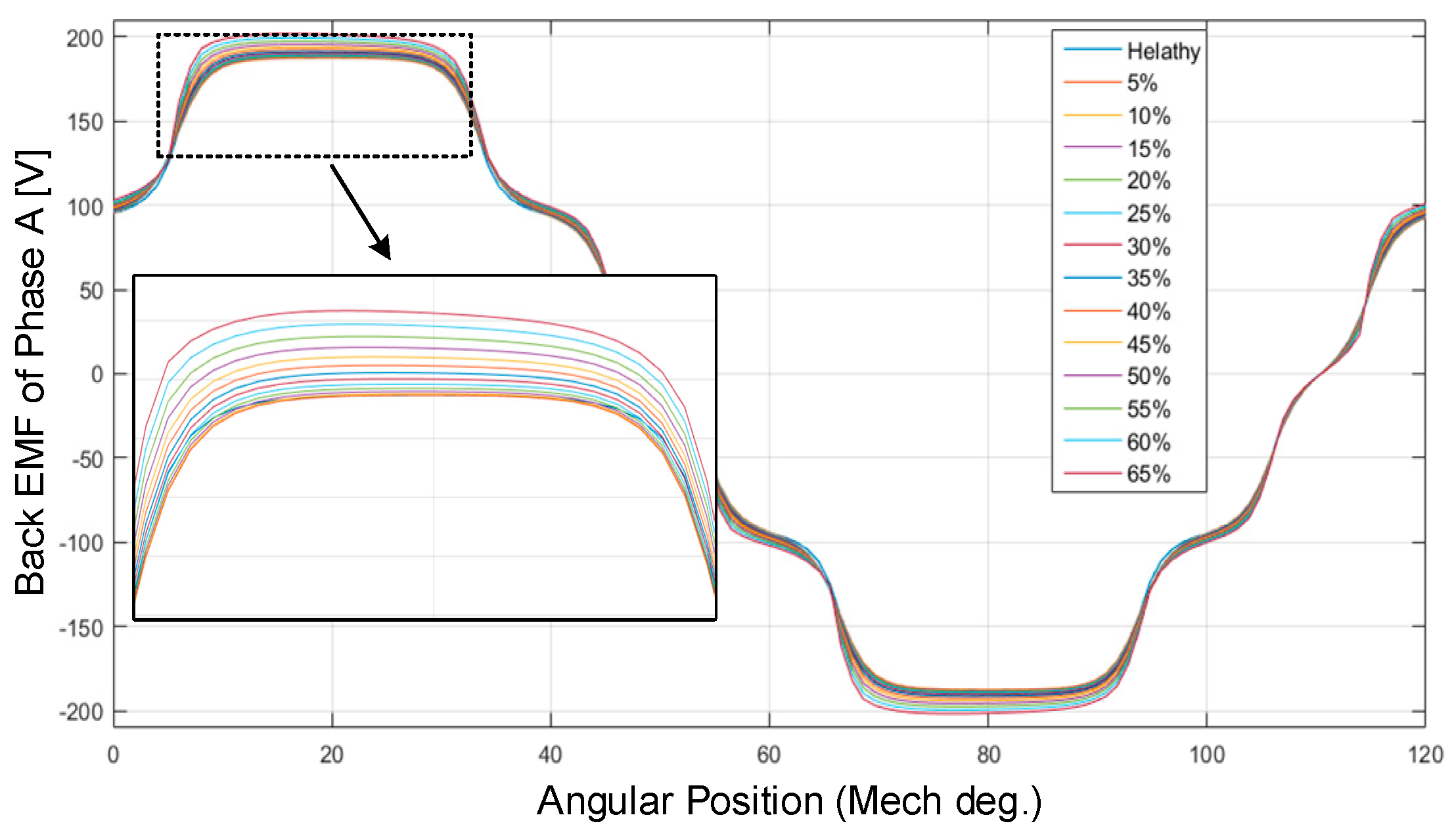
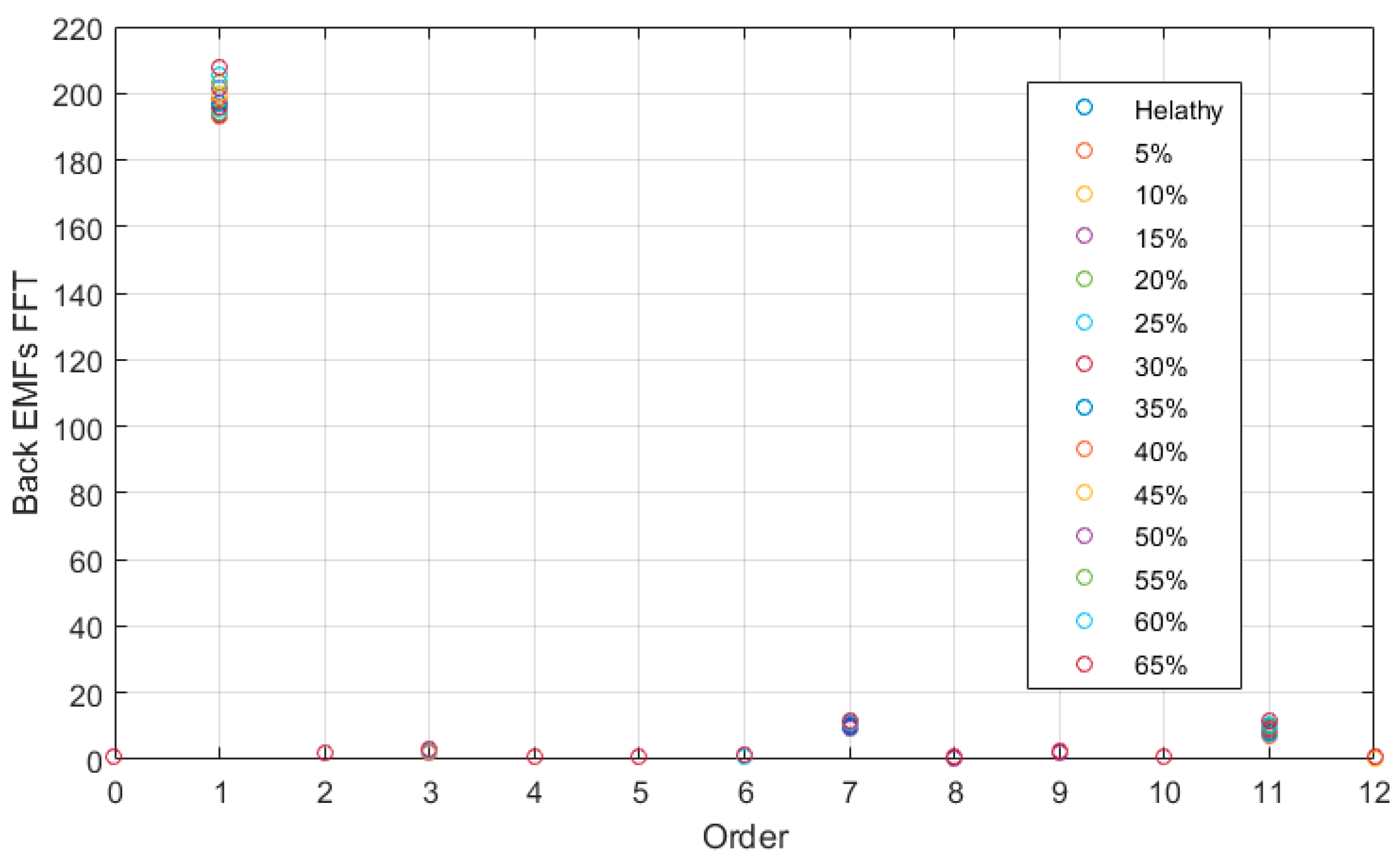
5.1. Machine Main Characteristics under No Load Condition
5.2. Machine Main Characteristics under on Load Condition
6. Experimental Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aydin, M.; Huang, S.; Lipo, T.A. Axial Flux Permanent Magnet Disc Machines: A Review; University of Wisconsin-Madison: Madison, WI, USA, 2004. [Google Scholar]
- Yang, Y.P.; Shih, G.Y. Optimal Design of an Axial-Flux Permanent-Magnet Motor for an Electric Vehicle Based on Driving Scenarios. Energies 2016, 9, 285. [Google Scholar] [CrossRef]
- Hua, W.; Zhou, L.K. Investigation of a Co-Axial Dual-Mechanical Ports Flux-Switching Permanent Magnet Machine for Hybrid Electric Vehicles. Energies 2015, 8, 14361–14379. [Google Scholar] [CrossRef]
- Bai, C.-J.; Wang, W.-C.; Chen, P.-W.; Chong, W.-T. System Integration of the Horizontal-Axis Wind Turbine: The Design of Turbine Blades with an Axial-Flux Permanent Magnet Generator. Energies 2014, 7, 7773–7793. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Tseng, K.-J.; Zhang, S.; Nguyen, T.D. A Novel Axial Flux Permanent-Magnet Machine for Flywheel Energy Storage System: Design and Analysis. IEEE Trans. Ind. Electron. 2011, 58, 3784–3794. [Google Scholar] [CrossRef]
- Mirimani, S.M.; Vahedi, A.; Marignetti, F. Effect of Inclined Static Eccentricity Fault in Single Stator-Single Rotor Axial Flux Permanent Magnet Machines. IEEE Trans. Magn. 2012, 48, 143–149. [Google Scholar] [CrossRef]
- Thiele, M.; Heins, G.; Patterson, D. Identifying manufacturing induced rotor and stator misalignment in brushless permanent magnet motors. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 2728–2733.
- Thiele, M.; Heins, G. Computationally Efficient Method for Identifying Manufacturing Induced Rotor and Stator Misalignment in Permanent Magnet Brushless Machines. IEEE Trans. Ind. Appl. 2016, 52, 3033–3040. [Google Scholar] [CrossRef]
- Li, J.; Qu, R.; Cho, Y.-H. Effect of unbalanced and inclined air-gap in double-stator inner-rotor axial flux permanent magnet machine. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 502–508.
- Bellini, A.; Filippetti, F.; Tassoni, C.; Capolino, G.A. Advances in Diagnostic Techniques for Induction Machines. IEEE Trans. Ind. Electron. 2008, 55, 4109–4126. [Google Scholar] [CrossRef]
- Marignetti, F.; Vahedi, A.; Mirimani, S.M. An Analytical Approach to Eccentricity in Axial Flux Permanent Magnet Synchronous Generators for Wind Turbines. Electr. Power Compon. Syst. 2015, 43, 1039–1250. [Google Scholar] [CrossRef]
- Mirimani, S.M.; Vahedi, A.; Marignetti, F.; di Stefano, R. An Online Method for Static Eccentricity Fault Detection in Axial Flux Machines. IEEE Trans. Ind. Electron. 2015, 62, 1931–1942. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Maroufian, S.S. Axial flux permanent magnet motor modeling using magnetic equivalent circuit. In Proceedings of the 2013 21st Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 14–16 May 2013.
- Azzouzi, J.; Barakat, G.; Dakyo, B. Quasi-3-D analytical modeling of the magnetic field of an axial flux permanent-magnet synchronous machine. IEEE Trans. Energy Convers. 2005, 20, 746–752. [Google Scholar] [CrossRef]
- Ajily, E.; Ardebili, M.; Abbaszadeh, K. Magnet Defect and Rotor Eccentricity Modeling in Axial-Flux Permanent-Magnet Machines via 3-D Field Reconstruction Method. IEEE Trans. Energy Convers. 2016, 31, 486–495. [Google Scholar] [CrossRef]
- Ajily, E.; Abbaszadeh, K.; Ardebili, M. Three-Dimensional Field Reconstruction Method for Modeling Axial Flux Permanent Magnet Machines. IEEE Trans. Energy Convers. 2015, 30, 199–207. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Rahimi, A. Analytical quasi 3D modeling of an axial flux PM motor with static eccentricity fault. Sci. Iran. Trans. Comput. Sci. Eng. Electr. 2015, 22, 2482. [Google Scholar]
- Zarko, D.; Ban, D.; Lipo, T.A. Analytical Solution for Electromagnetic Torque in Surface Permanent-Magnet Motors Using Conformal Mapping. IEEE Trans. Magn. 2009, 45, 2943–2954. [Google Scholar] [CrossRef]
- Žarko, D. A Systematic Approach to Optimized Design of Permanent Magnet Motors with Reduced Torque Pulsations. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2004. [Google Scholar]
- O’Connell, T.C.; Krein, P.T. A Schwarz–Christoffel-Based Analytical Method for Electric Machine Field Analysis. IEEE Trans. Energy Convers. 2009, 24, 565–577. [Google Scholar] [CrossRef]
- Hemeida, A.; Sergeant, P. Analytical Modeling of Surface PMSM Using a Combined Solution of Maxwell’s Equations and Magnetic Equivalent Circuit. IEEE Trans. Magn. 2014, 50, 1–13. [Google Scholar] [CrossRef]
- Calixto, W.P.; Alvarenga, B.; da Mota, J.C.; Brito, L.D.C.; Wu, M.; Alves, A.J.; Neto, L.M.; Antunes, C.F.R.L. Electromagnetic Problems Solving by Conformal Mapping: A Mathematical Operator for Optimization. Math. Probl. Eng. 2010, 2010, 742039. [Google Scholar] [CrossRef]
- Ogidi, O.O.; Barendse, P.S.; Khan, M.A. Detection of Static Eccentricities in Axial-Flux Permanent-Magnet Machines with Concentrated Windings Using Vibration Analysis. IEEE Trans. Ind. Appl. 2015, 51, 4425–4434. [Google Scholar] [CrossRef]
- Miroslav, M. Magnetic Field Analysis in Electric Motors Using Conformal Mapping; EPFL: Lausanne, Switzerland, 2004. [Google Scholar]
- Li, J.T.; Liu, Z.J.; Nay, L.H.A. Effect of Radial Magnetic Forces in Permanent Magnet Motors with Rotor Eccentricity. IEEE Trans. Magn. 2007, 43, 2525–2527. [Google Scholar] [CrossRef]
- Di Gerlando, A.; Foglia, G.M.; Iacchetti, M.F.; Perini, R. Evaluation of Manufacturing Dissymmetry Effects in Axial Flux Permanent-Magnet Machines: Analysis Method Based on Field Functions. IEEE Trans. Magn. 2012, 48, 1995–2008. [Google Scholar] [CrossRef]
- Barakat, G.; El-meslouhi, T.; Dakyo, B. Analysis of the cogging torque behavior of a two-phase axial flux permanent magnet synchronous machine. IEEE Trans. Magn. 2001, 37, 2803–2805. [Google Scholar] [CrossRef]


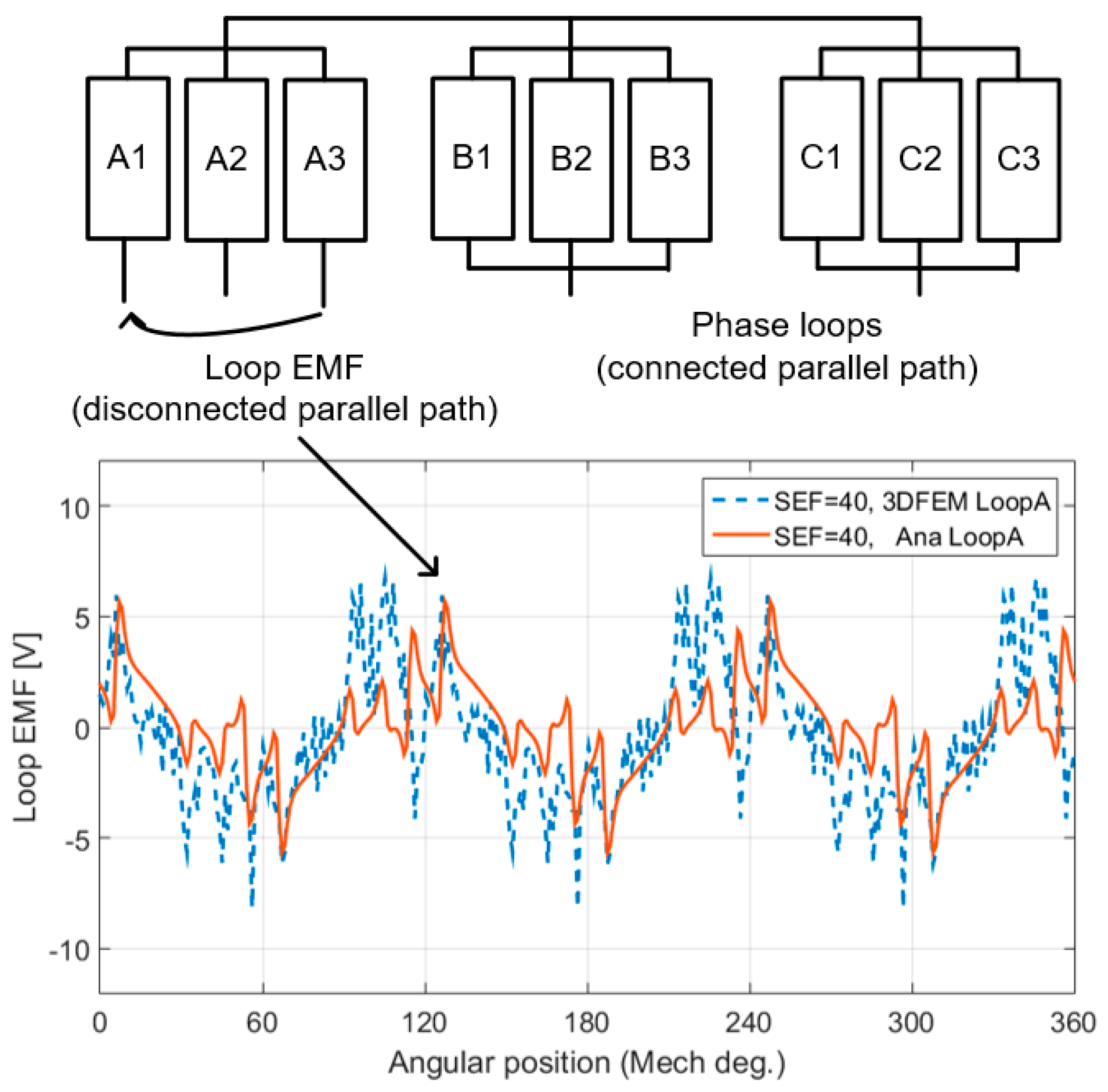
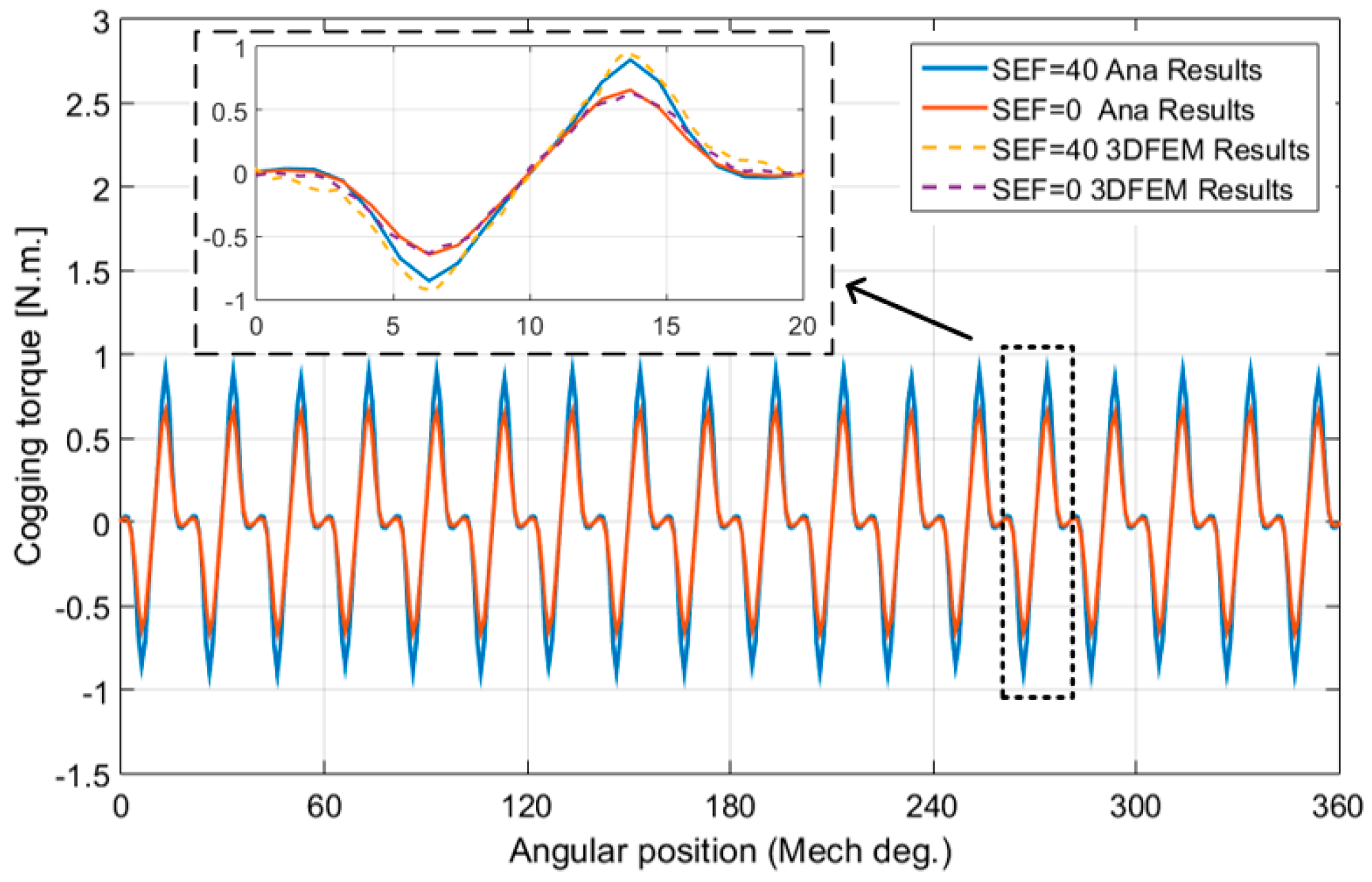
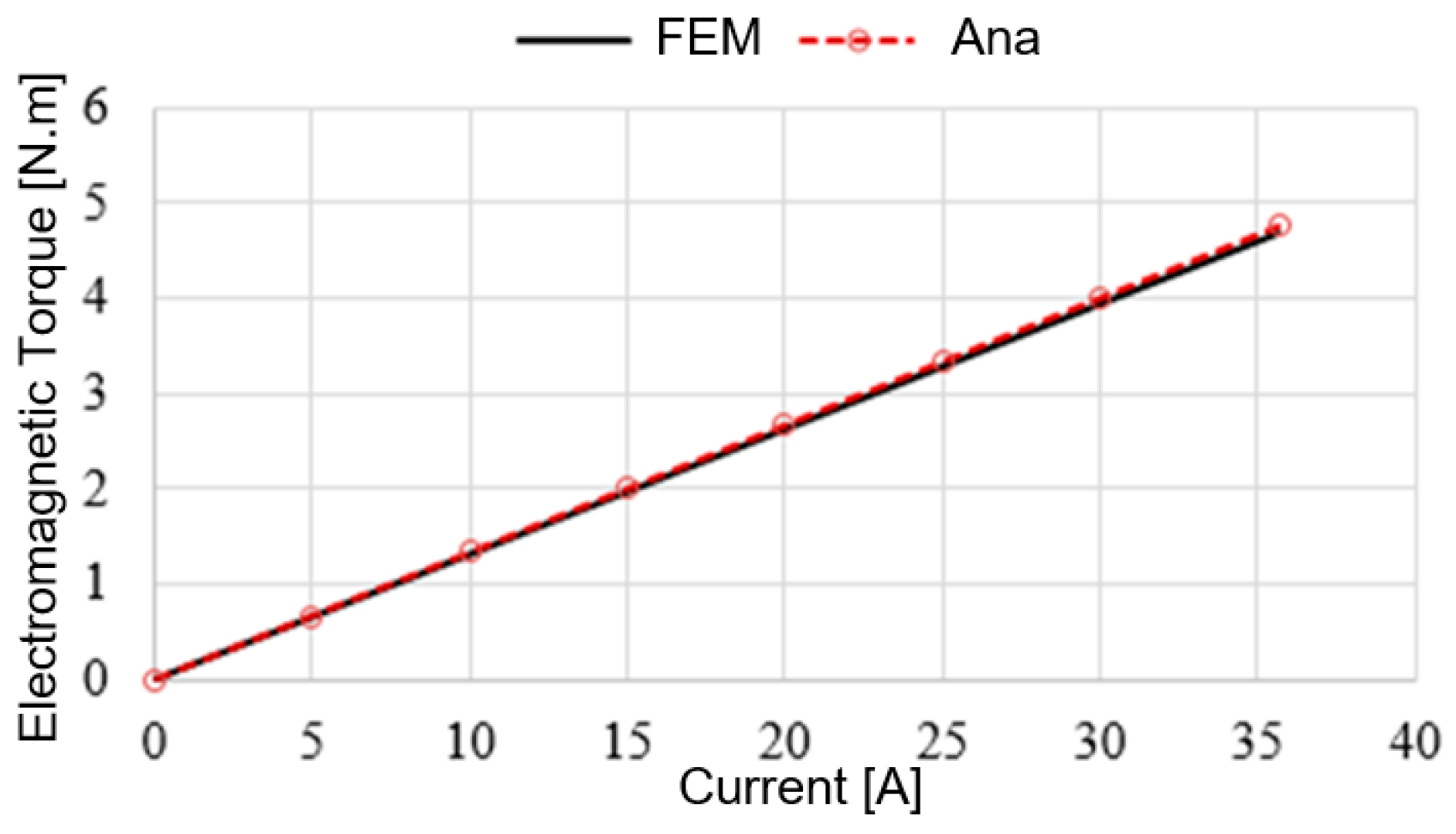

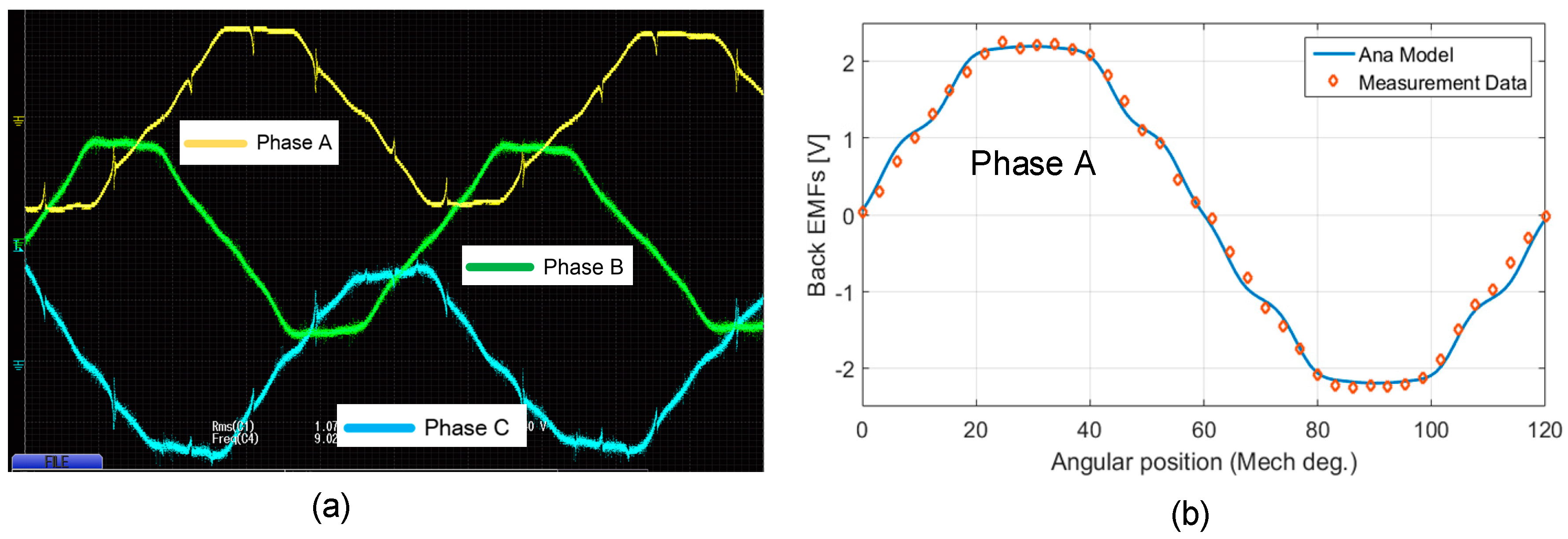
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Rated power | P | 10 | kW |
| Rated voltage | U | 200 | V |
| Rated speed | np | 20,000 | rpm |
| Number of poles/slots | p/Qs | 6/9 | - |
| Stator outer radius | Ro | 70 | mm |
| Stator inner radius | Ri | 45 | mm |
| Air gap length | g | 3 | mm |
| Remnant flux density of PM | Br | 1.03 | T |
| Stator core | - | SMC | - |
| Permanent magnet | - | NdFeB | - |
| Item | FE Model | Analytical Model | Experiment |
|---|---|---|---|
| Back EMF Coefficient | 5.30 | 5.30 | 5.28 |
| Error in Back-EMF | 0.37% | 0.37% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Guo, B.; Hemeida, A.; Sergeant, P. Analytical Modeling of Static Eccentricities in Axial Flux Permanent-Magnet Machines with Concentrated Windings. Energies 2016, 9, 892. https://doi.org/10.3390/en9110892
Huang Y, Guo B, Hemeida A, Sergeant P. Analytical Modeling of Static Eccentricities in Axial Flux Permanent-Magnet Machines with Concentrated Windings. Energies. 2016; 9(11):892. https://doi.org/10.3390/en9110892
Chicago/Turabian StyleHuang, Yunkai, Baocheng Guo, Ahmed Hemeida, and Peter Sergeant. 2016. "Analytical Modeling of Static Eccentricities in Axial Flux Permanent-Magnet Machines with Concentrated Windings" Energies 9, no. 11: 892. https://doi.org/10.3390/en9110892
APA StyleHuang, Y., Guo, B., Hemeida, A., & Sergeant, P. (2016). Analytical Modeling of Static Eccentricities in Axial Flux Permanent-Magnet Machines with Concentrated Windings. Energies, 9(11), 892. https://doi.org/10.3390/en9110892







