1. Introduction
The renewable energy industry is undergoing continuous improvement to cover the current demands of electricity, wind energy being one of the most important. The new technologies, communication systems and advances in mathematical models for signal processing aid in achieving that goal [
1]. The complexity of these devices causes a reduction of the reliability, availability, maintainability and safety of the system (RAMS) and increases the maintenance costs due to the occurrence of non-monitored failures [
2,
3,
4].
Nowadays, fault detection and diagnosis (FDD) by non-destructive testing (NDT) is employed in maintenance management [
5,
6,
7], for example in structural health monitoring (SHM) [
8]. SHM enables identifying and diagnosing the fault and its location by detecting changes in the static and dynamic features of the structure [
9,
10]. SHM can be remotely managed, reducing the costs of manual inspections and the time between the fault occurrences, and this has been noted [
11,
12]. This will lead to an increase in the productivity, reducing the potential downtimes for the wind farms and increasing the RAMS of the wind turbine [
13,
14,
15].
The purpose of this paper is to design an FDD model for the SHM of a wind turbine blade [
16,
17,
18]. The case study proposes a novel localization method using signals from macro-fiber composite (MFC) sensors. Three MFC sensors are strategically located along a blade section to detect incipient breakages in the structure [
19,
20]. The case study involves some considerations, e.g., the appearance of the scattering phenomena, the orientation of the sensors when the excitation is received,
etc. However, it will be demonstrated that the proposed method can set the location with high accuracy. The analysis identifies a single point obtained from a graphical method that is analytically set by nonlinear equations.
The accuracy of this method depends on the transducer sensitivity, the type of composite material, irregularities in the material, the environmental noise, etc. The localization precision of the emission source will be affected by the type of composite material, the sensitivity of the materials, environmental noise, false positives due to impacts on the piece, etc. Moreover, in real working conditions, considering environmental conditions, e.g., rain or hail, or impacts on the blade, it can cause false alarms.
In working conditions, it would be possible to distinguish between the frequencies associated with the vibration of the blade (low frequencies) and the frequencies associated with the acoustic emission of the fiber breakage (frequencies within the audible range and the ultrasonic range) [
21]. It is possible to filter the frequencies associated with the vibration from the collected signal. The authors demonstrated this in [
22].
2. Experiments
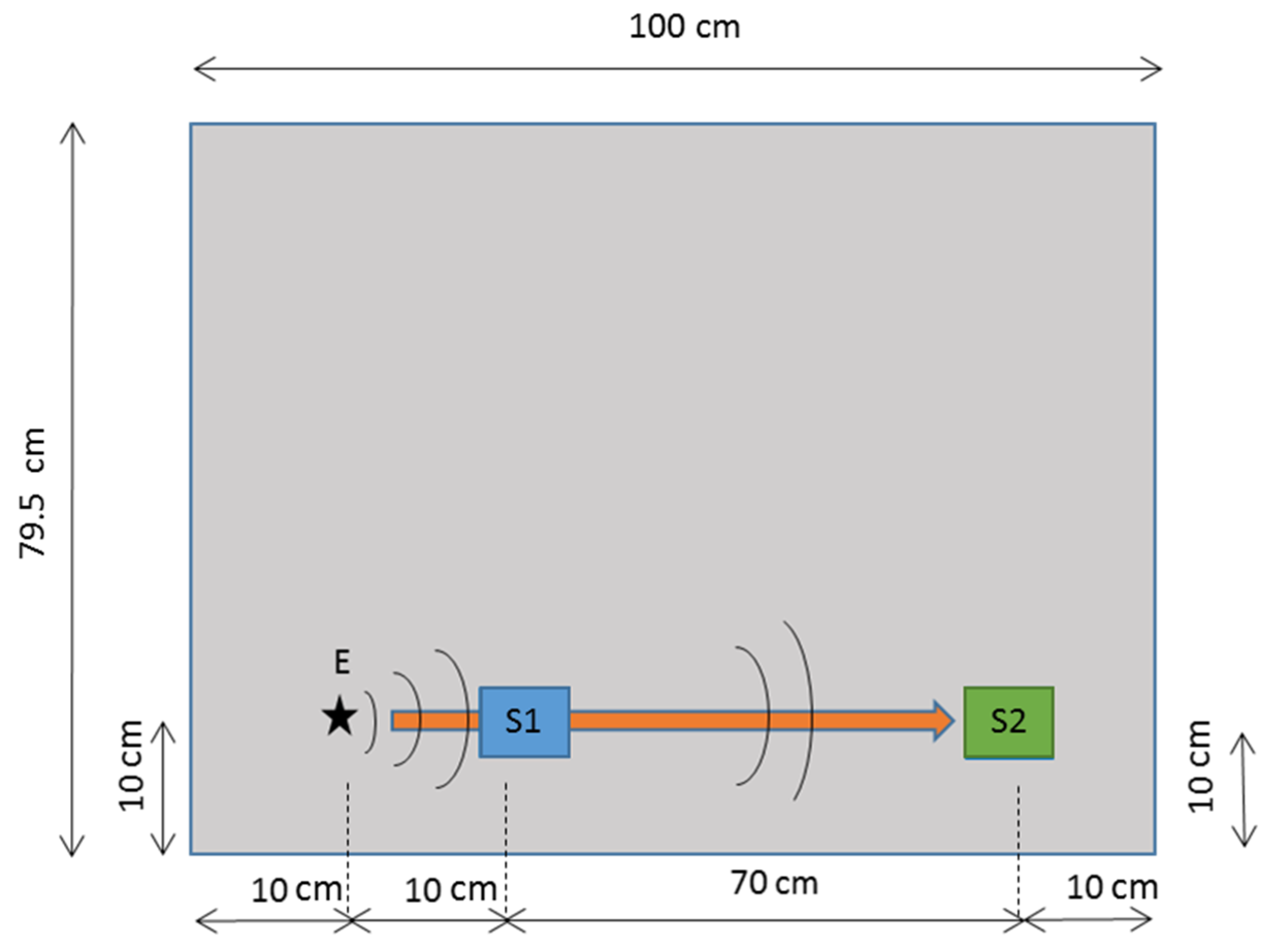
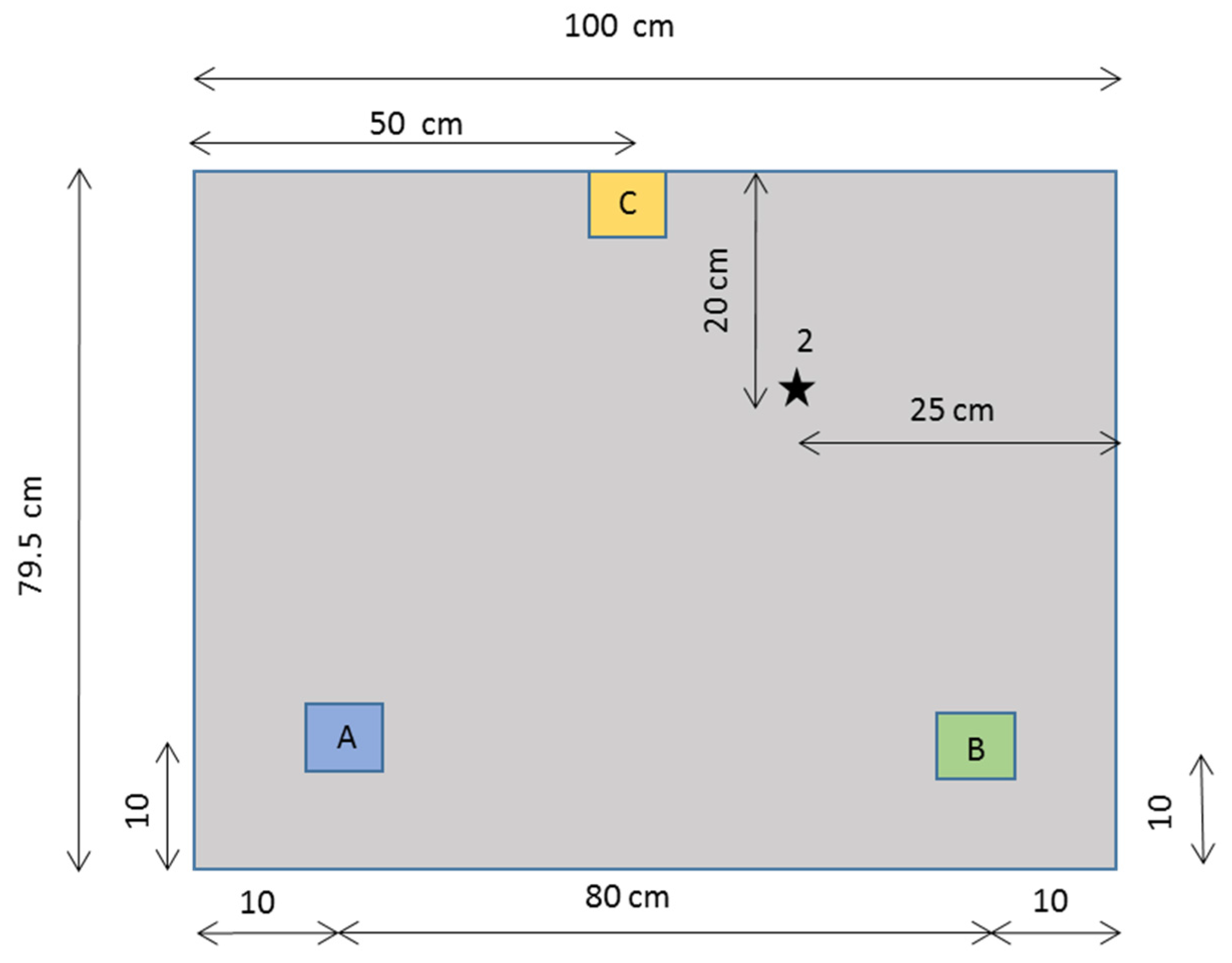
The experiments are done in a section of the wind turbine blade. The fragment, shown in
Figure 1, is made of glass fiber-reinforced polymer (GFRP), with dimensions of 100 × 79.5 cm. The section is composed of a honeycomb central layer embedded between two fiberglass layers made of polyester resin. This type of material has good structural properties, resistance to fatigue and other advantages. The attenuation of the acoustic emission in the blade is high, and it depends on the material, wave frequency and travelling distance between the failure source and the sensor location [
23].
Figure 1.
Wind turbine section with sensors for acoustic emission location.
Figure 1.
Wind turbine section with sensors for acoustic emission location.
The waves with the same velocity form a circular wave front when they propagate through an isotropic material. The velocity generally does not depend on the direction of propagation, but in anisotropic materials, e.g., the composite materials of the wind turbines, the velocity depends on the direction of propagation. A slowness factor could be introduced in order to consider the propagation direction, e.g., it has been observed that the configuration of layers (+45/−45) for a composite has a strong dependency of the direction of propagation. However, it has been demonstrated that the direction of propagation does not affect the velocity in the blade section studied in this paper. Therefore, the slowness factor has not been introduced in these experiments.
3. Location of the Fiber Breakage by the Triangulation Methodology
The SHM on wind turbine blades is employed to detect the defect online and to locate it with accuracy [
24]. The wind turbine blades are becoming larger and more complex, and this requires setting the exact location of a fiber breakage to reduce the maintenance cost and the productivity.
The glass fiber breakages of a wind turbine blade have been simulated in the laboratory on a real blade. A novel location method by triangulation has been developed. The aim of the paper is to locate the acoustic emission source in four different points on the blade section. The acoustic emission produced by the division of the glass fibers is simulated by breaking the tip of the lead from a mechanical pencil [
25,
26,
27]. Three MFC transducers (A, B and C) were used to detect the acoustic emissions. The three transducers are used as sensors that collect the wave front of the mechanical wave produced by the acoustic emission. These signals received by the sensors present a low amplitude, and therefore, they need to be pre-amplified before being acquired by the oscilloscope [
28].
In working conditions, there are many factors that could influence the configuration of the arrangement of the sensors on a blade, for example the length of the blades, the intensity of the acoustic emission, the accuracy of the sensors, the background noise, attenuation, etc. Depending on these factors, many groups of three sensors would be established, as they are required to cover the entire blade.
The propagation velocity of the acoustic emission (see
Figure 2) has been experimentally calculated by breaking a pencil lead and measuring the delays in the excitement of the sensors S1 and S2 (
Figure 3).
Figure 2.
Measuring the experimental propagation velocity in the composite material.
Figure 2.
Measuring the experimental propagation velocity in the composite material.
Figure 3.
Peak detection of the acoustical emission collected by Sensor 1 (blue) and Sensor 2 (green) to obtain the experimental propagation velocity in the composite material.
Figure 3.
Peak detection of the acoustical emission collected by Sensor 1 (blue) and Sensor 2 (green) to obtain the experimental propagation velocity in the composite material.
The delay between Signals 1 and 2 is 271 µs (542 samples), and the propagation velocity for the composite material is 2583 m/s.
Four experiments have been conducted at four different locations of the acoustic emission. Twelve tests have been done applying the same force, angle of inclination and length (1 mm approximately). The main objective is to get similar signals for all of the case studies. The data are also filtered for the signal processing, where undesired frequencies are filtered [
29]. The peak detection algorithm identifies the wave front of each signal. This process is complex because the waves are compounded by a large number of frequencies. Moreover, there are multiple elements in the blade that could affect the scattering of the acoustic signal, such as the edges of the geometry, the junction with the beam, adhesives,
etc.
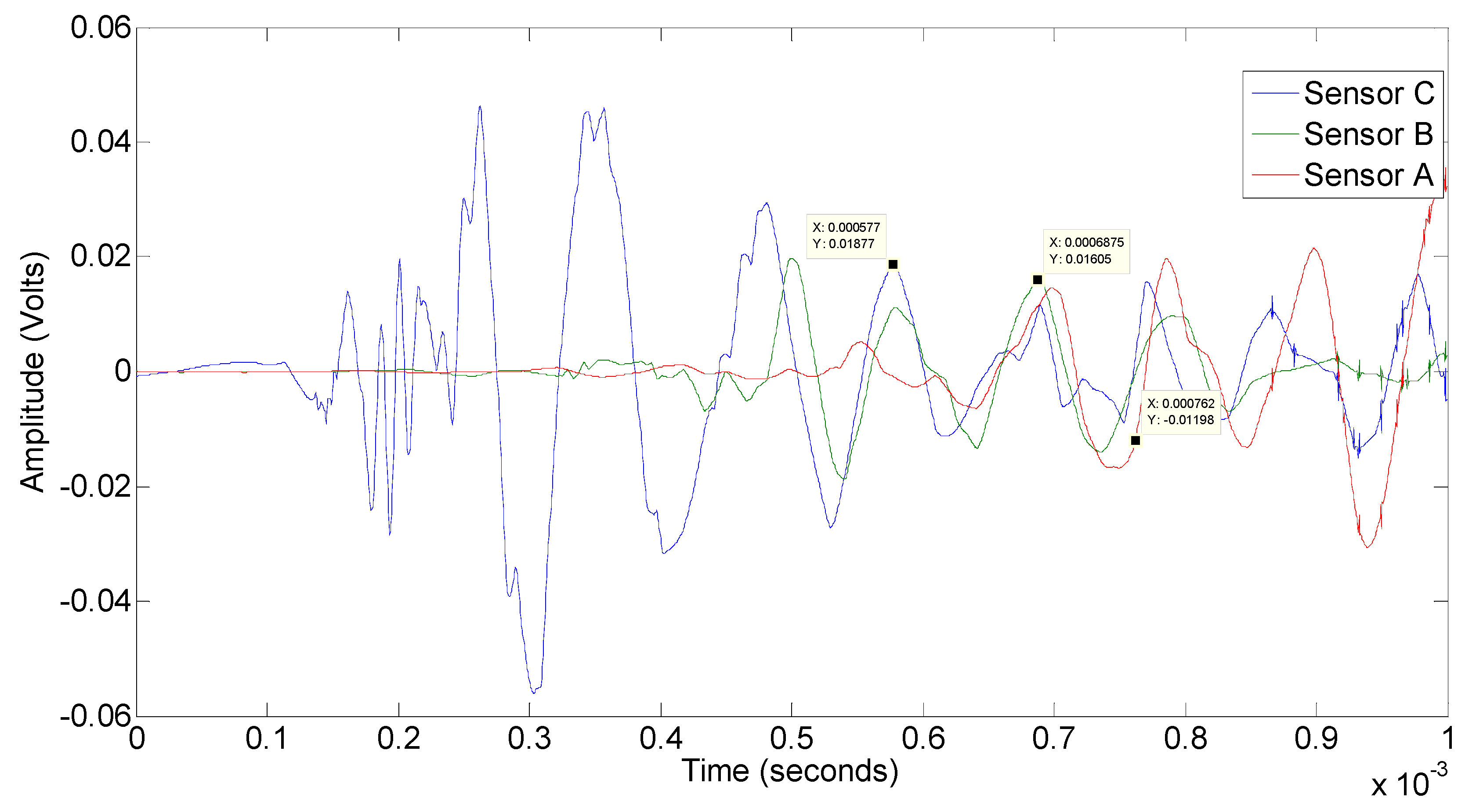
The signal processing consists of a pass band filter that eliminates low and high frequencies and carries out a comparison of the peaks of the wave front in the same frequency range of Signals A, B and C, generated by the above-mentioned MFC sensors, A, B and C (
Figure 4).
Figure 4.
Pre-processing of the signal. Wave front collected by Sensors C (blue), B (green) and A (red).
Figure 4.
Pre-processing of the signal. Wave front collected by Sensors C (blue), B (green) and A (red).
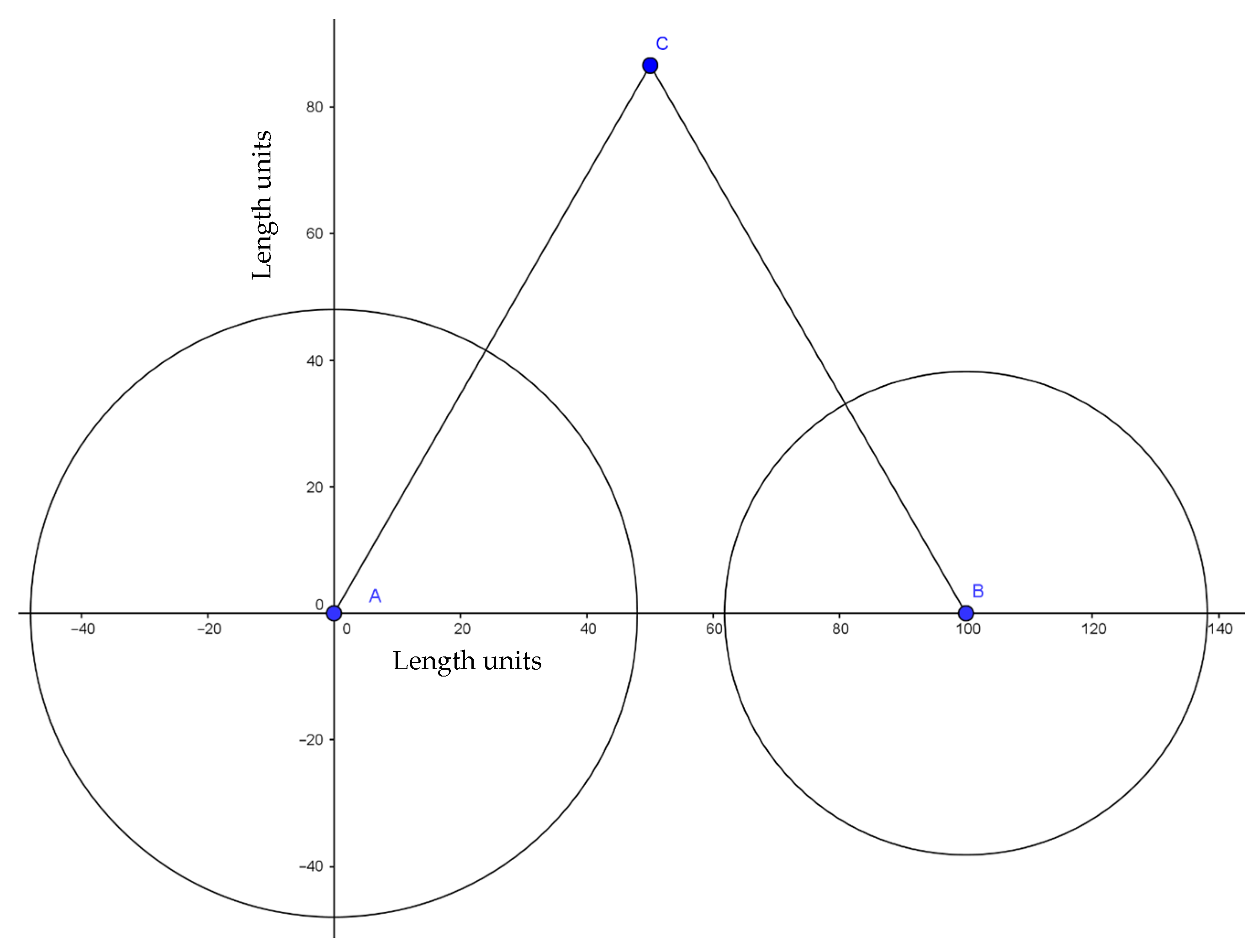
The MFC Sensors A, B and C are placed as an equilateral triangle (see
Figure 5). D is the location of the emission source by the breaking, D (D is known in this experiment).
Figure 5.
Location of Vertices A, B and C and the, defect D.
Figure 5.
Location of Vertices A, B and C and the, defect D.
The nearest Sensor C is the first to be excited due to the wave front coming from the acoustic emission (
Figure 6).
Figure 6.
Wave front of the acoustic emission collected by the nearest Sensor C.
Figure 6.
Wave front of the acoustic emission collected by the nearest Sensor C.
The delay between the excitation of the first Sensor C and the second closest Sensor B to the defect, D, is given by the distance from E to B (
Figure 7). The delay time and the speed of the wave propagation on the blade is calculated by Equation (1):
where
DEB is the distance between E and B,
v is the propagation velocity of the wave (obtained experimentally) and
tCB is the time delay between the excitation of Sensors C and B.
Figure 7.
Location of Point E, set by the delay between the excitation time in Sensors C and B.
Figure 7.
Location of Point E, set by the delay between the excitation time in Sensors C and B.
The delay between Sensor C and Sensor A, the farthest one from Defect D, is given by the distance from F to A
DFA in Equation (2).
where
tCA is the time delay between the excitation of Sensor C and Sensor A.
Figure 8 shows the scheme of the triangulation approach, the delay being represented by a circle.
Figure 8.
Scheme of the acoustic emission delays for locating the source.
Figure 8.
Scheme of the acoustic emission delays for locating the source.
In a real case study, Point D is unknown regarding the time and location, and the delays between the different sensors can be calculated. This condition is shown in
Figure 9, where the circumferences represent the delays of the signal that comes to each sensor with respect to the first sensor (C).
Figure 9.
Initial conditions to locate the source of the acoustic emission.
Figure 9.
Initial conditions to locate the source of the acoustic emission.
The objective is to find the source of the acoustic emission D mentioned above. This point is the center of a circle that is tangential to two given circles and passes through Point C (see
Figure 8). The solution is obtained in this paper employing a graphical method and an analytical method using a system of seven nonlinear equations.
5. Experimental Procedure and Results
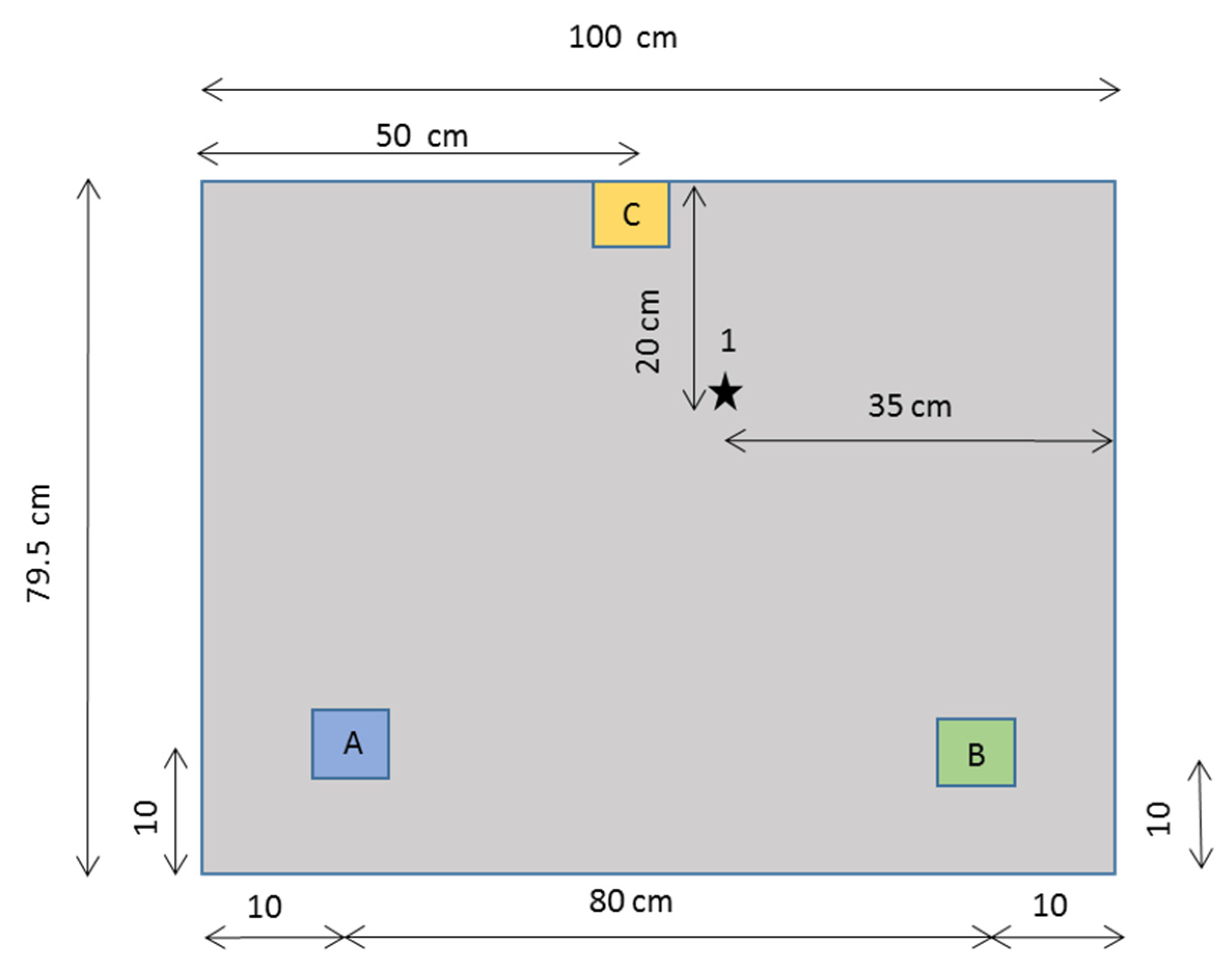
The time of flight and distances are set in this section for Sensors B and A regarding C, C being the first sensor to receive the acoustic signal of the breakage. The experiments are repeated four times to take into account the deviations of the results. The algorithm gives the exact location of the defect, as well as a graphic outline, knowing the radius of the circles with centers at B and C. The dimensions of the blade section, the distribution of the sensors and the emission source (star) in the wind turbine blade are shown in
Figure 10. The mathematical results obtained with the algorithm are given in
Table 1,
Table 2,
Table 3,
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8.
Figure 10.
First experiment. Case Study 1.
Figure 10.
First experiment. Case Study 1.
Table 1.
First case study: detection time; delay with C; delay; theoretical distance; experimental distance.
Table 1.
First case study: detection time; delay with C; delay; theoretical distance; experimental distance.
| Sensors | Detection Time (Samples) | Delay with C (Samples) | Delay (s) | Theoretical Distance (m) | Experimental Distance (m) |
|---|
| C | 1152 | - | - | - | - |
| B | 1381 | 229 | 1.15 × 10−4 | 0.30 | 0.30 |
| A | 1528 | 376 | 1.88 × 10−4 | 0.49 | 0.49 |
Table 2.
Initial data of the first case study.
Table 2.
Initial data of the first case study.
| Locations | x-Coordinate (m) | y-Coordinate (m) | Radius (m) |
|---|
| A | 0 | 0 | 0.49 |
| B | 0.8 | 0 | 0.30 |
| C | 0.4 | 0.69 | - |
| 1 | 0.55 | 0.495 | - |
Table 3.
Second case study: detection time; delay with C; delay; theoretical distance; experimental distance.
Table 3.
Second case study: detection time; delay with C; delay; theoretical distance; experimental distance.
| Sensors | Detection Time (Samples) | Delay with C (Samples) | Delay (s) | Theoretical Distance (m) | Experimental Distance (m) |
|---|
| C | 912 | - | - | - | - |
| B | 1063 | 151 | 7.55 × 10−5 | 0.20 | 0.20 |
| A | 1296 | 384 | 1.92 × 10−4 | 0.50 | 0.50 |
Table 4.
Initial data of the second case study.
Table 4.
Initial data of the second case study.
| Locations | x-Coordinate (m) | y-Coordinate (m) | Radius (m) |
|---|
| A | 0 | 0 | 0.50 |
| B | 0.8 | 0 | 0.20 |
| C | 0.4 | 0.69 | - |
| 2 | 0.65 | 0.495 | - |
Table 5.
Third case study: detection time; delay with C; delay; theoretical distance; experimental distance.
Table 5.
Third case study: detection time; delay with C; delay; theoretical distance; experimental distance.
| Sensors | Detection Time (Samples) | Delay with C (Samples) | Delay (s) | Theoretical Distance (m) | Experimental Distance (m) |
|---|
| C | 962 | - | - | - | - |
| B | 1298 | 336 | 1.68 × 10−4 | 0.43 | 0.43 |
| A | 1087 | 125 | 6.25 × 10−5 | 0.17 | 0.16 |
Table 6.
Initial data of the third case study.
Table 6.
Initial data of the third case study.
| Locations | x-Coordinate (m) | y-Coordinate (m) | Radius (m) |
|---|
| A | 0 | 0 | 0.16 |
| B | 0.8 | 0 | 0.43 |
| C | 0.4 | 0.69 | - |
| 3 | 0.2 | 0.445 | - |
Table 7.
Fourth case study: detection time; delay with C; delay; theoretical distance; experimental distance.
Table 7.
Fourth case study: detection time; delay with C; delay; theoretical distance; experimental distance.
| Sensors | Detection Time (Samples) | Delay with C (Samples) | Delay (s) | Theoretical Distance (m) | Experimental Distance (m) |
|---|
| C | 1155 | - | - | - | - |
| B | 1650 | 495 | 2.48 × 10−4 | 0.64 | 0.64 |
| A | 1385 | 230 | 1.15 × 10−4 | 0.29 | 0.30 |
Table 8.
Initial data of the fourth case study.
Table 8.
Initial data of the fourth case study.
| Locations | x-Coordinate (m) | y-Coordinate (m) | Radius (m) |
|---|
| A | 0 | 0 | 0.30 |
| B | 0.8 | 0 | 0.64 |
| C | 0.4 | 0.69 | / |
| 4 | 0.05 | 0.645 | / |
5.1. Case Study 1
The breaking of the lead is made in the following coordinates from Sensor A at Point 1 (star); see
Figure 10. Sensor A is the coordinate origin.
- -
Coordinate x: 0.55.
- -
Coordinate y: 0.495.
The location of the source employing the algorithm is: Point 1: (x: 0.5533, y: 0.4920). The error in the location is: coordinate x: 3.3 mm; coordinate y: 30 mm.
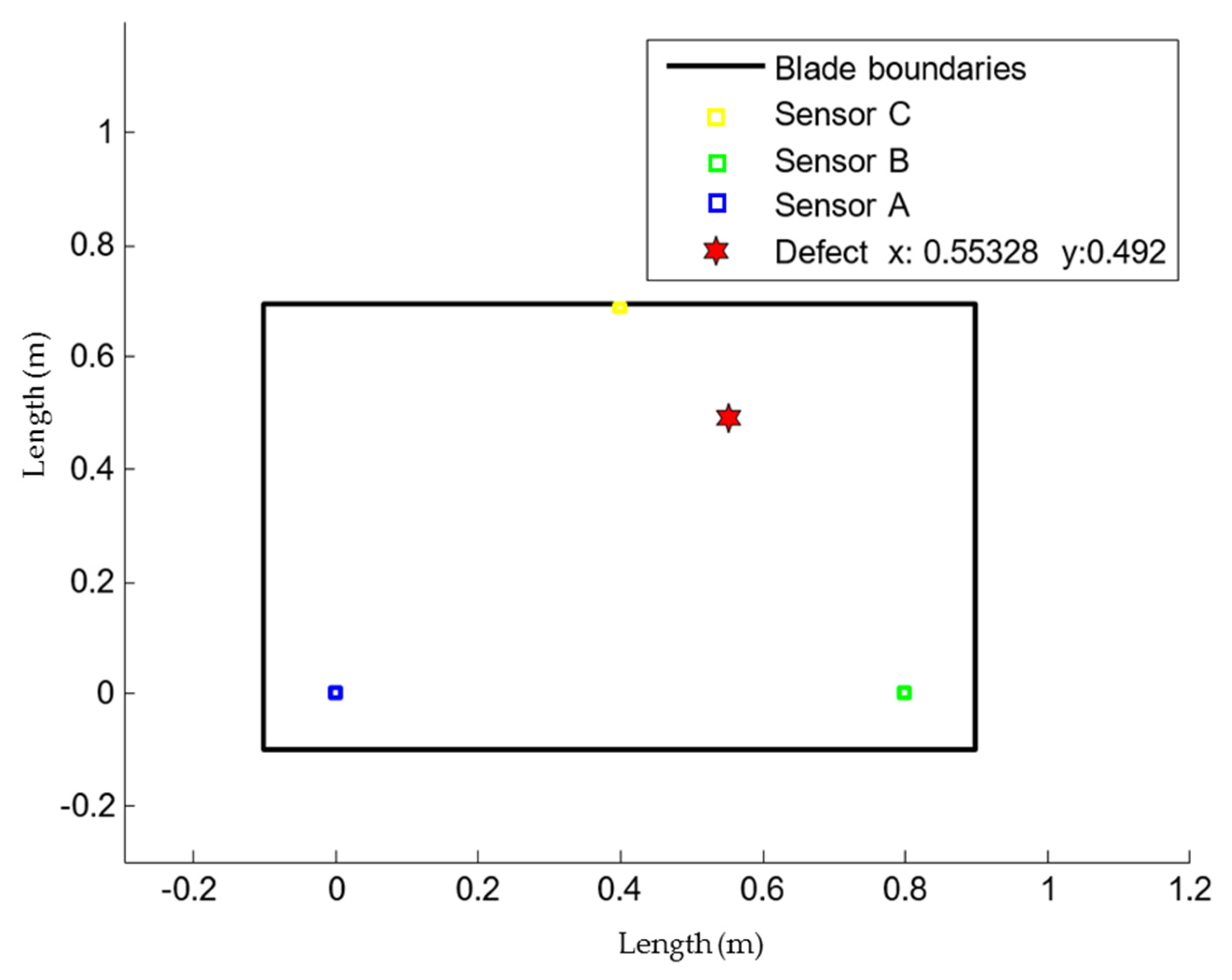
5.2. Case Study 2
In this case, the emission source was generated at Point 2 (star), shown in
Figure 11:
- -
Coordinate x: 0.65.
- -
Coordinate y: 0.495.
Figure 11.
Scheme for Case Study 2.
Figure 11.
Scheme for Case Study 2.
The location of the source employing the algorithm is: Point 2: (x: 0.6502, y: 0.4950). The errors in the location are: coordinate x: 0.2 mm; coordinate y: 0.00 mm.
5.3. Case Study 3
In this case, the emission source was generated at Point 3 (star); see
Figure 12:
- -
Coordinate x: 0.20.
- -
Coordinate y: 0.445.
Figure 12.
Scheme for Case Study 3.
Figure 12.
Scheme for Case Study 3.
The location of the source employing the algorithm is: Point 3 (x: 0.1914, y: 0.4434). The errors in the location are: coordinate x: 8.6 mm; coordinate y: 1.6 mm.
5.4. Case Study 4
In this case, the emission source was generated at Point 4 (star), and it is shown in
Figure 13:
- -
Coordinate x: 0.05.
- -
Coordinate y: 0.645.
Figure 13.
Scheme for Case Study 4.
Figure 13.
Scheme for Case Study 4.
The location of the source employing the algorithm is: Point 4: (x: 0.050, y: 0.6495). The errors in the location are: coordinate x: 0 mm; coordinate y: 4.5 mm.
Different waves with different speeds appear as a result of the scattering phenomena when a large number of frequencies are excited by the breakage. This makes the identification of peaks to measure the delays of the signals complicated. The orientation of the sensors, when they receive the excitation, can affect the shape of the signal collected.
It is observed that the algorithm provides correct and coherent results. It detects the location of the acoustic emission with an accuracy of two decimals (millimeters). The maximum error registered was 9 mm.
Finally, the algorithm shows the position of the acoustic emission point with the real dimensions of the blade.
Figure 14 shows the location of the acoustic emission for the first case study.
Figure 14.
Scheme of the location of the acoustic emission for the first case study.
Figure 14.
Scheme of the location of the acoustic emission for the first case study.
6. Conclusions
The development of a localization approach presented in this paper is set using macro-fiber composites to detect cracks in blades in an SHM system. This approach, based on NDT, automatically identifies and locates an acoustic emission source coming from a fiber’s breakage in a wind turbine blade section by a novel signal processing method. It can be extrapolated to other similar structures, e.g., airplane wings.
Three sensors are strategically located in the blade. It is demonstrated that the approach is able to detect the location of the simulated defect accurately employing acoustic emissions signals. The signal processing is based on a graphical method of triangulation and seven nonlinear equations. The signals are previously filtered. Different experiments are performed to demonstrate the effectiveness of the proposed method.
The approach detects the location of the acoustic emission with high accuracy, 9 mm being the maximum error registered.
There are conditions that affect the accuracy of the emission source location, e.g., the type of composite material, the sensitivity of the transducers, environmental noise, false positives due to impacts on the piece, etc. The method shows the position of the acoustic emission point with the real dimensions of the blade.