Theoretical Modelling Methods for Thermal Management of Batteries
Abstract
:1. Introduction

- The energy balance equation
- The heat generation equation—complex or simplified
- The boundary condition equations—linear/nonlinear, conduction, convection and or radiation
2. Numerical and Analytical Thermal Models
2.1. Overview of Numerical and Analytical Models
2.2. Lumped Capacitance Thermal Models
- The core and modules were assumed to be isothermal due to the high conductivity of the core.
- The temperature of the case is very close to the core/battery because of the low thermal mass of the case.
- The cell is a thermally homogenous body with effective thermo-physical properties.
- The cell properties are independent of temperature over the range of operating temperatures.
- Heat is generated uniformly throughout the cell.
| Thermodynamic formulas | Variables |
|---|---|
| Energy Balance | T = cell temperature (K) r = radial distance (mm) R = radius (mm) kcell = radial thermal conductivity (W·m−1·K−1) q = volumetric heat generation rate (W·L−1) t = time (s) α = thermal diffusivity (m2·s−1) Ta = ambient temperature (K) h = surface heat transfer coefficient (W·m−2·K−1) Q = overall heat generation (J) Q’ = overall heat generation rate (W) Wel = electric work (J) F = Faraday constant (96,486 mol−1) n = number of electrons Eeq = cell equilibrium voltage (V) E = cell voltage on load (V) S = entropy (J·mol−1·K−1) |
| Boundary Conditions | |
| Initial Conditions | |
| Heat Generation Rates |
2.3. Two-Dimensional Transient Finite Element Analysis Thermal Models
| Thermodynamic formulas | Variables |
|---|---|
| Heat Generation | Qt = total heat generation rate (W) Qn = Internal resistance (Ri) heat generation (W) Qs = reversible entropic heat generation/consumption (W) I = current (Idis > 0 and Ich < 0) (A) EOC = open circuit voltage (V) V = cell voltage (V) = rate of internal heat generation per unit volume (W·m−3) i = discharge current/unit volume (A·m−3) n = number of electrons (n = 1) |


2.4. Numerical Thermal Behaviour Model with Analytical Validation
2.5. Finite Volume Thermal Model
2.6. Adaptive Thermal Model
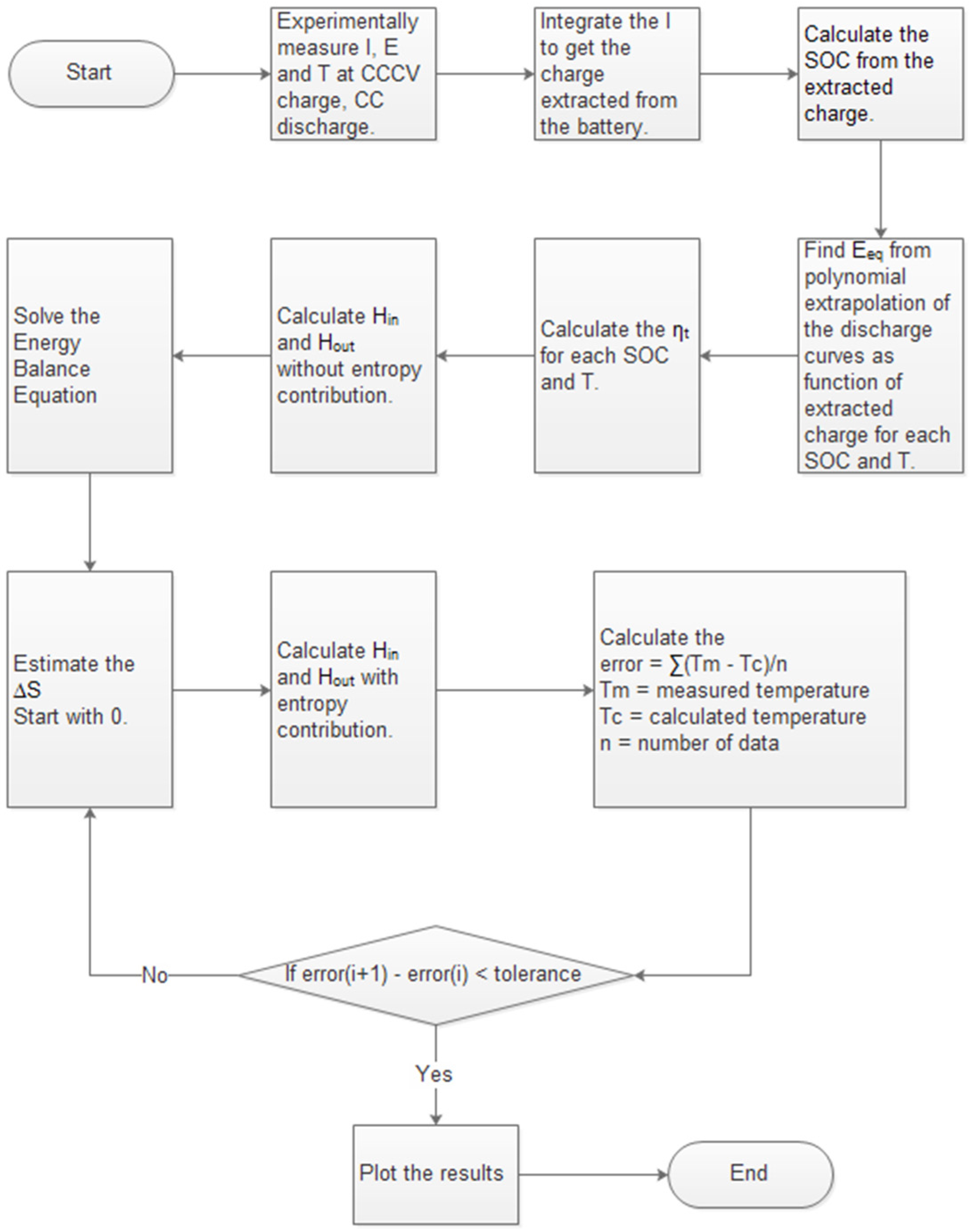
| Thermodynamic formulas | Variables |
|---|---|
| Energy Balance | m = mass of cell (g) CP = specific heat capacity (J·g−1·K−1) T = temperature (K) t = time (s) = all processes that generate heat (W) Qn = overpotential heat generation (W) ηt = total overpotential (V) Qs = entropic heat generation or consumption (W) = entropy change (J·mol−1·K−1) n = number of electrons transferred F = Faraday constant I = Current through individual electrodes (A) = Heat dissipate from cell (W) QC = Heat convection (W) QR = Heat radiation (W) h = convective heat transfer coefficient(W·m−2·K−1) A = surface area of cell (m2) Ta = ambient temperature (K) Nu = Nusselt number d = diameter of battery (m) k = air thermal conductivity (W·m−1·K−1) Ra = Rayleigh number Pr = Prandtl number σ = Stefan–Boltzmann constant (5.67 × 10−8 J·s−1·m−2·K−4) ε = emissivity factor of the battery surface material |
| Heat Generation | |
| Heat Dissipation |
2.7. Other Numerical Thermal Model Applications
3. Behavioural Models
Electrical Equivalent Circuit Thermal Models

4. Conclusions
| Method | Advantages | Disadvantages | Recommended applications |
|---|---|---|---|
| Lumped Capacitance Thermal Approach | The main advantage of the lumped parameters method is that it is a simple method with a minimum set of data required to develop a satisfactory model to predict the thermal behaviour of Li-ion batteries [40]. Rather than setting all the characteristics and material types like required in a FEA or CFD analysis, the method “lumps” the characteristics together assuming the differences within each of these groups are not critical [99]. This makes it quick to design and run providing directionally correct estimates of the thermal performance of the ESS. The lumped capacitance approach is commonly adopted within other approaches like the equivalent circuit approach and some numerical approaches in order to simplify the complex problem. | The main disadvantage of this method is that there is a physical constraint to the possible applications due to Bi number limitations. Lumped parameters can only be used to model applications with Bi < 1. Bi is affected by large cell diameters and/or high heat transfer coefficients, limiting the application of the lumped parameters approach. This can be the case for many liquid cooling situations which are high h applications [100]. Additionally the results of Hallaj, et al. [40] indicated inaccuracy at a higher discharge rate of 1C-rate and abnormal operating conditions like extreme hot or cold operating temperatures. | System level modelling that requires fast processing time. The lumped parameters method is suitable for ESS thermal behaviour modelling under normal conditions of battery use for example under non-extreme operating temperatures [52]. |
| Numerical and Analytical Thermal Models | The main advantage of numerical methods like FEM and CFD is that these approaches are not very complex but it can yield a good level of accuracy. Applying heterogeneous thermo-physical properties can further improve the level of accuracy at the expense of computational time [31]. Computational time can be saved if the model is symmetrical. Adopting curved fitted thermal properties for Ri and ΔS is convenient but marginally compromises accuracy [31,44]. In most instances this is acceptable. | The disadvantage of this methodology is that it relies on accurate measurement or representation of the physical ESS model as well as a sound knowledge of the chemical and material compositions for an accurate representation. Also this method can be computational intensive depending on the 2D/3D model designed. This can limit the system model size based on a practical computational time. Numerical methods like FEA and CFD are inflexible and specific to the particular battery analysed. | Applications where a high level accuracy is required. Symmetrical models can benefit from a reduced computational domain hence processing time. Ideal for ESS cell level modelling. Numerical methods are an ideal tool when specific knowledge of the battery thermo-physical properties are known. Useful tool for system design optimisation for example as applied in [80,81,82,83,84,85]. |
| Equivalent Circuit Thermal Models | General behavioural models like equivalent circuit models are faster, more flexible and easier to formulate compared to numerical models. Minimal computational effort is required since in behavioural models the information regarding the different materials and associated thermo-physical properties within the cell are minimal [29]. | Similar to the lumped capacitance approach the disadvantage of the equivalent circuit approach is that it is potentially less accurate because the models calculates an average temperature for the entire chemistry within the battery unit [96]. | System level modelling that requires fast processing time. On-field or compact ESS battery thermal management systems [29]. The equivalent circuit approach is an ideal approach for systems level integration of ESS. The equivalent circuit approach is also useful for electro-thermal modelling in which electrical behaviour modelling is also required. |
Author Contributions
Conflicts of Interest
References
- Wagner, R. Valve regulated lead-acid batteries for telecommunications and UPS applications. In Valve-Regulated Lead–Acid Batteries; Rand, D.J., Ed.; Elsevier B.V.: Oxford, UK, 2004; pp. 435–465. [Google Scholar]
- Percy, K. Ausnet Testing New Battery System to Curb Power Outages in Summer. Available online: http://www.abc.net.au/news/2015-01-07/ausnet-trialling-new-system-to-curb-power-outages-on-hot-days/6004454 (accessed on 30 May 2015).
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sci. 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Rothgang, S.; Rogge, M.; Becker, J.; Sauer, D.U. Battery design for successful electrification in public transport. Energies 2015, 8, 6715–6737. [Google Scholar] [CrossRef]
- Shabani, B.; Andrews, J. Standalone solar-hydrogen systems powering fire contingency networks. Int. J. Hydrogen Energy 2015, 40, 5509–5517. [Google Scholar] [CrossRef]
- Pesaran, A.; Vlahinos, A.; Stuart, T. Cooling and Preheating of Batteries in Hybrid Electric Vehicles; National Renewable Energy Laboratory (NREL): Colorado, CO, USA, 2003. [Google Scholar]
- Ji, Y.; Wang, Y. Heating strategies for Li-ion batteries operated from subzero temperatures. Electrochim. Acta 2013, 107, 664–674. [Google Scholar] [CrossRef]
- Szente-Varga, D.; Horvath, G.; Rencz, M. Thermal characterization and modelling of lithium-based batteries at low ambient temperature. In Proceedings of the 14th International Workshop on Thermal Inveatigation of ICs and Systems, 2008 (THERMINIC 2008), Rome, Italy, 24–26 September 2008.
- Bergveld, H.J.; Krujit, W.S.; Notten, P.H.L. Battery Management Systems-Design by Modelling, Philips Research Book Series Volume 1; Springer: Eindhoven, The Netherlands, 2002. [Google Scholar]
- Horie, H.; Abe, T.; Kinoshita, T.; Shimoida, Y. A study on an advanced lithium-ion battery system for EVs. World Electric Veh. J. 2008, 2, 25–31. [Google Scholar]
- Ye, Y.; Shi, Y.; Cai, N.; Lee, J.; He, X. Electro-thermal modeling and experimental validation for lithium ion battery. J. Power Sources 2012, 199, 227–238. [Google Scholar] [CrossRef]
- Vlahinos, A.; Pesaran, A. Energy Efficient Battery Heating in Cold Climates; SAE Technial Paper; SAE International: Warrendale, PA, USA, 2002; p. 10. [Google Scholar]
- Zhang, S.S.; Xu, K.; Jow, T.R. The low temperature performance of Li-ion batteries. J. Power Sources 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Trinidad, F.; Gimeno, C.; Gutierrez, J.; Ruiz, R.; Sainz, J.; Valenciano, J. The VRLA modular wound design for 42 V mild hybrid systems. J. Power Sources 2003, 116, 128–140. [Google Scholar] [CrossRef]
- Yuksel, T.; Michalek, J. Evaluation of the Effects of Thermal Management on Battery Life in Plug-in Hybrid Electric Vehicles. Available online: http://www.cmu.edu/me/ddl/publications/2012-Battery-Congress-Yuksel-Michalek-Thermal-Mgmt.pdf (accessed on 14 July 2015).
- Xun, J.; Liu, R.; Chen, J.; Jiao, K.; Du, Q. Numerical investigation of thermal behaviors in lithium-ion battery stack discharge. Appl. Energy 2014, 132, 288–297. [Google Scholar]
- Kim, G.-H.; Gonder, J.; Lustbader, J.; Pesaran, A. Thermal management of batteries in advanced vehicles using phase-change materials. World Electric Veh. J. 2008, 2, 46–59. [Google Scholar]
- Zhu, C.; Li, X.; Song, L. Development of a theoretically based thermal model for lithium ion battery pack. J. Power Sources 2013, 223, 155–164. [Google Scholar] [CrossRef]
- Motloch, C.G.; Christophersen, J.P.; Belt, J.R.; Wright, R.B.; Hunt, G.L.; Sutula, R.A.; Duong, T.Q.; Tartamella, T.J.; Haskins, H.J.; Miller, T.J. High-Power Battery Testing Procedures and Analytical Methodologies for HEV’s; SAE International: Warrendale, PA, USA, 2002. [Google Scholar]
- Hunter, H. Extreme Temperatures Affect Electric Vehicle Driving Range, AAA Says. Available online: http://newsroom.aaa.com/2014/03/extreme-temperatures-affect-electric-vehicle-driving-range-aaa-says/ (accessed on 18 July 2015).
- Zhang, T.; Gao, C.; Gao, Q.; Wang, G.; Liu, M.; Guo, Y.; Xiao, C.; Yan, Y.Y. Status and development of electric vehicle integrated thermal management from BTM to HVAC. Appl. Thermal Eng. 2015, 88, 398–409. [Google Scholar] [CrossRef]
- Park, C.-W.; Jaura, A.K. Dynamic Thermal Model of Li-Ion Battery for Predictive Behavior in Hybrid and Fuel Cell Vehicles; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- Mahamud, R.; Park, C. Reciprocating air flow for Li-ion battery thermal management to improve temperature uniformity. J. Power Sources 2011, 196, 5685–5696. [Google Scholar] [CrossRef]
- Taylor, J.N.A.C. Safety performance for phosphate based large format lithium-ion battery. In Proceedings of the 26th Annual International Telecommunications Energy Conference, 19–23 September 2004; pp. 146–148.
- Yamaki, J.; Ihara, M.; Okada, S. Improvement of thermal stability of lithium ion batteries by using methyl difluoroacetate as an electrolyte solvent. In Proceedings of the 25th Annual International Telecommunications Energy Conference, Yokohama, Japan, 23 October 2003; pp. 59–65.
- Ratnakumar, B.V.; Smart, M.C.; Halpert, G.; Kindler, A.; Frank, H.; DiStefano, S.; Ewell, R.; Surampudi, S. Lithium batteries on 2003 Mars Rover. In Proceedings of the 17th Annual Battery Conference on Applications and Advances, Long Beach, CA, USA, 15 January 2002; pp. 47–51.
- Semerie, J.P. Lithium-ion batteries for geosynchronous satellites. Qualification test results of the stentor battery. In Proceedings of the 35th Intersociety Energy Conversion Engineering Conference and Exhibit, Las Vegas, NV, USA, 24–28 July 2000; Volume 1, pp. 621–628.
- Amiribavandpour, P.; Shen, W.; Mu, D.; Kapoor, A. An improved theoretical electrochemical-thermal modelling of lithium-ion battery packs in electric vehicles. J. Power Sources 2015, 284, 328–338. [Google Scholar] [CrossRef]
- Xiao, Y. Model-based virtual thermal sensors for lithium-ion battery in EV applications. IEEE Trans. Ind. Electron. 2015, 62, 3112–3122. [Google Scholar] [CrossRef]
- Zhang, X.; Kong, X.; Li, G.; Jun, L. Thermodynamic assessment of active cooling/heating methods for lithium-ion batteries of electric vehicles in extreme conditions. Energy 2014, 64, 1092–1101. [Google Scholar] [CrossRef]
- Karimi, G.; Li, X. Thermal management of lithium-ion batteries for electric vehicles. Int. J. Energy Res. 2013, 37, 12–24. [Google Scholar] [CrossRef]
- Cooper, A. Development of a lead-acid battery for a hybrid electric vehicle. J. Power Sources 2004, 133, 116–125. [Google Scholar] [CrossRef]
- Cooper, A. Development of a high-performance lead–acid battery for new-generation vehicles. J. Power Sources 2005, 144, 385–394. [Google Scholar] [CrossRef]
- Karden, E.; Ploumen, S.; Fricke, B.; Miller, T.; Snyder, K. Energy storage devices for future hybrid electric vehicles. J. Power Sources 2007, 168, 2–11. [Google Scholar] [CrossRef]
- Lam, L.T.; Louey, R. Development of ultra-battery for hybrid-electric vehicle applications. J. Power Sources 2006, 158, 1140–1148. [Google Scholar] [CrossRef]
- Moseley, P.T.; Bonnet, B.; Copper, A.; Kellaway, M.J. Lead-acid battery chemistry adapted for hybrid electric vehicle duty. J. Power Sources 2007, 174, 49–53. [Google Scholar] [CrossRef]
- Pollet, B.; Staffell, I.; Shang, J. Current status of hybrid, battery and fuel cell electric vehicles: From electrochemistry to market prospects. Electrochem. Acta 2012, 84, 235–249. [Google Scholar] [CrossRef]
- Wu, B.; Yufit, V.; Marinescu, M.; Offer, G.J.M.-B.; Ricardo, F.; Brandon, N.P. Coupled thermal-electrochemical modelling of uneven heat generation in lithium-ion battery packs. J. Power Sources 2013, 243, 544–554. [Google Scholar] [CrossRef]
- Chen, K. Heat Generation Measurements of Prismatic Lithium Ion Batteries. Master’s Thesis, The University of Waterloo, Waterloo, ON, Canada, 2013. [Google Scholar]
- Hallaj, S.A.; Maleki, H.; Hong, J.S.; Selman, J.R. Thermal modeling and design considerations of lithium-ion batteries. J. Power Sources 1999, 83, 1–8. [Google Scholar] [CrossRef]
- Choi, S.S.; Lim, H.S. Factors that affect cycle-life and possible degradation mechanisms of a Li-ion cell based on LiCoO2. J. Power Sources 2002, 111, 130–136. [Google Scholar] [CrossRef]
- Cadex. Charging at High and Low Temperatures. Available online: http://batteryuniversity.com/learn/article/charging_at_high_and_low_temperatures (accessed on 25 May 2015).
- Plangklang, B.; Pornharuthai, P. Mathematical model and experiment of temperature effect on discharge of lead-acid battery for PV systems in tropical area. Energy Power Eng. 2013, 5, 43–49. [Google Scholar] [CrossRef]
- Rad, M.S.; Danilov, D.L.; Baghalha, M.; Kazemeini, M.; Notten, P.H.L. Adaptive thermal modeling of Li-ion batteries. Electrochim. Acta 2013, 102, 183–195. [Google Scholar]
- Rao, Z.; Wang, S. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Pesaran, A. Tools for Designing Thermal Management of Batteries in Electric Drive Vehicles; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Parsons, K.K. Design and Simulation of Passive Thermal Management System for Lithium-Ion Battery Packs on an Unmanned Ground Vehicle. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2012. [Google Scholar]
- Chen, S.; Wan, C.; Wang, Y. Thermal analysis of lithium-ion batteries. J. Power Sources 2005, 140, 111–124. [Google Scholar] [CrossRef]
- DeWitt, I.; Bergman, L. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kim, Y.; Siegel, J.B.; Stefanopoulou, A.G. A computationally efficient thermal model of cylindrical battery cells for the estimation of radially distributed temperatures. In Proceedings of the 2013 American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013.
- Ismail, N.H.F.; Toha, S.F.; Mohd Azubir, N.A.; Ishak, N.H.M.; Hassan, M.K.; Ibrahim, B.S. Simplified heat generation model for lithium ion battery used in electric vehicle. In Proceedings of the 5th International Conference on Mechatronics (ICOM’13), Kuala Lumpur, Malaysia, 2–4 July 2013.
- Maleki, H.; Hong, J.S.; Hallaj, S.A.; Selman, J.R. The Electrochemical Society and International Society of Electrochemistry Meeting Abstracts; The Electrochemical Society and International Society of Electrochemistry: Paris, France, 1997. [Google Scholar]
- Hong, J.S.; Maleki, H.; Al Hallaj, S.; Redley, L.; Selman, J.R. Electrochemical-calorimetric studies of lithium-ion cells. Electrochem. Soc. 1998, 145, 1489–1501. [Google Scholar] [CrossRef]
- Inui, Y.; Kobayashi, Y.; Watanabe, Y.; Watase, Y.; Kitamura, Y. Simulation of temperature distribution in cylindrical and prismatic lithium ion secondary batteries. Energy Convers. Manag. 2007, 48, 2103–2109. [Google Scholar] [CrossRef]
- Onda, K.; Ohshima, T.; Nakayama, M.; Fukuda, K.; Araki, T. Thermal behavior of small lithium-ion battery during rapid charge and discharge cycles. J. Power Sources 2006, 158, 535–542. [Google Scholar] [CrossRef]
- Xun, J.; Liu, R.; Jiao, K. Numerical and analytical modeling of lithium ion battery thermal behaviors with different cooling designs. J. Power Sources 2013, 223, 47–61. [Google Scholar] [CrossRef]
- Ling, Z.; Chen, J.; Fang, X.; Zhang, Z.X.; Tao, X.; Gao, X.; Wang, S. Experimental and numerical investigation of the application of phase change materials in a simulative power batteries thermal management system. Appl. Energy 2014, 121, 104–113. [Google Scholar] [CrossRef]
- Al-Hallaj, S.; Selman, J.R. Thermal modeling of secondary lithium batteries for electric vehicle/hybrid electric vehicle applications. J. Power Sources 2002, 110, 341–348. [Google Scholar] [CrossRef]
- Iraola, U.; Aizpuru, I.; Canales, J.M.; Etxeberria, A. Methodology for thermal modelling of lithium-ion batteries. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013.
- He, F.; Li, X.; Ma, L. Combined experimental and numerical study of thermal management of battery module consisting of multiple Li-ion cells. Int. J. Heat Mass Transf. 2014, 72, 622–629. [Google Scholar] [CrossRef]
- Hu, X. Advanced numerical simulation helps accelerate the development of safe, long-lasting and cost-effective batteries for electric vehicles. In Battery Thermal Management in Electric Vehicles; ANSYS Incorporated: Canonsburg, PA, USA, 2015. [Google Scholar]
- Javani, N.; Dincer, I.; Naterer, G.F.; Rohrauer, G.L. Modeling of passive thermal management for electric vehicle battery packs with PCM between cells. Appl. Thermal Eng. 2014, 73, 307–316. [Google Scholar] [CrossRef]
- Wang, T.; Tseng, K.J.; Zhao, J.; Wei, Z. Thermal investigation of lithium-ion battery module with different cell arrangement structures and forced air-cooling strategies. Appl. Energy 2014, 134, 229–238. [Google Scholar] [CrossRef]
- Xu, X.M.; He, R. Research on the heat dissipation performance of battery pack based on forced air cooling. J. Power Sci. 2013, 240, 33–41. [Google Scholar] [CrossRef]
- Chacko, S.; Chung, Y.M. Thermal modelling of Li-ion polymer battery for electric vehicle drive cycles. J. Power Sources 2012, 213, 296–303. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M.; Pesaran, A.A. A parametric study on thermal management of an air-cooled lithium-ion battery module for plug-in hybrid electric vehicles. J. Power Sources 2013, 238, 301–312. [Google Scholar] [CrossRef]
- Danilov, D.L.; Ledovskikh, A.; Notten, P.H.L. Adaptive thermal modeling of rechargeable batteries for advanced automotive battery management systems. In Prcoeedings of the 8th International Automotive Congress, Eindhoven, The Netherlands, 16–17 March 2011; p. 50.
- Chen, Y.; Evans, J.W. Thermal analysis of lithium-ion batteries. J. Electrochem. Soc. 1996, 143, 2708–2712. [Google Scholar] [CrossRef]
- Chen, Y.; Evans, J.W. Three-dimensional thermal modeling of lithium-polymer batteries under galvanostatic discharge and dynamic power profile. J. Electrochem. Soc. 1994, 141, 2947–2955. [Google Scholar] [CrossRef]
- Chen, Y.; Evans, J.W. Heat transfer phenomena in lithium/polymer-electrolyte batteries for electric vehicle applications. J. Electrochem. Soc. 1993, 140, 1833–1838. [Google Scholar] [CrossRef]
- Guo, G.; Long, B.; Cheng, B.; Zhou, S.; Xu, P.; Cao, B. Three-dimensional thermal finite element modeling of lithium-ion battery in thermal abuse application. J. Power Sources 2015, 195, 2393–2398. [Google Scholar] [CrossRef]
- Jeon, D.H.; Baek, S.M. Thermal modeling of cylindrical lithium ion battery during discharge cycle. Energy Convers. Manag. 2011, 52, 2973–2981. [Google Scholar] [CrossRef]
- Karimi, G.; Dehghan, A.R. Thermal analysis of high-power lithium-ion battery packs using flow network approach. Int. J. Energy Res. 2014, 38, 1793–1811. [Google Scholar] [CrossRef]
- Sun, H.; Wang, X.; Tossan, B.; Dixon, R. Three-dimensional thermal modeling of a lithium-ion battery pack. J. Power Sources 2012, 206, 349–356. [Google Scholar] [CrossRef]
- Jeon, D.H. Numerical modeling of lithium ion battery for predicting thermal behavior in a cylindrical cell. Curr. Appl. Phys. 2014, 14, 196–205. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Guo, B.; Deng, C. Numerical analysis and design of thermal management system for lithium ion battery pack using thermoelectric coolers. Adv. Mech. Eng. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Yang, L. A pseudo three-dimensional electrochemicalethermal model of a prismatic LiFePO4 battery during discharge process. Energy 2015, 80, 303–317. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. Two-dimensional electrochemicalethermal coupled modeling of cylindrical LiFePO4 batteries. J. Power Sources 2014, 256, 233–243. [Google Scholar] [CrossRef]
- Tong, W.; Somasundaram, K.; Birgersson, E.; Mujumdar, A.S.; Yap, C. Numerical investigation of water cooling for a lithium-ion bipolar battery pack. Int. J. Thermal Sci. 2015, 94, 259–269. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Li, Y. Thermal performance of mini-channel liquid cooled cylinder based battery thermal management for cylindrical lithium-ion power battery. Energy Convers. Manag. 2015, 103, 157–165. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Huo, Y.; Liu, X.; Li, Y. Thermal management of cylindrical power battery module for extending the life of new energy electric vehicles. Appl. Thermal Eng. 2015, 85, 33–43. [Google Scholar] [CrossRef]
- Pesaran, A.; Vlahinos, A.; Burch, S. Thermal Performance of EV and HEV Battery Modules and Packs; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 1997. [Google Scholar]
- Yu, K.; Yang, X.; Cheng, Y.; Li, C. Thermal analysis and two-directional air flow thermal management for lithium-ion battery pack. J. Power Sources 2014, 270, 193–200. [Google Scholar] [CrossRef]
- Park, H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles. J. Power Sources 2013, 239, 30–36. [Google Scholar] [CrossRef]
- Ye, Y.; Saw, L.H.; Shi, Y.; Tay, A.A.O. Numerical analyses on optimizing a heat pipe thermal management system for lithium-ion batteries during fast charging. Appl. Thermal Eng. 2015, 86, 281–291. [Google Scholar] [CrossRef]
- Tran, T.-H.; Harmand, S.; Sahut, B. Experimental investigation on heat pipe cooling for hybrid electric vehicle and electric vehicle lithium-ion battery. J. Power Sources 2014, 265, 262–272. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S.; Wu, M.; Lin, Z.; Li, F. Experimental investigation on thermal management of electric vehicle battery with heat pipe. Energy Convers. Manag. 2013, 65, 92–97. [Google Scholar] [CrossRef]
- Prasher, R.S. A simplified conduction based modeling scheme for design sensitivity study of thermal solution utilizing heat pipe and vapor chamber technology. J. Electron. Packag. 2003, 126, 378–385. [Google Scholar] [CrossRef]
- Greco, A.; Cao, D.; Jiang, X.; Yang, H. A theoretical and computational study of lithium-ion battery thermal management for electric vehicles using heat pipes. J. Power Sources 2014, 257, 344–355. [Google Scholar] [CrossRef]
- Forgez, C.; Do, D.V.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Huria, T.; Massimo, C.; Jackey, R.; Gazzarri, J. High fidelity electrical model with thermal dependence for characterization and simulation of high power lithium battery cells. In Proceedings of the 2012 IEEE International Electric Vehicle Conference (IEVC), Greenville, SC, USA, 4–8 March 2012; pp. 1–8.
- Jackey, R. A Simple, Effective Lead-Acid Battery Modeling Process for Electrical System Component Selection; SAE Paper; SAE International: Warrendale, PA, USA, 2007; pp. 1–9. [Google Scholar]
- Murashko, K.; Pyrhonen, J.; Laurila, L. Three-dimensional thermal model of a lithium ion battery for hybrid mobile working machines: Determination of the model parameters in a pouch cell. IEEE Trans. Energy Convers. 2013, 28, 335–343. [Google Scholar] [CrossRef]
- Erdinc, O.; Vural, B.; Uzunoglu, M. A dynamic lithium-ion battery model considering the effects of temperature and capacity fading. In Proceedings of the International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 383–386.
- Damay, N.; Forgez, C.; Bichat, M.-P.; Friedrich, G. Thermal modeling of large prismatic LiFePO4/graphite battery. Coupled thermal and heat generation models for characterization and simulation. J. Power Sources 2015, 283, 37–45. [Google Scholar] [CrossRef]
- Fathian, K.; Hassanipour, F.; Gans, N.R. Virtual thermal sensing and control of heat distribution using state estimation. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 1725–1738.
- L.H, S.; Ye, Y.; Tay, A.A.O. Electro-thermal characterization of lithium iron phosphate cell with equivalent circuit modeling. Energy Convers. Manag. 2014, 87, 367–377. [Google Scholar]
- Saw, L.H.; Ye, Y.; Tay, A.A.O. Electrochemical-thermal analysis of 18650 lithium iron phosphate cell. Energy Convers. Manag. 2013, 75, 162–167. [Google Scholar] [CrossRef]
- Warner, J. Chapter 6—Computer-aided design and analysis. In The Handbook of Lithium-Ion Battery Pack Design; Elsevier Science: Midland, MI, USA, 2015; pp. 59–63. [Google Scholar]
- Mahamud, R.; Park, C. Spatial-resolution, lumped-capacitance thermal model for cylindrical Li-ion batteries under high biot number conditions. Appl. Math. Model. 2013, 37, 2787–2801. [Google Scholar] [CrossRef]
- Lin, X.; Stefanopoulou, A.G.; Fu, H.; Perez, H.E.; Siegel, J.B.; Ding, Y.; Castanier, M.P. Parameterization and observability analysis of scalable battery clusters for onboard thermal management. Oil Gas Sci. Technol. 2013, 68, 165–178. [Google Scholar] [CrossRef]
- Lin, X.; Stefanopoulou, A.G.; Perez, H.E.; Siegel, J.B.; Li, Y.; Anderson, R.D. Quadruple adaptive observer of the core temperature in cylindrical Li-ion batteries and their health monitoring. In Proceedings of the 2012 American Control Conference, Fairmont Queen Elizabeth, Montréal, QC, Canada, 27–29 June 2012.
- Lin, X.; Perez, H.E.; Siegel, J.B.; Stefanopoulou, A.G. Online parameterization of lumped thermal dynamics in cylindrical lithium ion batteries for core temperature estimation and health monitoring. IEEE Trans. Control Syst. 2013, 21, 1745–1755. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shabani, B.; Biju, M. Theoretical Modelling Methods for Thermal Management of Batteries. Energies 2015, 8, 10153-10177. https://doi.org/10.3390/en80910153
Shabani B, Biju M. Theoretical Modelling Methods for Thermal Management of Batteries. Energies. 2015; 8(9):10153-10177. https://doi.org/10.3390/en80910153
Chicago/Turabian StyleShabani, Bahman, and Manu Biju. 2015. "Theoretical Modelling Methods for Thermal Management of Batteries" Energies 8, no. 9: 10153-10177. https://doi.org/10.3390/en80910153
APA StyleShabani, B., & Biju, M. (2015). Theoretical Modelling Methods for Thermal Management of Batteries. Energies, 8(9), 10153-10177. https://doi.org/10.3390/en80910153






