Thermal Behaviour Investigation of a Large and High Power Lithium Iron Phosphate Cylindrical Cell
Abstract
:1. Introduction
2. Methodology

3. Electrochemical-thermal Modelling of the Cell
| Physics | Governing equations | Mathematical expressions |
|---|---|---|
| Chemical kinetics | Butler-Volmer equation | |
| Electrode overpotential | ||
| Exchange current density | ||
| Charge conservation | Solid phase | |
| Electrolyte phase | ||
| Mass transfer | Species conservation in solid phase | |
| Species conservation in electrolyte | ||
| Heat transfer | Energy conservation |
Assumptions for Modelling and Numerical Implementations
| Parameters | Anode | Separator | Cathode |
|---|---|---|---|
| Thickness (m) [38] | 3.4 × 10 | 2.5 × 10 | 8 × 10 |
| Active material volume fraction [38] | 0.58 | 0.55 | 0.374 |
| Filler volume fraction [38] | 0.0326 | - | 0.0535 |
| Volume fraction electrolyte | 0.3874 | 0.45 | 0.5725 |
| Reaction rate coefficient [33] | 2 × 10 | - | 2 × 10 |
| Particule radius (m) [38] | 5 × 10 | - | 5 × 10 |
| Solid phase Li diffusion (m/s) [38] | 3 × 10 | - | 5.9 × 10 |
| Electrolyte phase Li diffusion (m/s) [38] | 2 × 10 | ||
| Initial electrolyte concentration (mol/m) [33] | 2000 | ||
| Maximum solid phase concentration (mol/m) [38] | 30,555 | - | 22,806 |
| Regions | (J/kg·K) | ρ(kg/m) | |
|---|---|---|---|
| Cell internal region | 1034.2 | 3345.5 | 0.33434 () |
| 57.515 () | |||
| Negative electrode [33] | 1437.4 | 1347.33 | 1.04 |
| Positive electrode [33] | 750 | 3600 | 0.20 |
| Separator electrode [33] | 1978.16 | 1008.98 | 0.344 |
| Negative current collector [33] | 385 | 8933 | 398 |
| Positive current collector [33] | 875 | 2770 | 170 |
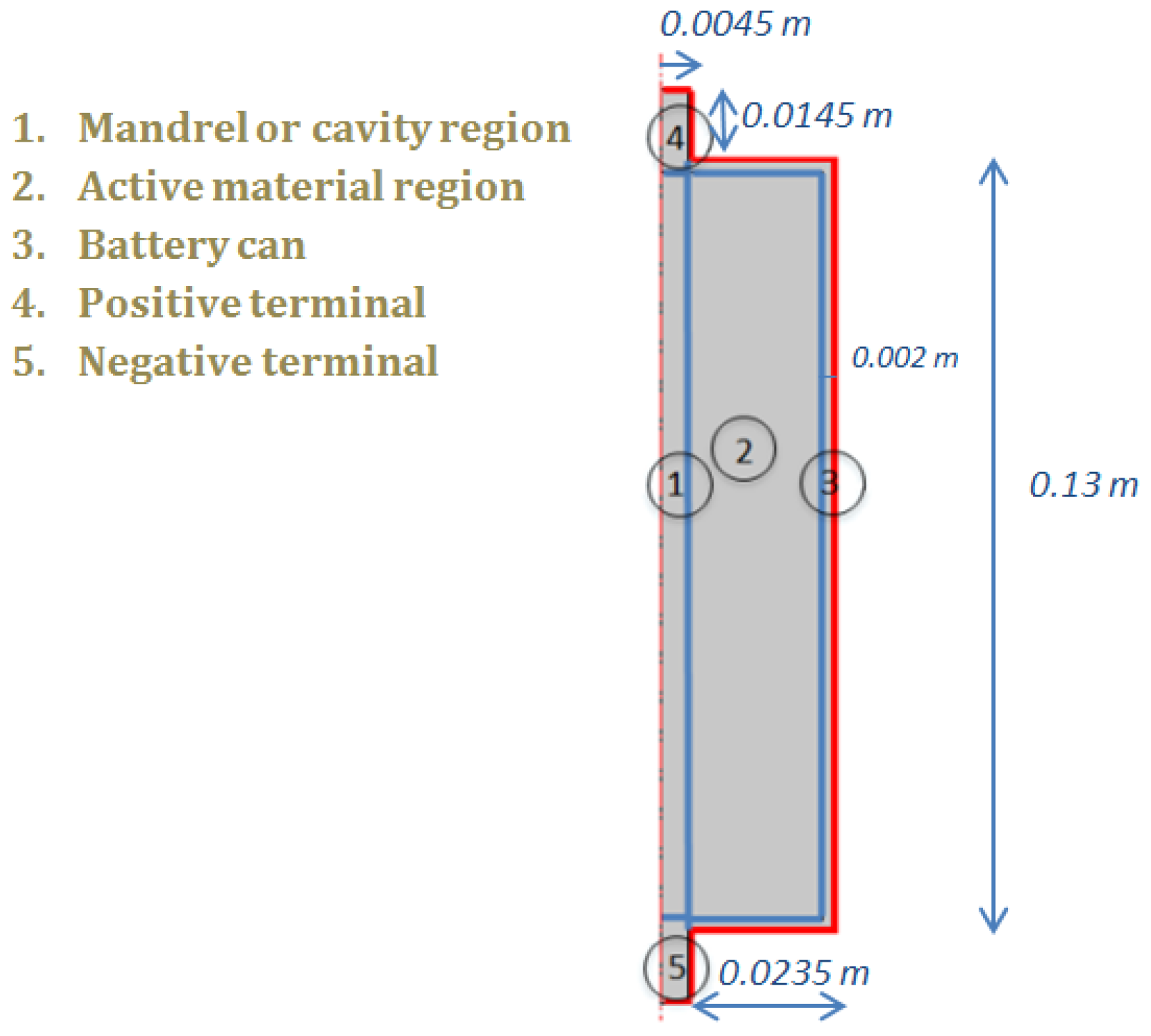
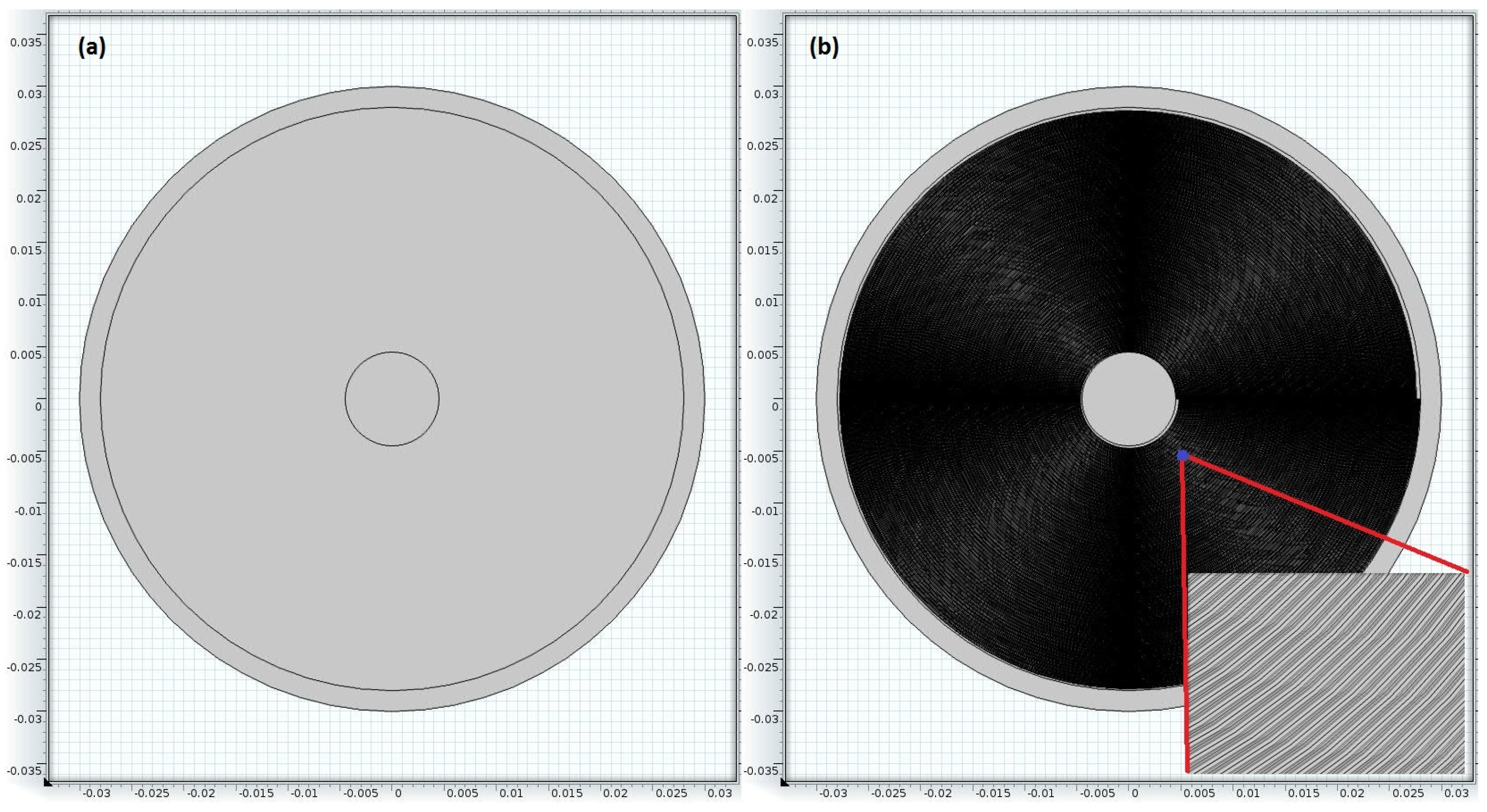
4. Experimental Conditions
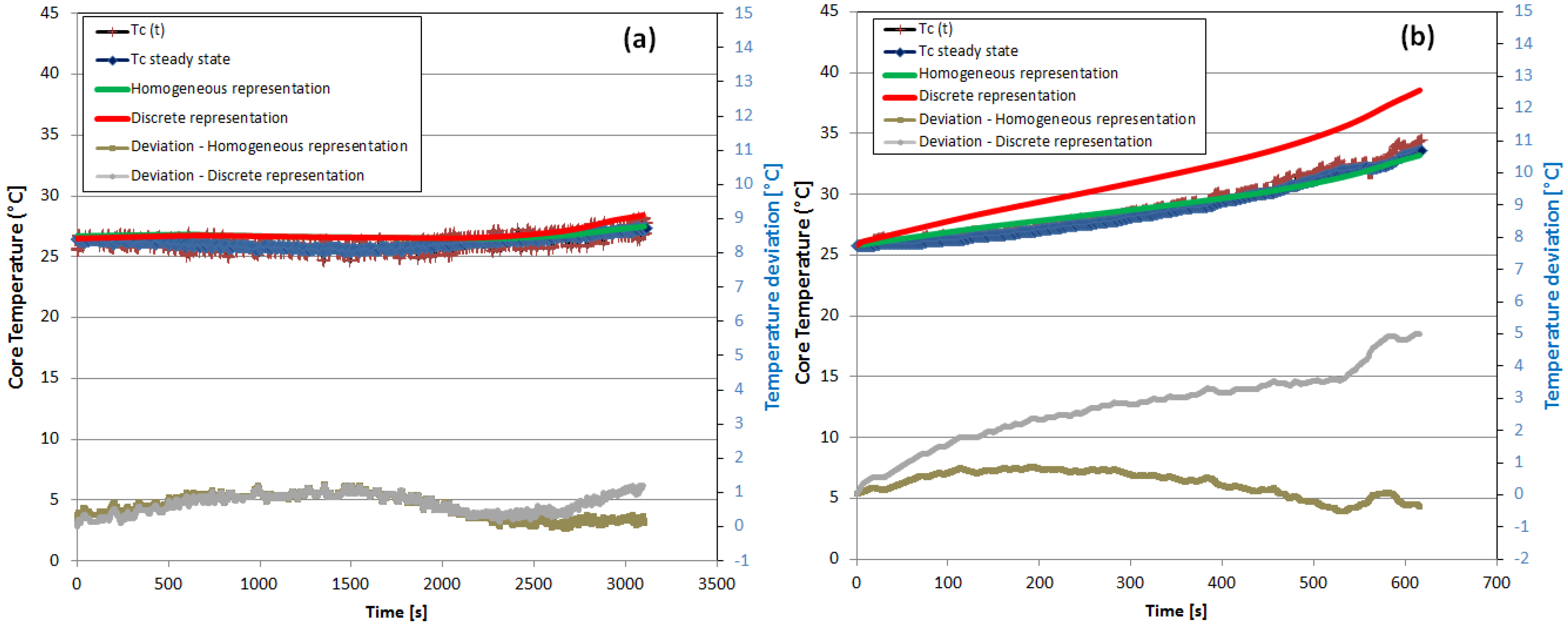
5. Validation of the Electrochemical-Thermal Modelling of the Cell
5.1. Cell Voltage

5.2. Cell Surface Temperature
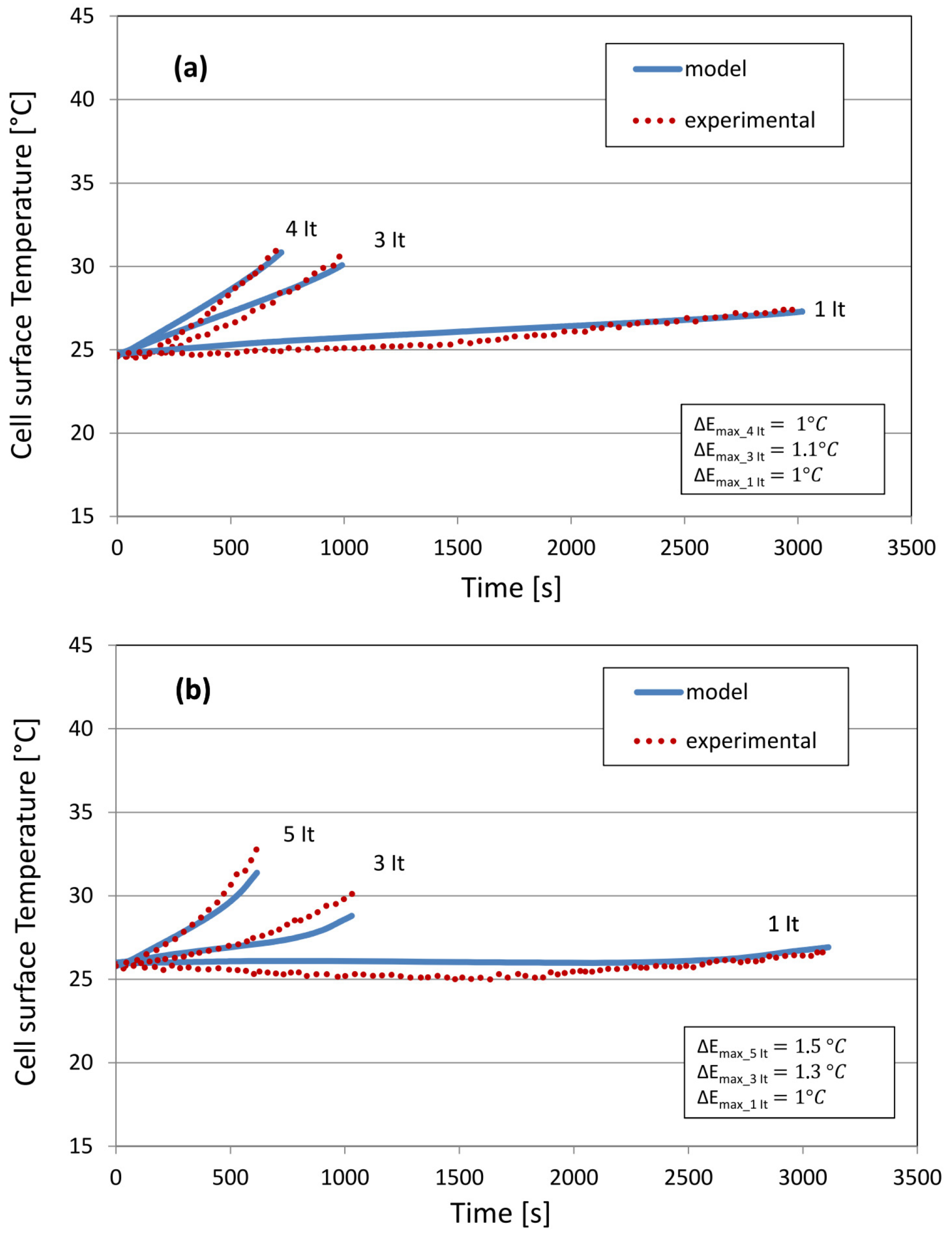
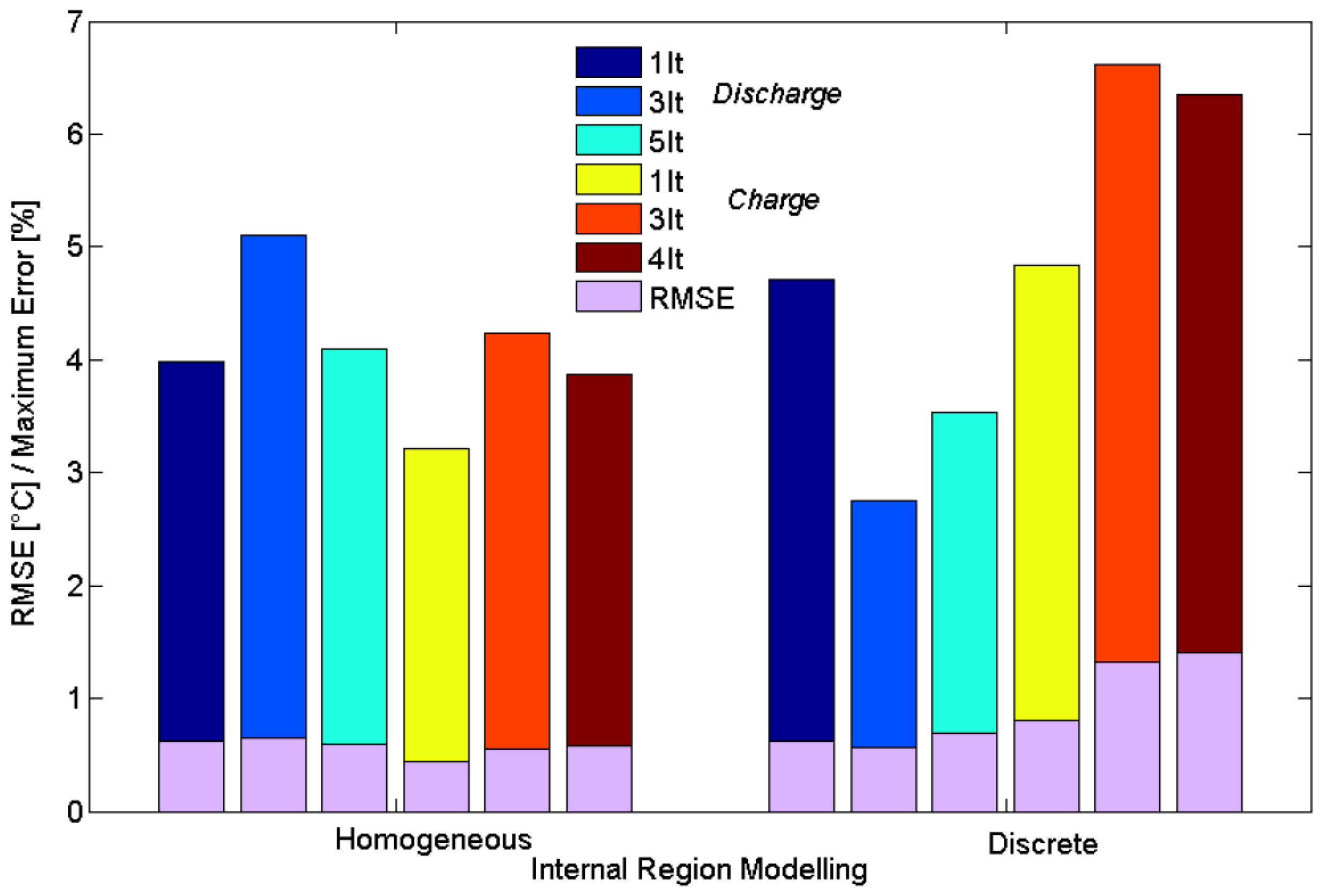


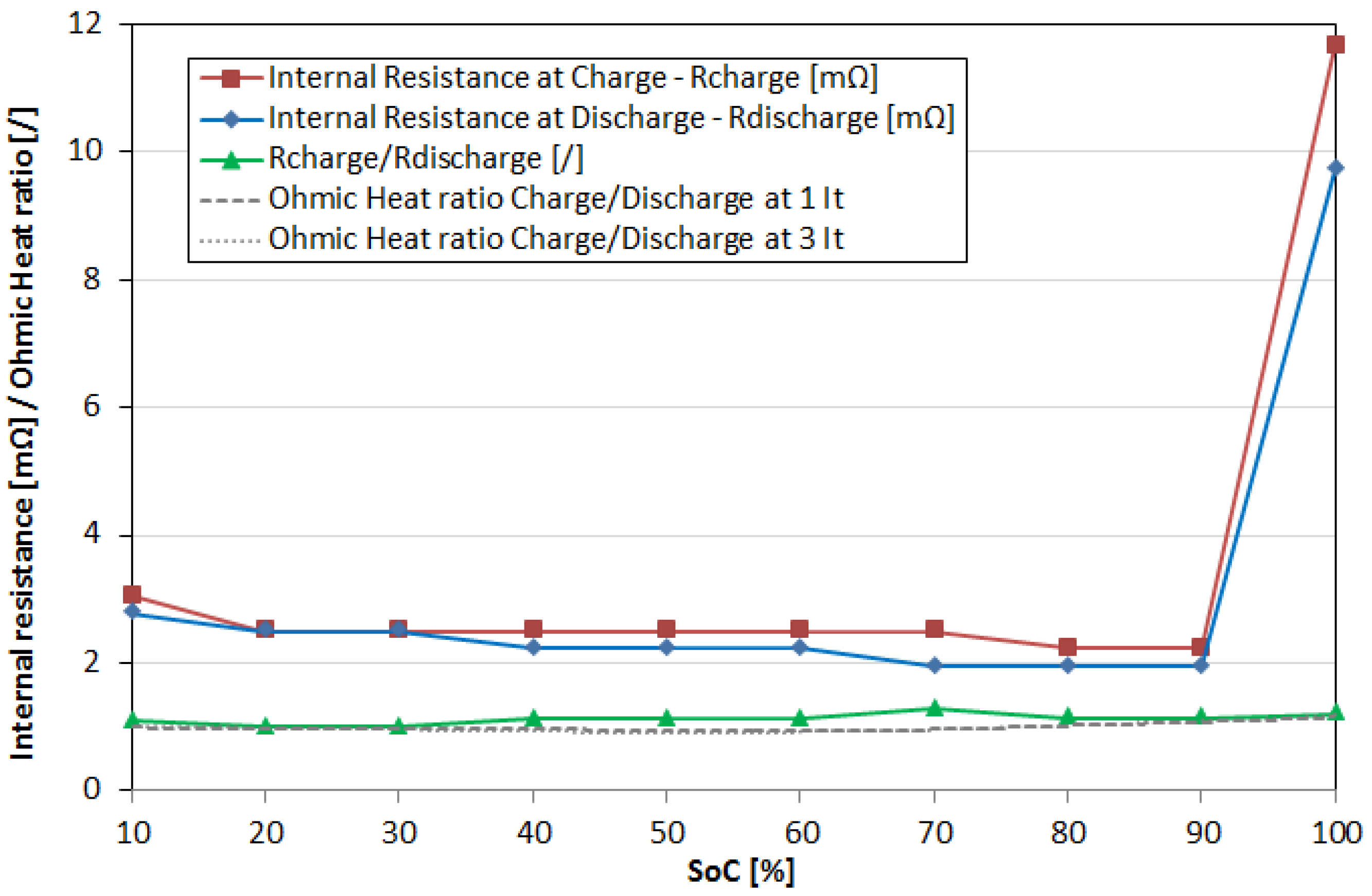
6. Results and Discussion
6.1. Evaluation of the Cell Internal Temperature Distribution
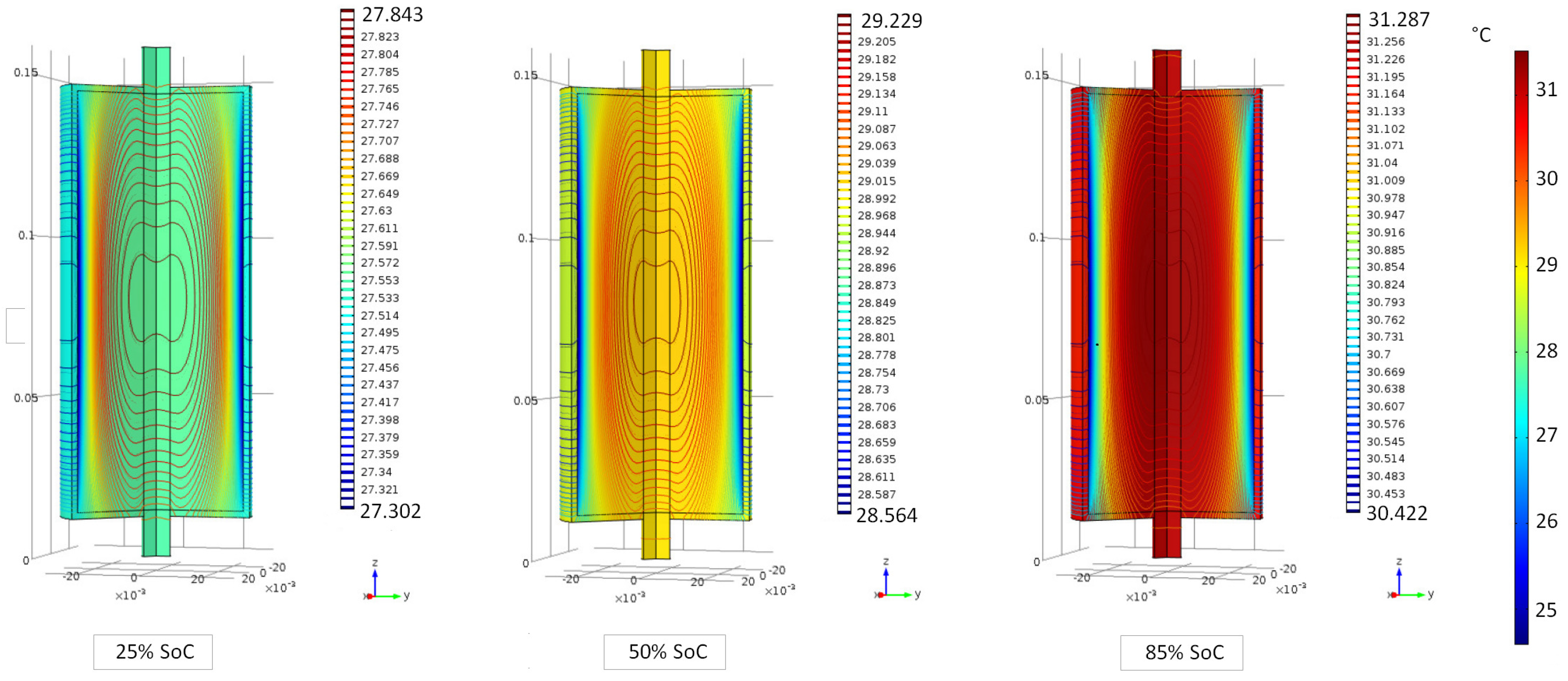
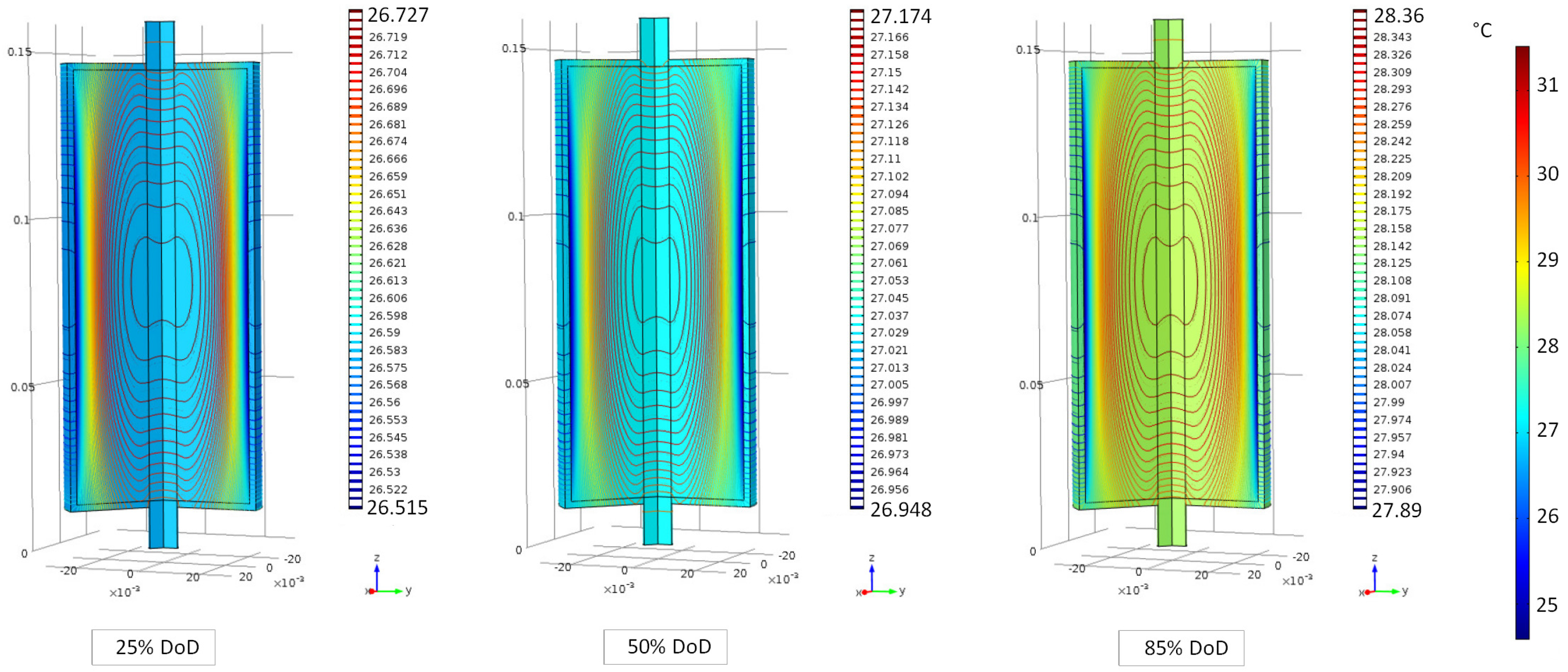

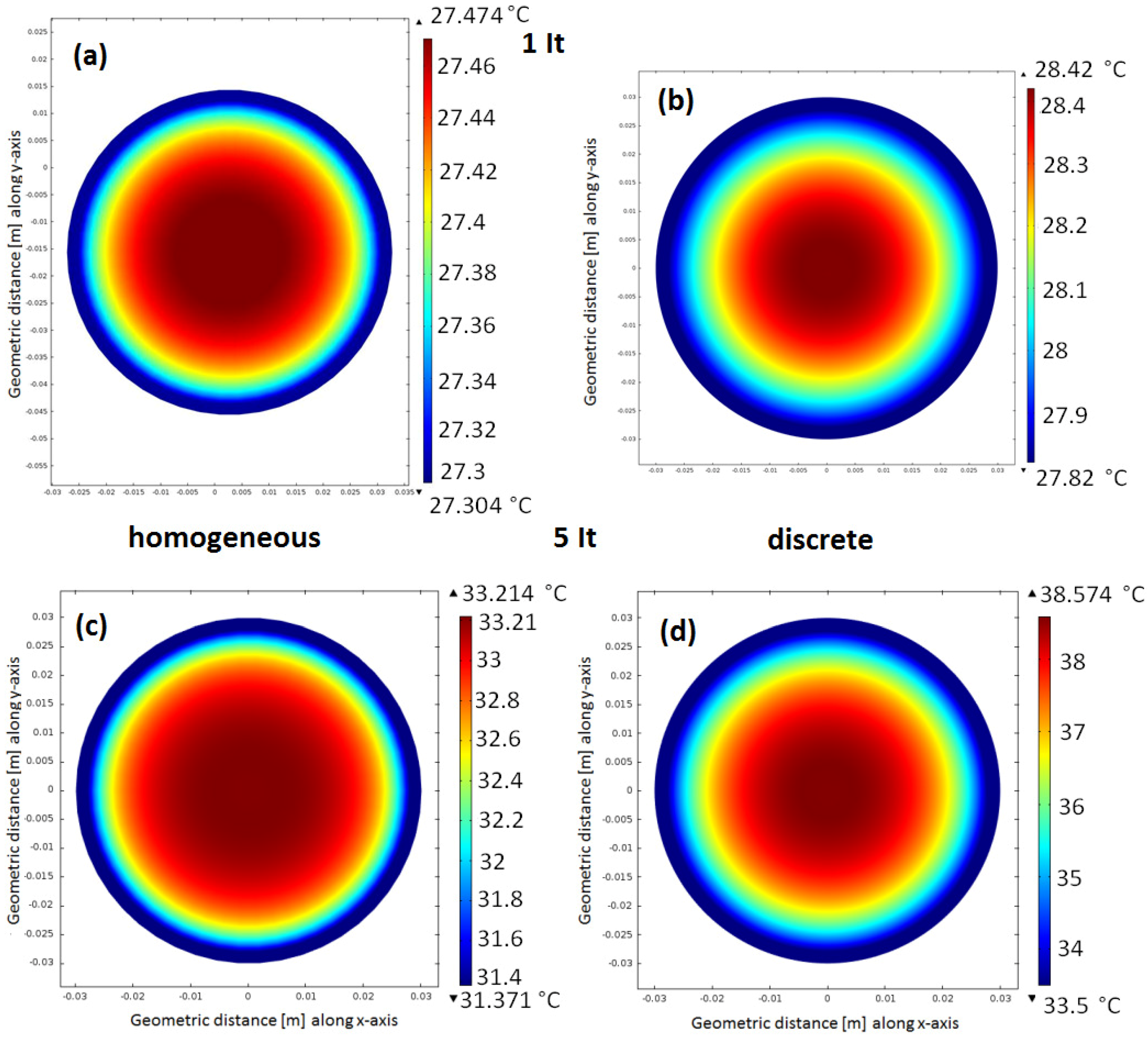
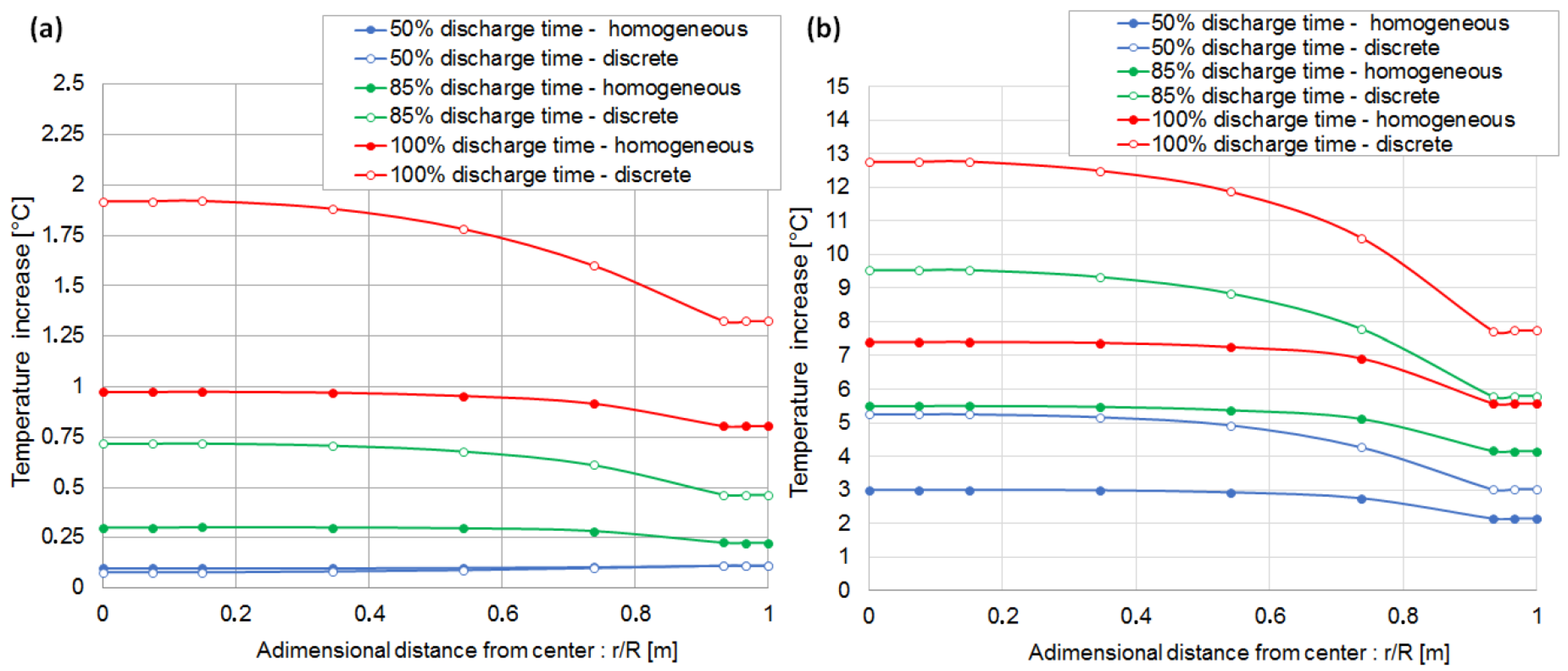
6.2. Evaluation of the Cell Temperature Rises

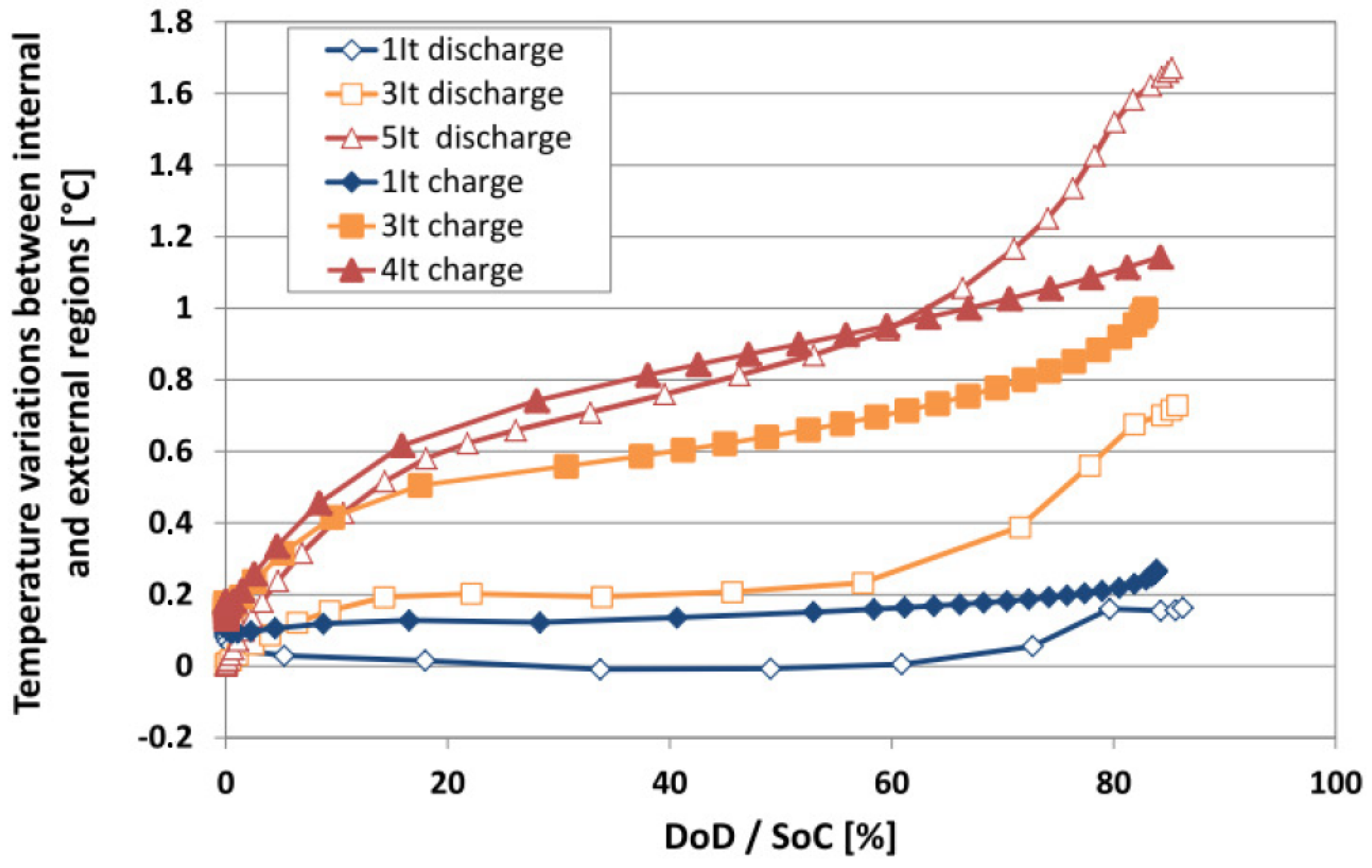
6.3. Evaluation of the Cell Temperature Gradients
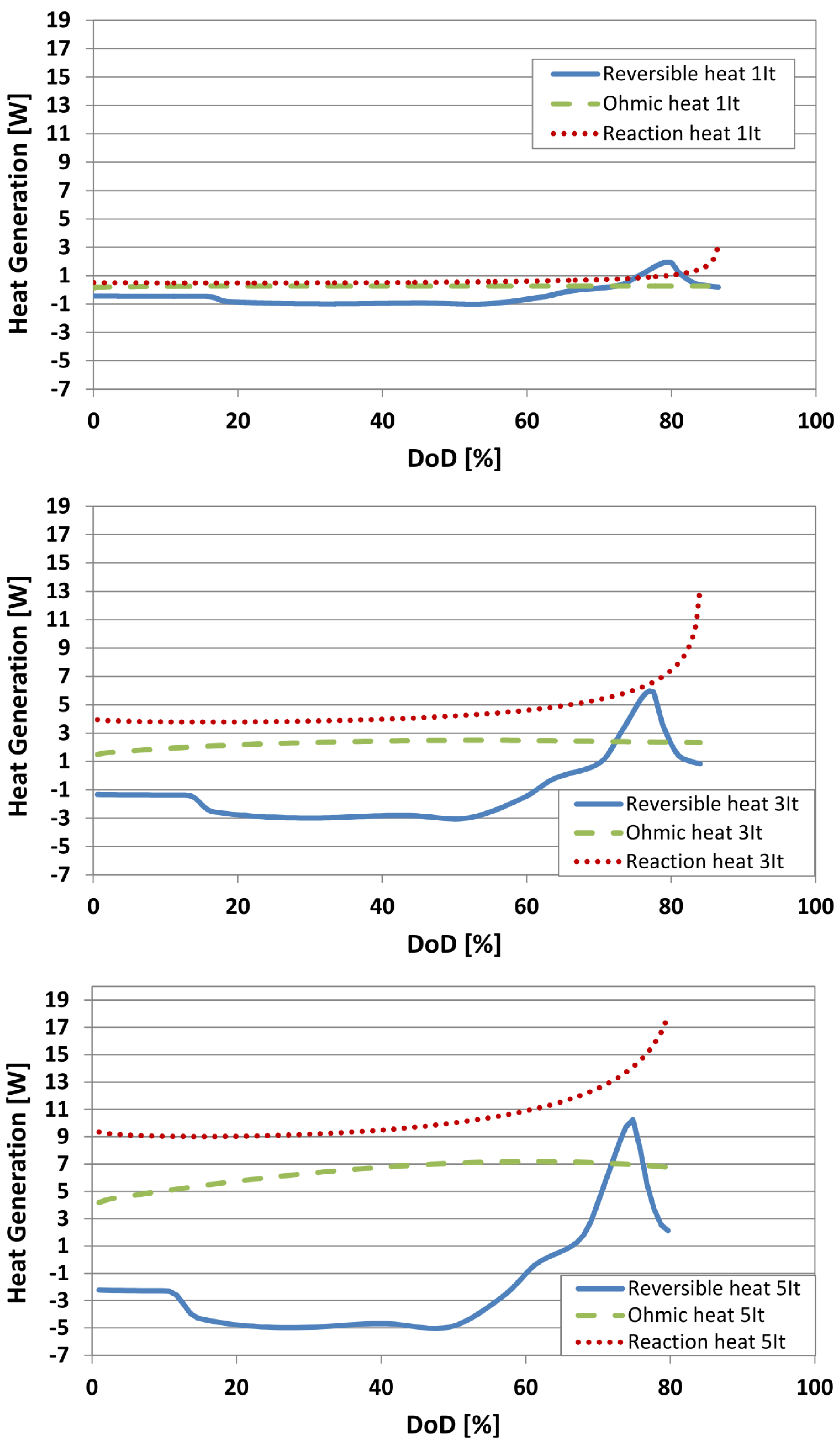
6.4. Evaluation of the Heat Generation
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Symbols
| as | Active surface area (1/m) |
| c | lithium ions concentration (mol/m3) |
| cp | Heat capacity (J/kg·K) |
| d | Diameter at the start of the spiral or internal diameter of the cell (m) |
| D | Diffusion coefficient (m2/s) |
| D | Diameter taken at the end of the spiral or cell diameter (m) |
| F | Faraday constant, 96,485 (C/mol) |
| h | Height of the battery (m) |
| i0 | Exchange current density of an electrode reaction (A/m2) |
| jLi | Transfer current due to the intercalation or deintercalation of lithium ions (A/m3) |
| k | Electrochemical reaction rate constant (m/s) |
| k | Thermal conductivity (W/m·K) |
| L | Total length of the spiral constituting the internal structure of the cell (m) |
| N | Total number of layers in the jelly roll structure of the cell (/) |
| Q | Heat generation (W/m3) |
| r | Radius of the spherical particle (m) |
| R | Universal gas constant 8.3145 (J/mol·K) |
| t | Time (s) |
| t+ | Transference number of lithium ions (/) |
| T | Temperature (°C) |
| U | Open circuit voltage (V) |
| V | Volume of layer (m3) |
| w | Width of the different layers constituting the jelly roll (m) |
Greek Letters
| α | Charge transfer coefficient (/) |
| £ | Volume fraction (/) |
| η | Overpotential (V) |
| κ | Ionic conductivity (S/m) |
| φ | Potential (V) |
| ρ | Density (kg/m3) |
| σ | Electrical conductivity (S/m) |
Subscripts
| a | Anode |
| c | Cathode |
| e or l | Electrolyte phase |
| eff | Effective |
| max | Maximum |
| measured | Measured by experiment |
| model | Modeled by simulation |
| s | Solid phase |
Abbreviations
| DoD | Depth of discharge |
| EV | Electric vehicle |
| FEM | Finite elements methods |
| FES | Flywheel energy storage |
| HEV | Hybrid electric vehicle |
| LFP | Lithium iron phosphate |
| MUMPS | Multifrontal massively parallel solver |
| PHEV | Plug-in hybrid vehicle |
| RMSE | Root mean square error |
| RMSD | Root mean square deviation |
| SoC | State of charge |
References
- Van Mierlo, J.; Maggetto, G.; van de Burgwal, E.; Gense, R. Driving style and traffic measures—Influence on vehicle emissions and fuel consumption. J. Automob. Eng. 2003, 218, 43–50. [Google Scholar] [CrossRef]
- Maggetto, G.; van Mierlo, J. Electric vehicles, hybrid electric vehicles and fuel cell electric vehicles: State of the art and perspectives. Ann. Chim. Sci. Mater. 2001, 26, 9–26. [Google Scholar] [CrossRef]
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Al Sakka, M.; Gualous, H.; van Mierlo, J.; Culcu, H. Thermal modeling and heat management of supercapacitor modules for vehicle applications. J. Power Sources 2009, 194, 581–587. [Google Scholar] [CrossRef]
- Omar, N.; Daowd, M.; van den Bossche, P.; Hegazy, O.; Smekens, J.; Coosemans, T.; van Mierlo, J. Rechargeable Energy Storage Systems for Plug-in Hybrid Electric Vehicles—Assessment of Electrical Characteristics. Energies 2012, 5, 2952–2988. [Google Scholar] [CrossRef]
- Omar, N.; Gualous, H.; Al Sakka, M.; van Mierlo, J.; van den Bossche, P. Electric and thermal characterization of advanced hybrid Li-ion capacitor rechargeable energy storage system. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives (Powereng), Istanbul, Turkey, 13–17 May 2013; pp. 1574–1580.
- Van den Bossche, P.; Omar, N.; Al Sakka, M.; Samba, A.; Gualous, H.; van Mierlo, J. The challenge of PHEV battery design and the opportunities of electrothermal modeling. In Lithium-Ion Batteries: Advances and Applications; Elsevier: Amsterdam, The Netherlands, 2014; Chapter 11. [Google Scholar]
- Van den Bossche, P.; Vergels, F.; van Mierlo, J.; Matheys, J.; van Autenboer, W. SUBAT: An assessment of sustainable battery technology. J. Power Sources 2006, 162, 913–919. [Google Scholar] [CrossRef]
- Mulder, G.; Omar, N.; Pauwels, S.; Meeus, M.; Leemans, F.; Verbrugge, B.; de Nijs, W.; van den Bossche, P.; Six, D.; van Mierlo, J. Comparison of commercial battery cells in relation to material properties. Electrochim. Acta 2013, 87, 473–488. [Google Scholar] [CrossRef]
- Van Mierlo, J.; van den Bossche, P.; Maggetto, G. Models of energy sources for EV and HEV: Fuel cells, batteries, ultracapacitors, flywheels and engine-generators. J. Power Sources 2004, 128, 76–89. [Google Scholar] [CrossRef]
- Kim, G.; Smith, K. Multi-dimensional electrochemical-thermal coupled model of large format cylindrical lithium-ion cells. In Proceedings of the 212th ECS Meeting, Washington, DC, USA, 7–12 October 2007.
- Jung, D.Y.; Lee, B.H.; Kim, S.W. Development of battery management system for nickel-metal hydride batteries in electric vehicle applications. J. Power Sources 2002, 109, 1–10. [Google Scholar] [CrossRef]
- Braun, P.V.; Cho, J.; Pikul, J.H.; King, W.P.; Zhang, H. High power rechargeable batteries. Curr. Opin. Solid State Mater. Sci. 2012, 16, 186–198. [Google Scholar] [CrossRef]
- Richard, M.; Dahn, J. Predicting electrical and thermal abuse behaviours of practical lithium-ion cells from accelerating rate calorimeter studies on small samples in electrolyte. J. Power Sources 1999, 79, 135–142. [Google Scholar] [CrossRef]
- MacNeil, D.; Dahn, J. test of reaction kinetics using both differential scanning and accelerating rate calorimetries as applied to the reaction of LixCoO2 in non-aqueous electrolyte. J. Phys. Chem. A 2001, 105, 4430–4439. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Karimi, G.; Li, X. Thermal management of lithium-ion batteries for electric vehicles. Int. J. Energy Res. 2013, 37, 13–24. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Sabbah, R.; Kizilel, R.; Selman, J.R. Active (air-cooled) vs. passive (phase change material) thermal management of high power lithium-ion packs: Limitation of temperature rise and uniformity of temperature distribution. J. Power Sources 2008, 182, 630–638. [Google Scholar] [CrossRef]
- Warner, J. Chapter 7: Lithium-ion battery packs for EVs. In Lithium-Ion Batteries: Advances and Applications; Elsevier: Amsterdam, The Netherlands, 2014; pp. 127–150. [Google Scholar]
- Matthe, R.; Eberle, U. The voltec system-energy storage and electric propulsion. In Lithium-Ion Batteries: Advances and Applications; Elsevier: Amsterdam, The Netherlands, 2014; Chapter 8; pp. 151–176. [Google Scholar]
- Pesaran, A.; Vlahinos, A.; Burch, S. Thermal Performance of EV and HEV Battery Modules and Packs; National Renewable Energy Laboratory: Golden, CO, USA, 1997. [Google Scholar]
- Pesaran, A. Battery thermal management in EVs and HEVs: Issues and solutions. Battery Man 2001, 43, 34–49. [Google Scholar]
- Pesaran, A.; Burch, S.; Keyser, M. An approach for designing thermal management systems for electric and hybrid vehicle battery packs. In Proceedings of the Fourth Vehicle Thermal Management Systems Conference and Exhibition, London, UK, 24–27 May 1999.
- Karimi, G.; Dehghan, A.R. Thermal analysis of high-power lithium-ion battery packs using flow network approach. Int. J. Energy Res. 2014, 38, 1793–1811. [Google Scholar] [CrossRef]
- Forgez, C.; Vinh Do, D.; Friedrich, G.; Morcrette, M.; Delacourt, C. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery. J. Power Sources 2010, 195, 2961–2968. [Google Scholar] [CrossRef]
- Rad, M.; Danilov, D.; Baghalha, M.; Kazemeini, M.; Notten, P. Thermal modeling of cylindrical LiFePO4 Batteries. J. Mod. Phys. 2013, 4, 1–7. [Google Scholar] [CrossRef]
- Jeon, D.H.; Baek, S.M. Thermal modeling of cylindrical lithium ion battery during discharge cycle. Energy Convers. Manag. 2011, 52, 2973–2981. [Google Scholar] [CrossRef]
- Jeon, D.H. Numerical modeling of lithium ion battery for predicting thermal behavior in a cylindrical cell. Curr. Appl. Phys. 2014, 14, 196–205. [Google Scholar] [CrossRef]
- Zhang, X. Thermal analysis of a cylindrical lithium-ion battery. Electrochim. Acta 2011, 56, 1246–1255. [Google Scholar] [CrossRef]
- Ye, Y.; Shi, Y.; Tay, A.A.O. Electro-thermal cycle life model for lithium iron phosphate battery. J. Power Sources 2012, 217, 509–518. [Google Scholar] [CrossRef]
- Samba, A.; Omar, N.; Gualous, H.; Capron, O.; van den Bossche, P.; van Mierlo, J. Impact of tab location on large format lithium-ion pouch cell based on fully coupled three-dimensional electrochemical-thermal modeling. Electrochim. Acta 2014, 147, 319–329. [Google Scholar] [CrossRef]
- Saw, L.; Ye, Y.; Tay, A.A.O. Electrochemical-thermal analysis of 18650 Lithium Iron Phosphate cell. Energy Convers. Manag. 2013, 75, 162–174. [Google Scholar] [CrossRef]
- Somasundaram, K.; Birgersson, E.; Mujumdar, A. Thermal-electrochemical model for passive thermal management of a spiral-wound lithium-ion battery. J. Power Sources 2012, 203, 84–96. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.; Doyle, M.; Newman, J. Simulation and optimization of the dual lithium ion insertion cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Somasundaram, K. Mathematical Modeling of Transport Phenomena in Electrochemical Energy Storage Systems. Ph.D. Thesis, Department of Mechanical Engineering, National University of Singapore, Singapore, 2012. [Google Scholar]
- Prada, E.; Di Domenico, D.; Creff, Y.; Bernard, J.; Sauvant-Moynot, V.; Huet, F. Simplified electrochemical and thermal model of LiFePO4, graphite Li-ion batteries for fast charge applications. J. Electrochem. Soc. 2012, 159, A1508–A1519. [Google Scholar] [CrossRef]
- Inui, Y.; Kobayashi, Y.; Watanabe, Y.; Watase, Y.; Kitamura, Y. Simulation of temperature distribution in cylindrical and prismatic lithium ion secondary batteries. Energy Convers. Manag. 2007, 48, 2103–2109. [Google Scholar] [CrossRef]
- Samba, A.; Omar, N.; Gualous, H.; Firouz, Y.; van den Bossche, P.; van Mierlo, J.; Boubekeur, T.I. Development of an advanced two-dimensional thermal model for large size lithium-ion pouch cells. Electrochim. Acta 2014, 117, 246–254. [Google Scholar] [CrossRef]
- PEC. Test Equipment, High Power Equipment for Cells: SBT0550. Available online: http://www.peccorp.com/SBT0550-tabs-glance.html (accessed on 12 September 2015).
- International Electrotechnical Commission (IEC). Secondary Cells and Batteries Containing Alkaline or Other Non-Acid Electrolytes—Guide to Designation of Current in Alkaline Secondary Cell and Battery Standards, 1996. Available online: https://webstore.iec.ch/publication/5453 (accessed on 12 September 2015).
- Simmons, K.; Guezennec, Y.; Onori, S. Modeling and energy management control design for a fuel cell hybrid passenger bus. J. Power Sources 2014, 246, 736–746. [Google Scholar] [CrossRef]
- Capron, O.; Samba, A.; Omar, N.; Coosemans, T.; Bossche, P.; van Mierlo, J. Lithium-ion batteries: Thermal behaviour investigation of unbalanced modules. Sustainability 2015, 7, 8374–8398. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capron, O.; Samba, A.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. Thermal Behaviour Investigation of a Large and High Power Lithium Iron Phosphate Cylindrical Cell. Energies 2015, 8, 10017-10042. https://doi.org/10.3390/en80910017
Capron O, Samba A, Omar N, Van Den Bossche P, Van Mierlo J. Thermal Behaviour Investigation of a Large and High Power Lithium Iron Phosphate Cylindrical Cell. Energies. 2015; 8(9):10017-10042. https://doi.org/10.3390/en80910017
Chicago/Turabian StyleCapron, Odile, Ahmadou Samba, Noshin Omar, Peter Van Den Bossche, and Joeri Van Mierlo. 2015. "Thermal Behaviour Investigation of a Large and High Power Lithium Iron Phosphate Cylindrical Cell" Energies 8, no. 9: 10017-10042. https://doi.org/10.3390/en80910017








