2. Numerical Model
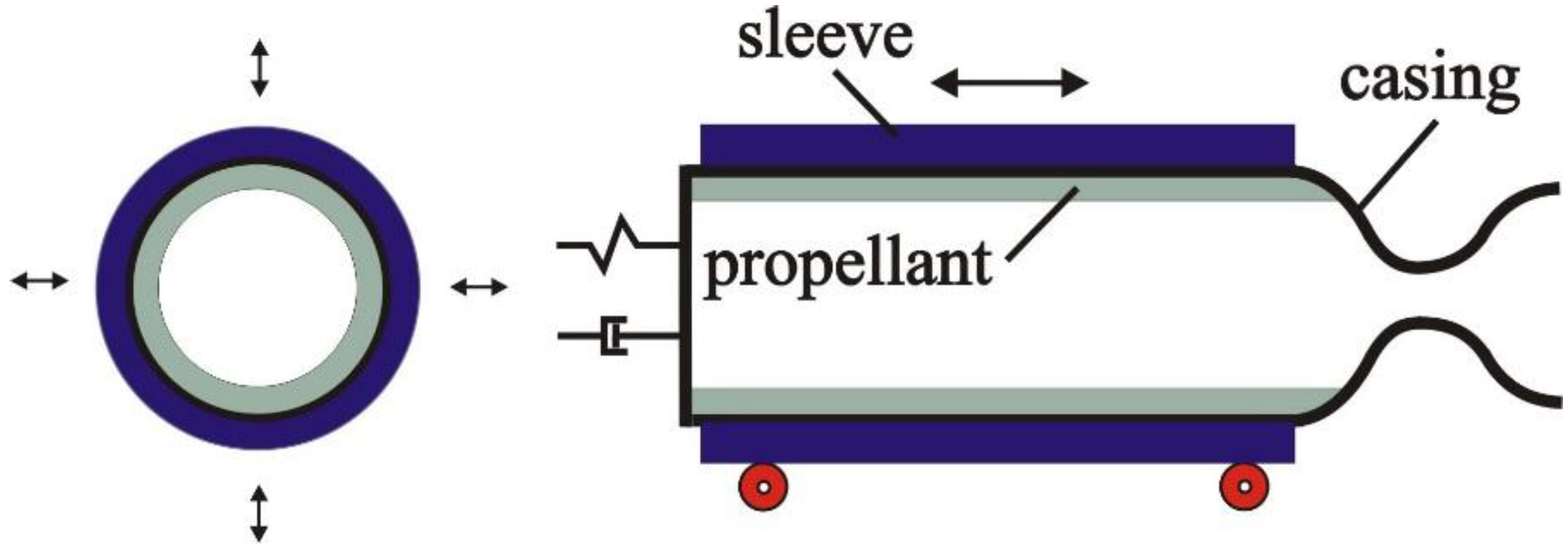
In the present investigation, the SRM is assumed to be positioned on a static test stand, as schematically represented in
Figure 1. In this case, the cylindrical-grain motor is free to vibrate radially without any external constraint (
i.e., only constrained in some cases by the thick steel static test sleeve surrounding the aluminum flight weight motor casing), while axial motion is constrained to a large degree by the thrust-measuring load cell (represented in the predictive model as a spring/damper system) at the left-hand boundary of the motor’s head end. Under normal (nominal) quasi-equilibrium operating conditions, the internal gas-particle flow moves smoothly from the burning propellant surface into the axial flow, from left-to-right, as per
Figure 1, through and beyond the exhaust nozzle.
Figure 1.
The reference solid-propellant rocket motor (SRM) model setup, for static test firing in the laboratory.
Figure 1.
The reference solid-propellant rocket motor (SRM) model setup, for static test firing in the laboratory.
The equations of motion describing the non-steady core flow within the SRM must be solved in conjunction with the local surface regression rate
rb of the solid propellant and the surrounding structure’s instantaneous geometric deformation. As pertains to the present study of a motor having a larger length-to-diameter ratio, the quasi-one-dimensional hydrodynamic conservation equations for the axial gas flow are given below:
The total specific energy of the gas is defined for an ideal gas as:
In Equation (1), for the conservation of mass, one can see the input of gas entering the central flow from the nominally spherical reactive particles, as specified by the final term on the right-hand side. With respect to the remaining (largest) mass input from the propellant burning surface, the loading fraction of solid particles in the propellant, αp, influences the amount of propellant gas entering into the central flow, as per the second term on the right-hand side of Equation (1). In Equation (2), for conservation of axial momentum, one sees the drag force of the particles on the gas in the last term on the right-hand side. In Equation (3), for the conservation of energy, one sees the contribution of high-temperature particle gas heat energy in the final term on the right-hand, while one sees the drag and heat energy transfer between the particles and gas in the term next to it.
A one-dimensional (1D) approach, as described by the above conservation equations, will not capture all of the physical phenomena at play in a motor’s interior flow (relative to what can potentially be obtained via a two-dimensional axisymmetric or three-dimensional flow model). However, for a motor with a larger length-to-diameter ratio, the 1D approach can capture at least some useful elements of the physical phenomena that are of interest for this study, as made evident later in this paper. In addition, one can note that a 1D numerical model has the nominal advantages of allowing for simpler modelling and quicker turnaround times for the computed results.
Assuming that one starts with a single set of reactive particles of one nominal starting diameter within the solid propellant, one would, in turn, need to account for the diminishing size of those particles once they exit the solid propellant surface and begin moving downstream in the internal core flow. One can separate the collection of different-sized particles appearing in a given volumetric element into their applicable size subset or bracket, e.g., for a 10-m starting particle diameter, employ 10 size subsets (
i = 1 to 10 subsets, for particles sized between 10 and 9 m for
i = 1, between 9 and 8 m for
i = 2,
etc., down to a zero particle diameter). For greater accuracy, one would want to use more size subsets with smaller size ranges between them, the trade-off being an increased computational turnaround time. One will need to keep track of particles transitioning from a higher sized bracket into the adjacent lower size bracket as they burn down at their respective regression rate
rb,pi. For example, particles being added into an
i-th bracket from its upper boundary with its adjacent higher size bracket (at
i − 1) over a small computational time increment will adjust the particle density therein as follows:
where Δ
rbracket is the
i-th bracket distance in terms of particle radius (0.5 m for the above example). Similarly, particles being lost from an
i-th bracket through its lower boundary with its adjacent lower size bracket (at
i + 1) will adjust the particle density in the
i-th bracket as follows:
For the simulation runs done in this study, the size brackets are initially empty and allowed to fill up to their quasi-equilibrium value with a sufficient period of time allotted. The number of particles in a given bracket at a given axial location (flow element of volume
) can be established via:
where the mass of an individual particle is ascertained via:
The corresponding equations of motion for an
i-th particle set within the axial flow may be described by the following:
The total specific energy of a local grouping of particles from an
i-th set is given by:
where
Tpi is the mean temperature of that group of particles. As noted in the pertinent conservation equations, terms associated with particle mass or particle energy input from the propellant surface are only applicable when
i = 1. The one-dimensional conservation equations above essentially prescribe the movement of a collection of particles of comparable size (for the
i-th set in question; in the sense as a quasi-continuous medium, but without exertion of any pressure of one particle on another). The given particle set moves through elemental volumes of length Δ
x, as one moves left to right from the motor’s head end downstream to and through the motor’s exhaust nozzle. As with the gas, the particles are allowed to move out of the nozzle expansion’s exit plane, with a transmissive right-side boundary at that point to avoid any artificial reflections of significance in regards to influencing flow activity upstream in the combustion chamber.
As noted above, gaseous mass and the associated energy evolving from the burning surface of the solid spherical reactive particles of varying diameters is accounted for in the gas-phase mass and energy conservation equations. The idealized “pre-heated” inert particle assumption, entering the central core flow at
Tf, is shown in Equation (11). As outlined in [
12], the viscous interaction between the gas and a particle from the
i-th particle set is represented by the drag force
Di, and the heat transfer from the core flow to a particle from the
i-th set is defined by
Qi. In the case of drag between the gas and a representative spherical particle at a given axial location, one notes that:
where
Cd is the drag coefficient for a sphere in a steady flow with low flow turbulence (determined as a function of the relative Reynolds number, relative flow Mach number and temperature difference between the particle and the gas). In the case of heat transfer from the core flow to a representative particle at a given axial location, the following applies in the inert particle case (this relation may need to be modified for the reactive particle case, given the presence of a high-temperature flame surrounding a given particle):
where the Nusselt number Nu can be found as a function of the Prandtl number and the relative Reynolds number for a sphere of mean diameter
dmi. One will need to solve Equations (9) to (11) for each of
Nset particle sets as part of the calculation process, where for the example particle subset family described above,
Nset has a value of 10 at quasi-equilibrium.
Longitudinal acceleration
aℓ appears in the gas and particle momentum and energy equations as a body force contribution within a fixed Eulerian reference (fixing of
x = 0 to the motor head end,
x positive moving right on the structure, as per
Figure 1; acceleration of the local surrounding structure rightward is designated positive
aℓ) and may vary both spatially along the length of the motor and with time. The effects of such factors as turbulence can be included through one or more additional equations that employ the information from the bulk flow properties arising from the solution of the above one-dimensional equations of motion. The principal differential equations themselves can be solved via a higher-order, explicit, finite-volume random-choice method (RCM) approach [
12,
13]. The RCM solver employs a Riemann solution technique noted for low artificial dispersion with the time of wave activity in tubes,
etc. The equations of motion of the gas and particles will be solved over a given time step Δ
t (on the order of 1 × 10
−7 s for the present study, given the motor solution node allocation in the axial direction from the head end to nozzle exit plane), in sequence with additional equations for structural motion and the propellant burning rate, as described below.
Structural vibration can play a significant role in non-steady SRM internal ballistic behaviour, as evidenced by the observed changes in combustion instability symptoms as allied with the changes in the structure surrounding the internal flow (e.g., propellant grain configuration, wall thickness, material properties). The level of sophistication required for modelling the motor structure (propellant, casing, static-test sleeve, nozzle) and applicable boundary conditions (load cell on a static test stand) can vary, depending on the particular application and motor design. Montesano
et al. [
14] employed a finite-element approach towards the structural modeling of the given motor configuration. In the present study, a cylindrical-grain configuration allows for a simpler approach via the thick wall theory, as reported in [
15]. The radial deformation dynamics of the propellant/casing/sleeve are modelled by a series of independent ring elements along the length of the motor. With that representation, the following ordinary differential equation applies for the movement of a radial position
r within the assembly:
where
ro is the reference radius under no chamber pressure and ψ is the local instantaneous radial displacement under static loading. Equation (15) may be solved using a backward difference scheme. Allowing for viscoelastic behavior, ξ
R is the radial damping ratio. The fundamental natural radial frequency, ω
nR, of the sleeve/casing/propellant assembly may be determined using a commercial finite element analysis software program, if the theoretical approximation is not considered adequate.
Axial motion along the length of the structure is modelled via beam theory and bounded by the spring/damper load cell at the motor’s head end. Viscous damping is applied in both the radial and axial directions. Reference structural properties are assumed for an ammonium-perchlorate/hydroxyl-terminated polybutadiene (AP/HTPB) composite propellant surrounded by an aluminum casing and steel sleeve.
With respect to transient, frequency-dependent burning rate modeling, which allows one to solve for the local
rb value for the burning propellant surface at a given time, a generalized Zeldovich-Novozhilov (Z-N) solid-phase energy conservation approach is used in the present simulation program. It may be represented by the following time-dependent temperature-based relationship [
16]:
where
rb,qs is the quasi-steady burning rate (the value for the burning rate as estimated from the steady-state information for a given set of local flow conditions above the propellant surface),
Ti is the initial propellant temperature (e.g., room or outside air temperature) and, in this context, ∆
T = T(
y,
t)
− Ti is the temperature distribution in moving from the burning propellant surface at
y = 0 (and
T = Ts) to that spatial location in the propellant where the temperature reaches
Ti. The net surface heat release term appearing in Equation 16, Δ
Hs, is commonly included as an add-on correction to the solid-phase energy contribution in an energy-conservation model involving solid propellants (e.g., see Equation (22) below for erosive burning). On a pragmatic level, adjusting the value of Δ
Hs positively upward (the more exothermic contribution) increases the burning response magnitude of the propellant at a given frequency, and
vice versa for a more endothermic contribution, which acts to deaden the response [
16].
For the numerical solution of the integral of Equation (16), the transient heat conduction in the solid phase can be solved by an appropriate finite-difference scheme. In Equation (16),
rb* is the nominal (unconstrained) instantaneous burning rate. The actual instantaneous burning rate
rb may be found as a function of
rb* through the rate limiting equation provided below [
16]:
The rate limiting coefficient
Kb effectively damps (“slows down”) the unconstrained burning rate
rb* to allow for a better comparison to experimental transient response data and to prevent artificial burning-rate divergence (“runaway”). A higher value for
Kb, moving closer to, but still less than 1/Δ
t (
i.e., the inverse of the numerical solution time step), tends to shift the peak combustion response frequency
fr to a higher value. Adjusting the value for
Kb and Δ
Hs permits one to better compare a given solid propellant’s experimentally observed transient response behaviour, for example as determined from a T-burner, where the “T” shape of the apparatus gives it its name [
1,
9].
The quasi-steady burning rate appearing in Equation (16) may be ascertained as a function of various parameters; in this study, as a function of local static pressure
p, core flow velocity
u (erosive burning component) and acceleration (combined effect of
an and
aℓ, the normal and lateral/longitudinal vector components), such that:
The pressure-based burning component may be found through de St. Robert’s empirical law:
The flow-based erosive burning component (negative and positive) is established through the following expression [
17]:
where at lower flow speeds, the negative component resulting from a stretched combustion zone thickness (δ
r > δ
o) may cause an appreciable drop in the base burning rate
ro, which, in this study, is predominantly the pressure-dependent burning component (when acceleration is present,
ro would be the sum of
rp and
ra). The stretching of the flame zone at low speed may be viewed as being the result of a laminar-like sliding process of the local axial flow in the boundary layer acting to extend and curve the path of a representative particle moving up from the burning surface towards the flame front, such that the effective reactive length is increased. From [
17], in the low-speed regime, the following expression may be applied, such that the core flow Darcy–Weisbach friction factor
f is below the limit value
flim, at which point negative erosive burning is no longer in effect:
The parameter
Kδ is a shear layer coefficient, whose value is set at 2600 m
−1, along with a value for
flim of 2.5 × 10
−4, producing a good comparison to experimental data for various propellants and motors [
17].
At higher flow speeds, the positive erosive burning component
re, which can be established from a phenomenological convective heat feedback premise [
16], should dominate:
For practical modelling purposes, the value for net surface heat release term Δ
Hs as specifically employed in Equation (22) is usually small in comparison to the available experimental quasi-steady erosive burning data [
17] and, thus, is commonly set to zero when calculating
re (as is done in this study). The comparable Δ
Hs term in Equation (16), for transient combustion response, is treated separately and may have a significant positive or negative value to better compare to transient experimental data. One can find the effective convective heat transfer coefficient
h of Equation (22) as a function of the zero-transpiration (zero blowing) value
h* and overall propellant burning rate
rb [
17]:
In turn, the value for
h* may be found as a function of the zero-transpiration Darcy–Weisbach friction factor
f*, via Reynolds’ analogy [
17]:
In the realm of fully-developed turbulent flow, Colebrook’s [
18] semi-empirical expression for
f* has proven accurate over a wide range of Reynolds numbers:
Through Equation (25), one can see the correlation of propellant surface roughness height ε and grain port diameter dp in influencing the magnitude of flow-dependent erosive burning. With composite propellants using ammonium perchlorate crystals, the roughness height can commonly be correlated with the AP crystal size.
The effect of normal acceleration
an on the burning rate, in this study resulting from radial propellant/casing/sleeve vibration, may be determined via [
19]:
where the compressive effect of normal acceleration and the dissipative effect of steady or oscillatory longitudinal (or lateral, if, say, for a star grain configuration) acceleration
aP are stipulated through the accelerative mass flux
Ga:
Note that the longitudinal/lateral acceleration-based displacement orientation angle φ
d is greater than the nominal acceleration vector orientation angle (φ; at the lower limit, φ and φ
d are zero when only normal acceleration
an relative to the burning propellant surface is present) [
19]. One should also note that
an is negative when acting to compress the combustion zone and treated as zero when directed away from the zone. For the above case, the base burning rate
ro is a function of the other flow mechanisms (pressure and core flow).
Past studies by some researchers have allowed for the propellant’s burning surface temperature
Ts to vary as a function of the propellant’s burning rate, while others, explicitly or implicitly, have assumed a mean or constant value [
11,
16]. Based on good comparisons in general to the experimental data for various burning mechanisms and conditions, a constant or mean burning surface temperature
Ts was employed or implicitly assumed in elements of the numerical combustion model, for the present investigation.
Finally, one needs to address the nominal rate at which the spherical aluminum particles will diminish in size as they move down the central flow. Following the approach that Yang and Yoon [
20] used for modelling the regression rate of aluminum particles, via the so-called D
2 law (D referring to particle diameter, this law is also known as the evaporation coefficient approach [
21,
22]), one can approximate a spherical aluminum particle’s nominal regression rate as a function of its current diameter
dm:
where
kr is the particle evaporation coefficient. The evaporation law itself (and the D
2 name) arises from the following relation for
kr, determined as a function of change in the square of the particle diameter over a time increment Δ
t:
Given that, in practice, the exponent
np acting on the particle diameter in the evaporation law of Equation (29) may, in some instances [
22], be somewhat to significantly lower than two, the more general expression for the particle regression rate can be given as:
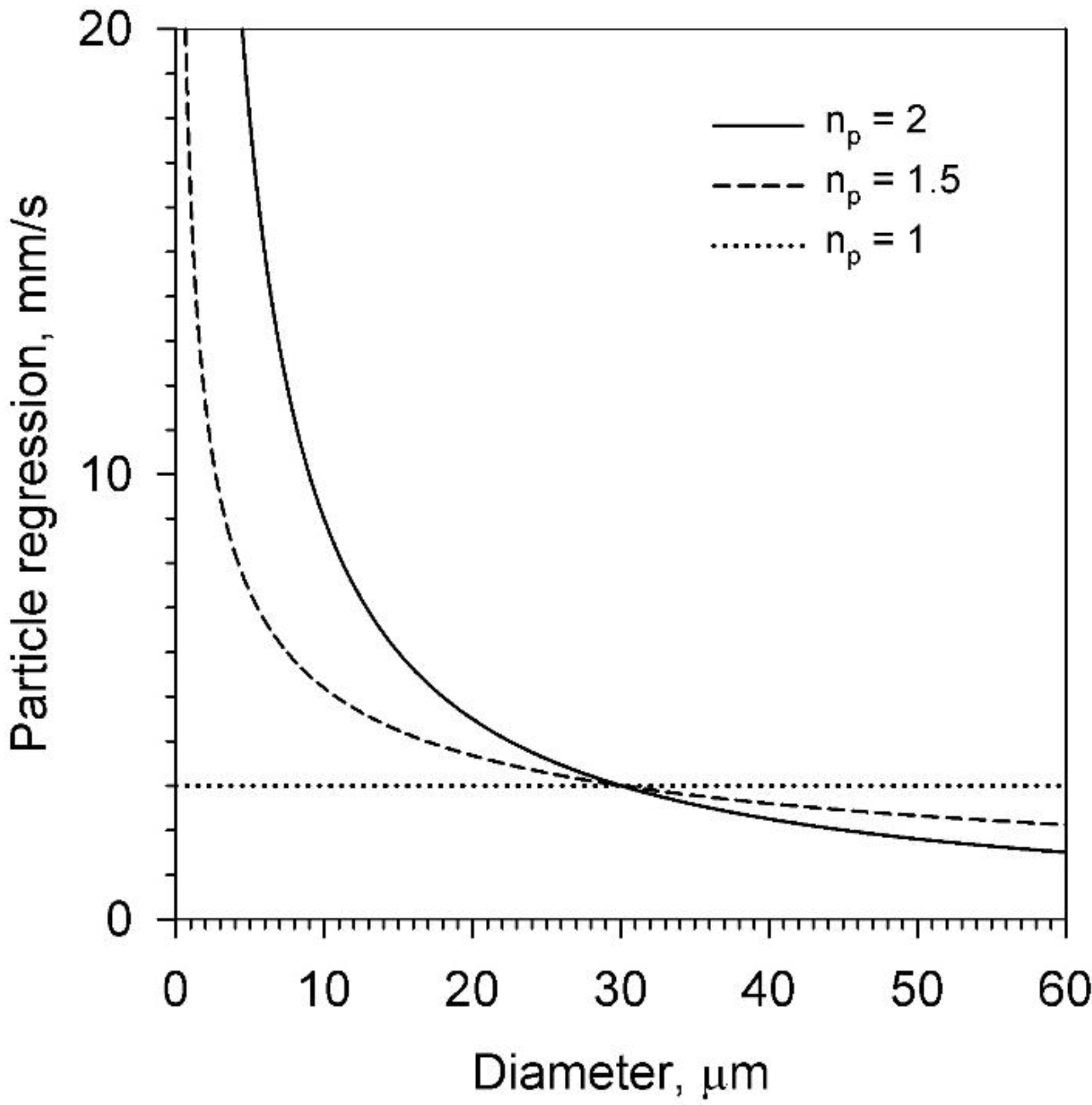
Figure 2 provides the particle regression rate as a function of its diameter, for the cases where
np is the nominal reference value of two (following the D
2 law),
np is a bit lower at a value of 1.5 and when
np is at its lower limit (uniform regression rate when
np = 1). In practice, one may observe the value of
np becoming lower as the particle diameter falls below a certain threshold size, in some cases with
np approaching unity at some point [
23]. The conversion of an aluminum particle to an effectively inert aluminum oxide (Al
2O
3) particle would potentially slow the regression rate down to zero. On the other hand, agglomeration of some molten particles within the propellant may take place near the burning surface, and thus, effectively larger particles, to some degree, may be entering into the central flow [
23]. That being said, results for the most part using the nominal evaporation law value of two for
np will be shown later in this paper, as a point of reference for future comparison. Other particle regression models, such as the semi-empirical model proposed by Beckstead [
22,
23], may prove more accurate when making direct comparisons to experimental firing data for some motors employing an aluminized propellant. For this study, the nominal aluminum particle regression rate is set as 3 mm/s when it is at a particle diameter of 30 m, as a point of reference, as reflected by
Figure 2.
Figure 2.
Predicted particle regression rate for np = 2 (D2 law, kr = 3.6 × 10−7 m2/s), for np = 1.5 (kr = 4.93 × 10−5 m1.5/s) and for np = 1 (kr = 6.0 × 10−3 m/s).
Figure 2.
Predicted particle regression rate for np = 2 (D2 law, kr = 3.6 × 10−7 m2/s), for np = 1.5 (kr = 4.93 × 10−5 m1.5/s) and for np = 1 (kr = 6.0 × 10−3 m/s).
3. Results and Discussion
The characteristics of the baseline reference motor for this study are listed in
Table 1. In the case where the given propellant characteristic was not directly measurable or available, such as mean propellant burning surface temperature
Ts, assigned values are estimates, for the most part taken from the open or confidential literature, for comparable propellants. Some of the structural properties listed in
Table 1, such as damping values, are estimations arising from previous studies involving comparisons to experimental vibration data. A nominal value of 2700 kg/m
3 is assigned for the aluminum particles’ density (Δ
m); one can note that, in practice, liquid (molten) aluminum has a somewhat lower density (around 2400 kg/m
3) should the particle’s core be liquid,
versus solid. In this regard, for some particles transferring from one state to another [
24], one can also note that aluminum oxide is significantly heavier, at 3800 kg/m
3. The motor, based in large part on a similar experimental motor [
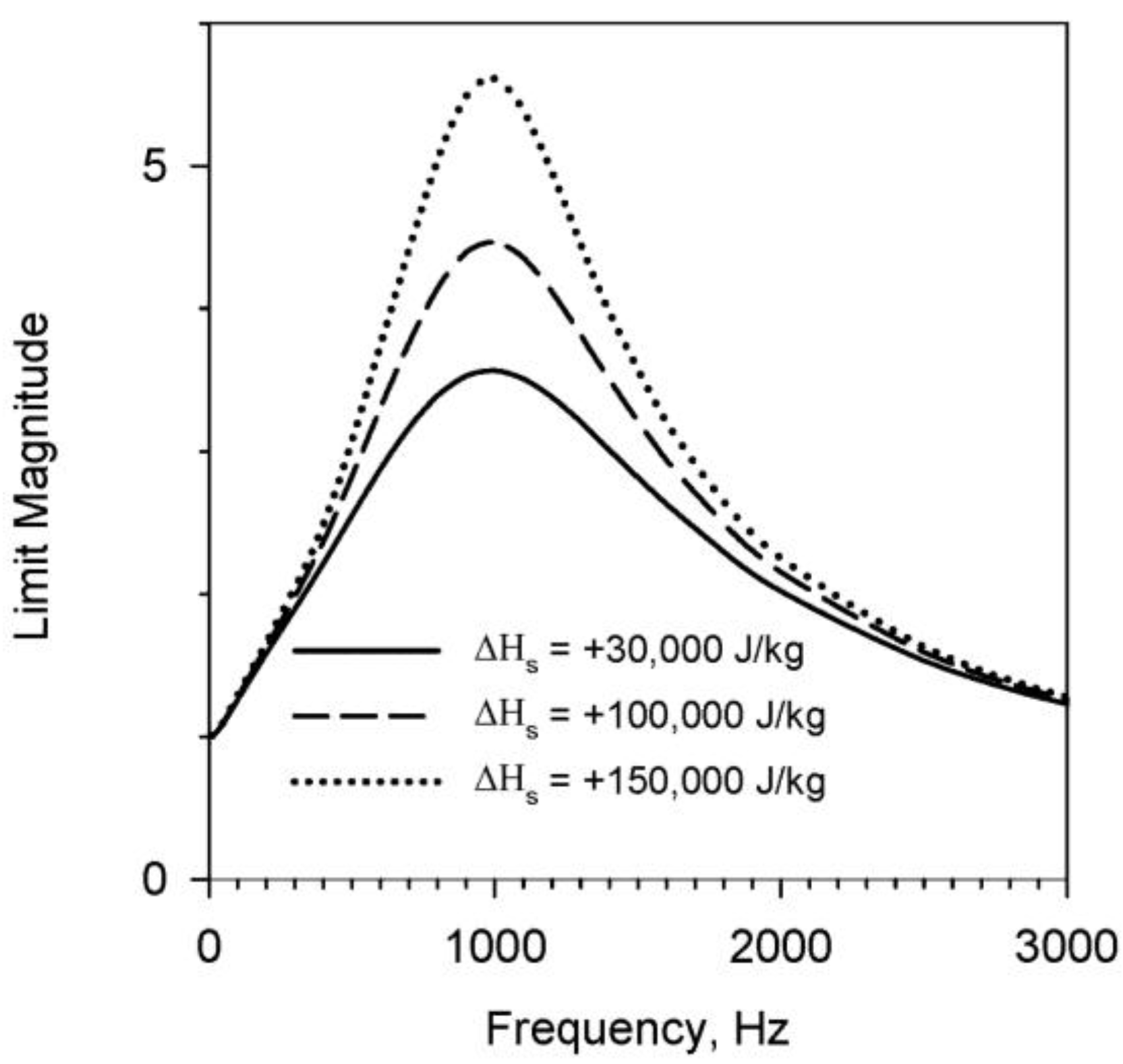
15], is a smaller cylindrical-grain design with an aluminum casing and static-test steel sleeve, with a relatively large length-to-diameter ratio. The motor at the time of pulsing has a moderate port-to-throat area ratio, with a considerable propellant web thickness remaining. The predicted frequency response for the AP/HTPB propellant at three different settings for the net surface heat release value may be viewed in
Figure 3 (positive value for Δ
Hs, exothermic heat release). The general response is given in terms of the non-dimensional limit magnitude,
Mℓ, defined by:
where the reference burning rate
rb,o in this case is the motor’s approximate mean burn rate at the point of pulsing (1.27 cm/s). The propellant’s resonant frequency
fr is set via the value of
Kb (20,000 s
−1) to be on the order of 1 kHz (a value within the range of what might be expected for this type of composite propellant at that base burning rate). This value for
fr is, in fact, relatively close to the fundamental longitudinal acoustic frequency
f1L of the combustion chamber, in providing examples later in this paper that are close to the worst-case scenario for susceptibility to axial combustion instability symptoms.
Table 1.
Reference motor characteristics.
Table 1.
Reference motor characteristics.
| Characteristic | Value |
|---|
| Propellant grain length, ࡁp | 52 cm |
| Initial port diameter, dp,i | 3.6 cm |
| Nozzle throat diameter, dt | 1.6 cm |
| Grain/nozzle-convergence length ratio, ࡁp/ࡁc | 16:1 |
| Propellant specific heat, Cs | 1500 J/kg·K |
| Propellant density, ρs | 1730 kg/m3 |
| Propellant thermal conductivity, ks | 0.4 W/m·K |
| Propellant thermal diffusivity, αs | 1.54 × 10−7 m2/s |
| Propellant flame temperature, Tf | 3000 K |
| Propellant surface temperature, Ts | 1000 K |
| Propellant initial temperature, Ti | 294 K |
| Gas specific heat, Cp | 1920 J/kg·K |
| Specific gas constant, R | 320 J/kg·K |
| Gas thermal conductivity, k | 0.2 W/m·K |
| Gas absolute viscosity, μ | 8.07 × 10−5 kg/m·s |
| Gas specific heat ratio, γ | 1.2 |
| De St. Robert exponent, n | 0.35 |
| De St. Robert coefficient, C | 0.05 cm/s·(kPa)n |
| Particle density, ρm | 2700 kg/m3 |
| Particle flame temperature, Tfp | 4200 K |
| Particle solid specific heat, Cm | 900 J/kg·K |
| Particle mass fraction, αp | 0% |
| Propellant elastic modulus, EA | 45 MPa |
| Propellant Poisson’s ratio, υA | 0.497 |
| Casing inner wall radius, rm | 3.24 cm |
| Casing wall thickness, hB | 0.127 cm |
| Casing material density, ρB | 2700 kg/m3 |
| Casing elastic modulus, EB | 80 GPa |
| Casing material Poisson’s ratio, υB | 0.33 |
| Sleeve wall thickness, hC | 0.47 cm |
| Sleeve material density, ρC | 7850 kg/m3 |
| Sleeve elastic modulus, EC | 200 GPa |
| Sleeve material Poisson’s ratio, υC | 0.30 |
| Casing/propellant radial damping ratio, ξR | 0.35 |
| Casing/propellant axial damping ratio, ξL | 0.10 |
Figure 3.
Frequency response of the reference propellant (Kb = 20,000 s−1; differing values for ΔHs; rb,o = 1.27 cm/s) in terms of the non-dimensional limit magnitude.
Figure 3.
Frequency response of the reference propellant (Kb = 20,000 s−1; differing values for ΔHs; rb,o = 1.27 cm/s) in terms of the non-dimensional limit magnitude.
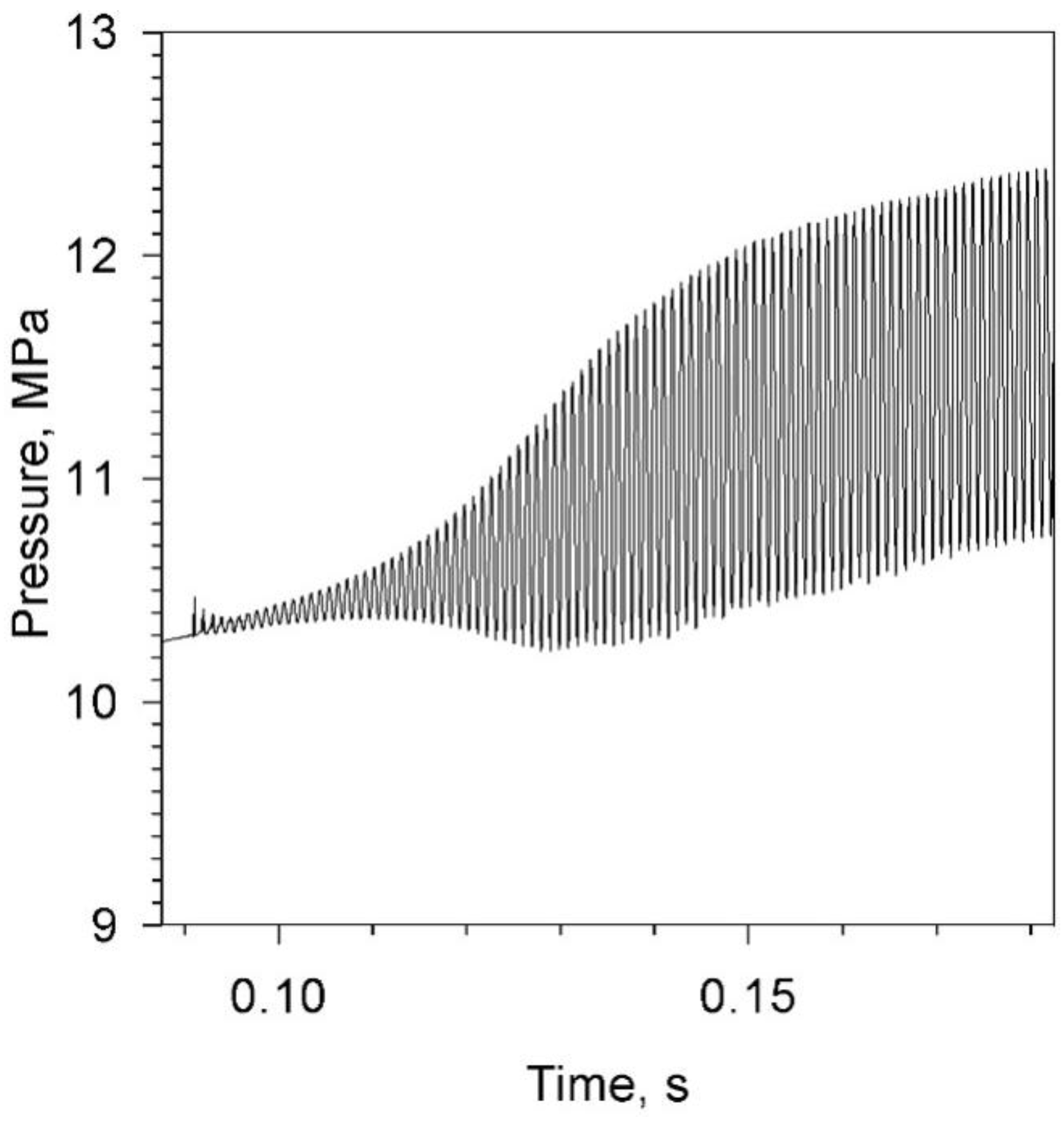
An initial pulsed-firing simulation run was completed as the starting reference for this study, in which no particles are present or no other suppression technique is applied. In
Figure 4 for head-end pressure
pc as a function of time, one can see that, at some point, the principal compression wave reaches its quasi-equilibrium strength from an initial disturbance pressure
∆pd of 2 atm, the sustained compression wave front arriving about every 1 ms, oscillating at the fundamental frequency
f1L of 1 kHz. The base pressure is not appreciably elevated over the nominal operating chamber pressure. The effect of normal acceleration on the burning process has been nullified for this simulation (in order to isolate the frequency-dependent Z-N combustion response as the predominant instability symptom driver), and this is certainly a factor in reducing the development of a dc shift (later results, with acceleration effects on burning included, will further illustrate this point). One can note that the limit pressure wave magnitude (
∆pw, peak-to-trough; here, 1.42 MPa at the reference time of 0.26 s) is decreasing gradually with time after first reaching its quasi-equilibrium level, as the cylindrical grain burns back and the base pressure rises.
Figure 4.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg; Δpd = 2 atm), no particles (αp = 0%), acceleration nullified.
Figure 4.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg; Δpd = 2 atm), no particles (αp = 0%), acceleration nullified.
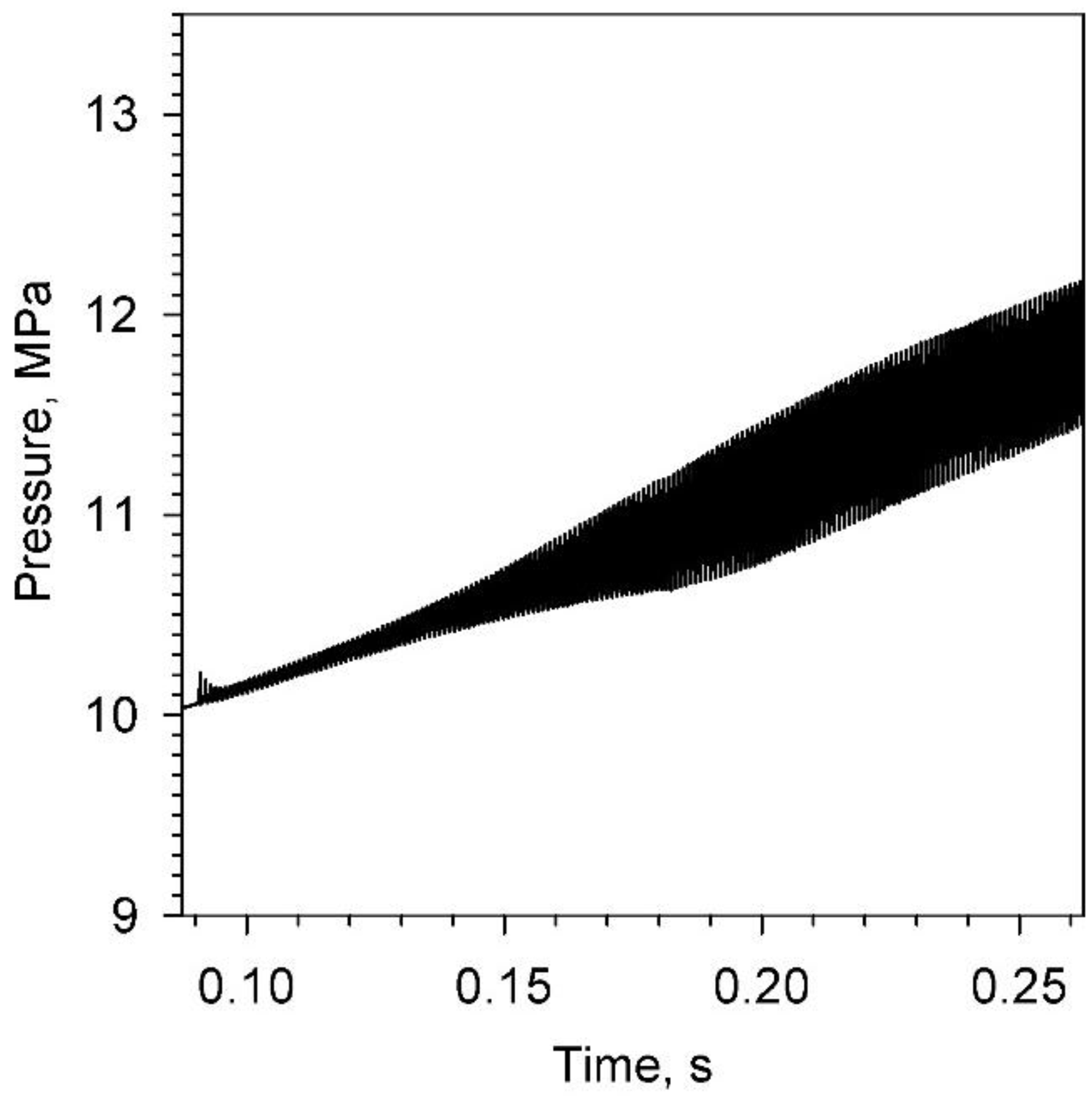
One can refer to
Figure 5 for the pressure-time profile for the same motor, but now with 10% particle loading (by mass) of reactive spherical aluminum particles having a starting diameter of 30 μm. The spherical particles regress in size at a rate governed by the D
2 law of Equation (28), as they enter and move downstream in the internal core flow. The value for the evaporation coefficient
kr is 3.6 × 10
−7 m
2/s, as estimated from the results reported in [
20], giving a regression rate of 3 mm/s when at a diameter of 30 m. Observing the results of
Figure 4, the suppression of axial wave development after an initial 2-atm pulse is moderately effective (the limit magnitude of the sustained pressure wave, at 0.26 s, is about 0.75 MPa (
∆pw), as compared to 1.42 MPa for the 0% loading case noted earlier (
∆pw,peak), giving a non-dimensional attenuation
Ma, defined by:
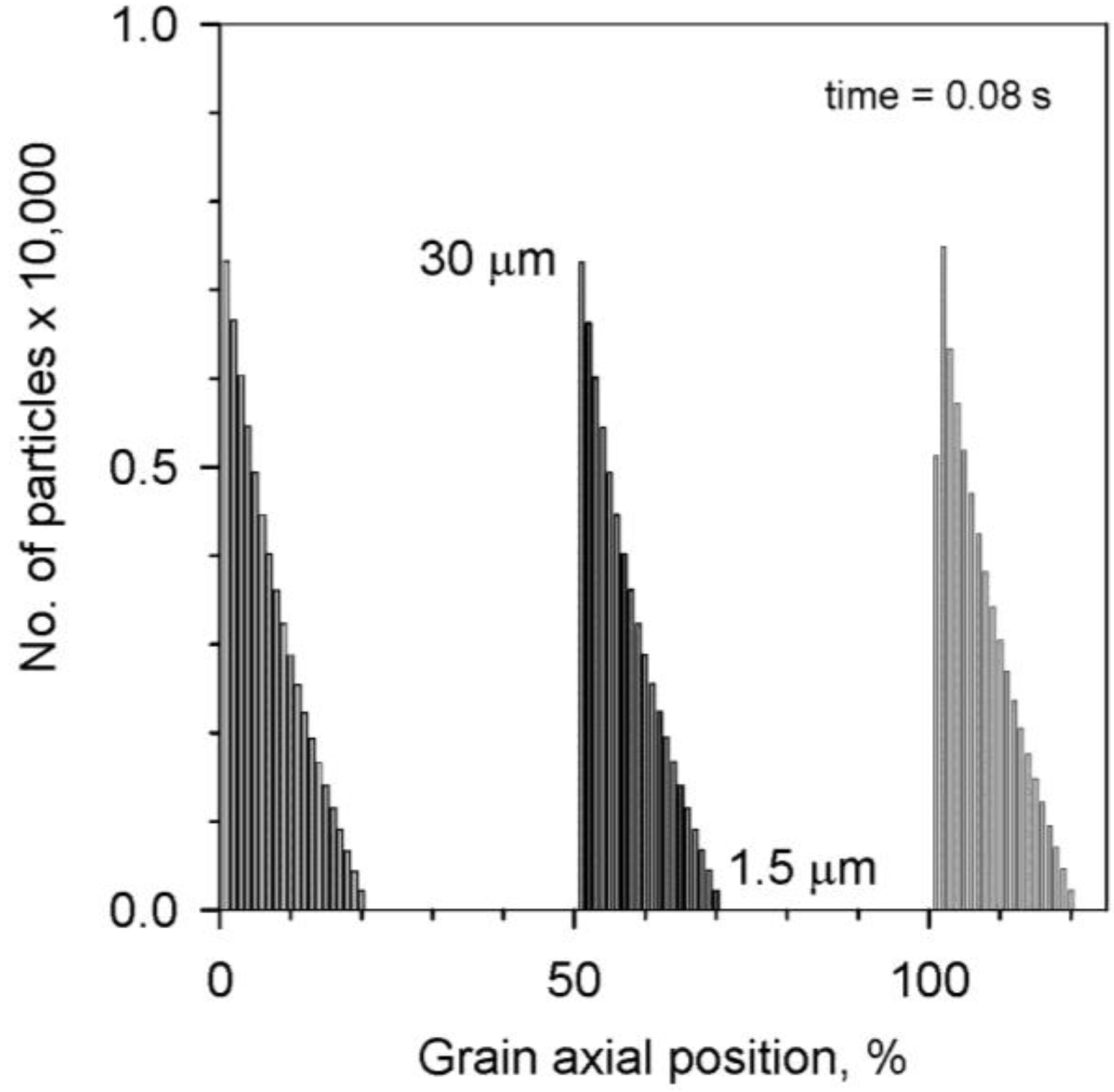
a value of 0.47, noting that a value of unity is a complete suppression. The particle size distribution before the introduction of the initial pressure pulse disturbance is provided in
Figure 6. As indicated by the graph, the particles are grouped into 1.5-m increments (30, 28.5, 27, …, 1.5) in the numerical model’s calculations, hence using 20 particle subsets. In the inert case, one would have around 140,000 particles in a given cell, while here, one notes that there are around 70,000 particles per cell, or a loss of some 70,000 particles per cell due to regression (
i.e., about half of the ideal total). One can note that the best case for suppression by an inert particle is from diameters from around 10 to 20 m, to give an
Ma of around 0.97 at a 5% loading [
7]. The choice of 30 m for the starting reactive particle diameter was made in light of this, given the regression in size that will be experienced by each particle while moving through the active system.
Figure 5.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 10%, dm,o = 30 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration nullified.
Figure 5.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 10%, dm,o = 30 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration nullified.
Figure 6.
For the simulated firing of
Figure 5, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.
Figure 6.
For the simulated firing of
Figure 5, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.
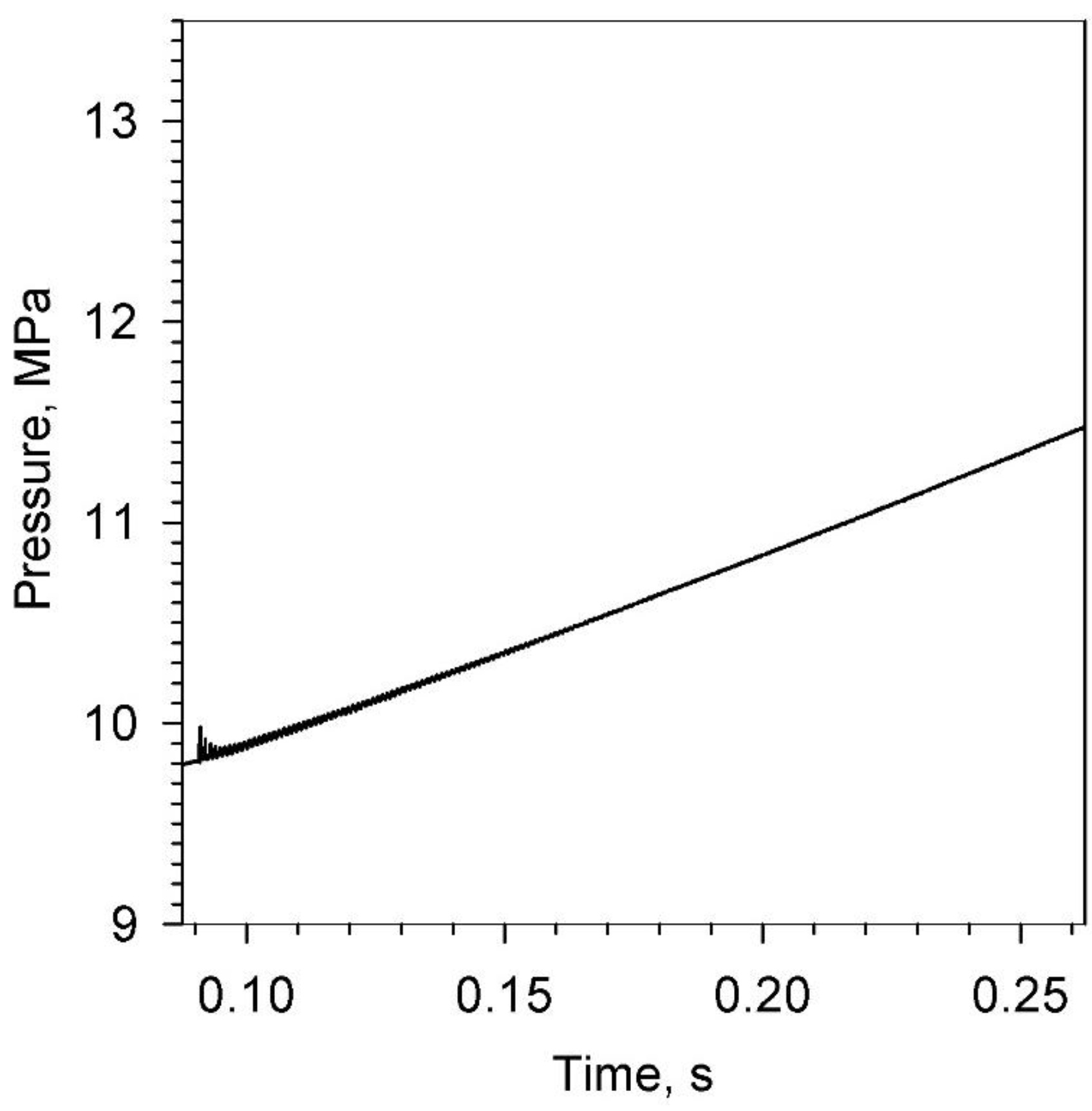
Figure 7 illustrates the pressure-time profile for the same motor, but now with 20% particle loading (by mass) of a single set of spherical aluminum particles having a 30-μm diameter initially, with the spherical particles regressing in size at a rate governed by the D
2 law noted above. Suppression of axial wave development after an initial 2-atm pulse is very effective (the limit magnitude of the sustained pressure wave, at the reference time of 0.26 s, is about 0.012 MPa, as compared to 1.42 MPa for the 0% loading case noted earlier, giving a non-dimensional attenuation
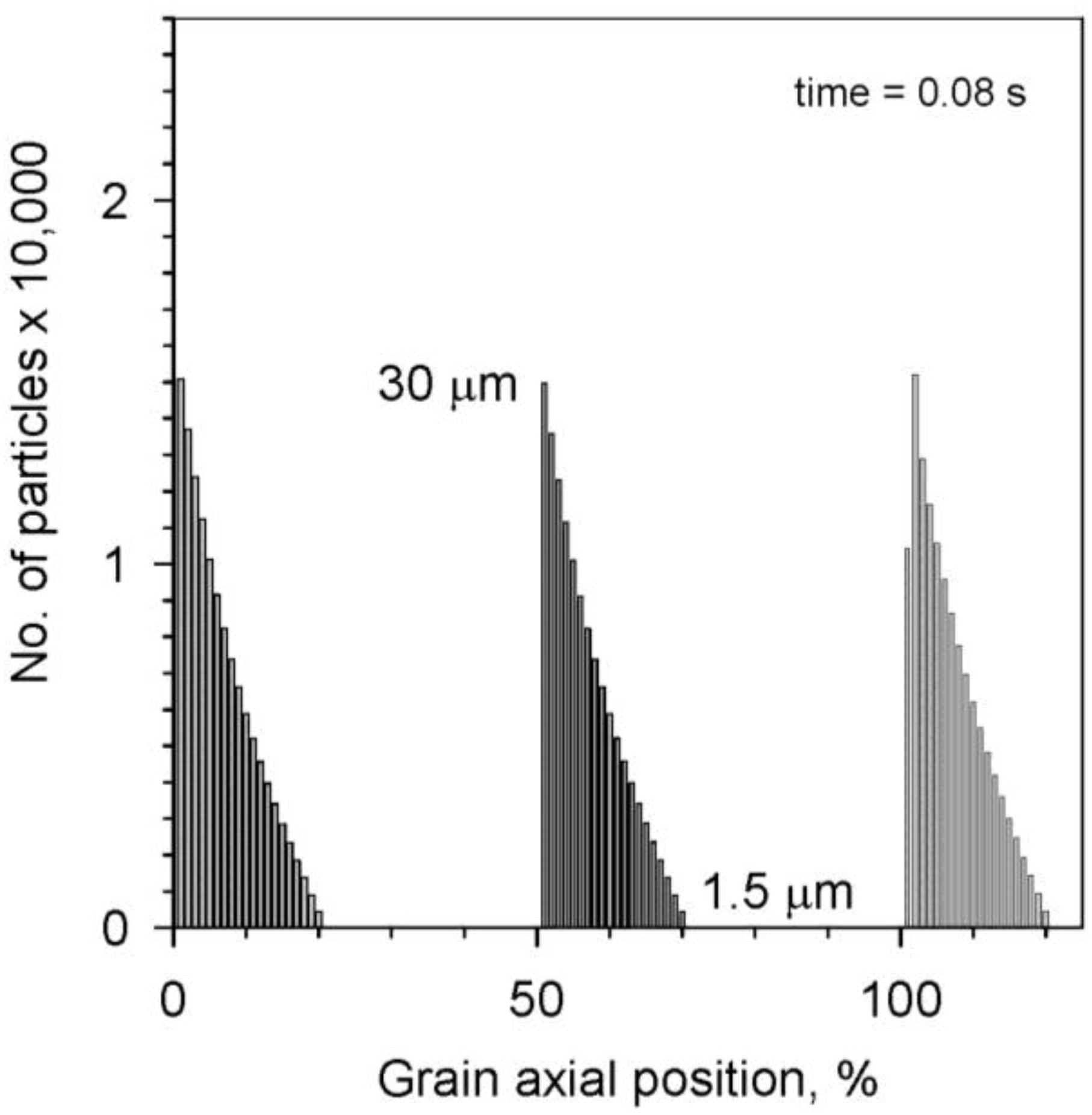
Ma value of 0.99). The particle size distribution before the introduction of the initial pressure pulse disturbance is provided in
Figure 8.
Figure 7.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 20%, dm,o = 30 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration nullified.
Figure 7.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 20%, dm,o = 30 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration nullified.
Figure 8.
For the simulated firing of
Figure 7, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.
Figure 8.
For the simulated firing of
Figure 7, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.
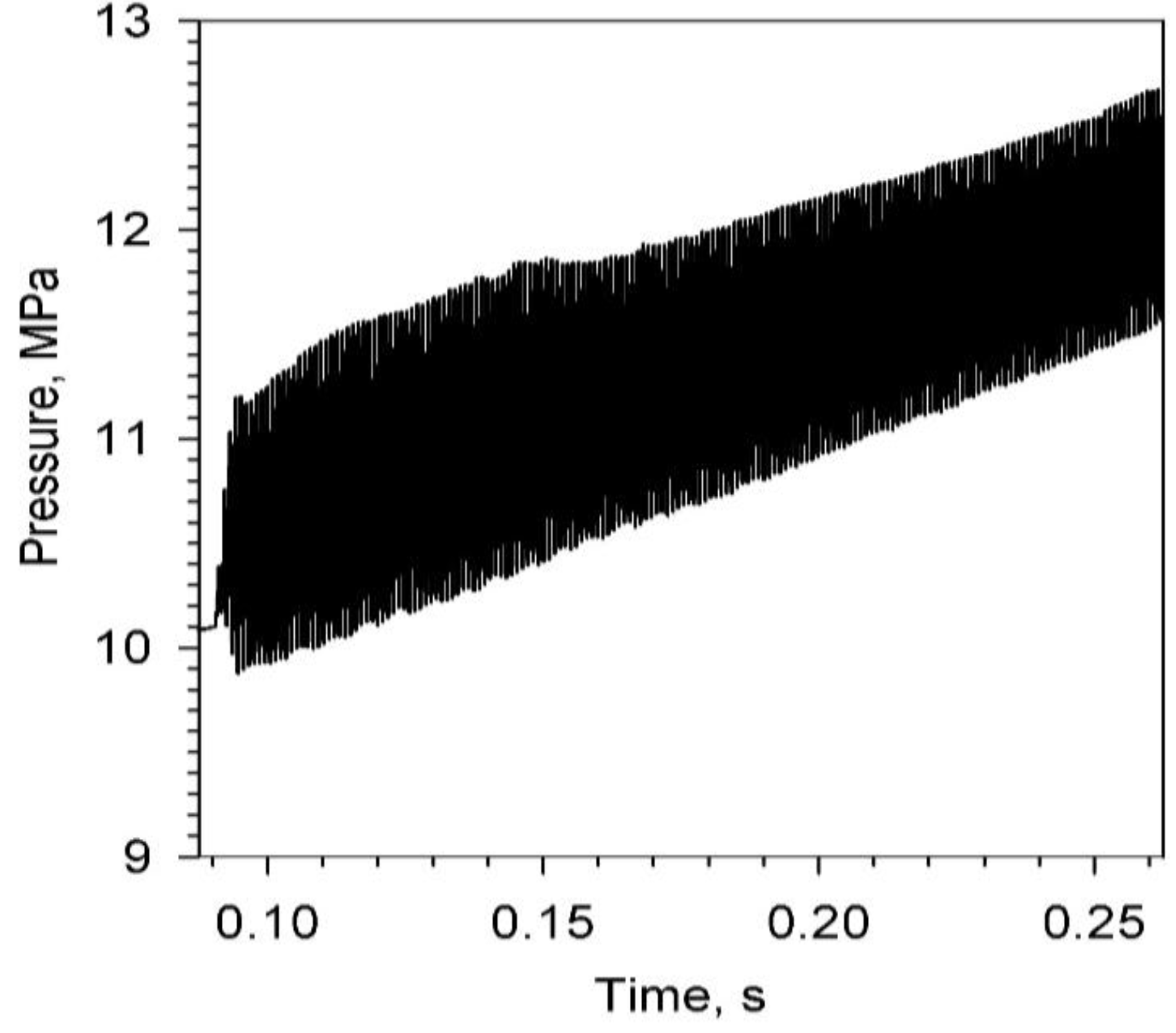
At this juncture, the influence of normal acceleration on the burning process will be considered. Referring to
Figure 9, allowing for the effect of vibration-induced acceleration on combustion in addition to the transient combustion response contribution, one has a very active motor in the absence of particles in the flow, with a large limit magnitude (around 10.2 MPa at 0.26 s) for the now shock-fronted axial pressure wave moving back and forth within the chamber, and a visible dc shift is present.
Figure 9.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg; Δpd = 2 atm), no particles (αp = 0%), acceleration active.
Figure 9.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg; Δpd = 2 atm), no particles (αp = 0%), acceleration active.
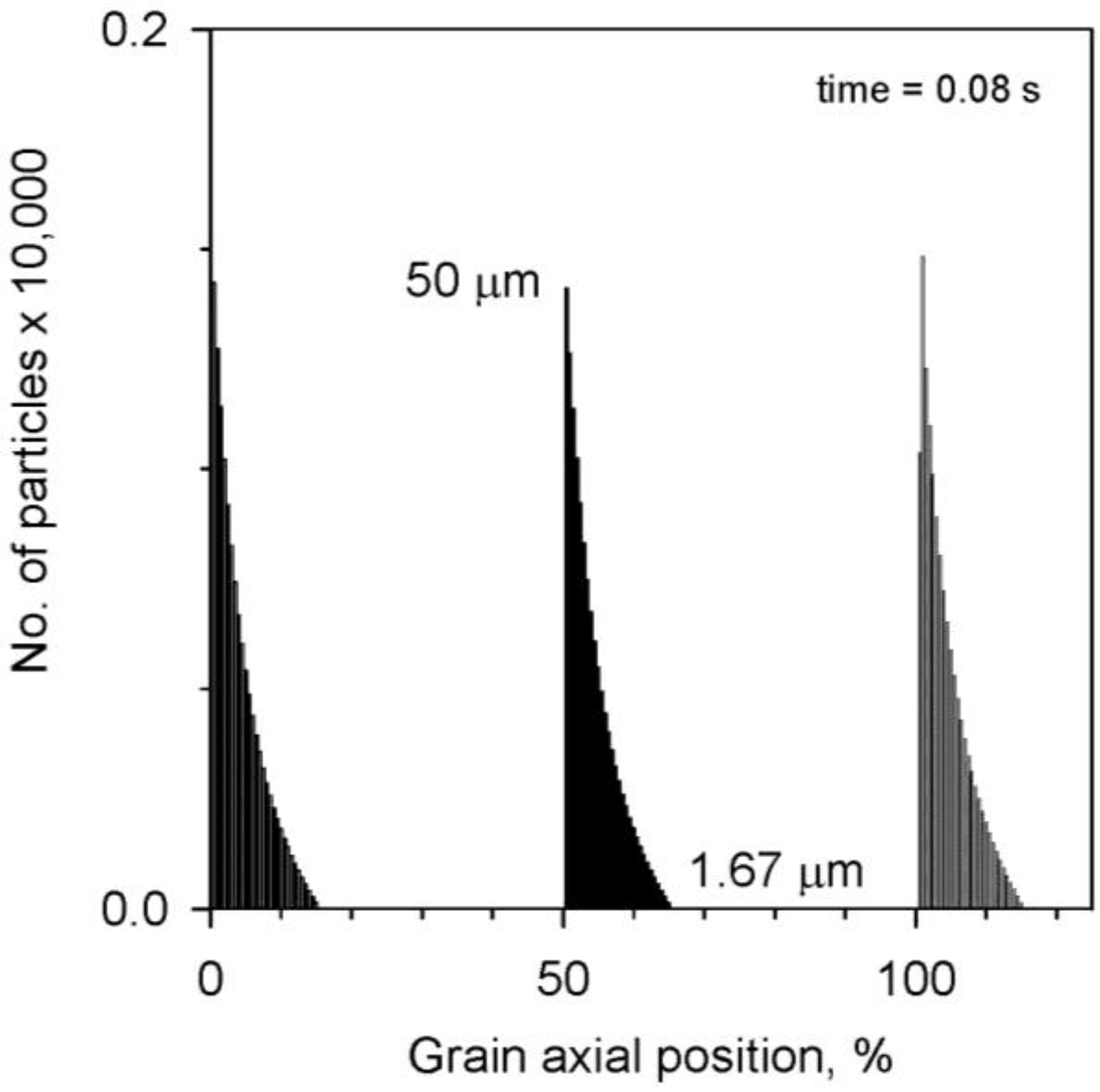
Employing reactive aluminum particles diminishing in size via the D
2 law, one can observe in
Figure 10 the predicted pressure-time profile for the same motor, but now with 5% particle loading (by mass) of reactive spherical aluminum particles having a starting diameter of 50 μm. The starting particle size is substantially larger than the previous case (30 μm), to allow for more effective suppression over the course of the continually diminishing reactive particle’s effective lifetime in the combustion chamber (inert particles are comparably effective in the 10- to 35-μm size range [
7], albeit at a lower loading percentage). The limit magnitude of the sustained axial pressure wave, at 0.26 s, is about 1.11 MPa, which corresponds to an
Ma value of 0.89, which is fairly effective. The particle size distribution before the introduction of the initial pressure pulse disturbance is provided in
Figure 11. As indicated by the graph, the particles are grouped into 1.67-m increments (50, 48.33, 46.67, …, 1.67) in the numerical model’s calculations, hence using 30 particle subsets.
Figure 10.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 5%, dm,o = 50 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration active.
Figure 10.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 5%, dm,o = 50 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration active.
Figure 11.
For the simulated firing of
Figure 10, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.
Figure 11.
For the simulated firing of
Figure 10, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.
Figure 12 illustrates the predicted pressure-time profile for a higher loading of 15% of the 50-μm reactive particles. The suppression of axial pressure wave development is considerably improved overall, but in this case, the system appears to be transitioning in a bipolar manner from one quasi-equilibrium wave activity level to another in a cyclic, but progressively decaying fashion, as one moves further in time into the simulated firing. At higher loading percentages, the qualitative pattern persists, albeit with the peak magnitudes of each cycle correspondingly getting smaller relative to that seen at lower particle loading percentages. The particle size distribution before the introduction of the initial pressure pulse disturbance is provided in
Figure 13.
Figure 12.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 15%, dm,o = 50 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration active.
Figure 12.
Predicted head-end pressure-time profile, reference motor (Kb = 20,000 s−1, ΔHs = 150,000 J/kg, αp = 15%, dm,o = 50 µm; Δpd = 2 atm), single regressing particle set (D2 law, kr = 3.6 × 10−7 m2/s), acceleration active.
Figure 13.
For the simulated firing of
Figure 12, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.
Figure 13.
For the simulated firing of
Figure 12, the particle size distribution in the element, at different positions along the propellant grain, before the introduction of the initial pressure pulse disturbance.