Finite Action-Set Learning Automata for Economic Dispatch Considering Electric Vehicles and Renewable Energy Sources
Abstract
:1. Introduction
2. Models of the Power Demand and Supply of EVs, Wind Power, and Load
2.1. Modeling of the Power Demand and Supply of EVs
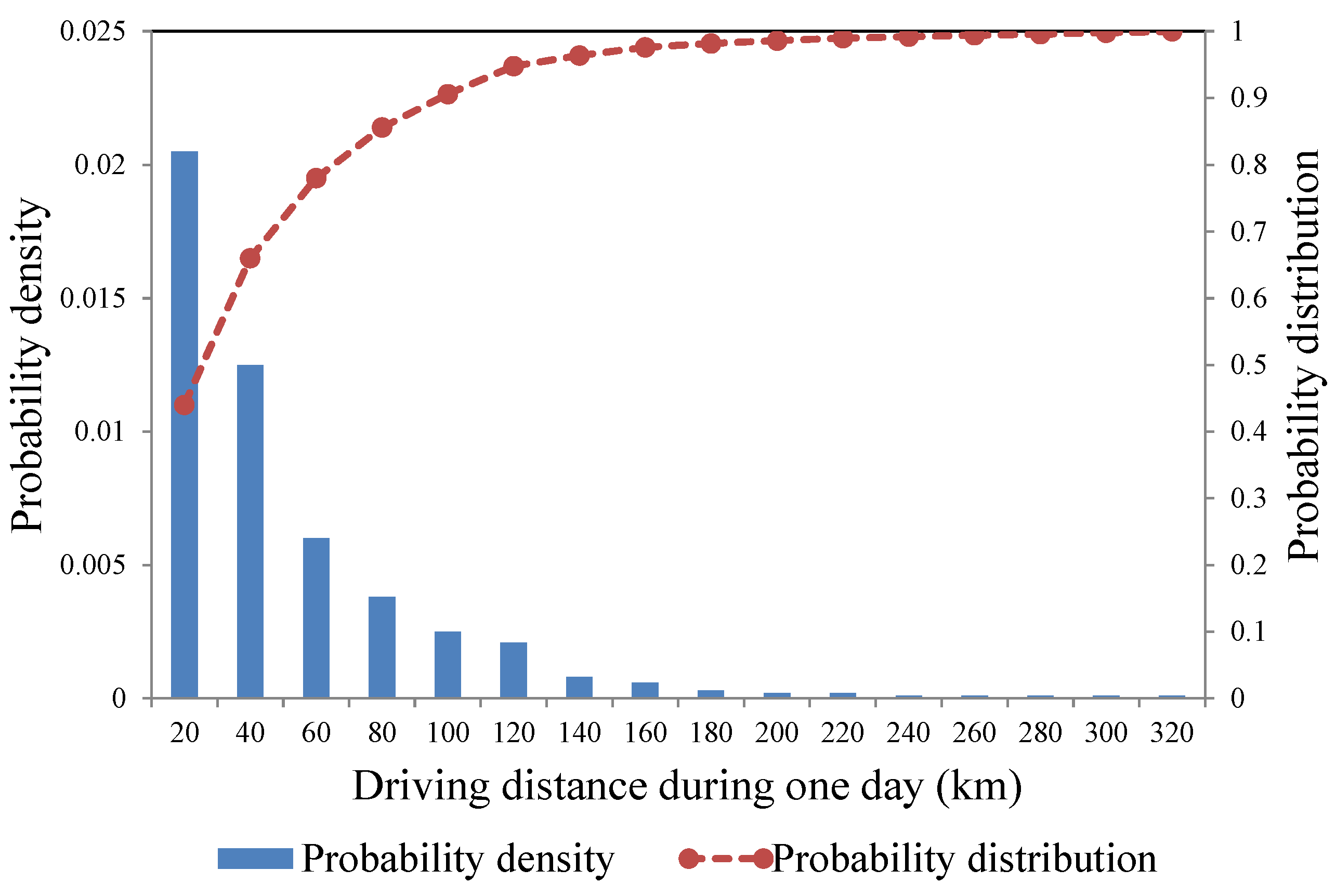
- The energy an EV has consumed is in direct proportion to the distance it has traveled.
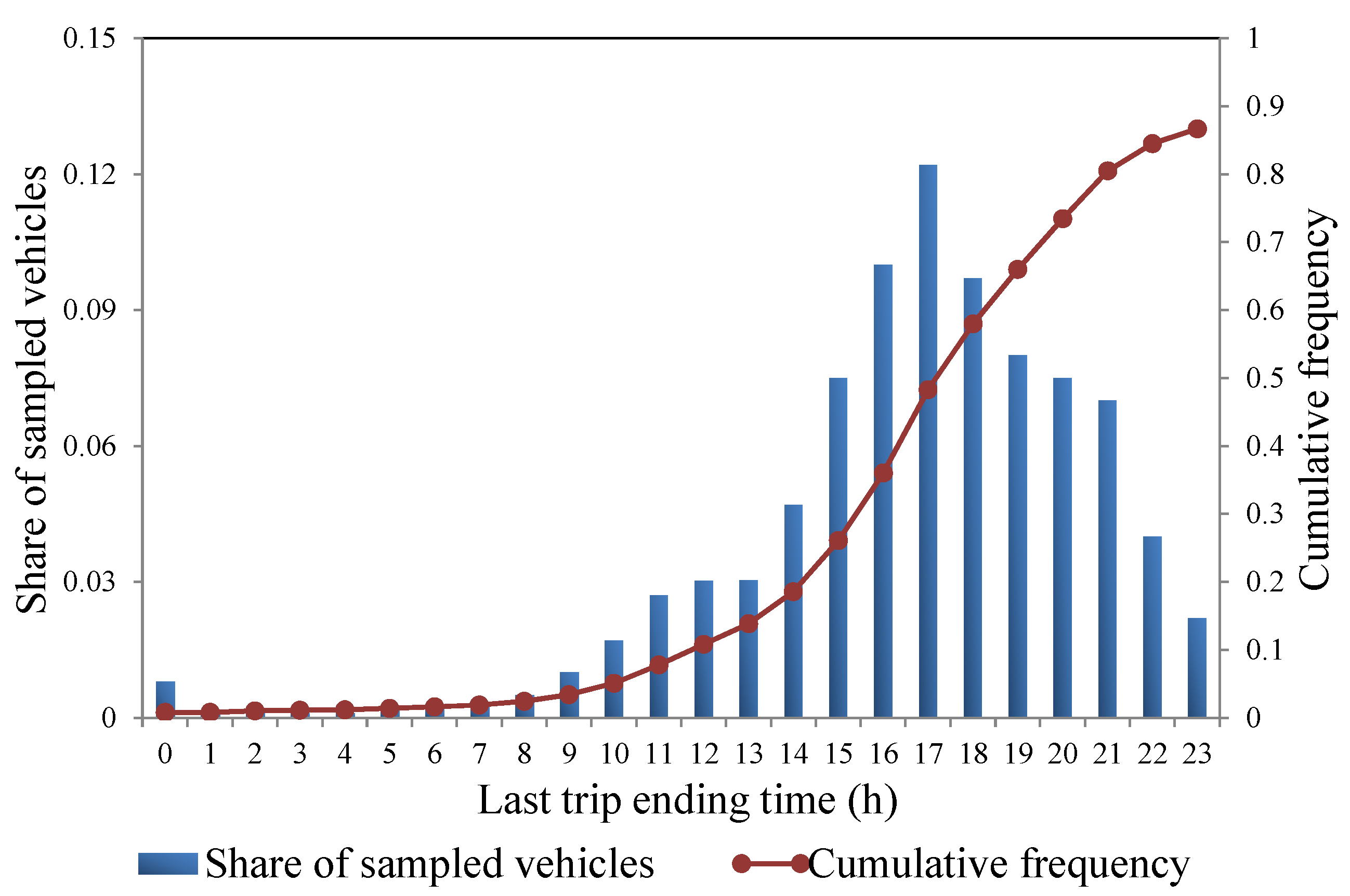
- The probability distributions of an EV’s arrival time and the distance the EV has traveled are derived from driving pattern data collected in the National Household Transportation Survey (NHTS) [26].
- The peaks of battery exchange demand are during the morning rush hour, lunch time, and afternoon rush hour.
2.1.1. Power Demand and Supply of NI EVs
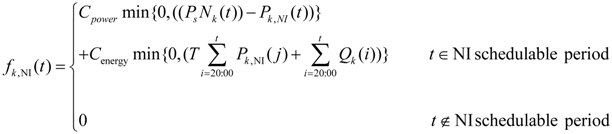
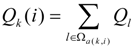
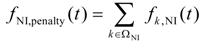
2.1.2. Power Demand/Supply of BE EVs
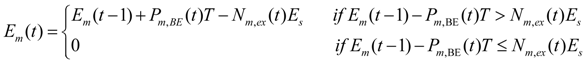
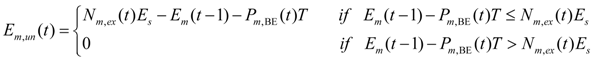
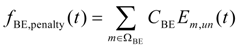
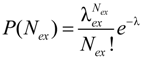
2.2. Modeling of Regular Load
2.3. Modeling of Wind Power
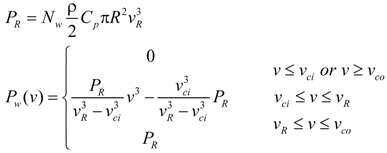
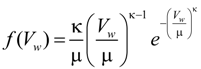
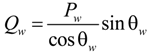
3. Economic Dispatch Formulation
3.1. Objective Function
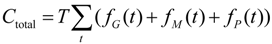
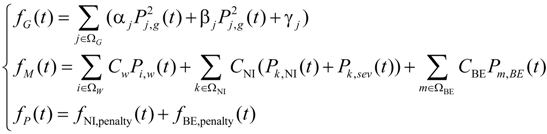
3.2. Constraints
- Power balance constraint:
- Generation limitation constraint:
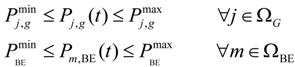
- Power line transmission limitation constraint:
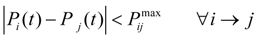
- Local voltage limitation constraint:
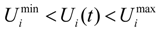
- Normal interaction station operational constraint:
- Battery exchange station operational constraint:


3.3. ED Problem Formulation
4. Description of the Proposed Approach
4.1. The FALA Method

4.2. FALA-Based Approach for the ED Problem

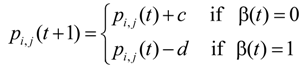
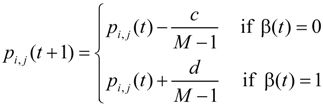
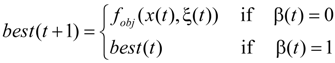
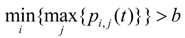
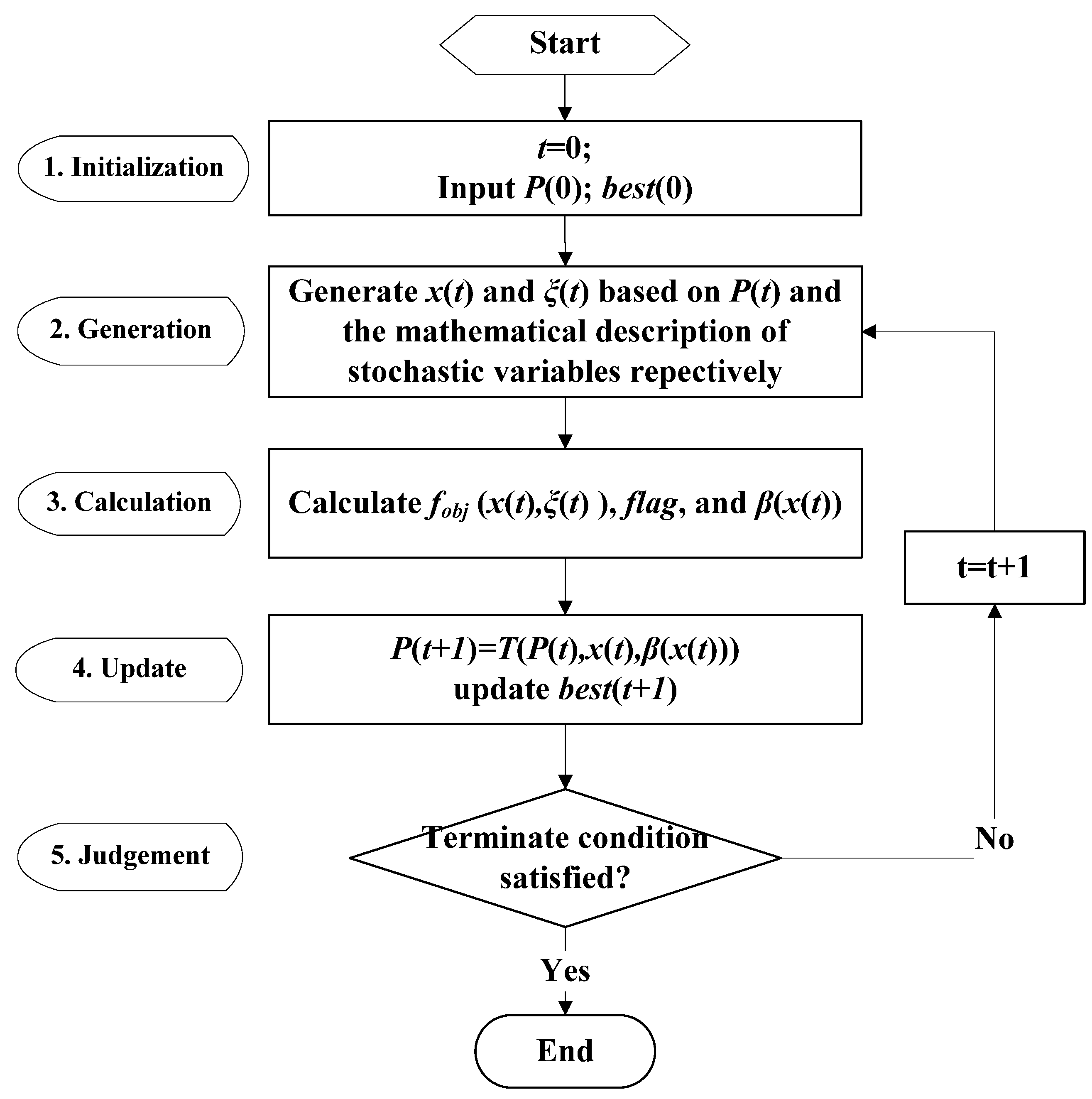
5. Case Studies
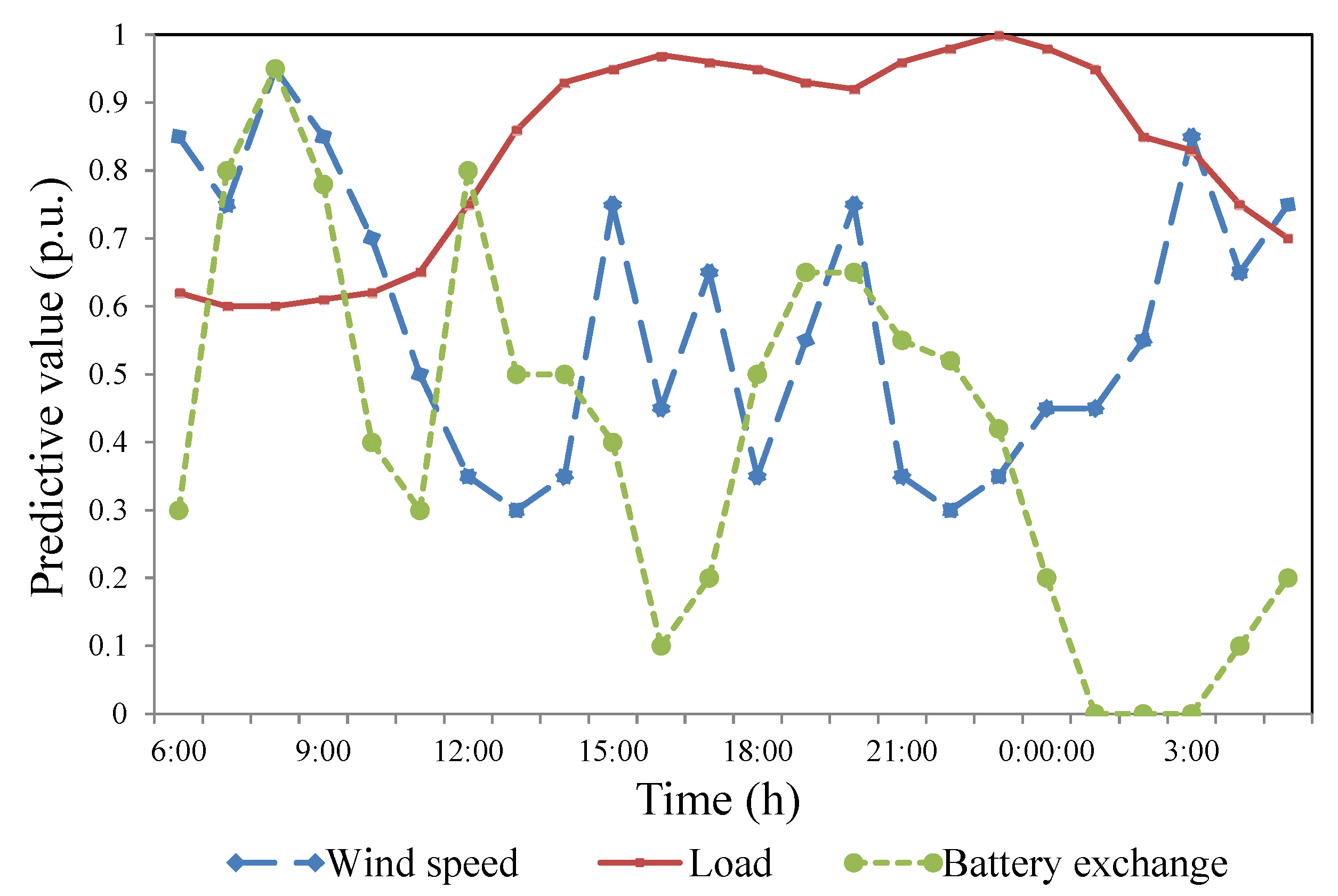
| Bus Number | α i (Ұ) | β i (Ұ/MW) | γi (Ұ/MW2) |  (MW) (MW) |  (MW) (MW) |
|---|---|---|---|---|---|
| 1 | 0.124 | 12.4 | 0 | 0 | 80 |
| 2 | 0.1085 | 10.85 | 0 | 0 | 80 |
| 22 | 0.3875 | 6.2 | 0 | 0 | 50 |
| 27 | 0.5171 | 20.15 | 0 | 0 | 55 |
| 23 | 0.155 | 18.6 | 0 | 0 | 30 |
| 13 | 0.155 | 18.6 | 0 | 0 | 40 |
5.1. Parameter Settings
- Step 1.
- The stochastic problem was transformed into a deterministic problem using CCP (see [32] for details). The parameters were set as: N = 10, N’ = 8.
- Step 2.
- The transformed problem was solved using the PSO algorithm (see Equation (6) in [33]). The parameters were set as: Popsize = 20, φic = 0.5, and φ1 = φ2 =2.
5.2. Results and Analysis
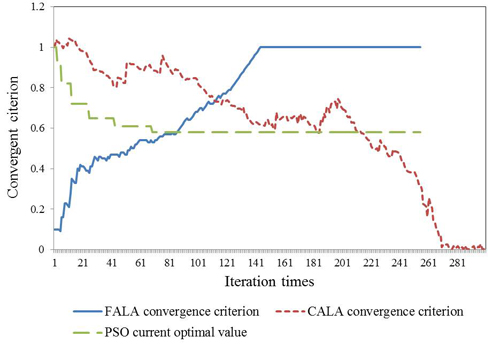
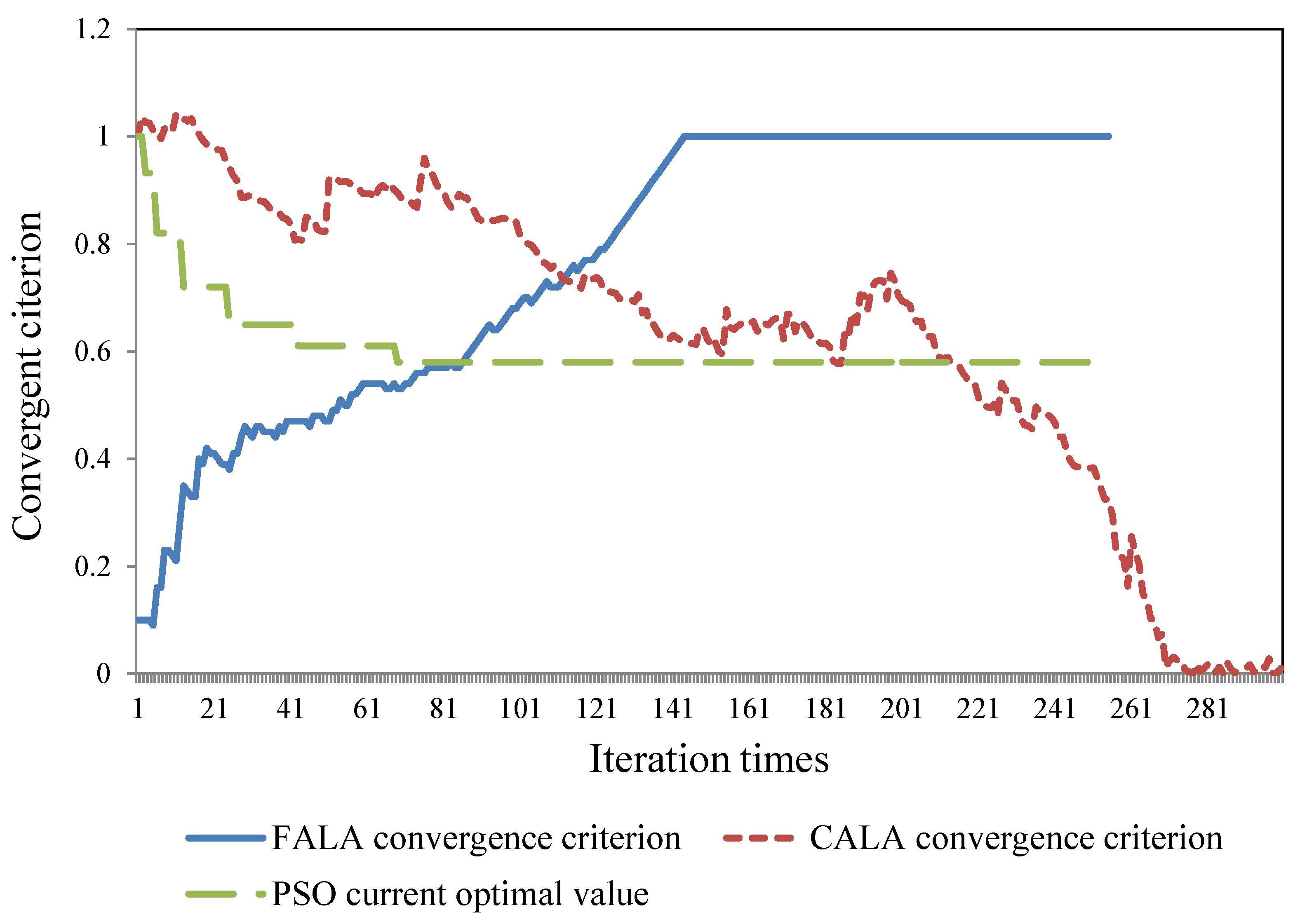
5.2.1. Comparison of Convergences
- (1)
- The convergence criterion of the FALA algorithm is given in Equation (35). It converged after approximately 150 iterations. In the first 30 iterations, the action probability vector changed rapidly because “best(t)” was not so small that the inequality constraint in Equation (36) was easily satisfied. During iterations 40–110 the action probability vector changed slowly as “best(t)” became smaller. After 120 iterations, the action probability vector had changed dramatically and there was a high probability that the control variables were selected in the optimal intervals, so the inequality in Equation (36) was easily satisfied. These results show that this algorithm is steady, and that, once converged, the action probability vector does not fluctuate:best(t) > fobj(x(t),ξ(t))
- (2)
- The CALA algorithm converged after approximately 270 iterations for this ED problem. The convergence criterion of the CALA algorithm fluctuated more dramatically than that of FALA algorithm, because it had the possibility to increase (opposite to the converging direction) even though the response of the current solution was good enough.
- (3)
- The characteristic curve of the PSO algorithm shows the change of the current global optimal value with each iteration. The value was transformed using:best(t)′ = exp(100 × (best(t) − best(1))/best(1))
5.2.2. Comparison of Computation Efficiency
| Algorithm | f0bj Calculation Times Each Iteration | Iteration Times | Total Times of f0bj Calculation | Computing Time(s) |
|---|---|---|---|---|
| FALA | 1 | 160 | 160 | 239 |
| CALA | 2 | 270 | 540 | 815 |
| PSO | 200 | 70 | 14,000 | 15,872 |
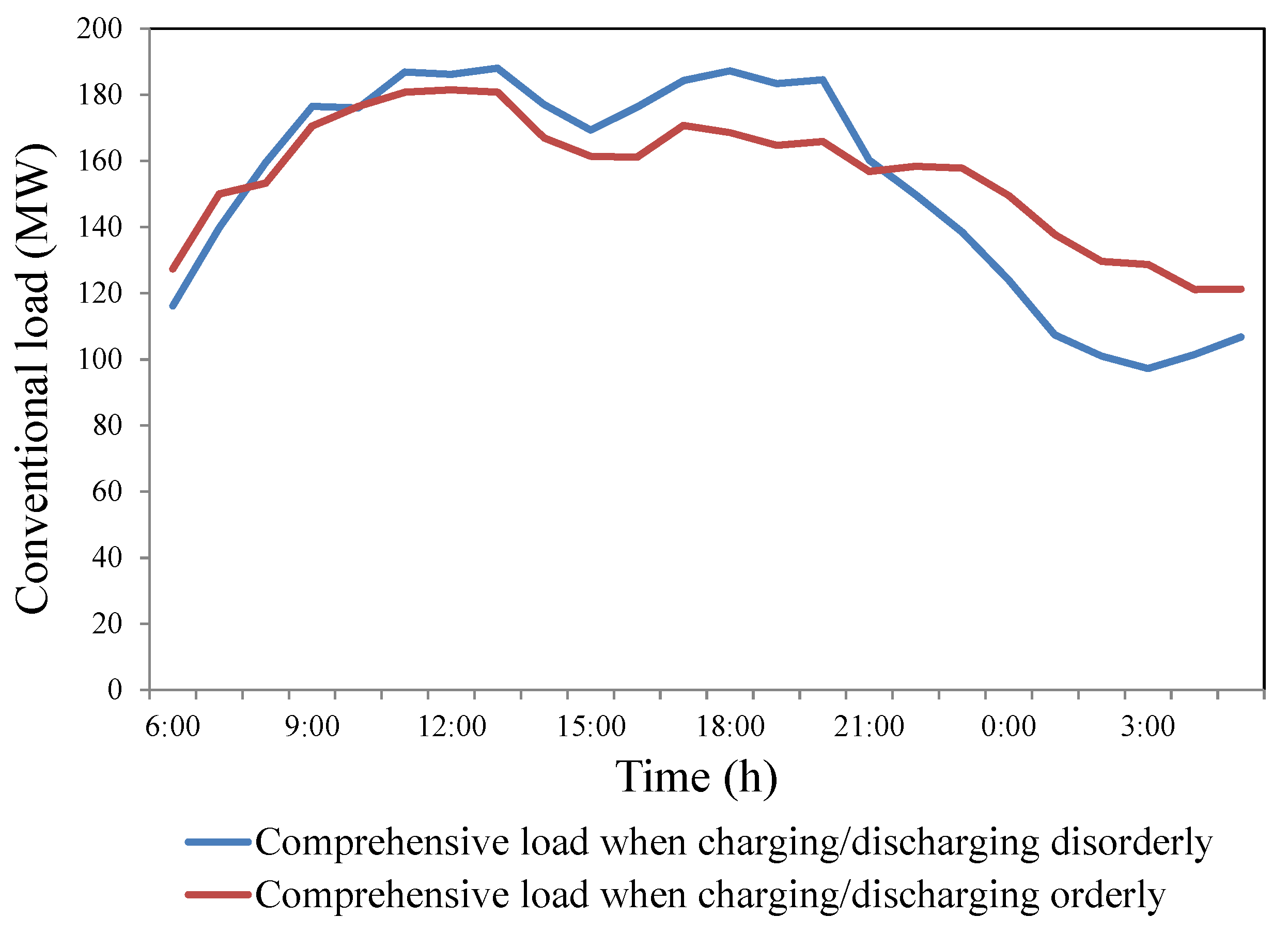
5.2.3. Comparison of the Solution Quality
| Algorithm | Mean Cost (Ұ) | Mean Diff (MW) | Mean Diff When Charging/Discharging Disorderly (MW) |
|---|---|---|---|
| FALA | 57,939 | 62.53 | 92.02 |
| CALA | 57,925 | 60.48 | 91.62 |
| PSO | 57,970 | 63.91 | 94.80 |
6. Conclusions
Nomenclature
| EV | Electrical vehicle |
| NI | Normal interaction model of EVs |
| BE | Battery exchange model of EVs |
| Ωa | Set of EVs arriving at the NI station |
| ΩNI ΩW ΩG | Set of buses connected with NI stations, wind farms and conventional generators |
| Nw | Number of wind turbines in a wind farm |
| Nk,s | Total number of EVs signing the dispatch agreement in the NI station k |
| X | Set of control variables |
| ξ | Set of random variables |
| Ps | Maximum power of EV charging/discharging |
| T | Time interval between operations |
| Cpower, Cenergy | Penalty parameters of unsatisfied battery charging demand |
| CBE | Penalty parameter of the unsatisfied battery exchange demand |
| Es | Battery capacity of a single EV |
| λex | Predictive value of the battery exchange demand |
| PR | Rated power of a wind farm |
| ρ | Air density |
| Cp | Energy conversion efficiency of a wind farm |
| R | Radius of the wind turbine blade |
| vR vci vco | Rated wind speed, cut-in wind speed and cut-out wind speed |
| μ | Predicted value of the wind speed |
| κ | Shape parameter of Weibull distribution |
| θw | Power factor of a wind farm |
| αj, βj, γj | Power generation cost parameters of a conventional generator |
| Cw | Cost of wind power generation per MW |
| CNI | Cost of interaction power between NI EVs and the power system per MW |
| CBE | Cost of interaction power between NI EVs and the power system per MW |
 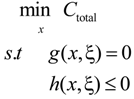 | Lower and upper generation limits of a conventional generator |
  | Lower and upper limits of interactive power of the battery exchange stations |
  | Lower and upper limits of the voltage of bus i. |
| Qev | Battery capacity of a EV |
 | Maximum energy storage capacity of the BE station m |
| Ql | Energy left in the battery of EV l |
| Qk | Total energy in the batteries of the EVs that arrive in the NI station k |
| Nk | Number of EVs that finish the last trip in the NI station k |
| Em | Stalled energy of the station m |
| Pm,BE | The power transmission between BE station m and the power system |
| Nm,ex | Number of the EVs that need battery exchange |
| Em,un | Unsatisfied battery exchange demand |
| Ctotal | Total operational cost of the whole sampling period |
| Pi,w | Wind farm output of bus i |
| Pk,sev | Interactive power between the power system and the NI EVs not signing the dispatch agreement in NI station k |
| PW PG PL | Output of the wind farms, output of conventional generators and power Loss through the transmission lines |
| PEV | Total interactive power between the power system and the EV installation |
| Pi | Injection power of bus i |
 | Maximum power transmission of the power line that connects bus i and bus j |
| Ui | Voltage of bus I |
| Em | Stalled energy of the BE station m |
| Pk,NI | Interactive power between the system and the NI EVs signing the user agreement in bus k |
| Pj,g | Output of a conventional generator of bus j, j ≠ 1. |
| fk,NI () | Penalty function of the NI station of bus k |
| fNI,penalty () | Penalty function of all NI stations |
| fBE,penalty () | Penalty function of all BE stations |
| fG() fM () fP() | Fuel cost, maintenance cost and penalty cost of the system |
| fobj() | Objective function of the optimization model |
| g(·,·) h(·,·) | Equality and inequality constraint function |
| F() | Reward function for the automation |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Juul, N.; Meibom, P. Road transport and power system scenarios for Northern Europe in 2030. Appl. Energy 2012, 92, 573–582. [Google Scholar] [CrossRef]
- Duvall, M.; Knipping, E.; Alexander, M. Environmental Assessment of Plug-in Hybrid Electric Vehicles; Volume 1, Nationwide Greenhouse Gas Emissions; Electric Power Research Institute: Palo Alto, CA, USA, 2007. [Google Scholar]
- Liu, W.; Lund, H.; Mathiesen, B.V. Large-scale integration of wind power into the existing Chinese energy system. Energy 2011, 36, 4753–4760. [Google Scholar] [CrossRef]
- Mathiesen, B.V.; Lund, H.; Karlsson, K. 100% Renewable energy systems, climate mitigation and economic growth. Appl. Energy 2011, 88, 488–501. [Google Scholar] [CrossRef]
- Li, J.F.; Shi, P.F.; Gao, H. Wind Power Development Report in China; Hainan Press: Haikou, China, 2010. [Google Scholar]
- Fernandez, L.P.; San Roman, T.G.; Cossent, R.; Domingo, C.M.; Frias, P. Assessment of the impact of plug-in electric vehicles on distribution networks. Power Syst. IEEE Trans. 2011, 26, 206–213. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. Power Syst. IEEE Trans. 2010, 25, 371–380. [Google Scholar] [CrossRef] [Green Version]
- Bessa, R.J.; Matos, M.A. Economic and technical management of an aggregation agent for electric vehicles: A literature survey. Electr. Power Eur. Trans. 2012, 22, 334–350. [Google Scholar] [CrossRef]
- Rogers, K.M.; Klump, R.; Khurana, H.; Aquino-Lugo, A.A.; Overbye, T.J. An authenticated control framework for distributed voltage support on the smart grid. Smart Grid IEEE Trans. 2010, 1, 40–47. [Google Scholar] [CrossRef]
- Lu, M.-S.; Chang, C.-L.; Lee, W.-J.; Wang, L. Combining the wind power generation system with energy storage equipment. Ind. Appl. IEEE Trans. 2009, 45, 2109–2115. [Google Scholar] [CrossRef]
- Borba, B.; Szklo, A.; Schaeffer, R. Plug-in hybrid electric vehicles as a way to maximize the integration of variable renewable energy in power systems: The case of wind generation in northeastern Brazil. Energy 2012, 37, 469–481. [Google Scholar] [CrossRef]
- Dallinger, D.; Gerda, S.; Wietschel, M. Integration of intermittent renewable power supply using grid-connected vehicles—A 2030 case study for California and Germany. Appl. Energy 2013, 104, 666–682. [Google Scholar] [CrossRef]
- Markel, T.; Kuss, M.; Denholm, P. Communication and control of electric drive vehicles supporting renewables. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 27–34.
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust energy management for microgrids with high-penetration renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar]
- Zhao, J.; Wen, F.; Dong, Z.Y.; Xue, Y.; Wong, K.-P. Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization. IEEE Trans. Ind. Inf. 2012, 8, 889–899. [Google Scholar] [CrossRef]
- Yu, H.J.; Gu, W.; Zhang, N.; Lin, D.Q. Economic dispatch considering integration of wind power generation and mixed-mode electric vehicles. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7.
- Aghaei, J.; Ahmadi, A.; Shayanfar, H.A.; Rabiee, A. Mixed integer programming of generalized hydro-thermal self-scheduling of generating units. Electr. Eng. 2013, 95, 109–125. [Google Scholar] [CrossRef]
- Silva, I.C.; do Nascimento, F.R.; de Oliveira, E.J.; Marcato, A.L.M.; de Oliveira, L.W.; Passos, J.A. Programming of thermoelectric generation systems based on a heuristic composition of ant colonies. Int. J. Electr. Power Energy Syst. 2013, 44, 134–145. [Google Scholar] [CrossRef]
- Vo, D.N.; Ongsakul, W. Economic dispatch with multiple fuel types by enhanced augmented Lagrange Hopfield network. Appl. Energy 2012, 91, 281–289. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Ding, Z.H. A bare-bones multi-objective particle swarm optimization algorithm for environmental/economic dispatch. Inf. Sci. 2012, 192, 213–227. [Google Scholar] [CrossRef]
- Liu, X.; Xu, W. Economic load dispatch constrained by wind power availability: A here-and-now approach. IEEE Trans. Sustain. Energy 2010, 1, 2–9. [Google Scholar] [CrossRef]
- Hetzer, J.; Yu, D.C.; Bhattarai, K. An economic dispatch model incorporating wind power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, T. Stochastic security-constrained unit commitment. Power Syst. IEEE Trans. 2007, 22, 800–811. [Google Scholar] [CrossRef]
- Gu, W.; Wu, Z.; Bo, R.; Liu, W.; Zhou, G.; Chen, W.; Wu, Z. Modeling, planning and optimal energy management of combined cooling, heating and power microgrid: A review. Int. J. Electr. Power Energy Syst. 2014, 54, 26–37. [Google Scholar] [CrossRef]
- Hayes, J.G.; de Oliveira, R.P.R.; Vaughan, S.; Egan, M.G. Simplified electric vehicle power train models and range estimation. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 6–9 September 2011; pp. 1–5.
- Santos, A.; McGuckin, N.; Nakamoto, H.Y.; Gray, D.; Liss, S. Summary of Travel Trends: 2009 National Household Travel Survey; Federal Highway Administration: Washington, DC, USA, 2009. [Google Scholar]
- Gu, W.; Wu, Z.; Yuan, X. Microgrid economic optimal operation of the combined heat and power system with renewable energy. In proceedings of IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–6.
- Wu, J.; Zhu, J.; Chen, G.; Zhang, H. A hybrid method for optimal scheduling of short-term electric power generation of cascaded hydroelectric plants based on particle swarm optimization and chance-constrained programming. Power Syst. IEEE Trans. 2008, 23, 1570–1579. [Google Scholar] [CrossRef]
- Guan, Y.C.; Wang, Y.S.; Tan, Z.Y. Environmental protection and security considered dynamic economic dispatch for wind farm integrated systems. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 May 2012; pp. 1–4.
- Thathachar, M.; Sastry, P.S. Varieties of learning automata: An overview. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2002, 32, 711–722. [Google Scholar] [CrossRef]
- Kachore, P.; Palandurkar, M.V. TTC and CBM calculation of IEEE-30 bus system. In Proceedings of 2009 2nd International Conference on Emerging Trends in Engineering and Technology (ICETET), Nagpur, India, 16–18 December 2009; pp. 539–542.
- Liu, B.D. Fuzzy random chance-constrained programming. Fuzzy Syst. IEEE Trans. 2001, 9, 713–720. [Google Scholar] [CrossRef]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, J.; Jiang, P.; Gu, W.; Sheng, W.; Meng, X.; Gao, J. Finite Action-Set Learning Automata for Economic Dispatch Considering Electric Vehicles and Renewable Energy Sources. Energies 2014, 7, 4629-4647. https://doi.org/10.3390/en7074629
Zhu J, Jiang P, Gu W, Sheng W, Meng X, Gao J. Finite Action-Set Learning Automata for Economic Dispatch Considering Electric Vehicles and Renewable Energy Sources. Energies. 2014; 7(7):4629-4647. https://doi.org/10.3390/en7074629
Chicago/Turabian StyleZhu, Junpeng, Ping Jiang, Wei Gu, Wanxing Sheng, Xiaoli Meng, and Jun Gao. 2014. "Finite Action-Set Learning Automata for Economic Dispatch Considering Electric Vehicles and Renewable Energy Sources" Energies 7, no. 7: 4629-4647. https://doi.org/10.3390/en7074629